Kernel Density Estimation of the Unknown Probability Density Function
14 699
2
Introduction
Improvement of MQL5 performance and steady growth of PC productivity allow MetaTrader 5 platform users to apply fairly sophisticated and advanced mathematical methods for the market analysis. These methods may belong to various areas of economics, econometrics or statistics but in any case we will have to deal with the concept of probability density function while using them.
Many common analysis methods have been developed based on the assumption of data distribution normality or errors normality in the used model. Besides, it is often necessary to know the distribution of various components of the used model to estimate the analysis results. In both cases we have a task to create a "tool" (a universal one, in ideal case) allowing to estimate the unknown probability density function.
In this article the attempt is made to create a class realizing more or less universal algorithm for estimating the unknown probability density function. The original idea was that no
external means would be used during the estimation, i.e. everything was to be realized by means of MQL5 only. But finally the original idea has been altered to some extent. It is clear that the task of probability density function visual estimation consists of two independent parts.
Namely, calculation of the estimation itself and its visualization, i.e. displaying as a chart or a diagram. Of course, calculations have been realized by means of MQL5, while
visualization must be implemented by creating a HTML page and its display in web browser. That solution has been used to eventually get graphics in vector form.
But as the calculation part and results display are realized separately, a reader can, of course, visualize using any other available method. Besides, we expect that various libraries, including graphics ones, will appear in MetaTrader 5 (the work is under way, as far as we know). It will not be difficult to alter the display part in the proposed solution, in case MetaTrader 5 provides the advanced means for building charts and diagrams.
It should be preliminarily noted that creation of a truly universal algorithm for estimation of sequences probability density function proved out to be an unachievable goal. Although the proposed solution is not a highly specialized one, it cannot be called completely universal either. The problem is that optimality criteria turns out to be quite different during density estimation, for example, for bell-shaped distributions, such as normal and exponential ones.
Therefore, it is always possible to choose the most suitable solution for each specific case, if there is some preliminary information concerning estimated distribution. But, nevertheless, we will assume that we know nothing about the nature of the estimated density. Such an approach will surely affect the quality of estimations, but let's hope that it will pay off by providing the possibility to estimate quite different densities.
Due to the fact that we often have to deal with non-stationary sequences during the market data analysis, we are most interested in estimation of short and medium sequences density. This is a critical moment that determines the selection of the used estimation method.
Histograms and P-spline can be successfully used for really long sequences containing more than a million values. But some issues appear when we try to effectively build the histograms for sequences containing 10-20 values. Therefore, we will focus mainly on the sequences having approximately from 10 up to 10 000 values further on.
1. Probability Density Function Estimation Methods
Quite a lot of more or less popular methods of probability density function estimation are known, nowadays. They can easily be found on the Internet, for example, by using such key expressions as "probability density estimation", "probability density","density estimation" etc. But, unfortunately, we have not managed to choose the best one among them. All of them possess some certain advantages as well as disadvantages.
Histograms are traditionally used for density estimation [1]. Using the histograms (including smooth ones) allows to provide the high quality of probability density estimations, but only in case we deal with long sequences. As it was mentioned earlier, it is not possible to divide a short sequence into a large number of groups, while a histogram consisting of 2-3 bars cannot illustrate the probability density distribution law of such a sequence. Therefore, we had to abandon the use of histograms.
Another fairly well-known estimation method is kernel density estimation [2]. The idea of using the kernel smoothing is shown quite well at [3]. Therefore, we have chosen that method, despite all its disadvantages. Some aspects related to the implementation of this method will be briefly discussed below.
It is also necessary to mention a very interesting density estimation method, which uses the "Expectation–maximization" algorithm [4]. This algorithm allows to divide a sequence into separate components having, for instance, a normal distribution. It is possible to get a density estimation by summing obtained distribution curves after separate components parameters have been determined. This method is mentioned at [5]. This method has not been implemented and tested when working on the article, as well as many others. A great number of density estimation methods described in various sources prevents from examining all of them in practice.
Let's proceed to the kernel density estimation method that has been chosen for implementation.
2. Kernel Density Estimation of the Probability Density Function
Kernel density estimation of the probability density function is based on the kernel smoothing method. The principles of that method can be found, for example, at [6], [7].
The basic idea of the kernel smoothing is quite simple. MetaTrader 5 users are familiar with Moving Average (MA) indicator. That indicator can be easily portrayed as a window sliding along a sequence with its weighted values being smoothed inside. The window may be rectangular, exponential or have some other shape. We can easily see the same sliding window during the kernel smoothing (for example, [3]). But in this case, it is symmetrical.
Examples of the windows that are most frequently used in the kernel smoothing can be found at [8]. In case a zero order regression is used in the kernel smoothing, the sequence weighted values that have got to the window (kernel) are simply smoothed, like in MA. We can see the same kind of the window function application when we deal with filtering issues. But now the same procedure is presented a little differently. Amplitude-frequency and phase-frequency characteristics are used, while the kernel (window) is
called a filter impulse characteristic.
These examples show the fact that one thing can often be represented in different ways. That contributes to the mathematical apparatus, of course. But it may also lead to confusion when discussing the issues of that sort.
Although kernel density estimation uses the same principles, as the already mentioned kernel smoothing, its algorithm differs a bit.
Let's go to the expression defining the density estimation at one point.
where
- x - sequence having length n;
- K - symmetrical kernel;
- h - range, smoothing parameter.
Only the Gaussian kernel will be used further on for density estimations:
As follows from the above expression, the density at point X is calculated as the sum of the kernel values for the quantities defined by the differences between the values of point X and the sequence. Furthermore, X points used for the density calculation, may not coincide with the values of the sequence itself.
Here are the basic steps of the implementation of the kernel density estimation algorithm.
- Evaluation of the mean value and the input sequence standard deviation.
- Normalizing the input sequence. Deducting the previously obtained mean from each of its value and dividing by the standard deviation value. After such normalization the original sequence will have a zero mean and standard deviation equal to one. Such normalization is not necessary for calculating the density but it allows to unify resulting charts, as for any sequence on X scale there will be values expressed in standard deviation units.
- Finding high and low values in the normalized sequence.
- Creating two arrays, the sizes of which correspond to the desired number of points displayed on the resulting chart. For example, if the chart is to be built using 200 points, the arrays size must appropriately include 200 values each.
- Reserving one of the created arrays for storing the result. The second one is used for forming the values of the points, for which the density estimation has been performed. To do this, we must form 200 (in this case) equally spaced values between the previously prepared high and low values and save them in the array we have prepared.
- Using the expression shown before, we should carry out the density estimation in 200 (in our case) test points saving the result in the array we have prepared at step 4.
Software implementation of this algorithm is shown below.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
NTpoints() method allows to set the required number of equally spaced test points, for which density estimation will be carried out. This method must be called before calling Density() method. The link to the array containing the input data and the range value (smoothing parameter) is passed to Density() method as its parameters when the method is called.
Density() method returns zero in case
of successful completion, while test points values and estimations
results are located in T[] and Y[] arrays of that class, respectively.
The arrays sizes are set when accessing NTpoints(), while being equal to 200 values by default.
The following sample script shows the use of presented CDens class.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
The arrays for storing the test points input sequence and estimation results are prepared in this example. Then, X[] array is filled with random values, by way of example. The copy of CDens class is created after all the data has been prepared.
Then, the necessary number of test points is set (npoint=300 in our case) by NTpoints() method invocation. In case there is no need in changing the default number of points, NTpoints() method invocation can be excluded.
Calculated values are copied to the pre-defined arrays after Density() method invocation. Then, the previously created copy of CDens class is deleted. This example shows only interaction with CDens class. No further actions with the obtained results (T[] and Y[] arrays) are performed.
If these results are meant to be used for creating a chart, it can be easily done by putting the values from T[] array on the X chart scale, while the appropriate values from Y[] array should be put on the Y scale.
3. Optimal Range Selection
Fig. 1 displays the density estimation charts for the sequence having the normal distribution law and various h range values.
Estimations are performed using CDens class described above. The charts have been built in the form of HTML pages. The method of building such charts will be presented at the end of the article. Creation of charts and diagrams in HTML format can be found at [9].
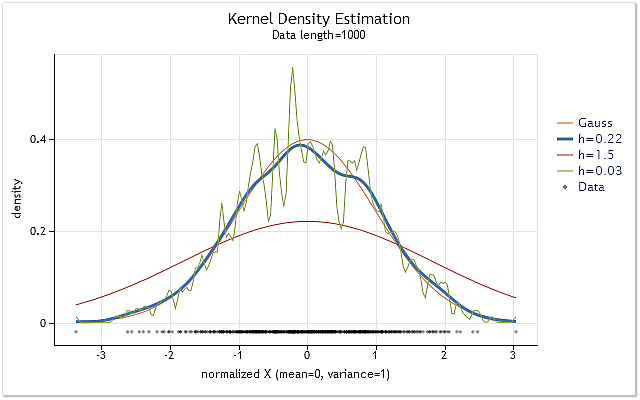
Fig. 1. Density estimation for various h range values
Fig. 1 also displays the true normal distribution density curve (Gaussian distribution) along with three density estimations. It can be easily seen that the most appropriate
estimation result has been obtained with h=0.22 in that case. In two other cases we can observe definite "oversmoothing" and "undersmoothing".
Figure 1 clearly shows the importance of correct h range selection when using kernel density estimation. In case h value has been chosen incorrectly, an estimation will be shifted greatly against the true density or considerably dispersed.
Lots of various works are dedicated to the optimal h range selection. Simple and well-proven Silverman's rule of thumb is often used for h selection (see [10]).
In this case A is the lowest value out of the sequence standard deviation values and the interquartile range divided by 1.34.
Considering that the input sequence has the standard deviation equal to one in the above mentioned CDens class, it is quite easy to implement this rule using the following code fragment:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
That estimation suits the sequences with the probability density function that is close to the normal one by its form.
In many cases, consideration of the interquartile range allows to adjust h value to the lower side when the form of the evaluated density deviates from the normal one. That makes this evaluation method versatile enough. Therefore, this rule of thumb is worth using as the initial basic h value estimation. Besides, it does not require any lengthy calculations.
In addition to the asymptotic and empirical h range value estimations, there are also various methods based on the analysis of the input sequence itself. In this case, the optimal h value is determined by considering the preliminary estimation of the unknown density. Comparison of the efficiency of some of these methods can be found at [11], [12].
According to the tests results published in various sources, Sheather-Jones plug-in method (SJPI) is one of the most effective range estimation methods. Let us opt for this method. In order not to overload the article by lengthy mathematical expressions, only some of the method's features will be discussed further on. If necessary, the mathematical basis of this method can be found at [13].
We use a Gaussian kernel, which is a kernel with unbounded support (i.e., it is specified when its parameter changes from minus to plus infinity). As it follows from the above expression, we will need O(M*N) operations when estimating the density in M points of the sequence having N length using the direct calculation method and the kernel with unbounded support. In case we need to make estimations at each of the sequence points, this value increases up to O(N*N) operations and the time spent on the calculation will increase proportionally with the square of the sequence length.
Such a high demand for computational resources is one of the major drawbacks of the kernel smoothing method. If we pass to SJPI method, we will see that it is not better in terms of the required amount of computation. Speaking short, we must first calculate the sum of two density derivatives along the whole length of the input sequence twice when implementing SJPI method.
Then, we should repeatedly calculate the estimation using the obtained results. The estimation value must be equal to zero. Newton-Raphson method [14] may be used to find the argument, at which this function is equal to zero. In case of the direct calculation, application of SJPI method for determining the optimal range value may require about ten times as much time as the density estimations calculation.
There are various methods of accelerating the calculations in the kernel smoothing and density kernel density estimation. In our case, the Gaussian kernel is used, the values of which can be assumed to be negligibly small for the argument values greater than 4. So, if the argument value is greater than 4, there is no
need to calculate the kernel values. Therefore, we can partially reduce the required number of calculations. We will hardly see any difference between the chart based on such an estimation and the fully calculated version.
Another simple way to accelerate the calculations is reducing the number of points, for which the estimation is performed. As it was mentioned above, if M is less than N, the number of required operations will be reduced from O(N*N) to O(M*N). If we have a long sequence, for example, N=100 000, we can perform estimations only in M=200 points. Therefore, we can considerably reduce the calculations time.
Also, more complex methods can be used to reduce the necessary number of calculations, for example, the estimations using a fast Fourier transform algorithm or wavelet transforms. The methods based on reducing the input sequence dimension (for example, "Data binning" [15]) can be successfully applied for really long sequences.
Fast Gaussian transform [16] can also be applied to speed up the calculations in addition to the methods mentioned above, in case the Gaussian kernel is used. We will use the algorithm based on the Gaussian transformation [17] to implement SJPI method of the range value estimation. The above mentioned link leads to the materials containing both the method description and program codes implementing the proposed algorithm.
4. Sheather-Jones plug-in (SJPI)
As in the case of the mathematical expressions determining the essence of SJPI method, we will not copy the mathematical basis of the implementation of the algorithm that can be found at [17] to this article. If necessary, you can examine the publications at [17].
CSJPlugin class has been created based on the materials located at [17]. This class is intended for calculation of the optimal h range value and includes only one public method –
double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
The following arguments are passed to this method when it is invoked:
- double &px[] – the link to the array containing the original sequence;
- double h is the initial h range value, relative to which the search is performed when solving the equations using Newton-Raphson algorithm. It is desirable that this value is as close to the searched one as possible. This may significantly reduce the time spent on solving the equations and decrease the probability of the cases when Newton-Raphson may lose its reliability. The value found by using Silverman's rule of thumb can be used as the initial h value;
- double stdev=1 – the value of the original sequence standard deviation. The default value is one. In this case, we do not have to change the default value as this method is meant to use together with the previously mentioned CDens class, in which the original sequence has been normalized already and has the standard deviation equal to one.
SelectH() method returns the obtained optimal h range value in case of successful completion. The initial h value is returned as a parameter in case of failure. The source code of CSJPlugin class is located in CSJPlugin.mqh file.
It is necessary to clarify some features of this implementation.
The source sequence is transformed to [0,1] interval at once, while the h range initial value is normalized proportionally with the original sequence transformation scale. Reversed normalization is applied to the optimal h value obtained during the calculations.
eps=1e-4 – the calculation accuracy of estimations of density and its derivatives and P_UL=500 – maximum allowable number of the algorithm inner iterations are set in CSJPlugin class constructor. For more information, see [17].
IMAX=20 – maximum allowable number of iterations for Newton-Raphson method and PREC=1e-4 – the accuracy of solving the equation using this method are set in SelectH() method.
The traditional use of Newton-Raphson method required the calculation of the target function and its derivative at the same point at each value iteration. In this case the calculation of the derivative has been replaced by its estimation calculated by adding a small increment to the value of its argument.
Figure 2 shows the example of using two different methods of the optimal h range value estimation.
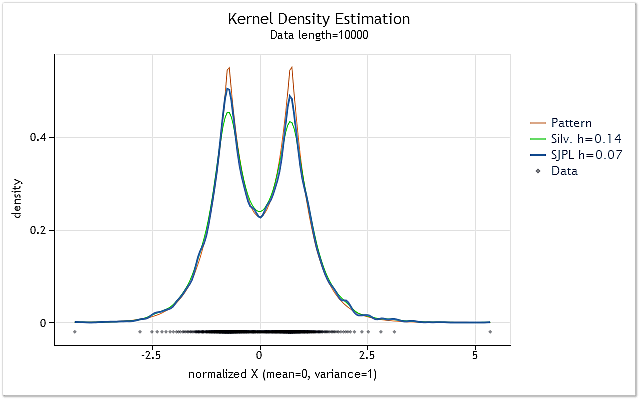
Fig. 2. Comparison of the optimal h range value estimations
Figure 2 displays two estimations for the random sequence, the true density of which is shown as the red chart (Pattern).
The estimations have been performed for the sequence having 10 000 elements in length. The h range value of 0.14 has been obtained for this sequence when using Silverman's rule of thumb, while it has been 0.07 when using SJPI method.
Examining the results of the kernel density estimation for these two h values shown in Figure 2, we can easily see that SJPI method application has helped to get more attractive h estimation comparing with Silverman's rule. As we can see, the sharp tops are shaped much better, while there is almost no dispersion increasing at sloping hollows in case of h=0.07.
As it was expected, the use of SJPI method allows in many cases to get quite successful h range estimations. Despite the fact that quite fast algorithms [17] have been used for CSJPlugin class creation, the h value estimation using this method may still take too much time for long sequences.
Another drawback of this method is its tendency to overestimate the h value for short sequences consisting of only 10-30 values. The estimations made using SJPI method may exceed h estimations made by Silverman's rule of thumb.
The following rules will be used in the further implementation to somehow compensate these drawbacks:
- The Silverman's estimation will be the default estimation for the h range, while it will be possible to activate SJPI method by a separate command;
- When using SJPI method, the lowest value out of the ones obtained by two mentioned methods will always be used as the h final value.
5. Boundary Effect
Desire to use as optimal range value in density estimation as possible has led to creation of the above mentioned and rather cumbersome CSJPlugin class. But there is one more issue in addition to specifying the range size and high resource intensity of the kernel smoothing method. That is the so-called boundary effect.
The issue is simple. It will be displayed using the kernel defined on the interval [-1,1]. Such kernel is called a kernel with finite support. It equals to zero outside the specified range (does not exist).
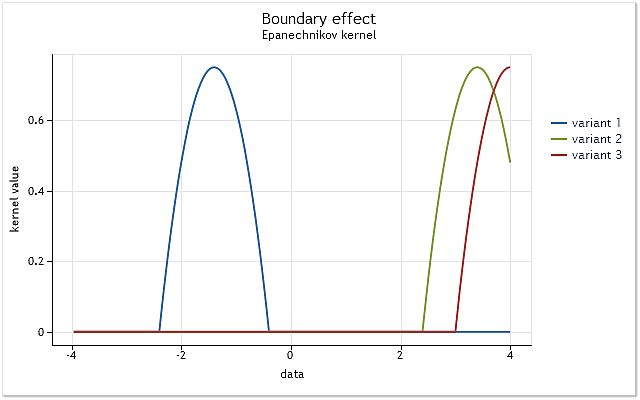
Fig. 3. The kernel reduction at the range boundary
As shown in Figure 3, in the first case, the core completely covers the original data located on the interval [-1,1] relative to its center. As the kernel is displacing (e.g., to the right), the situation emerges when the data is not enough to fully use the selected kernel function.
The kernel already covers less data than in the first case. The worst case is when the kernel center is located at the data sequence boundary. The amount of the data covered by the kernel is reduced to 50% in that case. Such a reduction in the number of the data used for density estimation leads to a significant shift of the estimations and increases their dispersion in the points close to the range boundaries.
Figure 3 shows an example of reduction for a kernel with finite support (Epanechnikov kernel) at the range boundary. It should be noted that the Gaussian kernel defined on the infinite range (unbounded support) has been used during the implementation of the kernel density estimation method. Theoretically, the cut-off of such a kernel must always take place. But considering the fact that the value of this kernel almost equals to zero for large arguments, the boundary effects appear to it the same way it does to the kernels with finite support.
This feature cannot affect the results of density estimation at the cases presented in Figures 1 and 2, as in the both cases the estimation has been performed for the distributions, the probability density function of which decreased at the boundaries almost down to zero.
Let's form the sequence consisting of positive integers X=1,2,3,4,5,6,…n to show the influence of the kernel cut-off at the range boundaries. Such a sequence has even law of the probability density distribution. It means that density estimation of this sequence must be a horizontal straight line, located on a non-zero level.
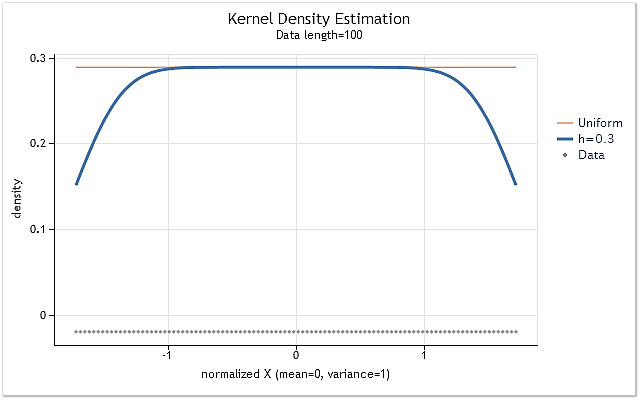
Fig. 4. Density estimation for the sequence having even law of distribution
As expected, figure 4 clearly shows that there is a considerable shift of density estimations at the range boundaries. There are several methods used to reduce that shift to greater or lesser extent. They can be roughly divided into the following groups:
- Data reflection methods;
- Data transformation methods;
- Pseudo-data methods;
- Boundary kernel methods.
The idea of using the reflected data is that the input sequence is intentionally increased by adding the data, which is a sort of a mirror reflection of that sequence relative to the sequence range boundaries. After such an increase, the density estimation is performed for the same points, as for the original sequence, but intentionally added data is also used in the estimation.
The methods involving data transformation are focused on the sequence transformation near its range boundaries. For example, it is possible to use logarithmic or any other transformation allowing to somehow deform the data scale when approaching to the range boundary during the density estimation.
The so-called pseudo-data may be used for the intentional extension (enlargement) of the original sequence. That is the data calculated on the basis of the original sequence values. That data serves to consider its behavior at the boundaries and complement it in the best appropriate way.
There are plenty of publications devoted to the boundary kernel methods. In these methods, the kernel by some means alters its form when approaching the boundary. The kernel form changes so that to compensate the estimations shift at the boundaries.
Some methods dedicated to the compensation of the distortions appearing at the range boundaries, their comparison and efficiency evaluation can be found at [18].
Data reflection method has been selected for further use after some short experiments. That choice was influenced by the fact that this method does not imply situations when the density estimation has a negative value. In addition, this method does not require complex mathematical calculations. The total number of operations still increases due to the need to make each estimation of the sequence, the length of which is deliberately increased.
There are two ways of implementing that method. Firstly, it is possible to complement the original sequence by necessary data and increase its size by three times in the process. Then, we will be able to make estimations the same way, as it is shown in the previously presented CDens class. Secondly, it is possible not to expand the input data array. We may just once again select the data from it in a certain way. The second way has been selected for implementation.
In the above mentioned CDens class the density estimation has been implemented in void kdens(double h) function. Let's change this function by adding boundary distortions correction.
The augmented function may look as follows.
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
The function is implemented assuming the fact that the source data in X[] array had already been sorted at the time when the function was called. This allows to easily exclude two sequence elements corresponding to the extreme range values from another processing. The attempt to put mathematical operations outside the loops whenever possible has been made when implementing this function. As a result, the function reflects the idea of the used algorithm less obviously.
It has already been mentioned before that it is possible to reduce the number of calculations, in case we will not calculate a kernel value for the arguments' large values. That is exactly what has been implemented in the above function. In this case, it is impossible to notice any changes after creation of the evaluated density chart.
When using modified version of kdens() function, density estimation shown in Figure 4 is transformed into a straight line and boundary hollows completely disappear. But such an ideal correction can be achieved only if the distribution near the boundaries has zero gradient, i.e. represented by a horizontal line.
If the estimated distribution density rises or falls sharply near the boundary, the selected data reflection method will not be able to fully adjust the boundary effect. This is displayed by the following figures.
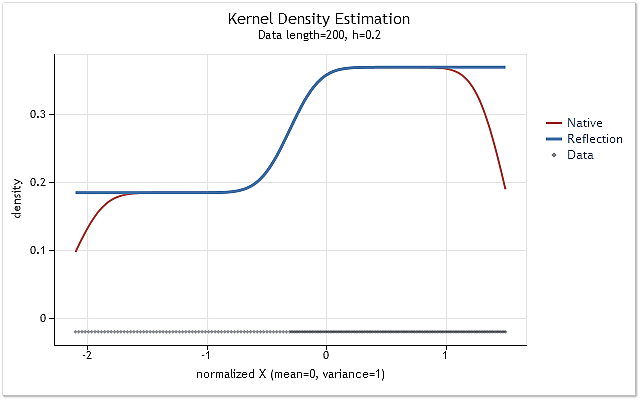
Fig. 5. The probability density function changing stepwise
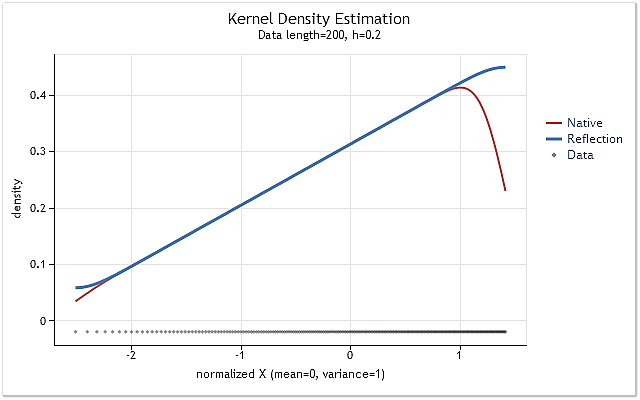
Fig. 6. The probability density function increasing linearly
Figures 5 and 6 display density estimation obtained using the original version of kdens() function (red) and the estimation obtained considering the applied changes that implement data reflection method (blue). The boundary effect has been fully corrected in Figure 5, while the shift near the boundaries has not been eliminated completely in Figure 6. If the estimated density rises or falls sharply near the boundary, then it appears to be a bit smoother near that boundary.
The data reflection method selected for adjusting the boundary effect is not the best or the worst of the known methods. Although this method cannot eliminate the boundary effect in all cases, it is stable enough and easy to implement. This method allows to get a logical and predictable result.
6. Final Implementation. CKDensity Class
Let's add the ability to automatically select h range value and the
boundary effect correction to the previously created CDens class.
Below is the source code of such a modified class.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Density(double &x[],double hh=-1) method is a basic one for that class. The first argument is the link to x[] array, at which the analyzed input sequence must be contained. The length of the input sequence should not be less than eight elements. The second (optional) argument is used for forced setting of h range value.
Any positive number may be specified. Set h value will always be limited by 0.005 from below. If this parameter has a negative value, the range value will be selected automatically. Density() method returns zero in case of successful completion and minus one in case of emergency completion.
After invoking Density() method and its successful completion, T[] array will contain test points values, for which the density estimation has been performed, while Y[] array will contain the values of these estimations. X[] array will contain the normalized and sorted input sequence. The average value of this sequence is equal to zero, while the standard deviation value is equal to one.
The following values are contained in the variables that are class members:
- N – input sequence length;
- Np – number of test points, at which the density estimation has been performed;
- Mean – input sequence mean value;
- Var – input sequence variance;
- StDev – input sequence standard deviation;
- H – value of the range (smoothing parameter);
- Pflag – flag of SJPI method application for determining the h range optimal value.
NTpoints(int n) method is used to set the number of test points, at which the density estimation will be carried out. Setting of the test points number must be performed before calling Density() basic method. If NTpoints(int n) method is not used, default points number of 200 will be set.
PluginMode(int m) method allows or prohibits the use of SJPI method to evaluate the optimal range value. If the parameter equal to one is used when invoking this method, SJPI method will be applied to specify h range. If the value of this parameter is not equal to one, SJPI method will not be used. If PluginMode(int m) method has not been invoked, SJPI method will be disabled by default.
7. Creating Charts
The method that can be found at [9] has been used when writing this article. That publication dealt with the application of ready-made HTML page including highcharts [19] JavaScript library and full specification of all its invocations. Further on, an MQL program forms a text file containing the data to be displayed and that file connects to the above mentioned HTML page.
In that case, it is necessary to edit HTML page by changing implemented JavaScript code to make any corrections in the displayed charts structure. To avoid this, a simple interface has been developed allowing to invoke JavaScript methods of highcharts library directly from the MQL program.
There has been no task to implement access to all possibilities of highcharts library when creating the interface. Therefore, only the possibilities allowing not to change previously created HTML file when writing the article have been implemented.
The source code of CLinDraw class is displayed below. This class has been used to provide the connection with highcharts library methods. This code should not be regarded as a complete software implementation. It is just an example showing how to create an interface having graphics JavaScript library.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
If we want to make this class operate properly, we need a ready-made HTML page having implemented JavaScript libraries. A size and location of the field for building chart(s) should also be specified. Example of such a page implementation can be found in the files attached to this article.
When AddGraph() method is invoked in a text file, an appropriate JavaScript code is formed. The text file is then included into the previously created HTML page. The mentioned code refers to the graphics library and provides creation of a chart using the data submitted to AddGraph() method as an argument. One or a few more charts can be added on the output field when invoking this method again.
Three versions of AddGraph() overloaded function are included into CLinDraw class. One of the versions requires that only one array with the displayed data is to be transferred to it as an argument. It is designed to build a sequence chart where that sequence element index is displayed on the X axis.
The second version gets two arrays as an argument. These arrays contain the values displayed on X and Y axis, respectively. The third version allows to set a constant value for Y axis. It can be used to build a horizontal line. The remaining arguments of these functions are similar:
- string type – displayed chart type. May have "line","spline" and "scatter" values;
- string name – name assigned to the chart;
- int w=0 – line width. Optional argument. If the value is 0, the default width value of 2 is used;
- string col="" – sets the line color and its opacity value. Optional argument.
LDraw() method must be invoked last. This method completes the output of JavaScript code and the data into the text file created in \MQL5\Files\ by default. Then the file is moved
to the directory containing graphics library files and the HTML file.
LDraw() method may possess a single optional argument. If the argument value is not set or is set to one, a default web browser will be invoked and the chart will be displayed after moving the data file to an appropriate directory. If the argument has any other value, the data file will also be completely formed but a web browser will not be invoked automatically.
Other available CLinDraw class methods allow to set chart headers and axes labels. We will not consider in details the issues of applying highcharts library and CLinDraw class in this article. Comprehensive information on highcharts graphics library can be found at [19], while examples of its application for creating charts and diagrams can be found at [9], [20].
The use of external libraries must be allowed in the terminal for normal operation of CLinDraw class.
8. Example of the Density Estimation and Files Arrangement
We have eventually got three classes - CKDensity, CSJPlugin and CLinDraw.
Below is the source code of the example dispaying how the classes may be used.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
The data, for which the evaluation of the probability density function will be performed, is prepared at the start of KDE_Example.mq5 script. To achieve this, "open" values of the current symbol and period are copied to X[] array. Logarithmic returns are then calculated on their basis.
The next step is creation of a copy of CKDensity class. Invoking its PluginMode() method allows to use SJPI method for h range evaluation. Density estimation is then performed for the sequence created in X[] array. Evaluation process is complete at this step. All further steps deal with visualization of the obtained density estimation.
The obtained estimations should be compared with any well-known distribution law. To do this, the values corresponding to Laplace distribution law are formed in Z[] array. Normalized and sorted-out input data is then stored in Sc[] array. If the input sequence length exceeds 400 elements, then not all its values will be included in Sc[]. Some of them will be skipped. Therefore, Sc[] array size will never contain more than 400 elements.
Once all the data that is necessary for display has been prepared, a copy of CLinDraw class is created. Next, the headers are specified and the necessary charts are added using AddGraph() method.
The first one is Laplace distribution law chart meant to be a template. It is followed by the chart of the density estimation obtained using input data. The bottom chart displaying the group of source data is added last. After defining all the elements necessary for display, LDraw() method is invoked.
As a result, we get the chart shown in Figure 7.
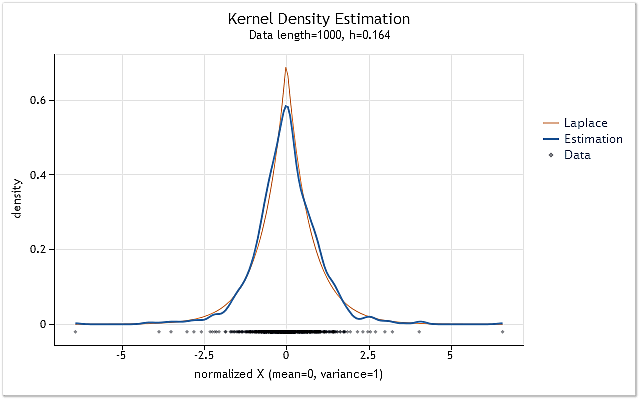
Fig. 7. Density estimation for logarithmic returns (USDJPY, Daily)
Estimation shown in Figure 7 has been performed for 1 000 values of logarithmic returns for USDJPY, Daily. As we can see, the estimation is very similar to the curve corresponding to the Laplace distribution.
All files necessary for density estimation and visualization are located in KDEFiles.zip archive below. The archive includes the following files:
- DensityEstimation\ChartTools\CLinDraw.mqh – class for interaction with highcharts.js;
- DensityEstimation\ChartTools\highcharts.js - Highcharts JS v2.2.0 library (2012-02-16);
- DensityEstimation\ChartTools\jquery.js – jQuery v1.7.1 library;
- DensityEstimation\ChartTools\LinDraw.htm – HTML page meant for display;
- DensityEstimation\CKDensity.mqh – class implementing density estimation;
- DensityEstimation\CSJPlugin.mqh – class implementing SJPI method of the optimal range value estimation;
- DensityEstimation\KDE_Example.mq5 – example of density estimation for logarithmic returns.
After unpacking the archive, DensityEstimation\ directory with all its contents must be placed in Scripts (or Indicators) directory of the terminal. It is afterwards possible to immediately compile and launch KDE_Example.mq5. DensityEstimation directory can be renamed, if necessary. That will not affect the program operation.
It should be mentioned again that the use of external libraries must be allowed in the terminal for CLinDraw class normal operation.
DensityEstimation\ directory includes ChartTools\ subdirectory containing all the components necessary for visualizing estimation results. Visualization files are located in a separate subdirectory, so that the contents of DensityEstimation\ directory can be easily seen. ChartTools\ subdirectory name is specified directly in source codes. Therefore, it should not be renamed, otherwise it will be necessary to make changes in source codes.
It has been already mentioned that the text file is created during visualization. This file contains the data necessary to build charts. This file is originally created in a special Files directory of the terminal. But then it is moved to the mentioned ChartTools directory. Thus, there will be no any traces of our test example activity left in Files\ or any other terminal directory. Therefore, you may simply delete DensityEstimation directory with all its contents to completely remove the installed files of this article.
Conclusion
The mathematical expressions explaining the essence of some particular methods have been included into the
article. That has been done deliberately in an attempt to simplify its reading. If necessary, all mathematical calculations can be found in numerous publications. The links at some of them are provided below.
The source codes provided in the article have not been subject to serious tests. Therefore, they must be considered only as examples, not as fully functional applications.
References
- Histogram.
- Kernel density estimation.
- Kernel smoother.
- Expectation–maximization algorithm.
- А.V. Batov, V.Y. Korolyov, А.Y. Korchagin. EM-Algorithm Having a Large Number of Components as a Means of Constructing Non-Parametric Density Estimations (in Russian).
- Hardle W. Applied Nonparametric Regression.
- Kernel (statistics).
- Charts and diagrams in HTML.
- Simon J. Sheather. (2004). Density Estimation.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). A Review and Comparison of Bandwidth Selection Methods for Kernel Regression.
- Clive R. Loader. (1999). Bandwidth Selection: Classical or Plug-In?.
- S. J. Sheather, M. C. Jones. (1991). A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation.
- Newton's method.
- Data binning.
- Changjiang Yang, Ramani Duraiswami and Larry Davis. (2004). Efficient Kernel Machines Using the Improved Fast Gauss Transform.
- Fast optimal bandwidth estimation for univariate KDE.
- R.J. Karunamuni and T. Alberts. (2005). A Locally Adaptive Transformation Method of Boundary Correction in Kernel Density Estimation.
- Highcharts JS.
- Analysis of the Main Characteristics of Time Series.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/396
Get 200 usd for your algorithmic trading article!
OpenCL: The Bridge to Parallel Worlds
Visualize a Strategy in the MetaTrader 5 Tester
MetaTrader 5 - More Than You Can Imagine!
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
So what is a practical part from trading point of view of this article ??
Krzysztof
This is a very usefull and good article, thanks, however I don't think that the code works properly even the first and simplest example.
I wonder if the author or somebody could recheck the code or someone would recommend any kind of 1D kernel density estimation code on C or MQL?