
Zaman Serisinin Temel Özelliklerinin Analizi
Tanıtım
Fiyat serileri tarafından temsil edilen süreçlerin analizi, genellikle önemli miktarda zaman ve çaba gerektiren oldukça zorlu bir iştir. Bu, çalışma altındaki dizilerin özellikleriyle ve çok sayıda çeşitli yayına rağmen, belirli bir sorun için yeterli bir programlama çözümü bulmanın bazen zor olduğu gerçeğiyle de ilgilidir.
Uygun bir komut dosyası veya gösterge bulunsa bile, kaynak kodunun eldeki göreve ayarlanması gerekmeyeceği anlamına gelmez.
Ayrıca, basit sorunların çözümü için bile, bu programlar, geliştiriciler tarafından iyi bilinen ancak bir kullanıcı için her zaman tamamen açık olmayan noktanın giriş parametrelerinin kullanılmasını gerektirebilir.
Bu zorluklar kesinlikle ciddi araştırmalarda dayanılmaz bir engel haline gelemez, ancak bir varsayımı kanıtlamak veya sadece merakını gidermek istediğinde, bu tür bir merak tatmin edilmeden daha sık kalacaktır. Bu yüzden, bir giriş dizisinin ana özelliklerinin ve parametrelerinin kolay ön analizine izin veren evrensel bir programlama aracı oluşturmak için bir fikrim vardı.
Böyle bir araç, kullanımını en üst düzeye çıkarmak için herhangi bir giriş parametresine gerek kalmadan kurulumunda tamamen basit olmalıdır. Aynı zamanda, tahmini parametreler ve özellikler, incelenen sıranın doğasını yeterince ve net bir şekilde yansıtmalıdır.
Özelliklerin ön tahmini, daha derinlemesine çalışmanın yollarını belirlemeye veya herhangi bir varsayımı erken bir aşamada reddetmeye ve daha fazla çalışma ile ilgili zaman kaybını önlemeye yardımcı olabilir.
Evrensel yazılımın özellikleri açısından genellikle özelleştirilmiş yazılımlarla karşılaştırıldığında kötü olduğu bilinmektedir. Bu, neredeyse her zaman tüm taviz sistemi ile elde edilen evrensellik için düzenli bir fiyattır. Ancak bu makale, dizilerin özelliklerinin ön analizini en üst düzeyde kolaylaştırmaya izin veren evrensel bir araç oluşturma çabasını temsil eder.
Kurulum ve Kapasite
TSAnalysis.zip makalenin sonunda bulunan dosya, iş için gerekli tüm dosyaları içeren \TSAnalysis dizinini içerir. Sıkıştırılmış dosyayı açtıktan sonra, tüm içeriğiyle birlikte dizin (adını değiştirmeden) \MQL5\Scripts dizinine kopyalanmalıdır. Kopyalanan dizin \TSAnalysis, derlendikten sonra çalıştırılabilen bir test komut dosyası TSAexample.mq5 içerir.
Bu komut dosyası verileri hazırlar ve TSAnalysis sınıfını kullanarak görüntülemek için varsayılan tarayıcıyı çağırır. TSAnalysis sınıfının normal çalışması için Terminalde harici DLL'lerin kullanımının etkinleştirileceği belirtilmelidir. Kaldırmak için yalnızca \TSAnalysis dizinini silmek yeterlidir.
Dizilerin analizi için kullanılan tüm kaynak kodu TSAnalysis sınıfı tarafından temsil edilir ve yalnızca TSAnalysis.mqh dosyasında bulunabilir.
Bu sınıfı bir giriş sırası için kullanırken, aşağıdaki bilgileri tahmin eder ve görüntüleyebilir:
- Listedeki elemanların toplam sayısı;
- Sıranın maksimum ve minimum değeri (maks., min);
- Medyan;
- Ortalama;
- Fark;
- Standart sapma;
- Tarafsız fark;
- Tarafsız standart sapma;
- Eğrilik;
- Basıklık;
- Aşırı basıklık;
- Jarque-Bera test;
- Jarque-Bera testi p-değeri;
- Düzeltilmiş Jarque-Bera testi;
- Düzeltilmiş Jarque-Bera testi p-değerleri;
- Verilen sıraya ait olmayan değerler için sınırlar (aykırı değerler);
- Histogram verileri;
- Normal Olasılık Grafiği verileri;
- Korelogram verileri;
- Otomatik ilişki fonksiyonu için %95 güven bantları;
- Otomatik ilişki işleviyle hesaplanan Spektral Grafiği verileri;
- Kısmi Otomatik İlişkilendirme İşlevi Grafiği verileri;
- Maksimum entropi yöntemi kullanılarak hesaplanan Spektral Tahmin Grafiği verileri.
Elde edilen sonuçların incelenen TSAnalysis sınıfında görsel olarak görüntülenmesi için, yalnızca önceden hazırlanmış bir bilgi görüntüleme yönteminden sorumlu bir sanal gösteri yöntemi kullanılır.
Bu nedenle, bu yöntemi TSAnalysis sınıfının alt öğelerinde yeniden tanımlayarak, sonuçların çıktısını mümkün olan herhangi bir şekilde düzenleyebilirsiniz, yalnızca grafikleri görüntülemek için bir veri dosyası oluşturma sırasında bir web tarayıcısının çağrıldığı temel sınıftaki gibi bir HTML dosyası kullanarak değil.
TSAnalysis sınıf incelemesine geçmeden önce, kullanım sonucunu bir veri test dizisi aracılığıyla göstereceğiz. Aşağıdaki şekilde TSAexample.mq5 komut dosyası işletim sonucu göstermektedir.
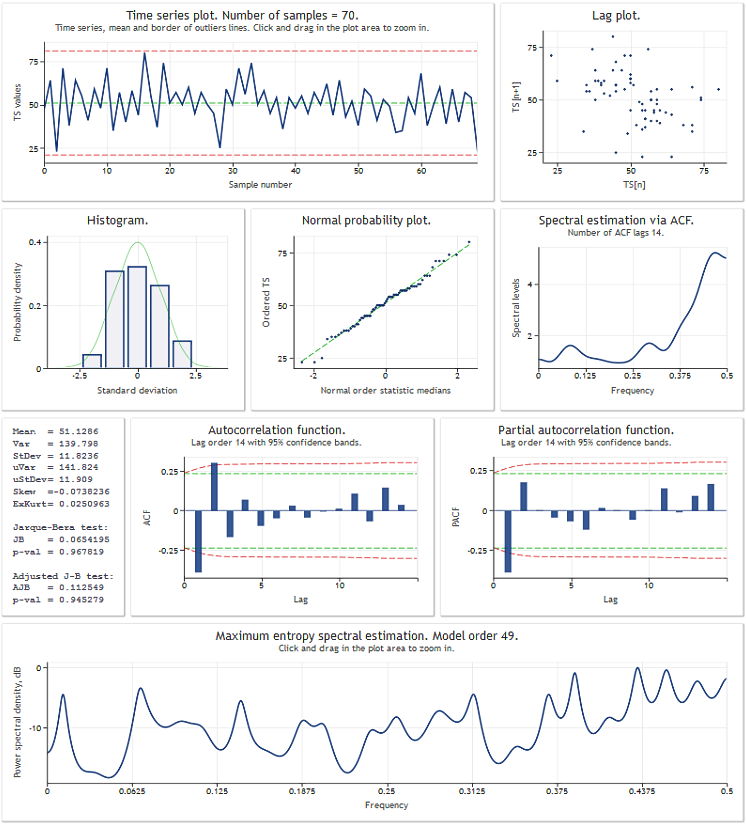
Şekil 1. TSAexample.mq5 komut dosyası işletim sonucu
TSAnalysis sınıf kapasitesine kısa bir aşinalık yaptıktan sonra, şimdi sınıfın kendisinin daha ayrıntılı bir değerlendirmesine geçeceğiz.
TSAnalysis Sınıfı
TSAnalysis sınıfı (bkz. TSAnalysis.mqh), sanal yöntem gösterisinin çağrıldığı gerekli tüm hesaplamalardan sorumlu olan yalnızca bir kullanılabilir (genel) yöntem Calc içerir. Gösteri yöntemi daha sonra kısaca gözden geçirilecek ve şimdi yapılan hesaplamaların ana noktasının adım adım açıklığa kavuşmasına devam edeceğiz.
TSAnalysis sınıfı kullanırken, incelenerek giriş sırasına bazı kısıtlamalar getirilir.
İlk olarak, sıra en az sekiz elementten oluşacaktır. Böyle bir kısıtlama muhtemelen çok katı değildir, çünkü bu kadar kısa dizileri pratik amaçlar için incelemek zor olacaktır.
Minimum sıra uzunluğu kısıtlamasına ek olarak, giriş sırası varyans değerinin sıfıra yakın olması gerekir. Bu gereksinim, varyans değerinin daha fazla hesaplamada kullanılmasından ve kararlı bir sonuç için belirli bir değerden daha az olamamasından kaynaklanmaktadır.
Çok düşük bir varyans değerine sahip diziler çok yaygın değildir, bu nedenle bu kısıtlama muhtemelen ciddi bir dezavantaj da olmayacaktır. Sıranın çok kısa olduğu ve sıfıra yakın bir fark değerinin olduğu durumlarda, hesaplamalar kesilir ve günlükte ilgili bir hata iletisi görüntülenir.
Bir giriş dizisinin izin verilen en uzun uzunluğuyla ilgili başka bir örtük kısıtlama daha vardır. Bu kısıtlama açıkça ayarlanmıyor ve kullanılan bir bilgisayarın performansına ve bellek kapasitesine bağlıdır ve komut dosyası yürütmesi için gereken zamana ve bir web tarayıcısında sonuçların çizilme hızına göre tamamen öznel bir şekilde belirlenir. 2-3 bin elementten oluşan dizilerin işlenmesinin ciddi zorluklara yol açmaması gerektiği varsayılıyor.
Sıranın istatistiksel parametrelerinin hesaplanması, Calc yöntemi kaynak kodunun aşağıdaki parçasına dayalı olacaktır (bkz. TSAnalysis.mqh).
Kullanılan algoritmanın açıklaması bu bağlantıyı izleyerek bulunabilir "VaryansıHesaplamak içintitlealgoritmalar http://www.answers.com/topic/algorithms-for-calculating-variancetitle".
. . . Mean=0; sum2=0; sum3=0; sum4=0; for(i=0;i<NumTS;i++) { n=i+1; delta=TS[i]-Mean; a=delta/n; Mean+=a; // Mean (average) sum4+=a*(a*a*delta*i*(n*(n-3.0)+3.0)+6.0*a*sum2-4.0*sum3); // sum of fourth degree b=TS[i]-Mean; sum3+=a*(b*delta*(n-2.0)-3.0*sum2); // sum of third degree sum2+=delta*b; // sum of second degree } . . .
Bu parçanın yürütülmesi sonucunda, aşağıdaki değerler hesaplanır
![]()
burada n = NumTS dizideki öğe sayısıdır.
Elde edilen değerleri kullanarak aşağıdaki parametreleri hesaplıyoruz.
Varyans ve standartsapma:
![]()
Tarafsız varyans ve standart sapma:
![]()
Eğrilik:
![]()
Basıklık. Minimum basıklık 1, normalde dağıtılan sıranın basıklığı 3 olacaktır.
![]()
Aşırı basıklık:
![]()
Bu durumda minimum basıklık -2'dir ve normalde dağıtılan sıranın basıklığı 0 olacaktır.
Geleneksel olarak, bir dizi üzerinde ilk uygun iyilik testi yapılırken, bilinen eğrilik ve basıklık değerleri kullanılarak kolayca hesaplanan Jarque-Bera istatistiği kullanılır. Jarque-Bera istatistiği için istatistiksel anlamlılık (p-değeri), dizi uzunluğunun artması üzerine asimptotik olarak iki serbestlik dereceli ters ki-kare dağılım fonksiyonuna yönelir.
Böylelikle,
![]()
Sıranın kısa olduğu durumlarda, bu şekilde elde edilen p değerinin kayda değer bir hataya sahip olması gerekir. Tam olarak bu hesaplama seçeneği yine de çok sık kullanılır. Nedenini söylemek zordur, belki de kullanılan basit ve net formüllerle ilgisi vardır veya Jarque-Bera istatistiğinin kendi başına ideal bir uygunluk testi temsil etmediği ve bu nedenle daha doğru hesaplamaların bir anlamı olmadığı gerçeği olabilir.
Bizim durumumuzda Jarque-Bera istatistiği ve ilgili p değeri yukarıdaki formüllere uygun olarak Calc yönteminde (TSAnalysis.mqh) hesaplanır.
Ayrıca, ayarlanmış bir Jarque-Bera testi ek olarak hesaplanır:
![]()
Burada:
![]()
Jarque-Bera testinin kısa diziler için ayarlanmış sürümü, belirtilen şekilde hesaplanan p değerinin hatasını azaltır, ancak tam olarak ortadan kaldırmaz.
Analizin nihai sonucunun, ortalamaya karşılık gelen satırı ve değerlerin geçersiz sayılacağı ve verilen sıraya (aykırı değerler) ait olmayan sınırları tanımlayan satırları görüntüleyen bir giriş sırası grafiği içermesi gerekir.
Bu sınırlar bu durumda aşağıdaki gibi hesaplanır:
![]()
![]()
Bu formül kitapta S. V. tarafından sağlanmıştır. Bulashev "Tüccarlar için İstatistikler" P. V.'nin kitabına atıfta bulunarak. Novitsky ve İçki. Zograf "Ölçüm Sonuçlarında Hata Tahmini". Sınırları belirledikten sonra, giriş sırasının işlenmesi amaçlanmamıştır; sınırların yalnızca bilgi için görüntülenmesi gerekir.
Giriş sırası grafiğine ek olarak, giriş sırası dağılımının ampirik tahminini yansıtan bir histogramın görüntülenmesi amaçlanmıştır. Histogramın aralık sayısı aşağıdaki gibi tanımlanır (S. V. Bulashev "Satıcılar için İstatistikler"):
![]()
Sonuç, en yakın tek tamsayı değerine yuvarlanır. Elde edilen değer beşten küçükse, 5 değeri kullanılır.
Histogramın X ekseni ve Y ekseni için veri dizilerindeki öğe sayısı, histogramın soluna ve sağına sıfır değer sütunu eklendiğinden, elde edilen aralık sayısı artı ikiye karşılık gelir.
Histogram oluşturmak için verileri hazırlayan kodun bir parçası (bkz. TSAnalysis.mqh) aşağıda verilmiştir.
. . . n=(int)MathRound((Kurt+1.5)*MathPow(NumTS,0.4)/6.0); if((n&0x01)==0)n--; if(n<5)n=5; // Number of bins ArrayResize(XHist,n); ArrayResize(YHist,n); ArrayInitialize(YHist,0.0); a=MathAbs(TSort[0]-Mean); b=MathAbs(TSort[NumTS-1]-Mean); if(a<b)a=b; v=Mean-a; delta=2.0*a/n; for(i=0;i<n;i++)XHist[i]=(v+(i+0.5)*delta-Mean)/StDev; // Histogram. X-axis for(i=0;i<NumTS;i++) { k=(int)((TS[i]-v)/delta); if(k>(n-1))k=n-1; YHist[k]++; } for(i=0;i<n;i++)YHist[i]=YHist[i]/NumTS/delta*StDev; // Histogram. Y-axis . . .
Yukarıdaki kodda:
- NumTS, dizideki öğelerin sayısıdır,
- XHist[] ve YHist[] sırasıyla X ve Y ekseni için değerler içeren dizilerdir.
- TSort[] sıralanmış bir giriş dizisi içeren dizidir.
Bu hesaplama yöntemi kullanılarak X ekseni değerleri standart sapma birimleri ile ifade edilecek ve Y ekseni değerleri olasılık yoğunluğuna karşılık gelecektir.
Normal dağıtım eksenine sahip bir grafik oluşturmak amacıyla, artan düzende sıralanmış giriş sırası Y ekseni değerleri olarak kullanılır. Y ve X ekseni değerlerinin sayısının eşit olması gerekir. X ekseni değerlerini hesaplamak için, önce tekdüze dağıtım yasasında olduğu gibi ortanca değerleri bulmak gerekir:
![]()
![]()
![]()
Ters normal dağılım işlevi ile X ekseni değerlerini hesaplamak için daha fazla kullanılırlar (bkz. ndtri yöntemi).
Otomatik ilişki işlevi (ACF) çizimi, kısmi otomatik ilişki işlevi (PACF) çizimi oluşturmak ve maksimum entropi yöntemini kullanarak spektral tahmini hesaplamak için, giriş sırası için otomatik ilişki işlev değerleri bulunmalıdır.
ACF ve PACF çizimlerinde görüntülenmesi gereken değerlerin sayısını aşağıdaki gibi tanımlayacağız:
![]()
![]()
![]()
Belirtilen şekilde belirlenen değerlerin sayısı, çizimdeki otomatik düzeltme işlevinin görüntülenmesi için oldukça yeterli olacaktır, ancak spektral tahminin daha fazla hesaplanması için, bizim durumumuzda kullanılan özbağlanımlı modelin sırasına eşit olacak daha fazla sayıda hesaplanan ACF değerine sahip olunması önerilir.
IP modeli sırası elde edilen NLags değeri tarafından tanımlanır:
![]()
![]()
Spektral tahmin için modelin en uygun sırasını belirleme sürecini resmileştirmek oldukça zordur. Düşük sıralı bir model son derece düzgün sonuçlar getirirken, yüksek sıralı bir model büyük olasılıkla çok çeşitli değerlere sahip kararsız bir spektral tahmine yol açacaktır.
Ayrıca, model sırası da giriş sırasının doğasından etkilenir, bu nedenle yukarıdaki formül kullanılarak belirlenen IP sırası bazı durumlarda çok yüksek ve diğer durumlarda çok düşük olacaktır. Ne yazık ki, gerekli model sırasını belirlemek için etkili bir yaklaşım bulunamadı.
Bu nedenle, giriş sırası için, sıranın spektral tahmini için kullanılan IP modeli sırasına eşit ACF değerlerinin sayısını belirlemelidir.
. . . ArrayResize(cor,IP); a=0; for(i=0;i<NumTS;i++)a+=TSCenter[i]*TSCenter[i]; for(i=1;i<=IP;i++) { c=0; for(k=i;k<NumTS;k++)c+=TSCenter[k]*TSCenter[k-i]; cor[i-1]=c/a; // Autocorrelation } . . .
Kaynak kodun bu parçası (bkz. TSAnalysis.mqh), otomatik ilişki işlevini (ACF) hesaplama işlemini gösterir. Hesaplama sonucu cor[] dizisine yerleştirilir. Görüldüğü gibi, önce sıfır otomatik ilişki katsayısı hesaplanır, ardından döngüde kalan katsayıların hesaplanması ve normalleştirilmesi. Bu tür bir normalleştirmede, sıfır katsayısı her zaman bire eşit olacaktır, bu nedenle cor[] dizisinde kaydetmeye gerek yoktur.
Bu dizi, ilkinden başlayarak IP'ye eşit katsayı sayısını içerir. ACF hesaplanırken TSCenter[] dizisi kullanılır; ortalama değerin sürülmüş olduğu öğelerin giriş sırasını içerir.
ACF'yi hesaplamak için gereken süreyi azaltmak için, FFT gibi hızlı dönüşüm algoritmalarını kullanan yöntemlerden yararlanılabilir. Ancak bu durumda ACF'yi hesaplamak için gereken süre oldukça kabul edilebilir, bu nedenle muhtemelen programlama kodunu karmaşıklaştırmaya gerek yoktur.
Bir ACF çizimi (korelogram), korelasyon katsayılarının elde edilen değerleri kullanılarak kolayca oluşturulabilir. Bu çizimde %95 güven bantlarını görüntüleyebilmek için değerleri aşağıdaki formüller kullanılarak hesaplanabilir.
Rastgeleliği test etmek için kullanılan bantlar için:
![]()
ARIMA model sırasını belirlemek için kullanılan bantlar için:
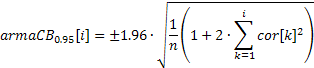
İlk durumda güven bandının değeri sabit olacak ve ikinci durumda otomatik ilişki katsayısının artmasıyla artacaktır.
Giriş dizisinin sadece frekans dağılımının genel eğilimini yansıtan çok düzgün bir frekans yanıtı bazen ilgi çekici olabilir. Örneğin, düşük veya yüksek frekans aralığında önemli artışlar, orta menzilli frekansların baskınlığı vb.
Baskın frekans aralıklarını güçlü bir şekilde vurgulamak için bu frekans yanıtının doğrusal ölçekte görüntülenmesi önerilir. Bu genlik frekansı yanıtı (AFR), daha önce elde edilen otomatik ilişki katsayılarına göre çizilebilir. AFR'nin hesaplanması için ACF çiziminde görüntülenen sayıya eşit katsayı sayısını kullanacağız.
Bu sayının büyük olmadığı göz önüne alındığında, sonuç olarak elde edilen spektral tahminler oldukça pürüzsüz olmalıdır.
Bu durumda sıranın frekans yanıtı, otomatik ilişki katsayıları ile aşağıdaki gibi ifade edilebilir:
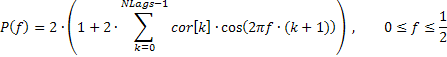
Sağlanan formüle dayalı olarak AFR'yi hesaplamak için kullanılan kodun bir parçası (bkz. TSAnalysis.mqh) aşağıda verilmiştir.
. . . n=320; // Number of X-points ArrayResize(Spect,n); v=M_PI/n; for(i=0;i<n;i++) { a=i*v; b=0; for(k=0;k<NLags;k++)b+=((double)NLags-k)/(NLags+1.0)*ACF[k]*MathCos(a*(k+1)); Spect[i]=2.0*(1+2*b); // Spectrum Y-axis } . . .
Yukarıdaki koddaki korelasyon katsayısı değerlerinin, daha fazla yumuşatma için üçgen pencere işleviyle çarpıldığı belirtilmelidir.
Daha ayrıntılı bir spektral analiz için, maksimum entropi yöntemi başka bir uzlaşma olarak seçildi. Evrensel spektral tahmin yönteminin seçimi oldukça zordur. Spektral analizin klasik parametrik olmayan yöntemleri ile ilişkili dezavantajları iyi bilinmektedir.
Periodogram ve korelogram yöntemleri, hızlı Fourier dönüştürme algoritmaları kullanılarak kolayca uygulanan bu tür yöntemlere örnek teşkil edebilir. Ancak sonuçların yüksek stabilitesine rağmen, bu yöntemler yeterli bir çözünürlük gücü elde etmek için çok uzun giriş dizileri gerektirir. Buna karşılık, spektral tahmin parametrik yöntemler (örneğin özbağlanımlı yöntemler) kısa diziler için çok daha yüksek çözünürlük sağlayabilir.
Ne yazık ki, bunları kullanırken, sadece bu yöntemlerin belirli bir uygulamasının özelliklerini değil, aynı zamanda giriş dizisinin doğasını da dikkate almak gerekir. Aynı zamanda, çözünürlük gücünün artmasına neden olan ancak elde edilen dağınık sonuçlara yol açan en uygun AR modeli sırasını belirlemek oldukça zordur. Çok yüksek sıralı modeller kullanılırsa, bu yöntemler kararsız sonuçlar vermeye başlar.
Farklı spektral tahmin algoritmalarının karşılaştırmalı özellikleri kitapta S. L. tarafından bulunabilir. Marple "Uygulamalarla Dijital Spektral Analiz". Daha önce de belirtildiği gibi, bu durumda maksimum entropi yöntemi seçildi. Bu yöntem, diğer özbağlanımlı yöntemlere kıyasla muhtemelen en düşük çözünürlük gücüyle sonuçlanır, ancak daha kararlı spektral tahminler elde etmek için bir görünümle seçilmiştir.
Özbağlanımlı spektral tahmin hesaplamalarının sırasına bir göz atalım. Model siparişinin seçimine daha önce değinildi, bu nedenle model sırasının ip'ye eşit olarak zaten seçildiğini ve IP otomatik ilişki katsayılarının hesaplandığını varsayacağız.
Bilinen otokorelasyon katsayılarını kullanarak özbağlanımlı katsayıları elde etmek için Levinson-Durbin algoritması LevinsonRecursion yöntemi olarak uygulanmaktadır.
//----------------------------------------------------------------------------------- // Calculate the Levinson-Durbin recursion for the autocorrelation sequence R[] // and return the autoregression coefficients A[] and partial autocorrelation // coefficients K[] //----------------------------------------------------------------------------------- void TSAnalysis::LevinsonRecursion(const double &R[],double &A[],double &K[]) { int p,i,m; double km,Em,Am1[],err; p=ArraySize(R); ArrayResize(Am1,p); ArrayInitialize(Am1,0); ArrayInitialize(A,0); ArrayInitialize(K,0); km=0; Em=1; for(m=0;m<p;m++) { err=0; for(i=0;i<m;i++)err+=Am1[i]*R[m-i-1]; km=(R[m]-err)/Em; K[m]=km; A[m]=km; for(i=0;i<m;i++)A[i]=(Am1[i]-km*Am1[m-i-1]); Em=(1-km*km)*Em; ArrayCopy(Am1,A); } return; }
Yöntemin üç giriş parametresi vardır. Her üç parametre de dizilere başvurudur. Bu yöntemi çağırırken, giriş otomatik ilişki katsayıları ilk dizi R[]'ye yerleştirilmelidir. Hesaplamalar boyunca bu değerler değişmeden kalır.
Elde edilen otomatik ilişki katsayıları A dizisine yerleştirilir[]. Bunun yanı sıra, dizi K[] ters işaretle alınan otomatik gerici model yansıma katsayılarına eşit kısmi otomatik ilişki işlev değerleri içerir. Model sırası giriş parametresi olarak geçirilmez; R[] giriş dizisindeki öğe sayısına eşit olduğu varsayılır.
Bu nedenle, çıkış dizisi boyutlarının giriş dizisi boyutundan küçük olmaması gerekir; bu gereksinimin yerine getirilmesi işlev içinde denetlenmez. Hesaplamalar tamamlandıktan sonra, kısmi otomatik ilişki işlevinin sıfır otomatik gerileme katsayısı ve sıfır katsayısı A[] ve K dizilerine kaydedilmez[].
Her zaman bire eşit oldukları varsayılır. Bu nedenle, çıkış dizileri, giriş dizisinde olduğu gibi, 1'den IP'ye kadar dizinlere sahip katsayılar içerir (0'dan başlayan dizi dizinleriyle karıştırılmamalıdır).
Kısmi otomatik ilişki işlevinin elde edilen değerleri yalnızca ilgili bir çizimde görüntülenmek için daha fazla kullanılır ve otoregren katsayıları, aşağıdaki formülle tanımlanan frekans yanıtı tahmininin hesaplanmasında temel teşkil eder:
![]()
Frekans yanıtı, 0 ile 0,5 aralığında 4096 normalleştirilmiş frekans değeri için hesaplanır. Yukarıdaki formülü kullanarak AFR değerlerinin doğrudan hesaplanması çok fazla zaman alır ve karmaşık üstellerin toplamını hesaplamak için hızlı Fourier dönüştürme algoritması kullanılarak önemli ölçüde azaltılabilir.
Bu amaçla, Calc yöntemi hızlı Fourier dönüşümü yerine hızlı Hartley dönüşümünü (FHT) kullanmaktadır.
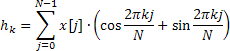
Hartley dönüşümü karmaşık işlemler içermez ve hem giriş hem de çıkış dizileri geçerlidir. Ters Hartley dönüşümü, yalnızca ek bir faktör 1/N gerektiren aynı formül kullanılarak hesaplanır.
Geçerli bir giriş dizisinde, bu dönüşümün katsayıları ile Fourier dönüşümünün katsayıları arasında basit bir bağlantı vardır.
![]()
Hızlı Hartley dönüşüm algoritmaları hakkında bilgi burada bulunabilir "FXT algoritma kütüphanesi" ve "Ayrık Fourier ve Hartley Dönüşümleri".
Verilen uygulamada, hızlı Hartley dönüştürme işlevi fht yöntemi ile temsil edilir.
//----------------------------------------------------------------------------------- // Radix-2 decimation in frequency (DIF) fast Hartley transform (FHT). // Length is N = 2 ** ldn //----------------------------------------------------------------------------------- void TSAnalysis::fht(double &f[], ulong ldn) { const ulong n = ((ulong)1<<ldn); for (ulong ldm=ldn; ldm>=1; --ldm) { const ulong m = ((ulong)1<<ldm); const ulong mh = (m>>1); const ulong m4 = (mh>>1); const double phi0 = M_PI / (double)mh; for (ulong r=0; r<n; r+=m) { for (ulong j=0; j<mh; ++j) { ulong t1 = r+j; ulong t2 = t1+mh; double u = f[t1]; double v = f[t2]; f[t1] = u + v; f[t2] = u - v; } double ph = 0.0; for (ulong j=1; j<m4; ++j) { ulong k = mh-j; ph += phi0; double s=MathSin(ph); double c=MathCos(ph); ulong t1 = r+mh+j; ulong t2 = r+mh+k; double pj = f[t1]; double pk = f[t2]; f[t1] = pj * c + pk * s; f[t2] = pj * s - pk * c; } } } if(n>2) { ulong r = 0; for (ulong i=1; i<n; i++) { ulong k = n; do {k = k>>1; r = r^k;} while ((r & k)==0); if (r>i) {double tmp = f[i]; f[i] = f[r]; f[r] = tmp;} } } }
Bu yöntemi çağırırken, giriş veri dizisi f[] ve N = 2 ** ldn dönüştürme uzunluğunu tanımlayan imzalanmamış tamsayı ldn'ye bir başvuru girişte geçirilir. F[] dizisinin boyutu dönüştürme uzunluğundan az olmamalıdır N. İşlevin içinde bunun için hiçbir denetimin olmadığını unutmayın. Ayrıca, dönüştürme sonucunun giriş verilerinin yerleştiği dizide depolandığını unutmayın.
Dönüştürmeden sonra, giriş verilerinin kendisi depolanmaz. İncelenen Calc yönteminde, 4096 AFR değerlerini hesaplamak için N=8192 uzunluğunda bir dönüşüm kullanılır. Dönüşüm kare büyüklüğünün hesaplanmasından ve karşılıklı olarak alınmasından sonra, elde edilen sonuç maksimum değerine normalleştirilir ve logaritmik olarak ölçeklendirilir.
Bunun dışında, Calc yönteminin önemli özellikleri yoktur; gerekirse, TSAnalysis.mqh'ye atıfta bulunarak uygulamasına daha yakından bakılabilir.
Hesaplamalar sonucunda elde edilen ve görüntülenmeye hazırlanan tüm değerler, TSAnalysis sınıfının üyeleri olan değişkenlere kaydedilir. Bu nedenle, sonuçları görüntülemek için sanal yöntem gösterisi çağrılırken bağımsız değişken olarak geçirilmeleri gerekmez.
Görselleştirme
Daha önce de belirtildiği gibi, gösterme yöntemi sanal olarak belirtilmiş. Bu nedenle, yeniden tanımlayarak, önerilenden farklı olacak hesaplama sonuçlarını görüntülemek için gerekli yöntemi uygulayabilirsiniz. Önerilen TSAnalysis sınıfında görselleştirme, veri dosyası hazırlama ve verilerin görüntülenmesi için bir web tarayıcısı çağırma yoluyla gerçekleştirilir.
Bir web tarayıcısının bu tür verileri görüntüleyebilmesi için, proje dosyalarının geri kalanıyla aynı dizinde bulunan TSA.htm dosyası kullanılır. Grafik bilgilerini görüntülemek için bu yöntem daha önce "HTML'de Grafikler ve Diyagramlar" makalesinde açıklanmıştır.
Show yönteminin TSAnalysis sınıfı, görüntülenmesi amaçlanan tüm hesaplama sonuçlarını biçimlendirmekten ve dize türü değişkenine kaydetmekten sorumludur (bkz. TSAnalysis.mqh). Bu şekilde oluşturulan uzun bir hat, tek bir adımda TSDat.txt kaydedilir. Bu dosyanın oluşturulması ve verilerin kaydedilme işlemi standart MQL5 araçları kullanılarak gerçekleştirilir, bu nedenle dosya \MQL5\Files dizininde oluşturulur.
Bu dosya daha sonra dış sistem işlevleri çağrılarak bu projenin dizinine taşınır. Bunu, TSDat.txt'daki verileri kullanan TSA.htm görüntüleyen bir web tarayıcısının çağrısı izler. Sistem işlevleri gösterme yönteminde çağrıldığından, TSAnalysis sınıfıyla çalışmak için Terminal'de harici DLL'lerin kullanımı etkinleştirilir.
Örnekler
TSAnalysis.zip arşivinde bulunan TSAexample.mq5, TSAnalysis sınıfını kullanmanın bir örneğidir.
//----------------------------------------------------------------------------------- // TSAexample.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "TSAnalysis.mqh" //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { double bd[]={47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50, 60,45,57,50,45,25,59,50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52, 38,59,55,41,53,49,34,35,54,45,68,38,50,60,39,59,40,57,54,23}; TSAnalysis *tsa=new TSAnalysis; tsa.Calc(bd); delete tsa; }
Görüldüğü gibi, sınıfa başvuru oldukça basittir; giriş sırasını içeren hazırlanmış bir dizi varsa, analiz için Calc yöntemine geçirmek için çok fazla çaba harcamaz. Ayrıca, silme komutunu çağırarak belleği boşaltmayı unutmamalısınız. Bu komut dosyasını çalıştırmanın sonucu makalenin başında zaten sağlanmıştır.
Üretilen spektral tahminlerin verimliliğini göstermek için, oluşturulan dizilerin kullanılacağı ek örneklere dönelim.
Başlangıç olarak, iki sinüzoidden oluşan bir dizi kullanacağız.
int i,n; double a,x[]; n=400; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i);
Aşağıdaki şekil, bu sıranın frekans yanıtı tahminini göstermektedir.
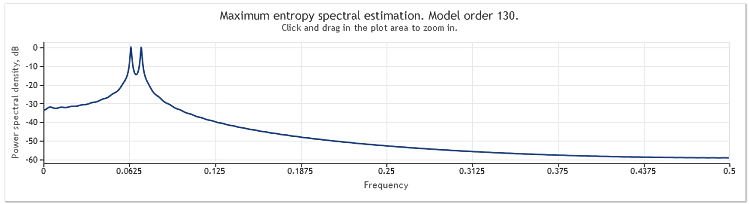 22
22
Şekil 2. Spektral tahmin. İki sinüzoid
Her iki sinüzoid de iyi gözlemlenebilir olsa da, ilgi alanına yakınlaştırmak, zirvelerin 0,0637 ve 0,0712 frekanslarında bulunduğunu keşfetmemizi sağladı. Başka bir deyişle, gerçek değerlerden biraz farklıdırlar. Bir dizi tek bir sinüzoidden oluştuğunda, bir tahminin böyle bir önyargısı gözlenmez. Bu oluşumu seçilen spektral analiz yönteminin etkisi olarak düşünelim.
Dizimize rastgele bir bileşen ekleyerek görevi daha da karmaşık hale getireceğiz. Bu amaçla, makalenin sonundaki RNDXor128.zip arşivinde bulunabilen RNDXor128 sınıfı tarafından temsil edilen sahte rastgele sıra oluşturucu kullanılacaktır.
Aşağıdaki kod parçası bir test sinyali oluşturmak için kullanıldı.
int i,n; double a,x[]; RNDXor128 *rnd=new RNDXor128; n=800; ArrayResize(x,n); a=2*M_PI; for(i=0;i<n;i++)x[i]=MathSin(0.064*a*i)+MathSin(0.071*a*i)+rnd.Rand_Norm(); delete rnd;
Bu örnekte, iki sinüzoide normal dağılım ve birim varyanslı rastgele bir sinyal eklendi.
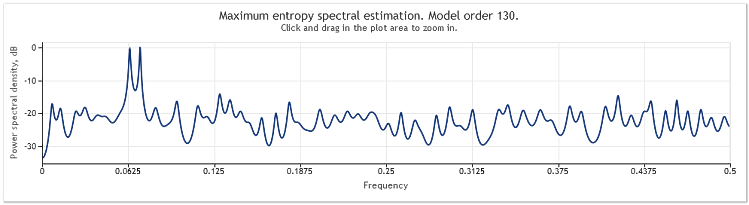
Şekil 3. Spektral tahmin. İki sinüzoid artı rastgele bir sinyal
Bu durumda, sinüzoidal bileşenler iyi ayırt edilebilir kalır.
Rastgele bileşenin genliğinde beş kat artış önemli ölçüde maskelenmiş sinüzoidlerle sonuçlanır.
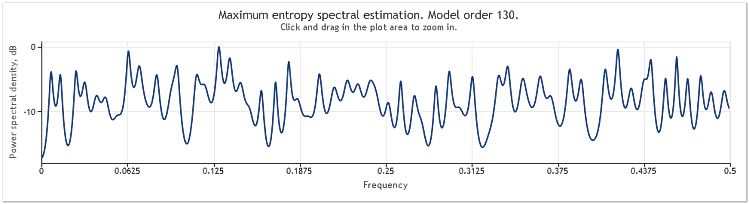
Şekil 4. Spektral tahmin. İki sinüzoid artı daha büyük genlikli rastgele bir sinyal
Dizi uzunluğu 400'den 800 elemente yükseltildiğinde, sinüzoidler tekrar iyi gözlemlenebilir hale gelir.
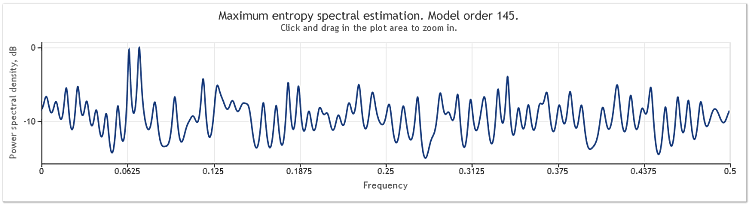
Şekil 5. İki sinüzoid artı daha büyük genlikli rastgele bir sinyal. N=800
Böylece otomatik gerileyen model sırası 130'dan 145'e yükselmiştir. Sıra uzunluğundaki artış modelin daha yüksek sırasına yol açtı ve sonuç olarak spektral tahminin çözünürlük gücü arttı - grafik zirveleri belirgin şekilde keskinleşti.
EURUSD, D1 için iki yıl boyunca (2009 ve 2010) tekliflerin spektral tahmini aşağıdaki gibi gösterilebilir.

Şekil 6. EURUSD alıntıları. 2009-2010. Dönem D1
Giriş sırası 519 değerden oluşuyordu ve model sırası, rakamdan aşağıdaki gibi, 135 olarak göründü.
Görüldüğü gibi, bu spektral tahmin bir dizi farklı zirve içerir. Ancak bu tahmin, bu zirvelerin tekliflerin periyodik bileşenleri olup olmadığını belirlemek için tek başına yeterli değildir.
Frekans yanıtında piklerin oluşması, tırnaklarda bulunan üst düzey rastgele bir bileşenden veya söz konusu sıranın açıkça sabitlenmemiş olmasından kaynaklanabilir.
Bu nedenle, periyodik bileşenin varlığıyla ilgili nihai bir sonuç çıkarmadan önce, sıranın başka bir kısmından veya başka bir zaman diliminden gelen verileri kullanarak elde edilen sonucu doğrulamanız her zaman tavsiye edilir. Ayrıca, döngüsel nüks incelerken, sıranın kendisi yerine sıra farklılıklarını kullanmayı deneyebilirsiniz.
Sonuç
Makalede kullanılan spektral tahmin yöntemi otomatik ilişki katsayılarına dayandığından, giriş sırasının ortalaması her zaman yöntemin uygulanmasından sonra diziden silinmiş gibi görünmektedir. Genellikle sabit bir bileşeni giriş dizisinden silmek kesinlikle gereklidir, ancak otomatik gerici yöntemler kullanırken, bu tür silme bazı durumlarda düşük frekans aralığında spektral tahminin bozulmasına neden olabilir.
Bu tür çarpıtmalara bir örnek, S. L.'nin kitabındaki "Spektral Tahminlere İlişkin Sonuçların Özeti" bölümünün sonunda verilmiştir. Marple "Uygulamalarla Dijital Spektral Analiz". Bizim durumumuzda, kullanılan spektral analiz yöntemi bize başka seçenek bırakmaz, bu nedenle spektral tahminin her zaman silinmiş bir ortalamaya sahip bir diziye göre gerçekleştirildiğini unutmayın.
Referanslar
- Wuertz, Diethelm ve Katzgraber, Helmut (2009): Precise finite-sample quantiles of the Jarque-Bera adjusted Lagrange multiplier test, Swiss Federal Institute of Technology, Zurich,2009.
- Tanweer-ul-Islam, Asad Zaman, Normality Testing - A new Direction, IIE, International Islamic University, Islamabad, Pakistan, 2008.
- Carlos M. Urzua, Portable and powerful tests for normality, Tecnologico de Monterrey, Campus Ciudad de Mexico, 2007.
- Comparison of Common Tests for Normality
- S. V. Bulashev. Statistics for Traders. - М.: Kompania Sputnik +, 2003. - 245 pp.
- P. V. Novitsky, I. A. Zograf. Ölçüm Sonuçlarında Hata Tahmini. Energoatomizdat, 1991.
- S. L. Marple, Jr. Uygulamalar ile Dijital Spektral Analiz. Moskova: Mir, 1990.
- David J. Sheskin, Parametrik ve Nonparametrik İstatistik Prosedürleri El Kitabı, Chapman ve Hall/CRC.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/292
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
Bu makale sitenin bir kullanıcısı tarafından yazılmıştır ve kendi kişisel görüşlerini yansıtmaktadır. MetaQuotes Ltd, sunulan bilgilerin doğruluğundan veya açıklanan çözümlerin, stratejilerin veya tavsiyelerin kullanımından kaynaklanan herhangi bir sonuçtan sorumlu değildir.
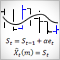 Üssel Düzeltme Kullanarak Zaman Serisi Tahmini
Üssel Düzeltme Kullanarak Zaman Serisi Tahmini
 MQL5'te Gelişmiş Uyarlanabilir Göstergeler Teorisi ve Uygulaması
MQL5'te Gelişmiş Uyarlanabilir Göstergeler Teorisi ve Uygulaması
 Göstergelerin İstatistiksel Parametrelerini Analiz Etme
Göstergelerin İstatistiksel Parametrelerini Analiz Etme
 Yeni Başlayanlar için MQL5 Sihirbazı
Yeni Başlayanlar için MQL5 Sihirbazı
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Zaman serilerinin temel özelliklerini analiz etme makalesi yayınlandı:
Yazar: Victor
Viktor, iyi günler.
Ne yazık ki nihai bilgileri alamıyorum. Orijinal formda görünen özellikler görüntülenir: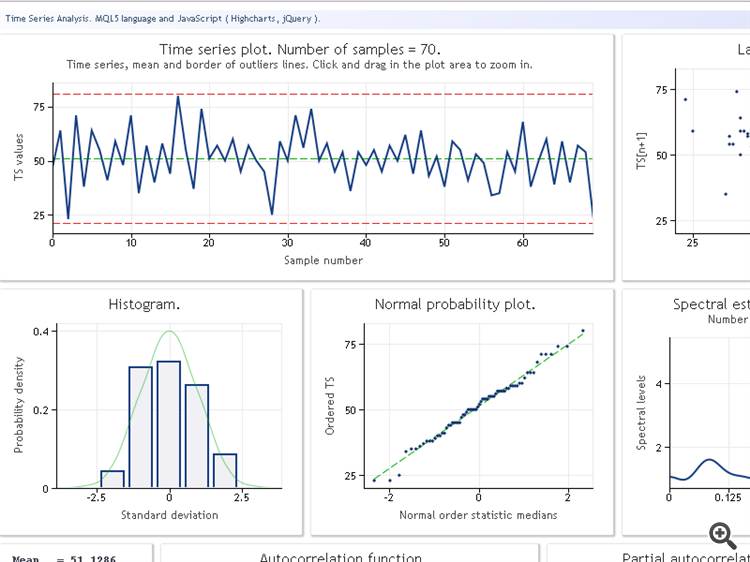
TSAexample.mq5 kodunun metnine bakın.
Burada, bd[] dizisi incelenen dizinin değerleriyle doldurulur ve daha sonra TSAnalysis sınıfının Calc yöntemi çağrılırken bir argüman olarak kullanılır.
Kendi kodunuzu (veya göstergenizi) yazın, mevcut herhangi bir yöntemle dizinizi içeren bir dizi oluşturun ve makalede verilen örneğe benzer şekilde Calc yöntemine bir argüman olarak aktarın.
Bana öyle geliyor ki bunu yapabilmelisiniz.
Victor.
Lütfen "IP" kısaltması ne anlama geliyor?
TSAexample.mq5 kodunun metnine bakın.
Burada, bd[] dizisi incelenen dizinin değerleriyle doldurulur ve daha sonra TSAnalysis sınıfının Calc yöntemi çağrılırken bir argüman olarak kullanılır.
Kendi kodunuzu (veya göstergenizi) yazın, mevcut herhangi bir yöntemle dizinizi içeren bir dizi oluşturun ve makalede verilen örneğe benzer şekilde Calc yöntemine bir argüman olarak aktarın.
Bana öyle geliyor ki bunu yapabilmelisiniz.
Victor.
Her şey gayet iyi çalışıyor! Çok kullanışlı bir araç! Teşekkür ederim!