La stima kernel di densità della funzione di densità di probabilità
556
0
Introduzione
Il miglioramento delle prestazioni MQL5 e la crescita costante della produttività del PC consentono agli utenti della piattaforma MetaTrader 5 di applicare metodi matematici abbastanza sofisticati e avanzati per l'analisi di mercato. Questi metodi possono appartenere a vari ambiti dell'economia, dell'econometria o della statistica, ma in ogni caso dovremo fare i conti con il concetto di funzione di densità di probabilità durante il loro utilizzo.
Sono stati sviluppati molti metodi di analisi comuni basati sull'assunzione della normalità della distribuzione dei dati o della normalità degli errori nel modello utilizzato. Inoltre, spesso è necessario conoscere la distribuzione delle varie componenti del modello utilizzato per stimare i risultati dell'analisi. In entrambi i casi, abbiamo il compito di creare uno "strumento" (universale, nel caso ideale) che permetta di stimare la funzione di densità di probabilità incognita.
In questo articolo si cerca di creare una classe che realizzi un algoritmo più o meno universale per la stima della funzione di densità di probabilità incognita. L'idea originale era che durante la stima non sarebbero stati utilizzati mezzi esterni, ovvero tutto doveva essere realizzato solo mediante MQL5. Ma, alla fine, l'idea originale è stata modificata in una certa misura. È chiaro che il compito della stima visiva della funzione di densità di probabilità consiste di due parti indipendenti.
Vale a dire calcolo della stima stessa e della sua visualizzazione, ovvero la visualizzazione come grafico o diagramma. Ovviamente i calcoli sono stati realizzati tramite MQL5, mentre la visualizzazione deve essere implementata creando una pagina HTML e la sua visualizzazione nel browser web. Quella soluzione è stata utilizzata per ottenere eventualmente la grafica in forma vettoriale.
Ma poiché la parte di calcolo e la visualizzazione dei risultati sono realizzate separatamente, un lettore può, ovviamente, visualizzare utilizzando qualsiasi altro metodo disponibile. Inoltre, ci aspettiamo che varie librerie, comprese quelle grafiche, appaiano su MetaTrader 5 (il lavoro è in corso, per quanto ne sappiamo). Non sarà difficile modificare la parte di visualizzazione nella soluzione proposta, nel caso in cui MetaTrader 5 fornisca i mezzi avanzati per costruire grafici e diagrammi.
Va preliminarmente notato che la creazione di un algoritmo veramente universale per la stima della funzione di densità di probabilità di sequenze si è rivelata un obiettivo irraggiungibile. Sebbene la soluzione proposta non sia altamente specializzata, non può nemmeno essere definita completamente universale. Il problema è che i criteri di ottimalità risultano essere abbastanza differenti durante la stima della densità, ad esempio per le distribuzioni a campana, come quelle normali ed esponenziali.
Pertanto, è sempre possibile scegliere la soluzione più adatta per ogni caso specifico se si dispone di alcune informazioni preliminari sulla distribuzione stimata. Tuttavia, supporremo di non sapere nulla sulla natura della densità stimata. Un tale approccio influenzerà sicuramente la qualità delle stime, ma speriamo che ripaghi fornendo la possibilità di stimare densità piuttosto diverse.
A causa del fatto che spesso abbiamo a che fare con sequenze non stazionarie durante l'analisi dei dati di mercato, siamo più interessati alla stima della densità di sequenze brevi e medie. Questo è un momento critico che determina la scelta del metodo di stima utilizzato.
Gli istogrammi e la P-spline possono essere utilizzati con successo per sequenze molto lunghe contenenti più di un milione di valori. Ma alcuni problemi compaiono quando proviamo a costruire in modo efficace gli istogrammi per sequenze contenenti 10-20 valori. Pertanto, ci concentreremo principalmente sulle sequenze aventi approssimativamente da 10 fino a 10 000 valori più avanti.
1. Metodi di stima della funzione densità di probabilità
Oggigiorno sono noti molti metodi più o meno popolari di stima della funzione di densità di probabilità. Possono essere facilmente trovati su Internet, ad esempio, utilizzando espressioni chiave come "stima della densità di probabilità", "densità di probabilità", "stima della densità" ecc. Ma, sfortunatamente, non siamo riusciti a scegliere il migliore tra loro. Tutti possiedono alcuni vantaggi e svantaggi.
Gli istogrammi sono tradizionalmente utilizzati per la stima della densità [1]. L'uso degli istogrammi (compresi quelli lisci) consente di fornire l'alta qualità delle stime della densità di probabilità, ma solo nel caso in cui si tratti di sequenze lunghe. Come accennato in precedenza, non è possibile dividere una sequenza breve in un grande numero di gruppi, mentre un istogramma composto da 2-3 barre non può illustrare la legge di distribuzione della densità di probabilità di tale sequenza. Pertanto, abbiamo dovuto abbandonare l'uso degli istogrammi.
Un altro metodo di stima abbastanza noto è la stima kernel di densità [2]. L'idea di usare lo smoothing kernel è mostrata abbastanza bene in [3]. Pertanto, abbiamo scelto quel metodo, nonostante tutti i suoi svantaggi. Alcuni aspetti relativi all'implementazione di questo metodo verranno brevemente discussi di seguito.
È inoltre necessario citare un metodo di stima della densità molto interessante, che utilizza l'algoritmo "Expectation–maximization" [4]. Questo algoritmo permette di dividere una sequenza in componenti separati aventi, ad esempio, una distribuzione normale. È possibile ottenere una stima della densità sommando le curve di distribuzione ottenute dopo aver determinato i parametri dei componenti separati. Questo metodo è menzionato in [5]. Questo metodo non è stato implementato e testato durante la stesura dell’articolo, così come per molti altri. Un gran numero di metodi di stima della densità descritti in varie fonti impedisce di esaminarli tutti in pratica.
Procediamo con il metodo di stima kernel di densità che è stato scelto per l'implementazione.
2. La stima kernel di densità della funzione densità di probabilità
La stima kernel di densità della funzione di densità di probabilità si basa sul metodo di smoothing kernel. I principi di tale metodo possono essere trovati, ad esempio, in [6], [7].
L'idea di base dello smoothing kernel è abbastanza semplice. Gli utenti di MetaTrader 5 hanno familiarità con l'indicatore Moving Average (MA). Questo indicatore può essere facilmente rappresentato come una finestra che scorre lungo una sequenza con i suoi valori ponderati che vengono smussati all'interno. La finestra può essere rettangolare, esponenziale o avere qualche altra forma. Possiamo facilmente vedere la stessa finestra scorrevole durante lo smoothing kernel (ad esempio, [3]). Ma in questo caso è simmetrico.
Esempi delle finestre più frequentemente utilizzate nello smoothing kernel possono essere trovati in [8]. Nel caso in cui venga utilizzata una regressione di ordine zero nello smoothing kernel, i valori ponderati della sequenza che sono arrivati alla finestra (kernel) vengono semplicemente livellati, come in MA. Possiamo vedere lo stesso tipo di applicazione della funzione finestra quando ci occupiamo di problemi di filtraggio. Ma ora la stessa procedura viene presentata in modo leggermente diverso. Vengono utilizzate le caratteristiche di ampiezza-frequenza e di fase-frequenza, mentre il kernel (finestra) è chiamato caratteristica dell'impulso di filtro.
Questi esempi mostrano il fatto che spesso una cosa può essere rappresentata in modi diversi. Ciò contribuisce all'apparato matematico, naturalmente. Ma può anche creare confusione quando si discutono questioni di questo tipo.
Sebbene la stima kernel di densità utilizzi gli stessi principi, come il già citato smoothing kernel, il suo algoritmo differisce leggermente.
Passiamo all'espressione che definisce la stima della densità in un punto.
dove
- x - sequenza di lunghezza n;
- K - kernel simmetrico;
- h - intervallo, parametro di livellamento.
Solo il kernel gaussiano verrà utilizzato più avanti per le stime della densità:
Come segue dall'espressione di cui sopra, la densità nel punto X è calcolata come somma dei valori kernel per le quantità definite dalle differenze tra i valori del punto X e la sequenza. Inoltre, X punti utilizzati per il calcolo della densità potrebbero non coincidere con i valori della sequenza stessa.
Ecco i passaggi fondamentali dell'implementazione dell'algoritmo di stima kernel di densità.
- Valutazione del valore medio e della deviazione standard della sequenza di input.
- Normalizzazione della sequenza di input. Sottraendo la media precedentemente ottenuta da ciascuno dei suoi valori e dividendo per il valore della deviazione standard. Dopo tale normalizzazione, la sequenza originale avrà media nulla e deviazione standard pari a uno. Tale normalizzazione non è necessaria per il calcolo della densità, ma permette di unificare i grafici risultanti in quanto, per qualsiasi sequenza sulla scala X, ci saranno valori espressi in unità di deviazione standard.
- Trovare valori alti e bassi nella sequenza normalizzata.
- Creazione di due array le cui dimensioni corrispondono al numero desiderato di punti visualizzati sul grafico risultante. Ad esempio, se il grafico deve essere creato utilizzando 200 punti, la dimensione degli array deve includere in modo appropriato 200 valori ciascuno.
- Riservando uno degli array creati per la memorizzazione del risultato. Il secondo è utilizzato per formare i valori dei punti per i quali è stata eseguita la stima della densità. Per fare ciò, dobbiamo formare 200 (in questo caso) valori equidistanti tra i valori alti e bassi precedentemente preparati e salvarli nell'array che abbiamo preparato.
- Utilizzando l'espressione mostrata prima, dobbiamo eseguire la stima della densità in 200 (nel nostro caso) test point salvando il risultato nell'array che abbiamo preparato al passaggio 4.
L'implementazione software di questo algoritmo è mostrata di seguito.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
Il metodo NTpoints() consente di impostare il numero richiesto di punti di prova equidistanti, per cui verrà effettuata la stima della densità. Questo metodo deve essere chiamato prima chiamando il metodo Density(). Il collegamento all'array contenente i dati input e il valore dell'intervallo (parametro di livellamento) viene passato al metodo Density() come suoi parametri quando il metodo viene chiamato.
Il metodo Density() restituisce zero in caso di completamento con successo, mentre i valori dei punti di prova e le stime dei risultati si trovano rispettivamente negli array T[] e Y[] di quella classe.
Le dimensioni degli array vengono impostate quando si accede a NTpoints(), pur essendo uguali a 200 valori per impostazione predefinita.
Il seguente script di esempio mostra l'uso della classe CDens presentata.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
In questo esempio vengono preparati gli array per la memorizzazione della sequenza di input dei punti di prova e dei risultati della stima. Quindi, l'array X[] viene riempito con valori casuali, a titolo di esempio. La copia della classe CDens viene creata dopo che tutti i dati sono stati preparati.
Quindi, il numero necessario di punti di prova viene impostato (npoint=300 nel nostro caso) chiamando il metodo NTpoints(). Nel caso in cui non sia necessario modificare il numero predefinito di punti, l'invocazione del metodo NTpoints() può essere esclusa.
I valori calcolati vengono copiati negli array predefiniti dopo l'invocazione del metodo Density(). Quindi, la copia creata in precedenza della classe CDens viene eliminata. Questo esempio mostra solo l'interazione con la classe CDens. Non vengono eseguite ulteriori azioni con i risultati ottenuti (array T[] e Y[]).
Se questi risultati devono essere utilizzati per creare un grafico, è possibile farlo facilmente inserendo i valori dell'array T[] sulla scala del grafico X, mentre i valori appropriati dell'array Y[] devono essere inseriti nella scala Y.
3. Selezione ottimale della gamma
La Fig.1 mostra i grafici di stima della densità per la sequenza avente la legge di distribuzione normale e vari valori dell'intervallo h.
Le stime vengono eseguite utilizzando la classe CDens descritta sopra. I grafici sono stati costruiti sotto forma di pagine HTML. Il metodo per costruire tali grafici sarà presentato alla fine dell'articolo. La creazione di grafici e diagrammi in formato HTML si trova in [9].
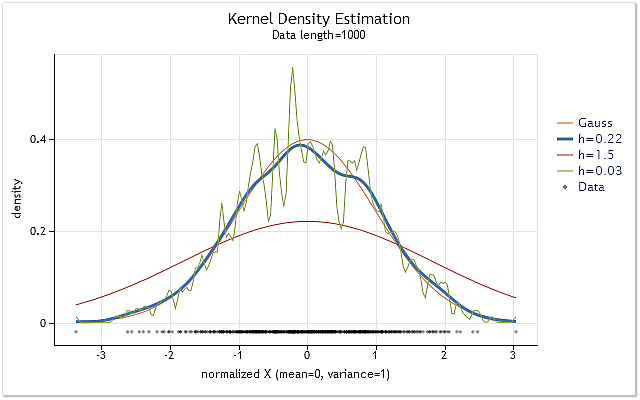
Fig.1. Stima della densità per vari valori dell'intervallo h
La Fig.1 mostra anche la vera curva di densità della distribuzione normale (distribuzione gaussiana) insieme a tre stime della densità. Si può facilmente vedere che il risultato più appropriato della stima è stato ottenuto con h=0.22 in quel caso. In altri due casi si osservano "oversmoothing" e "undersmoothing" definiti.
La figura 1 mostra chiaramente l'importanza della corretta selezione dell'intervallo h durante l'uso della stima kernel di densità. Nel caso in cui il valore di h sia stato scelto in modo errato, una stima sarà notevolmente spostata rispetto alla densità reale o notevolmente dispersa.
Numerosi lavori sono dedicati alla selezione ottimale della gamma h. La semplice e ben collaudata regola empirica di Silverman è spesso usata per la selezione di h (vedi [10]).
In questo caso, A è il valore più basso tra i valori di deviazione standard della sequenza e l'intervallo interquartile diviso per 1,34.
Considerando che la sequenza di input ha la deviazione standard pari a uno nella suddetta classe CDens, è abbastanza facile implementare questa regola utilizzando il seguente frammento di codice:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Tale stima si adatta alle sequenze con la funzione di densità di probabilità che è vicina a quella normale per la sua forma.
In molti casi, la considerazione dell'intervallo interquartile consente di regolare il valore di h verso il basso, quando la forma della densità valutata si discosta da quella normale. Ciò rende questo metodo di valutazione abbastanza versatile. Pertanto, vale la pena utilizzare questa regola empirica come stima iniziale del valore h di base. Inoltre, non richiede lunghi calcoli.
Oltre alle stime asintotiche ed empiriche del valore dell'intervallo h, esistono anche vari metodi basati sull'analisi della sequenza di input stessa. In questo caso, il valore di h ottimale è determinato considerando la stima preliminare della densità incognita. Il confronto dell'efficienza di alcuni di questi metodi può essere trovato in [11], [12].
Secondo i risultati dei test pubblicati in varie fonti, il metodo plug-in Sheather-Jones (SJPI) è uno dei metodi di stima dell'intervallo più efficaci. Optiamo per questo metodo. Per non sovraccaricare l'articolo con lunghe espressioni matematiche, solo alcune delle caratteristiche del metodo verranno discusse più avanti. Se necessario, la base matematica di questo metodo può essere trovata in [13].
Usiamo un kernel gaussiano, che è un kernel con supporto illimitato (cioè è specificato quando il suo parametro cambia da meno a più infinito). Come segue dall'espressione sopra, avremo bisogno di operazioni O(M*N) per stimare la densità in M punti della sequenza di lunghezza N usando il metodo di calcolo diretto e il kernel con supporto illimitato. Nel caso in cui sia necessario effettuare stime in corrispondenza di ciascuno dei punti della sequenza, questo valore aumenta fino a O(N*N) operazioni e il tempo impiegato per il calcolo aumenterà proporzionalmente al quadrato della lunghezza della sequenza.
Una richiesta così elevata di risorse computazionali è uno dei principali svantaggi del metodo di smoothing kernel. Se passiamo al metodo SJPI, vedremo che non è migliore in termini di quantità di calcolo richiesta. Parlando in breve, dobbiamo prima calcolare due volte la somma di due derivate di densità lungo l'intera lunghezza della sequenza di input quando implementiamo il metodo SJPI.
Quindi dobbiamo calcolare ripetutamente la stima utilizzando i risultati ottenuti. Il valore di stima deve essere uguale a zero. Il metodo di Newton-Raphson [14] può essere usato per trovare l'argomento in corrispondenza del quale questa funzione è uguale a zero. Nel caso del calcolo diretto, l'applicazione del metodo SJPI per la determinazione del valore ottimale dell'intervallo può richiedere circa dieci volte il tempo necessario per il calcolo delle stime di densità.
Esistono vari metodi per accelerare i calcoli nello smoothing kernel e nella stima kernel di densità. Nel nostro caso viene utilizzato il kernel gaussiano, i cui valori si possono assumere trascurabilmente piccoli per i valori dell'argomento maggiori di 4. Quindi, se il valore dell'argomento è maggiore di 4, non c'è bisogno di calcolare i valori del kernel. Pertanto, possiamo ridurre parzialmente il numero richiesto di calcoli. Difficilmente vedremo alcuna differenza tra il grafico basato su tale stima e la versione completamente calcolata.
Un altro modo semplice per accelerare i calcoli è ridurre il numero di punti per i quali viene eseguita la stima. Come accennato in precedenza, se M è minore di N, il numero di operazioni richieste sarà ridotto da O(N*N) a O(M*N). Se abbiamo una sequenza lunga, ad esempio N=100 000, possiamo eseguire stime solo in M=200 punti. Pertanto, possiamo ridurre notevolmente i tempi di calcolo.
Inoltre, è possibile utilizzare metodi più complessi per ridurre il numero necessario di calcoli, ad esempio le stime utilizzando un algoritmo di trasformata di Fourier veloce o trasformate wavelet. I metodi basati sulla riduzione della dimensione della sequenza di input (ad esempio, "Data binning" [15]) possono essere applicati con successo per sequenze molto lunghe.
La trasformata gaussiana veloce [16] può essere applicata anche per velocizzare i calcoli oltre ai metodi sopra menzionati, nel caso si utilizzi il kernel gaussiano. Utilizzeremo l'algoritmo basato sulla trasformazione gaussiana [17] per implementare il metodo SJPI della stima del valore del range. Il collegamento sopra menzionato conduce ai materiali contenenti sia la descrizione del metodo che i codici di programma che implementano l'algoritmo proposto.
4. Plug-in Sheather Jones (SJPI)
Come nel caso delle espressioni matematiche che determinano l'essenza del metodo SJPI, non copieremo le basi matematiche dell'implementazione dell'algoritmo che possono essere trovate in [17] in questo articolo. Se necessario, è possibile esaminare le pubblicazioni in [17].
La classe CSJPlugin è stata creata sulla base dei materiali che si trovano in [17]. Questa classe è destinata al calcolo del valore ottimale dell'intervallo h e include un solo metodo pubblico: double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
I seguenti argomenti vengono passati a questo metodo quando viene chiamato:
- double &px[], il link all’array contenente la sequenza originale;
- double h è il valore iniziale dell'intervallo h, rispetto al quale viene eseguita la ricerca quando si risolvono le equazioni utilizzando l'algoritmo di Newton-Raphson. È auspicabile che questo valore sia il più vicino possibile a quello cercato. Ciò può ridurre significativamente il tempo impiegato per risolvere le equazioni e diminuire la probabilità dei casi in cui Newton-Raphson potrebbe perdere la sua affidabilità. Il valore trovato utilizzando la regola empirica di Silverman può essere utilizzato come valore h iniziale;
- double stdev=1, il valore della deviazione standard della sequenza originale. Il valore predefinito è uno. In questo caso non è necessario modificare il valore di default in quanto questo metodo è pensato per essere utilizzato insieme alla già citata classe CDens, in cui la sequenza originale è già stata normalizzata e ha la deviazione standard pari a uno.
Il metodo SelectH() restituisce il valore dell'intervallo h ottimale ottenuto in caso di completamento con successo. Il valore h iniziale viene restituito come parametro in caso di errore. Il codice sorgente della classe CSJPlugin si trova nel file CSJPlugin.mqh.
È necessario chiarire alcune caratteristiche di questa implementazione.
La sequenza sorgente viene trasformata nell'intervallo [0,1] in una volta, mentre il valore iniziale dell'intervallo h viene normalizzato proporzionalmente con la scala di trasformazione della sequenza originale. La normalizzazione inversa viene applicata al valore h ottimale ottenuto durante i calcoli.
eps=1e-4, la precisione di calcolo delle stime della densità e delle sue derivate e P_UL=500, il numero massimo consentito di iterazioni interne dell'algoritmo è impostato nel costruttore della classe CSJPlugin. Per ulteriori informazioni, vedi [17].
IMAX=20, numero massimo consentito di iterazioni per il metodo Newton-Raphson e PREC=1e-4, l'accuratezza della risoluzione dell'equazione utilizzando questo metodo è impostata nel metodo SelectH().
L'uso tradizionale del metodo Newton-Raphson richiedeva il calcolo della funzione target e della sua derivata nello stesso punto ad ogni iterazione del valore. In questo caso, il calcolo della derivata è stato sostituito dalla sua stima calcolata aggiungendo un piccolo incremento al valore del suo argomento.
La figura 2 mostra l'esempio dell'utilizzo di due diversi metodi di stima del valore ottimale dell'intervallo h.
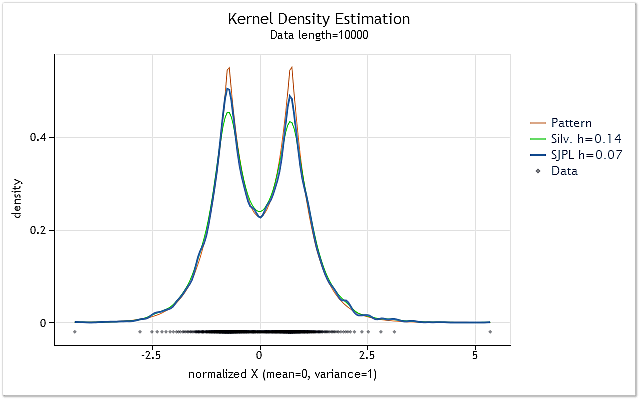
Fig.2. Confronto delle stime del valore ottimale dell'intervallo h
La figura 2 mostra due stime per la sequenza casuale, la cui densità reale è mostrata come grafico rosso (Pattern).
Le stime sono state eseguite per la sequenza avente una lunghezza di 10.000 elementi. Il valore dell'intervallo h di 0,14 è stato ottenuto per questa sequenza utilizzando la regola empirica di Silverman, mentre è stato 0,07 utilizzando il metodo SJPI.
Esaminando i risultati della stima kernel di densità per questi due valori h mostrati nella figura 2, possiamo facilmente vedere che l'applicazione del metodo SJPI ha aiutato a ottenere una stima h più interessante rispetto alla regola di Silverman. Come possiamo vedere, le punte affilate hanno una forma molto migliore, mentre non c'è quasi alcuna dispersione crescente nelle cavità inclinate in caso di h=0,07.
Come previsto, l'uso del metodo SJPI consente in molti casi di ottenere stime dell'intervallo h abbastanza efficaci. Nonostante il fatto che siano stati utilizzati algoritmi abbastanza veloci [17] per la creazione della classe CSJPlugin, la stima del valore h utilizzando questo metodo potrebbe richiedere ancora troppo tempo per sequenze lunghe.
Un altro inconveniente di questo metodo è la sua tendenza a sovrastimare il valore h per brevi sequenze costituite da soli 10-30 valori. Le stime effettuate utilizzando il metodo SJPI possono superare le stime h effettuate dalla regola empirica di Silverman.
Le seguenti regole verranno utilizzate nell'ulteriore implementazione per compensare in qualche modo questi inconvenienti:
- La stima di Silverman sarà la stima di default per l'intervallo h, mentre sarà possibile attivare il metodo SJPI con un comando separato;
- Quando si utilizza il metodo SJPI, come valore finale di h verrà sempre utilizzato il valore più basso tra quelli ottenuti con i due metodi menzionati.
5. Effetto di confine
Il desiderio di utilizzare il valore di intervallo ottimale nella stima della densità ha portato alla creazione della classe CSJPlugin sopra menzionata e piuttosto ingombrante. Ma c'è un altro problema oltre a specificare la dimensione dell'intervallo e l'elevata intensità di risorse del metodo di smoothing kernel. Questo è il cosiddetto effetto confine.
La questione è semplice. Verrà visualizzato utilizzando il kernel definito nell'intervallo [-1,1]. Tale kernel è chiamato kernel con supporto finito. È uguale a zero al di fuori dell'intervallo specificato (non esiste).
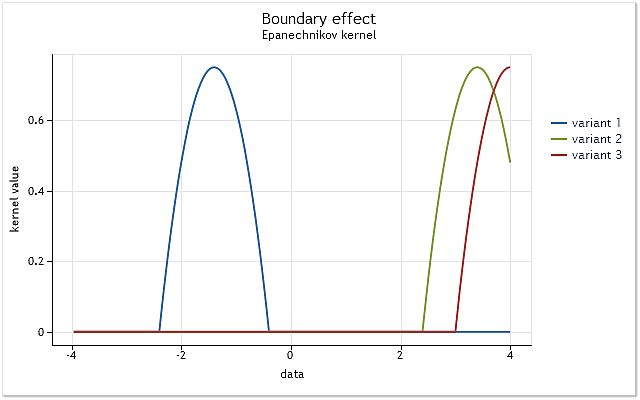
Fig.3. La riduzione del kernel al limite dell'intervallo
Come mostrato in figura 3, nel primo caso il nucleo copre completamente i dati originali situati sull'intervallo [-1,1] relativo al suo centro. Quando il kernel si sposta (ad esempio, a destra), emerge la situazione in cui i dati non sono sufficienti per utilizzare completamente la funzione del kernel selezionata.
Il kernel copre già meno dati rispetto al primo caso. Il caso peggiore è quando il centro del kernel si trova al confine della sequenza di dati. La quantità dei dati coperti dal kernel è ridotta al 50% in tal caso. Una tale riduzione del numero dei dati utilizzati per la stima della densità porta ad uno spostamento significativo delle stime e ne aumenta la dispersione nei punti vicini ai limiti di intervallo.
La figura 3 mostra un esempio di riduzione per un kernel con supporto finito (kernel Epanechnikov) al limite dell'intervallo. Va notato che il kernel gaussiano definito sull'intervallo infinito (supporto illimitato) è stato utilizzato durante l'implementazione del metodo di stima kernel di densità. In teoria, l’interruzione di un tale kernel deve sempre avvenire. Ma considerando il fatto che il valore di questo kernel è quasi uguale a zero per argomenti di grandi dimensioni, gli effetti di confine gli appaiono allo stesso modo dei kernel con supporto finito.
Questa caratteristica non può influenzare i risultati della stima della densità nei casi presentati nelle figure 1 e 2, poiché in entrambi i casi la stima è stata eseguita per le distribuzioni la cui funzione di densità di probabilità è diminuita ai bordi quasi fino a zero.
Formiamo la sequenza composta da interi positivi X=1,2,3,4,5,6,…n per mostrare l'influenza dell’interruzione del kernel ai limiti dell'intervallo. Tale sequenza ha una legge pari della distribuzione della densità di probabilità. Significa che la stima della densità di questa sequenza deve essere una linea retta orizzontale situata su un livello diverso da zero.
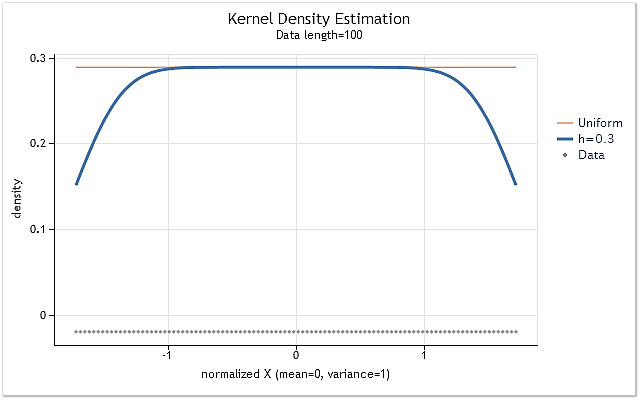
Fig.4. Stima della densità per la sequenza avente legge di distribuzione uniforme
Come previsto, la figura 4 mostra chiaramente che c'è un considerevole spostamento delle stime di densità ai confini dell'intervallo. Esistono diversi metodi utilizzati per ridurre tale spostamento in misura maggiore o minore. Possono essere grossolanamente suddivisi nei seguenti gruppi:
- metodi di riflessione dei dati;
- Metodi di trasformazione dei dati;
- metodi pseudo-dati;
- Metodi del limite kernel.
L'idea di utilizzare i dati riflessi è che la sequenza di input viene aumentata intenzionalmente aggiungendo i dati, il che è una sorta di riflesso speculare di quella sequenza rispetto ai limiti dell'intervallo di sequenza. Dopo tale aumento, la stima della densità viene eseguita per gli stessi punti, come per la sequenza originale, ma nella stima vengono utilizzati anche dati aggiunti intenzionalmente.
I metodi che coinvolgono la trasformazione dei dati sono focalizzati sulla trasformazione della sequenza vicino ai suoi limiti di intervallo. Ad esempio, è possibile utilizzare logaritmico o qualsiasi altra trasformazione che consente di deformare in qualche modo la scala dei dati quando ci si avvicina al limite dell'intervallo durante la stima della densità.
I cosiddetti pseudo-dati possono essere utilizzati per l'estensione intenzionale (ingrandimento) della sequenza originale. Questi sono i dati calcolati sulla base dei valori della sequenza originale. Quei dati servono a considerare il suo comportamento ai confini e ad integrarlo nel modo più appropriato.
Ci sono molte pubblicazioni dedicate ai metodi kernel di confine. In questi metodi, il kernel in qualche modo altera la sua forma quando si avvicina al confine. La forma del kernel cambia in modo che per compensare le stime si spostino ai confini.
Alcuni metodi dedicati alla compensazione delle distorsioni che si manifestano ai limiti di gamma, al loro confronto e alla valutazione dell'efficienza si trovano in [18].
Il metodo di riflessione dei dati è stato selezionato per un ulteriore utilizzo dopo alcuni brevi esperimenti. Tale scelta è stata influenzata dal fatto che questo metodo non implica situazioni in cui la stima della densità ha un valore negativo. Inoltre, questo metodo non richiede calcoli matematici complessi. Il numero totale delle operazioni aumenta ancora per la necessità di fare ogni stima della sequenza, la cui lunghezza è volutamente aumentata.
Ci sono due modi per implementare questo metodo. In primo luogo, è possibile integrare la sequenza originale con i dati necessari e aumentare le sue dimensioni di tre volte nel processo. Quindi saremo in grado di effettuare stime allo stesso modo, come mostrato nella classe CDens presentata in precedenza. In secondo luogo, è possibile non espandere l'array di dati di input. Possiamo ancora una volta selezionare i dati da esso in un certo modo. Il secondo modo è stato selezionato per l'implementazione.
Nella suddetta classe CDens, la stima della densità è stata implementata nella funzione void kdens(doppia h). Cambiamo questa funzione aggiungendo la correzione delle distorsioni di confine.
La funzione aumentata può avere il seguente aspetto.
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
La funzione viene implementata presupponendo che i dati di origine nell'array X[] siano già stati ordinati nel momento in cui è stata chiamata la funzione. Ciò consente di escludere facilmente da un'altra elaborazione due elementi di sequenza corrispondenti ai valori estremi dell'intervallo. Il tentativo di mettere le operazioni matematiche al di fuori dei cicli, quando possibile, è stato fatto durante l'implementazione di questa funzione. Di conseguenza, la funzione riflette in modo meno evidente l'idea dell'algoritmo utilizzato.
È già stato detto prima che è possibile ridurre il numero di calcoli, nel caso in cui non calcoliamo un valore del kernel per i grandi valori degli argomenti. Questo è esattamente ciò che è stato implementato nella funzione di cui sopra. In questo caso, è impossibile notare eventuali modifiche dopo la creazione del grafico della densità valutata.
Quando si utilizza la versione modificata della funzione kdens(), la stima della densità mostrata nella figura 4 viene trasformata in una linea retta e le cavità di confine scompaiono completamente. Ma una tale correzione ideale può essere ottenuta solo se la distribuzione vicino ai confini ha gradiente zero, cioè rappresentato da una linea orizzontale.
Se la densità di distribuzione stimata aumenta o diminuisce bruscamente vicino al confine, il metodo di riflessione dei dati selezionato non sarà in grado di regolare completamente l'effetto del confine. Questo è mostrato dalle figure seguenti.
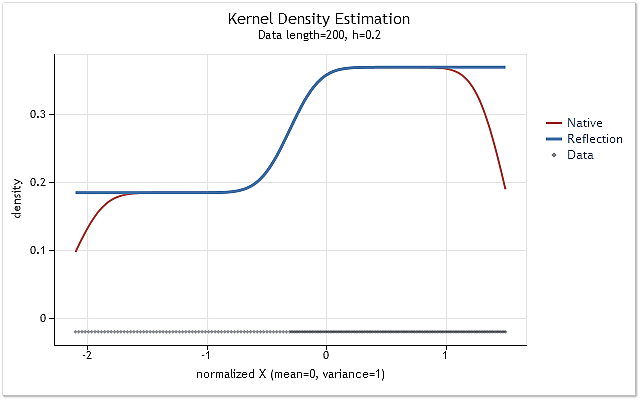
Fig.5. La funzione di densità di probabilità cambia gradualmente
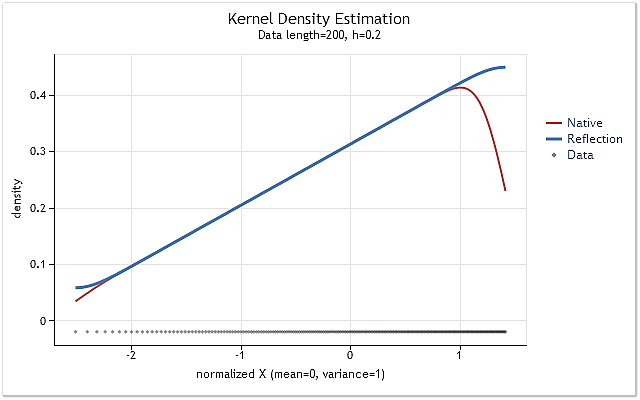
Fig.6. La funzione di densità di probabilità crescente linearmente
Le figure 5 e 6 mostrano la stima della densità ottenuta utilizzando la versione originale della funzione kdens() (rosso) e la stima ottenuta considerando le modifiche applicate che implementano il metodo di riflessione dei dati (blu). L'effetto confine è stato completamente corretto nella figura 5, mentre lo spostamento vicino ai confini non è stato eliminato completamente nella figura 6. Se la densità stimata aumenta o diminuisce bruscamente vicino al confine, allora sembra essere un po' più uniforme vicino a quel confine.
Il metodo di riflessione dei dati selezionato per regolare l'effetto contorno non è il migliore o il peggiore dei metodi noti. Sebbene questo metodo non possa eliminare in tutti i casi l'effetto limite, è sufficientemente stabile e facile da implementare. Questo metodo permette di ottenere un risultato logico e prevedibile.
6. Implementazione finale. Classe di densità CK
Aggiungiamo la possibilità di selezionare automaticamente il valore dell'intervallo h e la correzione dell'effetto contorno alla classe CDens creata in precedenza.
Di seguito è riportato il codice sorgente di tale classe modificata.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Il metodo Density(double &x[],double hh=-1) è la base per quella classe. Il primo argomento è il collegamento all'array x[] in cui deve essere contenuta la sequenza di input analizzata. La lunghezza della sequenza di input non deve essere inferiore a otto elementi. Il secondo argomento (opzionale) viene utilizzato per l'impostazione forzata del valore dell'intervallo h.
È possibile specificare qualsiasi numero positivo. Il valore impostato h sarà sempre limitato da 0,005 dal basso. Se questo parametro ha un valore negativo, il valore dell'intervallo verrà selezionato automaticamente. Il metodo Density() restituisce zero in caso di completamento con successo e meno uno in caso di completamento di emergenza.
Dopo aver invocato il metodo Density() e il suo completamento con successo, l'array T[] conterrà i valori dei punti di test per i quali è stata eseguita la stima della densità, mentre l'array Y[] conterrà i valori di queste stime. L'array X[] conterrà la sequenza di input normalizzata e ordinata. Il valore medio di questa sequenza è uguale a zero, mentre il valore della deviazione standard è uguale a uno.
I seguenti valori sono contenuti nelle variabili che sono membri della classe:
- N – lunghezza della sequenza di input;
- Np – numero di punti di prova, in corrispondenza dei quali è stata eseguita la stima della densità;
- Media – valore medio della sequenza di input;
- Var – variazione della sequenza di input;
- StDev – deviazione standard della sequenza di input;
- H – valore del range (parametro smoothing);
- Pflag – flag dell'applicazione del metodo SJPI per determinare il valore ottimale dell'intervallo h.
Il metodo NTpoints(int n) viene utilizzato per impostare il numero di punti di prova, in corrispondenza dei quali verrà eseguita la stima della densità. L'impostazione del numero dei punti di prova deve essere eseguita prima di chiamare il metodo di base Density(). Se il metodo NTpoints(int n) non viene utilizzato, verrà impostato il numero di punti predefinito di 200.
Il metodo PluginMode(int m) consente o vieta l'uso del metodo SJPI per valutare il valore dell'intervallo ottimale. Se viene utilizzato il parametro uguale a uno quando si richiama questo metodo, verrà applicato il metodo SJPI per specificare l'intervallo h. Se il valore di questo parametro non è uguale a uno, il metodo SJPI non verrà utilizzato. Se il metodo PluginMode(int m) non è stato invocato, il metodo SJPI sarà disabilitato per impostazione predefinita.
7. Creazione di grafici
Durante la stesura di questo articolo è stato utilizzato il metodo che si trova in [9]. Quella pubblicazione riguardava l'applicazione di pagine HTML già pronte, inclusa la libreria JavaScript highcharts [19] e la specifica completa di tutte le sue invocazioni. Successivamente, un programma MQL forma un file di testo contenente i dati da visualizzare e tale file si collega alla suddetta pagina HTML.
In tal caso, è necessario modificare la pagina HTML modificando il codice JavaScript implementato per apportare eventuali correzioni nella struttura dei grafici visualizzati. Per evitare ciò, è stata sviluppata una semplice interfaccia che consente di invocare i metodi JavaScript della libreria highcharts direttamente dal programma MQL.
Non è stato svolto alcun compito per implementare l'accesso a tutte le possibilità della libreria highcharts durante la creazione dell'interfaccia. Pertanto, sono state implementate solo le possibilità che consentono di non modificare il file HTML creato in precedenza durante la scrittura dell'articolo.
Il codice sorgente della classe CLinDraw è visualizzato di seguito. Questa classe è stata utilizzata per fornire la connessione con i metodi della libreria highcharts. Questo codice non deve essere considerato come un'implementazione software completa. È solo un esempio che mostra come creare un'interfaccia con una libreria JavaScript grafica.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Se vogliamo far funzionare correttamente questa classe, abbiamo bisogno di una pagina HTML già pronta con librerie JavaScript implementate. È inoltre necessario specificare una dimensione e una posizione del campo per la creazione di grafici. Un esempio di tale implementazione della pagina può essere trovato nei file allegati a questo articolo.
Quando il metodo AddGraph() viene richiamato in un file di testo, viene formato un codice JavaScript appropriato. Il file di testo viene quindi incluso nella pagina HTML precedentemente creata. Il codice citato fa riferimento alla libreria grafica e fornisce la creazione di un grafico utilizzando i dati inviati al metodo AddGraph() come argomento. È possibile aggiungere uno o più grafici nel campo di output quando si chiama nuovamente questo metodo.
Tre versioni della funzione sovraccarica AddGraph() sono incluse nella classe CLinDraw. Una delle versioni richiede che venga trasferito come argomento un solo array con i dati visualizzati. È progettato per creare un grafico di sequenza in cui l'indice dell'elemento di sequenza viene visualizzato sull'asse X.
La seconda versione ottiene due array come argomento. Questi array contengono i valori visualizzati rispettivamente sugli assi X e Y. La terza versione permette di impostare un valore costante per l'asse Y. Può essere usato per costruire una linea orizzontale. I restanti argomenti di queste funzioni sono simili:
- tipo stringa – tipo di grafico visualizzato. Può avere valori "line","spline" e "scatter";
- nome stringa – nome assegnato al grafico;
- int w=0 – larghezza della linea. Argomento facoltativo. Se il valore è 0, viene utilizzato il valore di larghezza predefinito di 2;
- string col="" – imposta il colore della linea e il suo valore di opacità. Argomento facoltativo.
Il metodo LDraw() deve essere invocato per ultimo. Questo metodo completa l'output del codice JavaScript e dei dati nel file di testo creato in \MQL5\Files\ per impostazione predefinita. Quindi il file viene spostato nella directory contenente i file della libreria grafica e il file HTML.
Il metodo LDraw() può possedere un singolo argomento opzionale. Se il valore dell'argomento non è impostato o è impostato su uno, verrà richiamato un browser predefinito e il grafico verrà visualizzato dopo aver spostato il file di dati in una directory appropriata. Se l'argomento ha un altro valore, anche il file di dati sarà completamente formato, ma non verrà richiamato automaticamente un browser web.
Altri metodi di classe CLinDraw disponibili consentono di impostare le intestazioni dei grafici e le etichette degli assi. Non considereremo in dettaglio i problemi relativi all'applicazione della libreria highcharts e della classe CLinDraw in questo articolo. Informazioni complete sulla libreria grafica highcharts possono essere trovate in [19], mentre esempi della sua applicazione per la creazione di grafici e diagrammi possono essere trovati in [9], [20].
L'uso di librerie esterne deve essere consentito nel terminale per il normale funzionamento della classe CLinDraw.
8. Esempio di stima della densità e disposizione dei file
Alla fine abbiamo tre classi: CKDensity, CSJPlugin e CLinDraw.
Di seguito è riportato il codice sorgente dell'esempio che mostra come possono essere utilizzate le classi.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
I dati per i quali verrà eseguita la valutazione della funzione di densità di probabilità vengono preparati all'inizio dello script KDE_Example.mq5. Per ottenere ciò, i valori "aperti" del simbolo e del punto correnti vengono copiati nell'array X[]. I rendimenti logaritmici vengono quindi calcolati sulla loro base.
Il passo successivo è la creazione di una copia della classe CKDensity. Invocare il suo metodo PluginMode() consente di utilizzare il metodo SJPI per la valutazione dell'intervallo h. La stima della densità viene quindi eseguita per la sequenza creata nell'array X[]. Il processo di valutazione è completo in questa fase. Tutti i passaggi successivi riguardano la visualizzazione della stima della densità ottenuta.
Le stime ottenute devono essere confrontate con qualsiasi nota legge di distribuzione. Per fare ciò, i valori corrispondenti alla legge di distribuzione di Laplace sono formati nell'array Z[]. I dati di input normalizzati e ordinati vengono quindi archiviati nell'array Sc[]. Se la lunghezza della sequenza di input supera i 400 elementi, non tutti i suoi valori verranno inclusi in Sc[]. Alcuni di essi verranno saltati. Pertanto, la dimensione dell'array Sc[] non conterrà mai più di 400 elementi.
Una volta preparati tutti i dati necessari per la visualizzazione, viene creata una copia della classe CLinDraw. Successivamente, vengono specificate le intestazioni e vengono aggiunti i grafici necessari utilizzando il metodo AddGraph().
Il primo è il grafico della legge sulla distribuzione di Laplace pensato per essere un modello. Segue il grafico della stima della densità ottenuta utilizzando i dati di input. Il grafico in basso che mostra il gruppo di dati di origine viene aggiunto per ultimo. Dopo aver definito tutti gli elementi necessari per la visualizzazione, viene invocato il metodo LDraw().
Di conseguenza, otteniamo il grafico mostrato in figura 7.
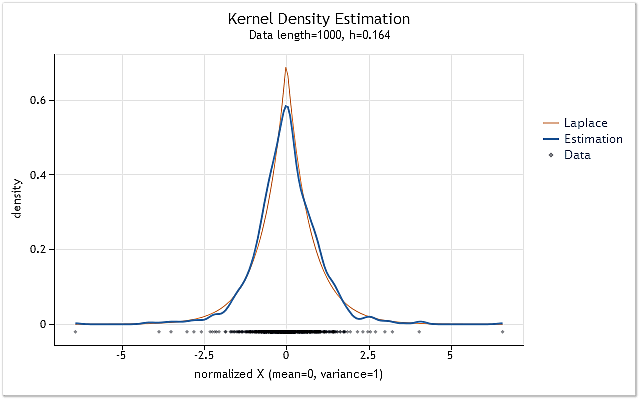
Fig.7. Stima della densità per i rendimenti logaritmici (USDJPY, giornaliero)
La stima mostrata nella figura 7 è stata eseguita per 1000 valori di rendimenti logaritmici per USDJPY, Giornaliero. Come si vede, la stima è molto simile alla curva corrispondente alla distribuzione di Laplace.
Tutti i file necessari per la stima e la visualizzazione della densità si trovano nell'archivio KDEFiles.zip di seguito. L'archivio comprende i seguenti file:
- DensityEstimation\ChartTools\CLinDraw.mqh – classe per l'interazione con highcharts.js;
- DensityEstimation\ChartTools\highcharts.js - Highcharts JS v2.2.0 library (2012-02-16);
- DensityEstimation\ChartTools\jquery.js – libreria jQuery v1.7.1;
- DensityEstimation\ChartTools\LinDraw.htm – Pagina HTML destinata alla visualizzazione;
- DensityEstimation\CKDensity.mqh – classe che implementa la stima della densità;
- DensityEstimation\CSJPlugin.mqh – classe che implementa il metodo SJPI della stima del valore del range ottimale;
- DensityEstimation\KDE_Example.mq5 – esempio di stima della densità per ritorni logaritmici.
Dopo aver decompresso l'archivio, la directory DensityEstimation\ con tutto il suo contenuto deve essere collocata nella directory Scripts (o Indicators) del terminale. Successivamente è possibile compilare e lanciare immediatamente KDE_Example.mq5. La directory DensityEstimation può essere rinominata, se necessario. Ciò non influirà sul funzionamento del programma.
Va ricordato ancora che l'uso di librerie esterne deve essere consentito nel terminale per il normale funzionamento della classe CLinDraw.
La directory DensityEstimation\ include la sottodirectory ChartTools\ contenente tutti i componenti necessari per visualizzare i risultati della stima. I file di visualizzazione si trovano in una sottodirectory separata, in modo che il contenuto della directory DensityEstimation\ possa essere facilmente visto. Il nome della sottodirectory ChartTools\ è specificato direttamente nei codici sorgente. Pertanto non dovrebbe essere rinominato, altrimenti sarà necessario apportare modifiche ai codici sorgente.
È già stato detto che il file di testo viene creato durante la visualizzazione. Questo file contiene i dati necessari per creare grafici. Questo file è originariamente creato in una speciale directory Files del terminale. Ma poi viene spostato nella directory ChartTools menzionata. Pertanto, non rimarranno tracce della nostra attività di esempio di test in Files\ o in qualsiasi altra directory del terminale. Quindi puoi semplicemente eliminare la directory DensityEstimation con tutto il suo contenuto per rimuovere completamente i file installati di questo articolo.
Conclusione
Le espressioni matematiche che spiegano l'essenza di alcuni metodi particolari sono state incluse nell’ articolo. Ciò è stato fatto deliberatamente nel tentativo di semplificarne la lettura. Se necessario, tutti i calcoli matematici possono essere trovati in numerose pubblicazioni. I collegamenti ad alcuni di essi sono forniti di seguito.
I codici sorgente forniti nell'articolo non sono stati sottoposti a test seri. Pertanto, devono essere considerati solo come esempi, non come applicazioni completamente funzionali.
Fonti
- Histogram.
- Kernel density estimation.
- Kernel smoother.
- Expectation–maximization algorithm.
- А.V. Batov, V.Y. Korolyov, А.Y. Korchagin. EM-Algorithm Having a Large Number of Components as a Means of Constructing Non-Parametric Density Estimations (in Russian).
- Hardle W. Applied Nonparametric Regression.
- Kernel (statistics).
- Charts and diagrams in HTML.
- Simon J. Sheather. (2004). Density Estimation.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). A Review and Comparison of Bandwidth Selection Methods for Kernel Regression.
- Clive R. Loader. (1999). Bandwidth Selection: Classical or Plug-In?.
- S. J. Sheather, M. C. Jones. (1991). A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation.
- Newton's method.
- Data binning.
- Changjiang Yang, Ramani Duraiswami and Larry Davis. (2004). Efficient Kernel Machines Using the Improved Fast Gauss Transform.
- Fast optimal bandwidth estimation for univariate KDE.
- R.J. Karunamuni and T. Alberts. (2005). A Locally Adaptive Transformation Method of Boundary Correction in Kernel Density Estimation.
- Highcharts JS.
- Analysis of the Main Characteristics of Time Series.
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/396
Ottieni 200 USD per il tuo articolo per il trading algoritmico!
Fondamenti di Statistica
Applicazione del metodo delle auto-coordinate all'analisi strutturale di distribuzioni statistiche non estensive
Chi è chi nella MQL5.community?
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso