Estimación de la densidad del kernel de la función de densidad de probabilidad desconocida
12 505
0
Introducción
La mejora del rendimiento de MQL5 y el crecimiento sostenido de la productividad de los ordenadores permiten a los usuarios de la plataforma MetaTrader 5 aplicar métodos matemáticos muy sofisticados y avanzados para el análisis del mercado. Estos métodos pueden pertenecer a diferentes áreas de la economía, econometría o estadística, pero en cualquier caso tendremos que tratar el concepto de función de densidad de probabilidad al usarlos.
Se han desarrollado muchos métodos de análisis basándose en la suposición de la normalidad en la distribución de los datos o la normalidad de los errores en el modelo utilizado. Además, a menudo es necesario conocer la distribución de distintos componentes del modelo utilizado para estimar los resultados del análisis. En ambos casos tenemos que crear una "herramienta" (una universal, en el caso ideal) que permita estimar la función de densidad de probabilidad desconocida.
En este artículo se pretende crear una clase mediante un algoritmo más o menos universal para la estimación de la función de densidad de probabilidad desconocida. La idea original era no utilizar medios externos durante la estimación, es decir, que todo fuese realizado mediante MQL5. Pero finalmente, dicha idea original fue modificada hasta cierto punto. Está claro que la tarea de estimar visualmente la función de densidad de probabilidad consta de dos partes independientes.
Estas dos partes son el cálculo de la propia estimación y su visualización, es decir, la representación como gráfico o diagrama. Por supuesto, los cálculos fueron realizados mediante MQL5, mientras que la visualización se implementó creando una página HTML y mostrándola en el navegador. Se utilizó esa solución para obtener gráficos en forma vectorial.
Pero como la parte de cálculo y la representación de resultados se ejecutan por separado, un lector puede, por supuesto, visualizarlos por medio de cualquier otro método disponible. Además, esperamos que en Meta Trader 5 se encuentren disponibles varias librerías, incluyendo las gráficas (esta tarea ya está siendo realizada por lo que sabemos hasta ahora). No será difícil modificar la parte a visualizar en la solución propuesta en caso de que Meta Trader 5 proporcione los medios avanzados para construir gráficos y diagramas.
Deber recordarse previamente que la creación de un algoritmo verdaderamente universal para la estimación de la función de densidad de probabilidad de series se ha mostrado como un objetivo inalcanzable. Aunque la solución propuesta no es muy especializada, tampoco puede considerarse una solución universal. El problema es que el criterio de optimización resulta bastante distinto durante la estimación de la densidad, por ejemplo, para las distribuciones con forma de campana, como las normales y exponenciales.
Por tanto, siempre es posible elegir la solución más adecuada para cada caso específico, si hay alguna información preliminar en relación a la distribución estimada. Aunque, no obstante, vamos a asumir que no sabemos nada sobre la naturaleza de la densidad estimada. Este enfoque afectará a la calidad de las estimaciones pero esperemos que de resultados y nos dé la posibilidad de estimar densidades muy distintas.
Como a menudo tenemos que trabajar con series no estacionarias durante el análisis de los datos del mercado, nos interesa más la estimación de densidades de series cortas y medias. Este es un momento crítico que determina la selección del método de estimación utilizado.
Los histogramas y las curvas p-spline pueden ser utilizadas con éxito para series realmente largas que contengan más de un millón de valores. Sin embargo, aparecerán algunos problemas al intentar construir los histogramas de series con 10-20 valores. Por tanto, nos centraremos principalmente en aquellas series que tengan un número de valores a partir de 10 a 10.000 aproximadamente.
1. Métodos de estimación de la función de densidad de probabilidad
Hoy en día se conocen una gran cantidad de métodos, más o menos populares, para la estimación de la función de densidad de probabilidad. Se pueden encontrar fácilmente en internet, por ejemplo, usando términos clave como "estimación de densidad de probabilidad", "densidad de probabilidad", "estimación de densidad", etc. Pero, por desgracia, no hemos podido elegir el mejor de ellos. Todos ellos poseen ciertas ventajas e inconvenientes.
Los histogramas se utilizan tradicionalmente para la estimación de la densidad [1]. El uso de histogramas (incluso los sencillos) permite obtener estimaciones de densidad de probabilidad de gran calidad, pero solo en el caso de series largas. Tal y como se mencionó anteriormente, no es posible dividir una serie corta en un gran número de grupos y un histograma formado por 2-3 barras no puede ilustrar la ley de distribución de densidad de probabilidad de dicha serie. Por tanto, tuvimos que abandonar el uso de histogramas.
Otro método de estimación bastante conocido es la estimación de densidad de kernel [2]. La idea del uso del ajuste de kernel se representa claramente en [3]. Por tanto, hemos elegido dicho método a pesar de todos sus inconvenientes. Más adelante trataremos brevemente algunos aspectos relativos a la implementación de este método.
Es preciso mencionar también un método de estimación de la densidad muy interesante que utiliza el algoritmo de "maximización de la esperanza" [4]. Este algoritmo permite dividir una serie en componentes separados con una distribución normal, por ejemplo. Es posible conseguir una estimación de la densidad sumando las curvas de distribución obtenidas después de determinar los parámetros de los componentes por separado. Este método es mencionado en [5]. Este método, al igual que muchos otros, no se ha implementado ni probado durante la elaboración de este artículo. Un buen número de métodos de estimación de la densidad, descritos en diferentes fuentes, evitan tener que examinarlos en la práctica.
Vamos a ver el método de estimación de densidad de kernel elegido para la implementación.
2. Estimación de la densidad del kernel de la función de densidad de probabilidad
La estimación de la densidad del kernel de la función de densidad de probabilidad está basada en el método de estimación del kernel. Los principios de dicho método pueden encontrarse, por ejemplo, en [6] y [7].
La idea básica del ajuste del kernel es simple. Los usuarios de Meta Trader 5 están familiarizados con el indicador media móvil (MA). Este indicador puede describirse como una ventana que se desliza a lo largo de una serie con sus valores ponderados ajustándose en su interior. La ventana puede ser rectangular, exponencial o tener alguna otra forma. Podemos ver fácilmente la misma ventana deslizante durante el ajuste del kernel (por ejemplo en [3]). Pero en este caso, es asimétrica.
Los ejemplos de ventanas utilizados con más frecuencia en el ajuste del kernel se encuentran en [8]. En caso de que se utilice una regresión de orden cero en el ajuste del kernel, los valores ponderados de la serie que se encuentran en la ventana (kernel) simplemente se ajustan, como en la media móvil. Podemos ver el mismo tipo de aplicación de la función ventana al trabajar con el filtrado. Aunque ahora se presenta el mismo procedimiento de forma ligeramente distinta. Se utilizan las características amplitud-frecuencia y fase-frecuencia, mientras que al kernel (ventana) se le denomina característica de impulso de filtro.
Estos ejemplos demuestran que un mismo aspecto puede representarse de diferentes formas. Eso contribuye al sistema matemático, por supuesto. Pero también puede provocar cierta confusión al discutir los aspectos de este tipo.
Aunque la estimación de la densidad del kernel utiliza los mismos principios, como el mencionado ajuste del kernel, su algoritmo es algo diferente.
Vamos a ver la expresión que define la estimación de la densidad en un punto.
donde:
- x - serie de longitud n;
- K - kernel simétrico;
- h - rango, parámetro de ajuste.
Solo se usará el kernel gausiano para las estimaciones de la densidad:
A partir de la expresión anterior, la densidad en un punto X se calcula como la suma de los valores del kernel para las cantidades definidas por las diferencias entre los valores del punto X y la serie. Además, los puntos X utilizados para el cálculo de la densidad pueden no coincidir con los valores de la propia serie.
Estos son algunos pasos básicos en la implementación del algoritmo de estimación de la densidad del kernel.
- Evaluación del valor medio y de la desviación estándar de la serie de entrada.
- Normalizar la serie de entrada. Deducir la media obtenida previamente de cada valor y dividir por la desviación estándar. Después de esta normalización, la serie original tendrá una media cero y una desviación estándar igual a uno. Dicha normalización no es necesaria para calcular la densidad, pero permite unificar los gráficos resultantes, ya que para cualquier serie en la escala X habrá valores expresados en unidades de la desviación estándar.
- Hallar valores altos y bajos en la serie normalizada.
- Crear dos matrices cuyos tamaños correspondan al número deseado de puntos representados en el gráfico obtenido. Por ejemplo, si debe construirse el gráfico usando 200 puntos, el tamaño de las matrices debe ser de 200 valores cada una, aproximadamente.
- Reservar una de las matrices creadas para almacenar el resultado. El segundo se utiliza para formar los valores de los puntos, para los que se ha realizado la estimación de la densidad. Para hacer esto debemos crear 200 valores (en este caso) igualmente espaciados entre los valores altos y bajos previamente preparados y guardarlos en la matriz que hemos preparado.
- Utilizando la expresión mostrada anteriormente podemos realizar la estimación de la densidad en 200 puntos de prueba (en nuestro caso) en la matriz que hemos preparado en el paso 4.
La implementación de este algoritmo se muestra a continuación.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": ¡Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": ¡Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
El método NTpoints() permite establecer el número requerido de puntos de prueba igualmente espaciados para los que se realizará la estimación de la densidad. Este método debe llamarse antes de la llamada al método Density(). El enlace a la matriz que contiene los datos de entrada y el valor del rango (parámetro de ajuste) se pasan al método Density() como sus parámetros cuando se llama a dicho método.
El método Density() devuelve cero si se completa con éxito y los valores y resultados de la estimación se ubican en las matrices T[] e Y[] de esa clase, respectivamente.
Los tamaños de las matrices se establecen al acceder a NTpoints, siendo igual a 200 valores por defecto.
El siguiente script de ejemplo muestra el uso de la clase CDens presentada.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
Las matrices para almacenar la serie de entrada y los resultados de la estimación de los puntos de prueba se preparan en este ejemplo. Luego, se rellena la matriz X[] con valores aleatorios a modo de ejemplo. La copia de la clase CDens se crea después de que se han preparado todos los datos.
Luego, se establecen todos los puntos de prueba necesarios (npoint=300 en nuestro caso) mediante la invocación del método NTpoints(). Si no es necesario cambiar el número por defecto de puntos, puede excluirse la invocación del método NTpoints().
Los valores calculados se copian en las matrices predefinidas después de la invocación del método Density(). Luego, se borra la copia de CDens previamente creada. Este ejemplo solo muestra la interacción con la clase CDens. No se realizan acciones adicionales con los resultados obtenidos (matrices T[] e Y[]).
Si se van a usar estos resultados para crear un gráfico se puede realizar fácilmente poniendo los valores de la matriz T[] en la escala del gráfico X, mientras que los valores correspondientes de la matriz Y[] deben ponerse en la escala Y.
3. Selección óptima del rango
La Fig. 1 muestra los gráficos de la estimación de la densidad para la serie con una ley de distribución normal y varios valores de rango h.
Las estimaciones se realizaron usando la clase CDens descrita anteriormente. Los gráficos se han construido en forma de páginas HTML. El método de construcción de dichos gráficos será presentado al final del artículo. La creación de gráficos y diagramas en formato HTML se encuentra disponible en [9].
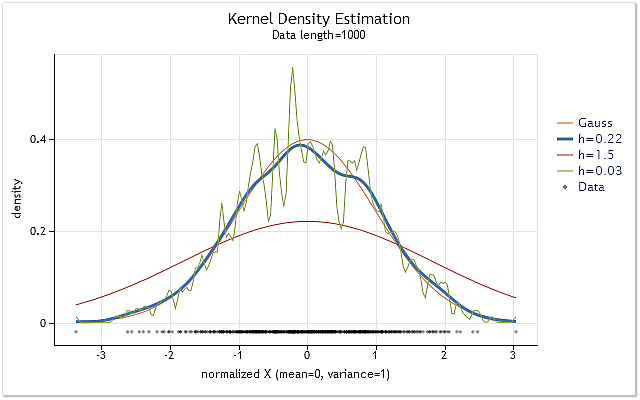
Fig. 1. Estimación de la densidad para varios valores de rango h
La Fig. 1 también muestra la curva de densidad de distribución normal verdadera (distribución gausiana) junto con las tres estimaciones de densidad. Puede verse fácilmente que el resultado de la estimación más adecuado se ha obtenido con h=0,22 en dicho caso. En los dos otros casos podemos observar claros "sobreajustes" y "subajustes".
La Fig. 1 muestra claramente la importancia de la elección de un rango h adecuado al usar la estimación de la densidad del kernel. Si el valor h se ha elegido incorrectamente, la estimación cambiará considerablemente con relación a la densidad verdadera o será muy dispersa.
Hay muchos trabajos dedicados a la elección del rango h óptimo. A menudo se utiliza la regla general simple y bien probada de Silverman para la selección de h (ver [10]).
En este caso, A es el valor más bajo de los valores de la desviación estándar de la serie y el rango del intercuartil dividido por 1,34.
Teniendo en cuenta que la serie de entrada tiene una desviación estándar igual a uno en la clase CDens anteriormente citada, es muy fácil implementar esta regla utilizando el siguiente fragmento de código:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Esa estimación le viene bien a las series con una función de densidad de probabilidad cercana a la norma por su forma.
En muchos casos, la consideración del rango del intercuantil permite ajustar los valores de h al lado inferior cuando la forma de la densidad evaluada se desvía de la normal. Esto hace que este método de evaluación sea la suficientemente versátil. Por tanto, esta regla general merece ser usada como estimación del valor h básica inicial. Además, no requiere cálculos extensos.
Además de las estimaciones del valor del rango h asintóticas y empíricas, hay también diferentes métodos basados en el análisis de la propia serie de entrada. En este caso, el valor de ha óptimo se determina considerando la estimación preliminar de la densidad desconocida. La comparación de la eficiencia de algunos de estos métodos se encuentra disponible en [11] y [12].
De acuerdo con los resultados publicados en diferentes fuentes, el método de extensión de Sheather-Jones (SJPI) es uno de los métodos de estimación del rango más efectivos. Vamos a optar por este método. Para no sobrecargar el artículo con expresiones matemáticas extensas, solo se incluirán algunas características del método. Si es necesario, pueden consultarse los fundamentos matemáticos de este método en [13].
Usamos un kernel gausiano que dispone de soporte ilimitado (es decir, se especifica cuando su parámetro cambia de menos a más infinito). Como puede deducirse de la expresión anterior, necesitaremos O(M*N) operaciones al estimar la densidad en M puntos de la serie con longitud N usando el método de cálculo directo y el kernel con soporte ilimitado. En caso de que necesitemos realizar estimaciones en cada punto de la secuencia, este valor se incrementa hasta O(N*N) operaciones y el tiempo empleado en el cálculo se incrementará proporcionalmente con el cuadrado de la longitud de la serie.
Esta demanda tan alta de recursos de cómputo constituye una de las mayores desventajas del método de ajuste del kernel. Si pasamos al método SJPI. veremos que no es mejor en términos de la cantidad requerida de cálculos. En pocas palabras, debemos primero calcular la suma de dos derivadas de la densidad a lo largo de toda la longitud de la serie de entrada dos veces al implementar el método SJPI.
Luego, debemos calcular repetidamente la estimación usando los resultados obtenidos. El valor de la estimación debe ser igual a cero. Puede usarse el método Newton-Raphson [14] para encontrar el argumento al que esta función será igual a cero. En el caso del cálculo directo, la aplicación del método SJPI para determinar el valor del rango óptimo puede requerir cerca de diez veces más tiempo que el cálculo de las estimaciones de densidad.
Hay varios métodos que permiten acelerar los cálculos en el ajuste del kernel y la estimación de la densidad del kernel. En nuestro caso utilizamos el kernel gausiano cuyos valores pueden considerarse insignificante para valores del argumento mayores que 4. Por tanto, si el valor del argumento es mayor que 4, no es necesario calcular los valores del kernel. Por ello, podemos reducir parcialmente el número necesario de cálculos. Es difícil que veamos alguna diferencia entre el gráfico basado en dicha estimación y la versión completamente calculada.
Otra forma simple de acelerar los cálculos consiste en reducir el número de puntos para los que se realiza la estimación. Como se mencionó anteriormente, si M es menor que N, el número de operaciones necesarias se reducirá de O(N*N) a O(M*N). Si tenemos una serie larga, por ejemplo, N=100.000, solo podemos realizar estimaciones en M=200 puntos. Por tanto, podemos reducir considerablemente el tiempo de cálculo.
Además, pueden utilizarse métodos más complejos para reducir el número de cálculos necesarios, por ejemplo, las estimaciones utilizando un algoritmo rápido de la transformada de Fourier o las transformadas de ondículas. Los métodos basados en la reducción de la dimensión de la serie de entrada (por ejemplo, la "discretización de datos" [data binning] [15]) puede aplicarse con éxito para series realmente largas.
La transformada rápida gausiana [16] puede utilizarse también para acelerar los cálculos además de los métodos mencionados anteriormente en caso de utilizarse el kernel gausiano. Utilizaremos el algoritmo basado en la transformación gausiana [17] para implementar el método SJPI de estimación del valor del rango. Los enlaces mencionados anteriormente conducen a los materiales que contienen tanto la descripción del método como los códigos de programa que implementan los algoritmos propuestos.
4. Sheather-Jones plug-in (SJPI)
Como ocurre en el caso de las expresiones matemáticas que determinan la esencia del método SJPI, no copiaremos los fundamentos matemáticos de la implementación del algoritmo que se encuentra disponible en el apartado [17] de este artículo. Si es necesario, podemos examinar las publicaciones que aparecen en dicho apartado [17].
Se ha creado la clase CSJPlugin en base a los materiales disponibles en [17]. Esta clase está pensada para el cálculo del valor óptimo del rango h e incluye un único método público, double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
Los siguientes argumentos se pasan a este método cuando es invocado:
- double &px[] – el enlace a la matriz que contiene el enlace original;
- double h es el valor inicial del rango h respecto al que se realiza la búsqueda al resolver las ecuaciones utilizando el algoritmo Newton-Raphson. Es aconsejable que este valor se encuentre tan cerca del valor buscado como sea posible. Esto puede reducir considerablemente el tiempo empleado en resolver las ecuaciones y la probabilidad de los casos en que el algoritmo Newton-Raphson puede perder su fiabilidad. El valor encontrado usando la regla general de Silverman puede utilizarse como valor h inicial.
- double stdev=1 – valor de la desviación estándar de la serie original. El valor por defecto es uno. En este caso, no tenemos que cambiar el valor por defecto ya que este método se utiliza conjuntamente con la clase CDens antes mencionada, donde la serie original ya se ha normalizado y posee una desviación estándar igual a uno.
El método SelectH() devuelve el valor óptimo del rango h obtenido en caso de finalización con éxito. El valor inicial h se devuelve como parámetro en caso de fallo. El código fuente de la clase CSJPlugin se encuentra en el archivo CSJPlugin.mqh
Es necesario aclarar algunas características de esta implementación.
La serie de origen se transforma en el intervalo [0,1] al instante, mientras que el valor inicial del rango h se normaliza proporcionalmente con respecto a la escala de transformación de la serie original. Se aplica la normalización inversa al valor h óptimo obtenido durante los cálculos.
eps=1e-4 es la precisión del cálculo de las estimaciones de la densidad y sus derivadas y P_UL=500, el número máximo permitido de iteraciones internas del algoritmo se establecen en el constructor de la clase CSJPlugin. Para más información véase el apartado [17].
IMAX=20 es el número máximo permitido de iteraciones del método Newton-Raphson y PREC=1e-4, la precisión en la resolución de la ecuación que utiliza este método establecido en el método SelectH().
El uso tradicional del método Newton-Raphson requirió el cálculo de la función objetivo y su derivada en el mismo punto en cada iteración del valor. En este caso, el cálculo de la derivada ha sido reemplazado por su estimación calculada añadiendo un pequeño incremento al valor de su argumento.
La Figura 2 muestra un ejemplo del uso de dos métodos diferentes de estimación del valor óptimo del rango h.
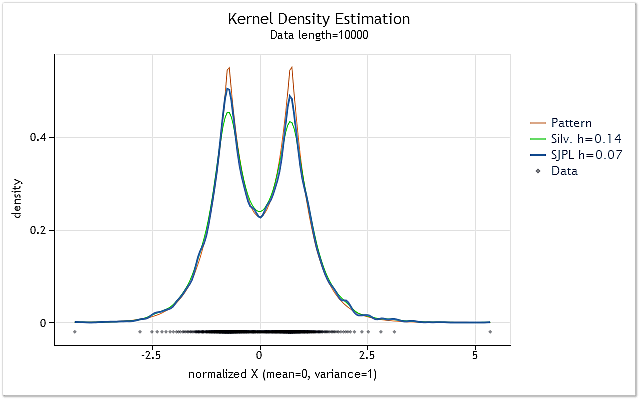
Fig. 2. Comparación de las estimaciones del valor del rango h óptimo
La Figura 2 muestra dos estimaciones de la serie aleatoria, la densidad verdadera mostrada como gráfico en color rojo (Pattern).
Se han realizado estimaciones para la serie con una longitud de 10.000 elementos. El valor del rango h de 0,14 se ha obtenido para esta serie utilizando la regla general de Silverman, mientras que dicho valor ha sido 0,07 al utilizar el método SJPI.
Al examinar los resultados de la estimación de la densidad del kernel para estos dos valores h de la Figura 2, podemos comprobar fácilmente que la aplicación del método SJPI ha ayudado a obtener una estimación de h más atractiva si la comparamos con la regla de Silverman. Como podemos ver, las zonas superiores más puntiagudas tienen una forma mucho más correcta mientras que casi no hay aumento de la dispersión en los huecos inclinados cuando h=0,07.
Como era de esperar, la utilización del método SJPI permite en muchos casos obtener estimaciones del rango h mucho más precisas. A pesar de que se han utilizado algoritmos mucho más rápidos de [17] para la creación de la clase CSJPlugin, la estimación del valor h utilizando este método puede llevar aún demasiado tiempo para series largas.
Otra desventaja de este método es su tendencia a sobreestimar el valor h para series cortas formadas solo por 10-30 valores. Las estimaciones realizadas a través del método SJPI puede exceder las estimaciones de h realizadas por la regla general de Silverman.
Se utilizarán las siguientes reglas en la implementación posterior para compensar de alguna forma estos inconvenientes:
- Se utilizará por defecto la estimación de Silverman para el rango de h, mientras que será posible activar el método SJPI mediante un comando separado;
- Al usar el método SJPI se utilizará siempre como valor final de h el valor más bajo de los obtenidos a través de los dos métodos mencionados.
5. Efecto frontera
El deseo de utilizar un valor del rango tan óptimo como sea posible en la estimación de la densidad ha llevado a la creación de la engorrosa clase antes citada CSJPlugin. Pero hay algo más además de especificar el tamaño del rango y una gran utilización de recursos del método de ajuste del kernel. El conocido efecto frontera.
La cuestión es simple. Se mostrará utilizando el kernel definido en el intervalo [-1,1]. A dicho kernel se le conoce como kernel con soporte finito. Se iguala a cero fuera del rango especificado (no existe).
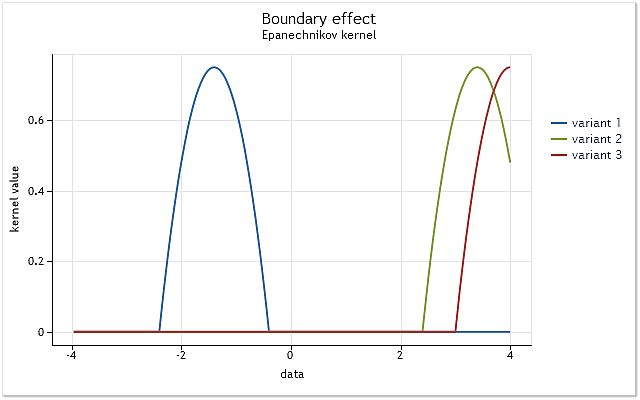
Fig. 3. Reducción del kernel en la frontera del rango
Como se muestra en la Figura 3, el núcleo cubre completamente los datos originales situados en el intervalo [-1,1] con respecto a su centro. A medida que el kernel se desplaza (p. ej. hacia la derecha) surge la situación cuando los datos no son suficientes para utilizar completamente la función del kernel seleccionada.
El kernel ya cubre menos datos en el primer caso. El peor caso ocurre cuando el centro del kernel se sitúa en la frontera de la serie de datos. La cantidad de datos cubiertos por el kernel se reduce al 50% en ese caso. Dicha reducción en el número de datos utilizados para la estimación de la densidad lleva a un cambio importante en las estimaciones e incrementa su dispersión en los puntos cercanos a los límites del rango.
La Figura 3 muestra un ejemplo de la reducción para un kernel con soporte finito (kernel de Epanechnikov) en la frontera del rango. Debe señalarse que el kernel gausiano definido en el rango infinito (soporte ilimitado) se ha usado durante la implementación del método de estimación de la densidad del kernel. En teoría, siempre debe producirse un corte en dicho kernel. Pero teniendo en cuenta que el valor de este kernel casi es igual a cero para grandes argumentos, los efectos de frontera aparecen de la misma forma que en los kernel con soporte finito.
Esta característica no puede afectar a los resultados de la estimación de la densidad en los casos presentados en las Figuras 1 y 2, ya que en ambos casos la estimación se ha realizado para las distribuciones cuya función de densidad de probabilidad ha disminuido en los límites has casi el valor cero.
Vamos a crear la serie formada por enteros positivos X=1,2,3,4,5,6,…n para mostrar la influencia del corte del kernel en los límites del rango. Dicha serie sigue aún una ley de distribución de densidad de probabilidad. Significa que la estimación de la densidad de esta serie debe ser una línea recta horizontal situada en un nivel distinto a cero.
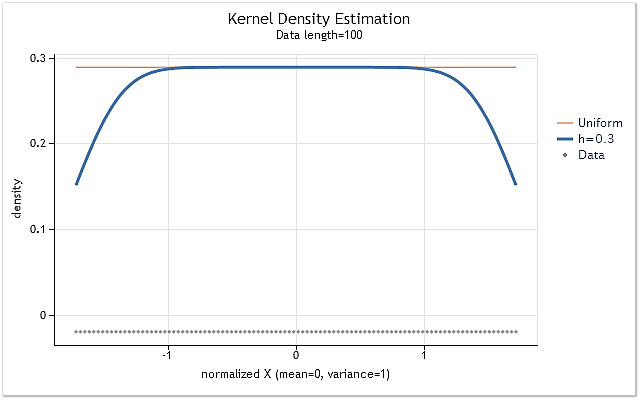
Fig. 4. Estimación de la densidad para la serie que sigue la ley de distribución
Como era de esperar, la figura 4 muestra claramente que hay un cambio considerable en las estimaciones de la densidad en los límites del rango. Se utilizan varios métodos para reducir dicho cambio en mayor o menor medida. Pueden clasificarse en términos generales en los siguientes grupos:
- Métodos de reflexión de datos;
- Métodos de transformación de datos;
- Métodos de seudodatos;
- Métodos de kernel de frontera.
La idea de utilizar los datos reflejados es que la serie se incrementa intencionadamente añadiendo los datos en una especia de imagen especular de dicha serie con relación a los límites del rango de la serie en cuestión. Después de dicho incremento se realiza la estimación de la densidad para los mismos puntos que para la serie original, pero los datos añadidos intencionadamente se utilizan también en la estimación.
Los métodos que implican la transformación de datos se entran en la transformación de la serie cercana a los límites del rango. Por ejemplo, es posible utilizar una transformación logarítmica o de otro tipo para poder deformar de alguna forma la escala de datos al acercarnos al límite del rango durante la estimación de la densidad.
Los llamados seudodatos pueden usarse para la extensión deliberada (ampliación) de la serie original. Esos son los datos calculados en base a los valores de la serie original. Dichos datos sirven para considerar su comportamiento en los límites y lo complementan de la forma más adecuada.
Hay muchas publicaciones dedicadas a los métodos de kernel de frontera. En estos métodos el kernel altera su forma de algún modo al aproximarse a la frontera. La forma del kernel cambia para compensar el cambio de las estimaciones en los límites.
En el apartado [18] pueden consultarse algunos métodos dedicados a la compensación de las distorsiones que aparecen en los límites del rango, su comparación y la evaluación de su eficiencia.
Se ha elegido el método de la reflexión de datos para su uso posterior después de algunos breves experimentos. Dicha elección se vio afectada por el hecho de que este método no implica situaciones en las que la estimación de la densidad pueda tener valores negativos. Además, este método no requiere cálculos matemáticos complejos. El número total de operaciones se incrementa todavía debido a la necesidad de realizar cada estimación de la serie cuya longitud se ha incrementado deliberadamente.
Hay dos formas de implementar ese método. En primer lugar, es posible complementar la serie original con datos necesarios e incrementar su tamaño tres veces en el proceso. A continuación, podremos realizar estimaciones en la forma mostrada en la clase CDens presentada anteriormente. En segundo lugar, es posible no tener que expandir la matriz de datos de entrada. Podemos seleccionar una vez más los datos de ella de algún modo. Se ha usado la segunda forma para la implementación.
En la clase CDens antes mencionada, se ha implementado la estimación de la densidad en la función kdens(double h). Vamos a cambiar esta función añadiendo una corrección de las distorsiones de frontera.
La función ampliada tendría la forma siguiente:
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
La función se implementa teniendo en cuenta que los datos de origen en la matriz X[] se han ordenado ya en el momento de la llamada a la función. Esto permite excluir con facilidad los dos elementos de la serie correspondientes a los valores del rango extremos de otro procesamiento. El intento de realizar operaciones matemáticas fuera de los bucles siempre que sea posible se ha llevado a cabo a la hora de implementar esta función. Como resultado, la función refleja la idea del algoritmo utilizado con menor claridad.
Se ha mencionado anteriormente que es posible reducir el número de cálculos en caso de que no calculemos el valor del kernel para los valores grandes de los argumentos. Eso es exactamente lo que se ha implementado en la anterior función. En este caso, es imposible observar algún cambio después de la creación del grafico de densidad evaluado.
Al utilizar la versión modificada de la función kdens(), la estimación de la densidad mostrada en la Figura 4 se transforma en una línea recta y los huecos en la frontera desaparecen por completo. Pero esta corrección ideal puede conseguirse solo si la distribución cerca de los límites tiene un gradiente cero, es decir, está representada por una línea horizontal.
Si la densidad de distribución estimada se eleva o desciende de forma acusada cerca de la frontera, el método de reflexión de datos seleccionado no podrá ajustar por completo el efecto frontera. Esto se muestra en las figuras siguientes.
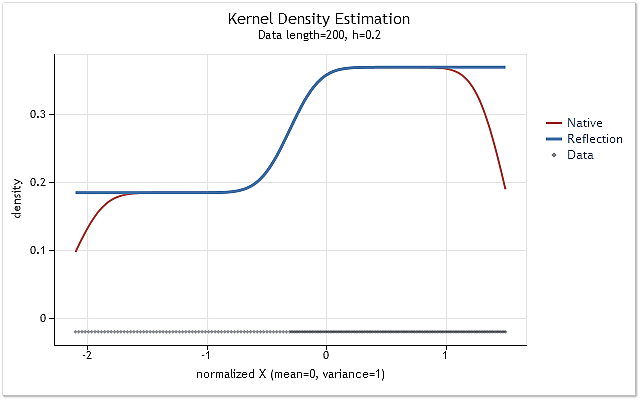
Fig. 5. La función de densidad de probabilidad cambiando paso a paso
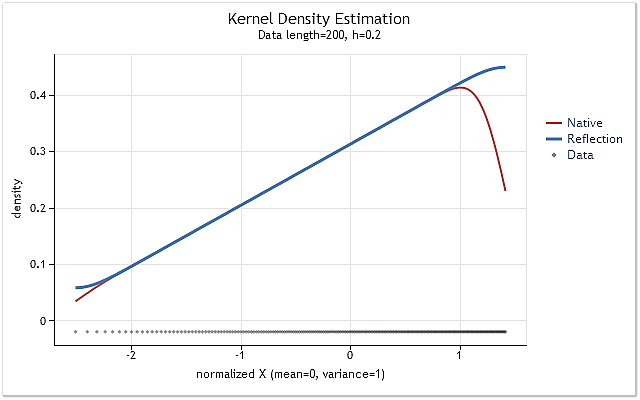
Fig. 6. La función de densidad de probabilidad aumentando linealmente
Las figuras 5 y 6 muestran la estimación de densidad obtenida usando la versión original de la función kdens() (rojo) y la estimación obtenida teniendo en cuenta los cambios aplicados que implementan los métodos de reflexión de datos (azul). El efecto frontera ha sido corregido completamente en la Figura 5, mientras que el cambio cerca de los límites no ha desaparecido por completo en la Figura 6. Si la densidad estimada aumenta o cae de forma acusada cerca de la frontera, entonces parece mostrarse algo más ajustada cerca de dicho límite.
El método de reflexión de datos seleccionado para ajustar el efecto frontera no es ni el mejor ni el peor de los métodos conocidos. Aunque este método no puede eliminar el efecto frontera en todos los casos, es lo suficientemente estable y fácil de implementar. Este método permite obtener un resultado lógico y predecible.
6. Implementación final. Clase CKDensity
Vamos a añadir la capacidad de seleccionar automáticamente el valor del rango h y la corrección del efecto frontera a la clase Cdens creada anteriormente.
A continuación se muestra el código fuente de la clase citada a la que nos referimos.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": ¡Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": ¡Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
El método Density(double &x[],double hh=-1) es de tipo básico para esa clase. El primer argumento es el enlace a la matriz x[] en la que la serie de entrada analizada debe estar contenida. La longitud de la serie de entrada no debe ser inferior a ocho elementos. El segundo argumento (opcional) se utiliza para el establecimiento forzado del valor del rango h.
Puede especificarse cualquier número positivo. El valor de h estará siempre limitado por 0,005 por abajo. Si este parámetro tiene un valor negativo, el valor del rango será seleccionado automáticamente. El método Density() devuelve cero en caso de una finalización con éxito y menos uno en caso de finalización de emergencia.
Después de invocar el método Density() y de su finalización con éxito, la matriz T[] contendrá los valores de los puntos de prueba para los que se ha realizado la estimación de la densidad, mientras que la matriz Y[] contendrá los valores de estas estimaciones. La matriz X[] contendrá la serie de entrada normalizada y ordenada. El valor promedio de esta serie es igual a cero, mientras que el valor de la desviación estándar es igual a uno.
Los valores siguientes se encuentran incluidos en las variables que son miembros de la clase:
- N – longitud de la serie de entrada;
- Np – número de puntos de prueba en los que se ha realizado la estimación de la densidad;
- Mean – valor medio de la serie de entrada;
- Var – varianza de la serie de entrada;
- StDev – desviación estándar de la serie de entrada;
- H – valor del rango (parámetro de ajuste);
- Pflag – flag de la aplicación del método SJPI para determinar el valor óptimo del rango h.
El método NTpoints(int n) se utiliza para establecer el número de puntos de prueba en los que se realiza la estimación de la densidad. La determinación del número de puntos de prueba debe realizarse antes de llamar al método básico Density(). Si no se utiliza el método NTpoints(), se establecerán 200 puntos por defecto.
El método PluginMode(int m) permite o prohíbe el uso del método SJPI para evaluar el valor del rango óptimo. Si el parámetro igual a uno se utiliza al invocar este método, el método SJPI se aplicará para especificar el rango h. Si el valor de este parámetro no es igual a uno, no se usará el método SJPI. Si no se ha invocado el método PluginMode(int m),el método SJPI será deshabilitado por defecto.
7. Crear gráficos
Al escribir este artículo se ha utilizado el método que está disponible en [9]. Dicha publicación trata sobre la aplicación de la página HTML prediseñada incluyendo la librería JavaScript de gráficos [19] y la especificación completa de todas sus invocaciones. Más adelante, un programa MQL forma un archivo de texto con los datos a mostrar y dicho archivo conecta con la página HTML antes mencionada.
En tal caso, es necesario editar la página HTML cambiando el código JavaScript implementado para hacer cualquier corrección en la estructura de gráficos mostrada. Para evitar esto, se ha desarrollado una sencilla interfaz que permite invocar los métodos JavaScript de la librería de gráficos directamente desde el programa MQL.
No ha sido necesario realizar ninguna tarea para implementar el acceso a todas las posibilidades de la librería de gráficos al crear la interfaz. Por tanto, solo se han implementado las posibilidades que permiten no cambiar el archivo HTML creado anteriormente al escribir el artículo.
El código fuente de la clase CLinDraw se muestra más abajo. Se ha utilizado esta clase para proporcionar la conexión con los métodos de la librería de gráficos. No debe considerarse este código como una implementación completa del software. Es solo un ejemplo que muestra cómo crear una interfaz con la librería JavaScript de gráficos.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": ¡Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Si queremos que esta clase funcione correctamente, necesitamos una página ya prediseñada que tenga implementadas las librerías JavaScript. También debe especificarse un tamaño y una ubicación del campo para poder construir los gráficos. Puede consultarse un ejemplo de la implementación de esta página en los archivos adjuntos a este artículo.
Cuando se invoca el método AddGraph() en un archivo de texto, se forma un código JavaScript adecuado. A continuación se incluye el archivo de texto en la página HTML previamente creada. El código mencionado se refiere a la librería de gráficos y permite la creación de un gráfico usando los datos enviados al método AddGraph() como argumento. Pueden añadirse uno o más gráficos en el campo de salida al invocar de nuevo a este método.
En la clase CLinDraw se incluyen tres versiones de la función sobrecargada AddGraph(). Una de las versiones requiere que se le transfiera como argumento solo una matriz con los datos representados. Está pensada para crear una gráfico de la serie donde el índice del elemento de esta sea mostrado en el eje X.
La segunda versión obtiene dos matrices como argumento. Estas matrices contienen los valores mostrados en los ejes X e Y, respectivamente. La tercera versión permite establecer un valor constante para el eje Y. Puede usarse para crear una línea horizontal. Los restantes argumentos de estas funciones son similares:
- string type – tipo de gráfico mostrado. Puede tener los valores "line","spline" y "scatter";
- string name – nombre asignado al gráfico;
- int w=0 – ancho de la línea. Argumento opcional. Si el valor es 0, se usará 2 como valor del ancho por defecto;
- string col="" – establece el color de la línea y el valor de su opacidad. Argumento opcional.
El método LDraw() debe invocarse en último lugar. Este método completa la salida del código JavaScript y los datos en el archivo de texto creado por defecto en \MQL5\Files\. A continuación se mueve el archivo al directorio que contiene los archivos de la librería de gráficos y el archivo HTML.
El método LDraw() puede tener un único argumento opcional. Si no se fija el valor del argumento o se hace igual a uno, se invocará a un navegador web por defecto y el gráfico se mostrará después de mover el archivo de datos al directorio correspondiente. Si el argumento tiene cualquier otro valor, el archivo de datos será también creado completamente pero no se invocará automáticamente a un navegador web.
Otros métodos de la clase CLinDraw disponibles permiten establecer los encabezados del gráfico y las etiquetas de los ejes. En este artículo, no vamos a ver en profundidad los aspectos relacionados con la aplicación de la librería de gráficos y la clase CLinDraw. En [19] puede consultarse la abundante información disponible sobre la librería de gráficos, mientras que los ejemplos de su aplicación para crear gráficos y diagramas se encuentran en [9] y [20].
Debe permitirse la utilización de librerías externas en el terminal para el funcionamiento normal de la clase CLinDraw.
8. Un ejemplo de estimación de la densidad y la distribución de los archivos
Hemos obtenido tres clases: CKDensity, CSJPlugin y CLinDraw.
A continuación se muestra el código fuente del ejemplo donde se muestra cómo pueden usarse las clases.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
Los datos para los que se realizará la evaluación de la densidad de probabilidad se preparan al inicio del script KDE_Example.mq5. Para conseguir esto, se copian a la matriz X[] los valores "abiertos" del símbolo y el periodo actuales. El resultado del logaritmo se calcula entonces en base a los mismos.
El siguiente paso es crear una copia de la clase CKDensity. La invocación del método PluginMode() permite utilizar el método SJPI para la evaluación del rango h. A continuación se realiza la estimación de la densidad para la serie creada en la matriz X[]. En este paso se completa el proceso de evaluación. Todos los pasos posteriores están relacionados con la visualización de la estimación de la densidad obtenida.
Las estimaciones obtenidas deben compararse con cualquier ley de distribución conocida. Para hacer esto, se crean los valores correspondiente a la ley de distribución de Laplace en la matriz Z[]. Posteriormente, todos los datos de entrada considerados se guardan en la matriz Sc[]. Si la longitud de la serie de entrada es superior a 400 elementos, no se incluirán todos sus valores en Sc[]. Algunos de ellos serán pasados por alto. Por ello, el tamaño de la matriz Sc[] nunca contendrá más de 400 elementos.
Una vez que se han preparado todos los datos necesarios para su representación en pantalla, se crea una copia de la clase CLinDraw. A continuación, se especifican los encabezados y los gráficos necesarios se añaden utilizando el método AddGraph().
El primero es el gráfico de la ley de distribución de Laplace, considerado una plantilla. A continuación le sigue el gráfico de la estimación de la densidad obtenido utilizando los datos de entrada. El gráfico inferior que muestra el grupo de datos de origen se añade en último lugar. Después de definir todos los elementos necesarios para realizar la representación en pantalla, se invoca el método LDraw().
Como resultado, obtenemos el gráfico mostrado en la Figura 7.
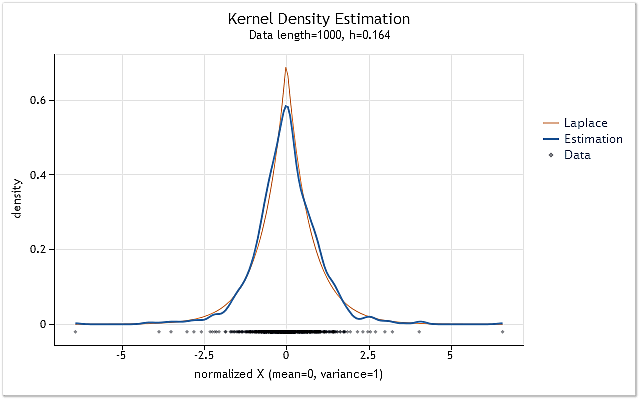
Fig. 7. Estimación de la densidad para los resultados del logaritmo (USDJPY, diario)
La estimación mostrada en la Figura 7 se ha realizado para 1.000 valores de los resultados del logaritmo para USDJPY, diario. Como podemos ver, la estimación es muy similar a la curva de la distribución de Laplace.
Todos los archivos necesarios para la estimación y visualización de la densidad se encuentran en el archivo KDEFiles.zip más abajo. El archivo incluye, a su vez, los siguientes:
- DensityEstimation\ChartTools\CLinDraw.mqh – clase para la interacción con highcharts.js;
- DensityEstimation\ChartTools\highcharts.js - librería Highcharts JS v2.2.0 (2012-02-16);
- DensityEstimation\ChartTools\jquery.js – librería jQuery v1.7.1;
- DensityEstimation\ChartTools\LinDraw.htm – página HTML para la visualización en pantalla;
- DensityEstimation\CKDensity.mqh – clase que implementa la estimación de la densidad;
- DensityEstimation\CSJPlugin.mqh – clase que implementa el método SJPI de la estimación del valor del rango óptimo;
- DensityEstimation\KDE_Example.mq5 – ejemplo de estimación de la densidad para los resultados del logaritmo.
Después de extraer el archivo, debe colocarse el directorio DensityEstimation\ con todo su contenido en el directorio de los Scripts (o Indicators) del terminal. Posteriormente es posible compilar y lanzar KDE_Example.mq5 inmediatamente. El directorio DensityEstimation puede renombrarse si es necesario. Esto no afectará al funcionamiento del programa.
Debe mencionarse de nuevo que debe permitirse el uso de librerías externas en el terminal para el funcionamiento normal de la clase CLinDraw.
El directorio DensityEstimation\ incluye el subdirectorio ChartTools\ que contiene todos los componentes necesarios para visualizar los resultados de la estimación. Los archivos de la visualización se encuentran en un subdirectorio separado, de forma que el contenido del directorio DensityEstimation\ pueda verse con facilidad. El nombre de directorio ChartTools\ se especifica directamente en los códigos fuente. Por tanto, no debe renombrarse, ya que de lo contrario será necesario realizar cambios en el código fuente.
Ya se ha mencionado que el archivo de texto se crea durante la visualización. Este archivo contiene los datos necesarios para construir gráficos. El archivo se crea originariamente en un directorio Files especial del terminal. Pero luego se mueve al mencionado directorio ChartTools. De esta forma, no quedará rastro de la actividad de nuestra prueba de ejemplo en Files\ o en cualquier otro directorio del terminal. Por tanto, puede simplemente borrar el directorio DensityEstimation con todo su contenido para eliminar por completo los archivos instalados de este artículo.
Conclusión
En este artículo se han incluido las expresiones matemáticas que explican la esencia de algunos métodos particulares. Esto ha sido realizado deliberadamente en un intento de simplificar su lectura. Si es necesario, pueden consultarse todos los cálculos matemáticos en numerosas publicaciones. Más abajo se proporcionan los enlaces a algunos de ellos.
El código fuente proporcionado en el artículo no ha sido sometido a pruebas rigurosas. Por ello, solo debe ser considerado como un ejemplo, no como funciones completamente operativas.
Bibliografía
- Histogram.
- Kernel density estimation.
- Kernel smoother.
- Expectation–maximization algorithm.
- А.V. Batov, V.Y. Korolyov, А.Y. Korchagin. EM-Algorithm Having a Large Number of Components as a Means of Constructing Non-Parametric Density Estimations (in Russian).
- Hardle W. Applied Nonparametric Regression.
- Kernel (statistics).
- Charts and diagrams in HTML.
- Simon J. Sheather. (2004). Density Estimation.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). A Review and Comparison of Bandwidth Selection Methods for Kernel Regression.
- Clive R. Loader. (1999). Bandwidth Selection: Classical or Plug-In?.
- S. J. Sheather, M. C. Jones. (1991). A Reliable Data-Based Bandwidth Selection Method for Kernel Density Estimation.
- Newton's method.
- Data binning.
- Changjiang Yang, Ramani Duraiswami and Larry Davis. (2004). Efficient Kernel Machines Using the Improved Fast Gauss Transform.
- Fast optimal bandwidth estimation for univariate KDE.
- R.J. Karunamuni and T. Alberts. (2005). A Locally Adaptive Transformation Method of Boundary Correction in Kernel Density Estimation.
- Highcharts JS.
- Analysis of the Main Characteristics of Time Series.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/396
Aplicación del método de coordenadas de Eigen al análisis estructural de distribuciones estadísticas no extensivas
La transformación Box-Cox
Introducción al método de descomposición de modo empírico
Análisis de regresión múltiple, generador y probador de estrategias en una sola aplicación
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso