Ticaret için kombinatorik ve olasılık teorisi (Bölüm IV): Bernoulli mantığı

İçindekiler

• Giriş
• Analizde doğru veri temsilinin önemi
• İki durumlu
• Çok durumlu
• Çok durumlu yazılım uygulaması
• Sonuç
• Referanslar

Giriş

Bu serinin önceki makalelerinde fraktalları piyasaları ve özellikle de fiyatlandırmayı tanımlamak için bir araç olarak tanımlamıştım. Bu model piyasayı mükemmel bir şekilde tanımlamaktadır - bu durum hesaplamalar ve simülasyonlar yoluyla teyit edilmiştir. Asıl amaç sadece en basit fiyatlandırma formlarını tanımlamak değil, aynı zamanda fiyatlandırma parametreleri setine benzer bir parametre setine sahip herhangi bir vektör serisinin ileri tanımlanmasını sağlamaktır. Genel durumda, bir ticaret işleminin, ticaret sürecinde ortaya çıkma olasılığı ve süresi ile karakterize edilen bir piyasa parçası olduğu ortaya çıkmaktadır. Hem fiyatlardan hem de işlemlerden eğriler oluşturulabilir. Fiyatlar için bu eğri fiyat geçmişidir, işlemler için ise işlem geçmişidir.

Fiyatla ilgili durum çok daha nettir, çünkü böyle bir serideki tüm üyeler açıkça birbirini takip eder. Elbette birbiriyle örtüşecek bu tür fiyat serileri oluşturmak mümkündür, ancak böyle bir analizden pratikte hiçbir fayda sağlanamayacağı için bu analiz kesinlikle yararsız olacaktır. Geriye dönük testler veya işlem geçmişi durumu daha karmaşıktır. Bu süreçleri incelerken, kârlı ve istikrarlı ticarete giden çok daha kolay ve doğru bir yol olduğu sonucuna vardım - işlem geçmişinin veya geriye dönük testlerin analizi yoluyla. Bu yaklaşımlardan birini açıklayan nihai bir makale olacaktır, ancak şimdilik bunun için çok erken.

Analizde doğru veri temsilinin önemi

İşlem geçmişini ve geriye dönük testleri matematik dilinde tanımlama olanaklarının analizini ele alacak olursak, öncelikle bu tür bir analizin amacını ve olası sonuçlarını anlamamız gerekir. Böyle bir analizin herhangi bir katma değeri var mı? Aslında hemen net bir cevap vermek mümkün değil. Ancak yavaş yavaş basit ve işe yarar çözümlere yol açabilecek bir cevap var. Ancak, önce daha fazla ayrıntıya girmeliyiz. Önceki makalelerdeki deneyimleri göz önünde bulundurarak aşağıdaki sorularla ilgilendim:

1. Herhangi bir stratejiyi ticaretin fraktal tanımına indirgemek mümkün mü?
2. Eğer mümkünse, nerede faydalı olur?
3. Eğer bu her zaman mümkün değilse, indirgenebilirliğin koşulları nelerdir?
4. İndirgenebilirlik koşulları karşılanıyorsa, indirgeme algoritmasını geliştir
5. Stratejiyi tanımlamak için diğer seçenekleri değerlendir ve genelleme yap

Tüm bu soruların cevapları şu şekildedir. Bazı stratejileri fraktal tanıma indirgemek mümkündür. Bu algoritmayı geliştirdim ve daha sonra açıklayacağım. Evrensel bir fraktal olduğu için başka amaçlar için de uygundur. Şimdi düşünelim ve şu soruyu yanıtlamaya çalışalım: Rastgele sayılar ve olasılık teorisi dilinde işlem geçmişi nedir? Cevap basittir: belirli bir zaman döneminde ortaya çıkması belirli bir olasılığa ve zaman kullanım faktörüne sahip olan bir izole varlık veya vektör kümesidir. Bu tür her bir varlığın temel özelliği, ortaya çıkma olasılığıdır. Zaman kullanım faktörü, mevcut zamanın ne kadarının ticaret için kullanıldığını belirlemeye yardımcı olan yardımcı bir değerdir. Aşağıdaki şekil bu fikrin anlaşılmasına yardımcı olabilir:

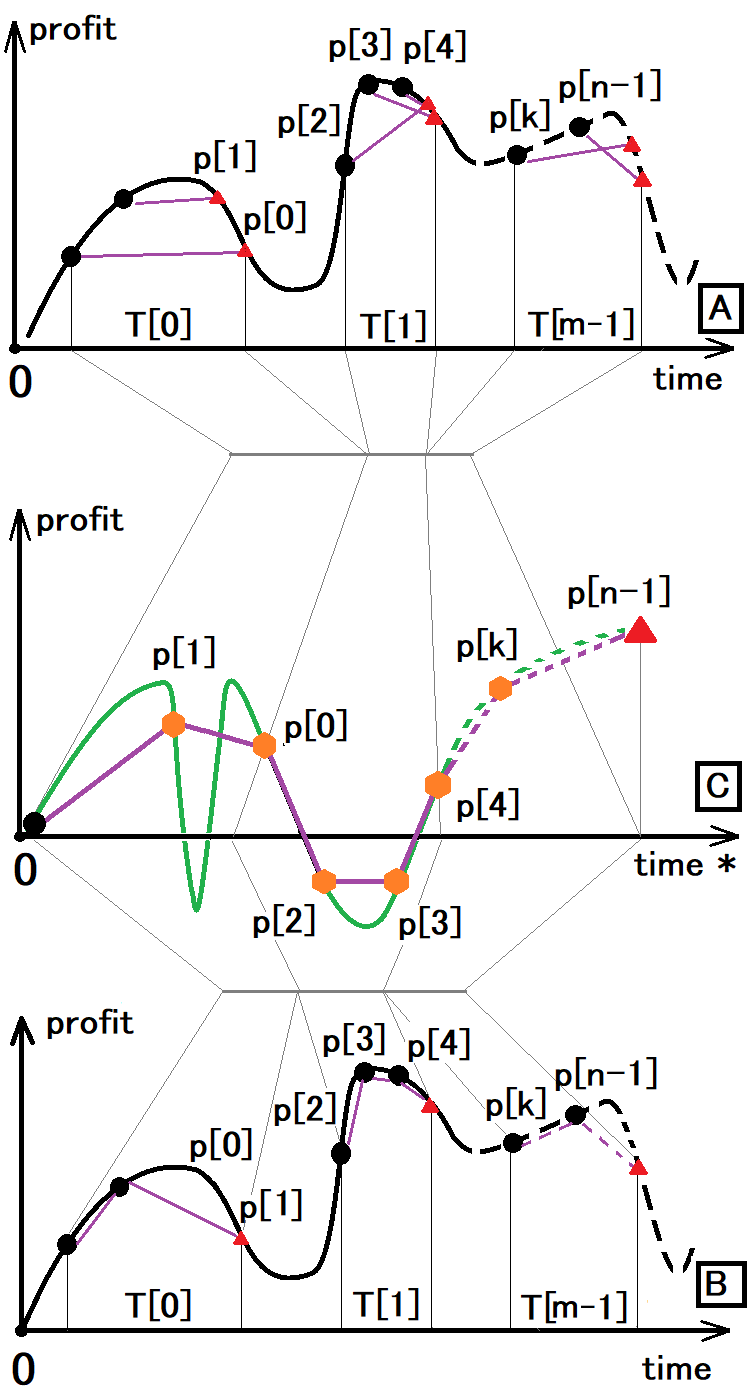
Şekilde aşağıdaki ifadeler kullanılmıştır:

1. Siyah nokta - işlemin başlangıcı
2. Kırmızı üçgen - işlemin sonu
3. Turuncu altıgen - hem bir önceki işlemin sonu hem de bir sonrakinin başlangıcı
4. T[i] - ilgili işlem penceresinin süresi
5. P[i] - ilgili işlemin kâr veya zararı
6. n - işlem sayısı
7. m - işlem penceresi sayısı

Şekilde, A ve B seçeneklerinin C seçeneğine indirgenebileceğini göstermek için üç grafik gösterilmektedir. Şimdi bu seçeneklerin neler olduğunu görelim:

1. A seçeneği, tüm olası tekniklerin, püf noktalarının, para yönetiminin vb. kullanıldığı keyfi ticareti nasıl gördüğümüzdür.
2. B seçeneği de aynısıdır ancak aynı anda yalnızca bir emrin açık olabileceği göz önünde bulundurulur.
3. C Seçeneği, Sinyaller hizmetinde veya geriye dönük testte ticareti nasıl gördüğümüzdür.

Burada C seçeneği en bilgilendirici olanıdır ve çoğu durumda bu ticaret temsiline güveniriz. Ayrıca, kesinlikle herhangi bir strateji bu türe indirgenebilir çünkü varlık çizgisi herhangi bir geriye dönük test veya ticaret sinyalinin ana özelliğidir. Bu çizgi, içinde bulunulan andaki gerçek kâr veya zararı yansıtır.

Keyfi bir stratejinin varlık çizgisinin analizi, çizgi değişmeden kalırsa, işlem açılış ve kapanış noktalarının kesinlikle keyfi konumlarda bulunabileceğini gösterecektir. Bu, bir ticaret stratejisinin çok sayıda farklı yolla temsil edilebileceği ve varlık çizgileri eşdeğer olacağından tüm bu yolların birbirine eşdeğer olacağı anlamına gelir. Bu nedenle, tüm eşdeğer seçenekleri aramanın bir anlamı yoktur. Onları bulmanın amacı nedir?

B tipi bir strateji kolayca C tipine dönüştürülebilir, çünkü yalnızca zaman aralıklarını oluştukları sırayla birbirine yapıştırmamız gerekir. Aslında sınayıcı ve Sinyaller hizmetinin yaptığı da tam olarak budur. A tipini C'ye dönüştürmeye çalışırsanız durum farklıdır. Bu dönüşümü uygulamak için önce A'yı B tipine indirgememiz gerekir ve ardından sonuç C tipine indirgenebilir. Artık strateji sınayıcının ve Sinyaller hizmetinin nasıl çalıştığını biliyorsunuz.

Bu dönüşüm kendi başına ticaret için herhangi bir pratik değer taşımamaktadır. Bununla birlikte, daha derin şeyleri anlamaya yardımcı olabilir. Örneğin, aşağıdaki strateji türleri olduğu sonucuna varabiliriz:

1. İki durum tarafından tanımlanan
2. Çok durum tarafından tanımlanan
3. Sonsuz sayıda durum tarafından tanımlanan

Bu makalede size ilk iki tür strateji için açıklama örnekleri göstereceğim. Üçüncü tür daha karmaşıktır ve ayrı bir makale gerektirir. Zamanı geldiğinde bu fikre geri döneceğim. Çünkü üçüncü tür stratejileri ele almadan önce ilk ikisini anlamak gerekir. Bu iki tür, üçüncü genel strateji türüne geçmeden önce zihnimizi hazırlayacaktır.

İki durumlu

Önceki makalelerde açıklanan fraktallar aslında iki durumlu bir modeli temsil etmektedir. Burada durumlar yukarı ve aşağı yönlü hareketlerdir. Modeli fiyatlandırma yerine bakiye çizgisine uygularsak, bu model tam olarak aynı şekilde çalışacaktır. Model Bernoulli şemasına dayanmaktadır. Bernoulli şeması iki durumlu en basit fraktalı tanımlar:

• P[k] = C(n, k)*Pow(p, k)*Pow(q, n-k) - Bernoulli formülü (P[k] belirli bir kombinasyonun olasılığıdır)
• p - tek bir deneyin sonucu olarak "1" durumunun olasılığı
• q - tek bir deneyin sonucu olarak "2" durumunun olasılığı

Bu formüller, "n" adımdan sonra bir bakiye eğrisine veya "k" ilk duruma ve "n-k" ikinci duruma sahip olacak başka bir eğriye sahip olma olasılığımızı hesaplayabilir. Bunların kâr olması gerekmez. Bu durumlar, teklik gördüğümüz herhangi bir parametre vektörünü sembolize edebilir. Belirli bir kombinasyonun tüm olasılıklarının toplamı bir tam grup oluşturmalıdır, bu da tüm bu olasılıkların toplamının bire eşit olması gerektiği anlamına gelir. Bu, "n" adımda bu tür kombinasyonlardan birinin mutlaka ortaya çıkması gerektiği gerçeğini sembolize eder:

• Summ(0...k…n)[P[k]] = 1

Bu durumda, bunları ya fiyatlandırmayı ya da geriye dönük testleri ve sinyalleri tanımlamak için kullanmakla ilgileniyoruz. Stratejimizin eşit uzaklıkta durma seviyeleri ile kapatılan işlemlerden oluştuğunu hayal edelim. Aynı zamanda, gelecekte beklenen fiyat hareketini hesaplamanın imkansız olduğunu biliyoruz. Bu olasılıkların dağılımı şu şekilde olacaktır:

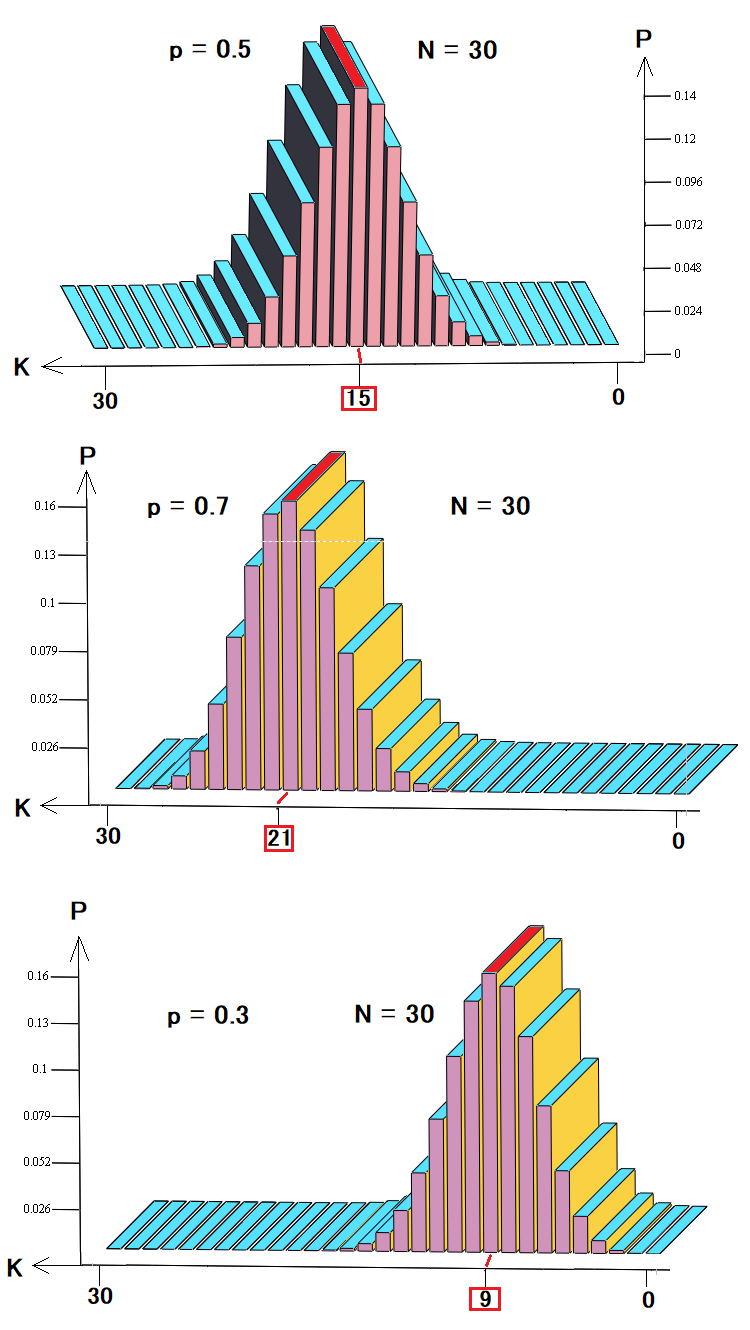
Bu üç çizim şunları göstermektedir:

1. Rastgele yürüyüş veya ticarette olasılık dağılımı
2. Kârlı ticaret veya yükseliş trendi için olasılık dağılımı
3. Zararlı ticaret veya düşüş trendi için olasılık dağılımı

Diyagramlardan görülebileceği gibi, bir adım yukarı olasılığına bağlı olarak, belirli kombinasyonların olasılıkları değişir ve en olası durum, diğer tüm olasılıklar gibi sola veya sağa kayar. Bu geriye dönük test veya fiyatlandırma temsili, analiz için en basit ve tercih edilen modeldir. Böyle bir model fiyatlandırmayı açıklamak için oldukça yeterlidir; ancak ticareti açıklamak için yeterli değildir. Aslında bakiye eğrisi, süre ve kâr/zarar açısından farklılık gösteren çeşitli ticaret işlemleri içerebilir. Hangi ticaret ölçütlerinin daha önemli olduğuna bağlı olarak, sadece iki değil, istediğimiz sayıda durum belirleyebiliriz.

Çok durumlu

Şimdi, şu örneği ele alalım. Hâlâ bir işlemin kâr veya zarar değeriyle ilgilendiğimizi varsayalım. Şimdi, kâr veya zarar durumunun kesin olarak tanımlanmış üç değer alabileceğini biliyoruz ve her bir değerin olasılıklarını biliyoruz. Eğer durum buysa, o zaman üç durumlu bir sistemimiz olduğunu söyleyebiliriz. İki durumlu bir sistem gibi tüm olası olay gelişmelerini tanımlamak mümkün mü? Aslında, bu mümkün. Bernoulli şemasını herhangi bir sayıda duruma sahip bir sistemle çalışabilecek şekilde biraz geliştireceğim.

Bernoulli mantığına göre, durum sayaçlarını tanımlamamız gerekir:

• i[0] - bağımsız deneyler zincirindeki ilk durumla elde edilen sonuç sayısı
• i[1] - bağımsız deneyler zincirinde ikinci durumla elde edilen sonuç sayısı
• . . .
• i[N] - N durumlu sonuç sayısı
• N - sistem durum sayısı
• s - durum sayısı

Belirli bir durumun gerçekleşme sayısını tek tek belirlersek, bir sonraki durum için mevcut sayı şu olacaktır:

• s[i] = N-Summ(0…k…i-1)[s[k]]

Basitleştirilebilir. Bir önceki durumun sonuç sayısını seçtiysek, bir sonraki durum için sonuç sayısı, bir önceki durum için seçilen durum sayısı ile tamamen aynı kalır. Tıpkı Bernoulli şemasında olduğu gibi, tutarsız ve aynı olasılığa sahip olasılık zincirleri vardır. Tüm durum sayısı aynı olan zincirlerin sayısı aşağıdaki gibi hesaplanır:

• A[h](N, i[0], i[1], …, i[n]) = C(N, i[0])*C(N-i[0], i[1])*…* C(N-Summ(0…k…n-1)[i[k] ], i[n])
• C - kombinasyonlar
• h - benzersiz bir adımlar kümesi

Açıkçası, bu tür kümelerin olasılıkları Bernoulli şemasında olduğu gibi hesaplanabilir. Bir kümenin olasılığını sayılarıyla çarpalım:

• P[k] = A[h](N, i[0], i[1], …, i[n])*Pow(p[0], i[0])*Pow(p[1], i[1])*…*Pow(1-Summ(0…j…N-1)[p[j]], i[1])
• p[j] - belirli bir durumun olasılığı

Daha anlaşılır olması için, önceki örnekte iki durum için olduğu gibi üç boyutlu grafikler oluşturdum. Yine 30 adımımız var, ancak burada iki yerine üç durum kullanıyoruz:

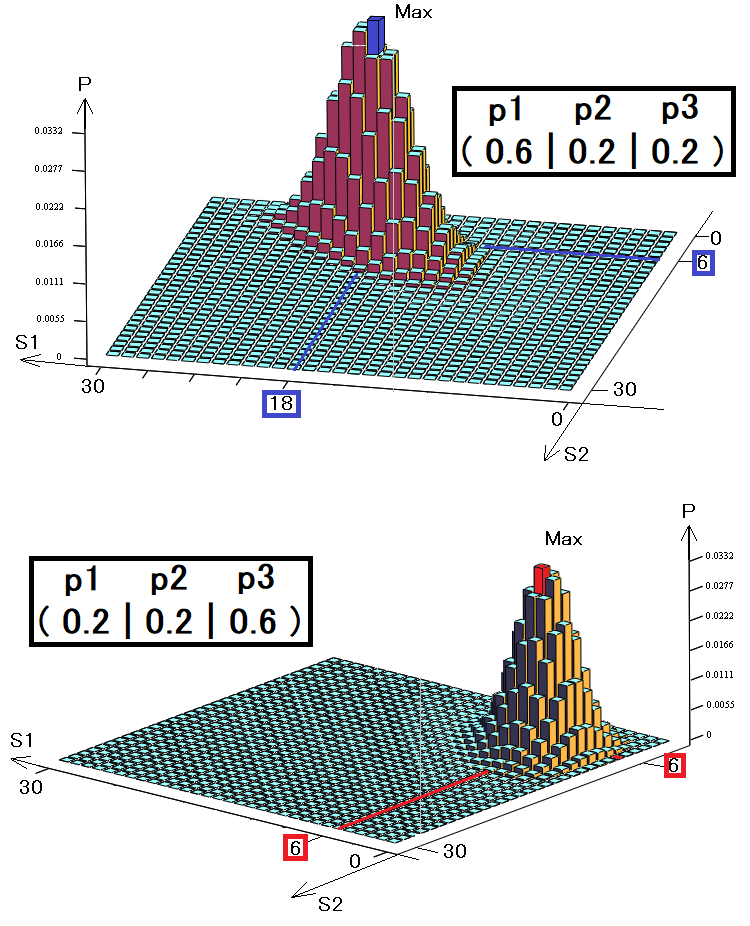
Böyle bir diyagramın hacmi tam olarak bire eşit olacaktır, çünkü her çubuk uyumsuz bir olayı sembolize eder ve tüm bu uyumsuz olaylar sadece bir tam grup oluşturur. Diyagramlar, farklı olasılık vektörlerine sahip iki farklı stratejiyi göstermektedir. Bu olasılıklar, üç durumdan birinin gerçekleşme şansını sembolize eder.

• S1 - ilk durum oluşumlarının sayısı
• S2 - ikinci durum oluşumlarının sayısı
• S3 = 30-S1-S2 - üçüncü durum oluşumlarının sayısı

Eğer sistemimiz dördüncü bir duruma sahip olsaydı, o zaman sadece dört boyutlu bir şekilde sunulabilirdi. Beş durum için beş boyutlu bir diyagrama ihtiyacımız olacaktır ve bu böyle devam edecektir. İnsan gözü için sadece 3 boyut mevcuttur, bu nedenle daha karmaşık sistemler grafiksel olarak temsil edilemez. Bununla birlikte, çok boyutlu fonksiyonlar da tıpkı diğerleri gibi işlevseldir.

Çok durumlu yazılım uygulaması

İki durumlu haller tek boyutlu bir dizi ile temsil edilebilir. Peki ya çok durum? Çok boyutlu bir dizi düşünebiliriz. Ancak, bildiğim kadarıyla, tüm programlama dilleri en fazla iki boyutlu diziler kullanır. Belki bazıları üç veya daha fazla boyutlu dizi oluşturma imkanı sunar, ancak bu uygun bir seçenek değildir. Koleksiyon veya veri grubu (tuple) kullanmak daha iyi bir seçenektir:

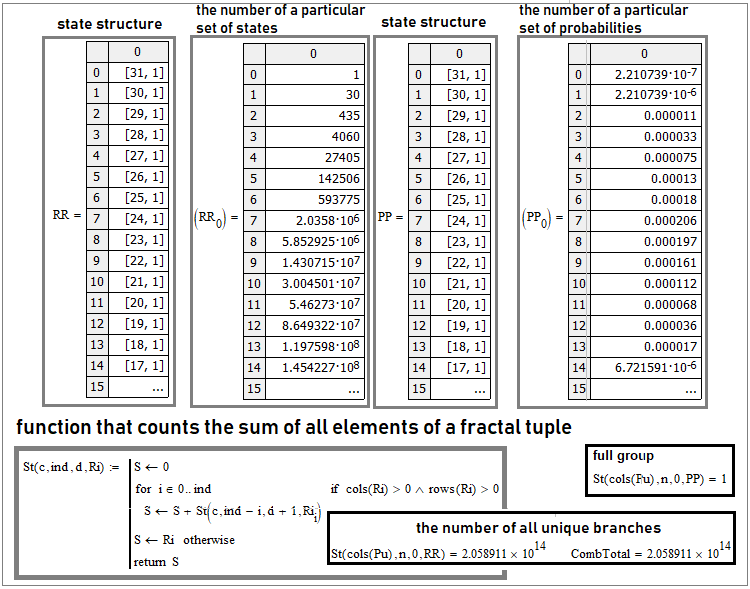
"30" adımlı durum. Birinci ve üçüncü sütunlar veri grubunun iç yapısını yansıtır. Bu sadece dizi içerisinde bir dizidir. Örneğin "[31,1]" yazıldığı yerde, bu matris elemanının aynı zamanda "31" satırlı ve bir sütunlu bir matris olduğu anlamına gelir. Bernoulli formülü ve Bernoulli şemasının tamamı, bu daha genel şemanın sadece özel bir durumudur. Eğer iki durum gerekiyorsa, veri grupları tek boyutlu dizilere dönüşecek ve bu durumda Bernoulli formülünde anahtar rolü oynayan basit kombinasyonlar elde edeceğiz.

Bu dizilerin içerisinde ne olduğuna bakarsak, "2" ve "4" sütunlarını elde ederiz. İkinci sütun, belirli benzersiz durum kümelerinin eşdeğer dallarının sayısıdır ve dördüncüsü, olasılıkları eşit olduğu için bu dalların toplam olasılığıdır.

Bu tür veri gruplarının hesaplanmasını doğrulamak için gerçekten açık bir kriter, tam olaylar grubunu ve tüm benzersiz dalların toplam sayısını kontrol etmektir. Bunu yapmak için, iç yapıları ne kadar karmaşık olursa olsun, karmaşık veri gruplarının tüm öğelerini toplayacak genel bir fonksiyon oluşturabiliriz. Yukarıdaki ekran görüntüsünde bir örnek gösterilmektedir. Böyle bir fonksiyon tekrarlı olmalıdır; kendisini içeriden çağırmalıdır - bu durumda herhangi bir sayıda durum ve adım sayısı için evrensel bir fonksiyon olacaktır. Benzersiz dal sayısı için gerçek değer aşağıdaki gibi hesaplanır:

• Pow(N, n)

Başka bir deyişle, sistem durum sayısı adım sayısının kuvvetine yükseltilmelidir - bu şekilde durumlarımızdan oluşan benzersiz zincirlerin tüm olası kombinasyonlarını elde edeceğiz. Şekilde bu sayı "CombTotal" değişkeni olarak gösterilmektedir. Elde edilen toplam bu değişkenle karşılaştırılacaktır.

Veri gruplarını saymak için aynı tekrarlayan yapıya sahip benzer fonksiyonlar kullanmalıyız:

Gördüğünüz gibi, birbirlerine çok benziyorlar. Sadece birkaç farklılık var. Her seviyede, ayrıca sonucu kalan serbest adımlardaki kombinasyon sayısıyla çarpmalıyız. Olasılıklar hesaplanırken, sonuç ayrıca o anda incelenmekte olan durumun olasılığı ile çarpılmalıdır. Ayrıca, zincirin halihazırda birikmiş olasılığı ile çarpmayı unutmamalıyız. Boş hücre kalmayana kadar tüm durumları teker teker biriktiririz (hücreler adım sayısıdır).

Bildiğimiz verilerden durumları çıkarmanın bir örneğini de düşünebiliriz. Örneğin, her emir için şu bilgilerin depolandığı işlem istatistiklerimiz olsun: ömür, işlem hacmi, zarar veya kâr vb. Örneklem sonlu olduğu için durum sayısı da sonludur. Örneğin, örneklemde kaç tane kâr seçeneği olduğunu belirleyebiliriz. Her bir benzersiz kâr değeri benzersiz bir durum olarak kabul edilebilir. Örneklem boyunca bu tür tüm kârların gerçekleşme sayısını sayarız, bunu tüm işlemlerin toplam sayısına böleriz ve belirli bir durumun olasılığını elde ederiz. Bunu tüm durumlar için tekrarlarız. Daha sonra tüm bu olasılıkları toplarsak, biri elde ederiz. Eğer öyleyse, her şey doğru yapılmıştır. Benzer bir şekilde, işlemleri emir ömrüne göre sınıflandırabiliriz. Başka bir deyişle, bir durum bir olayın herhangi bir benzersiz özelliği olabilir. Bu durumda, bir işlem bir olay olarak kabul edilirken, işlem parametreleri belirli bir olayın özellikleridir. Bizim durumumuzda, durum örnekleri aşağıdaki gibi olabilir:

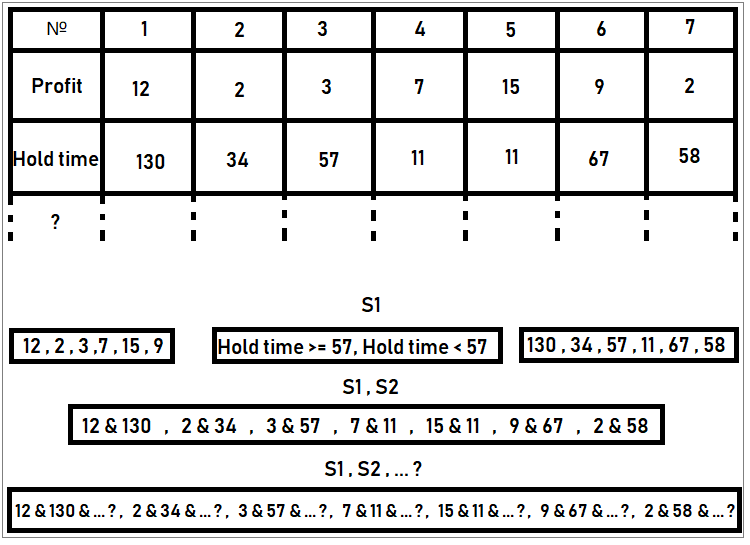
Şekilde durum kümelerinin oluşturulmasına bir örnek gösterilmektedir. Kurallara göre, durumlar bir tam olaylar grubu oluşturmalıdır, yani orada ortak durumlar olmamalıdır. Bu olayların olasılığı, tablodaki belirli durumlara sahip emirlerin sayısının tüm emirlerin sayısına (bizim durumumuzda 7'dir) bölünmesiyle hesaplanabilir. Bu, emirler örneğiydi; ancak diğer durumlarla da çalışabiliriz.

Sonuç

Bu makalede, veri örneklemlerinin nasıl değerlendirileceğini, verileri sınıflandırarak ve olasılıkları hesaplanabilen durum kümeleri halinde birleştirerek bu tür örneklemlerden yenilerinin nasıl yapılacağını göstermeye çalıştım. Bu verilerle ne yapacağınız size kalmış. Bence en iyi kullanım birden fazla örneklem oluşturmak ve bunları değerlendirmektir - buna örneklem kümeleme de denir. Örneklem kümeleme, mevcut sistemlerin ticaret performansını artırmak için iyi bir filtre görevi görebilir. Görünüşte kârlı olmayan bir stratejiden kâr elde etmek için de kullanılabilir - sadece verileri kümeleyin ve istenen kârlı örneklemleri bulun. Ve en önemlisi, bu tür mekanizmalar ölçeklenebilir ticaret sistemlerinde veri işleme aşamaları olarak kullanılabilir. Bu mekanizmaları daha sonra, kendi kendini uyarlayan bir ticaret sistemi kurmaya geçtiğimizde pratikte uygulayacağız. Şimdilik, bu sadece başka bir tuğla.

Referanslar

• Ticaret için kombinatorik ve olasılık teorisi (Bölüm I): Temel bilgiler
  
• Ticaret için kombinatorik ve olasılık teorisi (Bölüm II): Evrensel fraktal
  
• Ticaret için kombinatorik ve olasılık teorisi (Bölüm III): İlk matematiksel model