使用凯利准则与蒙特卡洛模拟的投资组合风险模型

引言

几十年来，交易员们一直使用凯利准则公式来确定投资或赌注的最优资本配置比例，其目标是在最大化长期增长的同时，最小化破产风险。然而，对于个人交易者而言，盲目地依据单次回测的结果来遵循凯利准则往往是危险的，因为在实盘交易中，交易优势会随着时间的推移而减弱，并且过往业绩并不能保证未来的结果。在本文中，我将提出一种在 MetaTrader 5 平台中，为一个或多个智能交易系统进行风险分配的现实方法，该方法将融合来自 Python 的蒙特卡洛模拟结果。

杠杆空间交易模型理论

杠杆空间交易模型 (LSTM) 是一种主要应用于金融市场和资产管理领域的理论框架。它将“杠杆”（即利用借入资金来放大潜在回报）的概念，与一种更具动态性和空间导向的市场行为建模方法相结合。 

LSTM 模型利用凯利准则来计算单一策略在每笔交易中应承担的投资组合风险百分比，其公式为：

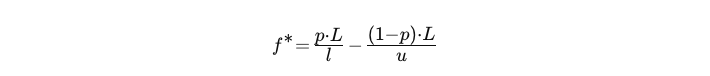
• L：杠杆因子
• p：成功概率
• u：杠杆化盈利比率
• l：杠杆化亏损比率

给定一个回测结果，我们可以通过以下公式获得各变量的值。

假设您正在使用 2:1 的杠杆进行交易。并设定以下条件：

• 交易成功的概率 = 0.6（即 60% 的胜率）。
• 预期盈利 = 0.1（无杠杆时为 10% 的收益，因此 2:1 杠杆下为 20% 的收益）。
• 预期亏损 = 0.05（无杠杆时为 5% 的亏损，因此 2:1 杠杆下为 10% 的亏损）。

将这些值代入凯利公式：

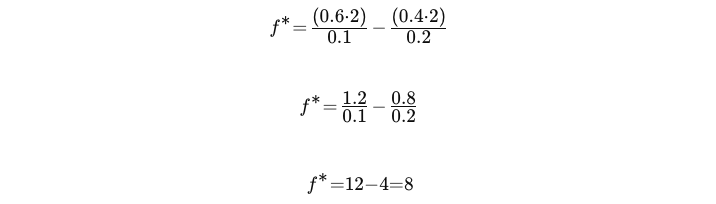
因此，在这笔交易中，您应承担风险的最优资本比例为您总资本的 8%。

当您将这个公式应用到您自己的某个智能交易系统上后，我相信您在看到自己每笔交易本应承担的风险额度时，会不可避免地感到一丝不安。的确，这个公式假设您未来的表现会和您的回测结果一样好，而这显然是不现实的。因此，在业界，人们通常会采用“分数凯利”来管理风险，也就是说，他们会将凯利公式的计算结果除以某个整数，以降低风险，并为未来可能出现的逆境留出缓冲空间。

现在，我们必须回答一个问题：应该选择多大的分数，才能让交易者在感到风险可控的同时，又能最大化每笔交易的预期回报？

根据拉尔夫·文斯所著的《杠杆空间交易模型》一书，通过随机优化过程可以得出结论：无论维度如何，回报期望函数都是凸函数。这意味着最优的预期回报存在唯一解，并且当f*值偏离该最优解时，预期回报会持续下降。

这暗示着，由于实盘交易并不像回测那样理想，我们预期那个能最大化我们回报的真实f*值，会小于通过凯利公式计算出的f*值。因此，我们要做的就是将分配的风险额度，提高到我们所能容忍的最高水平，同时确保它仍然小于凯利风险。

通常，交易者的风险容忍度是通过他们所能承受的最大回撤来衡量的。在本文的后续部分，我将假定一个合理的风险容忍水平，即 30% 的最大回撤。

在 MQL5 中应用杠杆风险

要在 MQL5 中应用杠杆风险，首先我们需将风险百分比声明为一个全局变量。在本例中，我们每笔交易承担 2% 的风险。

input double risk = 2.0;

接下来，我们将编写一个函数，根据以当前价格单位计算的止损点数来计算交易手数。例如，如果止损价格设为 0，那么止损点数将直接对应于当前价格，交易的结果将完全反映标的资产的价格变动。

//+------------------------------------------------------------------+
//| Calculate the corresponding lot size given the risk              |
//+------------------------------------------------------------------+
double calclots(double slpoints)
{
   double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;

   double ticksize = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_SIZE);
   double tickvalue = SymbolInfoDouble(_Symbol, SYMBOL_TRADE_TICK_VALUE);
   double lotstep = SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_STEP);

   double moneyperlotstep = slpoints / ticksize * tickvalue * lotstep;
   double lots = MathFloor(riskAmount / moneyperlotstep) * lotstep;
   lots = MathMin(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MAX));
   lots = MathMax(lots, SymbolInfoDouble(_Symbol, SYMBOL_VOLUME_MIN));
   return lots;
}

上述代码首先通过将账户余额乘以风险百分比，来确定具体的风险金额。

然后，它会获取交易品种的最小价格变动单位、最小价格变动价值以及最小手数变动单位，并基于止损距离，计算出每变动一个最小手数单位所对应的货币价值。

交易手数通过将风险金额除以每最小手数单位的货币价值，并将结果四舍五入到最接近的最小手数单位来确定。

最后，在返回结果之前，代码会确保计算出的交易手数处于该交易品种所允许的最小和最大交易量限制之内。

需要注意的是，并非所有的交易策略都采用固定的止损和止盈。但在杠杆交易领域，我们假设我们使用的是固定的止损点，因为在凯利准则中，我们必须在下单前就明确自己愿意承担多大的风险。

我们在执行任何交易操作前，都会调用这个函数。一个示例如下。

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy(double price) {
       double sl = price- slp*_Point;
       sl = NormalizeDouble(sl, _Digits);
       double lots = lotpoint;
       if (risk > 0) lots = calclots(slp*_Point);
       trade.BuyStop(lots,price,_Symbol,sl,0,ORDER_TIME_DAY,1);
       buypos = trade.ResultOrder();
       }

通常对于一个稳定盈利的EA来说，其回测结果应该看起来类似如下的指数函数曲线：

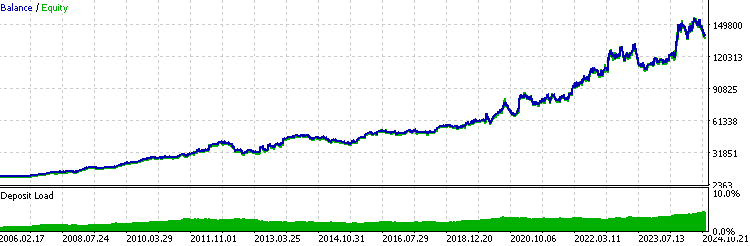
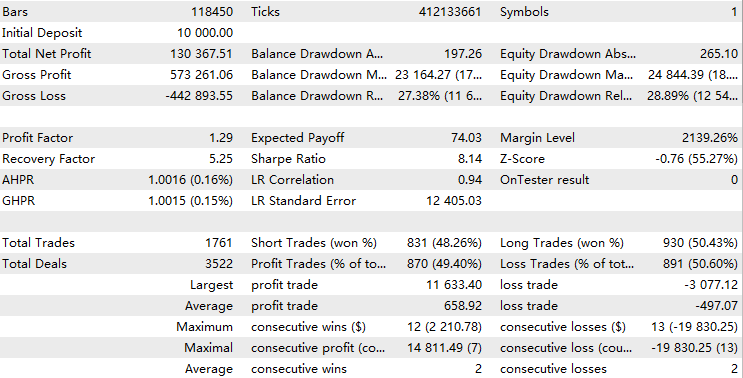
在使用此杠杆交易模型分析回测统计数据时，有几点需要特别注意：

• 如果你的智能交易系统是持续盈利的，那么近期的结果对整体回测性能的影响，会大于早期的结果。从本质上讲，你是在为近期表现的重要性赋予更高的权重。
• 线性回归相关性在此处不再适用，因为其图表会是一条指数曲线。
• 夏普比率也会变得不切实际，因为它假设风险与回报之间是线性关系。而杠杆会同时放大潜在的回报和风险，从而导致风险调整后的绩效指标出现偏斜。

如果你仍然希望评估上述指标，只需固定交易手数，然后重新进行一次测试即可。

最大回撤的蒙特卡洛模拟

我们将资金曲线视为账户余额的一系列百分比变动，而最大回撤则可以看作是该系列中累计百分比最小的那个片段。单次回测仅代表了该系列的一种可能排列，因此其统计稳健性是有限的。本节的目标是理解我们可能遇到的最大回撤范围，并选择其 95% 分位数作为我们最大容忍度的参考基准。

蒙特卡洛模拟可以通过以下几种方式来模拟可能的资金曲线：

1. 回报率随机抽样：基于历史表现或假定的统计分布（例如正态分布）生成随机回报率，然后通过将这些回报率随时间复利化，来模拟潜在的资金曲线。

2. 自助抽样法（Bootstrapping）：通过对历史回报率进行有放回的重抽样，来创建多条模拟的资金路径，这些路径反映了过去表现中观察到的波动性。

3. 洗牌法（Shuffling）：随机打乱历史回报率的顺序，并使用这个重新排列的序列来生成不同的资金路径，从而允许产生多样化的情景。

4. 风险/回报调整：根据指定的风险标准，修改输入参数（例如波动率或回撤限制），以生成在不同市场条件下更符合现实的资金曲线。

在本文中，我们将重点介绍“洗牌法”。

首先，我们像这样右键单击，从回测中获取交易记录报告。

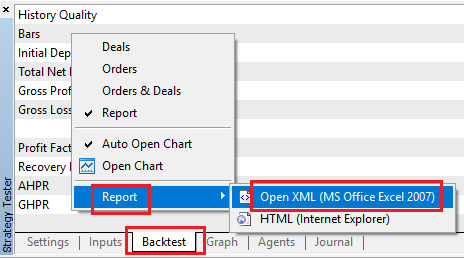
然后，我们打开 Python，并通过以下代码，从报告中提取出包含账户余额和每笔交易盈亏的有效数据行。

import pandas as pd
# Replace 'your_file.xlsx' with the path to your file
input_file = 'DBG-XAU.xlsx'
# Load the Excel file and skip the first {skiprows} rows
data = pd.read_excel(input_file, skiprows=10757)

# Select the 'profit' column (assumed to be 'Unnamed: 10') and filter rows as per your instructions
profit_data = data[['Profit','Balance']][1:-1] 
profit_data = profit_data[profit_data.index % 2 == 0]  # Filter for rows with odd indices
profit_data = profit_data.reset_index(drop=True)  # Reset index
# Convert to float, then apply the condition to set values to 1 if > 0, otherwise to 0
profit_data = profit_data.apply(pd.to_numeric, errors='coerce').fillna(0)  # Convert to float, replacing NaN with 0
# Save the processed data to a new CSV file with index
output_csv_path = 'processed-DBG-XAU.csv'
profit_data.to_csv(output_csv_path, index=True, header=['profit_loss','account_balance'])
print(f"Processed data saved to {output_csv_path}")

需要跳过的行，基本上就是该索引值（-1）以上的所有行。

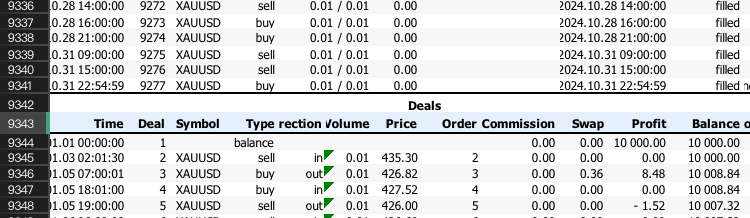
接下来，我们需要将每笔交易的利润转换为百分比变化，以确保重排后的序列能得出相同的最终余额。这是通过将账户余额列向下移动一行，并将每笔交易的盈亏计算为交易前余额的百分比来实现的。

initial_balance = account_balance.iloc[0] - profit_loss.iloc[0]

# Calculate the account balance before each trade
account_balance_before_trade = account_balance.shift(1)
account_balance_before_trade.iloc[0] = initial_balance

# Compute the percentage change made to the account balance for each trade
percentage_change = profit_loss / account_balance_before_trade

# Fill any NaN values that might have occurred
percentage_change.fillna(0, inplace=True)

最后，我们模拟 1000 个随机序列，并绘制出最大回撤最大的前 10 条曲线。请注意，最终的权益应该都是相同的，因为乘法具有交换律。无论百分比变化序列的值如何重排，将它们相乘都会得到相同的结果。

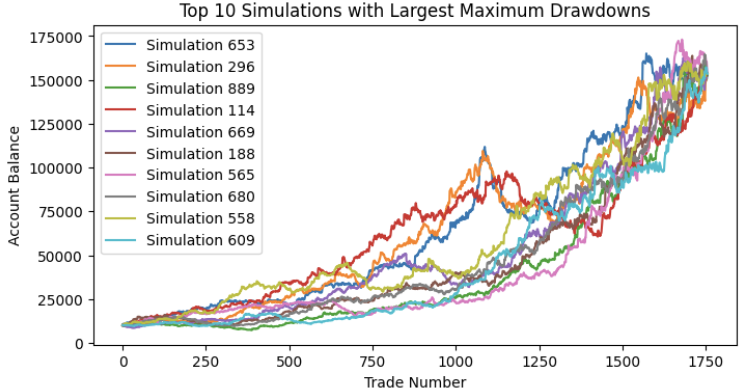
最大回撤的分布应接近正态分布，我们可以在这里看到其 95% 分位数（大约两个标准差）约为 30% 的最大回撤。

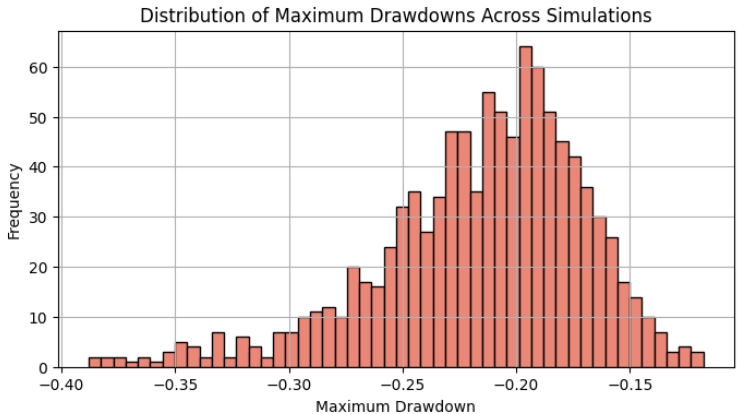
我们初始回测的最大回撤仅为 17%，小于该分布的均值。如果我们当初将其视为预期的最大回撤，那么与获得蒙特卡洛模拟结果所承担的风险相比，我们将风险放大了一倍。我们选择 95% 分位数，因为学者们普遍认为该结果接近于实盘交易的表现。很幸运，这里的 95% 分位数与我们最初设定的 30% 的最大容忍度非常接近。这意味着，如果我们在投资组合中只交易这一个EA，那么每笔交易 2% 的风险将使我们的利润最大化，同时又能很好地将我们控制在最大容忍度之内。如果结果不一致，我们应该重复上述过程，直到找到最优解。

用于投资组合优化的凯利准则

如果我们在一个账户上运行多个EA，我们首先需要为每个EA完成上述过程，以确定其最优风险。然后，我们将此风险应用于整个投资组合中为每个EA分配的资金。从整个账户的角度来看，每个EA的风险金额将是原始风险乘以其分配的权重比例。

每个EA所分配的凯利权重由其与其他EA的收益相关性及其整体回测表现决定。我们的主要目标是确保各个EA能够尽可能地相互抵消回撤，从而使整个投资组合的资金曲线更加平滑。需要注意的是，只有当新增的EA和策略之间不相关时，增加它们的数量才能提高投资组合的多样性；否则，这可能会增加整体风险，类似于放大单个EA的风险。

具体来说，我们使用以下公式，基于预期收益和收益的协方差矩阵来计算每个策略的凯利分配权重：

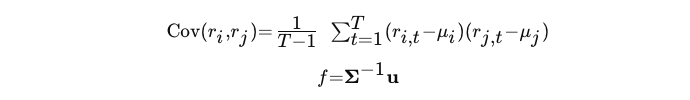
• r：EAi 或 EAj 在时间 t 的回报
• μ：EAi 或 EAj 的平均回报
  
• f：每个 EA 的凯利分配权重
• Σ−1：协方差矩阵的逆矩阵
  
• u：每个 EA 的预期回报向量

要提取上述变量的值，我们必须对每个策略进行回测，并将每个策略的百分比收益序列存储在一个单一的数据框中。接下来，根据所有 EA 的频率，我们选择合适的时间间隔进行记录，因为协方差是基于同一时间段内收益的相关性来计算的。我们使用以下 Python 代码执行此类操作：

# Read returns for each strategy
    for file in strategy_files:
        try:
            data = pd.read_csv(file, index_col='Time')
            # Ensure 'Time' is parsed correctly as datetime
            data.index = pd.to_datetime(data.index, errors='coerce')
            
            # Drop rows where 'Time' or 'return' is invalid
            data.dropna(subset=['return'], inplace=True)
            
            # Aggregate duplicate time indices by mean (or could use 'sum', but here mean can ignore the trade frequency significance)
            data = data.groupby(data.index).agg({'return': 'mean'})
            
            # Append results
            returns_list.append(data['return'])
            strategy_names.append(file)
        except Exception as e:
            print(f"Error processing {file}: {e}")
            continue 
    # Check if any data was successfully loaded
    if not returns_list:
        print("No valid data found in files.")
        return  
    # Combine returns into a single DataFrame, aligning by date
    returns_df = pd.concat(returns_list, axis=1, keys=strategy_names) 
    # Uncomment the below line if u wanna drop rows with missing values across strategies
    #returns_df.dropna(inplace=True)
    #Uncomment the below line if u wanna just fill unaligned rows with 0( I think this is best for backtest that may have years differences)
    returns_df.fillna(0, inplace=True)

确保所有回测结果的起止时间都保持一致。此外，选择一个合适的时间间隔来聚合结果，以避免任何间隔内出现过多交易，或完全没有交易的情况。如果时间间隔划分得过于离散，可能会导致在同一时间范围内的数据点不足，从而无法准确计算协方差。在我们的案例中，我们选择以一个月为间隔，并使用每个月的平均收益作为收益特征。

现在我们来进行计算：

    # Calculate expected returns (mean returns)
    expected_returns = returns_df.mean()
    
    # Calculate the covariance matrix of returns
    cov_matrix = returns_df.cov()
    
    # Compute the inverse of the covariance matrix
    try:
        inv_cov_matrix = np.linalg.inv(cov_matrix.values)
    except np.linalg.LinAlgError:
        # Use pseudo-inverse if covariance matrix is singular
        inv_cov_matrix = np.linalg.pinv(cov_matrix.values)
    
    # Calculate Kelly optimal fractions
    kelly_fractions = inv_cov_matrix @ expected_returns.values
    kelly_fractions = kelly_fractions / np.sum(kelly_fractions)

最终输出的结果如下：

         Strategy  Kelly Fraction
0  A1-DBG-XAU.csv        0.211095
1   A1-DBG-SP.csv        0.682924
2   A1-DBG-EU.csv        0.105981

我们可以将这个风险值直接应用到我们原始的 MQL5 代码中，因为最初的风险计算就已经是基于总账户余额的。随着账户余额的变化，分配给每个 EA 的资本将会自动重新计算，并应用到下一笔交易中。

double riskAmount = AccountInfoDouble(ACCOUNT_BALANCE) * risk / 100;

例如，要将计算出的凯利分数应用到我们的示例 EA 中，我们只需修改原始代码中的这一部分，任务就完成了。

input double risk = 2.0*0.211095;

我完全清楚，我们也可以选择根据每个 EA 分配资本的变化来重新计算风险，但基于整个投资组合进行计算是更优方案，原因如下：

1. 在我看来，追踪不同分配资本的变化是难以管理的。人们可能需要开设多个账户，或者编写一个程序在每笔交易后更新这些变化。
2. 凯利准则是用于最大化整个投资组合的长期增长。单个 EA 的表现会影响其他 EA 的风险，从而促进一个小型投资组合在规模扩大时实现高效增长。
3. 如果我们基于每个 EA 分配资金的变化来计算风险，那么表现良好的 EA 随着时间的推移，其被分配的资金会增加，从而导致这些 EA 的风险敞口也随之增大。这会破坏我们最初基于相关性来计算风险分配的初衷。

然而，我们的方法确实也存在一定的局限性：

1. 每个 EA 的风险会随着整个投资组合的表现而波动，这使得追踪单个 EA 的表现变得困难。整个投资组合可以被看作是一个类似标普 500（S&P 500）的指数。要评估单个 EA 的表现，就需要计算其百分比变化，而不是绝对利润。
2. 我们的风险分配计算并未考虑每个 EA 的交易频率。这意味着，如果同一账户上的 EA 交易频率差异巨大，那么即使进行了风险分配，也可能导致风险敞口不均。

总而言之，考虑到其为个人交易者最大化增长潜力的可能性，这种方法是值得采纳的。

结论

在本文中，我们在杠杆空间交易模型的背景下介绍了凯利准则，并阐述了其在交易中的应用。接着，我们提供了 MQL5 的实现代码。随后，我们使用蒙特卡洛模拟，基于单次回测来确定应考虑的最优最大回撤，并将其应用于评估单个 EA 的风险。最后，我们提出了一种基于 EA 回测表现和相关性，为每个 EA 进行资金分配的方法。

文件列表

名称	用法
KellyMultiFactors.ipynb	计算用于资金分配的凯利分数
MonteCarloDrawdown.ipynb	执行蒙特卡洛模拟