Теория категорий в MQL5 (Часть 19): Индукция квадрата естественности

Введение:

В этой серии статей мы рассмотрели применение теории категорий для классификации дискретных данных и на нескольких примерах показали, как торговые алгоритмы, в основном управляющие трейлинг-стопами, но также и те, которые управляют сигналами входа, а также размером позиции, могут быть органично включены в советник для реализации некоторых из его концепций. В этом очень помог мастер MQL5 Wizard в IDE, так как весь общий исходный код необходимо собрать с помощью мастера, чтобы получить тестируемую систему.

В этой статье мы рассмотрим, как использовать квадраты естественности, понятие которых мы ввели в прошлой статье, в индукции. Потенциальная польза от этого будет продемонстрирована на примере трех валютных пар, которые можно связать арбитражными операциями. Мы ищем классификацию данных об изменении цен для одной из пар с целью оценки возможности разработки алгоритма сигналов входа для этой пары.

Квадраты натуральности являются расширением преобразований на коммутативную диаграмму. Таким образом, если у нас есть две отдельные категории с более чем одним функтором между ними, то мы можем оценить отношения между двумя или более объектами в со-доменной категории и использовать этот анализ не только для соотнесения с другими аналогичными категориями, но и для прогнозирования внутри наблюдаемой категории, если объекты находятся во временном ряду.

Понимание настройки:

Наши две категории в этой статье будут иметь структуру, аналогичную той, которую мы рассматривали в предыдущей статье, поскольку между ними будут существовать два функтора. Но это и будет основным сходством, поскольку в данном случае мы будем иметь несколько объектов в обеих категориях, в то время как в предыдущем случае мы имели два объекта в доменной категории и только четыре в кодоменной.

Так, в доменной категории, содержащей один временной ряд, каждая ценовая точка в этом ряду представлена в виде объекта. Эти "объекты" будут связаны в хронологическом порядке морфизмами, которые просто инкрементируют их к таймфрейму графика, к которому привязан скрипт. Кроме того, поскольку мы имеем дело с временными рядами, это означает, что наша категория является несвязанной и, следовательно, не имеет кардинальности. И снова, как и в предыдущих статьях, нас интересует не столько общий размер и содержание категорий/объектов, сколько морфизмы и, более конкретно, функторы от этих объектов.

В категории codomain мы имеем два ценовых временных ряда для двух других валютных пар. Напомним, что для работы на требуется не менее трех валютных пар. Их может быть и больше, но в нашем случае мы используем минимум, чтобы сохранить относительную простоту реализации. Таким образом, в доменной категории будут находиться ценовые ряды для первой пары, которой будет USDJPY. Двумя другими парами, которые будут включены в кодомен как ценовые ряды, будут EURJPY и EURUSD.

Морфизмы, связывающие ценовые "объекты" во второй категории, будут находиться только в пределах конкретной серии, так как на начальном этапе у нас нет ни одного связывающего объекта в каждой серии.

Квадраты естественности и индукция:

Итак, концепция квадратов естественности в рамках теории категорий подчеркивает , которая в нашей прошлой статье использовалась как средство верификации классификации. В качестве примера можно привести приведенную ниже диаграмму, на которой представлены четыре объекта категории codomain:

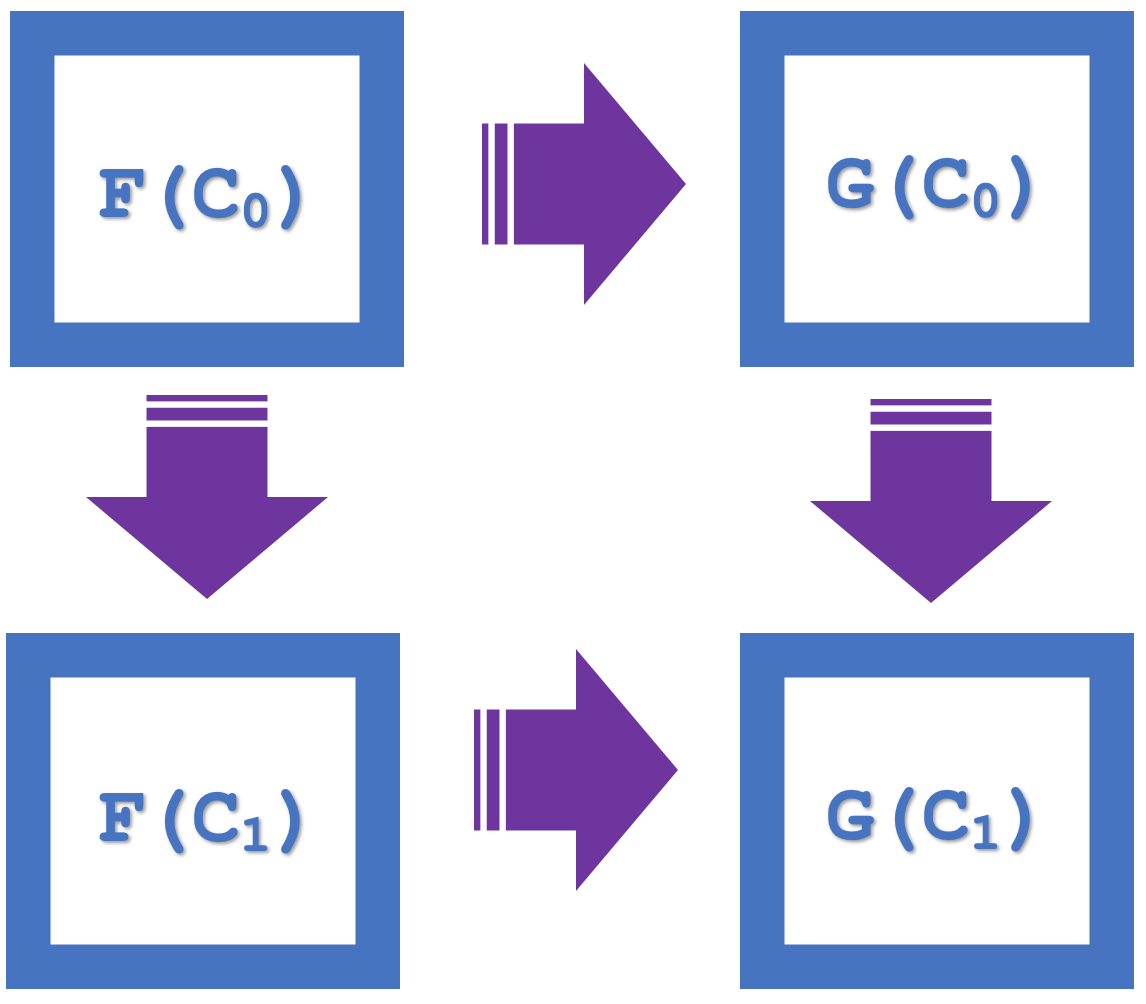
Мы видим, что существует коммутация F(C 0 ) - G(C 0 ) и затем G(C 1 ), эквивалентная F(C 0 ) - F(C 1 ) и затем G(C 1 ).

Понятие индукции, введенное в данной статье, подчеркивает возможность коммутации по сериям из нескольких квадратов, что упрощает проектирование и экономит вычислительные ресурсы. Если мы рассмотрим приведенную ниже диаграмму, на которой перечислены n квадратов:

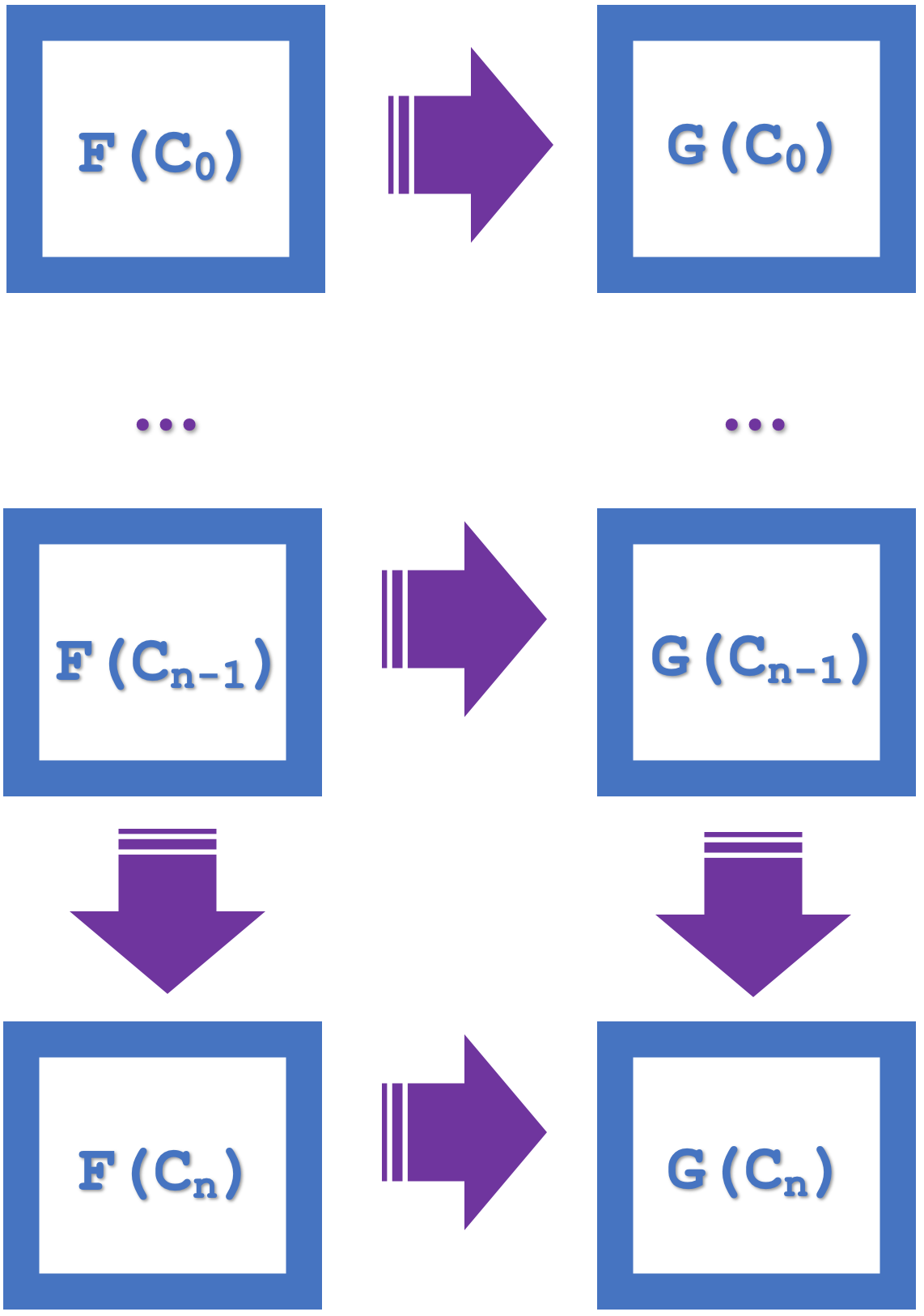
Если малые квадраты естественности коммутируют, то из этого следует, что коммутирует и больший прямоугольник. Эта большая коммутация влечет за собой морфизмы и функторы с шагом 'n'. Таким образом, оба наших функтора будут принадлежать серии USDJPY, но соединяться с разными сериями EURJPY и EURUSD. Поэтому естественные преобразования будут происходить из EURJPY в EURUSD. Поскольку для классификации мы, как и в прошлой статье, используем квадрат естественности, то прогнозы будут для кодомена естественных преобразований, а это EURUSD. Индукция позволяет рассматривать эти прогнозы на нескольких барах, а не на одном, как это было в предыдущей статье. В предыдущей статье попытка прогнозирования по нескольким барам требовала больших вычислительных затрат, поскольку приходилось использовать множество случайных лесов решений. С помощью индукции мы можем теперь начать классификацию с задержкой в n баров.

Визуальное представление этих квадратов естественности в виде единого прямоугольника показано ниже:

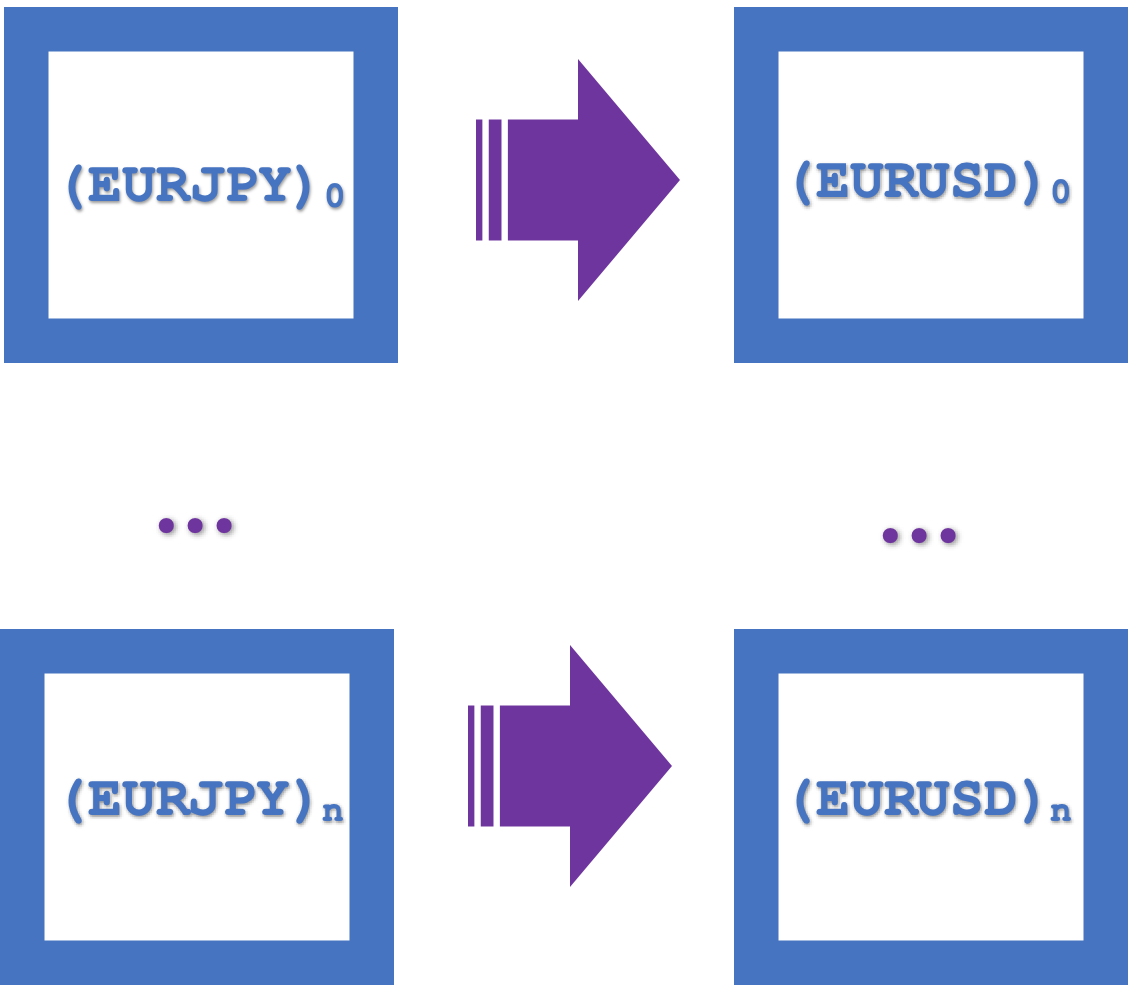
В этом большую роль играют функторы:

Сайт уже был представлен, поэтому данный параграф служит для того, чтобы подчеркнуть, как мы применяем его при работе с квадратами естественности. В предыдущей статье мы использовали многослойные перцептроны для определения отображения наших функторов, но в этой статье мы рассмотрим случайные леса решений для той же цели.

Decision Forests - это классификатор, использующий несколько методов обучения (лесов) для улучшения прогнозирования. Как и многослойный перцептрон (MLP), он является относительно сложным, и его часто называют методом ансамблевого обучения. Реализовывать это из первых принципов для наших целей было бы слишком утомительно, поэтому хорошо, что в Alglib уже есть классы реализации, которые доступны в библиотеке MQL5 в папке 'Include\Math'.

Таким образом, отображение с помощью Random Decision Forests (RDFs) определяется путем задания размера леса и приписывания весов различным деревьям и соответствующим ветвям леса. Однако для простоты описания можно представить RDF как команду небольших лиц, принимающих решения, где каждое лицо, принимающее решение, - это дерево, которое знает, как посмотреть на набор данных и сделать выбор. Все они получают один и тот же вопрос (данные), и каждый дает на него ответ (решение). После того как все команды сделали свой выбор, проводится голосование, в ходе которого выбирается наиболее понравившееся решение. Самое интересное в этом процессе то, что хотя всем командам (деревьям) были предоставлены одни и те же данные, они извлекали знания из разных частей, поскольку выборка была произвольной. Решения, принятые на основе этого, часто бывают умными и точными!

Я попробовал сделать свою собственную реализацию с нуля, и этот алгоритм, хотя и может быть описан просто, является достаточно сложным. Однако это можно сделать с помощью Alglib в нескольких форматах. Простейший из них требует только два входных параметра: количество лесов и входной параметр двойного типа R, который задает процент обучающего множества, используемого для построения деревьев. Для наших целей мы будем использовать именно его. Существуют и другие требования, такие как количество независимых переменных и количество зависимых переменных (они же классификаторы), но они характерны для большинства моделей машинного обучения.

Реализация сценариев на языке MQL5:

Для кодирования всего, что представлено в этих сериях, мы использовали исключительно среду разработки MQL5. Нелишним будет подчеркнуть, что помимо пользовательских индикаторов, советников и MQL5-скриптов, в этой среде можно кодировать/разрабатывать сервисы, библиотеки, базы данных и даже скрипты на языке python.

В данной статье мы просто используем скрипт для демонстрации классификации по квадратам естественности в индукции. Идеальным вариантом был бы экземпляр сигнального класса эксперта, а не просто скрипт, однако реализация мультивалютного сигнального класса хотя и возможна, но не настолько целесообразна, как это предусмотрено в данной статье, поэтому мы в неоптимизированных условиях выведем прогнозные и фактические изменения цены закрытия пары EURUSD и используем эти результаты для подтверждения или опровержения нашего тезиса о том, что квадраты естественности с индукцией полезны при построении прогнозов.

Итак, наш сценарий начинается с создания экземпляра доменной категории для хранения серии изменений цены закрытия USDJPY. Эта категория может быть использована для обучения и обозначена соответствующим образом. Хотя при обучении с его помощью будут установлены веса для функторов, переходящих из него в категорию кодомена (наши два функтора), эти веса не являются критичными для наших прогнозов (о чем говорилось в предыдущей статье), но здесь они упоминаются для перспективы.

      //create domain series (USDJPY-rates) in first category for training
      CCategory _c_a_train;_c_a_train.Let();
      int _a_size=GetObject(_c_a_train,__currency_a,__training_start,__training_stop);

Затем мы создаем экземпляр категории codomain, в котором, как уже говорилось, будут представлены два временных ряда - EURJPY и EURUSD. Поскольку каждая ценовая точка представляет собой объект, нам необходимо позаботиться о том, чтобы "сохранить" две серии внутри категории, последовательно добавляя объекты для каждой серии. Мы обозначаем их как b и c.

      //create 2 series (EURJPY and EURUSD rates) in second category for training
      CCategory _c_bc_train;_c_bc_train.Let();
      int _b_trains=GetObject(_c_bc_train,__currency_b,__training_start,__training_stop);
      int _c_trains=GetObject(_c_bc_train,__currency_c,__training_start,__training_stop);

Таким образом, наши прогнозы, как и в предыдущей статье, будут сосредоточены на объектах кодомена, образующих квадрат естественности. Морфизмы, соединяющие каждую серию вместе с естественными преобразованиями, связывающими объекты между сериями, мы будем отображать как RDF.

Наш скрипт имеет входной параметр для количества индукций, с помощью которого мы масштабируем квадрат и делаем проекции за пределы следующего 1 бара. Таким образом, наши квадраты естественности по n индукциям образуют единый квадрат, который мы примем за углы A, B, C и D, причем AB и CD будут нашими преобразованиями, а AC и BD - морфизмами.

При реализации этого отображения можно использовать как MLP, так и RDF, скажем, для преобразований и морфизмов соответственно. Я оставляю читателю возможность исследовать этот вопрос, поскольку мы уже видели, как можно использовать MLP. Однако, двигаясь дальше, нам необходимо наполнить наши обучающие модели для RDF данными, что и делается с помощью матрицы. Четыре RDF для каждого отображения из AB в CD будут иметь свою матрицу, которая заполняется листингом, представленным ниже:

      //create natural transformation, by induction across, n squares..., cpi to pmi
      //mapping by random forests
      int _training_size=fmin(_c_trains,_b_trains);
      int _info_ab=0,_info_bd=0,_info_ac=0,_info_cd=0;
      CDFReport _report_ab,_report_bd,_report_ac,_report_cd;
      CMatrixDouble _xy_ab;_xy_ab.Resize(_training_size,1+1);
      CMatrixDouble _xy_bd;_xy_bd.Resize(_training_size,1+1);
      CMatrixDouble _xy_ac;_xy_ac.Resize(_training_size,1+1);
      CMatrixDouble _xy_cd;_xy_cd.Resize(_training_size,1+1);
      
      double _a=0.0,_b=0.0,_c=0.0,_d=0.0;
      CElement<string> _e_a,_e_b,_e_c,_e_d;
      string _s_a="",_s_b="",_s_c="",_s_d="";
      for(int i=0;i<_training_size-__n_inductions;i++)
      {
         _s_a="";_e_a.Let();_c_bc_train.domain[i].Get(0,_e_a);_e_a.Get(1,_s_a);_a=StringToDouble(_s_a);
         _s_b="";_e_b.Let();_c_bc_train.domain[i+_b_trains].Get(0,_e_b);_e_b.Get(1,_s_b);_b=StringToDouble(_s_b);
         _s_c="";_e_c.Let();_c_bc_train.domain[i+__n_inductions].Get(0,_e_c);_e_c.Get(1,_s_c);_c=StringToDouble(_s_c);
         _s_d="";_e_d.Let();_c_bc_train.domain[i+_b_trains+__n_inductions].Get(0,_e_d);_e_d.Get(1,_s_d);_d=StringToDouble(_s_d);
         
         if(i<_training_size-__n_inductions)
         {
            _xy_ab[i].Set(0,_a);
            _xy_ab[i].Set(1,_b);
            
            _xy_bd[i].Set(0,_b);
            _xy_bd[i].Set(1,_d);
            
            _xy_ac[i].Set(0,_a);
            _xy_ac[i].Set(1,_c);
            
            _xy_cd[i].Set(0,_c);
            _xy_cd[i].Set(1,_d);
         }
      }

После того как наборы данных готовы, мы можем объявить экземпляры моделей для каждого RDF и приступить к индивидуальному обучению каждого из них. Это делается, как показано ниже:

      CDForest          _forest;
      CDecisionForest   _rdf_ab,_rdf_cd;
      CDecisionForest   _rdf_ac,_rdf_bd;
      
      _forest.DFBuildRandomDecisionForest(_xy_ab,_training_size-__n_inductions,1,1,__training_trees,__training_r,_info_ab,_rdf_ab,_report_ab);
      _forest.DFBuildRandomDecisionForest(_xy_bd,_training_size-__n_inductions,1,1,__training_trees,__training_r,_info_bd,_rdf_bd,_report_bd);
      _forest.DFBuildRandomDecisionForest(_xy_ac,_training_size-__n_inductions,1,1,__training_trees,__training_r,_info_ac,_rdf_ac,_report_ac);
      _forest.DFBuildRandomDecisionForest(_xy_cd,_training_size-__n_inductions,1,1,__training_trees,__training_r,_info_cd,_rdf_cd,_report_cd);

Выходные данные каждого обучения, которые нам необходимо оценить в целочисленном значении параметра 'info'. Как и в случае с MLP, эта величина должна быть положительной. Если все наши "информационные" параметры положительны, то можно приступать к тестированию.

Обратите внимание, что входные параметры нашего скрипта включают 3 даты: дату начала обучения, дату окончания обучения и дату окончания тестирования. В идеале эти значения должны проверяться перед использованием, чтобы убедиться, что они расположены по возрастанию в том порядке, в котором я их указал. Кроме того, не хватает даты начала тестирования, поскольку дата окончания обучения также является датой начала тестирования. Поэтому мы реализуем прямой тест с помощью приведенного ниже листинга:

      //
      if(_info_ab>0 && _info_bd>0 && _info_ac>0 && _info_cd>0)
      {
         //create 2 objects (cpi and pmi) in second category for testing
         CCategory _c_cp_test;_c_cp_test.Let();
         int _b_test=GetObject(_c_cp_test,__currency_b,__training_stop,__testing_stop);
         ...
      
         ...
         
         MqlRates _rates[];
         ArraySetAsSeries(_rates,true);
         if(CopyRates(__currency_c,Period(), 0, _testing_size+__n_inductions+1, _rates)>=_testing_size+__n_inductions+1)
         {
            ArraySetAsSeries(_rates,true);
            
            for(int i=__n_inductions+_testing_size;i>__n_inductions;i--)
            {
               _s_a="";_e_a.Let();_c_cp_test.domain[i].Get(0,_e_a);_e_a.Get(1,_s_a);_a=StringToDouble(_s_a);
               
               double _x_ab[],_y_ab[]; ArrayResize(_x_ab,1); ArrayResize(_y_ab,1);
               ArrayInitialize(_x_ab,0.0); ArrayInitialize(_y_ab,0.0);
               //
               _x_ab[0]=_a; _forest.DFProcess(_rdf_ab,_x_ab,_y_ab);
               
               ...
               
               double _x_cd[],_y_cd[]; ArrayResize(_x_cd,1); ArrayResize(_y_cd,1);
               ArrayInitialize(_x_cd,0.0); ArrayInitialize(_y_cd,0.0);
               //
               _x_cd[0]=_y_ac[0]; _forest.DFProcess(_rdf_cd,_x_cd,_y_cd);
               
               double _c_forecast=0.0;
               if((_y_bd[0]>0.0 && _y_cd[0]>0.0)||(_y_bd[0]<0.0 && _y_cd[0]<0.0))//abd agrees with acd on currency c change
               {
                  _c_forecast=0.5*(_y_bd[0]+_y_cd[0]);
               }
               
               double _c_actual=_rates[i-__n_inductions].close-_rates[i].close;
               
               if((_c_forecast>0.0 && _c_actual>0.0)||(_c_forecast<0.0 && _c_actual<0.0)){ _strict_match++; }
               else if((_c_forecast>=0.0 && _c_actual>=0.0)||(_c_forecast<=0.0 && _c_actual<=0.0)){ _generic_match++; }
               else { _miss++; }
            }
            //
            ...
         }
      }

Помните, что нас интересует прогноз изменения курса EURUSD, который в нашем квадрате представлен как D. При проверке наших прогнозов на форвард-тесте мы фиксируем значения, которые строго совпадают по направлению, значения, которые могли бы совпасть по направлению, учитывая, что у нас задействованы нули, и, наконец, мы также фиксируем пропуски. Все это отражено в приведенном выше листинге.

Таким образом, чтобы обобщить наш сценарий, мы начинаем с объявления обучающих категорий, одна из которых нам крайне необходима для предварительной обработки данных и обучения. В качестве арбитражных форекс-пар мы используем USDJPY, EURJPY и EURUSD. Мы сопоставляем объекты нашей кодоменной категории с помощью RDF, которые служат морфизмами в рядах и естественными преобразованиями в рядах для построения прогнозов на тестовых данных, которые определяются датой остановки обучения и датой остановки тестирования.

Результаты и анализ:

Если запустить приложенный в конце статьи скрипт, реализующий общий источник, приведенный выше, то мы получим следующие логи с индукциями по 1 на дневном графике USDJPY:

2023.09.01 13:39:14.500 ct_19_r1 (USDJPY.ln,D1) void OnStart() misses: 45, strict matches: 61, & generic matches: 166, for strict pct (excl. generic): 0.58, & generic pct: 0.83, with inductions at: 1

Однако если мы увеличим число индукций до 2, то получим вот что:

2023.09.01 13:39:55.073 ct_19_r1 (USDJPY.ln,D1) void OnStart() misses: 56, strict matches: 63, & generic matches: 153, for strict pct (excl. generic): 0.53, & generic pct: 0.79, with inductions at: 2

Наблюдается небольшое снижение, хотя и значительное, но все же положительное, так как строгих совпадений больше, чем промахов. Мы можем создать журнал регистрации количества введений по совпадениям и промахам. Это показано на графике ниже:

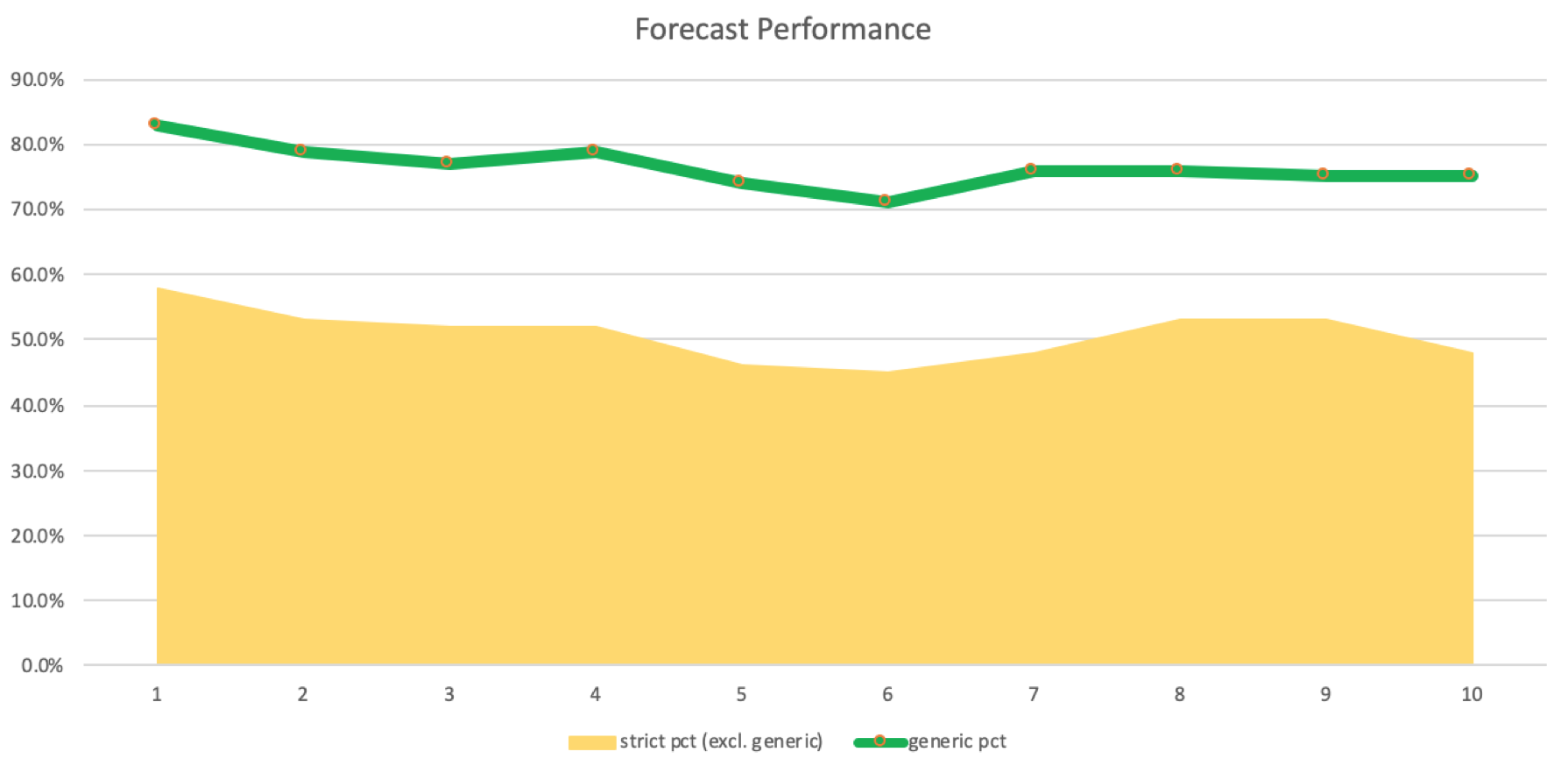
Точность этих прогнозов и совпадений необходимо подтвердить на реальной торговой системе, выполняющей прогоны с различными индукционными лагами, чтобы доказать или опровергнуть их эффективность. Довольно часто системы могут быть прибыльными и при меньшем проценте выигрыша, поэтому мы не можем однозначно утверждать, что использование индукционных лагов от 5 до 8 является идеальным для нашей системы. Тестирование с помощью советника, который может работать с несколькими валютами, подтвердит это.

Основные проблемы, с которыми столкнулась данная реализация, - невозможность тестирования в качестве экспертного класса сигналов эксперта-мастера MQL5. Мастер сборки по умолчанию инициирует индикаторы и ценовые буферы только для одного символа - символа графика. Обойти эту проблему, чтобы разместить несколько символов, можно, но для этого необходимо создать собственный класс, наследующий класс CExpert, и внести в него некоторые изменения. Мне показалось, что для данной статьи это слишком объемно, поэтому читатель может изучить этот вопрос самостоятельно.

Сравнение с традиционными методами:

По сравнению с "традиционными" методами, использующими такие простые индикаторы, как скользящая средняя, наш подход, основанный на индукции квадрата естественности, кажется сложным и, возможно, запутанным, если просто прочитать его описание. Я все же надеюсь, что благодаря обилию библиотек кода (например, Alglib), доступных в Интернете и в библиотеке MQL5, читатель получит представление о том, как можно легко закодировать сложный на первый взгляд подход или идею менее чем в 200 строках. Это позволяет изучить, принять или опровергнуть новые идеи. MQL5 IDE - это рай для филоматов.

Основными достоинствами этой системы являются ее адаптивность и потенциальная точность.

Реальные приложения:

Если мы и будем исследовать практическое применение нашей системы прогнозирования с арбитражными парами, то только в контексте попыток использования арбитражных возможностей внутри трех пар. Всем известно, что у каждого брокера своя политика спредов по парам на рынке Форекс, и если арбитражные возможности и существуют, то только потому, что одна из трех пар оценена неверно настолько, что разрыв превышает спред пары. Такие возможности существовали и раньше, но с годами, когда латентность для большинства брокеров уменьшилась, они стали вполне реальными. Более того, некоторые брокеры даже объявляют эту практику вне закона.

Поэтому если мы и будем заниматься арбитражем, то в псевдоформе, когда мы "не замечаем" спрэда и вместо него смотрим на сырые цены плюс прогноз наших квадратов естественности. Так, например, простая система для выхода в длинную позицию будет смотреть на то, чтобы арбитражная цена третьей пары, в нашем случае EURUSD, была выше текущей котировочной цены и прогноз также был на рост цены. Напомним, что арбитражная цена для пары EURUSD в нашем случае будет получена следующим образом:

EURJPY / USDJPY

Включение такой системы в ту, что мы имели из приведенного выше сценария, неизбежно приводит к уменьшению количества сделок с момента подтверждения. для каждого сигнала требуется либо более высокая, либо более низкая арбитражная цена для лонгов и шортов соответственно. Работа с классом экспертного сигнала для создания экземпляра класса, который кодирует это, является предпочтительным подходом, и поскольку поддержка мультивалютности в классах мастера MQL5 пока не так сильна, мы можем только упомянуть об этом здесь и предложить читателю модифицировать экспертный класс, как указано выше, или попробовать другой подход, который позволит протестировать этот мультивалютный подход с экспертами, собранными мастером.

Повторюсь, что тестирование идей с помощью советников, созданных мастерами на MQL5, позволяет не просто собрать что-то в единое целое с меньшим количеством кода, но и совместить другие выходящие сигналы с тем, над чем мы работаем, и посмотреть, есть ли среди них относительный вес, который удовлетворяет нашим целям. Так, например, если бы вместо скрипта, приложенного в конце, мы смогли реализовать мультивалютность и предоставить работоспособный сигнальный файл, то этот файл можно было бы комбинировать с другими библиотечными сигнальными файлами (такими как Awesome Oscillator, RSI и т.д.) или даже с другим пользовательским сигнальным файлом, чтобы разработать новую торговую систему с более значимыми или сбалансированными результатами, чем просто один сигнальный файл.

Подход к индукции квадратов естественности, помимо потенциально возможного получения сигнального файла, может быть использован для повышения эффективности риск-менеджмента и оптимизации портфеля, если вместо сигнального файла закодировать пользовательский экземпляр класса expert money. При таком подходе, хотя и рудиментарном, мы могли бы с определенными ограничениями размещать свои позиции пропорционально величине прогнозируемого движения цены.

Заключение:

Резюмируя основные выводы из этой статьи, мы рассмотрели, как квадраты естественности при расширении индукцией упрощают проектирование и экономят вычислительные ресурсы при классификации данных и, соответственно, прогнозировании будущего.

Точное прогнозирование рядов никогда не должно быть единственной и конечной целью торговой системы. Множество торговых методов стабильно приносят прибыль при небольшом проценте выигрыша, поэтому наша неспособность протестировать эти идеи в качестве класса экспертных сигналов удручает и явно делает результаты, полученные здесь, неубедительными в отношении роли и потенциала индукции.

Таким образом, читателям предлагается дополнительно протестировать приложенный код в настройках, обеспечивающих мультивалютную поддержку советников, чтобы сделать более точные выводы о том, какие индукционные лаги работают, а какие нет.

Ссылки:

Википедия в соответствии с общими ссылками в статье.

Приложение: Сниппеты кода MQL5

Прилагается скрипт (ct_19_r1.mq5), который для запуска необходимо скомпилировать в IDE, а затем прикрепить его файл *.ex5 к графику в терминале MetaTrader 5. Его можно запускать с различными настройками и разными арбитражными парами, помимо тех, что предлагаются по умолчанию. Во втором прикрепленном файле приведена часть теоретических классов, собранных на данном этапе серии. Как всегда, он должен находиться в папке include.