
모집단 최적화 알고리즘: 전자기 유사 알고리즘(ЕМ)
콘텐츠:
1. 소개
지난 수십 년 동안 전 세계의 많은 연구자들은 복잡한 글로벌 최적화 문제를 해결하기 위해 많은 메타휴리스틱 검색 방법과 이를 개선하는 방법을 고안해냈습니다.
전자기 유사(ЕМ) 알고리즘은 비교적 새로운 메타 휴리스틱 검색 알고리즘으로 물리적 공간에서 전자기 입자 움직임의 시뮬레이션을 기반으로 하며, I. Birbil과 S.С.에 의해 처음 소개되었습니다. 2003년 Fang. 이는 하전 입자 간의 상호작용의 전자기력에 기반한 무작위적인 노이즈와 모집단으로 구성된 진화 알고리즘으로 설명됩니다.
이 알고리즘은 연속 영역에서 제한 없이 비선형 최적화 문제를 해결하기 위해 전자기학 이론에서 전하의 인력 및 반발 메커니즘에서 영감을 얻은 것이며. 복잡한 글로벌 최적화 문제를 해결할 수 있는 능력 덕분에 여러 분야에서 최적화 도구로 널리 사용되고 있습니다.
전자기학과 전하에 관한 흥미로운 사실:
- 전하에는 양전하와 음전하의 두 가지 유형이 있습니다. 모든 전하는 양수 또는 음수입니다.
- 전자기장은 전파의 형태로 정보를 전송하는 데 사용될 수 있습니다. 우리는 매일 라디오를 듣거나 TV를 시청할 때 이 기능을 사용합니다.
- 태양풍과 우주선으로부터 우리를 보호하는 지구 자기장이 있습니다.
- 자석화될 수 있는 다양한 재료가 있으며 우리는 이를 통해 전자석을 만들 수 있습니다. 전자석은 발전기와 같은 다양한 도구에 사용됩니다.
- 전자기력을 기반으로 하는 많은 도구들이 있습니다. 예를 들어 컴퓨터, 휴대폰 및 기타 장치는 전자기 기술을 사용합니다.
- 모든 발광 물체(예: 전구 및 자동차 조명)는 전자기 방사선을 방출합니다.
- 전자기력은 의학에서도 중요한 역할을 합니다. MRI 및 CT와 같은 의료 기기는 전자기장을 사용하여 신체 내부의 이미지를 생성합니다.
- 상어와 전기 뱀장어와 같은 일부 동물은 전자기를 이용해 물속을 탐색할 수 있습니다.
- 전자기력은 중력, 약력, 강력과 함께 자연의 네 가지 기본 힘 중 하나입니다.
2. 알고리즘
전자기력의 이론에 따라 EM은 전하의 인력-반력 메커니즘을 시뮬레이션 하여 제한된 변수를 사용하여 글로벌 최적 솔루션을 달성합니다. 알고리즘에서 모든 솔루션은 검색 공간에서 하전된 입자로 간주되며 각 입자의 전하가 목표 함수의 값과 연관되어집니다. 목표 출력이 좋은 파티클은 인력을 가하고, 목표 값이 나쁜 파티클은 다른 파티클에 반발력을 가합니다. 목표 함수의 값이 클수록 입자 사이의 인력 또는 반발력이 커집니다.
알고리즘의 원리는 초기 단계에서 무작위 솔루션의 모집단이 형성되고 각 솔루션은 전자기 입자의 전하에 해당하는 좌표 벡터로 표현된다는 것입니다. 또한 알고리즘을 반복할 때마다 공간에서 이러한 전하의 움직임은 전자기력의 작용에 따라 시뮬레이션 되며 이동하는 동안 각 전하가 다른 전하와 상호작용하여 이동 방향과 속도가 달라집니다. 결과적으로 목표 함수의 최적 값에 대한 솔루션이 점진적으로 수렴합니다.
EM 알고리즘의 주요 구성 요소는 다음과 같습니다:
- 각 전하가 좌표 벡터로 표시되고 최적화 문제의 특정 해에 해당하는 해(전하)의 초기 모집단 형성.
- 전하 간 상호작용의 전자기력을 계산. 계산은 전하(솔루션) 사이의 거리에 따라 알고리즘을 반복할 때마다 수행됩니다.
- 전하는 전자기력의 상호작용에 영향을 받아 공간에서 이동합니다.
- 목표 함수에 의해 각 반복마다 솔루션 모집단을 업데이트합니다(예: 머신 러닝 문제에서 목표 함수는 손실 함수가 될 수 있음).
- 알고리즘을 중지하는 조건(예: 목표 함수의 특정 값에 도달)을 결정합니다.
입자는 전하와 입자 사이의 거리에 따라 서로 끌어당기거나 밀어내면서 상호작용합니다. 알고리즘은 여러 번의 반복으로 실행되며 각 반복마다 파티클의 좌표와 전하가 업데이트되고 적합도 함수의 새로운 값이 계산됩니다.
EM 최적화 알고리즘의 논리적 단위는 파티클이며 이는 검색 공간의 에이전트인 S_Particle 구조로 설명할 수 있습니다. 각 입자는 검색 공간에서 각각의 입자의 위치를 결정하는 c [] 좌표와 다른 입자와의 상호작용에 영향을 주는 C 전하를 갖습니다. 각 파티클에 대해 주어진 좌표에 해당하는 솔루션의 품질을 평가하는 적합성 함수 f의 값이 계산됩니다. 또한 각 파티클에 대해 다른 파티클과의 거리 R과 힘 벡터 F가 계산되어 검색 공간에서 파티클의 움직임의 방향을 결정합니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Particle { double c []; //coordinates double C; //charge double f; //fitness double R []; //euclidean distance to other particles double F []; //force vector }; //——————————————————————————————————————————————————————————————————————————————
C_AO_EM 클래스는 전자기력 최적화 알고리즘을 구현한 것으로 어떤 실수 집합에서 주어진 함수의 최적값을 찾는 데 사용됩니다. 이 알고리즘은 물리적 시스템에서 자성 입자와 전기 입자 간의 상호작용의 과정을 시뮬레이션 하는 것을 기반으로 합니다.
클래스에는 다음 필드가 포함됩니다:
- S_Particle p[] - 최적화 문제에 대한 잠재적 해결책을 나타내는 파티클 배열.
- double rangeMax[] - 각 좌표에 대한 최대 검색 범위 값의 배열.
- double rangeMin[] - 각 좌표에 대한 최소 검색 범위 값의 배열.
- double rangeStep[] - 각 좌표에 대한 검색 단계의 배열.
- double cB[] - 최적 솔루션의 좌표 배열.
- double fB - 최적의 솔루션 함수의 값.
이 클래스에는 다음과 같은 메서드가 포함되어 있습니다:
- void Init()은 좌표 수, 파티클 수, 환경 상수 및 이동 단계를 설정하여 알고리즘을 초기화합니다.
- void Moving(int iter)은 자기장과 전기장의 상호작용 규칙에 따라 파티클을 움직이는 알고리즘을 반복합니다.
- void Revision()은 파티클이 검색 범위를 벗어나는지 검사하고 필요한 경우 위치를 조정하는 파티클 수정을 수행합니다.
클래스에는 비공개 필드도 포함되어 있습니다:
- int coordinatesNumber - 좌표의 수.
- int particlesNumber - 파티클의 개수.
- double envConstant - 환경 상수.
- double movConstant - 이동 스텝.
- double exponent - 거리 지수.
- double vect[] - 벡터의 배열.
- bool revision - 파티클 개정이 필요함을 나타내는 플래그.
클래스에는 비공개 메서드가 포함되어 있습니다:
- double SeInDiSp(double In, double InMin, double InMax, double Step)는 균일한 그리드에 점을 분배합니다.
- double RNDfromCI(double min, double max)는 주어진 범위의 난수를 생성합니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_EM { //---------------------------------------------------------------------------- public: S_Particle p []; //particles public: double rangeMax []; //maximum search range public: double rangeMin []; //minimum search range public: double rangeStep []; //step search public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: void Init (const int coordinatesNumberP, //coordinates number const int particlesNumberP, //particles number const double envConstantP, //environmental constant const double movConstantP, //movement step const double exponentP); //exponent public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coordinatesNumber; //coordinates number private: int particlesNumber; //particles number private: double envConstant; //environmental constant private: double movConstant; //movement step private: double exponent; //exponent private: double vect []; //vector private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
'전자기 알고리즘' 최적화 알고리즘 초기화 방법은 난수 생성기를 재설정하고 일부 변수에 대한 초기값을 설정하는 것으로 시작됩니다. 그런 다음 이 메서드는 좌표 수, 파티클 수, 환경 값, 이동 단계 등 여러 파라미터를 입력으로 받습니다. 그런 다음 필요한 크기의 배열을 여러 개 생성하고 초기값으로 채웁니다.
배열에는 각 좌표 범위의 최대값과 최소값, 좌표 변경 단계, 벡터 및 각 파티클의 현재 위치가 저장됩니다. 그런 다음 파티클 배열을 생성하고 각 파티클에 대해 좌표, 다른 파티클과의 거리 행렬, 힘 벡터 및 함수의 현재 최적값을 저장하는 배열을 생성합니다. 마지막에는 모든 파티클의 최적 좌표를 저장하는 배열을 생성합니다. 따라서 이 방법은 '전자기 알고리즘' 최적화 알고리즘이 작동하는 데 필요한 모든 변수와 배열을 초기화합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_EM::Init (const int coordinatesNumberP, //coordinates number const int particlesNumberP, //particles number const double envConstantP, //environmental constant const double movConstantP, //movement step const double exponentP) //exponent { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coordinatesNumber = coordinatesNumberP; particlesNumber = particlesNumberP; envConstant = envConstantP; movConstant = movConstantP; exponent = exponentP; ArrayResize (rangeMax, coordinatesNumber); ArrayResize (rangeMin, coordinatesNumber); ArrayResize (rangeStep, coordinatesNumber); ArrayResize (vect, coordinatesNumber); ArrayResize (p, particlesNumber); for (int i = 0; i < particlesNumber; i++) { ArrayResize (p [i].c, coordinatesNumber); ArrayResize (p [i].R, particlesNumber); ArrayResize (p [i].F, coordinatesNumber); p [i].f = -DBL_MAX; } ArrayResize (cB, coordinatesNumber); } //——————————————————————————————————————————————————————————————————————————————
Moving() 메서드는 각 반복에서 가장 먼저 실행해야 하는 메서드로서. 솔루션 검색 공간에서 파티클의 이동을 담당합니다. 먼저 파티클이 이미 초기화되었는지 확인합니다. 그렇지 않은 경우 각 파티클은 주어진 한계 내에서 임의의 좌표를 받고 현재 추정치와 전하를 0으로 초기화합니다. 검색 공간의 각 차원에서 최대값과 최소값 사이의 차이 벡터 []도 계산됩니다.
//---------------------------------------------------------------------------- if (!revision) { fB = -DBL_MAX; for (int obj = 0; obj < particlesNumber; obj++) { for (int c = 0; c < coordinatesNumber; c++) { p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); p [obj].C = 0.0; p [obj].f = -DBL_MAX; } } for (int c = 0; c < coordinatesNumber; c++) { vect [c] = rangeMax [c] - rangeMin [c]; } revision = true; }
초기화가 이미 수행된 경우, 이 메서드는 모든 파티클의 글로벌 최대값 편차 합으로 정규화된 글로벌 최대값에서 얻어진 편차를 기준으로 각 파티클의 전하를 계산합니다. 차액의 합계는 다음과 같이 계산합니다:
//calculate the sum of the differences of the fitness of the particles with the global value for (int obj = 0; obj < particlesNumber; obj++) { sumDiff += fB - p [obj].f; }
파티클 전하량은 방정식에 의해 계산됩니다:
p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));보시다시피 방정식의 전하 값은 양수입니다. 전하의 부호는 나중에 알고리즘에서 고려됩니다. 글로벌 최대값에서 얻어진 편차 차이의 합이 0이면 파티클의 전하가 0인 것으로 간주됩니다. 파티클의 계산된 전하가 힘 계산 단계에서 파티클에서 다른 관련 파티클에 작용하는 힘의 진폭을 결정합니다. 파티클의 전하를 계산하는 코드는 다음과 같습니다://calculating the charge of particles======================================= for (int obj = 0; obj < particlesNumber; obj++) { if (sumDiff == 0.0) { p [obj].C = 0.0; } else { p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff)); } }
파티클 간의 거리 계산을 시작하기 전에 우리는 파티클에서 다른 파티클까지의 거리 배열을 재설정하고 파티클에 작용하는 힘의 벡터도 재설정해야 합니다:
//calculation of Euclidean distances between all particles================== for (int obj = 0; obj < particlesNumber; obj++) { ArrayInitialize (p [obj].R, 0.0); ArrayInitialize (p [obj].F, 0.0); }
그런 다음 모든 파티클 쌍 사이의 거리와 입자 사이에 작용하는 힘을 계산하며 이때 하전 입자 간의 상호작용을 설명하는 쿨롱의 법칙에 기반한 공식을 사용합니다. 각 파티클에 작용하는 힘은 다른 파티클에서 파티클에 작용하는 모든 힘의 벡터 합으로 계산됩니다.
전자기 이론에 따르면 한 파티클이 다른 파티클에 작용하는 힘은 두 입자 사이의 거리에 반비례하고 전하의 곱에 정비례합니다. 목표 값이 낮은 파티클은 상대적으로 높은 목표 값을 가진 파티클에 반발력을 가하고 마찬가지로 목표 값이 나쁜 영역에서는 좋은 파티클을 밀어냅니다. 반면 목표 값이 높은 파티클은 상대적으로 낮은 값을 가진 파티클에 인력을 가합니다.
다른 모든 파티클에 의해 생성된 모든 관련된 힘을 고려하여 파티클의 총 힘 벡터가 계산됩니다. 이 결합된 힘 벡터는 파티클 움직임 단계에서 파티클이 움직일 방향을 결정합니다. 알고리즘 작성자는 파티클의 힘 벡터를 모든 파티클 간의 힘 벡터로 정규화할 것을 권장합니다. 제가 실험한 바에 따르면 정규화 없이도 결과가 더 좋았고 코드는 정규화 없는 것으로 표시되는 것으로 나타났습니다.
어떤 파티클의 목적 함수의 값이 더 큰지에 따라 우리는 힘의 방향(전하 부호의 모방)을 설정합니다.
for (int obj = 0; obj < particlesNumber; obj++) { for (int obj2 = 0; obj2 < particlesNumber; obj2++) { if (obj != obj2) { if (p [obj].R [obj2] == 0.0) { for (int c = 0; c < coordinatesNumber; c++) { diffDist = p [obj].c [c] - p [obj2].c [c]; p [obj].R [obj2] += diffDist * diffDist; } p [obj].R [obj2] = sqrt (p [obj].R [obj2]); p [obj2].R [obj] = p [obj].R [obj2]; //calculation of the force------------------------------------------ Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent)); for (int c = 0; c < coordinatesNumber; c++) { if (p [obj].f > p [obj2].f) { p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp; p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp; } else { p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp; p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp; } } } } } }
마지막으로 각 파티클의 현재 위치와 작용하는 힘을 기반으로 각 파티클에 대한 새로운 좌표가 계산됩니다. 파티클은 질량이 없으므로 가속도가 없습니다. GSA 중력 검색 알고리즘과 달리 입자는 즉시 새로운 위치로 이동하며 이동 좌표는 검색 범위와 변경 단계에 따라 제한됩니다.
주석 처리된 코드는 파티클이 범위를 벗어난 경우 해당 좌표에서 멀리 떨어진 범위의 반대편에 있는 파티클을 반환합니다.
//calculation of particle motions=========================================== for (int obj = 0; obj < particlesNumber; obj++) { for (int c = 0; c < coordinatesNumber; c++) { r = RNDfromCI (0.0, 1.0); p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant; //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]); //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]); p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } }
EM 최적화 알고리즘에서 각 반복마다 실행해야 하는 두 번째 메서드인 Revision() 메서드는 현재 반복에서 파티클의 최적의 위치를 확인하는 역할을 담당하며 메서드 내부에서 모든 파티클을 반복하고 피트니스 함수의 값을 현재 최적값인 fB와 비교합니다. 현재 파티클의 적합도 함수 값이 fB보다 크면 fB가 업데이트되고 파티클의 위치가 cB 배열에 복사됩니다.
따라서 Revision() 메서드를 사용하면 알고리즘을 반복할 때마다 파티클의 최적 위치를 추적하고 이를 cB 배열에 저장할 수 있습니다. 이는 최적의 솔루션을 찾는 프로세스를 최적화하고 알고리즘의 효율성을 높이는 데 도움이 됩니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_EM::Revision () { for (int s = 0; s < particlesNumber; s++) { if (p [s].f > fB) { fB = p [s].f; ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
"전자기 알고리즘" 최적화 알고리즘의 SeInDiSp() 메서드는 스텝을 사용하여 주어진 범위[InMin, InMax] 내에서 In 변수 값을 제한하는 데 사용됩니다. In이 InMin보다 작거나 같으면 메서드는 InMin을 반환합니다. In이 InMax보다 크거나 같으면 메서드는 InMax를 반환합니다. 단계가 0이면 메서드는 원래의 In 값을 반환합니다. 그렇지 않으면 이 메서드는 방정식을 사용하여 새로운 In 값을 계산합니다: InMin + Step * (In - InMin) / Step, 여기서 MathRound()는 숫자를 가장 가까운 정수로 반올림하는 메서드입니다.
따라서 SeInDiSp() 메서드를 사용하면 지정된 한도 내에서 지정된 단계로 In 변수 값의 변화를 제어할 수 있으므로 함수를 보다 효율적이고 빠르게 최적화하는 데 도움이 됩니다.
//—————————————————————————————————————————————————————————————————————————————— // Choice in discrete space double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step) { if (In <= InMin) return (InMin); if (In >= InMax) return (InMax); if (Step == 0.0) return (In); else return (InMin + Step * (double)MathRound ((In - InMin) / Step)); } //——————————————————————————————————————————————————————————————————————————————
3. 테스트 결과
ME 알고리즘 테스트 스탠드 결과:
2023.03.26 18:27:39.259 C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259 =============================
2023.03.26 18:27:43.215 5 Rastrigin's; Func 10000 실행 결과: 59.939529106561224
2023.03.26 18:27:43.215 점수: 0.74268
2023.03.26 18:27:52.960 25 Rastrigin's; Func 10000 실행 결과: 59.780143424645416
2023.03.26 18:27:52.960 점수: 0.74071
2023.03.26 18:29:22.856 500 Rastrigin's; Func 10000 실행 결과: 63.94951378068386
2023.03.26 18:29:22.856 점수: 0.79237
2023.03.26 18:29:22.856 =============================
2023.03.26 18:29:28.901 5 숲의; Func 10000 실행 결과: 0.28698617113254693
2023.03.26 18:29:28.901 점수: 0.16233
2023.03.26 18:29:38.103 25 Forest's; Func 10000 실행 결과: 0.1571444033424823
2023.03.26 18:29:38.103 점수: 0.08889
2023.03.26 18:30:53.341 500 숲의; Func 10000 실행 결과: 0.11734383105881332
2023.03.26 18:30:53.341 점수: 0.06638
2023.03.26 18:30:53.341 =============================
2023.03.26 18:30:58.108 5 메가시티; Func 10000 실행 결과: 1.3599999999999999
2023.03.26 18:30:58.108 점수: 0.11333
2023.03.26 18:31:08.897 25 Megacity's; Func 10000 실행 결과: 0.776
2023.03.26 18:31:08.897 점수: 0.06467
2023.03.26 18:32:23.199 500 메가시티; Func 10000 실행 결과: 0.34320000000000006
2023.03.26 18:32:23.199 점수: 0.02860
2023.03.26 18:32:23.199 =============================
2023.03.26 18:32:23.199 전체 점수: 2.79996
테스트 함수에 대한 ME 알고리즘의 애니메이션에 주목하면 일종의 검색 공간의 '전기화'를 상상할 수 있습니다. 파티클은 테스트 함수 표면의 특징에 따라 높은 전하 그룹을 형성합니다. 안타깝게도 컨버전스 화질은 눈에 띄게 낮지만 이미지는 부인할 수 없을 정도로 아름답습니다.
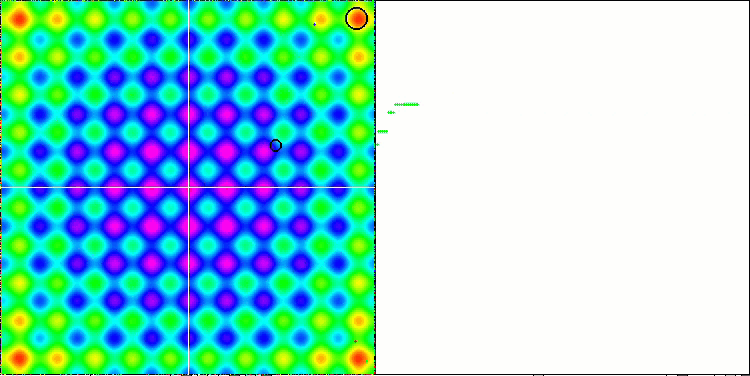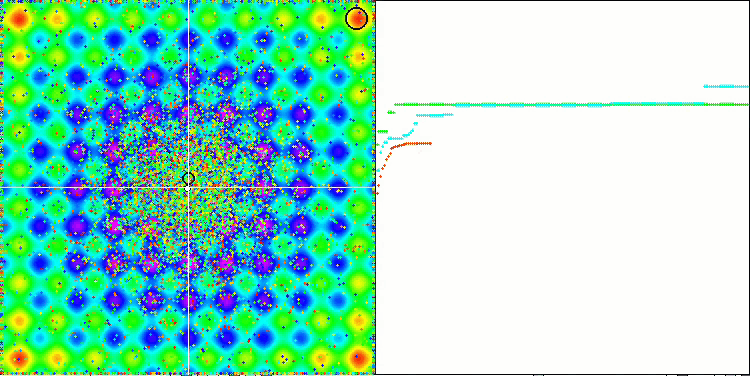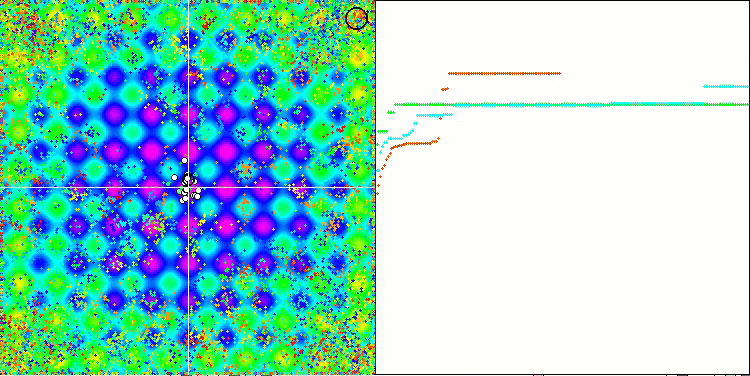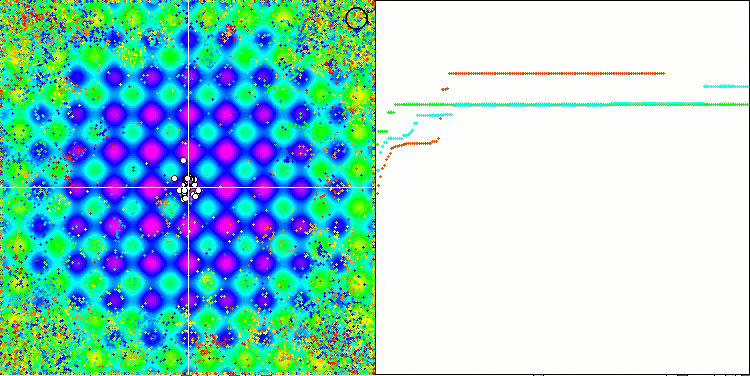
라스트진 테스트 함수에서 EM
포레스트 테스트 함수에서 EM
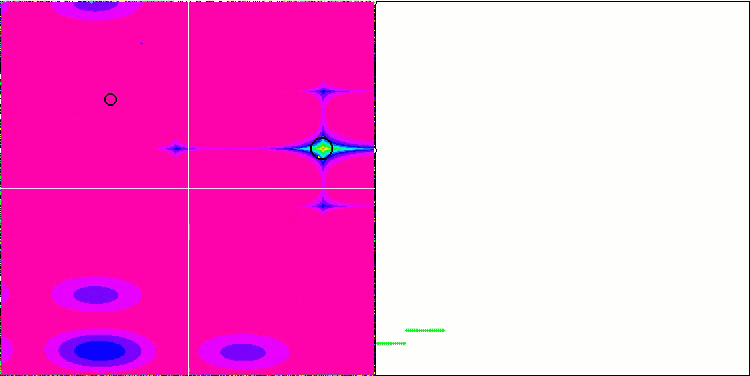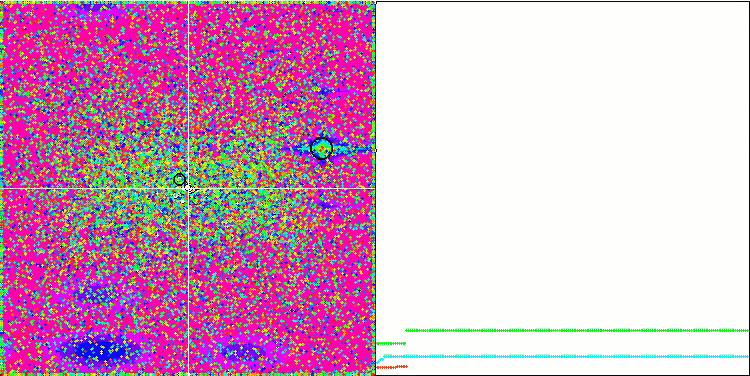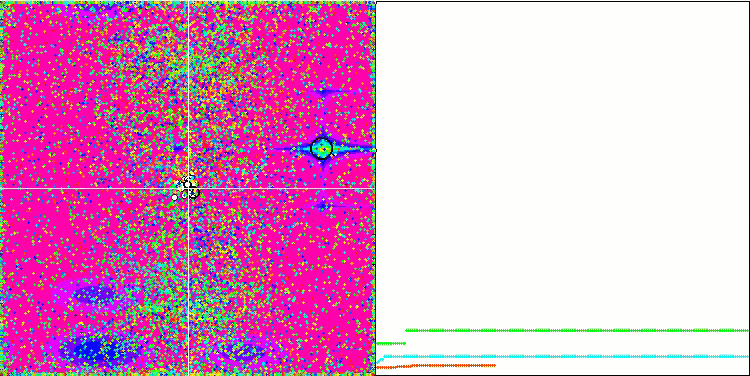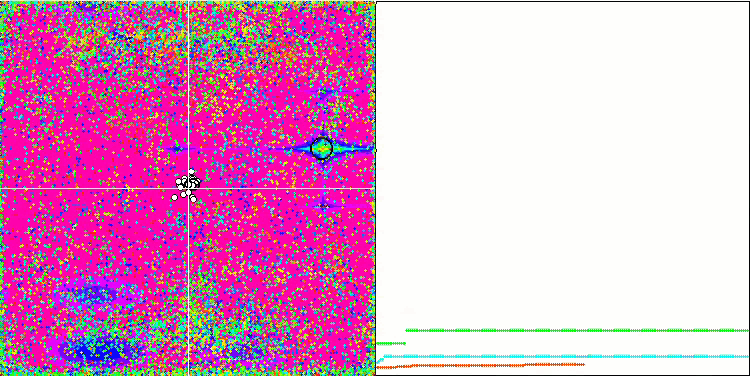
메가시티 테스트 함수에서 EM
EM 최적화 알고리즘의 테스트 결과로 넘어가 보겠습니다. EM은 최종 점수 22점으로 평균 이하의 성적을 거두었습니다. 알고리즘은 거의 모든 테스트에서 좋지 않은 결과를 보였습니다. 예외는 1000개의 매개변수가 있는 Rastrigin 함수 테스트인데 EM이 SSG 및 BA와 같은 강력한 알고리즘보다 나은 것으로 밝혀졌습니다. 또한 1000개의 매개변수에서 함수의 절대값은 10개와 50개의 매개변수를 사용한 테스트보다 더 높은 것으로 나타났습니다!
최적화된 매개변수의 수가 증가함에 따라 검색 결과가 개선된 것은 이번이 처음입니다. 대부분의 경우 이 현상은 EM 검색 전략 자체의 특성과 관련이 있습니다. 연구된 함수 정의의 전체 영역에 걸쳐 기울기 및 차별성의 존재에 대한 EM의 민감도에 주목할 필요가 있습니다.
| AO | 설명 | 라스트진 | 라스트진 최종 | 숲 | 숲 최종 | 메가시티(이산) | 메가시티 최종 | 최종 결과 | ||||||
| 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | ||||||
| SSG | 묘목 파종 및 성장 | 1.00000 | 1.00000 | 0.55665 | 2.55665 | 0.72740 | 0.94522 | 1.00000 | 2.67262 | 0.76364 | 0.85977 | 1.00000 | 2.62340 | 100.000 |
| HS | 하모니 검색 | 0.99676 | 0.95282 | 0.48178 | 2.43136 | 1.00000 | 0.98931 | 0.44806 | 2.43736 | 1.00000 | 1.00000 | 0.41537 | 2.41537 | 92.329 |
| ACOm | 개미 식민지 최적화 M | 0.34611 | 0.17985 | 0.17044 | 0.69640 | 0.86888 | 1.00000 | 0.77362 | 2.64249 | 1.00000 | 0.88930 | 0.05606 | 1.94536 | 65.347 |
| IWO | 침입성 잡초 최적화 | 0.95828 | 0.67083 | 0.29807 | 1.92719 | 0.70773 | 0.46349 | 0.31773 | 1.48896 | 0.80000 | 0.42067 | 0.33289 | 1.55356 | 61.104 |
| COAm | 뻐꾸기 최적화 알고리즘 M | 0.92400 | 0.46794 | 0.26004 | 1.65199 | 0.58378 | 0.34034 | 0.16526 | 1.08939 | 0.72727 | 0.33025 | 0.17083 | 1.22835 | 47.612 |
| FAm | 반딧불이 알고리즘 M | 0.59825 | 0.33980 | 0.17135 | 1.10941 | 0.51073 | 0.42299 | 0.49790 | 1.43161 | 0.34545 | 0.28044 | 0.35258 | 0.97847 | 41.537 |
| ABC | 인공 꿀벌 군집 | 0.78170 | 0.32715 | 0.20822 | 1.31707 | 0.53837 | 0.21455 | 0.13344 | 0.88636 | 0.56364 | 0.26569 | 0.13926 | 0.96858 | 36.849 |
| GSA | 중력 검색 알고리즘 | 0.70167 | 0.45217 | 0.00000 | 1.15384 | 0.31660 | 0.36416 | 0.33204 | 1.01280 | 0.59395 | 0.35054 | 0.00000 | 0.94448 | 36.028 |
| BA | 박쥐 알고리즘 | 0.40526 | 0.63761 | 0.84451 | 1.88738 | 0.20841 | 0.17477 | 0.25989 | 0.64308 | 0.29698 | 0.09963 | 0.17371 | 0.57032 | 35.888 |
| BFO | 박테리아 먹이 채집 최적화 | 0.67203 | 0.30963 | 0.11813 | 1.09979 | 0.39702 | 0.26623 | 0.20652 | 0.86976 | 0.52122 | 0.33211 | 0.18932 | 1.04264 | 34.693 |
| EM | 전자기 유사 알고리즘 | 0.12235 | 0.46278 | 1.00000 | 1.58513 | 0.00000 | 0.03498 | 0.34880 | 0.38377 | 0.00000 | 0.00000 | 0.10924 | 0.10924 | 22.091 |
| MA | 원숭이 알고리즘 | 0.33192 | 0.33451 | 0.14644 | 0.81287 | 0.10012 | 0.07891 | 0.08932 | 0.26836 | 0.21818 | 0.04243 | 0.10720 | 0.36781 | 13.603 |
| FSS | 물고기 떼 검색 | 0.46812 | 0.25337 | 0.11302 | 0.83451 | 0.12840 | 0.05013 | 0.06516 | 0.24369 | 0.16971 | 0.04796 | 0.08283 | 0.30050 | 12.655 |
| PSO | 파티클 스웜 최적화 | 0.20449 | 0.08200 | 0.07160 | 0.35809 | 0.18895 | 0.10486 | 0.21738 | 0.51119 | 0.23636 | 0.05903 | 0.01957 | 0.31496 | 10.031 |
| RND | 랜덤 | 0.16826 | 0.09743 | 0.08019 | 0.34589 | 0.13496 | 0.04810 | 0.04715 | 0.23021 | 0.16971 | 0.03875 | 0.04922 | 0.25767 | 5.302 |
| GWO | 회색 늑대 최적화 | 0.00000 | 0.00000 | 0.02256 | 0.02256 | 0.06570 | 0.00000 | 0.00000 | 0.06570 | 0.32727 | 0.07378 | 0.02557 | 0.42663 | 1.000 |
요약
- EM 알고리즘은 다양한 최적화 문제, 특히 대량의 데이터 처리 및 고차원의 매끄러운 함수 처리와 관련된 문제를 해결할 수 있는 효율적인 최적화 방법입니다.
- 이 알고리즘은 물리적 공간에서 전자기 입자의 움직임을 시뮬레이션하여 복잡한 다차원 함수로 작업할 때 결과의 높은 정확도를 달성할 수 있습니다.
- EM 알고리즘은 기울기 계산이 필요하지 않으므로 다양한 문제에 적용하기 쉽지만 최적화되는 함수에 기울기가 있는지 여부에 민감합니다.
- 특정 최적화 문제에 따라 알고리즘을 수정하고 사용자 지정할 수 있으므로 다양한 함수들을 최적화하는 데 유연한 도구가 됩니다.
- 기본 버전보다 개선되고 특정 최적화 문제에 맞게 조정할 수 있는 다양한 EM 알고리즘의 변경이 있습니다.
- EM 알고리즘은 머신러닝, 인공지능, 금융시장 최적화 등 다양한 분야에서 활용될 수 있습니다.
전자기 알고리즘의 가장 큰 장점은 결과의 높은 정확도를 유지하면서 다차원 공간과 큰 차원에서 최적화 문제를 해결할 수 있다는 것입니다.
따라서 EM 알고리즘은 다양한 함수들을 최적화하는 데 효과적인 도구이며 특히 대량의 데이터 및/또는 고차원성을 처리할 때 광범위한 최적화 문제에 사용할 수 있습니다.
이 평가는 특정 최적화 문제를 해결하는 데 가장 적합한 알고리즘을 선택하는 데 유용할 수 있습니다. 그러나 알고리즘의 효율성은 문제의 크기, 함수 유형, 변수 수 등 여러 요인에 따라 달라집니다. 따라서 알고리즘의 선택은 특정 문제의 철저한 분석을 기반으로 해야 합니다.
그림 1은 알고리즘의 테스트 결과를 보여줍니다.
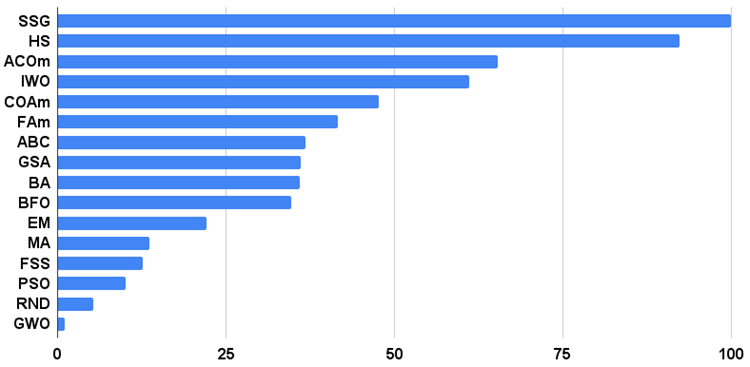
그림 1. 알고리즘 테스트 결과 히스토그램
전자기 알고리즘(EM)의 장단점:
1. 간편한 구현.
2. 부드러운 함수에 대한 확장성.
3. 적은 수의 외부 매개변수.
단점:
1. 높은 계산 복잡성.
2. 불연속 함수에 대해 결과가 좋지 않음.
3. 평평한 수평 '플랫폼'이 있는 함수에 갇힘.
각각의 기사에는 이전의 모든 기사에서 다룬 알고리즘 코드의 최신 버전이 업데이트된 아카이브가 포함되어 있습니다. 이 기사는 저의 축적된 경험을 바탕으로 작성되었으며 저의 개인적인 의견을 나타냅니다. 결론과 판단은 실험을 기반으로 합니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/12352
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.