
Risikobewertung durch die Abfolge von Positionen von Finanzanlagen
Vorwort
Dieser Artikel bezieht sich auf die Idee von Ralph Vince zur Bestimmung des Volumens der Positionen (in diesem Zusammenhang hilft es, sich mit der Kelly-Formel vertraut zu machen). Dies wird auch als optimales f bezeichnet. In dieser Theorie ist f der Anteil der Mittel, der in jedem Handelsgeschäft riskiert werden. Nach Vince wird f in Abhängigkeit von den Bedingungen der Optimierung (Maximierung) des Gewinns gewählt. Es gibt zwei Probleme, die sich bei der Anwendung dieser Theorie im Handel ergeben. Sie sind:
- Zu große Drawdowns auf dem Konto.
- f ist nur aus der Kontohistorie zu ermitteln.
Der Versuch, diese Probleme zu lösen, ist nur eines der Ziele dieses Artikels. Ein weiteres Problem ist ein erneuter Versuch, die Wahrscheinlichkeitstheorie und die mathematische Statistik zur Analyse von Handelssystemen zu verwenden. Deshalb wird gelegentlich vom Hauptthema abgeschweift. Ich werde die Grundlagen aber nicht erläutern. Bei Interesse kann sich der Leser dem Buch "The Mathematics of Technical Analysis: Applying Statistics to Trading Stocks, Options and Futures" zuwenden.
Dieser Artikel enthält Beispiele. Sie illustrieren die Theorie, die im Artikel beschrieben wird, folglich wird nicht empfohlen, sie im realen Handel zu verwenden.
Einführung, Die Abwesenheit von Unsicherheit
Der Einfachheit halber sei angenommen, dass der Preis einer Finanzanlage deren Wert in Geldwerten ausdrückt und nicht umgekehrt. Die kleinste Stufe, das Volumen zu ändern, ist ein fester Wert in der Einheit der Finanzanlage. Das kleinste Volumen größer Null entspricht dieser Stufe. Schauen wir uns ein einfaches Modell an.
Für jede Position sind seine Art (Kauf/Verkauf), sein Volumen v sowie der Einstiegs-, Ausstiegspreis und der Stop-Loss penter, pexit und pstop bekannt.
Offensichtliche Nebenbedingungen:
- Ein Volumen größer Null v≥0
- Bei einem Kauf muss der Stopppreis muss unter dem Einstiegspreis liegen: pstop<penter
- Bei einem Verkauf muss der Stopppreis muss über dem Einstiegspreis liegen: pstop>penter.
Verwenden wir die folgenden Notationen:
- C0 — Kapital vor dem Handel;
- C1 — Kapital nach dem Handel;
- Cs — Kapital, nachdem Stop-Loss ausgelöst wurde;
- r — der Anteil des Anfangskapitals, der beim Auslösen des Stop-Loss verlustig ginge;
das heißt C0−Cs=rC0.
Für einen Kauf: C1=C0+v(pexit−penter) und Cs=C0−v(penter−pstop).
Das Gleiche für einen Verkauf: C1=C0+v(penter−pexit) und Cs=C0−v(pstop−penter).
Nach einfachen Umstellungen erhalten wir C1=C0(1+ra) mit a=(pexit−penter)/(penter−pstop). Diese Ausdrücke gelten für Kauf und Verkauf. Bezeichnen wir jetzt den Wert von r als das Risiko der Position und den Wert a als den Ertrag der Position.
Betrachten wir die Risikokontrolle unseren Modells. Angenommen wir haben n Positionen mit den Erträgen ai mit i=1..n,. Jetzt wollen wir die Risiken ri abschätzen. Es sollte beachtet werden, dass die Werte ri bei einer neuen Position nur aus bereits bekannten Werten ermittelt werden können. Die Risiken werden allgemein als gleich angenommen ri=r mit 0≤r<1. r=rmax ist der Wert, der den Gewinn Maximiert Cn=C0(1+ra1)(1+ra2)…(1+ran).
Wir verwenden eine ähnlichen Ansatz, wenn auch mit ein paar Unterschieden, und wir berücksichtigen ein paar Nebenbedingungen. Diese sind der maximale Drawdown und der Durchschnittsertrag einer Abfolge von Positionen. Verwenden wir die folgenden Notationen:
- A0 der kleinste aller ai,
- A=(a1+a2+…+an)/n ist ihr arithmetischer Mittelwert.
Es gilt immer, dass A0≤A, und Gleichheit existiert nur, wenn alle ai=A0. Betrachtern wir die Nebenbedingungen von r im Detail.
- Cn=Cn(r)>0 woraus folgt 1+rA0>0. Wenn gilt A0≥−1, dann gilt für alle 0≤r<1. In diesem Fall, wenn A0<−1 erhalten wir 0≤r<−1/A0. Wir können erkennen, dass eine weitere Nebenbedingung für r nur dann auftritt, wenn Positionen durch Stop-Loss mit Slippage beendet werden. Im Ergebnis ergibt sich diese Nebenbedingung als 0≤r<rc mit rc=1, if A0≥−1 und rc=−1/A0 if A0<−1.
-
Wir definieren den durchschnittlichen Ertrag als g as Cn=C0(1+gr)^n, da
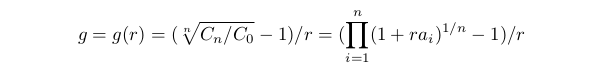
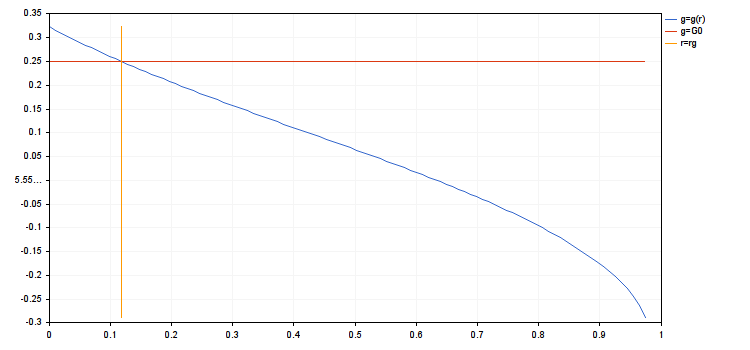
Anders ausgedrückt kann g als Durchschnittsertrag einer Abfolge von Positionen bezüglich des akzeptierten Risikos bezeichnet werden. Die Funktion g(r) wird bei der Umsetzung der Nebenbedingungen des vorherigen Punktes festgelegt. Sie hat eine entfernbare Singularität im Punkt r=0: wenn r→0 dann g(r)→A und wir können g(0)=A akzeptieren. Es kann gezeigt werden, dass g(r)≡A nur gilt, falls alle ai=A. Sind hingegen die ai unterschiedlich, dann fällt g(r), wenn r ansteigt. Diese Nebenbedingung stellt sich so dar g(r)≥G0>0. Die Konstante G0 hängt von Vielem ab - Handelsbedingungen, Vorlieben des Händlers etc. Im Rahmen dieses Modells können wir sagen, dass, wenn wir G0>A annehmen, die Menge r, die ungleich sind, leer sein wird. Wenn G0≤A, dass stell sich unsere Nebenbedingung wie folgt dar: 0≤r≤rg wobei rg die Lösung der Gleichung g(rg)=G0 ist. Wenn diese Gleichung keine Lösung hat, dann gilt rg=1.
-
Um den maximalen Drawdown auszuwerten, betrachten wir dessen Gegenteil:
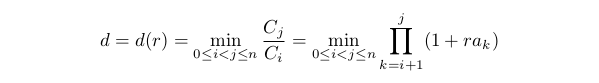
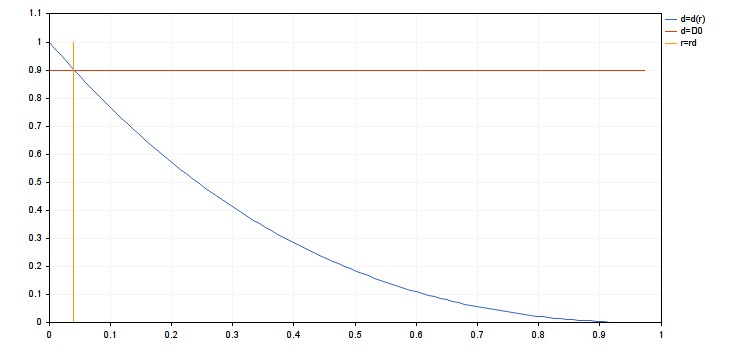
Dieser Wert kann als minimaler Ertrag bezeichnet werden. Es ist praktisch, da er immer positiv und endlich ist, wenn die im ersten Punkt angegebene Nebenbedingung erfüllt ist. Es ist offensichtlich, dass d(0)=1. Wenn A0<0, dann fällt d(r) wenn r steigt innerhalb der Grenzen aus dem ersten Punkt. Diese Nebenbedingung kann geschrieben werden in der Form d(r)≥D0 mit 0<D0<1. Je größer D0, desto kleiner ist der zulässige Drawdown. Formulieren wir die Nebenbedingung neu als 0≤r≤rd wobei rd die Lösung der Gleichung d(rd)=D0 ist (wenn die Gleichung eine Lösung hat, dann ist rd=1).
-
Wenn eine Position eröffnet wurde, darf das Volumen v keine beliebigen Wert annehmen. Der Wert muss ein Vielfaches von Δv>0, das heißt v=kΔv für die ganzen Zahl k≥0. Dann gilt für die ite Position:
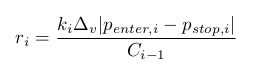
Offensichtlich ist das Zusammentreffen aller ri extrem unwahrscheinlich. Folglich hat die oben erwähnte Aufgabe keine präzise Lösung. Wir müssen also nach Näherung suchen. Wir beschränken uns auf die Berechnung des kleinsten rv, so dass jedes ri einen Wert größer Null innerhalb des Intervalls [0,rv] hat.
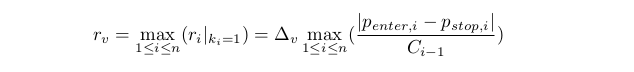
Bestimmen wir dazu noch eine grobe Schätzung für rvr≥rv. Um die Nebenbedingung des vorherigen Punktes zu erfüllen folgt Ci≥D0C0>0. Woraus folgt (bitte beachten Sie, d0 und D0 bedeuten dasselbe):
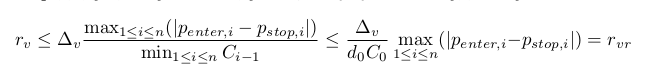
Diese Schätzung ist praktisch, weil sie eine einfachere Beziehung zum Kapital hat. Sie hängt nur vom Anfangswert des Kapitals ab.
Wir gehen davon aus, dass die Menge, die die ersten drei Nebenbedingungen erfüllt, nicht leer ist. Dann hat es die Form eines Intervalls [0,ra] mit ra=min(rc,rg,rd).
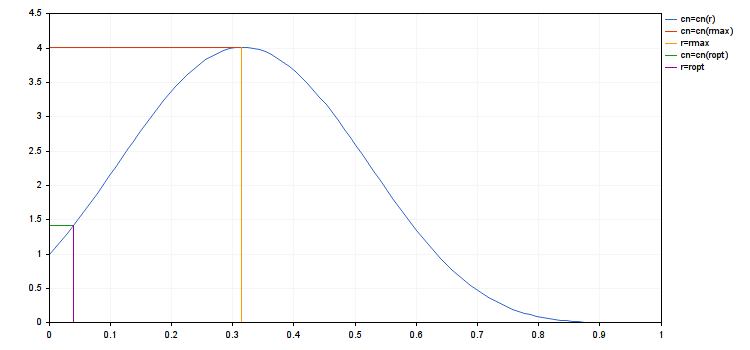
Wir nehmen auch an, dass die vierte Nebenbedingung erfüllt wird. Das erfordert ra≥rv. Betrachten wir jetzt das Problem der Maximierung Cn=Cn(r). Der für uns wichtige Punkt ist A>0 und A0<0. Diese Funktion steigt im Intervall [0,rmax] und fällt im Intervall [rmax,rc]. Hier ist rmax der Nullpunkt der ersten Ableitung dCn(r)/dr=0.
Jetzt ist ropt leicht zu ermitteln, er maximiert Cn(r) im Intervall [0,ra]: ropt=min(ra,rmax). Es bleiben zwei Fälle: 1) A0≤A≤0 und 2) 0≤A0≤A. Im ersten Fall ist ropt=rmax=0, und im zweiten rmax=rс und ropt=ra .
Betrachten wir jetzt den Fall, wenn die Menge durch die Nebenbedingungen leer ist. Das passiert in zwei Fällen: 1) G0>A or 2) ra<rv. Wir müssen nur davon ausgehen, dass ropt=0.
Jetzt könne wir die Werte ri unter Berücksichtigung der diskreten Natur der Volumina ermitteln. Es sei Ri eine nicht leere, finite Menge von Zahlen im Intervall [0,ra], die für den Risikowert ri in der iten Position geeignet sind. Wir wählen ropt,i, das Cn(r) in Ri maximiert. Wenn ropt∈Ri dann gilt ropt,i=ropt. Wenn gilt ropt∉Ri, gibt es zwei Möglichkeiten: 1) alle Punkte Ri befinden sich auf einer Seite von ropt und 2) die Punkte Ri befinden sich auf beiden Seiten von ropt. Im ersten Fall wählen wir ropt,i, ein Punkt aus Ri, der ropt am nächsten liegt. Im zweiten Fall wählen wir zwei Punkte aus Ri, die auf jeder Seite ropt am nächsten sind. Als ropt,i wird dann der ausgewählt, dessen Cn(r) größer ist.
Unsicherheit, Einführendes Beispiel
Machen wir das in der Einleitung betrachtete Modell etwas komplizierter. Nehmen wir an, wir kennen n Zahlen von ai, aber wir kennen nicht deren Reihenfolge. Ihre willkürliche Permutation ist somit erlaubt. Mal sehen, wie sich die oben erhaltenen Ergebnisse ändern. In den ersten beiden Punkte wird eine zufällige Permutation von ai nichts ändern. Es gibt auch keine Änderung im vierten Punkt, wenn die gröbere Evaluation rvr verwendet wird.
Im dritten Punkt allerdings könnten sich Änderungen ergeben. In der Tat, falls sich eine Reihenfolge ergibt, so dass es zwischen den negativen keine positiven gibt, wird der Drawdown maximal. Umgekehrt reduzieren gleichmäßig gemischte, positive und negative Ergebnisse den Drawdown. Die Gesamtzahl der Permutationen beträgt n!. Das ist eine sehr große Zahl, selbst wenn n nur wenige Vielfache von Zehn beträgt. Theoretisch könnten wir das Problem für jede einzelne Permutation j=1..n! der Werte ai lösen und erhalten die Zahlenmenge rd,j. Es gibt jedoch ein anhaltendes Problem. Wir wissen nicht für welche Permutation wir uns entscheiden sollen. Um mit dieser Unsicherheit umgehen zu können, müssen wir die Konzepte und Methoden der Wahrscheinlichkeitstheorie und der mathematischen Statistik anwenden.
Betrachten wir eine Reihe von Zahlen rd,j als Werte der Funktion ρd=ρd(j)=rd,j, die von den Permutationen abhängt. In der Wahrscheinlichkeitstheorie ist ρd eine Zufallsvariable, bei der die Menge der Ereignisse die Menge der n Permutationen entspricht. Wir behandeln sie alle als unterschiedlich, selbst wenn einige ai gleich sein sollten.
Wir nehmen weiters an, alle n Permutation sind gleich wahrscheinlich. Dadurch wird die Wahrscheinlichkeit von jeder 1/n!. Dies entzieht sich dem probabilistischen Maß an Elementarereignissen. Nun können wir die Wahrscheinlichkeitsverteilung ρρd(x)=n(x)/n! für Pd wobei n(x) die Anzahl von n Permutation für die gilt rd,j<x. An dieser Stelle muss die Nebenbedingung für den Drawdown angegeben werden. Neben dem minimal zulässigen D0 müssen wir ein Signifikanzniveau 0<δ<<1 für die Akzeptanz des Ergebnisses angeben. Der Wert δ gibt an, mit welcher Wahrscheinlichkeit wir ein Überschreiten der Grenze für den Drawdown als vernachlässigbar erachten. Dann können wir rd(δ) als das δ Quantil der Verteilung Pρd(x) bestimmen. Um eine ungefähre Lösung für dieses Problem zu finden, werden wir eine große Anzahl von nt erzeugen, mit 1<<nt<<n!, n Permutationen. Finden wir jetzt für jede den Wert rd,j, mit 1≤j≤nt. Dann können wir die Schätzung von rd(δ) das Quantil δ aus rd,j verwenden.
Obwohl dieses Modell ist etwas künstlich ist, es hat dennoch seinen Nutzen. Wir können zum Beispiel rd nehmen, berechnet für die ersten Positionen, und damit die Wahrscheinlichkeit von pd=Pρd(rd) ermitteln. Offensichtlich ist die Ungleichung 0≤pd≤1 erfüllt. pd nahe Null bedeutet, dass ein großer Drawdown durch nahe beieinander liegende Verlustpositionen verursacht wird. Ein pd nahe Eins zeigt, dass Gewinner und Verlierer gleichmäßig gemischt sind. Auf diese Weise kann man nicht nur eine Reihe von Verlusten in der Abfolge der Positionen entdecken (wie z. B. bei der Methode Z-Score), sondern auch einen gewissen Einfluss auf den Drawdown. Es können weitere Indices entweder aus Pρd() oder aus rd erzeugt werden.
Unsicherheit, Allgemeiner Fall
Nehmen wir an, es gibt eine Abfolge von Positionen mit Erträgen ai, 1≤i≤n. Nehmen wir weiters an, diese Sequenz sei die Umsetzung einer Folge von unabhängigen und identisch verteilten Zufallsvariablen λi einer Grundgesamtheit. Wir bezeichnen ihre Funktion der Wahrscheinlichkeitsverteilung mit Pλ(x). Es wird angenommen, dass sie folgende Eigenschaften hat:
- einen positiven mathematischen Erwartungswert Mλ
- eine Untergrenze. Es gibt eine Zahl λmin≤−1 für die gilt Pλ(x)=0 wenn x<λmin und Pλ(x)>0 wenn x>λ0
Diese Bedingungen bedeuten, dass der Durchschnittsertrag positiv ist. Obwohl Verlustpositionen wahrscheinlich sind, besteht jedoch immer die Möglichkeit, nicht das gesamte Kapital durch eine Position mit einer Risikobegrenzung zu verlieren.
Lassen Sie uns das Problem der Ermittlung der Größenordnung des Risikos feststellen. Ähnlich wie im Beispiel des vorigen Abschnitts sollte wir die Zufallsvariable ρopt statt ropt, berechnet in der Einleitung untersuchen. Dann setzen wir das Signifikanzniveau δ und berechnen ropt=ropt(δ) wobei δ ein Quantil der Verteilung Pρopt(x) ist. In Zukunft können wir unser System mit diesem Risiko nutzen, solange der Drawdown und der durchschnittliche Ertrag innerhalb der vorgegebenen Grenzen liegen. Werden diese Grenzen überschritten, muss das System abgelehnt werden. Die Fehlerwahrscheinlichkeit wird δ nicht überschreiten.
Ich möchte betonen, dass δ klein sein muss. Die Verwendung der erhaltenen Kriterien machen keinen Sinn für große δ . Nur bei einem kleinen δ kann angenommen werden, dass zwei Ereignisse miteinander verbunden sind: 1) das System funktioniert wegen eines veränderten Marktes nicht und 2) entweder der Drawdown ist zu groß oder der Ertrag ist zu klein. Zusätzlich zu dem Fehler, über den wir bereits gesprochen haben, kann eine andere Art von Fehler berücksichtigt werden. Wir erkennen durch ihn keine Veränderungen des Marktes, die einen Einfluss auf den Drawdown und die Profitabilität unseres Systems haben. Aus praktischer Sicht macht ein solcher Fehler natürlich keinen Sinn, weil er die Rentabilität des Systems nicht verändert.
In unserer Theorie zeigt sich dies darin, dass die Änderungen der Verteilungen Pλ(x) und Pρopt(x) nicht so wichtig für uns sind. Das einzige, was zählt, ist die Veränderung des δ Quantils Pρopt(x). Dies bedeutet insbesondere, dass in der Abfolge der Erträge keine stationäre Vorgabe erforderlich ist. Wenn wir das sagen, brauchen wir die Stationarität für die Wiederherstellung des Gesetzes der Ertragsverteilung auf der letzten Probe ai, 1≤i≤n. Dabei kann die Voraussetzung, dass sich die Verteilung nicht wesentlich ändert, anstelle der absoluten Stationarität ausreichend sein.
Im Endeffekt kann ρopt durch λi ausgedrückt werden, obwohl das eine komplexe Beziehung ist (sie wird durch andere zufällige Zwischenvariablen ausgedrückt). Dies verlangt die Untersuchung der Zufallsvariablen, die als Funktion von λi definiert sind und dem Erstellen von deren Verteilung. Dafür müssen wir Pλ(x) kennen. Zählen wir drei Varianten auf, welche Informationen wir über diese Distribution haben könnten.
- Es gibt einen genauen Ausdruck für Pλ(x) oder es gibt einen Weg, eine genügend genaue Näherung für ein zu analysierendes Handelssystem zu erstellen. Dies ist in der Regel nur möglich, wenn eine begründete Annahme über das Verhalten der Preise eine Finanzanlage vorliegt Zum Beispiel können wir die Hypothese des Random Walk als zutreffend erachten. Mit dieser Information ist ein Handel praktisch unmöglich. Die so gezogenen Schlussfolgerungen sind unrealistisch und verneinen in der Regel die Möglichkeit eines Gewinnes insgesamt. Dies kann anders genutzt werden. Mit dieser Hypothese können wir einen Nullhypothese aufstellen. Dann, mit Hilfe von empirischen Daten und Tests auf Konkordanz, können wir die Hypothese entweder verwerfen oder akzeptieren, dass wir sie mit unseren Daten nicht verwerfen können. In unserem Falls sind dies empirischen Daten die Abfolge der ai, 1≤i≤n.
- Pλ(x) ist bekannt dafür, dass es zu einer parametrischen Familie von Verteilungen gehört oder denen nahe kommt. Dies ist möglich, wenn die Annahmen über die Preise der Finanzanlagen aus dem vorherigen Punkt nicht weit entfernt sind. Natürlich wird der Typ der Verteilungsfamilie auch durch den Algorithmus des Handelssystems bestimmt. Die genauen Werte für die Parameter der Verteilung werden mit Hilfe der Abfolge ai, 1≤i≤n durch die Methode Parametric Statistics.
- Zusammen mit der Abfolge der ai, 1≤i≤n sind ein paar gemeinsame Eigenschaften von Pλ(x) bekannt (oder angenommen). Zum Beispiel kann dies eine Annahme über den existierenden endlichen Erwartungswert und Varianz sein. In diesem Fall verwenden wir eine Empirische Verteilungsfunktion als Näherung für Pλ(x). Wir werden sie auf der Grundlage der gleichen Abfolge ai, 1≤i≤n erstellen. Methoden, die die empirische Verteilungsfunktion anstelle der exakten verwenden, werden als Bootstrap bezeichnet. In einigen Fällen muss Pλ(x) nicht bekannt sein. Zum Beispiel kann die Zufallsvariable (λ1+λ2+…+λn)/n für große n kann als normalverteilt angesehen werden (mit endlicher Varianz λi).
Dieser Artikel wird fortgeführt, wo die in der dritten Variante beschriebenen Annahmen verwendet werden. Die ersten beiden Varianten werden im Folgenden beschrieben.
Wir werden untersuchen, wie sich die Berechnungen in der Einführung verändern werden. Statt absoluter Zahlen A0 und A, arbeiten wir auf die gleiche Art mit den Zufallsvariablen λi: Λ0=min(λ1, λ2, …, λn) und Λ=(λ1+λ2+…+λn)/n.
Betrachten wir ihr asymptotisches Verhalten bei uneingeschränkt wachsendem n. In diesem Fall gilt immer Λ0→λmin. Angenommen, dass λi eine endliche Varianz Dλ. Dann gilt Λ→Mλ. Wie bereits erwähnt können wir mit hoher Sicherheit sagen, dass Λ normalverteilt ist mit dem Erwartungswert Mλ und der Varianz Dλ/n. Wenn die genauen Werte von Mλ und Dλ unbekannt sind, können wir die entsprechend den ai berechneten Gegenstücke verwenden. Die empirischen Verteilungen für Λ0 und Λ können mit Bootstrap erstellt werden.
Bevor wir ropt(δ) mit der Bootstrap-Methode berechnen, sollten wir berücksichtigen, wie sich die Berechnungen in der Einleitung ändern werden:
- Zuerst kann aufgrund des asymptotischen Verhaltens von Λ0 die Schätzung einfach auf den Wert rc=−1/λmin gesetzt werden. Für eine ausgewählte Verteilung fällt der Wert λmin А0 zusammen und daher bleibt in diesem Punkt alles gleich.
- Es ist wichtig sicher zustellen, dass die Bedingung G0≤Λ mit einer Wahrscheinlichkeit von nicht größer als δ verletzt ist. dazu muss das Quantil δ von Λ kleiner sein als G0. Um dieses Quantil zu approximieren, verwenden wir die normale Näherung der Verteilung Λ. Als Ergebnis erhalten wir nmin — die untere Schätzung der Anzahl der Positionen, die für die Analyse notwendig sind. Die standardmäßige Bootstrap-Methode kann angepasst werden und es können Stichproben mit wachsender Umfang erstellt werden, um nmin zu finden. Theoretisch gesehen haben wir mehr oder weniger dasselbe wie bei einer Näherung durch die Normalverteilung.
- Im vierten Absatz verwenden wir wie zuvor eine grobe Schätzung von rvr.
Legen wir nb fest — die Anzahl von Ertragsabfolgen, die erzeugt werden. In der Schleife der Durchführung des Bootstraps müssen wir für jedes j=1..nb die Beschränkungen für das von uns in der Einleitung aufgeführte Risiko überschreiten. In Anbetracht des Vorstehenden bleibt es für uns rg(j), rd(j), rmax(j) und ropt(j) zu berechnen. Wenn die Menge von r für einige j leer ist, nehmen wir an, dass gilt ropt(j)=0.
Am Ende des Bootstrap haben wir einen Array mit den Werten ropt[]. Das aus diesem Array stammende Quantil δ wird als Lösung des Problems betrachtet.Schlussfolgerung
Alles, was oben zu lesen ist, ist nur der Anfang des Themas. Ich werde jetzt kurz erwähnen, welchen Themen die folgenden Artikel gewidmet sein werden.
- Um das Positionsmodell als eine Folge unabhängiger, identisch Verteilungen zu verwenden, müssen wir einige Annahmen und Annahmen zu den Preisen der Finanzanlagen und dem Handelsalgorithmus machen.
- Wir müssen die Theorie, mit welchen Methoden die Positionen geschlossen werden, konkretisieren: 1) fester Stop-Loss/Take-Profit, 2) fester Trailing-Stop.
- Es muss demonstriert werden, wie man die vorgestellte Theorie verwendet, um Handelssysteme aufzubauen. Besprechen werden wir die Möglichkeit, mit der Wahrscheinlichkeitstheorie ein System, das Kurslücken handelt, aufzubauen. Wir werden auch auf das Thema des maschinellen Lernens eingehen.
Anhang zur Einführung
Nachfolgend der Code des Skripts r_intro.mq5 und sein Ergebnis - in Form von Graphen und Zahlen.
#include <Graphics\Graphic.mqh> #define N 30 #define NR 100 #property script_show_inputs input int ngr=0; // Anzahl der angezeigten Charts double G0=0.25; // kleinster Durchschnittsertrag double D0=0.9; // kleinster Mindestgewinn // Anfangskapital c0 wird als 1 angenommen void OnStart() { double A0,A,rc,rg,rd,ra,rmax,ropt,r[NR],g[NR],d[NR],cn[NR],a[N]= { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // Positionsertrag 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; A0=a[ArrayMinimum(a)]; A=0; for(int i=0; i<N;++i) A+=a[i]; A/=N; rc=1; if(A0<-1) rc=-1/A0; double c[N]; r[0]=0; cn[0]=1; g[0]=A; d[0]=1; for(int i=1; i<NR;++i) { r[i]=i*rc/NR; cn[i]=1; for(int j=0; j<N;++j) cn[i]*=1+r[i]*a[j]; g[i]=(MathPow(cn[i],1.0/N)-1)/r[i]; c[0]=1+r[i]*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+r[i]*a[j]); d[i]=dcalc(c); } int nrg,nrd,nra,nrmax,nropt; double b[NR]; for(int i=0; i<NR;++i) b[i]=MathAbs(g[i]-G0); nrg=ArrayMinimum(b); rg=r[nrg]; for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0); nrd=ArrayMinimum(b); rd=r[nrd]; nra=MathMin(nrg,nrd); ra=r[nra]; nrmax=ArrayMaximum(cn); rmax=r[nrmax]; nropt=MathMin(nra,nrmax); ropt=r[nropt]; Print("rc = ",rc,"\nrg = ",rg,"\nrd = ",rd,"\nra = ",ra,"\nrmax = ",rmax,"\nropt = ",ropt, "\ng(rmax) = ",g[nrmax],", g(ropt) = ",g[nropt], "\nd(rmax) = ",d[nrmax],", d(ropt) = ",d[nropt], "\ncn(rmax) = ",cn[nrmax],", cn(ropt) = ",cn[nropt]); if(ngr<1 || ngr>5) return; ChartSetInteger(0,CHART_SHOW,false); CGraphic graphic; graphic.Create(0,"G",0,0,0,750,350); double x[2],y[2]; switch(ngr) { case 1: graphic.CurveAdd(r,g,CURVE_LINES,"g=g(r)"); x[0]=0; x[1]=r[NR-1]; y[0]=G0; y[1]=G0; graphic.CurveAdd(x,y,CURVE_LINES,"g=G0"); x[0]=rg; x[1]=rg; y[0]=g[0]; y[1]=g[NR-1]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rg"); break; case 2: graphic.CurveAdd(r,d,CURVE_LINES,"d=d(r)"); x[0]=0; x[1]=r[NR-1]; y[0]=D0; y[1]=D0; graphic.CurveAdd(x,y,CURVE_LINES,"d=D0"); x[0]=rd; x[1]=rd; y[0]=d[0]; y[1]=d[NR-1]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rd"); break; case 3: graphic.CurveAdd(r,cn,CURVE_LINES,"cn=cn(r)"); x[0]=0; x[1]=rmax; y[0]=cn[nrmax]; y[1]=cn[nrmax]; graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(rmax)"); x[0]=rmax; x[1]=rmax; y[0]=cn[NR-1]; y[1]=cn[nrmax]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rmax"); x[0]=0; x[1]=ropt; y[0]=cn[nropt]; y[1]=cn[nropt]; graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(ropt)"); x[0]=ropt; x[1]=ropt; y[0]=cn[NR-1]; y[1]=cn[nropt]; graphic.CurveAdd(x,y,CURVE_LINES,"r=ropt"); break; case 4: c[0]=1+ropt*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+ropt*a[j]); graphic.CurveAdd(c,CURVE_LINES,"Equity, ropt"); break; case 5: c[0]=1+rmax*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+rmax*a[j]); graphic.CurveAdd(c,CURVE_LINES,"Equity, rmax"); break; } graphic.CurvePlotAll(); graphic.Update(); Sleep(30000); ChartSetInteger(0,CHART_SHOW,true); graphic.Destroy(); } // Die Funktion dcalc() akzeptiert das Array mit c1, c2, ... cN Werten und // gibt den kleinsten Gewinn d zurück. Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(int i=1; i<N;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; }
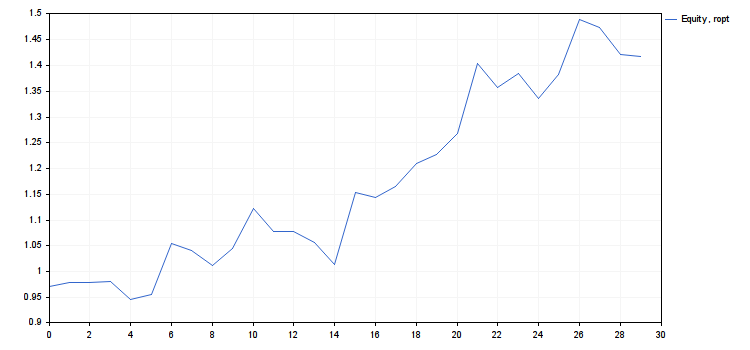
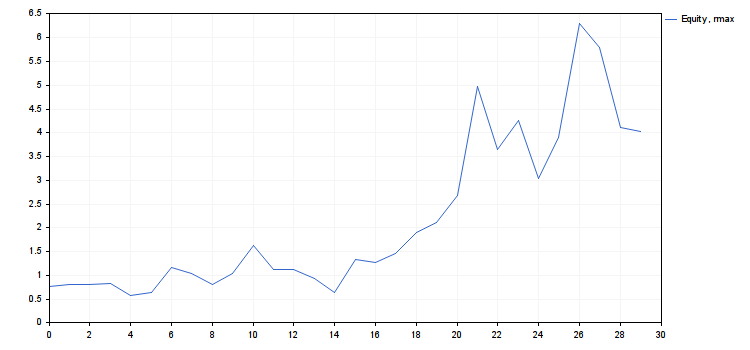
- rc = 0.9839614287119945
- rg = 0.1180753714454393
- rd = 0.03935845714847978
- ra = 0.03935845714847978
- rmax = 0.3148676571878383
- ropt = 0.03935845714847978
- g(rmax) = 0.1507064833125653, g(ropt) = 0.2967587621877231
- d(rmax) = 0.3925358395456308, d(ropt) = 0.9037200051227304
- cn(rmax) = 4.018198063206267, cn(ropt) = 1.416754202013712
- Verwendung von ropt als Risikowert des Systems.
- Das "freigegebene" Risiko von rmax−ropt kann dazu genutzt werden, neue Systeme hinzuzufügen (Diversifikation).
Anhang zum einleitenden Beispiel
Unten ist der Code des Skripts r_exmp.mq5 und dessen numerischen Resultate.
#include <Math\Stat\Uniform.mqh> #define N 30 // Länge der Abfolge von Positionen #define NR 500 // Anzahl der Segmente des Intervalls [0,rc] #define NT 500 // Anzahl der erzeugten Permutationen double D0=0.9; // kleinster Minimalgewinn double dlt=0.05; // Signifikanzniveau void OnStart() { double A0,rc,r[NR],d[NR],rd[NT],a[N]=//A,rg,ra,rmax,ropt,g[NR],cn[NR], { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,// Positionsgewinn 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; A0=a[ArrayMinimum(a)]; rc=1; if(A0<-1) rc=-1/A0; for(int i=0; i<NR;++i) r[i]=i*rc/NR; double b[NR],c[N]; int nrd; MathSrand(GetTickCount()); for(int j=0; j<NT;++j) { trps(a,N); for(int i=1; i<NR;++i) { c[0]=1+r[i]*a[0]; for(int k=1; k<N;++k) c[k]=c[k-1]*(1+r[i]*a[k]); d[i]=dcalc(c); } for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0); nrd=ArrayMinimum(b); rd[j]=r[nrd]; } double p[1],q[1]; p[0]=dlt; if(!MathQuantile(rd,p,q)) {Print("MathQuantile() error"); return;} PrintFormat("sample %f-quantile rd[] equals %f",p[0],q[0]); double rd0=0.03935845714847978; // Wert von rd aus der Einführung double pd0=0; // korrespondierender Wert von pd for(int j=0; j<NT;++j) if(rd[j]<rd0) ++pd0; pd0/=NT; PrintFormat("for rd = %f value pd = %f",rd0,pd0); } // Die Funktion dcalc() akzeptiert das Array mit c1, c2, ... cN Werten und // gibt den kleinsten Gewinn d zurück. Assume that c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(int i=1; i<N;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } // erste Zufallspermutation, die nicht größer ist als min(n,ArraySize(b)) // Elemente des Arrays b[] // Die Bibliothek MathSample() kann an Stelle von trps() verwendet werden void trps(double &b[],int n) { if(n<=1) return; int sz=ArraySize(b); if(sz<=1) return; if(sz<n) n=sz; int ner; double dnc=MathRandomUniform(0,n,ner); if(!MathIsValidNumber(dnc)) {Print("Error ",ner); ExpertRemove();} int nc=(int)dnc; if(nc>=0 && nc<n-1) { double tmp=b[n-1]; b[n-1]=b[nc]; b[nc]=tmp;} trps(b,n-1); }
- Das ausgewählte 0.05Quantil rd[] beträgt 0.021647
- für rd = 0.039358 pd = 0.584
Die erste Zeile der Ergebnisse sagt uns, dass wir das Risiko im Vergleich zu den Ergebnissen in der Einführung halbieren müssen. In diesem Fall bedeutet es, dass das System, wenn der Drawdown das Ziel (10%) überschreitet, wahrscheinlich Fehler aufweisen wird und es sollte nicht für den Handel verwendet werden. Die Fehlerwahrscheinlichkeit (Handelssystem wird abgelehnt) beträgt in diesem Fall δ (0.05 oder 5%). Die zweite Zeile des Ergebnisses besagt, dass die Inanspruchnahme in der ersten Abfolge der Positionen kleiner ist als sie durchschnittlich sein könnte. Es sei darauf hingewiesen, dass 30 Positionen möglicherweise nicht ausreichen, um dieses System zu bewerten. Daher wäre es sinnvoll, eine detaillierte Analyse mit einer größeren Anzahl von Positionen durchzuführen und zu sehen, wie sich dies auf die Ergebnisse auswirkt.
Anhang zum allgemeinen Fall
Unten ist das Skript r_cmn.mq5, in dem wir versuchen, den Wert nmin und die Ergebnisse der Arbeit des Skripts zu evaluieren:
#include <Math\Stat\Normal.mqh> #include <Math\Stat\Uniform.mqh> #include <Graphics\Graphic.mqh> #define N 30 // Länge der Positionsabfolge #define NB 10000 // Anzahl der erzeugten Stichproben für Bootstrap double G0=0.25; // kleinster Durchschnittsertrag double dlt=0.05; // Signifikanzniveau void OnStart() { double a[N]= { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // Positionsgewinn 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; double A=MathMean(a); double S2=MathVariance(a); double Sk=MathSkewness(a); double Md=MathMedian(a); Print("sample distribution parameters:"); PrintFormat("average: %f, dispersion: %f, asymmetry: %f, median: %f",A,S2,Sk,Md); PrintFormat("number of deals: %d, dlt value??: %f, G0value??: %f",N,dlt,G0); // Näherung dor die Normalverteilung Print("approximation by normal distribution:"); double q0, p0; int ner; q0=MathQuantileNormal(dlt,A,MathSqrt(S2/N),ner); if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;} Print("dlt quantile: ",q0); p0=MathCumulativeDistributionNormal(G0,A,MathSqrt(S2/N),ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;} Print("level of significance for G0: ",p0); // Bootstrap MathSrand(GetTickCount()); double b[N],s[NB]; p0=0; for(int i=0;i<NB;++i) { sample(a,b); s[i]=MathMean(b); if(s[i]<G0) ++p0; } p0/=NB; double p[1],q[1]; p[0]=dlt; if(!MathQuantile(s,p,q)) {Print("MathQuantile() error"); return;} Print("approximation by bootstrap"); Print("dlt quantile: ",q[0]); Print("level of significance for G0: ",p0); // Näherung nmin (Näherung durch die Normalverteilung) int nmin; for(nmin=1; nmin<1000;++nmin) { q0=MathQuantileNormal(dlt,A,MathSqrt(S2/nmin),ner); if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;} if(q0>G0) break; } Print("Minimal number of deals nmin (approximation by normal distribution):"); PrintFormat("no less than %d, value of the dlt quantile: %f",nmin,q0); } void sample(double &a[],double &b[]) { int ner; double dnc; for(int i=0; i<N;++i) { dnc=MathRandomUniform(0,N,ner); if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();} int nc=(int)dnc; if(nc==N) nc=N-1; b[i]=a[nc]; } }
Beispiel der Parameter:
- Durchschnitt: 0.322655
- Varianz: 1.419552
- Asymmetrie: 0.990362
- Median: 0.023030
- Anzahl der Positionen: 30
- Der Wert für dlt: 0.050000
- Der Wert für G0: 0.250000.
Näherung durch die Normalverteilung:
- dlt Quantil: -0.03514631247305994;
- Signifikanzniveau für G0: 0.3691880511783918.
Näherung durch Bootstrap:
- dlt Quantil: -0.0136361;
- Signifikanzniveau für G0: 0.3727.
- Minimale Anzahl der Positionen nmin (Näherung durch die Normalverteilung): nicht kleiner als 728
- Der Wert des dl-Quantils: 0.250022.
Es folgt aus diesen Ergebnissen, dass ropt(δ)=0. Dies bedeutet, dass unser Kriterium den Handel mit diesem System aufgrund der Daten verbietet oder die Historie der Positionen einen größeren Umfang erfordert. Dies trotz der so schönen Charts im ersten Anhang. Bootstrap lieferte annähernd die gleichen Ergebnisse wie die Näherung durch die Normalverteilung. Das führt zu zwei Fragen. 1. Warum sind die Ergebnisse so schlecht? und 2. Wie kann das System verbessert werden? Versuchen wir eine Antwort.
- Der Grund liegt sowohl im verwendeten Kriterium als auch im System selbst. Unsere Kriterien sind zu allgemein. Einerseits ist das gut, weil es so auf die meisten Fälle angewendet werden kann. Andererseits berücksichtigt es nicht das System selbst, sondern alle von uns betrachteten Systeme. Zum Beispiel produzieren alle unsere Systeme eine Verteilung mit einer abgeschnittenen linken Seite, und einige von ihnen können theoretisch unendliche Erwartungen haben. Deshalb sind in der Regel alle Verteilungen rechtsschief, und ihr Mittelwert nähert sich sehr langsam einer symmetrischen Normalverteilung an. Das System in unserem Beispiel hat so eine schiefe Verteilung. Das zeigt sich durch Schiefe oder durch einen auf die rechte Seite des Median verschobenen Erwartungswert. Das wird von einem System erwartet mit der Regel "Beschneide die Verluste und lass die Gewinne laufen".
- Wir benötigen Kriterien, die die Informationen über ein bestimmtes Handelssystem und eine Abfolge der Preise der Finanzanlage berücksichtigen. Ergo ohne Annahmen über die Preise funktioniert es nicht. Aber diese Annahmen sollten das reale Bild nicht zu sehr verzerren. Das bedeutet, dass wir uns in der Situation der zweiten Variante befinden sollten, die aus drei Punkten besteht, die zu Beginn des Abschnitts "Allgemeiner Fall"erörtert wurden. Deshalb sollten wir uns künftig auf parametrische Methoden konzentrieren. Aus rechnerischer Sicht sind sie schwieriger und weniger allgemein, können aber in jedem Einzelfall präziser sein.
Bis jetzt können wir folgendes festhalten. Verluste entstehen nicht nur durch unerwartete Veränderungen im Verhalten der Preise der Finanzanlagen (z. B. Trendwende). Dies kann auch durch Rauschen oder Volatilität verursacht werden. Die Methoden, die wir betrachten, ist eine der Möglichkeiten, diese Gründe zu trennen und ihren Einfluss zu verringern. Wenn dies für ein Handelssystem nicht möglich ist, wird die Verwendung eines solchen Systems nicht empfohlen.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3650
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Cross-Plattform Expert Advisor: Stopps
Cross-Plattform Expert Advisor: Stopps
 Universeller Expert Advisor: CUnIndicator und das Arbeiten mit Pending Orders (Teil 9)
Universeller Expert Advisor: CUnIndicator und das Arbeiten mit Pending Orders (Teil 9)
 Tiefe neuronale Netzwerke (Teil IV). Erstellen, trainieren und testen eines Modells des neuronalen Netzes
Tiefe neuronale Netzwerke (Teil IV). Erstellen, trainieren und testen eines Modells des neuronalen Netzes
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hochgeladen auf das Marktskript Volume Optimizer, unter Verwendung der im Artikel genannten Theorie. Es bestimmt das optimale Volumen des Geschäfts, basierend auf der Geschichte der Geschäfte.
Ich verlange eine Fortsetzung des Banketts! :-)
Es gibt eine Fortsetzung des Artikels. Oder meinen Sie etwas anderes? Im Film ist dieser Satz zu hören, wenn Iwan Wassiljewitsch das Bankett unbedingt beenden muss)
Es gibt eine Fortsetzung des Artikels. Oder meinen Sie etwas anderes? Im Film ist dieser Satz zu hören, als Iwan Wassiljewitsch das Bankett offensichtlich beenden muss)