
Redes neurais de maneira fácil (Parte 78): Detecção de objetos baseada em Transformador (DFFT)
Introdução
Nos artigos anteriores, dedicamos muito tempo à questão da previsão do movimento futuro dos preços. Analisamos os dados históricos. E com base nessa análise, buscamos diferentes maneiras de prever o movimento futuro mais provável dos preços. Alguns construíram um espectro completo de possíveis movimentos futuros dos preços e tentaram avaliar a probabilidade de cada uma das previsões feitas. Naturalmente, o treinamento e a utilização desses modelos exigem recursos computacionais significativos.
Mas precisamos realmente prever o movimento futuro dos preços? Ainda mais quando a precisão das previsões obtidas está longe do desejado.
Nosso objetivo final é obter lucro, que planejamos alcançar através do desempenho bem-sucedido do nosso Agente. Este, por sua vez, seleciona as melhores ações com base nas trajetórias de preços previstas que recebe.
Portanto, um erro na previsão das trajetórias de preços pode resultar em um erro ainda mais significativo na seleção das ações pelo Agente. Uso a expressão "pode resultar" porque, no processo de treinamento, o Ator pode se ajustar aos erros das previsões e reduzir um pouco o erro. No entanto, essa situação é possível com um erro relativamente constante nas previsões. No caso de um erro estocástico nas previsões, o erro das ações do Agente apenas se intensificará.
Quando isso acontece, procuramos maneiras de minimizar o erro. E se excluirmos a etapa intermediária de previsão da trajetória do movimento futuro dos preços. Voltemos à abordagem clássica de aprendizado por reforço. E permitamos que o Ator escolha ações com base na análise dos dados históricos. Mas ao fazer isso, não daremos um passo para trás, mas sim para o lado.
Proponho que você conheça um método interessante, que foi apresentado para resolver problemas na área de visão computacional. Este é o método Decoder-Free Fully Transformer-based (DFFT), que foi apresentado no artigo "Efficient Decoder-free Object Detection with Transformers".
O método DFFT proposto no artigo oferece alta eficiência tanto na etapa de treinamento quanto na de utilização. Os autores do método simplificam a detecção de objetos para uma tarefa unificada de previsão densa, utilizando apenas o codificador. E concentram seus esforços na resolução de 2 tarefas:
- Eliminação do decodificador ineficaz e utilização de 2 codificadores poderosos para manter a precisão da previsão de um mapa unificado de características;
- Exploração de características semânticas de baixo nível para a tarefa de detecção com recursos computacionais limitados.
Em particular, os autores do método propõem uma nova arquitetura leve de transformador, orientada para a detecção, que captura eficientemente características de baixo nível com rica semântica. Os experimentos apresentados no artigo mostram a redução dos custos computacionais e um menor número de épocas de treinamento.
1. Algoritmo DFFT
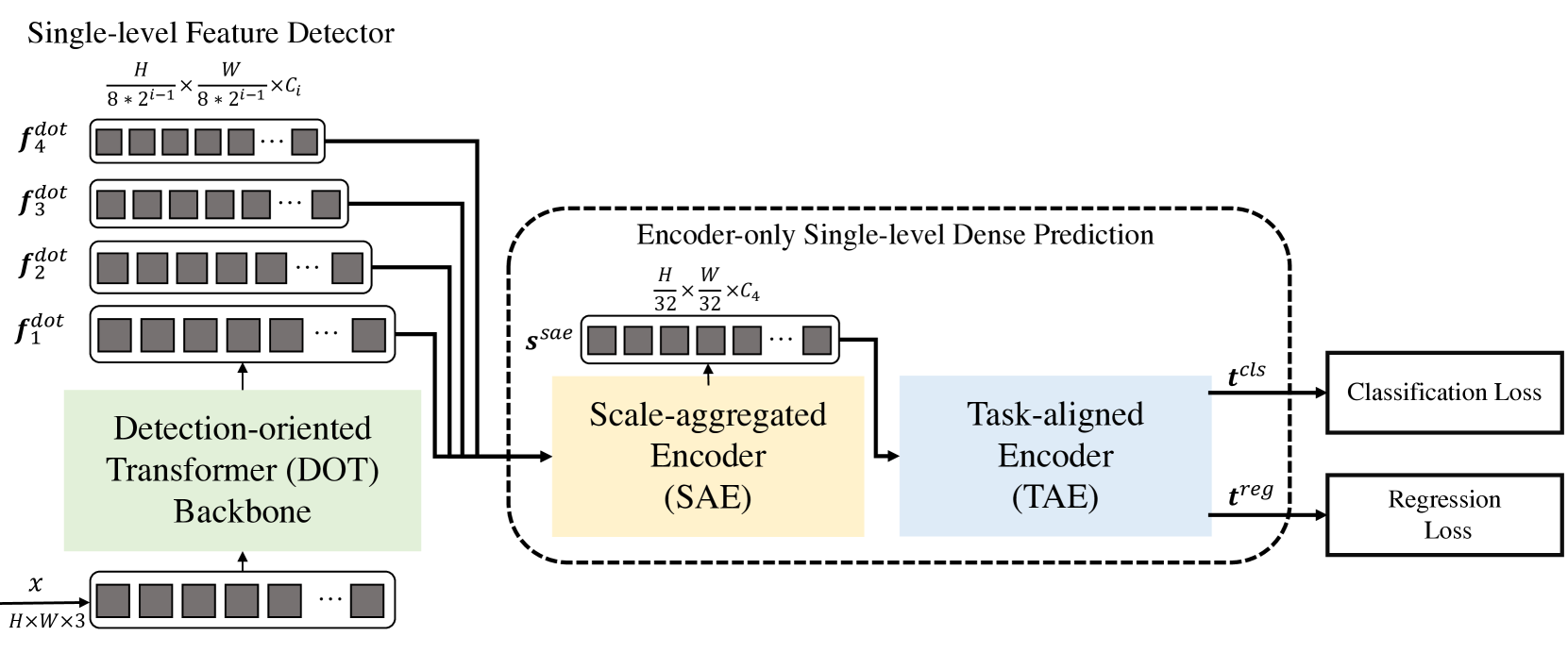
O método Decoder-Free Fully Transformer-based (DFFT) é um detector de objetos eficiente, totalmente baseado em Transformadores sem decodificador. A estrutura do Transformador é orientada para a detecção de objetos. Ele extrai objetos em quatro escalas e os envia para o próximo módulo de previsão densa, destinado apenas ao codificador. O módulo de previsão primeiro agrega o objeto multiescalar em um único mapa de objetos usando o codificador Scale-Aggregated Encoder.
Em seguida, os autores do método propõem o uso do codificador Task-Aligned Encoder para alinhar simultaneamente as funções para tarefas de classificação e regressão.
A estrutura do transformador orientada para a detecção (Detection-Oriented Transformer — DOT) é projetada para extrair características multiescalares com semântica rigorosa. Ela organiza hierarquicamente um módulo de Embeeding e quatro estágios de DOT. O novo módulo de atenção semanticamente expandido agrega informações semânticas de baixo nível de cada dois estágios consecutivos de DOT.
Ao processar mapas de características de alta resolução para previsão densa, os blocos transformadores comuns reduzem os custos computacionais substituindo a camada de Self-Attention com múltiplas cabeças (MSA) pela camada de atenção espacial local e Self-Attention com múltiplas cabeças de janela deslocada (SW-MSA). No entanto, tal estrutura reduz a performance de detecção, pois extrai apenas objetos multiescalares com semântica de baixo nível limitada.
Para mitigar essa limitação, os autores do método DFFT adicionam ao bloco DOT vários blocos de SW-MSA e um bloco global de atenção por canais. Observe que cada bloco de atenção contém uma camada de atenção e uma camada de FFN.
Os autores do método descobriram que colocar uma camada leve de atenção por canais após camadas sucessivas de atenção espacial local pode ajudar na extração da semântica do objeto em cada escala.
Enquanto o bloco DOT melhora as informações semânticas em características de baixo nível por meio da atenção global por canais, a semântica pode ser ainda mais aprimorada para melhorar a tarefa de detecção. Para isso, os autores do método propõem um novo módulo de atenção semanticamente aumentada (Semantic-Augmented Attention — SAA), que troca informações semânticas entre dois níveis consecutivos de DOT e complementa suas características. SAA consiste em uma camada de upsampling e um bloco global de atenção por canais. Os autores do método adicionam SAA a cada dois blocos consecutivos de DOT. Formalmente, SAA aceita os resultados do trabalho do bloco atual de DOT e da etapa anterior de DOT, e depois retorna uma função semanticamente expandida, que é enviada para a próxima etapa de DOT e também contribui para as características multiescalares finais.
Em geral, a etapa orientada para a detecção consiste em quatro camadas de DOT, onde cada etapa inclui um bloco de DOT e um módulo de SAA (exceto a primeira etapa). Em particular, a primeira etapa contém um bloco DOT e não contém o módulo SAA, pois as entradas do módulo SAA vêm de duas etapas consecutivas DOT. Em seguida, há uma camada de amostragem reduzida para restaurar a dimensão de entrada.
O próximo módulo é projetado para melhorar tanto a inferência quanto a eficiência do treinamento do modelo DFFT. Primeiro, é utilizado o codificador de escala agregada (Scale-Aggregated Encoder — SAE) para agregar objetos multiescalares da coluna vertebral DOT em um único mapa de objetos Ssae.
Em seguida, é utilizado o codificador alinhado por tarefa (Task-Aligned Encoder — TAE) para criar uma função de classificação alinhada 𝒕cls e uma função de regressão 𝒕reg simultaneamente em uma única cabeça.
O codificador de escala agregada é construído a partir de 3 blocos SAE. Cada bloco SAE aceita como dados de entrada dois objetos e os agrega passo a passo em todos os blocos SAE. Os autores do método usam a escala de agregação final dos objetos para equilibrar a precisão da detecção com os custos computacionais.
Normalmente, os detectores realizam a classificação e a localização dos objetos independentemente, usando dois ramos separados (cabeças não relacionadas). Essa estrutura de dois ramos não considera a interação entre as duas tarefas e leva a previsões inconsistentes. Enquanto isso, ao estudar características para as duas tarefas em uma cabeça conjunta, geralmente existem conflitos. Os autores do DFFT propõem o uso de um codificador orientado por tarefa, que proporciona um melhor equilíbrio entre o aprendizado de funções interativas e funções específicas da tarefa, combinando blocos de atenção de grupo por canais em uma cabeça conjunta.
Esse codificador é composto por dois tipos de blocos de atenção por canais. Primeiro, blocos de atenção de grupo multinível por canais alinham e dividem os objetos agregados Ssae em 2 partes. Em segundo lugar, os blocos de atenção globais por canais codificam um dos dois objetos divididos para a tarefa de regressão seguinte.
Em particular, as diferenças entre o bloco de atenção de grupo por canais e o bloco de atenção global por canais são que todas as projeções lineares, exceto as projeções de inserções Query/Key/Value no bloco de atenção de grupo por canais, são realizadas em dois grupos. Assim, as características interagem nas operações de atenção, enquanto são projetadas separadamente nas projeções de saída.
A visualização do método pelos autores pode ser encontrada aqui: visualização.
2. Implementação com MQL5
Após considerar os aspectos teóricos do método Decoder-Free Fully Transformer-based (DFFT), passamos à implementação prática dos métodos propostos utilizando MQL5. No entanto, nosso modelo será ligeiramente diferente do original. Isso ocorre porque, ao desenvolvê-lo, consideramos as diferenças entre as tarefas específicas de visão computacional para as quais o método foi projetado e o trabalho nos mercados financeiros, para o qual estamos criando nosso modelo.
2.1 Construção do bloco DOT
E, ao iniciar, é importante observar que os métodos propostos são bastante distintos dos modelos que desenvolvemos anteriormente. Por exemplo, o bloco DOT difere dos blocos de atenção que examinamos antes. Assim, começamos nosso trabalho com a criação de uma nova camada neural chamada CNeuronDOTOCL. Nossa nova camada será criada como herdeira da nossa classe base de camadas neurais CNeuronBaseOCL.
Semelhante a outros blocos de atenção, adicionaremos variáveis para armazenar os parâmetros-chave:
- iWindowSize — tamanho da janela de um elemento da sequência;
- iPrevWindowSize — tamanho da janela de um elemento da sequência da camada anterior;
- iDimension — tamanho do vetor de entidades internas Query, Key e Value;
- iUnits — número de elementos na sequência;
- iHeads — número de cabeças de atenção.
Acredito que você notou a variável iPrevWindowSize. Sua adição permitirá implementar a capacidade de compressão de dados de camada para camada, conforme previsto pelo método DFFT.
Além disso, para minimizar o trabalho diretamente na nova classe e maximizar o uso dos trabalhos anteriores, parte da funcionalidade será implementada utilizando camadas neurais aninhadas da nossa biblioteca. Nos familiarizaremos com essa funcionalidade durante a implementação dos métodos de propagação para frente e reversa.
class CNeuronDOTOCL : public CNeuronBaseOCL { protected: uint iWindowSize; uint iPrevWindowSize; uint iDimension; uint iUnits; uint iHeads; //--- CNeuronConvOCL cProjInput; CNeuronConvOCL cQKV; int iScoreBuffer; CNeuronBaseOCL cRelativePositionsBias; CNeuronBaseOCL MHAttentionOut; CNeuronConvOCL cProj; CNeuronBaseOCL AttentionOut; CNeuronConvOCL cFF1; CNeuronConvOCL cFF2; CNeuronBaseOCL SAttenOut; CNeuronXCiTOCL cCAtten; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool DOT(void); //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool updateRelativePositionsBias(void); virtual bool DOTInsideGradients(void); public: CNeuronDOTOCL(void) {}; ~CNeuronDOTOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint dimension, uint heads, uint units_count, uint prev_window, ENUM_OPTIMIZATION optimization_type, uint batch); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronDOTOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Em geral, a lista de métodos sobrescritos é bastante padrão.
No corpo da classe, usaremos objetos estáticos. Isso nos permite deixar o construtor e o destrutor da classe vazios.
A inicialização da classe é realizada no método Init. Nos parâmetros do método, transmitiremos todas as informações necessárias. O controle mínimo necessário é realizado no método correspondente da classe pai. É também nesse método que ocorre a inicialização dos objetos herdados.
bool CNeuronDOTOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint dimension, uint heads, uint units_count, uint prev_window, ENUM_OPTIMIZATION optimization_type, uint batch) { //--- if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Em seguida, verificamos se o tamanho dos dados de entrada e os parâmetros da camada atual estão certos. Se necessário, inicializamos a camada de escalonamento de dados.
if(prev_window != window) { if(!cProjInput.Init(0, 0, OpenCL, prev_window, prev_window, window, units_count, optimization_type, batch)) return false; }
Depois, salvamos as constantes principais recebidas do programa chamador, que definem a arquitetura da camada, em variáveis internas da classe.
iWindowSize = window; iPrevWindowSize = prev_window; iDimension = dimension; iHeads = heads; iUnits = units_count;
Após isso, inicializamos sequencialmente todos os objetos internos. Primeiro, inicializamos a camada de geração de entidades Query, Key e Value. Todas as 3 entidades serão geradas paralelamente no corpo de uma única camada neural cQKV.
if(!cQKV.Init(0, 1, OpenCL, window, window, dimension * heads, units_count, optimization_type, batch)) return false;
Depois, criaremos um buffer para gravar os coeficientes de dependência dos objetos iScoreBuffer. Aqui vale mencionar que no bloco DOT, primeiro analisamos a semântica local. Para isso, verificaremos a dependência entre o objeto e seus 2 vizinhos mais próximos. Portanto, o tamanho do buffer Score será definido como iUnits * iHeads * 3.
Além disso, os coeficientes salvos no buffer são recalculados a cada propagação para frente. E são usados apenas na próxima propagação reversa. Por isso, os dados do buffer não serão salvos no arquivo de salvamento do modelo. Além disso, não criaremos o buffer na memória do programa principal. Será suficiente criar o buffer na memória do contexto OpenCL. No lado do programa principal, manteremos apenas o ponteiro para o buffer.
//--- iScoreBuffer = OpenCL.AddBuffer(sizeof(float) * iUnits * iHeads * 3, CL_MEM_READ_WRITE); if(iScoreBuffer < 0) return false;
No mecanismo de Self-Attention com janelas, ao contrário do transformador clássico, cada token interage apenas com tokens dentro de uma janela específica. Isso reduz significativamente a complexidade computacional. No entanto, essa limitação também significa que os modelos devem levar em conta as posições relativas dos tokens dentro da janela. Para implementar essa funcionalidade, são introduzidos parâmetros treináveis cRelativePositionsBias. Para cada par de tokens (i, j) dentro da janela iWindowSize, cRelativePositionsBias contém um peso que determina a importância da interação entre esses tokens com base em sua posição relativa.
É fácil deduzir que o tamanho desse buffer é igual ao tamanho do buffer de coeficientes Score. No entanto, para o treinamento dos parâmetros, além do buffer dos próprios valores, também precisaremos de buffers adicionais. Com o objetivo de reduzir o número de objetos internos e a legibilidade do código, para cRelativePositionsBias declararemos um objeto de camada neural que contém todos os buffers adicionais.
if(!cRelativePositionsBias.Init(1, 2, OpenCL, iUnits * iHeads * 3, optimization_type, batch)) return false;
Da mesma forma, adicionaremos os outros elementos do mecanismo Self-Attention.
if(!MHAttentionOut.Init(0, 3, OpenCL, iUnits * iHeads * iDimension, optimization_type, batch)) return false; if(!cProj.Init(0, 4, OpenCL, iHeads * iDimension, iHeads * iDimension, window, iUnits, optimization_type, batch)) return false; if(!AttentionOut.Init(0, 5, OpenCL, iUnits * window, optimization_type, batch)) return false; if(!cFF1.Init(0, 6, OpenCL, window, window, 4 * window, units_count, optimization_type,batch)) return false; if(!cFF2.Init(0, 7, OpenCL, window * 4, window * 4, window, units_count, optimization_type, batch)) return false; if(!SAttenOut.Init(0, 8, OpenCL, iUnits * window, optimization_type, batch)) return false;
Como bloco de atenção global, utilizaremos a camada CNeuronXCiTOCL.
if(!cCAtten.Init(0, 9, OpenCL, window, MathMax(window / 2, 3), 8, iUnits, 1, optimization_type, batch)) return false;
Para minimizar as operações de cópia de dados entre os buffers, realizaremos a substituição de objetos e buffers.
if(!!Output) delete Output; Output = cCAtten.getOutput(); if(!!Gradient) delete Gradient; Gradient = cCAtten.getGradient(); SAttenOut.SetGradientIndex(cFF2.getGradientIndex()); //--- return true; }
E concluímos o trabalho do método.
Após a inicialização da classe, passamos para a construção do algoritmo de propagação para frente. E aqui começaremos a trabalhar com a organização do mecanismo Self-Attention com janelas no lado OpenCL do programa. Para isso, criaremos um kernel DOTFeedForward. Nos parâmetros do kernel, passaremos ponteiros para 4 buffers de dados:
- qkv — buffer de entidades Query, Key e Value,
- score — buffer de coeficientes de dependência,
- rpb — buffer de deslocamentos posicionais,
- out — buffer dos resultados do Self-Attention com janelas multiconectadas.
__kernel void DOTFeedForward(__global float *qkv, __global float *score, __global float *rpb, __global float *out) { const size_t d = get_local_id(0); const size_t dimension = get_local_size(0); const size_t u = get_global_id(1); const size_t units = get_global_size(1); const size_t h = get_global_id(2); const size_t heads = get_global_size(2);
Planejamos executar o kernel em um espaço tridimensional de tarefas. E no corpo do kernel, identificamos imediatamente o fluxo em todas as 3 dimensões. Aqui é importante notar que na primeira dimensão das entidades Query, Key e Value criamos um grupo de trabalho com uso conjunto do buffer na memória local.
Em seguida, definimos os deslocamentos nos buffers de dados até o início dos objetos analisados.
uint step = 3 * dimension * heads; uint start = max((int)u - 1, 0); uint stop = min((int)u + 1, (int)units - 1); uint shift_q = u * step + h * dimension; uint shift_k = start * step + dimension * (heads + h); uint shift_score = u * 3 * heads;
E também criamos um buffer local para troca de dados entre os fluxos de um grupo de trabalho.
const uint ls_d = min((uint)dimension, (uint)LOCAL_ARRAY_SIZE); __local float temp[LOCAL_ARRAY_SIZE][3];
Como mencionado anteriormente, a semântica local é determinada pelos 2 vizinhos mais próximos do objeto. Primeiro, determinamos a influência dos vizinhos no objeto analisado. Calculamos os coeficientes de dependência dentro do grupo de trabalho. Primeiro, multiplicamos os elementos das entidades Query e Key em fluxos paralelos.
//--- Score if(d < ls_d) { for(uint pos = start; pos <= stop; pos++) { temp[d][pos - start] = 0; } for(uint dim = d; dim < dimension; dim += ls_d) { float q = qkv[shift_q + dim]; for(uint pos = start; pos <= stop; pos++) { uint i = pos - start; temp[d][i] = temp[d][i] + q * qkv[shift_k + i * step + dim]; } } barrier(CLK_LOCAL_MEM_FENCE);
Em seguida, somamos os produtos obtidos.
int count = ls_d; do { count = (count + 1) / 2; if(d < count && (d + count) < dimension) for(uint i = 0; i <= (stop - start); i++) { temp[d][i] += temp[d + count][i]; temp[d + count][i] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); }
Aos valores obtidos, adicionamos os parâmetros de deslocamento e normalizamos com a função SoftMax.
if(d == 0) { float sum = 0; for(uint i = 0; i <= (stop - start); i++) { temp[0][i] = exp(temp[0][i] + rpb[shift_score + i]); sum += temp[0][i]; } for(uint i = 0; i <= (stop - start); i++) { temp[0][i] = temp[0][i] / sum; score[shift_score + i] = temp[0][i]; } } barrier(CLK_LOCAL_MEM_FENCE);
Salvamos o resultado no buffer de coeficientes de dependência.
Agora podemos multiplicar os coeficientes obtidos pelos elementos correspondentes da entidade Value para determinar os resultados do bloco de Self-Attention com janelas.
int shift_out = dimension * (u * heads + h) + d; int shift_v = dimension * (heads * (u * 3 + 2) + h); float sum = 0; for(uint i = 0; i <= (stop - start); i++) sum += qkv[shift_v + i] * temp[0][i]; out[shift_out] = sum; }
Os valores obtidos são salvos nos elementos correspondentes do buffer de resultados e o kernel é concluído.
Após criar o kernel, voltamos ao nosso programa principal, onde criamos os métodos da nossa nova classe CNeuronDOTOCL. Primeiro, criaremos o método DOT, que coloca o kernel recém-criado na fila de execução.
O algoritmo do método é bastante simples. Apenas transmitimos os parâmetros externos ao kernel.
bool CNeuronDOTOCL::DOT(void) { if(!OpenCL) return false; //--- uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iDimension, iUnits, iHeads}; uint local_work_size[3] = {iDimension, 1, 1}; if(!OpenCL.SetArgumentBuffer(def_k_DOTFeedForward, def_k_dot_qkv, cQKV.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTFeedForward, def_k_dot_score, iScoreBuffer)) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTFeedForward, def_k_dot_rpb, cRelativePositionsBias.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTFeedForward, def_k_dot_out, MHAttentionOut.getOutputIndex())) return false;
Depois, enviamos o kernel para a fila de execução.
ResetLastError(); if(!OpenCL.Execute(def_k_DOTFeedForward, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Lembrando de controlar o processo de execução das operações em cada etapa.
Após concluir o trabalho preparatório, passamos a criar o método CNeuronDOTOCL::feedForward, no qual definiremos em alto nível o algoritmo de propagação para frente da nossa camada.
Nos parâmetros do método, recebemos um ponteiro para a camada anterior da rede neural. Para conveniência, salvamos o ponteiro recebido em uma variável local.
bool CNeuronDOTOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
{
CNeuronBaseOCL* inputs = NeuronOCL;
Em seguida, verificamos se o tamanho dos dados de entrada difere dos parâmetros da camada atual. Se necessário, escalonamos os dados de entrada e calculamos as entidades Query, Key e Value.
Se os buffers de dados forem iguais, omitimos a etapa de escalonamento e geramos imediatamente as entidades Query, Key e Value.
if(iPrevWindowSize != iWindowSize) { if(!cProjInput.FeedForward(inputs) || !cQKV.FeedForward(GetPointer(cProjInput))) return false; inputs = GetPointer(cProjInput); } else if(!cQKV.FeedForward(inputs)) return false;
Na etapa seguinte, chamamos o método criado anteriormente de Self-Attention com janelas.
if(!DOT()) return false;
Reduzimos a dimensionalidade dos dados.
if(!cProj.FeedForward(GetPointer(MHAttentionOut))) return false;
E somamos o resultado com o buffer dos dados de entrada.
if(!SumAndNormilize(inputs.getOutput(), cProj.getOutput(), AttentionOut.getOutput(), iWindowSize, true)) return false;
Passamos o resultado pelo bloco FeedForward.
if(!cFF1.FeedForward(GetPointer(AttentionOut))) return false; if(!cFF2.FeedForward(GetPointer(cFF1))) return false;
E novamente somamos os buffers de resultados. Desta vez com a saída do bloco de Self-Attention com janelas.
if(!SumAndNormilize(AttentionOut.getOutput(), cFF2.getOutput(), SAttenOut.getOutput(), iWindowSize, true)) return false;
No final do bloco, há uma etapa de Self-Attention global. Para isso, utilizamos a camada CNeuronXCiTOCL.
if(!cCAtten.FeedForward(GetPointer(SAttenOut))) return false; //--- return true; }
Verificamos os resultados das operações e concluímos o método.
Com isso, finalizamos a implementação da propagação para frente da nossa classe e passamos a trabalhar nos métodos de para propagação reversa. Aqui, começamos criando o kernel de para propagação reversa do bloco Self-Attention com janelas DOTInsideGradients. Assim como o kernel de propagação para frente, o novo kernel será executado em um espaço tridimensional de tarefas. Desta vez, sem a criação de grupos locais.
Nos parâmetros, o kernel recebe ponteiros para todos os buffers de dados necessários.
__kernel void DOTInsideGradients(__global float *qkv, __global float *qkv_g, __global float *scores, __global float *rpb, __global float *rpb_g, __global float *gradient) { //--- init const uint u = get_global_id(0); const uint d = get_global_id(1); const uint h = get_global_id(2); const uint units = get_global_size(0); const uint dimension = get_global_size(1); const uint heads = get_global_size(2);
No corpo do kernel, identificamos imediatamente o fluxo em todas as 3 dimensões. E definimos o espaço de tarefas, que nos indicará a dimensionalidade dos buffers recebidos.
Aqui também definimos os deslocamentos nos buffers de dados.
uint step = 3 * dimension * heads; uint start = max((int)u - 1, 0); uint stop = min((int)u + 1, (int)units - 1); const uint shift_q = u * step + dimension * h + d; const uint shift_k = u * step + dimension * (heads + h) + d; const uint shift_v = u * step + dimension * (2 * heads + h) + d;
Depois disso, passamos à distribuição do gradiente. Primeiro, determinamos o gradiente do erro para o elemento Value. Para isso, multiplicamos o gradiente recebido pelo coeficiente de influência correspondente.
//--- Calculating Value's gradients float sum = 0; for(uint i = start; i <= stop; i ++) { int shift_score = i * 3 * heads; if(u == i) { shift_score += (uint)(u > 0); } else { if(u > i) shift_score += (uint)(start > 0) + 1; } uint shift_g = dimension * (i * heads + h) + d; sum += gradient[shift_g] * scores[shift_score]; } qkv_g[shift_v] = sum;
Na próxima etapa, determinamos o gradiente do erro para a entidade Query. Aqui o algoritmo é um pouco mais complexo. Primeiro, precisamos determinar o gradiente do erro para o vetor de coeficientes de dependência correspondente. Ajustar o gradiente recebido pela derivada da função SoftMax. E só depois disso, podemos multiplicar o gradiente de erro dos coeficientes de dependência pelo elemento correspondente do tensor de entidades Key.
Aqui é importante notar que antes da normalização dos coeficientes de dependência, somamos esses coeficientes com os elementos do deslocamento posicional da atenção. Como você sabe, ao somar, o gradiente é transmitido integralmente em ambas as direções. A dupla contagem do erro é facilmente neutralizada por um pequeno coeficiente de aprendizado. Portanto, transferimos o gradiente de erro no nível da matriz de coeficientes de dependência para o buffer de gradientes de erro do deslocamento posicional.
//--- Calculating Query's gradients float grad = 0; uint shift_score = u * heads * 3; for(int k = start; k <= stop; k++) { float sc_g = 0; float sc = scores[shift_score + k - start]; for(int v = start; v <= stop; v++) for(int dim=0;dim<dimension;dim++) sc_g += scores[shift_score + v - start] * qkv[v * step + dimension * (2 * heads + h) + dim] * gradient[dimension * (u * heads + h) + dim] * ((float)(k == v) - sc); grad += sc_g * qkv[k * step + dimension * (heads + h) + d]; if(d == 0) rpb_g[shift_score + k - start] = sc_g; } qkv_g[shift_q] = grad;
Em seguida, precisamos determinar da mesma forma o gradiente de erro para a entidade Key. O algoritmo é semelhante ao Query, mas em outra dimensão da matriz de coeficientes.
//--- Calculating Key's gradients grad = 0; for(int q = start; q <= stop; q++) { float sc_g = 0; shift_score = q * heads * 3; if(u == q) { shift_score += (uint)(u > 0); } else { if(u > q) shift_score += (uint)(start > 0) + 1; } float sc = scores[shift_score]; for(int v = start; v <= stop; v++) { shift_score = v * heads * 3; if(u == v) { shift_score += (uint)(u > 0); } else { if(u > v) shift_score += (uint)(start > 0) + 1; } for(int dim=0;dim<dimension;dim++) sc_g += scores[shift_score] * qkv[shift_v-d+dim] * gradient[dimension * (v * heads + h) + d] * ((float)(d == v) - sc); } grad += sc_g * qkv[q * step + dimension * h + d]; } qkv_g[shift_k] = grad; }
Com isso, concluímos o trabalho com o kernel e retornamos ao trabalho com nossa classe CNeuronDOTOCL, na qual criaremos o método DOTInsideGradients para chamar o kernel criado anteriormente. O algoritmo permanece o mesmo:
- definimos o espaço de tarefas
bool CNeuronDOTOCL::DOTInsideGradients(void) { if(!OpenCL) return false; //--- uint global_work_offset[3] = {0, 0, 0}; uint global_work_size[3] = {iUnits, iDimension, iHeads};
- passamos os parâmetros
if(!OpenCL.SetArgumentBuffer(def_k_DOTInsideGradients, def_k_dotg_qkv, cQKV.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTInsideGradients, def_k_dotg_qkv_g, cQKV.getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTInsideGradients, def_k_dotg_scores, iScoreBuffer)) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTInsideGradients, def_k_dotg_rpb, cRelativePositionsBias.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTInsideGradients, def_k_dotg_rpb_g, cRelativePositionsBias.getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_DOTInsideGradients, def_k_dotg_gradient, MHAttentionOut.getGradientIndex())) return false;
- colocamos na fila de execução
ResetLastError(); if(!OpenCL.Execute(def_k_DOTInsideGradients, 3, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
- verificamos o resultado das operações e concluímos o método.
Descrevemos o algoritmo de para propagação reversa de forma abrangente no método calcInputGradients. Nos parâmetros, esse método recebe um ponteiro para o objeto da camada anterior, para a qual passaremos o gradiente de erro. No corpo do método, verificamos imediatamente a validade do ponteiro recebido. Se o ponteiro for inválido, não temos para onde passar o gradiente de erro. E o sentido lógico de todas as operações é próximo de "0".
bool CNeuronDOTOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Em seguida, repetimos as operações do feedforward em ordem inversa. Na inicialização da nossa classe CNeuronDOTOCL, fizemos a substituição dos buffers. Agora, ao receber o gradiente de erro da camada neural subsequente, ele é recebido diretamente na camada de atenção global. Portanto, pulamos as operações desnecessárias de cópia de dados e chamamos imediatamente o método homônimo da camada interna de atenção global.
if(!cCAtten.calcInputGradients(GetPointer(SAttenOut))) return false;
Aqui também utilizamos a substituição dos buffers e passamos imediatamente o gradiente de erro pelo bloco FeedForward.
if(!cFF2.calcInputGradients(GetPointer(cFF1))) return false; if(!cFF1.calcInputGradients(GetPointer(AttentionOut))) return false;
Depois, somamos o gradiente de erro de dois fluxos.
if(!SumAndNormilize(AttentionOut.getGradient(), SAttenOut.getGradient(), cProj.getGradient(), iWindowSize, false)) return false;
E distribuímos entre as cabeças de atenção.
if(!cProj.calcInputGradients(GetPointer(MHAttentionOut))) return false;
Chamamos nosso método de distribuição do gradiente de erro através do bloco Self-Attention com janelas.
if(!DOTInsideGradients()) return false;
Após isso, verificamos a correspondência dos tamanhos das camadas anterior e atual. Se necessário, escalonamos os dados de erro para a camada de escalonamento. Somamos os gradientes de erro de dois fluxos. E só então escalonamos o gradiente de erro para a camada anterior.
if(iPrevWindowSize != iWindowSize) { if(!cQKV.calcInputGradients(GetPointer(cProjInput))) return false; if(!SumAndNormilize(cProjInput.getGradient(), cProj.getGradient(), cProjInput.getGradient(), iWindowSize, false)) return false; if(!cProjInput.calcInputGradients(prevLayer)) return false; }
No caso de igualdade das camadas neurais, passamos imediatamente o gradiente de erro para a camada anterior. E depois complementamos com o gradiente de erro do segundo fluxo.
else { if(!cQKV.calcInputGradients(prevLayer)) return false; if(!SumAndNormilize(prevLayer.getGradient(), cProj.getGradient(), prevLayer.getGradient(), iWindowSize, false)) return false; } //--- return true; }
Após distribuir o gradiente de erro entre todas as camadas neurais, precisamos atualizar os parâmetros do modelo para minimizar o erro. E isso seria trivial, se não fosse por um detalhe. Lembra do buffer dos parâmetros de influência posicional dos elementos? Precisamos atualizar seus parâmetros. Para realizar essa funcionalidade, criamos o kernel RPBUpdateAdam. Nos parâmetros, passamos ao kernel ponteiros para o buffer dos parâmetros atuais, gradiente de erro. Bem como tensores auxiliares e constantes do método Adam.
__kernel void RPBUpdateAdam(__global float *target, __global const float *gradient, __global float *matrix_m, ///<[in,out] Matrix of first momentum __global float *matrix_v, ///<[in,out] Matrix of seconfd momentum const float b1, ///< First momentum multiplier const float b2 ///< Second momentum multiplier ) { const int i = get_global_id(0);
No corpo do kernel, identificamos o fluxo, que nos indica o deslocamento nos buffers de dados.
Em seguida, declaramos variáveis locais e salvamos nelas os valores necessários dos buffers globais.
float m, v, weight; m = matrix_m[i]; v = matrix_v[i]; weight = target[i]; float g = gradient[i];
De acordo com o método Adam, primeiro determinamos os momentos.
m = b1 * m + (1 - b1) * g; v = b2 * v + (1 - b2) * pow(g, 2);
Com base nos momentos obtidos, calculamos a correção necessária do parâmetro.
float delta = m / (v != 0.0f ? sqrt(v) : 1.0f);
E salvamos todos os dados nos elementos correspondentes dos buffers globais.
target[i] = clamp(weight + delta, -MAX_WEIGHT, MAX_WEIGHT); matrix_m[i] = m; matrix_v[i] = v; }
Voltamos à nossa classe CNeuronDOTOCL e criamos o método updateRelativePositionsBias para chamar o kernel, seguindo o esquema clássico. Aqui utilizamos um espaço de tarefas unidimensional.
bool CNeuronDOTOCL::updateRelativePositionsBias(void) { if(!OpenCL) return false; //--- uint global_work_offset[1] = {0}; uint global_work_size[1] = {cRelativePositionsBias.Neurons()}; if(!OpenCL.SetArgumentBuffer(def_k_RPBUpdateAdam, def_k_rpbw_rpb, cRelativePositionsBias.getOutputIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_RPBUpdateAdam, def_k_rpbw_gradient, cRelativePositionsBias.getGradientIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_RPBUpdateAdam, def_k_rpbw_matrix_m, cRelativePositionsBias.getFirstMomentumIndex())) return false; if(!OpenCL.SetArgumentBuffer(def_k_RPBUpdateAdam, def_k_rpbw_matrix_v, cRelativePositionsBias.getSecondMomentumIndex())) return false; if(!OpenCL.SetArgument(def_k_RPBUpdateAdam, def_k_rpbw_b1, b1)) return false; if(!OpenCL.SetArgument(def_k_RPBUpdateAdam, def_k_rpbw_b2, b2)) return false; ResetLastError(); if(!OpenCL.Execute(def_k_RPBUpdateAdam, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
O trabalho preparatório está concluído. E passamos à criação do método de alto nível para atualização dos parâmetros do bloco updateInputWeights. Nos parâmetros, o método recebe um ponteiro para o objeto da camada anterior. Nesse caso, pulamos a verificação do ponteiro recebido, pois ela será realizada nos métodos das camadas internas.
Primeiro, verificamos a necessidade de atualizar os parâmetros da camada de escalonamento. E, se necessário, chamamos o método homônimo da camada especificada.
if(iWindowSize != iPrevWindowSize) { if(!cProjInput.UpdateInputWeights(NeuronOCL)) return false; if(!cQKV.UpdateInputWeights(GetPointer(cProjInput))) return false; } else { if(!cQKV.UpdateInputWeights(NeuronOCL)) return false; }
Depois, atualizamos os parâmetros da camada de geração de entidades Query, Key e Value.
Da mesma forma, atualizamos os parâmetros de todas as camadas internas.
if(!cProj.UpdateInputWeights(GetPointer(MHAttentionOut))) return false; if(!cFF1.UpdateInputWeights(GetPointer(AttentionOut))) return false; if(!cFF2.UpdateInputWeights(GetPointer(cFF1))) return false; if(!cCAtten.UpdateInputWeights(GetPointer(SAttenOut))) return false;
E, ao final do método, atualizamos os parâmetros do deslocamento posicional.
if(!updateRelativePositionsBias()) return false; //--- return true; }
Ao fazer isso, não esquecemos de controlar o processo de execução das operações em cada etapa.
Com isso, concluímos a revisão dos métodos da nova camada neural CNeuronDOTOCL. Você pode encontrar o código completo da classe e todos os seus métodos, incluindo os que não foram descritos neste artigo, no anexo.
Agora, seguimos adiante e passamos à construção da arquitetura do nosso novo modelo.
2.2 Arquitetura do modelo
Como de costume, a arquitetura do nosso modelo será descrita no método CreateDescriptions. Nos parâmetros, o método recebe ponteiros para 3 arrays dinâmicos para salvar a descrição dos modelos. No corpo do método, verificamos imediatamente a validade dos ponteiros recebidos e, se necessário, criamos novas instâncias dos arrays.
bool CreateDescriptions(CArrayObj *dot, CArrayObj *actor, CArrayObj *critic) { //--- CLayerDescription *descr; //--- if(!dot) { dot = new CArrayObj(); if(!dot) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; }
Como você pode ter notado, criaremos 3 modelos:
- DOT
- Actor
- Critic.
O bloco DOT está previsto na arquitetura DFFT, o que não pode ser dito do Actor e do Critic. Mas quero lembrar que o método DFFT propõe a criação do bloco TAE com saídas de classificação e regressão. O uso sequencial de Actor e Critic deve emular o bloco TAE. O Actor é um classificador de ações, e o Critic é uma regressão de recompensas.
Alimentamos o modelo DOT com a descrição do estado atual do ambiente.
//--- DOT dot.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!dot.Add(descr)) { delete descr; return false; }
Os dados "brutos" são processados na camada de normalização por lote.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!dot.Add(descr)) { delete descr; return false; }
Depois, criamos um embedding dos últimos dados e os adicionamos à pilha.
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {prev_count}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize; if(!dot.Add(descr)) { delete descr; return false; }
Em seguida, adicionamos a codificação posicional dos dados.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout; if(!dot.Add(descr)) { delete descr; return false; }
Até esse ponto, repetimos a arquitetura de embeddings de trabalhos anteriores. Mas a partir daí começam as mudanças. Adicionamos o primeiro bloco DOT, onde é realizada a análise de estados individuais.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDOTOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = prev_wout / descr.step; if(!dot.Add(descr)) { delete descr; return false; }
No próximo bloco, comprimimos os dados pela metade, mas continuamos a análise de estados individuais.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDOTOCL; descr.count = prev_count; prev_wout = descr.window = prev_wout / 2; descr.step = 4; descr.window_out = prev_wout / descr.step; if(!dot.Add(descr)) { delete descr; return false; }
Em seguida, agrupamos os dados para análise em grupos de 2 estados consecutivos.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDOTOCL; prev_count = descr.count = prev_count / 2; prev_wout = descr.window = prev_wout * 2; descr.step = 4; descr.window_out = prev_wout / descr.step; if(!dot.Add(descr)) { delete descr; return false; }
E comprimimos os dados mais uma vez.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDOTOCL; descr.count = prev_count; prev_wout = descr.window = prev_wout / 2; descr.step = 4; descr.window_out = prev_wout / descr.step; if(!dot.Add(descr)) { delete descr; return false; }
A última camada do modelo DOT vai além do método DFFT. Aqui, adicionei uma camada de cross-attention.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMH2AttentionOCL; descr.count = prev_wout; descr.window = prev_count; descr.step = 4; descr.window_out = prev_wout / descr.step; descr.optimization = ADAM; if(!dot.Add(descr)) { delete descr; return false; }
O modelo Actor recebe como entrada os estados do ambiente processados no modelo DOT.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = prev_count*prev_wout; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Os dados obtidos são combinados com o estado atual da conta.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count * prev_wout; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!actor.Add(descr)) { delete descr; return false; }
Os dados são processados por 2 camadas totalmente conectadas.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
E na saída, geramos a política estocástica do Actor.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
O Critic também usa os estados do ambiente processados como dados de entrada.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.Copy(actor.At(0)); if(!critic.Add(descr)) { delete descr; return false; }
A descrição do estado do ambiente é complementada pelas ações do Agente.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.Copy(actor.At(0)); descr.step = NActions; descr.optimization = ADAM; descr.activation = SIGMOID; if(!critic.Add(descr)) { delete descr; return false; }
Os dados são processados por 2 camadas totalmente conectadas, com um vetor de recompensas na saída.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
2.3 EA de interação com o ambiente
Após compor a arquitetura dos modelos, passamos a criar o EA de interação com o ambiente em "...\Experts\DFFT\Research.mq5". Este EA é destinado à coleta da amostra inicial de treinamento e à atualização subsequente do buffer de reprodução. O EA também pode ser usado para testar o modelo treinado. Embora para essa funcionalidade haja o EA "...\Experts\DFFT\Test.mq5". Ambos os EAs têm um algoritmo semelhante. A única diferença é que o último não salva dados no buffer de reprodução para treinamento subsequente. Isso é feito para um teste "justo" do modelo treinado.
Desde já, digo que ambos os EAs são amplamente copiados de trabalhos anteriores. Neste artigo, abordaremos apenas as mudanças específicas dos modelos.
Dentro da funcionalidade de coleta de dados, não usaremos o modelo Critic.
CNet DOT; CNet Actor;
No método de inicialização do EA, primeiro conectamos os indicadores necessários.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- if(!Symb.Name(_Symbol)) return INIT_FAILED; Symb.Refresh(); //--- if(!RSI.Create(Symb.Name(), TimeFrame, RSIPeriod, RSIPrice)) return INIT_FAILED; //--- if(!CCI.Create(Symb.Name(), TimeFrame, CCIPeriod, CCIPrice)) return INIT_FAILED; //--- if(!ATR.Create(Symb.Name(), TimeFrame, ATRPeriod)) return INIT_FAILED; //--- if(!MACD.Create(Symb.Name(), TimeFrame, FastPeriod, SlowPeriod, SignalPeriod, MACDPrice)) return INIT_FAILED; if(!RSI.BufferResize(HistoryBars) || !CCI.BufferResize(HistoryBars) || !ATR.BufferResize(HistoryBars) || !MACD.BufferResize(HistoryBars)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); return INIT_FAILED; } //--- if(!Trade.SetTypeFillingBySymbol(Symb.Name())) return INIT_FAILED; //--- load models float temp;
Depois tentamos carregar os modelos previamente treinados.
if(!DOT.Load(FileName + "DOT.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *dot = new CArrayObj(); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(dot, actor, critic)) { delete dot; delete actor; delete critic; return INIT_FAILED; } if(!DOT.Create(dot) || !Actor.Create(actor)) { delete dot; delete actor; delete critic; return INIT_FAILED; } delete dot; delete actor; delete critic; }
Se não for possível carregar os modelos, inicializamos novos modelos com parâmetros aleatórios. Em seguida, transferimos ambos os modelos para um único contexto OpenCL.
Actor.SetOpenCL(DOT.GetOpenCL());
E realizamos uma verificação mínima da arquitetura do modelo.
Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; } //--- DOT.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
E salvamos o estado do saldo em uma variável local.
PrevBalance = AccountInfoDouble(ACCOUNT_BALANCE); PrevEquity = AccountInfoDouble(ACCOUNT_EQUITY); //--- return(INIT_SUCCEEDED); }
A interação direta com o ambiente e a coleta de dados são realizadas no método OnTick. No corpo do método, primeiro verificamos se ocorreu a abertura de um novo candle. Toda a análise é feita apenas na nova vela.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- if(!IsNewBar()) return;
Depois atualizamos os dados históricos.
int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), HistoryBars, Rates); if(!ArraySetAsSeries(Rates, true)) return; //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); Symb.Refresh(); Symb.RefreshRates();
E preenchemos o buffer de descrição do estado do ambiente.
float atr = 0; for(int b = 0; b < (int)HistoryBars; b++) { float open = (float)Rates[b].open; float rsi = (float)RSI.Main(b); float cci = (float)CCI.Main(b); atr = (float)ATR.Main(b); float macd = (float)MACD.Main(b); float sign = (float)MACD.Signal(b); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- int shift = b * BarDescr; sState.state[shift] = (float)(Rates[b].close - open); sState.state[shift + 1] = (float)(Rates[b].high - open); sState.state[shift + 2] = (float)(Rates[b].low - open); sState.state[shift + 3] = (float)(Rates[b].tick_volume / 1000.0f); sState.state[shift + 4] = rsi; sState.state[shift + 5] = cci; sState.state[shift + 6] = atr; sState.state[shift + 7] = macd; sState.state[shift + 8] = sign; } bState.AssignArray(sState.state);
A próxima etapa é coletar dados sobre o estado atual da conta.
sState.account[0] = (float)AccountInfoDouble(ACCOUNT_BALANCE); sState.account[1] = (float)AccountInfoDouble(ACCOUNT_EQUITY); //--- double buy_value = 0, sell_value = 0, buy_profit = 0, sell_profit = 0; double position_discount = 0; double multiplyer = 1.0 / (60.0 * 60.0 * 10.0); int total = PositionsTotal(); datetime current = TimeCurrent(); for(int i = 0; i < total; i++) { if(PositionGetSymbol(i) != Symb.Name()) continue; double profit = PositionGetDouble(POSITION_PROFIT); switch((int)PositionGetInteger(POSITION_TYPE)) { case POSITION_TYPE_BUY: buy_value += PositionGetDouble(POSITION_VOLUME); buy_profit += profit; break; case POSITION_TYPE_SELL: sell_value += PositionGetDouble(POSITION_VOLUME); sell_profit += profit; break; } position_discount += profit - (current - PositionGetInteger(POSITION_TIME)) * multiplyer * MathAbs(profit); } sState.account[2] = (float)buy_value; sState.account[3] = (float)sell_value; sState.account[4] = (float)buy_profit; sState.account[5] = (float)sell_profit; sState.account[6] = (float)position_discount; sState.account[7] = (float)Rates[0].time;
Consolidamos os dados coletados no buffer de descrição do estado da conta.
bAccount.Clear(); bAccount.Add((float)((sState.account[0] - PrevBalance) / PrevBalance)); bAccount.Add((float)(sState.account[1] / PrevBalance)); bAccount.Add((float)((sState.account[1] - PrevEquity) / PrevEquity)); bAccount.Add(sState.account[2]); bAccount.Add(sState.account[3]); bAccount.Add((float)(sState.account[4] / PrevBalance)); bAccount.Add((float)(sState.account[5] / PrevBalance)); bAccount.Add((float)(sState.account[6] / PrevBalance));
Aqui também adicionamos um carimbo de tempo do estado atual.
double x = (double)Rates[0].time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(2.0 * M_PI * x)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(2.0 * M_PI * x)); x = (double)Rates[0].time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(2.0 * M_PI * x)); //--- if(bAccount.GetIndex() >= 0) if(!bAccount.BufferWrite()) return;
Após coletar os dados iniciais, realizamos a propagação para frente do codificador.
if(!DOT.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); return; }
E imediatamente realizamos a propagação para frente do Actor.
//--- Actor if(!Actor.feedForward((CNet *)GetPointer(DOT), -1, (CBufferFloat*)GetPointer(bAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); return; }
Obtemos os resultados do modelo.
PrevBalance = sState.account[0]; PrevEquity = sState.account[1]; //--- vector<float> temp; Actor.getResults(temp); if(temp.Size() < NActions) temp = vector<float>::Zeros(NActions);
E os decodificamos executando operações comerciais.
double min_lot = Symb.LotsMin(); double step_lot = Symb.LotsStep(); double stops = MathMax(Symb.StopsLevel(), 1) * Symb.Point(); if(temp[0] >= temp[3]) { temp[0] -= temp[3]; temp[3] = 0; } else { temp[3] -= temp[0]; temp[0] = 0; } //--- buy control if(temp[0] < min_lot || (temp[1] * MaxTP * Symb.Point()) <= stops || (temp[2] * MaxSL * Symb.Point()) <= stops) { if(buy_value > 0) CloseByDirection(POSITION_TYPE_BUY); } else { double buy_lot = min_lot + MathRound((double)(temp[0] - min_lot) / step_lot) * step_lot; double buy_tp = NormalizeDouble(Symb.Ask() + temp[1] * MaxTP * Symb.Point(), Symb.Digits()); double buy_sl = NormalizeDouble(Symb.Ask() - temp[2] * MaxSL * Symb.Point(), Symb.Digits()); if(buy_value > 0) TrailPosition(POSITION_TYPE_BUY, buy_sl, buy_tp); if(buy_value != buy_lot) { if(buy_value > buy_lot) ClosePartial(POSITION_TYPE_BUY, buy_value - buy_lot); else Trade.Buy(buy_lot - buy_value, Symb.Name(), Symb.Ask(), buy_sl, buy_tp); } }
//--- sell control if(temp[3] < min_lot || (temp[4] * MaxTP * Symb.Point()) <= stops || (temp[5] * MaxSL * Symb.Point()) <= stops) { if(sell_value > 0) CloseByDirection(POSITION_TYPE_SELL); } else { double sell_lot = min_lot + MathRound((double)(temp[3] - min_lot) / step_lot) * step_lot; double sell_tp = NormalizeDouble(Symb.Bid() - temp[4] * MaxTP * Symb.Point(), Symb.Digits()); double sell_sl = NormalizeDouble(Symb.Bid() + temp[5] * MaxSL * Symb.Point(), Symb.Digits()); if(sell_value > 0) TrailPosition(POSITION_TYPE_SELL, sell_sl, sell_tp); if(sell_value != sell_lot) { if(sell_value > sell_lot) ClosePartial(POSITION_TYPE_SELL, sell_value - sell_lot); else Trade.Sell(sell_lot - sell_value, Symb.Name(), Symb.Bid(), sell_sl, sell_tp); } }
Os dados recebidos do ambiente são salvos no buffer de reprodução.
sState.rewards[0] = bAccount[0]; sState.rewards[1] = 1.0f - bAccount[1]; if((buy_value + sell_value) == 0) sState.rewards[2] -= (float)(atr / PrevBalance); else sState.rewards[2] = 0; for(ulong i = 0; i < NActions; i++) sState.action[i] = temp[i]; if(!Base.Add(sState)) ExpertRemove(); }
Os demais métodos do EA foram transferidos sem alterações. Você pode consultá-los no anexo.
2.4 EA de treinamento dos modelos
Após coletar a amostra de treinamento, passamos a construir o EA de treinamento dos modelos "...\Experts\DFFT\Study.mq5". Como os EAs de interação com o ambiente, seu algoritmo foi amplamente fundamentado em pesquisas anteriores. Portanto, neste artigo, proponho considerar apenas o método de treinamento direto dos modelos Train.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
No corpo do método, primeiramente geramos um vetor de probabilidades para a escolha de trajetórias a partir da amostra de treinamento, com base em sua rentabilidade. As passagens mais lucrativas serão usadas com mais frequência para o treinamento dos modelos.
Em seguida, declararemos as variáveis locais necessárias.
vector<float> result, target; bool Stop = false; //--- uint ticks = GetTickCount();
Após concluir o trabalho preparatório, realizamos um sistema de ciclos de treinamento dos modelos. Lembro que no modelo do Codificador usamos uma pilha de dados históricos. Esse modelo é altamente sensível à ordem cronológica dos dados fornecidos. Portanto, no ciclo externo, amostraremos a trajetória do buffer de reprodução de experiência e o estado inicial para o treinamento nessa trajetória.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - PrecoderBars - batch)); if(state <= 0) { iter--; continue; }
Depois, limpamos a pilha interna do modelo.
DOT.Clear();
E executamos um ciclo aninhado de extração de estados históricos sequenciais do buffer de reprodução de experiência para o treinamento do modelo. O pacote de treinamento do modelo foi definido para 2 dias a mais que a profundidade da pilha interna do modelo.
int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars); for(int i = state; i < end; i++) { bState.AssignArray(Buffer[tr].States[i].state);
No corpo do ciclo aninhado, extraímos um estado do ambiente do buffer de reprodução de experiência e o usamos para a propagação para frente do Codificador.
//--- Trajectory if(!DOT.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Para treinar a política do Ator, primeiro precisamos preencher o buffer de descrição do estado da conta, como fizemos no EA de interação com o ambiente. Só que agora não interrogamos o ambiente, mas extraímos dados do buffer de reprodução de experiência.
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Também adicionamos uma marca temporal.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
Depois, realizamos a propagação para frente do Ator e do Crítico.
//--- Actor if(!Actor.feedForward((CNet *)GetPointer(DOT), -1, (CBufferFloat*)GetPointer(bAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } //--- Critic if(!Critic.feedForward((CNet *)GetPointer(DOT), -1, (CNet*)GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Em seguida, treinamos o Ator com ações do buffer de reprodução de experiência, transmitindo o gradiente para o modelo do Codificador. Classificação de objetos no bloco TAE, conforme proposto pelo método DFFT.
Result.AssignArray(Buffer[tr].States[i].action); if(!Actor.backProp(Result, (CBufferFloat *)GetPointer(bAccount), (CBufferFloat *)GetPointer(bGradient)) || !DOT.backPropGradient((CBufferFloat*)NULL) ) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Depois, determinamos a recompensa para a próxima transição para um novo estado do ambiente.
result.Assign(Buffer[tr].States[i+1].rewards); target.Assign(Buffer[tr].States[i+2].rewards); result=result-target*DiscFactor;
E treinamos o modelo do Crítico, transmitindo o gradiente de erro para ambos os modelos.
Result.AssignArray(result); if(!Critic.backProp(Result, (CNet *)GetPointer(Actor)) || !DOT.backPropGradient((CBufferFloat*)NULL) || !Actor.backPropGradient((CBufferFloat *)GetPointer(bAccount), (CBufferFloat *)GetPointer(bGradient)) || !DOT.backPropGradient((CBufferFloat*)NULL) ) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Aqui vale notar que em muitos algoritmos anteriores tentávamos evitar a adaptação mútua dos modelos. Com receio de obter resultados indesejados. Os autores do método DFFT, por outro lado, afirmam que essa abordagem permitirá ajustar melhor os parâmetros do Codificador para extrair o máximo de informações.
Após o treinamento dos modelos, informamos o usuário sobre o progresso do processo de treinamento e passamos para a próxima iteração do ciclo.
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Critic", percent, Critic.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
Após concluir com sucesso todas as iterações do processo de treinamento, limpamos o campo de comentários no gráfico. Exibimos os resultados do treinamento no diário. E iniciamos a finalização do trabalho do EA.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic", Critic.getRecentAverageError()); ExpertRemove(); //--- }
Com isso, concluímos a análise dos métodos do EA de treinamento dos modelos. Você pode encontrar o código completo do EA no anexo. Além disso, todos os programas utilizados na preparação deste artigo também estão incluídos lá.
3. Teste
Foi realizado um trabalho bastante extenso na implementação do método Decoder-Free Fully Transformer-based (DFFT) usando MQL5. E agora é hora da 3ª parte do nosso artigo — testar o trabalho realizado. Como sempre, o treinamento e teste do novo modelo são realizados com dados históricos do instrumento EURUSD no timeframe H1. Os parâmetros de todos os indicadores são utilizados no padrão.
Para o treinamento do modelo, foram coletadas 500 trajetórias aleatórias no período dos primeiros 7 meses de 2023. O teste do modelo treinado foi realizado com dados históricos de agosto de 2023. Como pode ser observado, o intervalo de teste não fazia parte da amostra de treinamento. Isso permite avaliar o desempenho do modelo com novos dados.
Devo admitir que o modelo ficou bastante "leve" em termos de consumo de recursos computacionais tanto no processo de treinamento quanto na operação em modo de teste.
O processo de treinamento foi bastante estável, com uma redução suave do erro tanto do Ator quanto do Crítico. Durante o treinamento, foi obtido um modelo capaz de gerar um lucro pequeno tanto nos dados de treinamento quanto nos dados de teste. No entanto, gostaria de obter um nível de rentabilidade mais alto e uma linha de saldo mais estável.
Considerações finais
Neste artigo, conhecemos o método DFFT — um detector de objetos eficiente baseado em transformador sem uso de decodificador, que foi apresentado para resolver problemas de visão computacional. As principais características dessa abordagem incluem o uso do transformador para extrair características e a previsão densa em um único mapa de características. O método propõe novos módulos para melhorar a eficiência do treinamento e da operação do modelo.
Os autores do método demonstraram que DFFT oferece alta precisão na detecção de objetos com custos computacionais relativamente baixos.
Na parte prática deste artigo, implementamos as abordagens propostas usando MQL5. Realizamos o treinamento e o teste do modelo construído com dados históricos reais. Os resultados obtidos confirmam a eficácia dos algoritmos propostos e merecem uma investigação prática mais detalhada.
Gostaria de lembrar que todos os programas apresentados no artigo são exclusivamente para fins informativos. E foram criados apenas para demonstrar as abordagens propostas, bem como suas capacidades. Antes de usar nos mercados financeiros reais, os programas devem ser aprimorados e testados cuidadosamente.
Links
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | EA | EA de coleta de exemplos |
| 2 | ResearchRealORL.mq5 | EA | EA de coleta de exemplos com o método Real-ORL |
| 3 | Study.mq5 | EA | EA de treinamento de modelos |
| 4 | Test.mq5 | EA | EA para teste de modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de rede neural |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código do programa OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14338
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Desenvolvendo um sistema de Replay (Parte 58): Voltando a trabalhar no serviço
Desenvolvendo um sistema de Replay (Parte 58): Voltando a trabalhar no serviço
 Ciência de dados e aprendizado de máquina (Parte 20): Escolha entre LDA e PCA em tarefas de algotrading no MQL5
Ciência de dados e aprendizado de máquina (Parte 20): Escolha entre LDA e PCA em tarefas de algotrading no MQL5
 Classe base de algoritmos populacionais como alicerce para otimização eficiente
Classe base de algoritmos populacionais como alicerce para otimização eficiente
 Vantagens do Assistente MQL5 que você precisa saber (Parte 12): Polinômio de Newton
Vantagens do Assistente MQL5 que você precisa saber (Parte 12): Polinômio de Newton
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Привет Dmitriy!
Antes de mais nada, muito obrigado por esse algoritmo. É possível treinar o modelo com base em dados históricos e usar os dados treinados em uma situação ativa?
Rgs
Andreas