Análise Fractal dos Movimentos Conjuntos de Moedas

Introdução

Você muitas vezes ouve as pessoas discutindo as diferentes relações entre as moedas no mercado Forex.

Geralmente o principal ponto em questão se resume a fatores fundamentais, experiência prática ou meras especulações resultantes de estereótipos pessoais falando em voz alta. A hipótese de uma ou mais 'arrastando' todo o resto das moedas 'globais' pode ser considerado um caso extremo.

De fato, qual é a natureza das relações entre as várias cotações? São os seus movimentos coordenados ou não? O movimento de uma moeda sugere o movimento de outra? O artigo tenta resolver esta questão usando uma dinâmica não-linear e métodos geométricos fractais.

1. Parte Teórica

1.1. Variáveis dependentes e independentes

Vamos dar uma olhada em duas variáveis (cotações) x e y. Em qualquer dado momento, estes valores instantâneos das variáveis determinam um ponto no plano-XY (Fig. 1). O movimento do ponto no decurso do tempo forma uma trajetória. A forma e o tipo de tal trajetória dependerá do tipo de relação entre as variáveis.

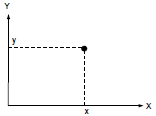
Figura 1. Ponto no plano

Por exemplo, se a variável x não tem relação com a variável y, você vai não observar nenhuma estrutura regular - o plano XY será uniformemente cheio de pontos, desde que o seu número seja suficiente (Figura 2).

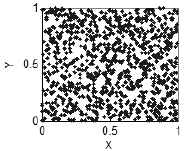
Figura 2. Nenhuma correlação - plano uniformemente preenchido

Se, no entanto, existe uma relação entre x e y, uma estrutura regular aparece, neste caso mais simples representa uma curva (Fig. 3),

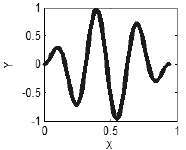
Figura 3. Presença de correlações - uma curva

ou ainda, uma estrutura mais complexa (Fig. 4).

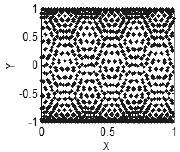
Figura 4. Presença de correlações - uma estrutura no plano

O mesmo possui características de um espaço tridimensional: se todas as variáveis são interrelacionados ou interdependentes, os pontos irão formar uma curva (Fig. 5), se existem duas variáveis independentes no conjunto, então neste caso os pontos irão formar uma superfície ( A Fig. 6) de três variáveis independentes, os pontos preencherão um espaço tridimensional, etc.

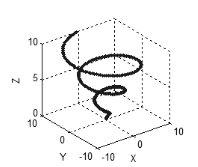
Figura 5. Uma curva no espaço tridimensional

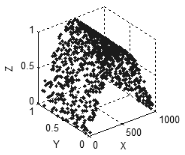
Figura 6. Uma superfície no espaço tridimensional

Se não existe uma relação entre as variáveis, os pontos serão uniformemente distribuídas em todas as dimensões disponíveis (Fig. 7). Assim, podemos falar sobre a natureza das relações entre as variáveis com base na forma como os pontos preenchem o espaço.

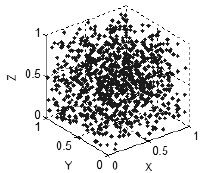
Figura 7. Nenhuma correlação - pontos uniformemente distribuídos no espaço

Neste caso a forma da estrutura resultante (linha, de superfície, a forma 3-D, etc.) é qualquer importância.

O que importa é a dimensão fractal do que a estrutura: 1 para conjuntos descrevendo linhas, 2 para conjuntos descrevendo superfícies, 3 para conjuntos descrevendo volumes, etc. Usualmente presume-se que um valor da dimensão fractal corresponde ao número de variáveis independentes num conjunto de dados.

Nós também podemos nos deparar com uma dimensão fracionada, por exemplo: 1.61 ou 2.68. Este pode ser o caso, se a estrutura resultante é um fractal, ou seja, um conjunto auto similar de dimensão não integral. Um exemplo de um fractal é dado na Figura 8, a sua dimensão é de cerca de 1.89, não é mais uma linha (dimensão 1) e ainda não é uma superfície (dimensão 2).

Figura 8. O tapete de Sierpinski

A dimensão fractal de um único e mesmo conjunto podem ser diferentes em diferentes escalas.

Por exemplo, se você der uma olhada no conjunto na Figura 9 de 'longe', você vai ver claramente uma linha, ou seja, uma dimensão fractal do conjunto 1. Um olhar 'plano fechado' para o mesmo conjunto deixará de revelar uma linha, mas um 'tubo difuso', onde os pontos não formam uma linha clara, mas se acumulam em torno dela de forma aleatória. A dimensão fractal do 'tubo' será igual à dimensão do espaço na qual nossa estrutura é considerada, pois os pontos no 'tubo' serão uniformemente distribuídos em todas as dimensões disponíveis.

Um aumento na dimensão fractal em escalas menores permite estimar uma dimensão em que as relações entre as variáveis se tornam indiscernível, devido à presença de ruído aleatório.

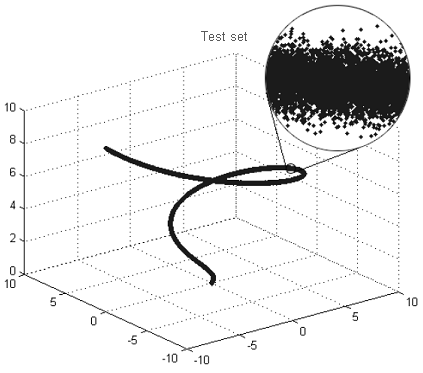
Figura 9. Exemplo de um 'tubo' fractal

1.2. Estimando a dimensão fractal

A dimensão fractal pode ser estimada usando o método de contagem de caixa com base na análise da dependência do número de caixas, contendo pontos de um conjunto sobre o comprimento do lado da caixa ( não tem de ser uma caixa 3D - uma "caixa" no espaço unidimensional será representado por um segmento; no espaço bidimensional, por um quadrado, etc)

Teoricamente, essa dependência é dada por N(ε) ~ 1/ε^D, Onde D é a dimensão fractal do conjunto, ε é o comprimento do lado da caixa, N(ε) - caixas de tamanho ε contendo pontos do conjunto. A fórmula permite estimar a dimensão fractal

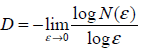
Sem entrar em mais pormenores, o funcionamento do algoritmo pode ser descrito como se segue:

1. Um determinado conjunto de pontos é dividido em caixas de tamanho ε, o número de N caixas contêm pelo menos um ponto no conjunto contado.

2. Para várias Épsilon (ε), um respectivo valor de N é determinado, ou seja, acumulamos dados para plotar a dependência N(ε).

3. A dependência N(ε) é representada por coordenadas logarítmicas duplas onde a inclinação da dependência corresponderá ao valor da dimensão fractal.

Por exemplo, a Figura 10 mostra dois conjuntos: uma figura plana (a) e uma linha (b). Células que contêm pontos do conjunto são preenchidas na cor cinza. Contando o número de células 'cinzas' com tamanhos diferentes de células, obtemos as dependências ilustradas na Figura 11. A inclinação das linhas retas que se aproximam destas dependências ajudam a estimar as dimensões fractais: Da≈2, Db≈1.

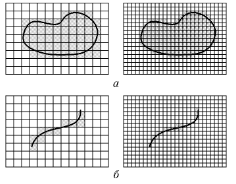
Figura 10. Mensurando os conjuntos

Normalmente, uma dimensão fractal é estimada na prática utilizando o algoritmo Grassberger-Procaccia, em vez do método de contagem de caixa, pois produz resultados mais precisos em espaços dimensionais grandes. A ideia do algoritmo é: a obtenção de uma dependência С(ε) da probabilidade de dois pontos de um conjunto obtido numa célula de tamanho ε, sobre o tamanho da célula, e para determinar o declive de uma seção linear de tal dependência.

Infelizmente, é impossível abranger todos os aspectos para estimar a dimensão fractal dentro do âmbito deste artigo. Outras informações, se necessárias, podem ser encontradas na literatura especializada.

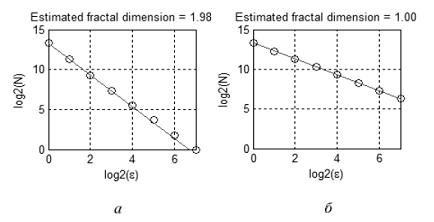
Figura 11. Dimensão fractal estimada dos conjuntos

1.3. Exemplo de dimensão fractal estimada dos conjuntos

Para verificar o desempenho da técnica proposta, vamos determinar o nível de ruído e o número de variáveis independentes para o conjunto mostrado na Figura 9. Este conjunto tridimensional é composto por 3000 pontos e representa uma linha (uma variável independente) com ruído sobreposto. O ruído é normalmente distribuído, com erro médio de raiz quadrada igual a 0.01.

A Figura 12 demonstra a dependência С(ε) em escala logarítmica. Existem duas seções lineares se cruzando em ε≈2^-4.6≈0.04. A inclinação da primeira linha é ≈2.6, a inclinação da segunda linha é ≈1.0.

Os resultados obtidos sugerem que o conjunto de teste tem apenas uma variável independente na escala maior do que 0.0 e 'quase três' variáveis independentes ou ruído sobrepostos na escala menor do que 0.04. Isto está em boa concordância com os dados iniciais: de acordo com a regra três Sigma, 99.7% dos pontos formam um "tubo" com um diâmetro de 2 * 3 * 0.01≈0.06.

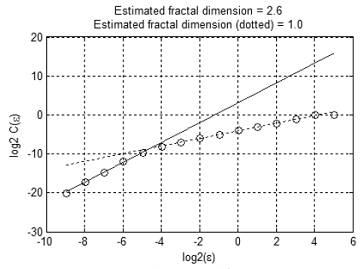
Figura 12. Dependência С(ε) em escala logarítmica

2. Parte Prática

2.1. Dados iniciais

As propriedades fractais do mercado Forex foram estudadas usando dados públicos durante o período de 2000 a 2009, inclusive. O estudo foi realizado nos fechamento dos preços dos sete principais pares de moeda: EURUSD, USDJPY, GBPUSD, AUDUSD, USDCHF, USDCAD, NZDUSD.

2.2. Implementação

Algoritmos para estimar a dimensão fractal foram implementados na forma de funções do ambiente MATLAB, com base em desenvolvimentos feitos pelo Dr. Michael Small (http://www.eie.polyu.edu.hk/~ensmall/matlab/). Funções com exemplos de implementação estão disponíveis no arquivo frac.rar anexado a este artigo.

Para acelerar os cálculos, a parte mais demorada foi escrita em linguagem C. Antes de começar, compilar a função C "interbin.c" usando o comando MATLAB "mex interbin.c".

2.3. Os resultados do estudo

A Figura 13 mostra um movimento do conjunto de preços do EURUSD e GBPUSD no ano de 2000 a 2010. Os valores dos preço são demonstrados nas Figuras 14 e 15.

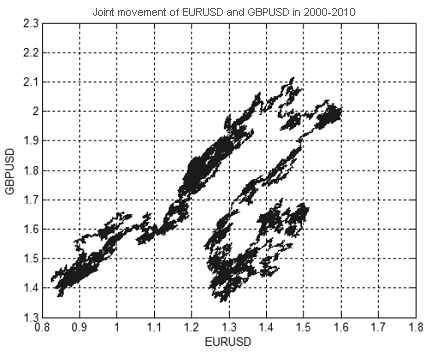
Figura 13. A movimentação conjunta dos preços de EURUSD e GBPUSD no ano de 2000 a 2010

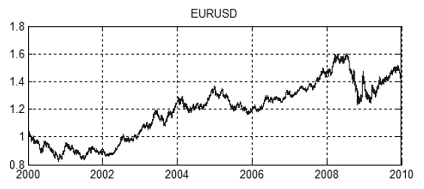
Figura 14. Tabela de preços EURUSD no ano de 2000 a 2010

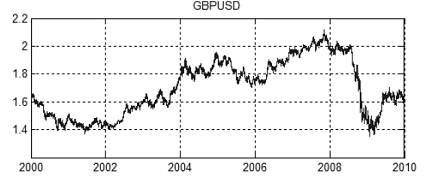
Figura 15. Tabela de preços GBPUSD no ano de 2000 a 2010

A dimensão fractal do conjunto mostrado na Figura 13 é aproximadamente igual a 1,7 (Fig. 16). Isso significa que o movimento EURUSD + GBPUSD não representa um passeio "puramente" aleatório, do contrário sua dimensão teria sido 2 (dimensão de um passeio aleatório em espaços bidimensionais ou maiores é sempre igual a 2).

No entanto, uma vez que o movimento do preço é muito parecido com o passeio aleatório, não podemos analisar os valores de preços por si mesmos - dimensão fractal muda insignificante quando novos pares de moedas são adicionados (Tabela 1) e é impossível tirar qualquer conclusão.

Os pares de moedas	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
Dimensão	1.7	1.9	1.9	1.9	1.9	1.9

Tabela 1. Mudança na dimensão sobre o aumento no número de moedas

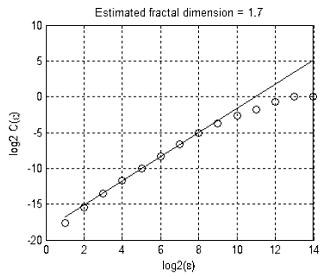
Figura 16. Dimensão fractal estimada

Para obter resultados mais interessantes, devemos proceder a partir de interações entre as cotações.

Valores de dimensão para vários intervalos incrementados e número diferente de pares de moedas são apresentados na Tabela 2.

	Datas	Número de pontos	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
M5	14 Aug 2008 — 31 Dec 2009	100000	1.9	2.8	3.7	4.4	5.3	6.2
M15	18 Nov 2005 — 31 Dez 2009	100000	2	2.8	3.7	4.5	5.9	6.7
M30	16 Nov 2001 — 31 Dez 2009	100000	2	2.8	3.7	4.5	5.7	6.8
H1	03 Jan 2000 — 31 Dez 2009	61765	2	2.9	3.8	4.6	5.6	6.5
H4	03 Jan 2000 — 31 Dez 2009	15558	2	3	4	4.8	5.9	6.3
D1	03 Jan 2000 — 31 Dez 2009	2601	2	3	4	5.1	5.7	6.5

Tabela 2. Mudança na dimensão em diferentes intervalos incrementados

Se as moedas estão inter-relacionadas, cada vez que um novo par de moedas é adicionado, a dimensão fractal deve aumentar menos e menos significativamente para finalmente chegar a um certo valor, determinando o número de 'variáveis livres' no mercado cambial de moedas.

Se nós também assumirmos, que o 'ruído do mercado' é sobreposto aos preços, todas as dimensões disponíveis podem obter preenchimento com o ruído nos timeframes (М5, М15, М30) e este efeito deve desaparecer em timeframes longos, 'revelando' as dependências entre as cotações (como no exemplo do teste).

Essa hipótese não foi confirmada por dados reais, mas a Tabela 2 sugere: o conjunto é distribuído em todas as dimensões disponíveis em todos os prazos, ou seja, todas as moedas são independentes uma da outra.

É um pouco conflitante com as hipóteses intuitivas sobre as relações monetárias. Parece que as moedas vizinhas, por exemplo: GBP e CHF ou AUD e NZD, devem apresentar uma dinâmica semelhante. Por exemplo, a Figura 17 mostra o incremento das dependências entre as correlações no par NZDUSD e AUDUSD; prazo M5 (coeficiente de correlação: 0,54) M5 e D1 (coeficiente de correlação: 0,84).

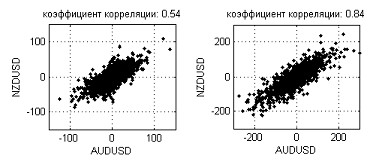
Figura 17. Incremento de dependências no par NZDUSD e AUDUSD entre os prazos de M5 (0,54) e D1 (0,84)

Como pode ser visto nesta figura, a dependência recebe mais e mais esticada diagonal e o valor do coeficiente de correlação sobe, assim como o intervalo aumenta. No entanto, em termos de dimensão fractal, o nível de ruído é demasiado elevado para considerar tal dependência como uma linha unidimensional. Dimensões fractais em intervalos mais longos (semanas, meses) talvez convergem para um determinado valor, mas não temos facilidades de verificar isso devido ao número insuficiente de pontos para estimar a dimensão.

Conclusão

Certamente seria mais interessante limitar os movimentos das moedas a uma ou mais variáveis independentes para simplificar consideravelmente a tarefa de reconstruir o atrator de mercado e prever os preços. O mercado, no entanto, produz um resultado diferente: dependências são fracamente pronunciadas e "bem escondidas" numa grande quantidade de ruído. O mercado é muito eficaz a este respeito.

Métodos de dinâmica não-linear que constantemente produzem bons resultados em áreas como a medicina, física, química, biologia e outras, requerem uma atenção especial e cuidadosa interpretação dos resultados quando utilizados na análise do preço de mercado.

Os resultados obtidos não sugerem expressamente a presença ou ausência de relações entre as moedas. Nós só podemos dizer que o nível de ruído nos prazos indicados é comparável à "força" do relacionamento, de modo que a questão das relações entre as moedas permanece em aberto.