货币联动的分形分析

简介

经常可以听到人们讨论外汇市场中不同货币之间的关系。

讨论的要点通常归结为基本因素、实践经验或纯粹的推测，均来自说话者的个人成见。 一种或多种‘全球’货币‘拖动’所有其他货币，这种假设可以认为是一种极端情形。

而各种报价之间的关系本质，究竟是什么呢？ 它们的走势是协同呢？还是一种货币的走势跟其他货币的走势截然无关？ 本文描述了如何使用非线性动力学和分形几何方法解决该问题。

1. 理论部分

1.1. 依赖和独立变量

我们来看两个变量（报价） x 和 y。 在任意时点上，这些变量的同步值在 XY-平面上确定了一个点。 点随时间运动形成了轨迹。 这种轨迹的形态和类型将取决于变量之间的关系类型。

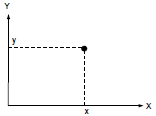
图 1 平面上的点

例如，如果变量 x 跟变量 y 没有关系，你就会看到不规则的结构——只要数量足够，点就会在 XY-平面上均匀分布。

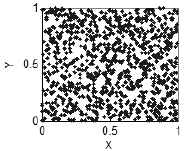
图 2 没有关联——均匀分布在平面上

如果 x 和 y 之间存在关系，就会出现规则的结构，在最简单的情况下出现一条曲线（图 3）。

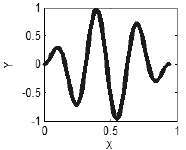
图 3 存在关联 ——曲线

或更加复杂的结构（图 4）。

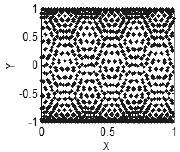
图 4 存在关联——平面上的结构

三维和多维空间中的特征相同：如果所有的变量相互关联或相互依赖，这些点会形成一条曲线（图 5），如果一组内有两个独立变量，这些点会形成一个面（图 6），在三个独立变量的情况下，这些点会填充这个三维空间。

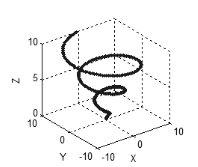
图 5 三维空间中的曲线

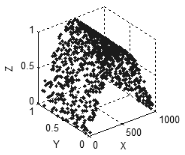
图 6 三维空间中的面

如果变量之间没有关系，这些点就会均匀分布在所有可用维数内（图 7）。 这样，我们就可以用点填充空间的方式来描述变量之间的关系本质。

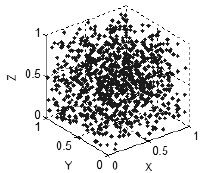
图 7 没有关联——点在空间均匀分布

生成的结构形态（线、面和三维形状等）在本例中并不重要。

重要的是结构的分形维数： 1 用于描述线的集合，2 用于描述面的集合，3 用于描述体的集合等等。通常认为，分形维数值对应着数据集内独立变量的数量。

我们也会遇到比如 1.61 或 2.68 的分形维数。 如果生成的结构是一个分形，即非整数维数的自相似集，可能就是这种情况。 图 8 中给出了一个分形示例，其维数约为 1.89，即不再是一条线（维数 1）或者一个面（维数 2）。

图 8 谢尔宾斯基地毯

同一个集的分形维数在不同的比例下可能不同。

例如，如果从远处看图 9 的集，可以清晰的看到一条线，即给定集的分形维数为 1。 ‘近距离’观察同一个集会发现它不再是一条线，而是一个‘模糊的管道’，其中的点没有形成一条清晰的线，而是以随机的方式聚集在线的周围。 该‘管道’的分形维数应等于我们考虑的结构中的空间维数，因为‘管道’中的点会均匀分布在所有可用维数内。

在较小比例下分形维数的增加可以估算维数，由于随机噪音的出现，该维数下变量之间的关系变得无法识别。

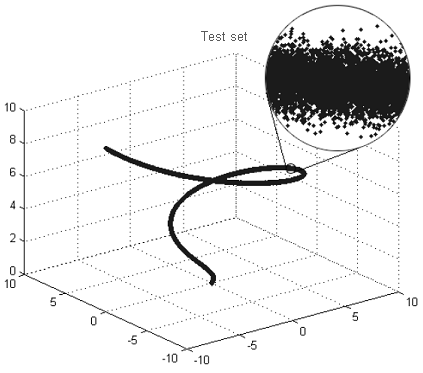
图 9 分形‘管道’的示例

1.2. 估算分形维数

可以使用盒维数方法估算分形维数，该方法基于对盒子数量的依存度分析，其中盒子数量包含了盒子边长上点集中的点（盒子不一定是三维的——在一维空间中‘盒子’可以用一条线段表示，二维空间中用正方形表示，等等）。

理论上，这种依存度由 N(ε)~1/ε^D 给出，其中 D 是点集的分形维数，ε 是盒子的边长，N(ε) 是包含点集中的点且边长为 ε 的盒子数量。 它可以估算分形维数。

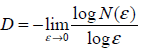
简单而言，算法运行的描述如下：

1. 将给定的点集分解为边长为 ε 的盒子，且计算至少包含点集中一个点的盒子的数量 N。

2. 对于各种 ε，分别确定相应的 N 值，也就是说，我们积累数据以绘制依存度 N(ε)。

3. 依存度 N(ε) 绘制在双对数坐标上，其中依存度的斜率对应分形维数的数值。

例如，图 10 显示了两个点集：平面图形（a）和线（b）。 包含点集的点的格子由灰色填充。 计算具有不同格子大小的‘灰色’格子数量，得到图 11 中显示的依存度。 接近这些依存度的直线的斜率有助于估算分形维数： Da≈2, Db≈1.

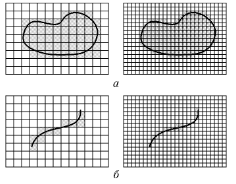
图 10 测量点集

在实践中通常使用 Grassberger-Procaccia 算法而不是计盒维数法来估算分形维数，因为这样可以在多维空间内得到更加精确的结果。 该算法的理念是获得一个点集内两个点进入一个边长为 ε 的格子的概率的依存度，并确定该依存度的线性部分的斜率。

不幸的是，限于本文的范围，无法涉及估算分形维数的所有方面。 如果需要更多信息，请查阅专业文献。

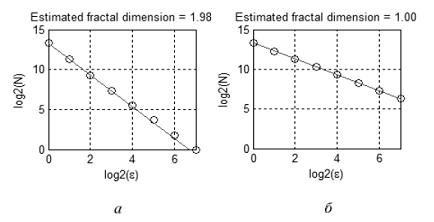
图 11 估算点集的分形维数

1.3. 估算分形维数示例

为了验证所述方法的效果，我们为图 9 所示点集确定噪音水平和独立变量的数量。 这个三维点集包含 3000 个点，表现为一条具有叠加噪音的线（一个独立变量）。 噪音为正态分布，均方根误差为 0.01。

图 12 展示了对数标度下的依存度 С(ε)。 有两个线性部分相交于 ε≈2^-4.6≈0.04。 第一条线的斜率≈2.6，第二条线的斜率≈1.0。

得到的结果显示，测试集在大于 0.0 的标度上只有一个独立变量，在小于 0.04 的标度上有‘接近三个’独立变量或叠加噪音。 这跟初始数据非常吻合：根据三标准差规则，99.7% 的点形成了一个直径为 2*3*0.01≈0.06 的‘管道’。

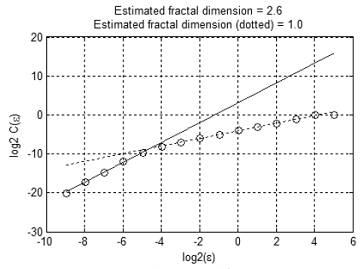
图 12 对数标度下的依存度 C(e)

2. 实践部分

2.1. 初始数据

对外汇市场分形特性的研究采用了 从 2000 年到 2009 年（含 2000 年和 2009 年）期间的公开数据。 对七个主要货币对的收盘价进行了研究： EURUSD、USDJPY、GBPUSD、AUDUSD、USDCHF、USDCAD、NZDUSD。

2.2. 实施

估算分形维数的算法是基于 Michael Small 博士的开发，以 MATLAB 环境函数的形式实现(http://www.eie.polyu.edu.hk/~ensmall/matlab/)。 本文随附的 frac.rar 文件中，包含了带有应用示例的函数。

为了加快计算，最耗时的部分使用 C 语言编写。 在开始之前，使用 MATLAB 命令“mex interbin.c”编译 C 语言函数“interbin.c”。

2.3. 研究结果

图 13 显示了 2000 年到 2010 年期间 EURUSD 和 GBPUSD 价格的联动情况。 价格值如图 14 和 15 所示。

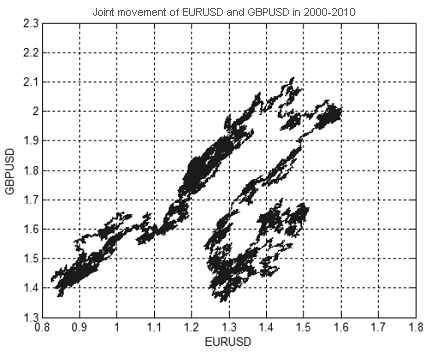
图 13 2000 年到 2010 年期间 EURUSD 和 GBPUSD 价格的联动情况

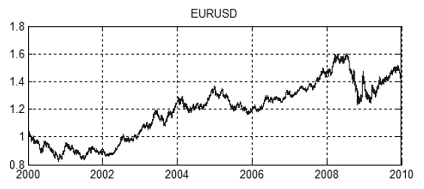
图 14 2000 年到 2010 年的 EURUSD 价格图表

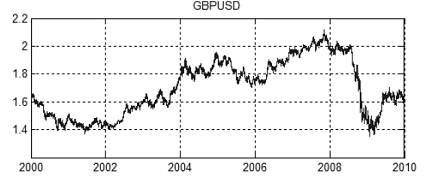
图 15 2000 年到 2010 年的 GBPUSD 价格图表

图 13 所示点集的分形维数约等于 1.7（图 16）。 这表明 EURUSD + GBPUSD 的变动 并非是‘纯’随机游动，否则其维数应等于 2（在两维和多维空间中随机游动的维数始终等于 2）。

但是，由于价格变动跟随机游动非常相似，我们无法根据它们分析价格值——当添加新的货币对时，分形维数变化并不明显（表 1），无法得出任何结论。

货币对	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
维数	1.7	1.9	1.9	1.9	1.9	1.9

表 1 货币数量增加时的维数变化

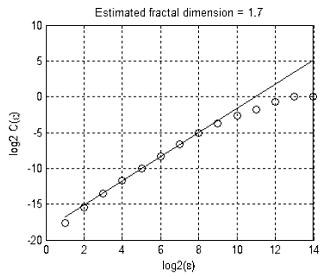
图 16 估算的分形维数

为了获得更加有趣的结果，我们应该从报价转到报价的变化。

表 2 中提供了不同增量间隔和不同货币对数的维数值。

	日期	点数	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
M5	2008 年 8 月 14 号——2009 年 12 月 31 号	100000	1.9	2.8	3.7	4.4	5.3	6.2
M15	2005 年 11 月 18 号——2009 年 12 月 31 号	100000	2	2.8	3.7	4.5	5.9	6.7
M30	2001 年 11 月 16 号——2009 年 12 月 31 号	100000	2	2.8	3.7	4.5	5.7	6.8
H1	2000 年 1 月 03 号——2009 年 12 月 31 号	61765	2	2.9	3.8	4.6	5.6	6.5
H4	2000 年 1 月 03 号——2009 年 12 月 31 号	15558	2	3	4	4.8	5.9	6.3
D1	2000 年 1 月 03 号——2009 年 12 月 31 号	2601	2	3	4	5.1	5.7	6.5

表 2 在不同增量间隔下的维数变化

如果货币相互关联，随着每次添加新的货币对，分形维数应该增加的越来越不明显，最终得到一个特定值，该值将确定外汇市场上‘自由变量’的数量。

如果我们另假设价格上叠加‘市场噪音’，则所有可用的维数都可能在较短的时间范围（М5、М15 和 М30）上充满了噪音，而且这种效果应该在‘反映’报价之间依存度的较长时间范围上减弱（如测试示例）。

如表 2 所示，该假设未经实际数据确认：点集中的点在所有时间范围上分布在所有可用维数内，也就是说，所有的货币都彼此独立。

这跟对货币关系的直觉假设有些冲突。 关系密切的货币，例如 GBP 和 CHF，或者 AUD 和 NZD，似乎应该表现出相似的动态。 例如，图 17 显示了 NZDUSD 和 AUDUSD 在 M5（相关系数为 0.54）以及 D1 时间范围上的增量依存度（相关系数为 0.84）。

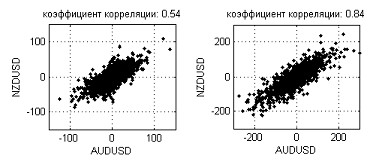
图 17 NZDUSD 和 AUDUSD 在 M5（0.54）和 D1（0.84）时间范围上的增量依存度

从图中可以看出，随着间隔增加，依存度变得对角拉伸越来越大，相关系数值也随之上升。 但是，对于分形维数而言，噪音水平过高，不能将这种依存度视为一条一维线。 更长间隔（周、月）上的分形维数可能会收敛到一个特定值，但我们没有工具对其检查，因为没有足以估算维数的点数。

总结

将货币变动限定到一个或多个独立变量上，以显著简化重新构建市场吸引子和预测价格的任务，将会更加有趣。 但是市场产生了不同的结果：依存度非常不明显，“深深的隐藏”在大量的噪音中。 在这方面，市场是非常有效的。

对于已经在医学、物理、化学、生物和其他领域产生稳定良好结果的非线性动力学方法，在用于市场价格分析时需要特别注意和谨慎解读结果。

获得的结果没有明确表明货币之间存在或不存在关系。 我们只能说，在给定时间范围上的噪音水平跟关系的‘强度’相当，所以货币之间关系的问题仍悬而未决。