合同通貨の動きのフラクタル解析

はじめに

Forex市場で異なる通貨間の関係について論じているのを聞くことがあると思います。

重要な問題点は、ファンダメンタルな要因や、実践の経験、話者の個人的なステレオタイプに由来する単なる推測になるということです。すべての通貨に影響する、一つか、それ以上の「グローバル」通貨の仮説は、極端なケースだと考えられます。

実際、様々な通貨の関係の本質はなんでしょうか？それらの動きは協調しているのか、それとも、ある通貨の動きはその他の動きに影響しないのでしょうか？この記事は、非線形力学やフラクタル幾何学を用いたこの問題への取り組みを紹介します。

1. 理論的な側面

1.1. 依存と独立変数

xとyの二つの変数を見てみましょう。特定の時間でのこれらの変数の瞬間的な値は、XY平面のポイントを決定します。（図１）ポイントの動きが起動を描きます。そのような起動の形や種類は、その変数館の関係の種類に依存する。

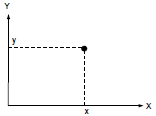
図1. 平面のポイント

例えば、もしその変数xは、変数yに何の関係もない場合、規則的な構造は観測されません - XY平面は、その数が充分であれば（図2）、そのポイントで一様に塗りつぶされます。

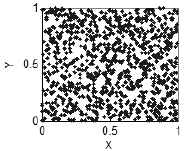
図2. 相関関係なし - 単一に塗りつぶされた平面

しかし、もしxとyに関係性があれば、規則的な構造が現れ、カーブを描きます（図3）

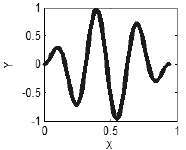
図3. 相関関係あり - カーブ

、もしくは、より複雑な構造（図4）

図4. 相関関係あり - 平面の構造

三次元、それ以上の次元での空間でも同じです：もしすべての変数が相互に依存し、関連している場合、ポイントはカーブを描き（図5）、もし二つの相互依存する変数があれば、ポイントは面を形成し（図6）、３つの相互依存する変数の場合、ポイントは３次元のスペースを形成します。

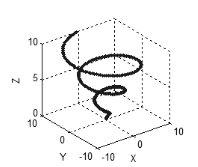
図5. ３次元空間でのカーブ

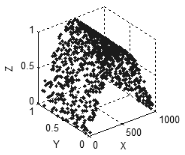
図6. ３次元の表面

もし変数に関係性がなければ、ポイントは、すべての使用可能な次元にて均一に分散されます (図7). 従って、ポイントがスペースを塗りつぶす方法に基づいて変数間の関係性の本質を語ることができます。

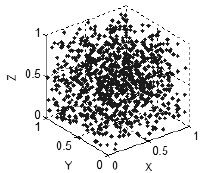
図7. 相関関係なし - ポイントは、そのスペースで均一に分散されます。

結果として生じる構造の形（線、平面、３Dの形状など）は、この場合重要ではありません。

重要な点は、その構造のフラクタル次元です：線を描画するセットの１、面を描画するセットの２、量を記述するセットの３などです。フラクタル次元の値は、データセットの相互依存変数の数に一致すると想定します。

また、1.61や2.68などのフラクショナル次元を取得できます。これは、 結果として生じる構造がフラクタルの場合、つまり非整数次元の類似したセットの場合、事実です。フラクタルの例は、図8にて提示されています。その次元は、おおよそ1.89になり、これはもはや線ではなく、平面でもありません。

図8. シェルピンスキーのカーペット

同じセットのフラクタル次元は、異なる規模では異なります。

例えば、もし図９の'afar'のセットを見てみれば、その線をはっきりと見ることができると思います。つまり、その特定のセットのフラクタル次元は、１になります。同じセットをより詳細に見ると、線ではなく、ポイントが明確な線を形成せず、ランダムにその周りをポイントが蓄積されている'fuzzy tube'を示しています。その'tube'のフラクタル次元がそのスペースの次元に等しく、そのストラクチャーは'tube'のポイントがすべての次元において均一に分配されていると考えられます。

より小さい規模でのフラクタル次元の増大で、変数間の関係がランダムなノイズのために識別できなくなります。

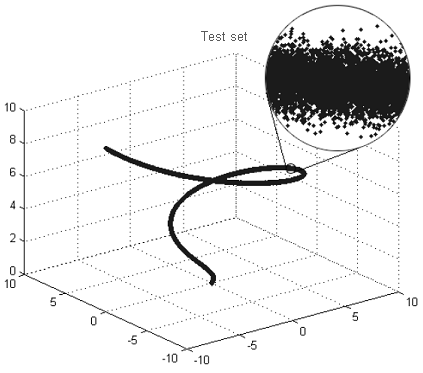
図9. フラクタル'tube'の例

1.2. フラクタル次元の評価

フラクタル次元は、そのボックスの側の長さでの特定のセットのポイントを含むボックスの数の依存の分析に基づいたボックスを数えるメソッドを用いて推測できます。（3Dボックスである必要はなく、一次元スペースのボックスは、一つのセグメントにより表現され、二次元では、正方形により表現されます）

理論的に、この依存は、N(ε)~1/ε^Dにより提示され、Dは、そのセットのフラクタル次元で、ε はボックスの側面の長さ、N(ε)は、そのセットのポイントを保持するεのサイズのボックスの数です。それにより、フラクタル次元を評価することができます。

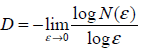
あまり詳細に触れなければ、そのアルゴリズムの処理は次の通りに記述できます。

1. 特定のセットのポイントがεのサイズぼボックスに分けられ、少なくとも１ポイントを持つNボックスの数が計測されます。

2. 様々な ε のために、それぞれのNの値が判断されます。依存 N(ε)を記述するためにデータを蓄積します。

3. その依存 N(ε) は、その依存の傾きがフラクタル次元の値に一致する二重の対数座標に記述されます。

例えば、図10は二つのセットを示します：平面図(a)と線(b)そのセットのポイントを保持するセルは、グレーで塗りつぶされます。異なるセルのサイズのグレーのセルの数を数え、図11で示される依存性を取得します。これらの依存に近い直線の傾きは、フラクタル次元の評価を助けます：Da≈2, Db≈1

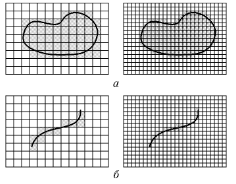
図10. セットの測定

通常、フラクタル次元は、高次元の空間でより正確な結果を弾き出すことができるので、ボックスを数えるメソッドではなく、Grassberger-Procacciaアルゴリズムを用いてひょうっかされます。そのアルゴリズムの考えは、εのサイズのセルで、そのサイズのセルに入る特定のセットの二つのポイントの確率の依存C(ε)を取得し、そのような依存の線形のセクションの傾きを決定します。

不幸にも、この記事の範囲にてフラクタル次元を評価するすべての側面をカバーすることは不可能です。さらに詳しい情報が必要であれば、特化した文献でご覧になれます。

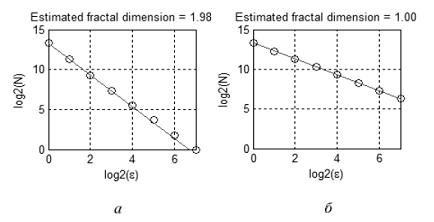
図11. 評価されるフラクタル次元

1.3. フラクタル次元の評価例

提示されたテクニックのパフォーマンスを確かめるために、図9で示されるセットにおけるノイズのレベルと依存する変数の数を決定しましょう。この３次元のセットは3000ポイントからなり、重ねられたノイズを持つ線を表示します。通常、そのノイズは0.01の二乗平均根エラーで分散されます。

図12は、対数スケールの依存 C(ε)を示します。ε≈2^-4.6≈0.04.で交差する二つの線形セクションがあります。最初の線の傾きは、≈2.6で、２番目は≈1.0です。

取得された結果によると、そのテストセットは、0.0以上のスケールにて相互依存する変数を持ち、0.04以下のスケールでほとんど３つの相互依存する変数かノイズを持ちます。これは、最初のデータと同調します：３つのシグマのルールによれば、99.7%のポイントは、直径2*3*0.01≈0.06で'tube'を形成します。

図12. 対数スケールの依存C(e)

2. 実践的な側面

2.1. 初期のデータ

2000から2009年までの期間をカバーする公的なデータを用いて、Forexマーケットのフラクタル特性は研究されました。その研究は、以下７つの主要な通貨のクロージング価格にて実行されました: EURUSD, USDJPY, GBPUSD, AUDUSD, USDCHF, USDCAD, NZDUSD.

2.2. 実装

フラクタル次元を評価するアルゴリズムは、Dr. Michael Smallによる開発に基づくMATLAB環境関数の形で実装されました. 実装例のある関数はこの記事に添付されているfrac.rar アーカイブにて取得できます。

計算を高速化するために、最も時間のかかる部分はC言語で書かれました。始める前に、MATLABコマンド "mex interbin.c"を用いてC関数"interbin.c"をコンパイルしてください。

2.3. 研究結果

図13 は、2000から2010年までのEURUSDとGBPUSD価格の関節運動を示します。その価格値は、図14、15で示されています。

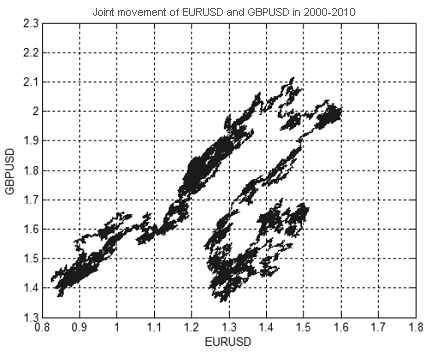
図13. EURUSDとGBPUSD価格の2000年から2010年までの関節運動

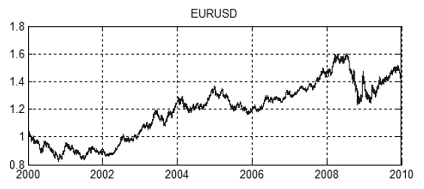
図14. 2000年から2010年までのEURUSD価格チャート

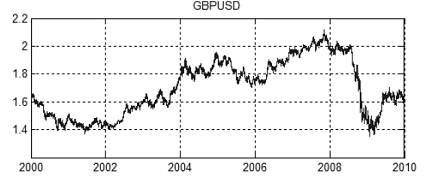
図15. 2000年から2010年までのGBPUSD価格チャート

図13に示されているセットのフラクタル次元は、おおよそ1.7に等しくなります(図16). EURUSD + GBPUSDの動き は、純粋なランダムウォークを示さないことを意味し、さもなければ、その次元は、二次元になります（二次元かそれ以上の次元でのランダムウォークの次元は、2に常に等しいです。）

しかしながら、その価格の動きはランダムウォークに類似しているので、それら自身で価格の値を分析できません - (表

通貨ペア	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
次元	1.7	1.9	1.9	1.9	1.9	1.9

表1. 通貨数の上昇に伴う次元の変化

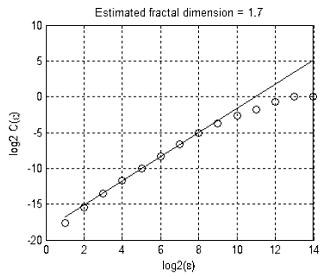
図16. 評価されるフラクタル次元

より興味深い結果を取得するために、その通貨相場からそれらの変化に進む必要があります。

様々な増大インターバルや異なる通貨ペアの数における次元の値は、表１に示されています。

	日付	ポイント数	EURUSD GBPUSD	+USDJPY	+AUDUSD	+USDCHF	+USDCAD	+NZDUSD
M5	142008年8月 — 2009年12月31日	100000	1.9	2.8	3.7	4.4	5.3	6.2
M15	182005年11月 — 2009年12月31日	100000	2	2.8	3.7	4.5	5.9	6.7
M30	162001年11月 — 2009年12月31日	100000	2	2.8	3.7	4.5	5.7	6.8
H1	032000年1月 — 2009年12月31日	61765	2	2.9	3.8	4.6	5.6	6.5
H4	032000年1月 — 2009年12月31日	15558	2	3	4	4.8	5.9	6.3
D1	032000年1月 — 2009年12月31日	2601	2	3	4	5.1	5.7	6.5

表2. 異なる増大インターバルでの次元の変化

もし通貨が相互依存していれば、新しい通貨が追加されるたびにそのフラクタル次元はより少なく増えるようになり、最終的に通貨交換市場で”自由変数”の数を決定する特定の値に至る必要があります。

もし'市場のノイズ'が価格に付加されたと想定すれば、全ての次元は短期間のフレーム（M5, M15, M30）にてそのノイズにより塗りつぶされ、（テストの例のように）通貨間の依存を示すより長いタイムフレームに影響します。

表2が示すように、この仮説は正確なデータにより確証されていませんでした：そのセットは、すべてのタイムフレームでの全次元に分散されます。つまり、全ての通貨はお互いに依存します。

それは通貨の関係に関する直感的な想定と合致しません。クローズ通貨、GBP、CHFやAUD、NZDは似た変遷を示すようです。例えば、図17は、M5(相関係数:0.54)とD1(相関係数：0.84)におけるNZDUSDとAUDSD間の増大する依存を示しています。

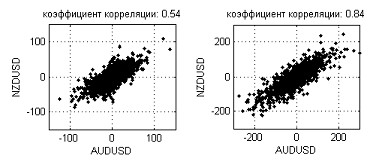
図17. M5 (0.54)とD1 (0.84)タイムフレームでのNZDUSDとAUDUSD間の増大する依存

ご覧の通り、その依存は対角線的に伸び、相関係数値はインターバルが増加するごとに増えています。しかし、フラクタル次元の観点ではそのノイズのレベルは一つの対角線を考察するためには高すぎます。長いインターバルでのフラクタル次元は、おそらく特定の値に収束しますが、その次元の評価のために不十分なポイント数であるためにこれをチェックすることはできません。

まとめ

マーケットアトラクターや予測値を再構築するタスクを単純化するために一つかそれ以上の相互依存する変数に通貨の動きを絞ることは確実により興味深いと思います。しかし、そのマーケットは異なる結果を出します：依存ははっきりと示されず、かなりのノイズの中で隠されてしまいます。この観点ではそのマーケットはとても効果的です。

物理学や化学、生物学などのような領域では良い結果を算出する非線形力学のメソッドは、マーケットの価格分析にて使用される際は特定の注意や発見の注意深い解釈を必要とします。

取得された結果は、通貨間の関係があるか、ないかを明確に示しません。特定のタイムフレームでのノイズレベルはその関係の強さに匹敵するとしか言えないので、依然通貨の関係に対する質問は議論の余地があります。