Implementando um algoritmo de treinamento ARIMA em MQL5

Introdução

A maioria dos negociantes de forex e criptomoedas que buscam explorar movimentos de curto prazo sofrem com a falta de informações fundamentais que poderiam auxiliar seus esforços. É aqui que as técnicas padrão de séries temporais podem ajudar. George Box e Gwilym Jenkins desenvolveram o que é, sem dúvida, o método mais reverenciado de previsão de séries temporais. Embora várias melhorias tenham surgido para aprimorar o método original, os princípios subjacentes ainda são relevantes hoje.

Um dos derivados de seus métodos é a Média Móvel Integrada Autoregressiva (ARIMA), que se tornou um método popular para previsão de séries temporais. É uma classe de modelos que captura dependências temporais em uma série de dados e oferece uma estrutura para modelar séries temporais não estacionárias. Neste artigo, usaremos o método Powell de minimização de função como base para a criação de um algoritmo de treinamento ARIMA usando a linguagem de programação mql5.

Visão geral do ARIMA

Box e Jenkins afirmaram que a maioria das séries temporais pode ser modelada usando uma ou ambas das duas estruturas. Box e Jenkins afirmaram que a maioria das séries temporais poderia ser modelada por um ou ambos os frameworks. Um é Autoregressivo (AR), o que significa que um valor de uma série pode ser explicado em relação aos seus valores anteriores, junto com um deslocamento constante e uma pequena diferença, geralmente referida como inovação ou ruído. Note-se que, neste texto, nos referiremos ao componente de ruído ou erro como inovação. A inovação é responsável pela variação aleatória que não pode ser explicada.

O segundo framework subjacente ao modelo ARIMA é a Média Móvel (MA). Esse modelo afirma que um valor de uma série é a soma proporcional de um número específico de termos de inovação anteriores, a inovação atual e, novamente, um deslocamento constante. Existem inúmeras outras condições estatísticas que definem esses modelos, mas não nos aprofundaremos nos detalhes. Há muitos recursos disponíveis online que fornecem mais informações. Estamos mais interessados em sua aplicação.

Não estamos limitados apenas aos modelos MA e AR puros, podemos combiná-los para produzir modelos mistos chamados modelos de Média Móvel Autoregressiva (ARMA). Em um modelo ARMA, especificamos um número finito de séries atrasadas e termos de ruído, além de um deslocamento constante e um termo de inovação atual.

Um dos requisitos fundamentais que afeta a aplicação de todos esses frameworks é que a série sendo modelada precisa ser estacionária. Dependendo de quão estrita seja sua definição de estacionariedade, os modelos descritos até agora tecnicamente não são apropriados para aplicação em séries temporais financeiras. É aqui que o ARIMA entra. A integração matemática é o inverso da diferenciação. Quando uma série temporal não estacionária é diferenciada uma ou mais vezes, a série resultante geralmente possui melhor estacionariedade. Ao diferenciar primeiro uma série, torna-se possível aplicar esses modelos à série resultante. O I em ARIMA refere-se à necessidade de reverter (Integrar) a diferenciação aplicada para retornar a série modelada ao seu domínio original.

Notação do modelo autoregressivo

Existe uma notação padrão que rege a descrição de um modelo. O número de termos AR (não incluindo o termo constante) geralmente é chamado de p. Os termos MA são denotados como q e d descreve o número de vezes que a série original foi diferenciada. Usando esses termos, um modelo ARIMA é especificado como ARIMA(p,d,q). Processos puros podem ser representados como MA(q) e AR(p). Modelos mistos sem diferenciação são escritos como ARMA(p,q). Esta notação pressupõe que os termos são contíguos. Por exemplo, ARMA(4,2) significa que a série pode ser descrita por 4 termos AR consecutivos e dois termos de inovação anteriores consecutivos. Usando ARIMA, podemos representar processos puros especificando p, q ou d como zero. Um ARIMA(1,0,0), por exemplo, reduz-se a um modelo AR(1) puro.

A maioria dos modelos autoregressivos especifica que os termos respectivos são contíguos, desde um atraso de 1 até o atraso p e atraso q para os termos AR e MA, respectivamente. O algoritmo que será demonstrado permitirá a especificação de atrasos não contíguos para termos MA e/ou AR. Outra flexibilidade que o algoritmo introduzirá é a capacidade de especificar modelos com ou sem um deslocamento constante.

Por exemplo, será possível construir modelos definidos pela função abaixo:
                                 

                                                        y(t) = AR1* y(t-4) + AR2*y(t-6) + E(t)         (1)

A função acima descreve um processo AR(2) puro sem um deslocamento constante, com o valor atual definido pelos valores da série 4 e 6 intervalos de tempo atrás. A notação padrão não fornece uma maneira de especificar tal modelo, mas não precisamos ser limitados por tais restrições.
 

Cálculo dos coeficientes do modelo e do deslocamento constante

Um modelo pode ter coeficientes p+q que devem ser calculados. Para fazer isso, usamos a especificação do modelo para fazer previsões de valores conhecidos da série e, em seguida, comparamos os valores previstos com os valores conhecidos e calculamos a soma dos erros quadráticos. Os coeficientes ótimos serão aqueles que produzem a menor soma de erros quadráticos.

Deve-se ter cuidado ao fazer previsões por causa das limitações impostas pela indisponibilidade de dados que se estendem ao infinito. Se a especificação do modelo tiver quaisquer termos AR, só podemos começar a fazer previsões após o número de valores que correspondem ao maior atraso de todos os termos AR.

Usando o exemplo especificado por (1) acima, só seríamos capazes de começar a fazer previsões a partir do sétimo intervalo de tempo. Pois quaisquer previsões anteriores referenciariam valores desconhecidos antes do início da série.

Deve-se observar que se (1) tivesse quaisquer termos MA, neste ponto, o modelo seria tratado como sendo puramente autoregressivo, uma vez que ainda não temos uma série de inovação. A série de valores de inovação será construída à medida que as previsões forem feitas. Voltando ao exemplo, a primeira previsão no sétimo intervalo de tempo será calculada com coeficientes AR iniciais arbitrários.

 A diferença entre a previsão calculada e o valor conhecido no sétimo intervalo de tempo será a inovação para aquele intervalo. Se houver algum termo MA especificado, ele será incluído no cálculo de uma previsão à medida que os valores atrasados da inovação se tornem conhecidos. Caso contrário, os termos MA são simplesmente definidos como zero. No caso de um modelo MA puro, um procedimento semelhante é seguido, exceto que, desta vez, se um deslocamento constante deve ser incluído, ele é inicializado como a média da série.

Há apenas uma limitação óbvia para o método recém-descrito. A série conhecida precisa conter um número proporcional de valores em relação à ordem do modelo que está sendo aplicado. Quanto mais termos e/ou quanto maiores os atrasos desses termos, mais valores precisamos para ajustar efetivamente o modelo. O processo de treinamento é então finalizado aplicando um algoritmo de minimização global apropriado para otimizar os coeficientes. O algoritmo que usaremos para minimizar o erro de previsão é o método de Powell. Os detalhes de implementação aplicados aqui estão documentados no artigo Previsão de séries temporais utilizando suavização exponencial.

A classe CArima

O algoritmo de treinamento ARIMA estará contido na classe CArima definida em Arima.mqh. A classe tem dois construtores, cada um dos quais inicializa um modelo autoregressivo. O construtor padrão cria um modelo AR(1) puro com um deslocamento constante.

CArima::CArima(void)
  {
   m_ar_order=1;
//---
   ArrayResize(m_arlags,m_ar_order);
   for(uint i=0; i<m_ar_order; i++)
      m_arlags[i]=i+1;
//---
   m_ma_order=m_diff_order=0;
   m_istrained=false;
   m_const=true;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

O construtor parametrizado permite mais controle na especificação de um modelo. Ele aceita quatro argumentos listados abaixo:

Parâmetros	Tipo de parâmetro	Descrição do parâmetro
p	inteiro sem sinal	quantidade de componentes AR para o modelo
d	inteiro sem sinal	define o grau de diferenciação aplicado à série modelada
q	inteiro sem sinal	indica a quantidade de componentes MA que o modelo deve conter
use_const_term	bool	estabelece o uso de um deslocamento constante no modelo

CArima::CArima(const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }


   m_istrained=false;
   m_const=use_const_term;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

Além dos dois construtores fornecidos, um modelo também pode ser especificado usando um dos métodos Fit() sobrecarregados. Ambos os métodos aceitam como primeiro argumento a série de dados a ser modelada. Um método Fit() tem apenas um argumento, enquanto um segundo requer quatro argumentos adicionais, todos idênticos aos já documentados na tabela acima.

bool CArima::Fit(double &input_series[])
  {

   uint input_size=ArraySize(input_series);

   uint in = m_ar_order+ (m_ma_order*2);

   if(input_size<=0 || input_size<in)
      return false;

   if(m_diff_order)
      difference(m_diff_order,input_series,m_differenced,m_leads);
   else
      ArrayCopy(m_differenced,input_series);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   double parameters[];
   ArrayResize(parameters,(m_const)?m_ar_order+m_ma_order+1:m_ar_order+m_ma_order);
   ArrayInitialize(parameters,0.0);

   int iterations = Optimize(parameters);

   if(iterations>0)
      m_istrained=true;
   else
      return false;

   m_sse=PowellsMethod::GetFret();

   ArrayCopy(m_model,parameters);

   return true;

  }

Usando o método com mais parâmetros, sobrescreve-se qualquer modelo que tenha sido previamente especificado e também se assume que os atrasos dos termos são adjacentes entre si. Ambos assumem que a série de dados especificada como primeiro parâmetro não é diferenciada. Portanto, a diferenciação será aplicada se especificada pelos parâmetros do modelo. Os métodos retornam ambos um valor booleano indicando sucesso ou falha no processo de treinamento do modelo.

bool CArima::Fit(double&input_series[],const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }

   m_istrained=false;
   m_const=use_const_term;

   ZeroMemory(m_innovation);
   ZeroMemory(m_model);
   ZeroMemory(m_differenced);

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);

   return Fit(input_series);

  }

Em relação à definição dos atrasos para os termos AR e MA, a classe fornece os métodos SetARLags() e SetMALags() respectivamente. Ambos funcionam de forma semelhante, aceitando um único argumento de array cujos elementos devem ser os atrasos correspondentes para um modelo já especificado por qualquer um dos construtores. O tamanho do array deve corresponder à ordem correspondente dos termos AR ou MA. Os elementos no array podem conter qualquer valor maior ou igual a um. Vamos ver um exemplo de especificação de um modelo com atrasos AR e MA não adjacentes.

O modelo que desejamos construir é especificado pela função abaixo:
         

                                        y(t) = AR1*y(t-2) + AR2*y(t-5) + MA1*E(t-1) + MA2*E(t-3) + E(t)                 (2)

Este modelo é definido por um processo ARMA(2,2) usando atrasos AR de 2 e 5 e atrasos MA de 1 e 3.
O código abaixo mostra como tal modelo pode ser especificado.

CArima arima(2,0,2);

uint alags [2]= {2,5};
uint mlags [2]= {1,3};

if(arima.SetARLags(alags) && arima.SetMALags(mlags))
   Print(arima.Summary());

Ao ajustar com sucesso um modelo a uma série de dados usando um dos métodos Fit(), os coeficientes ótimos e o deslocamento constante podem ser recuperados chamando o método GetModelParameters(). Ele requer um argumento de array no qual todos os parâmetros otimizados do modelo serão escritos. O deslocamento constante virá primeiro, seguido pelos termos AR e os termos MA sempre serão listados por último.

class CArima:public PowellsMethod
  {
private:
   bool              m_const,m_istrained;
   uint              m_diff_order,m_ar_order,m_ma_order;
   uint              m_arlags[],m_malags[];
   double            m_model[],m_sse;
   double            m_differenced[],m_innovation[],m_leads[];

   void              difference(const uint difference_degree, double &data[], double &differenced[], double &leads[]);
   void              integrate(double &differenced[], double &leads[], double &integrated[]);
   virtual double    func(const double &p[]);


public :
                     CArima(void);
                     CArima(const uint p,const uint d, const uint q,bool use_const_term=true);
                    ~CArima(void);

   uint              GetMaxArLag(void)    { if(m_ar_order) return m_arlags[ArrayMaximum(m_arlags)]; else return 0;}
   uint              GetMinArLag(void)    { if(m_ar_order) return m_arlags[ArrayMinimum(m_arlags)]; else return 0;}
   uint              GetMaxMaLag(void)    { if(m_ma_order) return m_malags[ArrayMaximum(m_malags)]; else return 0;}
   uint              GetMinMaLag(void)    { if(m_ma_order) return m_malags[ArrayMinimum(m_malags)]; else return 0;}
   uint              GetArOrder(void)     { return m_ar_order;  }
   uint              GetMaOrder(void)     { return m_ma_order;  }
   uint              GetDiffOrder(void)   { return m_diff_order;}
   bool              IsTrained(void)      { return m_istrained; }
   double            GetSSE(void)         { return m_sse;      }
   uint              GetArLagAt(const uint shift);
   uint              GetMaLagAt(const uint shift);


   bool              SetARLags(uint &ar_lags[]);
   bool              SetMALags(uint &ma_lags[]);
   bool              Fit(double &input_series[]);
   bool              Fit(double &input_series[],const uint p,const uint d, const uint q,bool use_const_term=true);
   string            Summary(void);
   void              GetModelParameters(double &out_array[]) { ArrayCopy(out_array,m_model);      }
   void              GetModelInnovation(double &out_array[]) { ArrayCopy(out_array,m_innovation); }

  };

GetModelInnovation() escreve em seu único argumento de array os valores de erro que são calculados com os coeficientes otimizados após ajustar um modelo. Enquanto a função Summary() retorna uma descrição em string que detalha o modelo completo. GetArOrder(), GetMaOrder() e GetDiffOrder() retornam o número de termos AR, termos MA e o grau de diferenciação, respectivamente, para um modelo.

GetArLagAt() e GetMaLagAt() cada um aceita um argumento inteiro sem sinal que corresponde à posição ordinal de um termo AR ou MA. O deslocamento zero refere-se ao primeiro termo. GetSSE() retorna a soma dos erros quadrados para um modelo treinado. IsTrained() retorna verdadeiro ou falso, dependendo de se um modelo especificado foi treinado ou não.

Uma vez que CArima herda de PowellsMethod, vários parâmetros do algoritmo de Powell podem ser ajustados. Mais detalhes sobre PowellsMethod podem ser encontrados aqui.

Usando a classe CArima

O código do script abaixo demonstra como um modelo pode ser construído e seus parâmetros estimados para uma série determinística. Na demonstração apresentada no script, uma série determinística será gerada com a opção de especificar o valor do deslocamento constante e a adição de um componente aleatório que simulará ruído.

O script inclui Arima.mqh e preenche o array de entrada com uma série construída a partir de um componente determinístico e aleatório.

#include<Arima.mqh>

input bool Add_Noise=false;
input double Const_Offset=0.625;

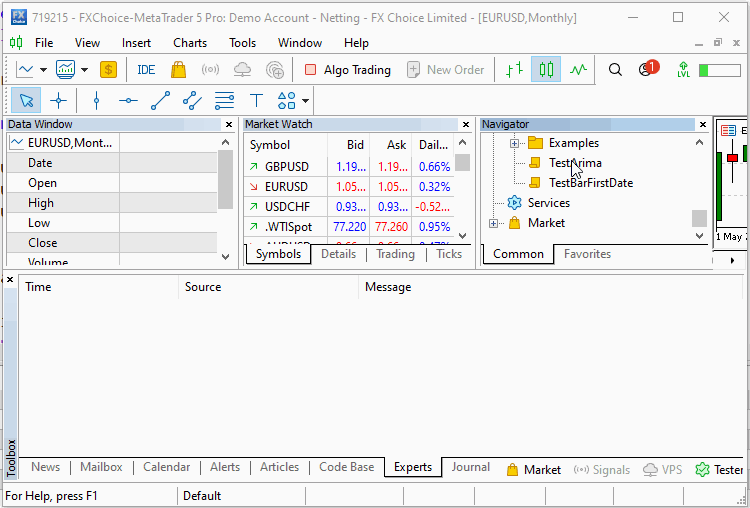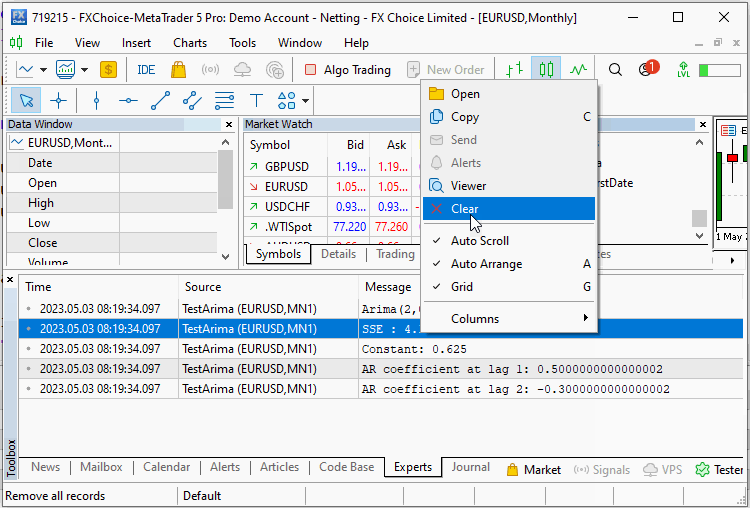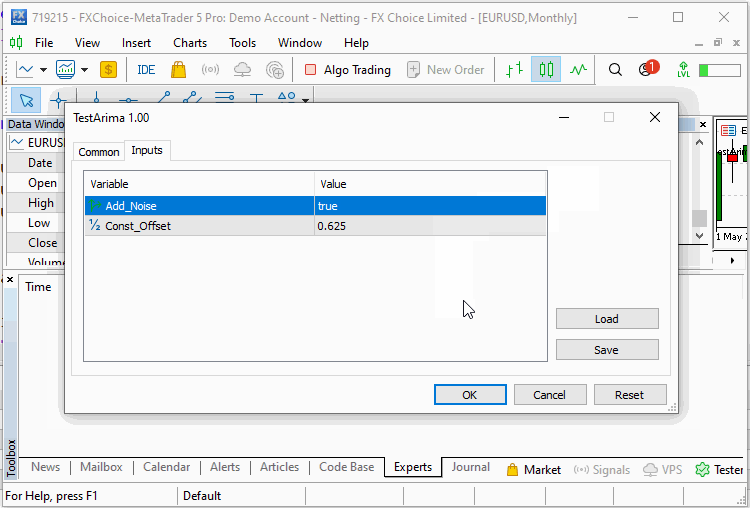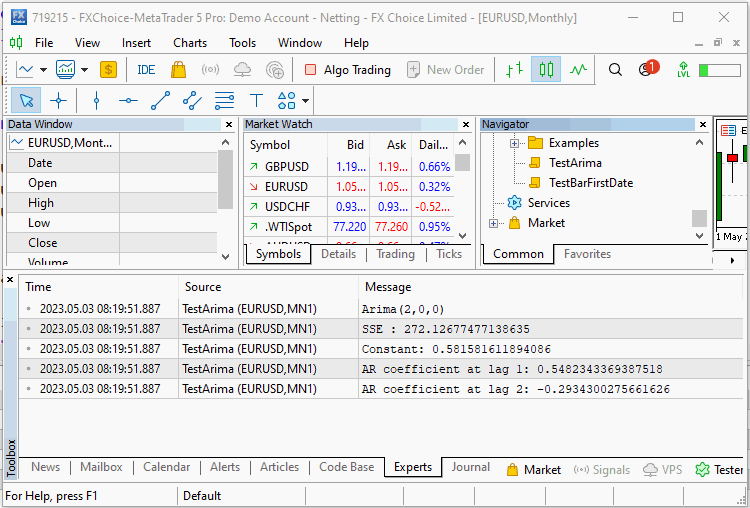
Declaramos o objeto CArima especificando um modelo AR(2) puro. O método Fit() com o array de entrada é chamado e os resultados do treinamento são exibidos com a ajuda da função Summary(). A saída do script é mostrada abaixo.

double inputs[300];
   ArrayInitialize(inputs,0);

   int error_code;

   for(int i=2; i<ArraySize(inputs); i++)
     {
      inputs[i]= Const_Offset;
      inputs[i]+= 0.5*inputs[i-1] - 0.3*inputs[i-2];
      inputs[i]+=(Add_Noise)?MathRandomNormal(0,1,error_code):0;
     }

   CArima arima(2,0,0,Const_Offset!=0);

   if(arima.Fit(inputs))
      Print(arima.Summary());

O script é executado duas vezes, com e sem o componente de ruído. Na primeira execução, vemos que o algoritmo foi capaz de estimar os coeficientes exatos da série. Na segunda execução, com ruído adicionado, o algoritmo fez um bom trabalho ao reproduzir o deslocamento constante verdadeiro e os coeficientes que definiram nossa série.

O exemplo demonstrado obviamente não é representativo do tipo de análise que encontraremos no mundo real. O ruído adicionado à série foi moderado em relação ao encontrado em séries temporais financeiras.

Projetando modelos ARIMA

Até agora, examinamos a implementação de um algoritmo de treinamento autoregressivo sem indicar como derivar ou escolher a ordem apropriada para um modelo. Treinar um modelo provavelmente é a parte fácil, em contraste com determinar um bom modelo.

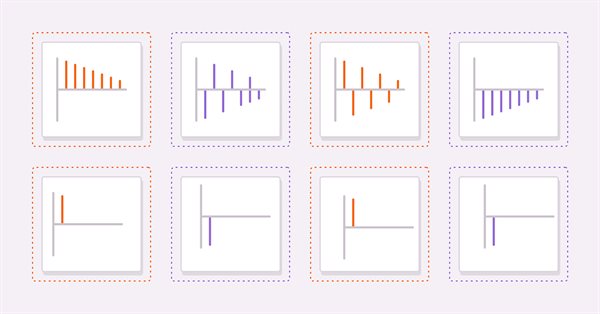
Duas ferramentas úteis para derivar um modelo adequado são calcular a autocorrelação e a autocorrelação parcial de uma série em estudo. Como guia para ajudar os leitores na interpretação de gráficos de autocorrelação e autocorrelação parcial, consideraremos quatro séries hipotéticas:
                                                                  y(t) = AR1* y(t-1) +  E(t)           (3) 

                 
                                                                  y(t) = E(t) - AR1 * y(t-1)            (4) 

            
                                                                  y(t) = MA1 * E(t-1) +  E(t)          (5) 

                
                                                                   y(t) = E(t) - MA1 * E(t-1)           (6) 

    
(3) e (4) são processos AR(1) puros com coeficientes positivos e negativos, respectivamente. (5) e (6) são processos MA(1) puros com coeficientes positivos e negativos, respectivamente.  

As figuras acima são as autocorrelações de (3) e (4) respectivamente. Em ambos os gráficos, os valores de correlação tornam-se menores à medida que o atraso aumenta. Isso faz sentido, pois o efeito de um valor anterior sobre o atual diminui à medida que se avança na série.

As próximas figuras mostram os gráficos de autocorrelações parciais do mesmo par de séries. Vemos que os valores de correlação se interrompem após o primeiro atraso. Essas observações fornecem a base para uma regra geral sobre modelos AR. Em geral, se as autocorrelações parciais se interromperem após um certo atraso e as autocorrelações começarem a decair simultaneamente além do mesmo atraso, a série pode ser modelada por um modelo AR puro até o atraso observado no gráfico de autocorrelação parcial.

 Examinando os gráficos de autocorrelação para a série MA, notamos que os gráficos são idênticos às autocorrelações parciais do AR(1).

Em geral, se todas as autocorrelações após um certo pico ou vale forem zero e as autocorrelações parciais se tornarem cada vez menores à medida que mais atrasos são amostrados, a série pode ser definida por um termo MA no atraso observado no gráfico de autocorrelação.

 
Outras maneiras de determinar os parâmetros p e q de um modelo incluem:

• Critérios de informação: Existem vários critérios de informação, como o Critério de Informação de Akaike (AIC) e o Critério de Informação Bayesiano (BIC), que podem ser usados para comparar diferentes modelos ARIMA e escolher o melhor.

• A busca em grade envolve a seleção de diferentes modelos ARIMA com diferentes ordens no mesmo conjunto de dados e comparar seu desempenho. A ordem que produz os melhores resultados é escolhida como a ordem ARIMA ideal.

• A validação cruzada de séries temporais envolve a divisão dos dados de séries temporais em conjuntos de treinamento e teste, ajustando diferentes modelos ARIMA ao conjunto de treinamento e avaliando sua eficácia no conjunto de teste. A ordem ARIMA que apresenta o menor erro de teste é selecionada como a ordem ideal

É importante notar que não existe uma abordagem única para selecionar a ordem ARIMA, e pode ser necessário algum método de tentativa e erro e conhecimento do domínio para determinar a melhor ordem para sua série temporal específica.

Considerações finais

Demonstramos a classe CArima que encapsula um algoritmo de treinamento autoregressivo usando o método Powell de minimização de função. O código para a classe completa é fornecido no arquivo zip anexado abaixo, juntamente com um script demonstrando seu uso.

Arquivo	Descrição
Arima.mqh	arquivo Include com definição da classe CArima
PowellsMethod.mqh	arquivo Include com definição da classe PowellsMethod
TesteArima	script que demonstra o uso da classe CArima para analisar uma série parcialmente determinística