Implementierung eines ARIMA-Trainingsalgorithmus in MQL5

Einführung

Die meisten Devisen- und Krypto-Händler, die kurzfristige Bewegungen ausnutzen wollen, leiden unter dem Mangel an fundamentalen Informationen, die ihnen bei ihren Bemühungen helfen könnten. Hier könnten Standard-Zeitreihenverfahren helfen. George Box und Gwilym Jenkins entwickelten die wohl bekannteste Methode der Zeitreihenvorhersage. Obwohl es eine Reihe von Fortschritten gegeben hat, die die ursprüngliche Methode verbessern, sind die zugrunde liegenden Prinzipien auch heute noch relevant.

Eine der Ableitungen ihrer Methoden ist der Autoregressive Integrierte Gleitende Durchschnitt (ARIMA), der sich zu einer beliebten Methode für Zeitreihenprognosen entwickelt hat. Es handelt sich um eine Klasse von Modellen, die zeitliche Abhängigkeiten in einer Datenreihe erfassen und einen Rahmen für die Modellierung nicht-stationärer Zeitreihen bieten. In diesem Artikel werden wir Powells Methode der Funktionsminimierung als Grundlage für die Erstellung eines ARIMA-Trainingsalgorithmus unter Verwendung der Programmiersprache mql5 verwenden.

Überblick über ARIMA

Box und Jenkins stellten fest, dass die meisten Zeitreihen mit einem oder beiden Rahmen modelliert werden können. Eine davon ist autoregressiv (AR), was bedeutet, dass ein Wert einer Reihe in Bezug auf seine vorherigen Werte zusammen mit einem konstanten Offset und einer kleinen Differenz, die gewöhnlich als Innovation oder Rauschen bezeichnet wird, erklärt werden kann. Bitte beachten Sie, dass wir in diesem Text die Rausch- oder Fehlerkomponente als Innovation bezeichnen werden. Die Innovation berücksichtigt die zufällige Variation, die nicht erklärt werden kann.

Der zweite Rahmen, der dem ARIMA-Modell zugrunde liegt, ist der gleitende Durchschnitt (MA), der besagt, dass der Wert einer Reihe die proportionale Summe einer bestimmten Anzahl vorhergehender Innovationsterme, der aktuellen Innovation und wiederum eines konstanten Offsets ist. Es gibt noch zahlreiche andere statistische Bedingungen, die diese Modelle definieren, aber wir werden uns nicht mit den Einzelheiten befassen. Es gibt zahlreiche Online-Ressourcen, die mehr Informationen bieten, aber wir sind mehr an ihrer Anwendung interessiert.

Wir sind nicht nur auf reine MA- und AR-Modelle beschränkt, wir können sie auch zu gemischten Modellen kombinieren, die als Autoregressive Moving Average-Modelle (ARMA) bezeichnet werden. In einem ARMA-Modell wird neben einem konstanten Offset und einem aktuellen Innovationsterm eine endliche Anzahl von verzögerten Reihen und Termen für Rauschen angegeben.

Eine der grundlegenden Anforderungen, die sich auf die Anwendung all dieser Rahmenwerke auswirkt, besteht darin, dass die zu modellierende Reihe stationär sein muss. Je nachdem, wie streng man den Begriff der Stationarität definiert, sind die bisher beschriebenen Modelle technisch nicht für die Anwendung auf finanzielle Zeitreihen geeignet. An dieser Stelle kommt ARIMA ins Spiel. Die mathematische Integration ist das Gegenteil der Differenzierung. Wenn eine nicht-stationäre Zeitreihe einmal oder mehrmals differenziert wird, weist die resultierende Reihe in der Regel eine bessere Stationarität auf. Das I in ARIMA bezieht sich auf die Anforderung, die angewandte Differenzierung umzukehren (zu integrieren), um die modellierte Reihe in ihren ursprünglichen Bereich zurückzuführen

Notation des autoregressiven Modells

Es gibt eine Standardnotation, die die Beschreibung eines Modells regelt. Die Anzahl der AR-Terme (ohne den konstanten Term) wird üblicherweise mit p bezeichnet. Die MA-Terme werden mit q bezeichnet und d beschreibt die Anzahl der Differenzierungen der ursprünglichen Reihe. Mit diesen Begriffen wird ein ARIMA-Modell als ARIMA(p,d,q) spezifiziert. Reine Prozesse können als MA(q) und AR(p) dargestellt werden. Gemischte Modelle ohne Differenzenbildung werden als ARMA(p,q) geschrieben. Diese Schreibweise setzt voraus, dass die Begriffe fortlaufend sind. ARMA(4,2) bedeutet zum Beispiel, dass die Reihe durch 4 aufeinander folgende AR-Terme und zwei vorhergehende aufeinander folgende Innovationsterme beschrieben werden kann. Mit ARIMA können wir reine Prozesse abbilden, indem wir entweder p, q oder d als Null angeben. Ein ARIMA(1,0,0) zum Beispiel reduziert sich auf ein reines AR(1)-Modell.

Die meisten autoregressiven Modelle legen fest, dass die jeweiligen Terme zusammenhängend sind, von einer Verzögerung (lag) von 1 bis p bzw. Verzögerung q für AR- und MA-Terme. Der vorgestellte Algorithmus ermöglicht die Angabe von nicht zusammenhängenden Verzögerungen für MA- und/oder AR-Terme. Eine weitere Flexibilität, die der Algorithmus einführen wird, ist die Möglichkeit, Modelle mit oder ohne konstanten Offset anzugeben.

Zum Beispiel wird es möglich sein, Modelle zu erstellen, die durch die folgende Funktion definiert sind:
                                 

                                                        y(t) = AR1* y(t-4) + AR2*y(t-6) + E(t)         (1)

Die obige Funktion beschreibt einen reinen AR(2)-Prozess ohne konstanten Offset, wobei der aktuelle Wert durch die 4 und 6 Zeitfenster zurückliegenden Reihenwerte definiert ist. Die Standardnotation bietet keine Möglichkeit, ein solches Modell zu spezifizieren, aber wir müssen uns von solchen Einschränkungen nicht aufhalten lassen.
 

Berechnung der Modellkoeffizienten und des konstanten Offsets

Ein Modell kann p+q Koeffizienten haben, die berechnet werden müssen. Zu diesem Zweck verwenden wir die Spezifikation des Modells, um Vorhersagen für bekannte Reihenwerte zu treffen, vergleichen dann die vorhergesagten Werte mit den bekannten Werten und berechnen die Summe der quadratischen Fehler. Die optimalen Koeffizienten sind diejenigen, die die kleinste Summe der quadratischen Fehler ergeben.

Bei der Erstellung von Prognosen ist Vorsicht geboten, da die Verfügbarkeit von Daten, die sich bis ins Unendliche erstrecken, Grenzen setzt. Wenn die Modellspezifikation AR-Terme enthält, können wir mit den Vorhersagen erst nach der Anzahl der Werte beginnen, die der größten Verzögerung aller AR-Terme entsprechen.

In dem unter (1) genannten Beispiel könnten wir erst ab dem Zeitfenster 7 mit den Vorhersagen beginnen. Denn alle Vorhersagen würden sich auf unbekannte Werte vor Beginn der Reihe beziehen.

Es ist anzumerken, dass, wenn (1) irgendwelche MA-Terme enthielte, das Modell an dieser Stelle als rein autoregressiv behandelt würde, da wir noch keine Innovationsreihen haben. Die Reihe der Innovationswerte wird im Laufe der Zeit durch weitere Maßnahmen ergänzt werden. Um auf das Beispiel zurückzukommen, wird die erste Vorhersage für das siebte Zeitfenster mit willkürlichen anfänglichen AR-Koeffizienten berechnet.

 Die Differenz zwischen der berechneten Vorhersage und dem bekannten Wert beim siebten Zeitfenster ist die Innovation für dieses Zeitfenster. Wenn MA-Terme angegeben sind, werden sie in die Berechnung einer Vorhersage einbezogen, sobald die entsprechenden verzögerten Werte der Innovation bekannt sind. Andernfalls werden die MA-Terme einfach auf Null gesetzt. Im Falle eines reinen MA-Modells wird ein ähnliches Verfahren angewandt, mit dem Unterschied, dass dieses Mal ein konstanter Offset als Mittelwert der Reihe initialisiert wird, wenn er einbezogen werden soll.

Es gibt nur eine offensichtliche Einschränkung der soeben beschriebenen Methode. Die bekannte Reihe muss eine angemessene Anzahl von Werten in Bezug auf die Reihenfolge des angewandten Modells enthalten. Je mehr Terme und/oder je größer die Verzögerungen dieser Terme, desto mehr Werte benötigen wir, um das Modell effektiv anzupassen. Der Trainingsprozess wird dann durch die Anwendung eines geeigneten globalen Minimierungsalgorithmus zur Optimierung der Koeffizienten abgerundet. Der Algorithmus, den wir zur Minimierung des Vorhersagefehlers verwenden werden, ist die Powells-Methode. Die hier angewandten Implementierungsdetails sind in dem Artikel Zeitreihenprognose mit Exponentialglättung.

Die Klasse CArima

Der ARIMA-Trainingsalgorithmus wird in der Klasse CArima enthalten sein, die in Arima.mqh definiert ist. Die Klasse hat zwei Konstruktoren, von denen jeder ein autoregressives Modell initialisiert. Der Standardkonstruktor erstellt ein reines AR(1)-Modell mit einem konstanten Offset.

CArima::CArima(void)
  {
   m_ar_order=1;
//---
   ArrayResize(m_arlags,m_ar_order);
   for(uint i=0; i<m_ar_order; i++)
      m_arlags[i]=i+1;
//---
   m_ma_order=m_diff_order=0;
   m_istrained=false;
   m_const=true;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

Der parametrisierte Konstruktor ermöglicht mehr Kontrolle bei der Angabe eines Modells. Er benötigt vier Argumente, die im Folgenden aufgeführt sind:

Parameter	Parameter-Typ	Parameter-Beschreibung
p	Ganzzahl ohne Vorzeichen	gibt die Anzahl der AR-Terme für das Modell an
d	Ganzzahl ohne Vorzeichen	gibt den Grad der Differenzierung an, die auf eine zu modellierende Reihe angewendet werden soll
q	Ganzzahl ohne Vorzeichen	gibt die Anzahl der MA-Terme an, die das Modell enthalten soll
use_const_term	bool	legt die Verwendung eines konstanten Offsets in einem Modell fest

CArima::CArima(const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }


   m_istrained=false;
   m_const=use_const_term;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

Zusätzlich zu den beiden Konstruktoren kann ein Modell auch mit Hilfe einer der überladenen Fit()-Methoden spezifiziert werden. Beide Methoden benötigen als erstes Argument die zu modellierende Datenreihe. Eine Fit()-Methode hat nur ein Argument, während eine zweite Methode vier weitere Argumente erfordert, die alle mit den bereits in der obigen Tabelle aufgeführten identisch sind.

bool CArima::Fit(double &input_series[])
  {

   uint input_size=ArraySize(input_series);

   uint in = m_ar_order+ (m_ma_order*2);

   if(input_size<=0 || input_size<in)
      return false;

   if(m_diff_order)
      difference(m_diff_order,input_series,m_differenced,m_leads);
   else
      ArrayCopy(m_differenced,input_series);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   double parameters[];
   ArrayResize(parameters,(m_const)?m_ar_order+m_ma_order+1:m_ar_order+m_ma_order);
   ArrayInitialize(parameters,0.0);

   int iterations = Optimize(parameters);

   if(iterations>0)
      m_istrained=true;
   else
      return false;

   m_sse=PowellsMethod::GetFret();

   ArrayCopy(m_model,parameters);

   return true;

  }

Die Verwendung der Methode mit mehr Parametern überschreibt jedes zuvor angegebene Modell und geht außerdem davon aus, dass die Verzögerungen der Terme nebeneinander liegen. Beide gehen davon aus, dass die als erster Parameter angegebene Datenreihe nicht differenziert ist. Die Differenzierung wird also angewandt, wenn dies durch die Modellparameter vorgegeben ist. Die Methoden geben beide einen booleschen Wert zurück, der den Erfolg oder Misserfolg des Modelltrainings angibt.

bool CArima::Fit(double&input_series[],const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }

   m_istrained=false;
   m_const=use_const_term;

   ZeroMemory(m_innovation);
   ZeroMemory(m_model);
   ZeroMemory(m_differenced);

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);

   return Fit(input_series);

  }

Für die Einstellung der Lags für die AR- und MA-Terme bietet die Klasse die Methoden SetARLags() bzw. SetMALags(). Beide funktionieren ähnlich, indem sie ein einzelnes Array-Argument annehmen, dessen Elemente die entsprechenden Lags für ein Modell sein sollten, das bereits von einem der Konstruktoren angegeben wurde. Die Größe des Arrays sollte mit der entsprechenden Reihenfolge der AR- oder MA-Terme übereinstimmen. Die Elemente in dem Array können jeden Wert größer oder gleich eins enthalten.  Betrachten wir ein Beispiel für die Spezifikation eines Modells mit nicht benachbarten AR- und MA-Verzögerung.

Das Modell, das wir erstellen wollen, wird durch die nachstehende Funktion festgelegt:
         

                                        y(t) = AR1*y(t-2) + AR2*y(t-5) + MA1*E(t-1) + MA2*E(t-3) + E(t)                 (2)

Dieses Modell wird durch einen ARMA(2,2)-Prozess mit AR-Verzögerungen von 2 und 5 und MA-Verzögerungen von 1 und 3 definiert.
Der folgende Code zeigt, wie ein solches Modell spezifiziert werden kann.

CArima arima(2,0,2);

uint alags [2]= {2,5};
uint mlags [2]= {1,3};

if(arima.SetARLags(alags) && arima.SetMALags(mlags))
   Print(arima.Summary());

Nach erfolgreicher Anpassung eines Modells an eine Datenreihe mit Hilfe einer der Fit()-Methoden können die optimalen Koeffizienten und der konstante Offset durch Aufruf der Methode GetModelParameters() abgerufen werden. Sie erfordert ein Array-Argument, in das alle optimierten Parameter des Modells geschrieben werden. Der konstante Offset steht an erster Stelle, gefolgt von den AR-Termen, und die MA-Terme werden immer zuletzt aufgeführt.

class CArima:public PowellsMethod
  {
private:
   bool              m_const,m_istrained;
   uint              m_diff_order,m_ar_order,m_ma_order;
   uint              m_arlags[],m_malags[];
   double            m_model[],m_sse;
   double            m_differenced[],m_innovation[],m_leads[];

   void              difference(const uint difference_degree, double &data[], double &differenced[], double &leads[]);
   void              integrate(double &differenced[], double &leads[], double &integrated[]);
   virtual double    func(const double &p[]);


public :
                     CArima(void);
                     CArima(const uint p,const uint d, const uint q,bool use_const_term=true);
                    ~CArima(void);

   uint              GetMaxArLag(void)    { if(m_ar_order) return m_arlags[ArrayMaximum(m_arlags)]; else return 0;}
   uint              GetMinArLag(void)    { if(m_ar_order) return m_arlags[ArrayMinimum(m_arlags)]; else return 0;}
   uint              GetMaxMaLag(void)    { if(m_ma_order) return m_malags[ArrayMaximum(m_malags)]; else return 0;}
   uint              GetMinMaLag(void)    { if(m_ma_order) return m_malags[ArrayMinimum(m_malags)]; else return 0;}
   uint              GetArOrder(void)     { return m_ar_order;  }
   uint              GetMaOrder(void)     { return m_ma_order;  }
   uint              GetDiffOrder(void)   { return m_diff_order;}
   bool              IsTrained(void)      { return m_istrained; }
   double            GetSSE(void)         { return m_sse;      }
   uint              GetArLagAt(const uint shift);
   uint              GetMaLagAt(const uint shift);


   bool              SetARLags(uint &ar_lags[]);
   bool              SetMALags(uint &ma_lags[]);
   bool              Fit(double &input_series[]);
   bool              Fit(double &input_series[],const uint p,const uint d, const uint q,bool use_const_term=true);
   string            Summary(void);
   void              GetModelParameters(double &out_array[]) { ArrayCopy(out_array,m_model);      }
   void              GetModelInnovation(double &out_array[]) { ArrayCopy(out_array,m_innovation); }

  };

GetModelInnovation() schreibt in sein einzelnes Array-Argument die Fehlerwerte, die mit den optimierten Koeffizienten nach der Anpassung eines Modells berechnet wurden. GetArOrder(), GetMaOrder() und GetDiffOrder() geben die Anzahl der AR-Terme, MA-Terme bzw. den Grad der Differenzierung für ein Modell zurück.

GetArLagAt() und GetMaLagAt() werden jeweils ein vorzeichenloses Ganzzahlargument übergeben, das der Ordinalposition eines AR- oder MA-Terms entspricht. Die Nullpunktverschiebung bezieht sich auf den ersten Term. GetSSE() gibt die Summe der quadratischen Fehler für ein trainiertes Modell zurück. IsTrained() gibt true oder false zurück, je nachdem, ob ein bestimmtes Modell trainiert wurde oder nicht.

Da CArima von PowellsMethod erbt, können verschiedene Parameter des Powellschen Algorithmus angepasst werden. Weitere Einzelheiten zu PowellsMethod finden Sie hier.

Verwendung der Klasse CArima

Der Code des nachstehenden Skripts zeigt, wie ein Modell konstruiert und seine Parameter für eine deterministische Reihe geschätzt werden können. In der im Skript dargestellten Demonstration wird eine deterministische Reihe mit der Option erzeugt, den konstanten Offset-Wert und die Hinzufügung einer Zufallskomponente, die das Rauschen nachahmt, anzugeben.

Das Skript enthält Arima.mqh und füllt das Eingabefeld mit einer Reihe, die aus einer deterministischen und einer zufälligen Komponente besteht.

#include<Arima.mqh>

input bool Add_Noise=false;
input double Const_Offset=0.625;

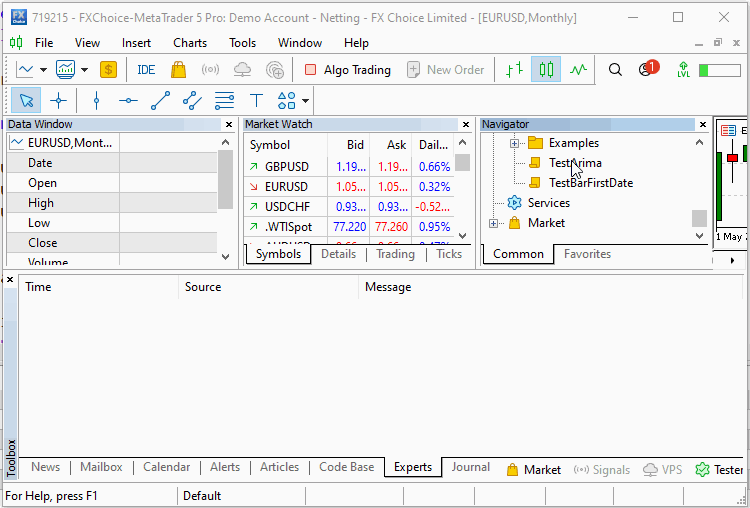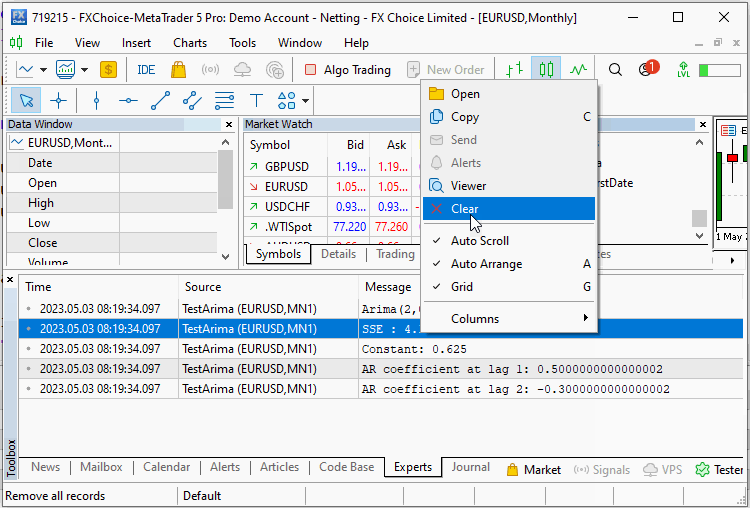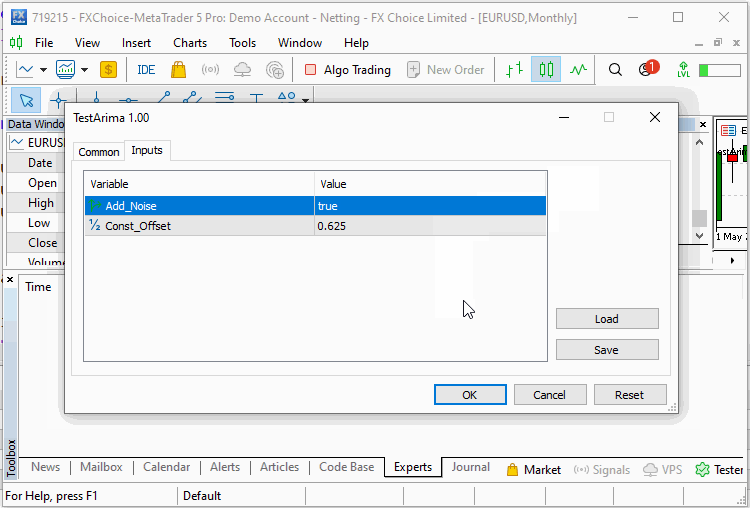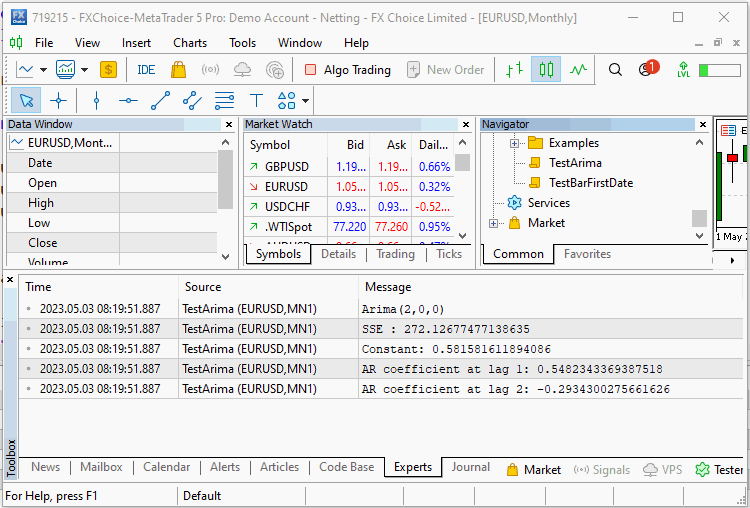
Wir deklarieren ein CArima-Objekt, das ein reines AR(2)-Modell spezifiziert. Die Fit()-Methode mit dem Eingabe-Array wird aufgerufen und die Ergebnisse des Trainings werden mit Hilfe der Summary()-Funktion angezeigt. Die Ausgabe des Skripts wird unten angezeigt.

double inputs[300];
   ArrayInitialize(inputs,0);

   int error_code;

   for(int i=2; i<ArraySize(inputs); i++)
     {
      inputs[i]= Const_Offset;
      inputs[i]+= 0.5*inputs[i-1] - 0.3*inputs[i-2];
      inputs[i]+=(Add_Noise)?MathRandomNormal(0,1,error_code):0;
     }

   CArima arima(2,0,0,Const_Offset!=0);

   if(arima.Fit(inputs))
      Print(arima.Summary());

Das Skript wird zweimal mit und ohne die Komponenten für das Rauschen ausgeführt. Im ersten Durchlauf sehen wir, dass der Algorithmus in der Lage war, die genauen Koeffizienten der Reihe zu schätzen. Im zweiten Durchlauf mit hinzugefügtem Rauschen gelang es dem Algorithmus recht gut, den wahren konstanten Offset und die Koeffizienten, die unsere Serie definierten, zu reproduzieren.

Das gezeigte Beispiel ist natürlich nicht repräsentativ für die Art der Analyse, die wir in der realen Welt antreffen werden. Das zu den Reihen hinzugefügte Rauschen war im Vergleich zu den Finanzzeitreihen moderat.

Entwurf von ARIMA-Modellen

Bisher haben wir uns mit der Implementierung eines autoregressiven Trainingsalgorithmus befasst, ohne anzugeben, wie man die geeignete Reihenfolge für ein Modell ableitet oder auswählt. Die Ausbildung eines Modells ist wahrscheinlich der einfachste Teil, im Gegensatz zur Bestimmung eines guten Modells.

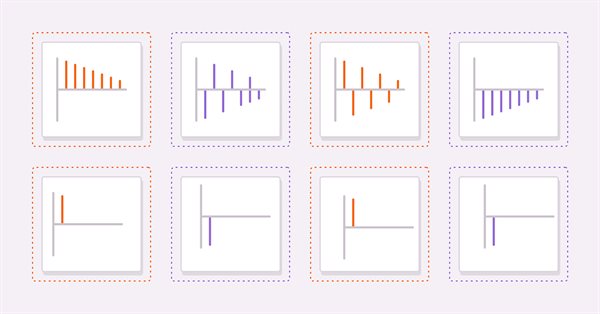
Zwei nützliche Instrumente zur Ableitung eines geeigneten Modells sind die Berechnung der Autokorrelation und der partiellen Autokorrelation einer untersuchten Reihe. Als Leitfaden für die Interpretation von Autokorrelations- und partiellen Autokorrelationsdiagrammen werden wir vier hypothetische Reihen betrachten.
                                                                  y(t) = AR1* y(t-1) +  E(t)           (3) 

                 
                                                                  y(t) = E(t) - AR1 * y(t-1)            (4) 

            
                                                                  y(t) = MA1 * E(t-1) +  E(t)          (5) 

                
                                                                   y(t) = E(t) - MA1 * E(t-1)           (6) 

    
(3) und (4) sind reine AR(1)-Prozesse mit positiven bzw. negativen Koeffizienten. (5) und (6) sind reine MA(1)-Prozesse mit positiven bzw. negativen Koeffizienten.  

Die obigen Zahlen sind die Autokorrelationen von (3) bzw. (4). In beiden Diagrammen werden die Korrelationswerte mit zunehmender Verzögerung kleiner. Dies ist sinnvoll, da die Auswirkung eines früheren Wertes auf den aktuellen Wert abnimmt, je weiter man in der Reihe nach oben geht.

Die nächsten Abbildungen zeigen die Diagramme der partiellen Autokorrelationen desselben Paares von Reihen. Wir sehen, dass die Korrelationswerte nach der ersten Verzögerung abnehmen. Diese Beobachtungen bilden die Grundlage für eine allgemeine Regel über AR-Modelle. Wenn die partiellen Autokorrelationen nach einer bestimmten Verzögerung abfallen und die Autokorrelationen gleichzeitig nach derselben Verzögerung abzufallen beginnen, kann die Reihe im Allgemeinen durch ein reines AR-Modell bis zu der beobachteten Verzögerung auf der partiellen Autokorrelationstabelle modelliert werden.

 Betrachtet man die Autokorrelationsdiagramme für die MA-Reihen, so stellt man fest, dass die Diagramme mit den partiellen Autokorrelationen der AR(1) identisch sind.

Wenn im Allgemeinen alle Autokorrelationen jenseits eines bestimmten Höchst- oder Tiefstwertes Null sind und die partiellen Autokorrelationen mit zunehmender Anzahl von Verzögerungen immer kleiner werden, kann die Reihe durch einen MA-Term bei der beobachteten Abschneideverzögerung auf dem Autokorrelationsdiagramm definiert werden.

 
Weitere Möglichkeiten zur Bestimmung der p- und q-Parameter eines Modells sind:

• Kriterien für die Information: Es gibt mehrere Informationskriterien, wie Information Criterion (AIC) und Bayesian Information Criterion (BIC), die zum Vergleich verschiedener ARIMA-Modelle und zur Auswahl des besten Modells verwendet werden können.

• Gittersuche: Dabei werden verschiedene ARIMA-Modelle mit unterschiedlichen Ordnungen an denselben Datensatz angepasst und ihre Leistung verglichen. Die Reihenfolge, die die besten Ergebnisse liefert, wird als optimale ARIMA-Reihenfolge gewählt.

• Zeitreihen-Kreuzvalidierung: Dies beinhaltet die Aufteilung Ihrer Zeitreihendaten in Trainings- und Testsätze, die Anpassung verschiedener ARIMA-Modelle an den Trainingssatz und die Bewertung ihrer Leistung auf dem Testsatz. Die ARIMA-Reihenfolge, die den besten Testfehler ergibt, wird als optimale Reihenfolge gewählt.

Es ist wichtig zu beachten, dass es keine Einheitslösung für die Auswahl der ARIMA-Reihenfolge gibt und dass es möglicherweise einiger Versuche und Fachkenntnisse bedarf, um die beste Reihenfolge für Ihre spezifische Zeitreihe zu bestimmen.

Schlussfolgerung

Wir haben die Klasse CArima vorgestellt, die einen autoregressiven Trainingsalgorithmus mit der Powells Methode der Funktionsminimierung einkapselt. Der Code für die vollständige Klasse ist in der unten angehängten Zip-Datei enthalten, zusammen mit einem Skript, das seine Verwendung demonstriert.

Datei	Beschreibung
Arima.mqh	Include-Datei mit der Definition der KlasseCArima
PowellsMethod.mqh	Include-Datei mit der Definition der PowellsMethod-Klasse
TestArima	Skript, das die Verwendung der CArima-Klasse zur Analyse einer teilweise deterministischen Reihe demonstriert.