以 MQL5 实现 ARIMA 训练算法

概述

众多外汇和加密货币交易者都希望从短期走势当中获益，但缺乏可以帮助他们奋斗的基本面信息，因而备受困扰。 而这恰是标准时间序列技术可以提供帮助的地方。 George Box 和 Gwilym Jenkins 开发出可以说是最受尊崇的时间序列预测方法。 尽管已经取得了许多大幅进步，改进了原始方法，但其基本原则在今天仍然适用。

他们方法的衍生物之一是自回归综合移动平均线（ARIMA），其已成为时间序列预测的流行方法。 它是一类模型，用于捕获数据序列中的时间依赖关系，并提供了针对非稳态时间序列进行建模的框架。 在本文中，我们将采用函数最小化 Powells 方法作为基础创建 ARIMA 训练算法，并利用 mql5 编程语言实现。

ARIMA 概览

Box 和 Jenkins 表示，大多数时间序列可以由两个框架中之一个或两个来建模。 其一是自回归（AR），这意味着序列的值可以由与其先前的值相关性来解释，而当中的恒定偏移量和微小的差异，通常称为创新或噪声。 请注意，在本文中，我们将噪声或误差部分称为创新。 创新解释了无法解释的随机变化。

ARIMA 模型的第二个框架是移动平均线（MA）。该模型指出，序列的值是特定数量的前期创新项、当前创新、和恒定偏移量的比例和。 还有许多其它统计条件可以定义这些模型，但我们不会深入研究细节。 网上有许多资源可以提供更多信息。我们对它们的应用更感兴趣。

我们不会受限于纯 MA 和 AR 模型，我们可以将它们组合在一起，生成称为自回归移动平均模型（ARMA）的混合模型。 在 ARMA 模型当中，除了恒定偏移量和当前创新项外，我们还指定了有限数量的滞后序列和噪声项。

影响所有这些框架应用的基本要求之一是，被建模的序列必须是稳态的。 取决于您对稳态定义的严格程度，到目前为止所描述的模型在技术上都不适合应用于金融时间序列。 这就是 ARIMA 的用武之地。 数学积分是微分的逆向。 当非稳态时间序列相差一次或更多次时，成果序列通常具有更好的稳态。 首先对序列进行微分，可以将这些模型应用于成果序列。ARIMA 中的 “I” 是指逆向（积分）所应用的差分的要求，以便将建模的序列返回到其原始域。

自回归模型标注法

有一个标准标注法来管控模型的描述。 AR 项（不包括常数项）的个数通常称为 p。 MA 项表示为 q，且 d 表示原始序列差异的次数。 使用这些术语，ARIMA 模型被指定为 ARIMA(p,d,q)。 纯过程可以描述为 MA(q) 和 AR(p)。 没有差分的混合模型写为 ARMA(p,q)。 此标注法假定这些术语是连续的。 例如，ARMA(4,2) 表示序列可以用 4 个连续的 AR 项，和两个连续的创新项来描述。 采用 ARIMA，我们可以通过将 p、q 或 d 指定为零值来描绘纯过程。 例如，ARIMA(1,0,0) 简化为纯 AR(1) 模型。

大多数自回归模型指定各自的项是连续的，分别是 AR 项从滞后 1 到滞后 p，及 MA 项滞后 q。 将要演示的算法将允许指定 MA 和/或 AR 项的非连续滞后。 该算法将引入的另一个灵活性是能够指定模型是否带有恒定偏移量。

例如，可以构建由以下函数定义的模型：                                  

                                                        y(t) = AR1* y(t-4) + AR2*y(t-6) + E(t)         (1)

上面的函数描述了一个纯 AR(2) 过程，该过程没有恒偏移量，当前值由前期第 4 和第 6 时隙的序列值定义。 标准标注法没有提供指定这种模型的方法，但我们不必被这些限制所束缚。
 

计算模型系数和恒定偏移量

模型可以具有必须经计算的 p+q 系数。 为此，我们使用模型的规范对已知序列值进行预测，然后将预测值与已知值进行比较，并计算误差的平方和。 最优系数将是产生最小误差平方和的系数。

在进行预测时必须小心，无限延伸的数据并不可用，因此会施加限制。 如果模型规范有任何 AR 项，我们只能跳过与所有 AR 项的最大滞后值对应的数值个数之后，再开始进行预测。

使用上面（1）指定的示例，我们只能从时隙 7 开始进行预测。 因为任何超前的预测都会在序列开始之前引用未知值。

应该注意的是，如果（1）有任何 MA 项，此时该模型将被视为纯自回归，因为我们还没有创新序列。 随着预测的推进，一系列的创新数值就会不断积累。 回到这个示例，第 7 处时隙的第一个预测将利用人工初始 AR 系数进行计算。

 计算出的预测值与第 7 处时隙的已知值之间的差值就是该时隙的创新值。 如果指定了任何 MA 项，则当相应的创新滞后值已知时，在计算预测时将包含它们在内。 否则，MA 项将清零。 在纯 MA 模型的情况下，遵循类似的过程，除了这次，如果应包含恒定偏移量，则将其初始化为序列的均值。

刚才讲述的方法只有一个明显的局限性。 已知序列需要包含与其所应用模型按顺序等量的数值。 更多的项和/或滞后越大，我们需要的值就越多，才能有效地拟合模型。 然后，通过应用相应的全局最小化算法来优化系数，从而完善训练过程。 我们将采用的最小化预测误差的算法是 Powells 方法 。 该实现于此应用的详情记录在文章利用指数平滑进行时间序列预测之中。

CArima 类

ARIMA 训练算法将被包含在 Arima.mqh 文件定义的 CArima 类当中。 该类有两个构造函数，每个构造函数初始化一个自回归模型。 默认构造函数创建一个具有恒定偏移量的纯 AR(1) 模型。

CArima::CArima(void)
  {
   m_ar_order=1;
//---
   ArrayResize(m_arlags,m_ar_order);
   for(uint i=0; i<m_ar_order; i++)
      m_arlags[i]=i+1;
//---
   m_ma_order=m_diff_order=0;
   m_istrained=false;
   m_const=true;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

参数化构造函数允许在指定模型时进行更多控制。 它需要下面列出的四个参数：

参数	参数类型	参数说明
p	无符号整数	指定了模型的 AR 项数
d	无符号整数	指定要应用于正在建模的序列的差异程度
q	无符号整数	指示模型应包含的 MA 项数
use_const_term	布尔值	设置启用模型中恒定偏移量

CArima::CArima(const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }


   m_istrained=false;
   m_const=use_const_term;

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);
  }

除了提供的两个构造函数外，还可以使用重载的 Fit() 方法之一来指定模型。 这两种方法都把建模的数据序列作为其第一个参数。 第一个 Fit() 方法只有一个参数，而第二个方法需要更多的四个参数，所有这些参数都与上表中所记录的参数相同。

bool CArima::Fit(double &input_series[])
  {

   uint input_size=ArraySize(input_series);

   uint in = m_ar_order+ (m_ma_order*2);

   if(input_size<=0 || input_size<in)
      return false;

   if(m_diff_order)
      difference(m_diff_order,input_series,m_differenced,m_leads);
   else
      ArrayCopy(m_differenced,input_series);

   ArrayResize(m_innovation,ArraySize(m_differenced));

   double parameters[];
   ArrayResize(parameters,(m_const)?m_ar_order+m_ma_order+1:m_ar_order+m_ma_order);
   ArrayInitialize(parameters,0.0);

   int iterations = Optimize(parameters);

   if(iterations>0)
      m_istrained=true;
   else
      return false;

   m_sse=PowellsMethod::GetFret();

   ArrayCopy(m_model,parameters);

   return true;

  }

调用更多参数的方法会覆盖以前指定的任何模型，并且还假定每一项的滞后是彼此相邻的。 两者都假定第一个参数指定的数据序列并无差别。 因此，如果由模型参数指定，则会应用差别。 这两种方法都返回一个布尔值，表示模型训练过程的成功或失败。

bool CArima::Fit(double&input_series[],const uint p,const uint d,const uint q,bool use_const_term=true)
  {
   m_ar_order=m_ma_order=m_diff_order=0;

   if(d)
      m_diff_order=d;
   if(p)
     {
      m_ar_order=p;
      ArrayResize(m_arlags,p);
      for(uint i=0; i<m_ar_order; i++)
         m_arlags[i]=i+1;
     }
   if(q)
     {
      m_ma_order=q;
      ArrayResize(m_malags,q);
      for(uint i=0; i<m_ma_order; i++)
         m_malags[i]=i+1;
     }

   m_istrained=false;
   m_const=use_const_term;

   ZeroMemory(m_innovation);
   ZeroMemory(m_model);
   ZeroMemory(m_differenced);

   ArrayResize(m_model,m_ar_order+m_ma_order+m_const);
   ArrayInitialize(m_model,0);

   return Fit(input_series);

  }

关于设置 AR 和 MA 项的滞后，该类分别提供了 SetARLags() 和 SetMALags() 方法。 两者的工作方式类似，取单个数组参数，其元素应该是任何一个构造函数所指定模型的相应滞后。 数组的大小应与 AR 或 MA 项的相应顺序匹配。 数组中的元素可以包含大于或等于 1 的任何值。我们来看一个示例，该示例指定具有非相邻 AR 和 MA 滞后的模型。

我们希望构建的模型由以下函数指定：          

                                        y(t) = AR1*y(t-2) + AR2*y(t-5) + MA1*E(t-1) + MA2*E(t-3) + E(t)                 (2)

该模型由 ARMA(2,2) 过程定义，并取 AR 第 2 和 第 5 处的滞后。 MA 滞后为第 1 和第 3 处时隙。
下面的代码展示了如何指定这样的模型。

CArima arima(2,0,2);

uint alags [2]= {2,5};
uint mlags [2]= {1,3};

if(arima.SetARLags(alags) && arima.SetMALags(mlags))
   Print(arima.Summary());

使用 Fit() 方法之一成功将模型与数据序列拟合后，可以通过调用 GetModelParameters() 方法提取最优系数和恒定偏移量。 它需要一个数组参数，模型的所有优化参数都将写入其内。 恒定偏移量将首先出现在 AR 项之后，MA 项将始终列于最后。

class CArima:public PowellsMethod
  {
private:
   bool              m_const,m_istrained;
   uint              m_diff_order,m_ar_order,m_ma_order;
   uint              m_arlags[],m_malags[];
   double            m_model[],m_sse;
   double            m_differenced[],m_innovation[],m_leads[];

   void              difference(const uint difference_degree, double &data[], double &differenced[], double &leads[]);
   void              integrate(double &differenced[], double &leads[], double &integrated[]);
   virtual double    func(const double &p[]);


public :
                     CArima(void);
                     CArima(const uint p,const uint d, const uint q,bool use_const_term=true);
                    ~CArima(void);

   uint              GetMaxArLag(void)    { if(m_ar_order) return m_arlags[ArrayMaximum(m_arlags)]; else return 0;}
   uint              GetMinArLag(void)    { if(m_ar_order) return m_arlags[ArrayMinimum(m_arlags)]; else return 0;}
   uint              GetMaxMaLag(void)    { if(m_ma_order) return m_malags[ArrayMaximum(m_malags)]; else return 0;}
   uint              GetMinMaLag(void)    { if(m_ma_order) return m_malags[ArrayMinimum(m_malags)]; else return 0;}
   uint              GetArOrder(void)     { return m_ar_order;  }
   uint              GetMaOrder(void)     { return m_ma_order;  }
   uint              GetDiffOrder(void)   { return m_diff_order;}
   bool              IsTrained(void)      { return m_istrained; }
   double            GetSSE(void)         { return m_sse;      }
   uint              GetArLagAt(const uint shift);
   uint              GetMaLagAt(const uint shift);


   bool              SetARLags(uint &ar_lags[]);
   bool              SetMALags(uint &ma_lags[]);
   bool              Fit(double &input_series[]);
   bool              Fit(double &input_series[],const uint p,const uint d, const uint q,bool use_const_term=true);
   string            Summary(void);
   void              GetModelParameters(double &out_array[]) { ArrayCopy(out_array,m_model);      }
   void              GetModelInnovation(double &out_array[]) { ArrayCopy(out_array,m_innovation); }

  };

GetModelInnovation() 将模型拟合后依据优化系数计算的误差值写入其单一数组参数。 而 Summary() 函数返回一个详细说明完整模型的字符串描述。GetArOrder()、GetMaOrder() 和 GetDiffOrder() 分别返回模型的 AR 项数、MA 项数和差异程度。

GetArLagAt( 和 GetMaLagAt() 各自采用一个无符号整数参数，该参数对应于 AR 或 MA 项的序号位置。 零位移引用第一项。 GetSSE() 返回训练模型的误差平方之和。 IsTrained() 返回 true 或 false，具体取决于指定的模型是否经过训练。

由于 CArima 继承自 PowellsMethod，因此可以调整 Powell 算法的各种参数。 关于 PowellsMethod 的更多细节可以在这里找到。

使用 CArima 类

下面的脚本代码演示了如何构造模型，以及如何为确定性序列估算其参数。 在脚本中展示的演示中，将生成一个确定性序列，其中包含指定恒定偏移值的选项，并添加一个随机组件模拟噪声。

该脚本包括 Arima.mqh，且输入数组会由确定性和随机组件构造的序列填充。

#include<Arima.mqh>

input bool Add_Noise=false;
input double Const_Offset=0.625;

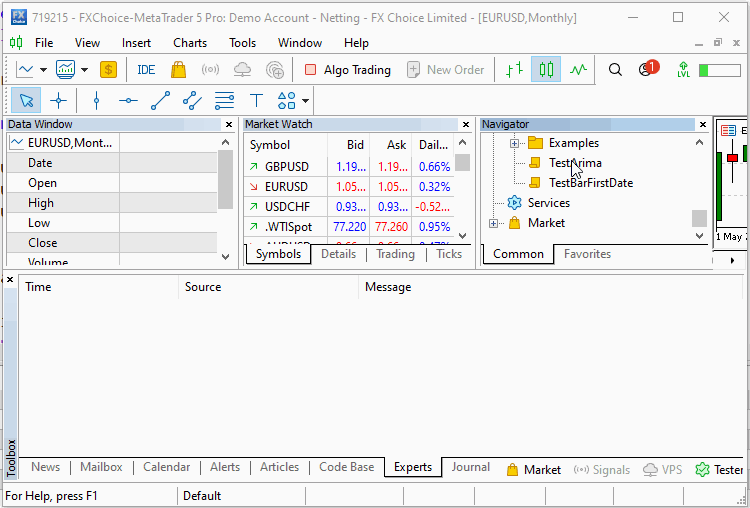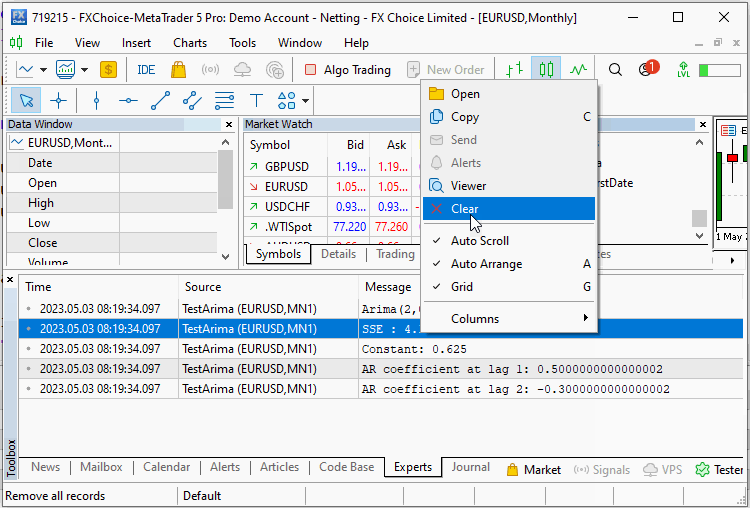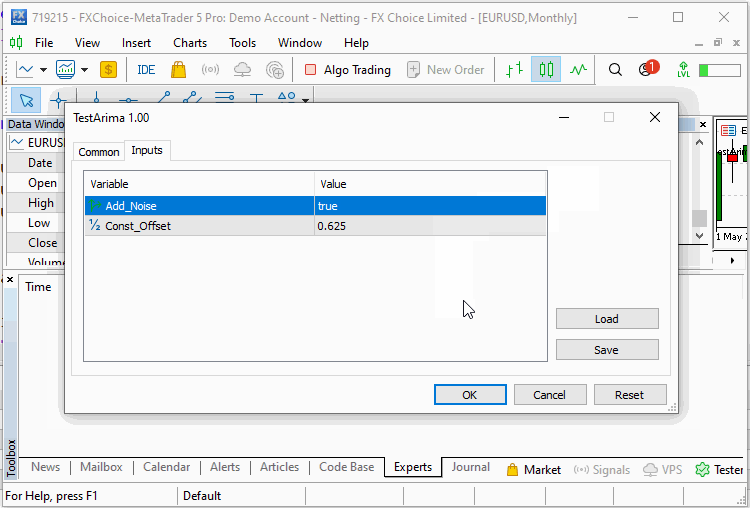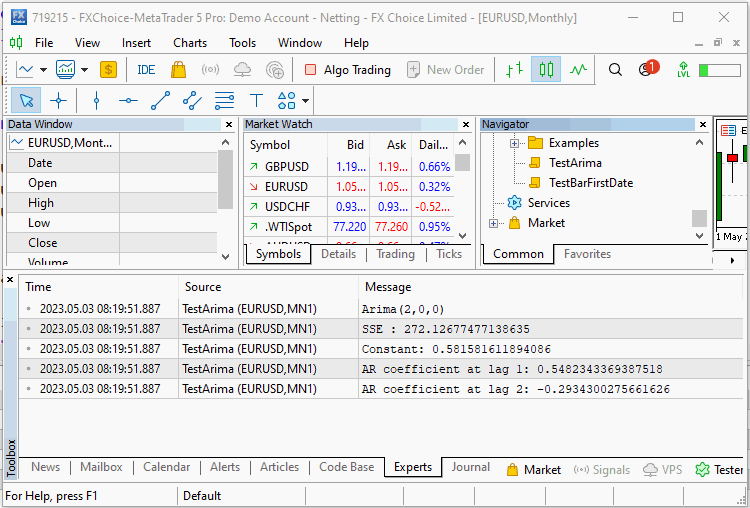
我们声明一个 CArima 对象，指定一个纯 AR(2) 模型。 调用带有输入数组的 Fit() 方法，并在 Summary( 函数的帮助下显示训练结果。 脚本的输出如下所示。

double inputs[300];
   ArrayInitialize(inputs,0);

   int error_code;

   for(int i=2; i<ArraySize(inputs); i++)
     {
      inputs[i]= Const_Offset;
      inputs[i]+= 0.5*inputs[i-1] - 0.3*inputs[i-2];
      inputs[i]+=(Add_Noise)?MathRandomNormal(0,1,error_code):0;
     }

   CArima arima(2,0,0,Const_Offset!=0);

   if(arima.Fit(inputs))
      Print(arima.Summary());

该脚本会运行两次，分别对应有和没有噪声组件的情况。 在第一次运行中，我们看到该算法能够估算序列的确切系数。 在第二次运行中，随着噪声的加入，该算法复现我们的序列所定义的真实恒定偏移量和系数之时相当不错。

示例演示显然不能代表我们在现实世界中将遇到的分析类型。 与金融时间序列相比，加入到序列中的噪声是适度的。

设计 ARIMA 模型

到目前为止，我们已经研究了自回归训练算法的实现，但没有讲明如何为模型推导或选择相应的顺序。 训练模型可能是最容易的部分，这是相较于判定一个好的模型。

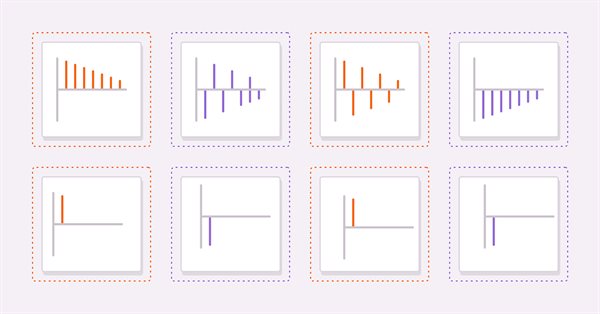
推导合适模型的两个有用工具是计算所研究序列的自相关和偏自相关。 作为指南，为了帮助读者解释自相关图和偏自相关图，我们将考虑四个假设序列。
                                                                  y(t) = AR1* y(t-1) +  E(t)           (3) 

                 
                                                                  y(t) = E(t) - AR1 * y(t-1)            (4) 

            
                                                                  y(t) = MA1 * E(t-1) +  E(t)          (5) 

                
                                                                   y(t) = E(t) - MA1 * E(t-1)           (6) 

    
（3）和（4）分别是具有正系数和负系数的纯 AR(1) 过程。 （5）和（6）分别是具有正系数和负系数的纯 MA(1) 过程。  

上图分别是（3）和（4）的自相关。 在这两个图中，随着滞后的增加，相关值会变小。 这是有道理的，因为随着序列的进一步增长，前期值对当期值的影响会减弱。

下图显示了同一序列对的偏自相关图。 我们看到，相关值在第一个滞后后被截断。 这些观察结果为有关 AR 模型的一般规则提供了基础。 一般来说，如果偏自相关在超过一定滞后之后被切断，并且自相关同时在超过同一滞后时开始衰减，那么可以通过纯 AR 模型对序列进行建模，直到在偏自相关图上观察到滞后截止。

 检查 MA 序列的自相关图，我们注意到这些图与 AR(1) 的偏自相关图相同。

通常，如果超过某个峰值或波谷的所有自相关都为零，并且随着更多的滞后采样，偏自相关变得越来越小，则序列可以由自相关图上观察到的滞后截止处的 MA 项来定义。

 
判定模型的 p 和 q 参数的其它方式包括：

• 信息准则：有若干种信息准则，例如 Akaike 信息准则（AIC）和 贝叶斯信息准则（BIC），可用于比较不同的 ARIMA 模型，并选择最佳模型。

• 网格搜索：这涉及在同一数据集上拟合具有不同顺序的不同 ARIMA 模型，并比较它们的效能。 产生最佳结果的顺序被选为最优 ARIMA 顺序。

• 时间序列交叉验证：这涉及将时间序列数据拆分为训练集和测试集，在训练集上拟合不同的 ARIMA 模型，并评估它们在测试集上的效能。 产生最佳测试误差的 ARIMA 顺序被选为最优阶数。

需要注意的是，没有一种放之四海而皆准的方法来选择 ARIMA 顺序，可能需要一些反复试验和领域知识才能判定特定时间序列的最佳顺序。

结束语

我们演示了 CArima 类，该类封装了采用 函数最小化 Powells 方法 的自回归训练算法。 完整的类代码在下面随附的 zip 文件中给出，并附有演示其用法的脚本。

文件	说明
Arima.mqh	包含 CArima 类定义的文件
PowellsMethod.mqh	内有 PowellsMethod 类定义的包含文件
TestArima	脚本，演示如何使用 CArima 类来分析部分确定性序列。