Teoria das Categorias em MQL5 (Parte 1)

Introdução

A Teoria das Categorias é um ramo da matemática que surgiu em meados dos anos 1940 por Eilenberg e Mac Lane. Suas ideias nasceram numa época quando a teoria da relatividade de Einstein estava levando à percepção de que não há uma única perspectiva de como ver o mundo, mas sim que o verdadeiro poder está em ser capaz de traduzir entre essas diferentes perspectivas. Portanto, ele serve como uma forma de classificação que não se concentra nos objetos que estão sendo classificados, mas se concentra na inter-relação desses objetos para chegar a definições muito concisas. A importância dessa abordagem é que os conceitos retirados de uma área de estudo ou disciplina podem ser intuitivos ou mesmo aplicáveis em um campo diferente. Em seus primórdios, porém, o uso principal era para o estudo das relalções entre a geometria e álgebra. Hoje, os usos claramente transcendem a matemática e são muito amplos para esses artigos da série, então vamos nos debruçar sobre o seu possível uso para os traders que usam a linguagem de programação em MQL.

No contexto de negociação e da escrita de expert advisors em MQL5, a teoria das Categorias pode ser usada para analisar e entender as relações entre diferentes estratégias de negociação, instrumentos e condições de mercado. Ele pode ajudar os traders a identificar padrões e estruturas comuns em seus sistemas de negociação e a desenvolver algoritmos de negociação mais gerais e flexíveis que possam se adaptar às mudanças nas condições do mercado.

A teoria das categorias também pode ser útil para verificar a correção e consistência dos sistemas de negociação e para desenvolver modelos formais de comportamento de negociação. Ao fornecer uma linguagem clara e rigorosa para expressar e raciocinar sobre os conceitos de negociação, a teoria das Categorias pode ajudar os traders a escrever expert advisors mais confiáveis e sustentáveis, bem como a comunicar as suas ideias e estratégias de forma mais eficaz com outros traders e pesquisadores.

Domínios e Morfismos

Domínios e morfismos das categorias são os conceitos fundamentais na teoria das categorias. Na teoria das categorias, uma categoria é uma coleção de domínios (também conhecidos como conjuntos) de elementos e os morfismos (também conhecidos setas, mapas ou funções) entre eles. Para esses artigos, nós consideraremos as setas, funções ou mapas como as unidades básicas de um morfismo. Esses morfismos codificam as relações entre os elementos em cada domínio dentro da categoria, e eles podem ser compostos para formar morfismos mais complexos.

Os conjuntos são um conceito fundamental em matemática e desempenham um papel fundamental na teoria das categorias. Na teoria das categorias, nos referimos a eles como domínios que são usados para definir os elementos de uma 'espécie' específica. Normalmente, se nós estivéssemos estudando a categoria dos domínios, os 'elementos' da categoria seriam o próprio domínio. Esses domínios, geralmente, mas nem sempre, passam a conter outros elementos que formam a base do morfismo. Os morfismos nesta categoria seriam funções entre domínios, que são regras que associam cada elemento de um domínio com um elemento único de outro domínio. Por exemplo, se nós tivéssemos dois domínios A e B, um morfismo de A para B seria uma regra que atribui cada elemento de A a um único elemento de B. Quando um morfismo vai de A para B, A é referido como 'o domínio' enquanto B é o 'contradomínio'. Todos os elementos do domínio terão uma relação com pelo menos um dos elementos do contradomínio. Nenhum elemento no domínio permanece não mapeado. No entanto, alguns elementos no contradomínio podem não estar mapeados. Isso geralmente é denotado da seguinte maneira.

//+------------------------------------------------------------------+
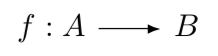
//| ELEMENT CLASS                                                    |
//+------------------------------------------------------------------+
class CElement
   {
      protected:
      
      int                           cardinal;
      vector                        element;
      
      public:
      
      bool                          Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; element.Init(cardinal); return(true); } return(false); }
      int                           Cardinality() { return(cardinal); }
      
      double                        Get(int Index) { if(Index>=0 && Index<Cardinality()) { return(element[Index]); } return(EMPTY_VALUE); }
      bool                          Set(int Index,double Value) { if(Index>=0 && Index<Cardinality()) { element[Index]=Value; return(true); } return(false); }
      
                                    CElement(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CElement(void) {};
   };

Portanto, na listagem acima, nós podemos começar definindo um elemento. Esta é a unidade básica de um domínio que você pode considerar como 'um membro de um conjunto'. Esta unidade pode assumir qualquer tipo de dados, seja duplo ou inteiro, no entanto, o tipo de vetor seria mais flexível à medida que tipos de dados e operações mais complexas forem atendidas. Ele permite escalabilidade. Seu tamanho, o parâmetro 'cardinal' é protegido e só pode ser acessado ou modificado através das funções 'Cardinality()'. Proteger o seu acesso garante que, sempre que ele for modificado, o vetor seja redimensionado adequadamente. O próprio 'elemento' do vetor também é protegido para evitar erros de índice inválido. Portanto, o acesso só é permitido através das funções 'Get()' e 'Set()'. A função 'Set()' também retorna um booleano para verificar se a atribuição foi bem-sucedida.

//+------------------------------------------------------------------+
//| DOMAIN CLASS                                                     |
//+------------------------------------------------------------------+
class CDomain
   {
      protected:
      
      int                           cardinal;
      CElement                      elements[];
      
      public:
      
      bool                          Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; ArrayResize(elements,cardinal); return(true); } return(false); }
      int                           Cardinality() { return(cardinal); }
      
      bool                          Get(int Index,CElement &Element) { if(Index>=0 && Index<Cardinality()) { Element=elements[Index]; return(true); } return(false); }
      bool                          Set(int Index,CElement &Value,bool IsNew=false) { if(Index>=0 && Index<Cardinality()) { if(!IsNew||New(Value)<0) { elements[Index]=Value; return(true); }} return(false); }
      
      //only unique elements allowed
      int                           New(CElement &Value)
                                    {
                                       bool _new=-1;
                                       //
                                       for(int o=0; o<cardinal; o++)
                                       {
                                          if(ElementMatch(Value,elements[o]))
                                          {
                                             _new=o;
                                             break;
                                          }
                                       }
                                       
                                       return(_new);
                                    }
      
                                    CDomain(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CDomain(void) {};
   };

A classe de domínio, portanto, é o que inclui nossos elementos cuja classe é abordada acima. Suas variáveis principais 'elements[]' e seu tamanho 'cardinal' são protegidos como na classe elemento pelas razões já mencionadas. O que é um pouco diferente aqui é a adição do método 'New()'. Esta função ajuda a verificar os novos objetos que serão adicionados ao domínio e garantir que eles sejam exclusivos. Os domínios da categoria contêm apenas objetos exclusivos. Não são permitidas duplicatas. 

Como nós temos essas duas classes, nós poderíamos tentar construir alguns domínios. Vamos tentar ter um domínio de números pares e outro de números ímpares. Poderíamos fazer isso executando um script que referencia essas classes. A listagem disso é mostrada a seguir.

//+------------------------------------------------------------------+
//| INPUTS                                                           |
//+------------------------------------------------------------------+
input int __domain_elements=3;
input int __domain_morphisms=5;

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
   {
      //Declare a sets of natural even & odd numbers
      CDomain _evens,_odds;
      CreateNumberDomain(_evens,__domain_elements,2);
      CreateNumberDomain(_odds,__domain_elements,2,1);
      
      printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens));
      
      printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds));
   }

A função de criação do número é um método direto para preencher um domínio com os números naturais. Todo o código está anexado a este artigo, no entanto, seu conjunto é mostrado aqui para maior clareza.

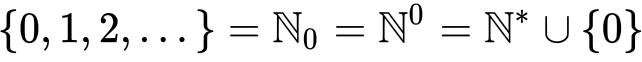
A função 'PrintSet()' é um método engenhoso ao qual nos referiremos com frequência. Ele simplesmente nos permite visualizar o conteúdo de um domínio com parênteses e vírgulas apropriados, tomando o cuidado de separar a(s) estrutura(s) do elemento vetorial da estrutura do domínio. Se executarmos o script acima, é isso que devemos ver.

2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() evens are... {(2.0),(4.0),(6.0),(8.0),(10.0),(12.0),(14.0)}

2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() odds are... {(1.0),(3.0),(5.0),(7.0),(9.0),(11.0),(13.0)}

Os vários elementos de cada domínio estão entre colchetes porque são do tipo de dados vetoriais, o que significa que eles próprios podem ter várias entradas. Quando isso acontece, vírgulas aparecem entre cada entrada com os colchetes, ajudando a definir os limites de cada elemento.

Os morfismos também são um conceito importante na teoria das categorias e são usados para codificar as relações entre os elementos no(s) domínio(s). De acordo com as regras da teoria das categorias, cada morfismo mapeia um elemento no domínio para um elemento no contradomínio. Essas funções podem ser compostas para formar morfismos mais complexos e podem ser usadas para estudar as propriedades de conjuntos e suas relações com outros conjuntos, conforme veremos.

Para começar, porém, existem 5 tipos principais de morfismos, que podem ser usados para descrever as relações entre objetos em uma determinada categoria. Alguns dos tipos mais comuns são:

1. Monomorfismos: são morfismos injetivos, o que significa que eles mapeiam cada elemento no domínio de origem para um único objeto no contradomínio. Não há dois morfismos mapeados para o mesmo objeto no contradomínio. Neste caso, você pode ter alguns objetos no destino não mapeados.
2. Epimorfismos: são morfismos sobrejetivos, o que significa que os elementos no domínio são mapeados para todos os elementos no contradomínio. Em outras palavras, nenhum elemento no contradomínio é deixado sem mapeamento. Também neste caso, é comum ter menos elementos no contradomínio do que no conjunto de origem.
3. Isomorfismos: Isomorfismos são morfismos bijetivos, o que significa que eles estabelecem uma correspondência um-para-um entre objetos nas categorias de origem e destino. Eles são injetivos e sobrejetivos, pois os conjuntos de origem e destino têm o mesmo número de objetos.
4. Endomorfismos: Endomorfismos são morfismos de um elemento para si mesmo. É o que constitui um mapa de identidade, ou seja, um grupo de endomorfismos ligando de volta ao domínio.
5. Automorfismos: Os automorfismos são uma combinação de mapas de isomorfismos e endomorfismos.

Vejamos como uma classe de morfismo e seu agrupamento com domínios chamados de homomorfismo podem ser implementados em MQL.

//+------------------------------------------------------------------+
//| MORPHISM CLASS                                                   |
//+------------------------------------------------------------------+
class CMorphism
   {
      public:
      
      int                           domain;
      int                           codomain;
      
      CElement                      morphism;
      
      bool                          Morph(CDomain &D,CDomain &C,CElement &DE,CElement &CE,bool Add=true)
                                    {
                                       int _d=D.New(DE),_c=C.New(CE);
                                       //
                                       if(_d>=0 && _c>=0)
                                       {
                                          if(DE.Cardinality()==CE.Cardinality())
                                          {
                                             domain=_d;
                                             codomain=_c;
                                             
                                             morphism.Cardinality(DE.Cardinality());
                                             
                                             if(Add)
                                             {
                                                for(int c=0;c<morphism.Cardinality();c++)
                                                {
                                                   morphism.Set(c,CE.Get(c)-DE.Get(c));
                                                }
                                             }
                                             else
                                             {
                                                for(int c=0;c<morphism.Cardinality();c++)
                                                {
                                                   if(DE.Get(c)!=0.0){ morphism.Set(c,CE.Get(c)/DE.Get(c)); }
                                                }
                                             }
                                          }
                                       }
                                       
                                       return(false);
                                    }
      
      
                                    CMorphism(void){ domain=-1; codomain=-1; };
                                    ~CMorphism(void){};
   };

A classe de morfismo é muito básica com apenas os parâmetros de índice de domínio e contradomínio mais uma função 'Morph' com a qual não nos preocuparemos neste artigo. A referência aos respectivos conjuntos de domínio e contradomínio é omitida aqui porque eles estão listados na classe Homomorfismo, conforme mostrado abaixo.

//+------------------------------------------------------------------+
//| HOMO-MORPHISM CLASS                                              |
//+------------------------------------------------------------------+
class CHomomorphism
   {
      protected:
      
      int                           cardinal;
      
      CMorphism                     morphism[];
      
      public:
      
      bool                          init;
      
      CDomain                       domain;
      CDomain                       codomain;
      
      bool                          Cardinality(int DomainIndex,int CodomainIndex,bool Add=true)
                                    { 
                                       bool _morphed=true; 
                                       
                                       if
                                       (
                                       !init
                                       )
                                       {
                                          _morphed=false; return(_morphed); 
                                       }
                                       
                                       if
                                       (
                                       DomainIndex<0 || DomainIndex>=domain.Cardinality() ||
                                       CodomainIndex<0 || CodomainIndex>=codomain.Cardinality()
                                       )
                                       {
                                          _morphed=false; return(_morphed); 
                                       }
                                       
                                       for(int m=0;m<cardinal;m++)
                                       {
                                          if(DomainIndex==morphism[m].domain)
                                          {
                                             _morphed=false; break;
                                          }
                                       } 
                                       
                                       if(_morphed)
                                       {
                                          cardinal++;
                                          ArrayResize(morphism,cardinal);
                                          CElement _de,_ce;
                                          if(domain.Get(DomainIndex,_de) && codomain.Get(CodomainIndex,_ce))
                                          {
                                             morphism[cardinal-1].Morph(domain,codomain,_de,_ce,Add);
                                          }
                                       }
                                       
                                       return(_morphed); 
                                    };
      
      int                           Cardinality()
                                    {
                                       return(cardinal);
                                    };
                                    
      bool                          Get(int Index,CMorphism &Morphism)
                                    {
                                       if(Index>=0 && Index<Cardinality())
                                       {
                                          
                                          return(true);
                                       }
                                       
                                       return(false);
                                    };
                                    
      bool                          Set(int Index,CMorphism &Value)
                                    {
                                       if
                                       (
                                       Index>=0 && Index<Cardinality() && 
                                       Value.domain>=0 && Value.domain<domain.Cardinality() &&
                                       Value.codomain>=0 && Value.codomain<codomain.Cardinality()
                                       )
                                       {
                                          if(!MorphismMatch(Index,Value,morphism,Cardinality()))
                                          {
                                             morphism[Index]=Value;
                                             return(true);
                                          }
                                          
                                       }
                                       
                                       return(false);
                                    };
                                    
      void                          Init(CDomain &Domain,CDomain &Codomain)
                                    {
                                       domain=Domain;
                                       codomain=Codomain;
                                       
                                       init=true;
                                    }
      
      
                                    CHomomorphism(void){ init=false; cardinal=0; };
                                    ~CHomomorphism(void){};
   };

Na classe Homomorfismo, a variável 'morphism[]' junto com seus tamanhos 'morfismos' são protegidos pelos motivos mencionados acima, os quais eu não repetirei. Basta dizer que as duas funções 'Morphism()' e as funções 'Get()' e 'Set()' seguem de forma semelhante às funções nos objetos e classes de conjuntos. O que é adicionado aqui é um parâmetro booleano 'init' que indica se a classe foi inicializada atribuindo os conjuntos públicos 'domain' e 'codomain'. A adição de um morfismo ao array protegido 'morphism[]' é feita através do fornecimento de um índice de domínio e um índice de contradomínio. Esses índices precisam estar dentro do intervalo de seus respectivos tamanhos de domínio. Depois de passarem por isso, é necessário verificar se o índice de domínio em particular não foi usado. De acordo com as regras da Teoria das Categorias, todos os objetos no domínio devem ser mapeados para um objeto no contradomínio, mas eles são mapeados apenas uma vez. Portanto, um índice de contradomínio pode ser usado duas vezes, mas um índice de domínio é usado apenas uma vez.

Vamos divagar um pouco e olhar para os subdomínios (conhecido como Subconjuntos). Os subdomínios são uma ferramenta útil na Teoria das categorias e a capacidade de enumerar os subdomínios dentro de um domínio e verificar se um domínio é um possível subdomínio para um determinado domínio pode ser uma ferramenta muito engenhosa. Vejamos as funções que realizam essas duas tarefas.

//+------------------------------------------------------------------+
//| Domain Match function                                            |
//+------------------------------------------------------------------+
bool DomainMatch(CDomain &A,CDomain &B)
   {
      if(A.Cardinality()!=B.Cardinality())
      {
         return(false);
      }
      
      bool _matched=true;
      
      for(int o=0; o<A.Cardinality(); o++)
      {
         CElement _a,_b;
         
         if(A.Get(o,_a) && B.Get(o,_b) && !ElementMatch(_a,_b))
         {
            _matched=false; break;
         }
      }
      
      return(_matched);
   }
//+------------------------------------------------------------------+
//| Is Subdomain function                                            |
//+------------------------------------------------------------------+
bool IsSubdomain(CDomain &Domain,CDomain &SubDomain)
   {
      bool _is_subdomain=false;
      
      int _subdomain_count=0; CDomain _subdomains[];
      GetSubdomains(Domain,_subdomain_count,_subdomains);
      
      for(int c=0;c<_subdomain_count;c++)
      {
         if(DomainMatch(SubDomain,_subdomains[c]))
         {
            _is_subdomain=true;
            break;
         }
      }
      
      return(_is_subdomain);
   }

Se, portanto, executarmos o script abaixo:

//+------------------------------------------------------------------+
//| INPUTS                                                           |
//+------------------------------------------------------------------+
input int __domain_elements=3;
input int __domain_morphisms=5;

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
   {
      //Declare a sets of natural even & odd numbers
      CDomain _evens,_odds;
      CreateNumberDomain(_evens,__domain_elements,2);
      CreateNumberDomain(_odds,__domain_elements,2,1);
      
      printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens));
      
      printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds));
    
      int _subdomain_count=0; CDomain _subdomains[];
      GetSubdomains(_evens,_subdomain_count,_subdomains);
      printf(__FUNCSIG__+" evens subs are... "+IntegerToString(_subdomain_count));
      for(int s=0; s<_subdomain_count; s++)
      {
         printf(" with: "+PrintDomain(_subdomains[s])+", at: "+IntegerToString(s+1));
      }
   } 

Ele deve nos fornecer esses logs:

2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) void OnStart() evens subs are... 7

2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) with: {(2.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 1

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 2

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 3

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 4

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 5

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 6

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0),(6.0)}

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 7

O número real de subconjuntos possíveis é 8 se incluirmos o conjunto vazio que também é um subconjunto.

O código adicional para verificar um subconjunto pode ser composto conforme mostrado:

      CDomain _smaller_evens;
      CreateNumberDomain(_smaller_evens,__domain_elements-2,2);
      
      printf(__FUNCSIG__+" smaller evens are... "+PrintDomain(_smaller_evens));
      
      bool _is_subdomain=IsSubdomain(_evens,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of evens. ");
      _is_subdomain=IsSubdomain(_odds,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of odds. ");
      

Seus logs devem gerar isso:

2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) void OnStart() smaller evens are... {(2.0)}

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1)

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: true that 'smaller-evens' is a subset of evens. 

2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: false that 'smaller-evens' is a subset of odds. 

Na teoria das categorias, um homomorfismo é uma definição que preserva a estrutura de um grupo de morfismos entre dois domínios. Ela é uma função que preserva as relações e operações definidas nos elementos. Os homomorfismos são importantes na teoria das categorias porque fornecem um meio de estudar as relações entre diferentes elementos e de construir novos elementos a partir dos existentes.

Ao considerar os homomorfismos entre os elementos, é possível obter informações sobre a natureza dos elementos e seu comportamento sob diferentes operações. Por exemplo, a existência de um homomorfismo entre dois domínios pode ser usada para definir uma noção de equivalência entre eles, permitindo o estudo das relações entre eles.

Outro significado dos homomorfismos na teoria das categorias é que eles fornecem um meio de construir novos objetos a partir dos existentes por meio da herança dessas propriedades. Exemplos destes, juntamente com a equivalência, serão abordados em artigos subsequentes e são mencionados aqui apenas para estabelecer a base para a definição dessa classe aparentemente 'não útil'.

Vamos tentar encorajar a Teoria das categorias para os nossos propósitos, criando uma instância da classe de homomorfismo que tenha conjuntos de domínio e contradomínio de tempo e preços de fechamento.

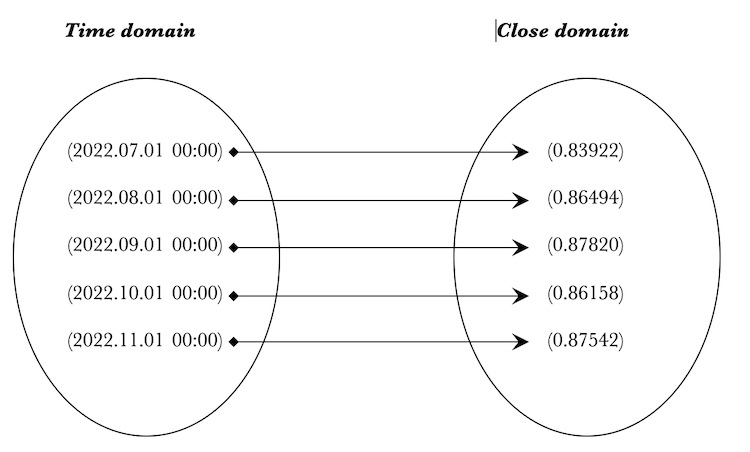
Em seguida, nós visualizaremos esta instância usando a função 'PrintHomomorphism()'. Essas funções de impressão personalizadas serão muito úteis na visualização de objetos, conjuntos, morfismos e homomorfismos criados. Aqui está a listagem:

//+------------------------------------------------------------------+
//| Print Element function                                            |
//+------------------------------------------------------------------+
string PrintElement(CElement &O,int Precision=1,bool IsTime=false)
   {
      string _element="(";
      //
      for(int r=0; r<O.Cardinality(); r++)
      {
         if(!IsTime)
         {
            _element+=DoubleToString(O.Get(r),Precision);
         }
         else if(IsTime)
         {
            _element+=TimeToString(datetime(int(O.Get(r))));
         }
         
         if(r<O.Cardinality()-1){ _element+=","; }
      }
      //
      return(_element+")");
   }
//+------------------------------------------------------------------+
//| Print Set function                                               |
//+------------------------------------------------------------------+
string PrintDomain(CDomain &S,int Precision=1,bool IsTime=false)
   {
      string _set="{";
      //
      CElement _e;
      for(int o=0; o<S.Cardinality(); o++)
      {
         S.Get(o,_e);
         _set+=PrintElement(_e,Precision,IsTime);if(o<S.Cardinality()-1){ _set+=","; }
      }
      //
      return(_set+"}\n");
   }
//+------------------------------------------------------------------+
//| Print Morphism function                                          |
//+------------------------------------------------------------------+
string PrintMorphism(CMorphism &M, CDomain &Domain,CDomain &Codomain,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false)
   {
      string _morphism="";
      //
      CElement _d,_c;
      if(Domain.Get(M.domain,_d) && Codomain.Get(M.codomain,_c))
      {
         _morphism=PrintElement(_d,Precision,DomainIsTime);
         _morphism+="|----->";
         _morphism+=PrintElement(_c,Precision,CodomainIsTime);
         _morphism+="\n";
      }
      //
      return(_morphism);
   }
//+------------------------------------------------------------------+
//| Print Homomorphism function                                      |
//+------------------------------------------------------------------+
string PrintHomomorphism(CHomomorphism &H,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false)
   {
      string _homomorphism="\n\n"+PrintDomain(H.domain,Precision,DomainIsTime);
      //
      _homomorphism+="|\n";
      
      CMorphism _m;
      for(int m=0;m<H.Cardinality();m++)
      {
         if(H.Get(m,_m))
         {
            _homomorphism+=(PrintMorphism(_m,H.domain,H.codomain,Precision,DomainIsTime,CodomainIsTime));
         }
      }
      //
      _homomorphism+="|\n";
      
      _homomorphism+=PrintDomain(H.codomain,Precision,CodomainIsTime);
      //
      return(_homomorphism);
   }

Entradas notáveis aqui são 'Precision' e 'IsTime'. Esses dois definem casas decimais para exibição de dados flutuantes (o padrão para vetores) e se é necessário converter os dados do objeto/vetor como tempo para fins de apresentação na string retornada. 

Então, para criar o nosso homomorfismo, nós usaremos este script:

//Declare sets to store time & close prices
      CDomain _time,_close;
      
      MqlRates _rates[];
      
      //Fill domain with 5 most recent bar time & MA values from chart
      if(CopyRates(_Symbol,_Period,0,__domain_morphisms,_rates)>=__domain_morphisms && _time.Cardinality(__domain_morphisms) && _close.Cardinality(__domain_morphisms))
      {
         for(int m=0;m<__domain_morphisms;m++)
         {
            //Create uni row element
            CElement _t,_m;
            if(_t.Cardinality(1) && _m.Cardinality(1))
            {
               datetime _t_value=_rates[m].time;//iTime(_Symbol,_Period,m);
               _t.Set(0,double(int(_t_value)));
               _time.Set(m,_t);
               
               double _m_value=_rates[m].close;//iClose(_Symbol,_Period,5);//,m,MODE_SMA,PRICE_CLOSE);
               _m.Set(0,_m_value);
               _close.Set(m,_m);
            }
         }
      }
      
      //Create homomorphism from time to close
      CHomomorphism _h;_h.Init(_time,_close);
      
      if(_h.init)
      {
         //Create 1-1 morphisms from time to MA
         int _morphisms=0;
         for(int m=0;m<__domain_morphisms;m++)
         {
            if(_h.Cardinality(m,m)){ _morphisms++; }
         }
         
         if(_morphisms>=__domain_morphisms)
         { 
            printf(__FUNCSIG__+" homomorphism: "+PrintHomomorphism(_h,_Digits,true)); 
         }
      }

Criamos dois conjuntos '_time' e "_close". Em seguida, os preenchemos com dados de um array MqlRates. '__set_morphisms' é um parâmetro de entrada que determina o tamanho do conjunto. Neste caso, ambos os conjuntos '"time' e "_close' são do mesmo tamanho e correspondem ao parâmetro de entrada. A instância da classe de homomorfismo '_h" é então inicializada com esses dois conjuntos. Morfismos simples um-para-um são criados entre os dois conjuntos usando a função 'Morphisms()' que é verificada, pois retorna um booleano. Se true, o parâmetro '_morphisms' é incrementado e uma vez que chegamos ao tamanho do parâmetro de entrada, imprimimos o homomorfismo '_h' usando a função PrintHomomorphism()'. Nossos logs devem gerar isso:

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) void OnStart() homomorphism: 

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(2022.07.01 00:00),(2022.08.01 00:00),(2022.09.01 00:00),(2022.10.01 00:00),(2022.11.01 00:00)}

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) |

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.07.01 00:00)|----->(0.83922)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.08.01 00:00)|----->(0.86494)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.09.01 00:00)|----->(0.87820)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.10.01 00:00)|----->(0.86158)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.11.01 00:00)|----->(0.87542)

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) |

2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(0.83922),(0.86494),(0.87820),(0.86158),(0.87542)}

Na Teoria das Categorias também pode ser útil enumerar o conjunto de imagens de um homomorfismo. Uma imagem simplesmente se refere a um subconjunto do contradomínio que apresenta apenas os objetos mapeados do domínio. Para nossos propósitos, nós podemos enumerar isso usando a função abaixo:

//+------------------------------------------------------------------+
//| Image function                                                   |
//+------------------------------------------------------------------+
void Image(CHomomorphism &H,CSet &Output)
   {
      for(int m=0;m<H.Morphisms();m++)
      {
         CObject _o;
         CMorphism _m;
         if(H.Get(m,_m) && H.codomain.Get(_m.codomain_index,_o))
         {
            bool _matched=false;
            for(int o=0;o<Output.Objects();o++)
            {
               CObject _oo;
               if(Output.Get(o,_oo) && ObjectMatch(_o,_oo))
               {
                  _matched=true; break;
               }
            }
            
            if(!_matched)
            {
               Output.Objects(Output.Objects()+1);
               Output.Set(Output.Objects()-1,_o);
            }
         }
      }
   }

Para ver este código em ação, nós usaremos este script:

      //Create homomorphism from time to close
      CHomomorphism _h_image;_h_image.Init(_time,_close);
      
      if(_h_image.init)
      {
         //Create 1-1 morphisms from time to MA
         int _morphisms=0;
         for(int m=0;m<__set_morphisms;m++)
         {
            int _random_codomain=MathRand()%__set_morphisms;
            if(_h_image.Morphisms(m,_random_codomain)){ _morphisms++; }
         }
         
         if(_morphisms>=__set_morphisms)
         { 
            CSet _image;_image.Objects(0);
            Image(_h_image,_image);
            printf(__FUNCSIG__+" image from homomorphism: "+PrintSet(_image,_Digits)); 
         }
      }

Tudo o que estamos fazendo aqui é usar os dois conjuntos criados anteriormente em uma nova classe de homomorfismo chamada '_h_image'. A diferença desta vez é que, ao adicionar morfismos, nós escolhemos aleatoriamente os valores do contradomínio e, portanto, temos repetição. Isso significa que o contradomínio definido será diferente daquele na instância '_h'. Nossos logs devem produzir isto:

2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2) void OnStart() image from homomorphism: {(145.847),(145.188)}

2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2)

Claramente, o contradomínio tem apenas dois objetos dos três possíveis, portanto, nós podemos recuperar facilmente os objetos mapeados de um determinado conjunto. Continuaremos daqui no próximo artigo onde começaremos com os isomorfismos e endomorfismos.

Conclusão

Nós examinamos alguns conceitos introdutórios da teoria das categorias, um método cada vez mais rico em matemática para classificar as informações. Entre eles está um elemento, um domínio e um morfismo. Um elemento forma a unidade fundamental e é normalmente pensado como um membro de um conjunto que, na teoria de conjuntos, é referido como um domínio. Este domínio através de seus elementos pode ter relacionamentos com outros domínios (referidos como contradomínios). Essas relações são chamadas de morfismos. Para um trader, a teoria das categorias pode servir como um classificador para informações financeiras de séries temporais e, portanto, uma ferramenta para avaliar e prever as condições do mercado. Nós retomaremos daqui no próximo artigo.