Теория категорий в MQL5 (Часть 1)
Введение
Теория категорий - раздел математики, созданный Эйленбергом и Маклейном в 1940-х годах. Теория относительности Эйнштейна привела к осознанию того, что не существует единой точки зрения, с которой можно смотреть на мир, а реальная перспектива для развития заключается в умении переводить одну точку зрения на язык другой. Теория представляет собой разновидность классификации, которая не останавливается на классифицируемых объектах как таковых, а скорее фокусируется на взаимосвязи этих объектов, чтобы дать очень краткое определение. Значение этого подхода заключается в том, что концепции, взятые из одной области исследования или дисциплины, могут быть интуитивно понятны или даже применимы в другой области. Изначально теория применялась для изучения связей между геометрией и алгеброй. Сегодня области ее применения явно выходят за рамки математики и слишком широки для статей этой серии, поэтому мы остановимся на возможном ее использовании для трейдеров, использующих язык программирования MQL.
В контексте торговли и написания советников на MQL5 теория категорий может использоваться для анализа и понимания взаимосвязей между различными торговыми стратегиями, инструментами и рыночными условиями. Она может помочь трейдерам определить общие модели и структуры в своих торговых системах и разработать более общие и гибкие торговые алгоритмы, которые могут адаптироваться к изменяющимся рыночным условиям.
Теория категорий также может быть полезна для проверки правильности и непротиворечивости торговых систем, а также для разработки формальных моделей торгового поведения. Предоставляя четкий и строгий язык для выражения и рассуждения о торговых концепциях, теория категорий может помочь трейдерам писать более надежных и удобных в сопровождении советников, а также более эффективно делиться своими идеями и стратегиями с другими трейдерами и исследователями.
Домены и морфизмы
Домены категорий и морфизмы являются основополагающими понятиями теории категорий. Категория — это набор доменов (наборов) элементов и морфизмов (или стрелок, также известных как карты, или функции) между ними. В рамках этой серии статей примем стрелки, функции, или карты в качестве основных единиц морфизма. Эти морфизмы кодируют отношения между элементами в каждом домене внутри категории, и они могут быть составлены для формирования более сложных морфизмов.
Множества являются фундаментальным понятием в математике и играют ключевую роль в теории категорий. В теории категорий мы называем их доменами, используемыми для определения элементов определенного "вида". Обычно при изучении категории доменов, "элементами" категории являются сами домены. Эти домены обычно (хотя и не всегда) содержат другие элементы, которые составляют основу морфизма. Морфизмы в этой категории являются функциями между доменами, которые представляют собой правила, связывающие каждый элемент одного домена с уникальным элементом другого домена. Например, у нас есть два домена A и B, при этом морфизм от A до B будет правилом, которое присваивает каждый элемент A уникальному элементу B. Когда морфизм выполняется от A до B, A называется "доменом", а B - "кодоменом". Все элементы в домене будут связаны по крайней мере с одним из элементов в домене кодов. Ни один элемент в домене не остается несопоставленным. Однако некоторые элементы в домене кода могут быть не отображены. Обычно это обозначается так.
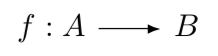
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ class CElement { protected: int cardinal; vector element; public: bool Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; element.Init(cardinal); return(true); } return(false); } int Cardinality() { return(cardinal); } double Get(int Index) { if(Index>=0 && Index<Cardinality()) { return(element[Index]); } return(EMPTY_VALUE); } bool Set(int Index,double Value) { if(Index>=0 && Index<Cardinality()) { element[Index]=Value; return(true); } return(false); } CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
Итак, пользуясь приведенным выше листингом, мы можем начать с определения элемента. Это базовая единица домена, которую вы можете рассматривать как «член множества». Этот блок может принимать любой тип данных, будь то двойной или целочисленный, однако векторный тип будет более гибким, поскольку мы имеем дело с более сложными типами данных и операциями. Векторный тип обеспечивает масштабируемость. Его размер (параметр cardinal) защищен и может быть доступен или изменен только c помощью функции 'Cardinality()'. Защита доступа гарантирует, что всякий раз, когда он изменяется, размер вектора изменяется соответствующим образом. Сам "элемент" вектора также защищен, чтобы предотвратить ошибки индекса. Таким образом, доступ разрешен только через функции 'Get()' и 'Set()'. Функция 'Set()' также возвращает булево значение для проверки успешности присваивания.
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ class CDomain { protected: int cardinal; CElement elements[]; public: bool Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; ArrayResize(elements,cardinal); return(true); } return(false); } int Cardinality() { return(cardinal); } bool Get(int Index,CElement &Element) { if(Index>=0 && Index<Cardinality()) { Element=elements[Index]; return(true); } return(false); } bool Set(int Index,CElement &Value,bool IsNew=false) { if(Index>=0 && Index<Cardinality()) { if(!IsNew||New(Value)<0) { elements[Index]=Value; return(true); }} return(false); } //only unique elements allowed int New(CElement &Value) { bool _new=-1; // for(int o=0; o<cardinal; o++) { if(ElementMatch(Value,elements[o])) { _new=o; break; } } return(_new); } CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
Таким образом, доменный класс включает в себя наши элементы, класс которых описан выше. Его основные переменные 'elements[]' и размер ('cardinal') защищены, как и в классе элементов, по уже упомянутым причинам. Что здесь немного отличается, так это добавление метода 'New()'. Эта функция помогает проверять новые объекты, добавляемые в домен, и обеспечивать их уникальность. Домены категорий содержат только уникальные объекты. Дубликаты не допускаются.
Поскольку у нас есть эти два класса, мы могли бы попытаться создать несколько доменов. Попробуем получить домен четных чисел и домен нечетных чисел. Запустим скрипт, который ссылается на эти классы. Листинг представлен ниже.
//+------------------------------------------------------------------+ //| INPUTS | //+------------------------------------------------------------------+ input int __domain_elements=3; input int __domain_morphisms=5; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //Declare a sets of natural even & odd numbers CDomain _evens,_odds; CreateNumberDomain(_evens,__domain_elements,2); CreateNumberDomain(_odds,__domain_elements,2,1); printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens)); printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds)); }
Функция создания числа — это простой метод заполнения домена натуральными числами. Весь код приложен к этой статье. Приведем здесь соответствующее множество для большей ясности.
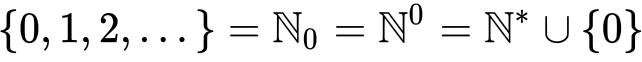
Мы будем часто обращаться к функции 'PrintSet()'. Она позволяет нам легко просматривать содержимое домена с соответствующими круглыми скобками и запятыми, отделяя структуру (структуры) вектора элемента от общей структуры домена. При запуске приведенного выше скрипта мы увидим следующее.
2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() odds are... {(1.0),(3.0),(5.0),(7.0),(9.0),(11.0),(13.0)}
Различные элементы каждого домена заключены в скобки, потому что они являются векторным типом данных, что означает, что они сами могут иметь несколько записей. Когда это происходит, между каждой записью и скобками появляются запятые, что помогает определить границы элемента.
Морфизмы также являются важным понятием в теории категорий. Они используются для кодирования отношений между элементами в домене (доменах). В соответствии с правилами теории категорий каждый морфизм отображает один элемент домена в один элемент кодомена. Эти функции можно комбинировать для формирования более сложных морфизмов. Как мы увидим, их можно использовать для изучения свойств множеств и их отношений с другими множествами.
Начнем с того, что есть 5 основных типов морфизмов, которые можно использовать для описания отношений между объектами в данной категории. Некоторые из наиболее распространенных типов:
- Мономорфизмы: инъективные морфизмы, отображающие каждый элемент исходного домена на уникальном объекте кодомена. Никакие два морфизма не могут отображаться на одном объекте кодомена. В этом случае у нас могут быть неотображенные объекты в цели.
- Эпиморфизмы: сюръективные морфизмы. Элементы домена отображают все элементы кодомена. Другими словами, ни один элемент в домене кода не остается неотображенным. В этом случае в кодомене обычно содержится меньше элементов, чем в исходном наборе.
- Изоморфизмы: биективные морфизмы, устанавливающие однозначное соответствие между объектами в исходной и целевой категориях. Они и инъективны, и сюръективны, поскольку исходное и целевое множества имеют одинаковое количество объектов.
- Endomorphisms: морфизм объекта категории в себя. Это то, что составляет карту идентичности, то есть группу эндоморфизмов, возвращающихся к домену.
- Автоморфизмы: комбинация карт изоморфизмов и эндоморфизмов.
Давайте посмотрим, как класс морфизмов и его группировка с областями, называемыми гомоморфизмами, могут быть реализованы в MQL.
//+------------------------------------------------------------------+ //| MORPHISM CLASS | //+------------------------------------------------------------------+ class CMorphism { public: int domain; int codomain; CElement morphism; bool Morph(CDomain &D,CDomain &C,CElement &DE,CElement &CE,bool Add=true) { int _d=D.New(DE),_c=C.New(CE); // if(_d>=0 && _c>=0) { if(DE.Cardinality()==CE.Cardinality()) { domain=_d; codomain=_c; morphism.Cardinality(DE.Cardinality()); if(Add) { for(int c=0;c<morphism.Cardinality();c++) { morphism.Set(c,CE.Get(c)-DE.Get(c)); } } else { for(int c=0;c<morphism.Cardinality();c++) { if(DE.Get(c)!=0.0){ morphism.Set(c,CE.Get(c)/DE.Get(c)); } } } } } return(false); } CMorphism(void){ domain=-1; codomain=-1; }; ~CMorphism(void){}; };
Класс Morphism является очень простым и содержит только параметры индекса домена и кодомена, а также функцию 'Morph', которую мы не будем рассматривать в этой статье. Ссылка на соответствующие наборы доменов и кодоменов здесь не приводится, потому что они перечислены в зонтичном классе Homomorphism, показанном ниже.
//+------------------------------------------------------------------+ //| HOMO-MORPHISM CLASS | //+------------------------------------------------------------------+ class CHomomorphism { protected: int cardinal; CMorphism morphism[]; public: bool init; CDomain domain; CDomain codomain; bool Cardinality(int DomainIndex,int CodomainIndex,bool Add=true) { bool _morphed=true; if ( !init ) { _morphed=false; return(_morphed); } if ( DomainIndex<0 || DomainIndex>=domain.Cardinality() || CodomainIndex<0 || CodomainIndex>=codomain.Cardinality() ) { _morphed=false; return(_morphed); } for(int m=0;m<cardinal;m++) { if(DomainIndex==morphism[m].domain) { _morphed=false; break; } } if(_morphed) { cardinal++; ArrayResize(morphism,cardinal); CElement _de,_ce; if(domain.Get(DomainIndex,_de) && codomain.Get(CodomainIndex,_ce)) { morphism[cardinal-1].Morph(domain,codomain,_de,_ce,Add); } } return(_morphed); }; int Cardinality() { return(cardinal); }; bool Get(int Index,CMorphism &Morphism) { if(Index>=0 && Index<Cardinality()) { return(true); } return(false); }; bool Set(int Index,CMorphism &Value) { if ( Index>=0 && Index<Cardinality() && Value.domain>=0 && Value.domain<domain.Cardinality() && Value.codomain>=0 && Value.codomain<codomain.Cardinality() ) { if(!MorphismMatch(Index,Value,morphism,Cardinality())) { morphism[Index]=Value; return(true); } } return(false); }; void Init(CDomain &Domain,CDomain &Codomain) { domain=Domain; codomain=Codomain; init=true; } CHomomorphism(void){ init=false; cardinal=0; }; ~CHomomorphism(void){}; };
В классе Homomorphism переменная 'morphism[]' защищена вместе со своим размером 'morphisms' по уже упомянутым причинам. Достаточно сказать, что две функции 'Morphism()', а также функции 'Get()' и 'Set()' аналогичны функциям в классах объектов и множеств. Здесь добавлен логический параметр 'init', который указывает, был ли класс инициализирован путем назначения общедоступных множеств 'domain' и 'codomain'. Добавление морфизма в защищенный массив 'morphism[]' осуществляется путем предоставления индексов домена и кодомена. Эти индексы должны находиться в пределах диапазона размеров соответствующих доменов. После прохождения диапазона нужно проверить, в частности, что индекс домена не использовался. В соответствии с правилами теории категорий все объекты в домене должны сопоставляться с объектом кодомена только один раз. Таким образом, индекс кодомена можно использовать дважды, а индекс домена — только один раз.
Немного отвлечемся и посмотрим на субдомены (также известные как подмножества). Субдомены являются полезным инструментом в теории категорий и позволяют перечислять субдомены внутри домена и/или проверять является ли домен возможным субдоменом для данного домена. Давайте посмотрим на функции, которые выполняют эти две задачи.
//+------------------------------------------------------------------+ //| Domain Match function | //+------------------------------------------------------------------+ bool DomainMatch(CDomain &A,CDomain &B) { if(A.Cardinality()!=B.Cardinality()) { return(false); } bool _matched=true; for(int o=0; o<A.Cardinality(); o++) { CElement _a,_b; if(A.Get(o,_a) && B.Get(o,_b) && !ElementMatch(_a,_b)) { _matched=false; break; } } return(_matched); } //+------------------------------------------------------------------+ //| Is Subdomain function | //+------------------------------------------------------------------+ bool IsSubdomain(CDomain &Domain,CDomain &SubDomain) { bool _is_subdomain=false; int _subdomain_count=0; CDomain _subdomains[]; GetSubdomains(Domain,_subdomain_count,_subdomains); for(int c=0;c<_subdomain_count;c++) { if(DomainMatch(SubDomain,_subdomains[c])) { _is_subdomain=true; break; } } return(_is_subdomain); }
Соответственно, если мы запустим скрипт ниже:
//+------------------------------------------------------------------+ //| INPUTS | //+------------------------------------------------------------------+ input int __domain_elements=3; input int __domain_morphisms=5; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //Declare a sets of natural even & odd numbers CDomain _evens,_odds; CreateNumberDomain(_evens,__domain_elements,2); CreateNumberDomain(_odds,__domain_elements,2,1); printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens)); printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds)); int _subdomain_count=0; CDomain _subdomains[]; GetSubdomains(_evens,_subdomain_count,_subdomains); printf(__FUNCSIG__+" evens subs are... "+IntegerToString(_subdomain_count)); for(int s=0; s<_subdomain_count; s++) { printf(" with: "+PrintDomain(_subdomains[s])+", at: "+IntegerToString(s+1)); } }
В логах видим следующие записи:
2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) void OnStart() evens subs are... 7 2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) with: {(2.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 1 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 2 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 3 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 4 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 5 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 6 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 7
Фактическое количество возможных подмножеств равно 8, если мы включим пустое множество, которое также является подмножеством.
Дополнительный код для проверки подмножества может выглядеть следующим образом:
CDomain _smaller_evens; CreateNumberDomain(_smaller_evens,__domain_elements-2,2); printf(__FUNCSIG__+" smaller evens are... "+PrintDomain(_smaller_evens)); bool _is_subdomain=IsSubdomain(_evens,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of evens. "); _is_subdomain=IsSubdomain(_odds,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of odds. ");
В логах увидим следующее:
2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) void OnStart() smaller evens are... {(2.0)} 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: true that 'smaller-evens' is a subset of evens. 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: false that 'smaller-evens' is a subset of odds.
В теории категорий гомоморфизм — это сохраняющее структуру определение группы морфизмов между двумя доменами. Это функция, которая сохраняет отношения и операции, определенные для элементов. Гомоморфизмы важны в теории категорий, потому что они предоставляют средства изучения отношений между различными элементами и построения новых элементов из существующих.
Рассматривая гомоморфизмы между элементами, можно получить представление о природе элементов и их поведении при различных операциях. Например, существование гомоморфизма между двумя областями можно использовать для определения понятия эквивалентности между ними, что позволяет изучать отношения между ними.
Еще одно значение гомоморфизмов в теории категорий состоит в том, что они обеспечивают средства построения новых объектов из существующих путем наследования этих свойств. Соответствующие примеры вместе с эквивалентностью будут рассмотрены в последующих статьях и упомянуты здесь только для того, чтобы установить основу для определения этого, казалось бы, "бесполезного" класса.
Давайте попробуем оживить теорию категорий для наших целей, создав экземпляр класса гомоморфизма, который имеет множества доменов и кодоменов времени и цен закрытия.
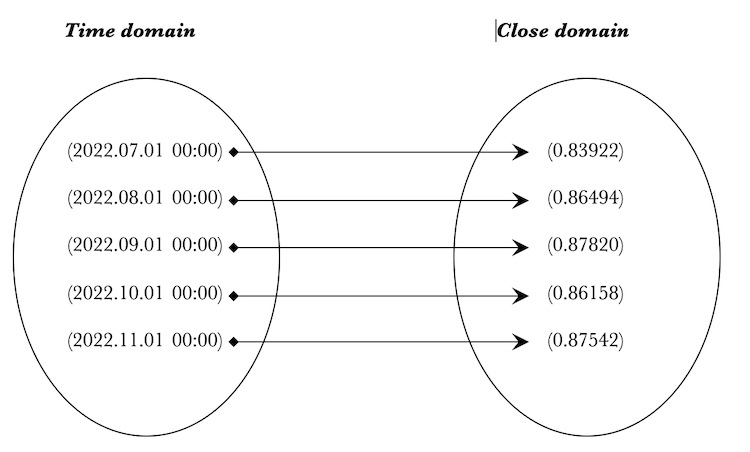
Затем мы просмотрим этот экземпляр с помощью функции 'PrintHomomorphism()'. Эти пользовательские функции будут очень полезны при просмотре созданных объектов, множеств, морфизмов и гомоморфизмов. Листинг приведен ниже:
//+------------------------------------------------------------------+ //| Print Element function | //+------------------------------------------------------------------+ string PrintElement(CElement &O,int Precision=1,bool IsTime=false) { string _element="("; // for(int r=0; r<O.Cardinality(); r++) { if(!IsTime) { _element+=DoubleToString(O.Get(r),Precision); } else if(IsTime) { _element+=TimeToString(datetime(int(O.Get(r)))); } if(r<O.Cardinality()-1){ _element+=","; } } // return(_element+")"); } //+------------------------------------------------------------------+ //| Print Set function | //+------------------------------------------------------------------+ string PrintDomain(CDomain &S,int Precision=1,bool IsTime=false) { string _set="{"; // CElement _e; for(int o=0; o<S.Cardinality(); o++) { S.Get(o,_e); _set+=PrintElement(_e,Precision,IsTime);if(o<S.Cardinality()-1){ _set+=","; } } // return(_set+"}\n"); } //+------------------------------------------------------------------+ //| Print Morphism function | //+------------------------------------------------------------------+ string PrintMorphism(CMorphism &M, CDomain &Domain,CDomain &Codomain,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false) { string _morphism=""; // CElement _d,_c; if(Domain.Get(M.domain,_d) && Codomain.Get(M.codomain,_c)) { _morphism=PrintElement(_d,Precision,DomainIsTime); _morphism+="|----->"; _morphism+=PrintElement(_c,Precision,CodomainIsTime); _morphism+="\n"; } // return(_morphism); } //+------------------------------------------------------------------+ //| Print Homomorphism function | //+------------------------------------------------------------------+ string PrintHomomorphism(CHomomorphism &H,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false) { string _homomorphism="\n\n"+PrintDomain(H.domain,Precision,DomainIsTime); // _homomorphism+="|\n"; CMorphism _m; for(int m=0;m<H.Cardinality();m++) { if(H.Get(m,_m)) { _homomorphism+=(PrintMorphism(_m,H.domain,H.codomain,Precision,DomainIsTime,CodomainIsTime)); } } // _homomorphism+="|\n"; _homomorphism+=PrintDomain(H.codomain,Precision,CodomainIsTime); // return(_homomorphism); }
Примечательными входными параметрами здесь являются 'Precision' и 'IsTime'. Эти два параметра устанавливают десятичные разряды для отображения плавающих данных (по умолчанию для векторов) и определяют, необходимо ли преобразовывать данные объекта/вектора как время для целей представления в возвращаемой строке.
Для создания гомоморфизма мы будем использовать следующий скрипт:
//Declare sets to store time & close prices CDomain _time,_close; MqlRates _rates[]; //Fill domain with 5 most recent bar time & MA values from chart if(CopyRates(_Symbol,_Period,0,__domain_morphisms,_rates)>=__domain_morphisms && _time.Cardinality(__domain_morphisms) && _close.Cardinality(__domain_morphisms)) { for(int m=0;m<__domain_morphisms;m++) { //Create uni row element CElement _t,_m; if(_t.Cardinality(1) && _m.Cardinality(1)) { datetime _t_value=_rates[m].time;//iTime(_Symbol,_Period,m); _t.Set(0,double(int(_t_value))); _time.Set(m,_t); double _m_value=_rates[m].close;//iClose(_Symbol,_Period,5);//,m,MODE_SMA,PRICE_CLOSE); _m.Set(0,_m_value); _close.Set(m,_m); } } } //Create homomorphism from time to close CHomomorphism _h;_h.Init(_time,_close); if(_h.init) { //Create 1-1 morphisms from time to MA int _morphisms=0; for(int m=0;m<__domain_morphisms;m++) { if(_h.Cardinality(m,m)){ _morphisms++; } } if(_morphisms>=__domain_morphisms) { printf(__FUNCSIG__+" homomorphism: "+PrintHomomorphism(_h,_Digits,true)); } }
Мы создаем два множества - '_time' и "_close'. Затем мы заполняем их данными из массива MqlRates. '__set_morphisms' — это входной параметр, определяющий размер множества. В этом случае множества '"time' и "_close' имеют одинаковый размер и соответствуют входному параметру. Экземпляр класса гомоморфизма '_h" затем инициализируется этими двумя наборами. Простые взаимно-однозначные морфизмы создаются между двумя множествами с помощью функции 'Morphisms()'. Она проверяется, так как возвращает логическое значение. При true параметр '_morphisms' увеличивается. Как только мы получаем размер входного параметра, мы печатаем гомоморфизм '_h', используя функцию Print Homomorphism()'. В логах видим следующее:
2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) void OnStart() homomorphism: 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(2022.07.01 00:00),(2022.08.01 00:00),(2022.09.01 00:00),(2022.10.01 00:00),(2022.11.01 00:00)} 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) | 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.07.01 00:00)|----->(0.83922) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.08.01 00:00)|----->(0.86494) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.09.01 00:00)|----->(0.87820) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.10.01 00:00)|----->(0.86158) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.11.01 00:00)|----->(0.87542) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) | 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(0.83922),(0.86494),(0.87820),(0.86158),(0.87542)}
В теории категорий также может быть полезно перечислить множество изображений гомоморфизма. Изображение просто относится к подмножеству кодомена, в котором представлены только объекты, сопоставленные с доменом. Для наших целей мы можем сделать перечисление, используя функцию ниже:
//+------------------------------------------------------------------+ //| Image function | //+------------------------------------------------------------------+ void Image(CHomomorphism &H,CSet &Output) { for(int m=0;m<H.Morphisms();m++) { CObject _o; CMorphism _m; if(H.Get(m,_m) && H.codomain.Get(_m.codomain_index,_o)) { bool _matched=false; for(int o=0;o<Output.Objects();o++) { CObject _oo; if(Output.Get(o,_oo) && ObjectMatch(_o,_oo)) { _matched=true; break; } } if(!_matched) { Output.Objects(Output.Objects()+1); Output.Set(Output.Objects()-1,_o); } } } }
Чтобы увидеть этот код в действии, мы будем использовать следующий скрипт:
//Create homomorphism from time to close CHomomorphism _h_image;_h_image.Init(_time,_close); if(_h_image.init) { //Create 1-1 morphisms from time to MA int _morphisms=0; for(int m=0;m<__set_morphisms;m++) { int _random_codomain=MathRand()%__set_morphisms; if(_h_image.Morphisms(m,_random_codomain)){ _morphisms++; } } if(_morphisms>=__set_morphisms) { CSet _image;_image.Objects(0); Image(_h_image,_image); printf(__FUNCSIG__+" image from homomorphism: "+PrintSet(_image,_Digits)); } }
Все, что мы здесь делаем, — это используем два ранее созданных набора в новом классе гомоморфизма под названием '_h_image'. Разница на этот раз заключается в том, что при добавлении морфизмов мы случайным образом выбираем значения кодомена и таким образом получаем повтор. Это означает, что набор кодоменов будет отличаться от того, что указан в экземпляре '_h'. В логах видим следующие записи:
2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2) void OnStart() image from homomorphism: {(145.847),(145.188)}
2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2)
Очевидно, что кодомен имеет только два объекта из трех возможных, поэтому мы можем легко получить объекты, сопоставленные с заданным множеством. В следующей статье мы рассмотрим изоморфизмы и эндоморфизмы.
Заключение
Мы рассмотрели некоторые вводные понятия теории категорий - продуктивного математического метода классификации информации. Среди них были элемент, домен и морфизм. Элемент образует фундаментальную единицу и обычно рассматривается как член множества, которое в теории категорий называется доменом. Этот домен через свои элементы может иметь отношения с другими доменами (называемые кодоменами). Эти отношения называются морфизмами. Для трейдера теория категорий может служить классификатором финансовой информации о временных рядах, являясь, таким образом, инструментом оценки и прогнозирования рыночных условий.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/11849
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Рецепты MQL5 — База данных макроэкономических событий
Рецепты MQL5 — База данных макроэкономических событий
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования