MQL5 中的范畴论 (第 1 部分)
952
0
概述
范畴论是数学的一个分支，由艾伦伯格（Eilenberg）和麦克莱恩（Mac Lane）于 1940 年代赋予生命。 当爱因斯坦的相对论导致人们意识到没有单一视角来看待世界，但真正的力量在于能够在这些不同的视角之间进行转换，由此诞生了这一思路。因此，它作为一种分类形式，它并不详述被分类的对象本身，而是关注这些对象的内部关系，从而提炼出非常简洁的定义。 这种方式的重要性在于，从一个研究领域或学科中获取的概念可以是直观的，甚至可应用于不同的领域。 然而，在一开始，其主要用途是研究几何和代数之间的联系。 时至今日，这些用途显然超越了数学，所有内容对于本系列文章来说过于广泛，因此我们只详述它对于采用 MQL 编程语言的交易者的可能用途。
以 MQL5 编写智能系统，并进行交易的背景下，范畴论可用于分析和理解不同交易策略、工具和行情条件之间的关系。 它可以帮助交易者识别其交易系统中的常见形态和结构，并开发更加通用和灵活的交易算法，从而适应不断变化的市场条件。
范畴论也可验证交易系统的正确性和一致性，以及开发交易行为的正规模型。 提供清晰严谨的语言来表达和推理交易概念，范畴论可以帮助交易者编写更可靠和可维护的智能系统，并更有效地与其他交易者和研究人员交流他们的思路和策略。
域（Domains）和态射（Morphisms）
范畴域和态射（Morphisms）是范畴论的基本概念。 在范畴论中，范畴是元素的域（又名集合），以及态射（或箭头又名映射，又名函数）它们之间的集合。 在这些文章中，我们取箭头、函数或映射作为态射的基本单位。 这些态射针对范畴内每个域中的元素之间的关系进行编码，并且可将它们组合成更复杂的态射。
集合是数学中的基本概念，它们在范畴论中起着关键作用。 在范畴论中，我们将它们称为用于定义特定“种类”元素的域。 典型情况，如果我们研究域范畴，范畴的“元素”将是域本身。 这些域，通常但又并非总是，继续包含构成态射基础的其它元素。 此范畴中的态射将是域之间的函数，这些函数是一个域的每个元素与另一个域的唯一元素相关联的规则。 例如，如果我们有两个域 A 和 B，则从 A 到 B 的态射将是一个规则，它将 A 的每个元素分配给 B 的唯一元素。当态射从 A 转运到 B 时，A 被称为“本域”，而 B 是“协域”。 本域中的所有元素都将与协域中的至少一个元素有关系。 本域中的任何元素都不会保持“未映射”状态。 然而，协域中的某些元素可能是“未映射”的。 这经常表示如下。
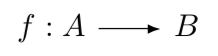
//+------------------------------------------------------------------+ //| ELEMENT CLASS | //+------------------------------------------------------------------+ class CElement { protected: int cardinal; vector element; public: bool Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; element.Init(cardinal); return(true); } return(false); } int Cardinality() { return(cardinal); } double Get(int Index) { if(Index>=0 && Index<Cardinality()) { return(element[Index]); } return(EMPTY_VALUE); } bool Set(int Index,double Value) { if(Index>=0 && Index<Cardinality()) { element[Index]=Value; return(true); } return(false); } CElement(void) { Cardinality(0); }; ~CElement(void) {}; };
故此，从上面的清单中，我们可以从定义一个元素开始。 这是一个域的基本单位，您可以把它当作一个“集合的成员”。 该单元可以采用任何数据类型，无论是双精度型还是整数型，不过若要满足更复杂的数据类型和运算时，向量类型将更加灵活。 它允许可扩展性。 其大小，'cardinal' 参数受到保护，只能通过 Cardinality()' 函数访问或修改。 保护其访问可确保无论何时修改向量，都会相应调整其大小。 向量 “element” 本身也受到保护，以防止无效的索引错误。 故此，仅允许通过 “Get()” 和 “Set()” 函数进行访问。 'Set()' 函数还返回一个布尔值来验证赋值是否成功。
//+------------------------------------------------------------------+ //| DOMAIN CLASS | //+------------------------------------------------------------------+ class CDomain { protected: int cardinal; CElement elements[]; public: bool Cardinality(int Value) { if(Value>=0 && Value<INT_MAX) { cardinal=Value; ArrayResize(elements,cardinal); return(true); } return(false); } int Cardinality() { return(cardinal); } bool Get(int Index,CElement &Element) { if(Index>=0 && Index<Cardinality()) { Element=elements[Index]; return(true); } return(false); } bool Set(int Index,CElement &Value,bool IsNew=false) { if(Index>=0 && Index<Cardinality()) { if(!IsNew||New(Value)<0) { elements[Index]=Value; return(true); }} return(false); } //only unique elements allowed int New(CElement &Value) { bool _new=-1; // for(int o=0; o<cardinal; o++) { if(ElementMatch(Value,elements[o])) { _new=o; break; } } return(_new); } CDomain(void) { Cardinality(0); }; ~CDomain(void) {}; };
因此，其内包括元素的域类，已在上面介绍过了。 它的主要变量 “elements[]” 和它的大小 “cardinal” 如同上述在元素类中一样受到保护。 这里略有不同的是添加了 “New()” 方法。 该函数帮助检查所要添加到域中的新对象，并确保它们的唯一性。 范畴域仅包含唯一对象。 不允许有重复。
由于我们有这两个类，我们可以尝试构造一些域。 我们来尝试一个偶数和一个奇数域。 我们可以运行一个脚本来引用这些类。 脚本清单如下所示。
//+------------------------------------------------------------------+ //| INPUTS | //+------------------------------------------------------------------+ input int __domain_elements=3; input int __domain_morphisms=5; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //Declare a sets of natural even & odd numbers CDomain _evens,_odds; CreateNumberDomain(_evens,__domain_elements,2); CreateNumberDomain(_odds,__domain_elements,2,1); printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens)); printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds)); }
创建数字函数是一种使用自然数填充域的简单方法。 所有代码都附在文末，但为清楚起见，此处展示出它的设置。
'PrintSet()' 函数是我们经常提到的一种资源丰富的方法。 它简单地令我们能使用相应的括号和逗号查看域的内容，精心将元素向量结构与整体域结构分离。 如果我们运行上面的脚本，这就是我们应该看到的。
2022.12.08 18:49:13.890 ct_1 (EURGBP.ln,MN1) void OnStart() odds are... {(1.0),(3.0),(5.0),(7.0),(9.0),(11.0),(13.0)}
在括号中都是每个域的各种元素，因为它们是向量数据类型，这意味着它们本身可以有多个条目。 若发生这种情况时，在每个带有括号的条目之间出现逗号，如此来帮助定义元素边界的位置。
态射也是范畴论中的一个重要概念，它们为域中元素之间的关系进行编码。 根据范畴论规则，每个态射将域中的一个元素映射到协域中的一个元素。 这些函数可以组合成更复杂的态射，它们可以用来研究集合的性质，以及它们与其它集合的关系，正如我们将看到的。
通览伊始，态射有 5 种主要类型，可用于描述给定类别中对象之间的关系。 一些最常见的类型是：
- 单态：这些是单射（injective）态射，这意味着它们将源域中的每个元素映射到协域中的唯一对象。 不会有两个态射映射到协域中的同一对象。 在这种情况下，您也许有一些对象在目标中无映射。
- 表态：这些是漫射（surjective）态射，这意味着域中的元素映射到协域中的所有元素。 换言之，协域中没有任何元素会保持无映射。 在这种实例下，协域中的元素通常少于源集合中的元素。
- 同构：同构是双射（bijective）态射，这意味着它们在源和目标范畴中的对象之间建立一对一的对应关系。 它们既是单射的，也是漫射的，因为源集合和目标集合具有相同数量的对象。
- 自同态：自同态是从元素到自身的态射。 它构成了一个恒等映射，即一组链接回域的自同态。
- 自同构：自同构是同构和自同态的映射组合。
我们看看如何以 MQL 实现态射类，以及它与域的分组作为同态。
//+------------------------------------------------------------------+ //| MORPHISM CLASS | //+------------------------------------------------------------------+ class CMorphism { public: int domain; int codomain; CElement morphism; bool Morph(CDomain &D,CDomain &C,CElement &DE,CElement &CE,bool Add=true) { int _d=D.New(DE),_c=C.New(CE); // if(_d>=0 && _c>=0) { if(DE.Cardinality()==CE.Cardinality()) { domain=_d; codomain=_c; morphism.Cardinality(DE.Cardinality()); if(Add) { for(int c=0;c<morphism.Cardinality();c++) { morphism.Set(c,CE.Get(c)-DE.Get(c)); } } else { for(int c=0;c<morphism.Cardinality();c++) { if(DE.Get(c)!=0.0){ morphism.Set(c,CE.Get(c)/DE.Get(c)); } } } } } return(false); } CMorphism(void){ domain=-1; codomain=-1; }; ~CMorphism(void){}; };
态射类是非常基本的，只有域和协域索引参数以及一个 “Morph” 函数，本文当中我们不会关注该函数。 此处省略了对相应域集合和协域集合的引用，因为它们列在伞形同态类中，如下所示。
//+------------------------------------------------------------------+ //| HOMO-MORPHISM CLASS | //+------------------------------------------------------------------+ class CHomomorphism { protected: int cardinal; CMorphism morphism[]; public: bool init; CDomain domain; CDomain codomain; bool Cardinality(int DomainIndex,int CodomainIndex,bool Add=true) { bool _morphed=true; if ( !init ) { _morphed=false; return(_morphed); } if ( DomainIndex<0 || DomainIndex>=domain.Cardinality() || CodomainIndex<0 || CodomainIndex>=codomain.Cardinality() ) { _morphed=false; return(_morphed); } for(int m=0;m<cardinal;m++) { if(DomainIndex==morphism[m].domain) { _morphed=false; break; } } if(_morphed) { cardinal++; ArrayResize(morphism,cardinal); CElement _de,_ce; if(domain.Get(DomainIndex,_de) && codomain.Get(CodomainIndex,_ce)) { morphism[cardinal-1].Morph(domain,codomain,_de,_ce,Add); } } return(_morphed); }; int Cardinality() { return(cardinal); }; bool Get(int Index,CMorphism &Morphism) { if(Index>=0 && Index<Cardinality()) { return(true); } return(false); }; bool Set(int Index,CMorphism &Value) { if ( Index>=0 && Index<Cardinality() && Value.domain>=0 && Value.domain<domain.Cardinality() && Value.codomain>=0 && Value.codomain<codomain.Cardinality() ) { if(!MorphismMatch(Index,Value,morphism,Cardinality())) { morphism[Index]=Value; return(true); } } return(false); }; void Init(CDomain &Domain,CDomain &Codomain) { domain=Domain; codomain=Codomain; init=true; } CHomomorphism(void){ init=false; cardinal=0; }; ~CHomomorphism(void){}; };
在同态类中，“morphism[]” 变量及其大小 “morphisms” 由于上述原因而受到保护，我不再啰嗦。 可以说，两个 “Morphism()” 函数和 “Get()” 和 “Set()” 函数遵循类似于对象和集合类中的函数风格。 这里添加了一个 “init” 布尔参数，该参数指示类是否已进行初始化，即分配公开的 “domain” 和 “codomain” 集合。 将态射添加到受保护的 “morphism[]” 数组是通过提供域索引和协域索引来实现的。 这些索引需要限定在其各自的域大小范围内。 一旦它们传递到这里，就需要检查域索引是否没有被实际用过。 根据范畴论的规则，域中的所有对象都必须映射到协域中的对象，但它们只能映射一次。 故此，协域索引可以使用两次，但域索引只能使用一次。
我们稍微离题一点，看看子域（又名： 子集）。 子域是范畴论中有用的工具，其能力是列举域内的子域，并检查域是否是给定域的可能子域，这可能是一个资源非常丰富的工具。 我们来看一下完成这两项任务的函数。
//+------------------------------------------------------------------+ //| Domain Match function | //+------------------------------------------------------------------+ bool DomainMatch(CDomain &A,CDomain &B) { if(A.Cardinality()!=B.Cardinality()) { return(false); } bool _matched=true; for(int o=0; o<A.Cardinality(); o++) { CElement _a,_b; if(A.Get(o,_a) && B.Get(o,_b) && !ElementMatch(_a,_b)) { _matched=false; break; } } return(_matched); } //+------------------------------------------------------------------+ //| Is Subdomain function | //+------------------------------------------------------------------+ bool IsSubdomain(CDomain &Domain,CDomain &SubDomain) { bool _is_subdomain=false; int _subdomain_count=0; CDomain _subdomains[]; GetSubdomains(Domain,_subdomain_count,_subdomains); for(int c=0;c<_subdomain_count;c++) { if(DomainMatch(SubDomain,_subdomains[c])) { _is_subdomain=true; break; } } return(_is_subdomain); }
因此，如果我们运行下面的脚本：
//+------------------------------------------------------------------+ //| INPUTS | //+------------------------------------------------------------------+ input int __domain_elements=3; input int __domain_morphisms=5; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //Declare a sets of natural even & odd numbers CDomain _evens,_odds; CreateNumberDomain(_evens,__domain_elements,2); CreateNumberDomain(_odds,__domain_elements,2,1); printf(__FUNCSIG__+" evens are... "+PrintDomain(_evens)); printf(__FUNCSIG__+" odds are... "+PrintDomain(_odds)); int _subdomain_count=0; CDomain _subdomains[]; GetSubdomains(_evens,_subdomain_count,_subdomains); printf(__FUNCSIG__+" evens subs are... "+IntegerToString(_subdomain_count)); for(int s=0; s<_subdomain_count; s++) { printf(" with: "+PrintDomain(_subdomains[s])+", at: "+IntegerToString(s+1)); } }
它应该给我们出示这些日志：
2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) void OnStart() evens subs are... 7 2022.12.08 20:25:21.314 ct_1 (EURGBP.ln,MN1) with: {(2.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 1 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 2 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 3 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 4 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 5 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(4.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 6 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) with: {(2.0),(4.0),(6.0)} 2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) , at: 7
如果我们把空集也算作子集，则可能子集的实际数量为 8。
可以按如下所示编写附加检查子集的代码：
CDomain _smaller_evens; CreateNumberDomain(_smaller_evens,__domain_elements-2,2); printf(__FUNCSIG__+" smaller evens are... "+PrintDomain(_smaller_evens)); bool _is_subdomain=IsSubdomain(_evens,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of evens. "); _is_subdomain=IsSubdomain(_odds,_smaller_evens);printf(__FUNCSIG__+" it is: "+string(_is_subdomain)+" that 'smaller-evens' is a subdomain of odds. ");
其日志应该产生如下结果：
2022.12.08 20:25:21.315 ct_1 (EURGBP.ln,MN1) void OnStart() smaller evens are... {(2.0)} 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: true that 'smaller-evens' is a subset of evens. 2022.12.08 20:25:21.316 ct_1 (EURGBP.ln,MN1) void OnStart() it is: false that 'smaller-evens' is a subset of odds.
在范畴论中，同态是两个域之间一组态射的结构保持定义。 它是一个保留元素的关系和操作定义的函数。 同态在范畴论中很重要，因为它们提供了一种研究不同元素之间关系的方法，以及从现有元素构建新元素的方法。
考虑到元素之间的同态，可以深入了解元素的性质，及其在不同操作下的行为。 例如，两个域之间存在同态，可定义它们之间的等价概念，从而允许研究它们之间的关系。
范畴论中同态的另一个意义是，它们提供了一种通过继承这些属性从现有对象构建新对象的方法。 这些示例以及等价性将在后续文章中介绍，此处仅提及这些示例，以便为定义这个看似“无用”的类奠定基础。
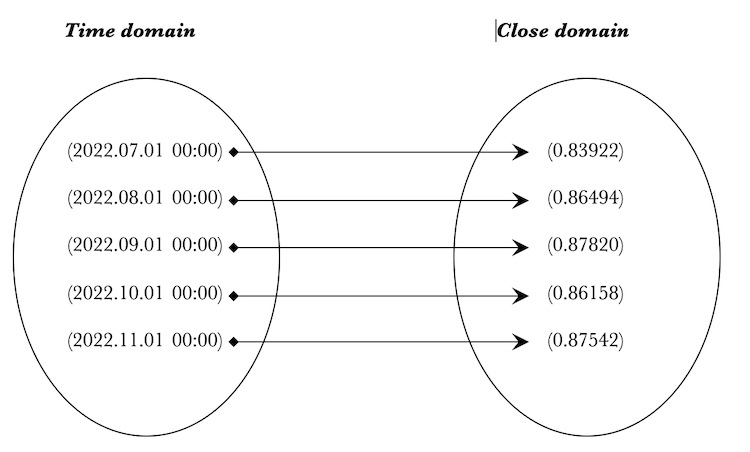
我们来尝试创建一个同态类的实例，含有时间和收盘价集合的域和协域，令范畴论更生动。
然后，我们调用 'PrintHomomorphism()' 函数查看此实例。 这些自定义打印函数在查看创建的对象、集合、态射和同态时非常有用。 此为清单:
//+------------------------------------------------------------------+ //| Print Element function | //+------------------------------------------------------------------+ string PrintElement(CElement &O,int Precision=1,bool IsTime=false) { string _element="("; // for(int r=0; r<O.Cardinality(); r++) { if(!IsTime) { _element+=DoubleToString(O.Get(r),Precision); } else if(IsTime) { _element+=TimeToString(datetime(int(O.Get(r)))); } if(r<O.Cardinality()-1){ _element+=","; } } // return(_element+")"); } //+------------------------------------------------------------------+ //| Print Set function | //+------------------------------------------------------------------+ string PrintDomain(CDomain &S,int Precision=1,bool IsTime=false) { string _set="{"; // CElement _e; for(int o=0; o<S.Cardinality(); o++) { S.Get(o,_e); _set+=PrintElement(_e,Precision,IsTime);if(o<S.Cardinality()-1){ _set+=","; } } // return(_set+"}\n"); } //+------------------------------------------------------------------+ //| Print Morphism function | //+------------------------------------------------------------------+ string PrintMorphism(CMorphism &M, CDomain &Domain,CDomain &Codomain,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false) { string _morphism=""; // CElement _d,_c; if(Domain.Get(M.domain,_d) && Codomain.Get(M.codomain,_c)) { _morphism=PrintElement(_d,Precision,DomainIsTime); _morphism+="|----->"; _morphism+=PrintElement(_c,Precision,CodomainIsTime); _morphism+="\n"; } // return(_morphism); } //+------------------------------------------------------------------+ //| Print Homomorphism function | //+------------------------------------------------------------------+ string PrintHomomorphism(CHomomorphism &H,int Precision=1,bool DomainIsTime=false,bool CodomainIsTime=false) { string _homomorphism="\n\n"+PrintDomain(H.domain,Precision,DomainIsTime); // _homomorphism+="|\n"; CMorphism _m; for(int m=0;m<H.Cardinality();m++) { if(H.Get(m,_m)) { _homomorphism+=(PrintMorphism(_m,H.domain,H.codomain,Precision,DomainIsTime,CodomainIsTime)); } } // _homomorphism+="|\n"; _homomorphism+=PrintDomain(H.codomain,Precision,CodomainIsTime); // return(_homomorphism); }
这里值得注意的输入是 “Precision” 和 “IsTime”。 这两个设置小数位以便显示浮点数据（向量的默认值），以及是否需要将对象/向量数据转换为时间，以便在返回的字符串中表示。
因此，为了创建我们的同态，我们将使用此脚本：
//Declare sets to store time & close prices CDomain _time,_close; MqlRates _rates[]; //Fill domain with 5 most recent bar time & MA values from chart if(CopyRates(_Symbol,_Period,0,__domain_morphisms,_rates)>=__domain_morphisms && _time.Cardinality(__domain_morphisms) && _close.Cardinality(__domain_morphisms)) { for(int m=0;m<__domain_morphisms;m++) { //Create uni row element CElement _t,_m; if(_t.Cardinality(1) && _m.Cardinality(1)) { datetime _t_value=_rates[m].time;//iTime(_Symbol,_Period,m); _t.Set(0,double(int(_t_value))); _time.Set(m,_t); double _m_value=_rates[m].close;//iClose(_Symbol,_Period,5);//,m,MODE_SMA,PRICE_CLOSE); _m.Set(0,_m_value); _close.Set(m,_m); } } } //Create homomorphism from time to close CHomomorphism _h;_h.Init(_time,_close); if(_h.init) { //Create 1-1 morphisms from time to MA int _morphisms=0; for(int m=0;m<__domain_morphisms;m++) { if(_h.Cardinality(m,m)){ _morphisms++; } } if(_morphisms>=__domain_morphisms) { printf(__FUNCSIG__+" homomorphism: "+PrintHomomorphism(_h,_Digits,true)); } }
我们创建两个集合 “_time” 和 “_close”。 然后，我们用来自 MqlRates 数组的数据填充它们。 '__set_morphisms' 是确定设置大小的输入参数。 在这种情况下，“time” 和 “_close” 集合的大小相同，并且它们与输入参数匹配。 然后用这两个集合初始化同态类实例 '_h”。 调用 “Morphisms()” 函数在两个集合之间创建简单的一对一态射，可检查该函数结果，因为它返回一个布尔值。 若为 true，则 '_morphisms' 参数将递增，一旦我们达到输入参数的大小，我们就调用 ‘Print Homomorphism()' 函数打印同态 '_h'。 我们的日志应该产生这个：
2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) void OnStart() homomorphism: 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(2022.07.01 00:00),(2022.08.01 00:00),(2022.09.01 00:00),(2022.10.01 00:00),(2022.11.01 00:00)} 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) | 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.07.01 00:00)|----->(0.83922) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.08.01 00:00)|----->(0.86494) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.09.01 00:00)|----->(0.87820) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.10.01 00:00)|----->(0.86158) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) (2022.11.01 00:00)|----->(0.87542) 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) | 2022.12.08 20:25:21.317 ct_1 (EURGBP.ln,MN1) {(0.83922),(0.86494),(0.87820),(0.86158),(0.87542)}
在范畴理论中，列举同态的集合图像也需要应对自如。 图像仅指协域的子集，该子集仅含有从域映射的对象。 出于我们的目的，我们可用以下函数列举它：
//+------------------------------------------------------------------+ //| Image function | //+------------------------------------------------------------------+ void Image(CHomomorphism &H,CSet &Output) { for(int m=0;m<H.Morphisms();m++) { CObject _o; CMorphism _m; if(H.Get(m,_m) && H.codomain.Get(_m.codomain_index,_o)) { bool _matched=false; for(int o=0;o<Output.Objects();o++) { CObject _oo; if(Output.Get(o,_oo) && ObjectMatch(_o,_oo)) { _matched=true; break; } } if(!_matched) { Output.Objects(Output.Objects()+1); Output.Set(Output.Objects()-1,_o); } } } }
为了查看此代码的实际效果，我们用到此脚本：
//Create homomorphism from time to close CHomomorphism _h_image;_h_image.Init(_time,_close); if(_h_image.init) { //Create 1-1 morphisms from time to MA int _morphisms=0; for(int m=0;m<__set_morphisms;m++) { int _random_codomain=MathRand()%__set_morphisms; if(_h_image.Morphisms(m,_random_codomain)){ _morphisms++; } } if(_morphisms>=__set_morphisms) { CSet _image;_image.Objects(0); Image(_h_image,_image); printf(__FUNCSIG__+" image from homomorphism: "+PrintSet(_image,_Digits)); } }
我们在这里所做所有事就是在一个名为 '_h_image' 的新同态类中使用之前创建的两个集合。 这次的区别在于，当添加态射时，我们随机选择共域值，故此会有重复。 这意味着协域集合将与 “_h” 实例中的协域集合不同。 我们的日志应该产生这样：
2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2) void OnStart() image from homomorphism: {(145.847),(145.188)}
2022.12.08 21:55:54.568 ct_1 (EURJPY.ln,H2)
显然，协域只有可能的三个对象中的两个对象，因此我们可以轻松地从给定集合中检索映射到的对象。 我们将在下一篇文章离继续从同构和自同态开始。
结束语
我们已经研究了范畴论的一些入门级概念，这是数学中用于对信息进行分类的一种越来越应对自如的方法。 其中包括一个元素、一个域和一个态射。 元素形成基本单元，它通常被认为是集合的成员，在范畴论中称为域。 本域通过其元素可以与其它域（称为协域）建立关系。 这些关系称为态射。 对于交易者来说，范畴论可以作为时间序列财经信息的分类器，从而作为评估和预测市场状况的工具。 我们将在下一篇文章里从此处继续。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/11849
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
矩阵实用工具，扩展矩阵和向量的标准库功能
种群优化算法：鱼群搜索（FSS）
DoEasy. 控件（第 二十九 部分）：滚动条（ScrollBar）辅助控件
