MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português Türkçe
preview
パターン検索への総当たり攻撃アプローチ(第IV部): 最小限の機能

パターン検索への総当たり攻撃アプローチ(第IV部): 最小限の機能

MetaTrader 5 — テスター | 25 5月 2021, 09:35
1 118 0
Evgeniy Ilin
Evgeniy Ilin
本稿では、最小限の機能を取得し、取引の作業設定を抽出できる新バージョンの製品を紹介します。変更は主に、使いやすさの向上と最小エントリしきい値の改善を目的としています。主な目標は、設定の検索と市場調査にできるだけ多くのユーザーを引き付けることのままです。取引の詳細を議論する代わりに、可能な限り多くの有用な情報を提供します。この方法の使い方をわかりやすく説明し、長所と短所を説明し、実用化の見通しを考えていきます。


新バージョンでの変更

前回の記事と同様に、プログラムは機能性と使いやすさの点で大幅に改善されています。以前のバージョンは非常に不便で、さまざまな不具合やエラーがありました。このバージョンには最大限の変更が含まれています。エキスパートアドバイザーテンプレートとソフトウェアを最新化するために多くのことが行われました。次は変更点のリストです。

  1. インターフェイスを再設計
  2. 総当たり攻撃の別の多項式を追加(改訂されたフーリエ級数に基づく)
  3. 乱数生成メカニズムを強化
  4. メソッドの概念を利便性と使いやすさに向けて拡張
  5. 超短セクションのロット変動メカニズムを追加
  6. スプレッド計算メカニズムを追加
  7. スプレッドノイズを低減するメカニズムを追加
  8. バグ修正

以前に計画されていた変更のほとんどが実装されました。それ以上のアルゴリズムの修正はそれほど重要ではありません


最初のデモンストレーションと新しい概念

EAを作成しているときに、常にEA名を作成して多数の設定を処理するのは難しいかもしれないことに気づきました。名前が重複したり、設定が混乱したりする場合があります。この問題の解決策は、エキスパートアドバイザーが設定を受け取ることです。プログラムは通常のtxt形式で構成ファイルを生成でき、エキスパートアドバイザーがそれを読み取ります。このアプローチにより、このソリューションでの作業がスピードアップし、よりシンプルで理解しやすくなります。ソリューションスキームは次のようになります。

Forex Awaiterの使用法


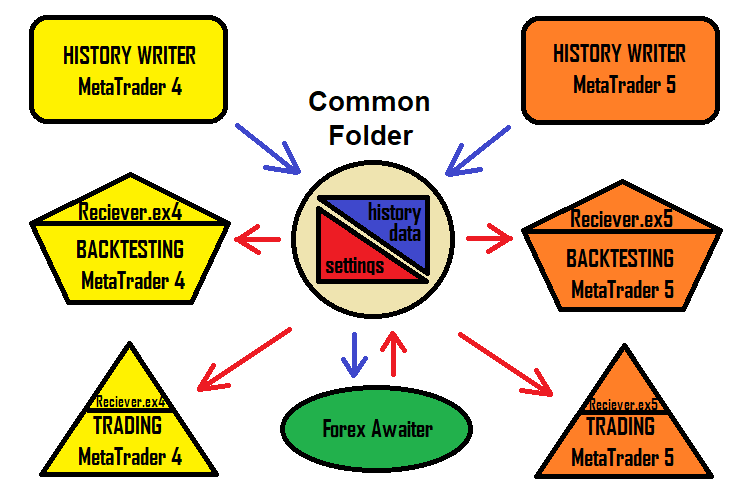
もちろん、ロボットを生成するプログラムのバージョンは引き続き利用できます。しかし、この記事では、MetaTrader 4およびMetaTrader 5ターミナルのために特別に発明された新しい概念を説明しています。それは一般ユーザーがこのソリューションを可能な限り簡単かつ迅速に利用し始めることを可能にするものです。このソリューションの最も便利な部分は、設定がMetaTrader 4とMetaTrader 5で同じように機能することです。

新しいインターフェイスは非常に大きく記事でスペースをとりすぎるため、一部のみを示します。これが最初のタブです。

新しいAwaiterインターフェイス


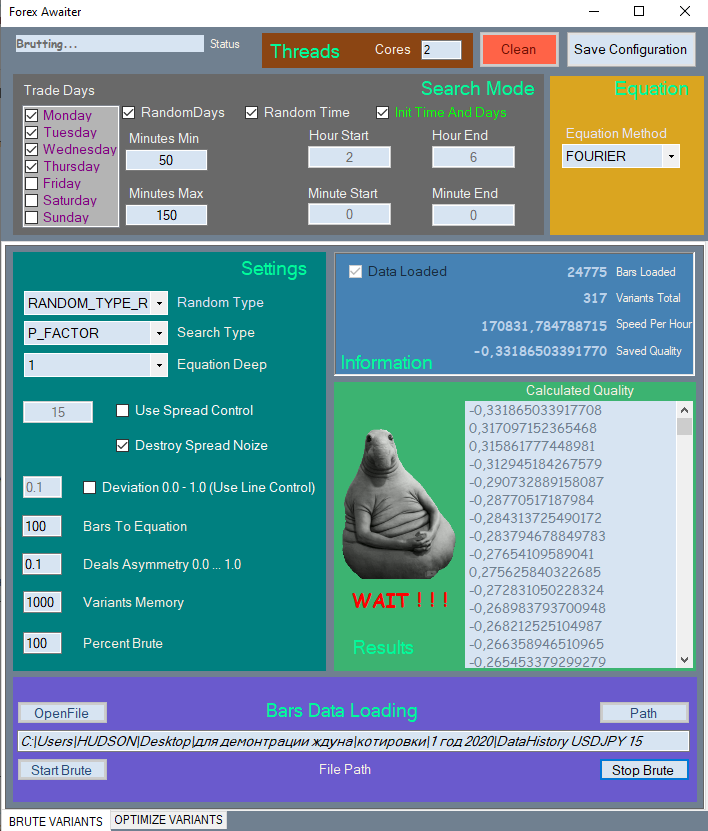
ナビゲーションを容易にするために、すべての要素は対応するセクションに分割されています。未使用の要素は、使用しても意味がない場合はブロックされます。

プログラムの操作を紹介する特別なビデオを作成しました。



通常のセットファイルで設定を渡すことができないのはなぜでしょうか。このメソッドは入力として浮動長の配列を使用するが、セットファイルに配列を含めることはできないためです。この場合、最も便利な解決策は通常のテキストファイルを使用することです。


修正されたフーリエ級数に基づく新しい多項式

機械学習に精通している多くの人々は、さまざまな目的でアルゴリズムにフーリエ級数を積極的に使用しています。フーリエ級数は元々、関数を[-π;π]の範囲の級数に分解するために作成されました。ここで知る必要があるのは、関数を級数に分解する方法と、そのような分解が必要かどうかです。さらに、分解は[-π; π]ではなく異なる間隔で実行できるため、変数置換方法の詳細を知ることが重要です。これにはすべて、数学の十分な知識と、それを取引に使用する目的があるかどうかの理解が必要です。フーリエ級数の一般的な見方は次のとおりです。

フーリエ級数の概観

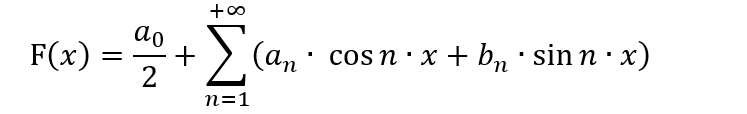
この形式では、この多項式は、取引パターンをより便利な形式で提示する場合、および価格が波のプロセスであると仮定して価格の動きを予測する場合にのみ役立ちます。この仮定は有効であるように見えますが、この場合、手法の概念全体を根本的に変更する必要があるため、この形式では総当たり攻撃には適用できません。代わりに、この手法に適用できるように多項式を変換します。多くのバリエーションがありますが、数式を本来の目的に使用せずにフーリエ級数に近づけるために、次のようにすることをお勧めします。

最初の変換

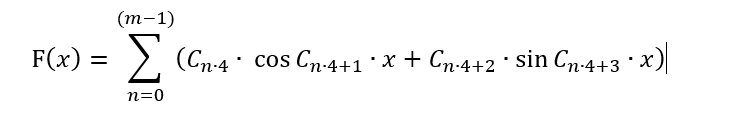
ここでは、級数の自由度が高いことを除いて、何も変更されていません。その期間はプラスとマイナスの両方で変動しています。また、現在、項の数には限りがあります。これは、適切な式を見つけるために組み合わせる係数が配列C[]に含まれているためです。そのような係数の数は限られています。この級数は無限ではないため、「m」バーに制限する必要があります。また、対称性を維持するために最初の項を削除しました。数式値は、「+」と「-」の範囲で最も対称的なシグナルを生成するはずです。しかし、この方法は、1バーに依存する機能を選択するためにのみ使用できます。すべてのバーの値が数式で使用できることを確認する必要があります。さらに、バーには1つではなく6つのパラメータがあります。これらの6つのパラメータは、この連載の2番目の記事で検討されました。ここでは、残りのすべてのバーを考慮に入れるために、1つのバーの処理精度を犠牲にする必要があります。理想的には、この量は別の量に包まれるべきですが、多項式を複雑にしたくないので、今のところ最も単純なバージョンを使用します。

最終多項式

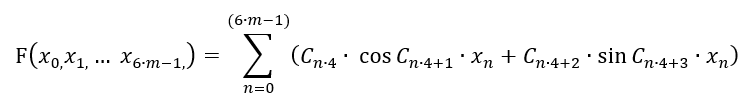
実際、1次元関数は多次元関数に変わりましたが、この多項式が選択された多次元超立方体の任意の多次元関数を記述できるわけではありません。とにかく、この関数は、テイラー級数では適切にカバーできない他の規則性を記述することができる別の種類の多次元関数を提供します。これにより、同じデータサンプルでより適切なパターンを見つける可能性が高くなります。 

コードでは、この関数は次のようになります。

if ( Method == "FOURIER" )
   {
      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(Close[i+1]-Open[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Close[i+1]-Open[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(High[i+1]-Open[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(High[i+1]-Open[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(Open[i+1]-Low[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Open[i+1]-Low[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(High[i+1]-Close[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(High[i+1]-Close[i+1])/_Point);
         iterator+=4;
         }

      for ( int i=0; i<CNum; i++ )
         {
         Val+=C1[iterator]*MathSin(C1[iterator+1]*(Close[i+1]-Low[i+1])/_Point)+C1[iterator+2]*MathCos(C1[iterator+3]*(Close[i+1]-Low[i+1])/_Point);
         iterator+=4;
         }         

   return Val;
   }

これは関数全体ではなく、多項式を実装する部分だけです。単純であるにかかわらず、そのような式でさえ市場には適応可能です。

この式が機能することを示すために、この方法を使用して、昨年の履歴データに対して非常に高速な総当たり攻撃を実行しました。ただし、それがうまく機能するかどうかを確認する必要があります。実際、この式を使用して本当に効率的な解決策を見つけることができなかったのですが、それは時間とコンピューティング能力の問題だと思います。最初のバージョンでは多くの時間を費やしました。これは、昨年1念の履歴のUSDJPY M15で達成できた結果です。

フーリエ法


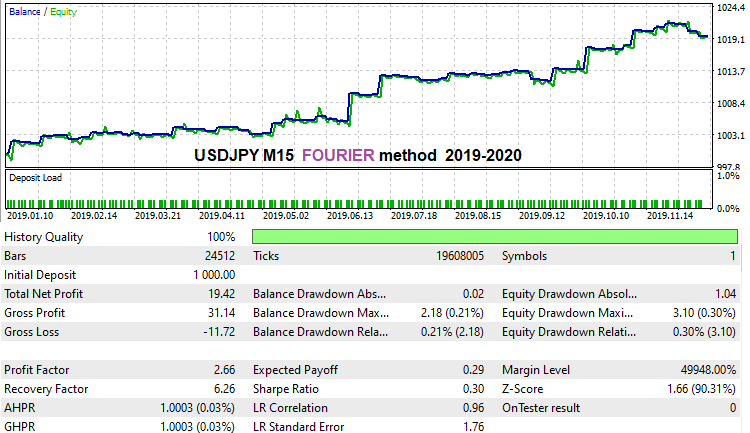
この式について気に入らなかったのは、スプレッドによるノイズ抑制の点で非常に不安定であるということです。おそらくこれは、この方法の枠組み内の調和関数の詳細に関連しています。おそらく、定式化に間違えがあったのだと思います。2番目のタブのスプレッド制御オプションを必ず有効にしてください。これにより、最適化中にスプレッドノイズ抑制メカニズムが無効になり、非常に優れたバリアントが生成されます。おそらく、式は非常に「穏やか」ですが、それでもかなり良いバリアントを見つけることができます。


内部からのソフトウェア実装について

これらの質問は、私の以前の記事ではほとんど取り上げられていませんでしたが、この部分を明らかにして、内部からどのように機能するかを示すことにしました。最も興味深く簡単な部分は、数式の係数を生成することです。この部分の説明は、係数がどのように生成されるかを理解するのに役立ちます。

public void GenerateC(Tester CoreWorker)
   {
   double RX;
   TYPE_RANDOM RT;
   RX = RandomX.NextDouble();
   if (RandomType == TYPE_RANDOM.RANDOM_TYPE_R) RT = (TYPE_RANDOM)RandomX.Next(0, Enum.GetValues(typeof(TYPE_RANDOM)).Length-1);
   else RT = RandomType;

   for (int i = 0; i < CoreWorker.Variant.ANum; i++)
      {
      if (RT == TYPE_RANDOM.RANDOM_TYPE_0) 
         {
         if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i-1]*RandomX.NextDouble();
         else CoreWorker.Variant.Ci[0]=1.0;
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_5)
         {
         if (RandomX.NextDouble() >= 0.5)
            {
            if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i - 1] * RandomX.NextDouble();
            else CoreWorker.Variant.Ci[0] = 1.0;
            }
         else
            {
            if (i > 0) CoreWorker.Variant.Ci[i] = CoreWorker.Variant.Ci[i - 1] * (-RandomX.NextDouble());
            else CoreWorker.Variant.Ci[0] = -1.0;
            }
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_1) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
      if (RT == TYPE_RANDOM.RANDOM_TYPE_2)
         {
         if (RandomX.NextDouble() >= 0.5) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
         else CoreWorker.Variant.Ci[i] = -RandomX.NextDouble();
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_3)
         {
         if (RandomX.NextDouble() >= RX)
            {
            if (RandomX.NextDouble() >= RX + (1.0 - RX) / 2.0) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
            else CoreWorker.Variant.Ci[i] = -RandomX.NextDouble();
            }
         else CoreWorker.Variant.Ci[i] = 0.0;
         }
      if (RT == TYPE_RANDOM.RANDOM_TYPE_4)
         {
         if (RandomX.NextDouble() >= RX) CoreWorker.Variant.Ci[i] = RandomX.NextDouble();
         else CoreWorker.Variant.Ci[i] = 0.0;
         }
      }
   }

非常に単純です。乱数生成にはいくつかの固定タイプがあり、すべてを一度に実装する一般的なタイプがあります。各生成タイプは実際にテストされています。一般的な生成タイプ「RANDOM_TYPE_R」が最大の効率を示していることがわかりました。さまざまな商品や時間枠での相場の性質が異なるため、固定タイプで常に結果が得られるとは限りません。視覚的には、ほとんどの場合、これらの違いはわかりませんが、マシンはすべてを認識します。固定タイプの中には、一部の時間枠でより多くの最高品質のシグナルを提供するものもありますが、たとえば、NZDUSD H1では、RANDOM_TYPE_4を使用すると、結果の品質が急激に上昇することに気付きました。これは、「ゼロと正の数のみ」を意味します。これは、目にアクセスできない隠れた波のプロセスの明確なヒントかもしれません。さまざまな商品について詳しく調べたいのですが、一人で行うのは難しいです。


スプレッドのノイズと戦い、スプレッドを説明するための新しいメカニズム

前の記事で述べたように、スプレッドは価格データを歪め、見つかったパターンのほとんどがスプレッド内にあるようにします。ほとんどのストラテジーではスプレッドをカバーするために十分な数学的期待値を提供できないため、スプレッドはストラテジーの最悪の敵でもあります。このデータサンプルは小さすぎて将来のパフォーマンスを評価できないため、実口座のバックテストや肯定的な取引統計にだまされてはいけません。「ナイトスキャルパー」と呼ばれる別のクラスの取引ストラテジーと自動取引システムがあります。これらのロボットは、限られた期間でわずかな利益を得ます。証券会社は深夜以降にスプレッドを拡大することで、このようなシステムと積極的に戦っています。スプレッドは、ほとんどのストラテジーが不採算になるようなレベルに設定されています。

ほとんどの証券会社でほぼ同じ値が1つあります。

  • Spread = (Ask - Bid) / _Point
  • MidPrice = ( Ask + Bid ) / 2

この価格は緑色で強調表示されていて、取引板の真ん中です。取引板は通常、この価格に対して並べられており、両方の価格はこの価格から等距離にあります。実際、取引板の古典的な定義を見ると、この価格では取引注文がないため意味がありません。すべての証券会社が独自のスプレッドを持っていると仮定しても、この価格はすべての証券会社でほぼ同じになる可能性があります。以下が図です。

スプレッド

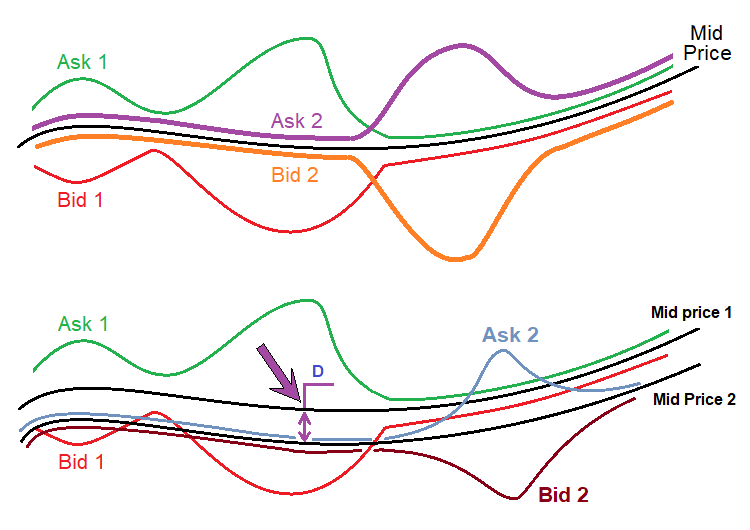
上の図は、ランダムに選択された証券会社2社の価格シリーズを示しています。売買価格を象徴する「売呼値」と「買呼値」は常にあります。黒い線は両方の価格帯で同じです。上に示したように、この価格は簡単に計算できます。最も重要なことは、すべての変更が特定の価格に対してほぼ均等であるため、この値は特定の証券会社のスプレッドの拡大や縮小に実質的に依存しないということです。

下の図は、さまざまな証券会社からの相場で実際に発生する実際の状況を示しています。問題は、この平均価格でさえ、ストリームごとに異なるということです。理由は分かりませんし、分かったとしても、取引にはほとんど役に立ちません。これらすべてのニュアンスが非常に重要である裁定取引を実践していたときに、この事実を発見しました。ここでの手法に関連して、それは重要です。

  • MidPrice1=f(t)
  • MidPrice2=MidPrice1-D
  • MidPrice1 '(t) =  MidPrice2 '(t)

言い換えると、両方の価格系列の平均価格(時間関数として表されている場合)は、定数「D」のみが異なるため、同じ導関数を持ちます。ここでの多項式は価格ではなく価格差を使用するため、すべての値はこれらの平均価格関数の導関数の汎関数になります。これらの導関数はすべての証券会社で同じであるため、異なる証券会社で設定が効率的になることが期待できます。別のケースでは、見つかった設定は、実際のティックでバックテストが成功する可能性や、他の証券会社に適用できる可能性が非常に低くなります。上記の概念は、そのような問題を回避します。

このメカニズムを実装するには、すべての要素を適切に変更する必要がありました。まず、相場ファイルを作成する際に、バーでのすべての重要なポイントでスプレッドを記録する必要があります。これらは、Open[]、Close[]、High[]、Low[]のポイントです。バーは買呼値に基づいているため、スプレッドは値を調整し、売呼値を取得するために使用されます。相場を書くEAは、現在、バーではなくティックに基づいています。これらのバーを記録するための関数は次のようになります。

void WriteBar()
   {
   FileWriteString(Handle0x,"\r\n");
   FileWriteString(Handle0x,DoubleToString(Close[1],8)+"\r\n");
   FileWriteString(Handle0x,DoubleToString(Open[1],8)+"\r\n");
   FileWriteString(Handle0x,DoubleToString(High[1],8)+"\r\n");
   FileWriteString(Handle0x,DoubleToString(Low[1],8)+"\r\n");         
   FileWriteString(Handle0x,IntegerToString(int(Time[1]))+"\r\n");
   FileWriteString(Handle0x,IntegerToString(PrevSpread)+"\r\n");
   FileWriteString(Handle0x,IntegerToString(CurrentSpread)+"\r\n");
   FileWriteString(Handle0x,IntegerToString(PrevHighSpread)+"\r\n");
   FileWriteString(Handle0x,IntegerToString(PrevLowSpread)+"\r\n");   
   MqlDateTime T;
   TimeToStruct(Time[1],T);
   FileWriteString(Handle0x,IntegerToString(int(T.hour))+"\r\n");
   FileWriteString(Handle0x,IntegerToString(int(T.min))+"\r\n");
   FileWriteString(Handle0x,IntegerToString(int(T.day_of_week))+"\r\n");         
   }      

緑色で強調表示されている4行はバーの4点すべてでのスプレッドを記録しています。以前のバージョンでは、これらの値は記録されず、計算で考慮されませんでした。これらのデータは簡単に取得して記録できます。次の単純なティックベースの関数は、高値と安値でのスプレッドを取得するために使用されます。

void RecalcHighLowSpreads()
   {
   if ( Close[0] > LastHigh )
      {
      LastHigh=Close[0];
      HighSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD));
      }
   if ( Close[0] < LastLow )
      {
      LastLow=Close[0];
      LowSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD));
      }      
   }

この関数は、現在のバーが形成されている間、バーの最高点と最低点でのスプレッドのみを決定します。新しいバーが表示されると、現在のバーは完全に形成されていると見なされ、そのデータがファイルに書き込まれます。この関数は、別のバーベースの関数と連携して機能します。

bool bNewBar()
   {
   ArraySetAsSeries(Close,false);                        
   ArraySetAsSeries(Open,false);                           
   ArraySetAsSeries(High,false);                        
   ArraySetAsSeries(Low,false);                              
   CopyOpen(_Symbol,_Period,0,2,Open);
   CopyClose(_Symbol,_Period,0,2,Close);
   CopyHigh(_Symbol,_Period,0,2,High);
   CopyLow(_Symbol,_Period,0,2,Low);
   ArraySetAsSeries(Close,true);                        
   ArraySetAsSeries(Open,true);                           
   ArraySetAsSeries(High,true);                        
   ArraySetAsSeries(Low,true);                                 
   if ( Time0 < Time[1] )
      {
      if (Time0 != 0)
         {
         Time0=Time[1];
         PrevHighSpread=HighSpread;
         PrevLowSpread=LowSpread;         
         PrevSpread=CurrentSpread;
         CurrentSpread=int(SymbolInfoInteger(_Symbol,SYMBOL_SPREAD));
         HighSpread=CurrentSpread;
         LowSpread=CurrentSpread;         
         return true;
         }
      else
         {
         Time0=Time[1];
         return false;
         }
      }
   else return false;
   }

この関数は、述語であると同時に論理の重要な要素であり、4つのスプレッドすべてが最終的に決定されます。プログラム内でも同様に実装されています。OnTickハンドラで非常に簡単に機能します。

RecalcHighLowSpreads();
if ( bNewBar()) WriteBar();

相場ファイルには、次のデータが含まれます。

バーの構造

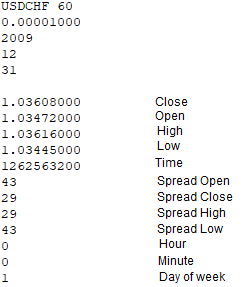
平均価格の配列は、プログラム内で同じように実装されます。

OpenX[1]=Open[1]+(double(PrevSpread)/2.0)*_Point;
CloseX[1]=Close[1]+(double(Spread)/2.0)*_Point;
HighX[1]=High[1]+(double(PrevHighSpread)/2.0)*_Point;
LowX[1]=Low[1]+(double(PrevLowSpread)/2.0)*_Point;

このアプローチは、スプレッドノイズの抑制を実装するために使用できるように思えるしれませんが、問題は、特定の数の収集されたティックが必要になることです(時間枠が長いほど、バーごとにより多くのティックが必要になります)。多数のティックを集めるには時間がかかります。さらに、バーは売呼値やスプレッド値を保存しないため、計算に買呼値を使用しました。

追加オプションとして、結果を最適化するときにスプレッドを考慮するメカニズムを追加しました。テストでは、このメカニズムはオプションであることが示されていますが、十分な計算能力があれば、非常に良い結果が得られます。重要なのは、スプレッドが必要な値を超えない場合にのみ、アルゴリズムが注文を開閉することを要求することです。現在のバージョンはスプレッドをバーデータに記録するため、値を制御でき、スプレッドを除いた実際のテスト値を計算できます。


短いセクションの多くのバリエーション

ロットバリエーション(種類の1つ)は、非常に短いセクションだけでなく、長いセクションでも使用できます。2つのリスク/ロット管理メカニズムがあります。

  • ロット増加
  • ロット減少

最初のメカニズムは、シグナルがすぐに反転すると予想される場合、反転取引で使用する必要があります。2番目のオプションは、信号が安定していて長時間続くことがわかっている場合にのみ機能します。任意の制御機能を使用できます。私は最も単純なもの、つまり線形関数を使用しました。言い換えれば、ロットは時間とともに変化します。実際のメカニズムの動作を見てみましょう。

これは、USDJPYM15見積もりを使用して行われます。この場合、ロボットのMQL4バージョンをデモンストレーションに使用します。これは、ロボットが拡散ポイントで取引されるため、実際のティックでのバックテストに失敗するためです。私は、短い時間枠での優れた総当たり攻撃アプローチが、総当たり攻撃期間などに等しい間隔で優れたフォワード結果を提供できることを証明したかったのです。私の計算能力は限られているので、仕事はそれほど広くはありませんでした。ただし、この結果は、これらのフォワードセクションに2つのロット管理メカニズムがあるため、かなり長いフォワード期間を示すのに十分です。検索間隔で見つかったバリアントのデモンストレーションから始めましょう。間隔は1年に相当します。

USDJPYM15総当たり攻撃の歴史

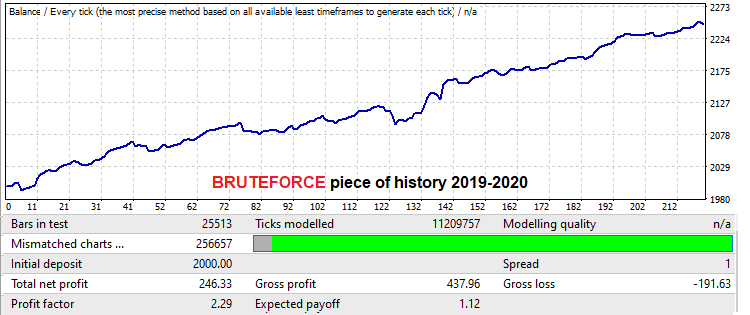
ここでの数学的な期待値は12ポイント強です(スプレッドなし。今回はスプレッドを無視するため、これは重要ではありません)。利益率を見ていきます。1年間のフォワードテストは次のようになります。

1年先

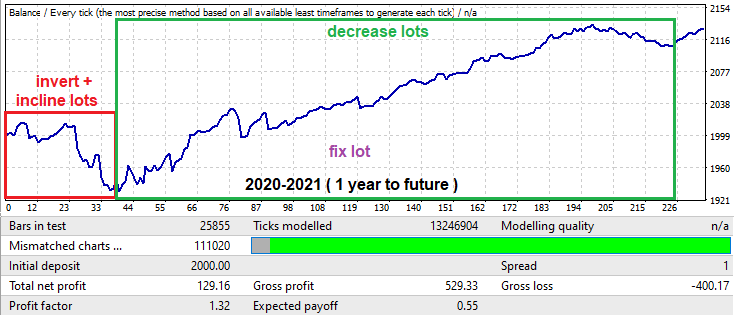
検索には1年しかかからなかったにもかかわらず、1年以上も機能し続けました。実際には、優れたコンピュータがあれば、スプレッドの低いすべての主要通貨ペアを1〜2週間で分析し、それらの中から最良のものを選択して、少なくとももう1年はパターンを活用できるということです。システムがMetaTrader 5のリアルティックバックテストに合格することを確認することを忘れないでください。さらに多くの証拠を収集するには、小さなチームに参加して複数のコンピュータ上のデータを分析し、結果を収集して統計を作成することをお勧めします。

ここで、フォワードテストを見てみましょう。最初は非常に大きなドローダウンがあります。これは通常、1年などの短い期間のパターンを探しているさいには非常に一般的です。それにもかかわらず、このドローダウンでさえ自分自身の目的のために使用することができます。この間隔は、上のグラフの赤い枠で示されています。ここでのEAの稼働時間は、設定で50取引日に制限されています(土曜日と日曜日はカウントされません)。また、ドローダウンを利益に変えるためにシグナルが反転されました。これは、反転後に負のグラフ部分に変わるため、ドローダウン後にグラフ部分を切り取るために行われます。結果のバックテストは次のとおりです。

反転+50日先までロットを固定

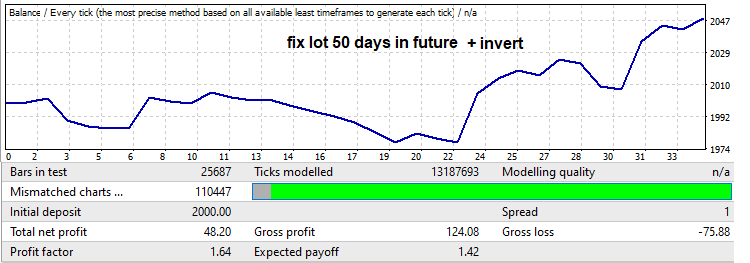
利益率に注意してください。増やしていきます。逆転が発生するかどうか、およびその逆転がどこまで進むかは実際にはわかりませんが、通常、総当たり攻撃セグメントで発生した動きのかなりの部分でロールバックします。最小値から最大値までロットの線形ゲインを適用することにより、このようなバックテストと利益率の増加が得られます。

反転+50日先までロットを増加

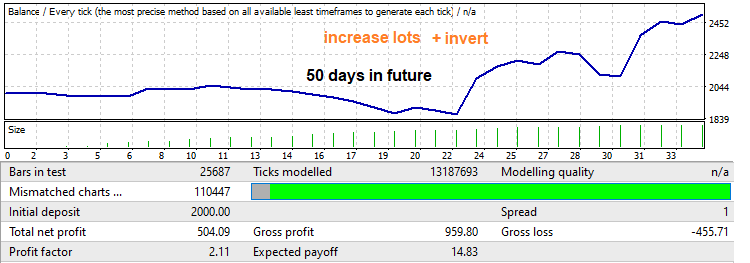
ここで、1年間のフォワードテストで緑色の枠で示されている逆のメカニズムを見てみましょう。この部分は、大きく成長している部分とそれに続くパターンの反転を示しています。この状況では、ロット減少を使用します。ロボットは、このセグメントの終わりまで取引するように設定されています。まず、後で結果を比較できるように、固定ロットでテストしてみましょう。

グリーンボックス固定ロット

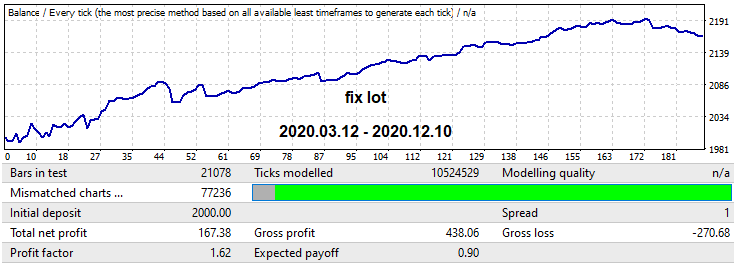
ここで、時間の経過に伴うロット減少を実装するメカニズムを有効にしましょう。これにより、利益率も増加しますが、グラフは滑らかになり、最後にドローダウンはありません。

グリーンボックス+ロット減少

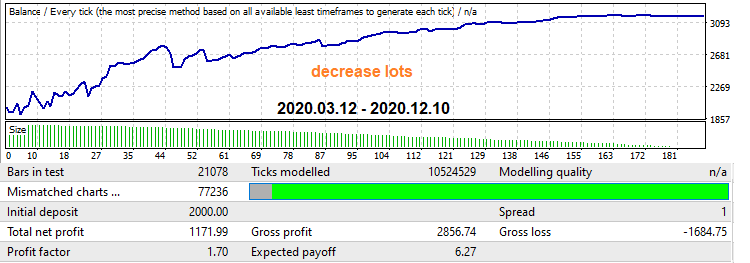
多くの市場の売り手はこれらの手法を使用しています。適切なタイミングで適切な場所に適用すると、収益性を高め、損失を減らすことができます。しかし現実はもっと複雑です。とにかく、これらのメカニズムは私のプログラムによって生成されたエキスパートアドバイザーで提供されているので、必要なときにいつでも有効または無効にできます。


グローバル履歴の作業バリアント

多くの読者は、実際のティック履歴でグローバルバックテストに合格できる少なくともいくつかの動作設定バリアントを特定することに興味があると思います。そのような設定を見つけました。コンピューティング機能が限られているとともに総当たり攻撃だけを実行しているため、検索にはかなりの時間がかかりましたが、いくつかのバリアントを見つけました。これです。

USDCAD H1 2010-2020

USDJPY H1 2017-2021

EURUSD H1 2010-2021

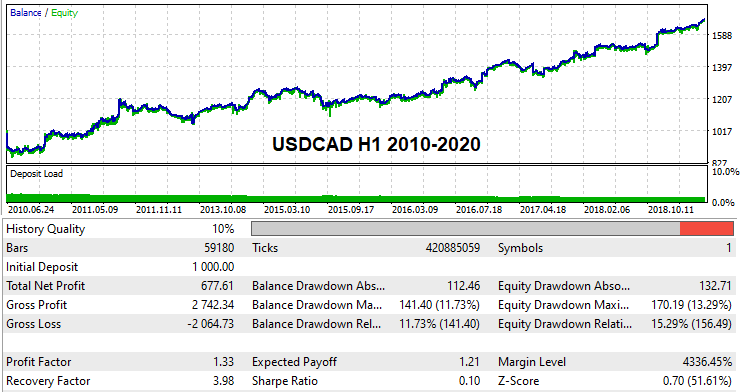
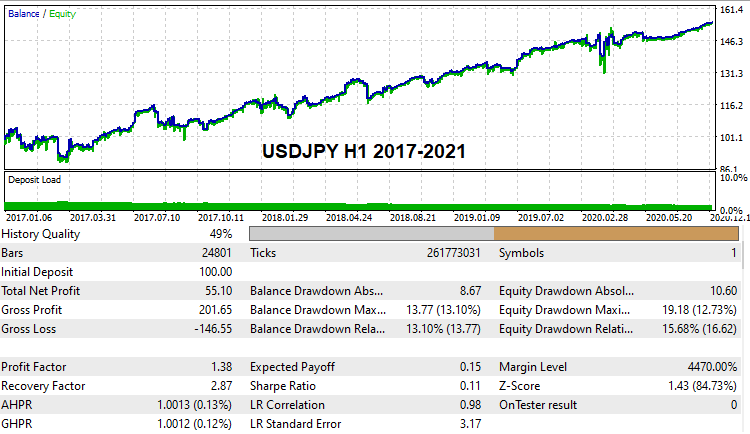
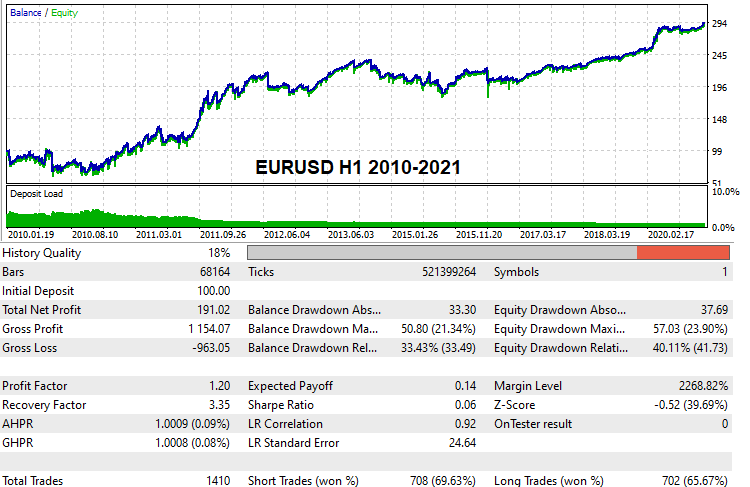
これらの設定は以下に添付されているため、必要に応じてテストできます。独自の設定を見つけて、デモ口座でバックテストすることもできます。このバージョンのプログラムから、どなたでもこの方法をお試しになれます。


総当たり攻撃の数学

このセクションでは、基本的な計算の原則を理解するために徹底的な説明が必要です。プログラムの最初のタブがどのように機能し、その結果をどのように解釈するかから始めましょう。

最初のタブの総当たり攻撃

実際、総当たり攻撃アルゴリズムで発生するすべてのことは、常に確率論に関連しています。これは、常に何らかのモデルと反復があるためです。ここでの反復は、現在のストラテジーバリアントの分析の完全なサイクルです。完全なサイクルは、特定のアプローチに応じて、1つまたは複数のテストで構成できます。テストやその他の操作の数は、すべてを1回の反復として分類できるため、それほど重要ではありません。結果の要件に応じて、反復は成功または失敗と見なすことができます。分析方法によっては、さまざまな定量値が良好な結果の基準として役立ちます。

アルゴリズムは常に、要件に適合する1つ以上のバリアントを出力します。どのくらいの結果をメモリに保存するかについてアルゴリズムに指示できます。要件を満たしているがストレージに収まらない他のすべての結果は破棄されます。総当たり攻撃アルゴリズムにいくつの手順があるとしても、このプロセスは常に実行されます。そうしないと、意図的に低品質のデータを処理するのに多くの時間を浪費することになります。これによって、単一のバリアントが失われることはありませんが、検索速度が低下する可能性があります。どのアプローチを使用するかは、最終的にはあなた次第です。

ここで、本論に直接入りましょう。結果検索プロセスは、最終的にはベルヌーイスキームに従った独立したテストのプロセスになります(アルゴリズムが固定されている場合)。すべては良いバリアントを取得する可能性に依存し、この確率は、固定アルゴリズムでは常に固定されています。この場合、この確率は次の値に依存します。

  • サンプルサイズ
  • アルゴリズムの変動性
  • ベースへの近接
  • 最終結果の要件の厳格さ

この点で、得られる結果の量と質は、ベルヌーイの公式に従って、反復回数とともに増加します。ただし、これは純粋に確率的なプロセスであることを忘れないでください。つまり、どの結果セットが得られるかを確実に予測することは不可能です。可能なのは、望ましい結果を見つける確率を計算することだけです。

  • Pk - 反復によって指定された要件で機能するバリアントが生成される確率(この確率は要件によって大きく異なる可能性があります)
  • C(n,m) - 「n」から「m」の組み合わせの数
  • Pa=Sum(m0...m...n)[C(n,m)*Pow(Pk ,m)*Pow(1-Pk ,n-m)] - n回の反復後に 要件を満たす少なくともm0のプライマリバリアントがある確率
  • m0 - 満足のいくプロトタイプの最小数
  • Pa -「n」回の反復から少なくとも「m0」以上を取得する確率
  • n — 動作するプロトタイプを検索するために利用可能な最大サイクル数(結果を待つ準備ができている時間)

サイクル数は時間で表すこともできます。最初のタブのカウンタから総当たり攻撃の速度を取得し、現在のデータの処理に費やす準備ができている時間を取得します。

  • Sh - 1時間あたりの反復回数としての速度
  • T - 待つ準備ができている時間
  • n = Sh*T

同様に、特定の品質要件に従ってバリアントが見つかる確率を計算することもできます。上記の式により、結果の線形性の要件である「偏差」フィルタに該当するバリアントを見つけることができました。このフィルタが有効になっていない場合、各反復は成功したと見なされ、常にバリアントが存在します。見つかったバリアントは、品質スコアで並べ替えられます。必要な品質に応じて、「Ps」値はモジュロで取得された品質値の関数になります。必要な品質が高いほど、この関数の値は低くなります。

  • Ps - 特定の追加の品質要件で結果を見つける確率
  • q - 必要な品質
  • qMax - 利用可能な最高の品質
  • Ps = Ps(|q|) = K * Px(|q|) , q <= qMax
  • K = Pk - この係数は、いくつかのランダムなバリアントを取得する確率を考慮に入れています(品質ベースのバリアントはそのようなバリアントから選択されます)
  • Ps ' (|q|) < 0
  • Lim (q-->qMax) [  Ps(|q|) ] = 0

この関数の一次導関数は負であり、要件が増加するにつれて、要件を満たす確率がゼロになる傾向があることを示しています。「q」が利用可能な最大値になる傾向がある場合、これは確率であるため、この関数の値は「0」になる傾向があります。「q」が最大値より大きい場合、選択されたアルゴリズムはそれぞれより高い品質を実現できないため、この関数は無意味です。この関数は、確率変数「q」の確率密度関数に従います。次の図は、Ps(q)と確率変数P(q)の確率密度、および追加の重要な量を示しています。

バラエティ

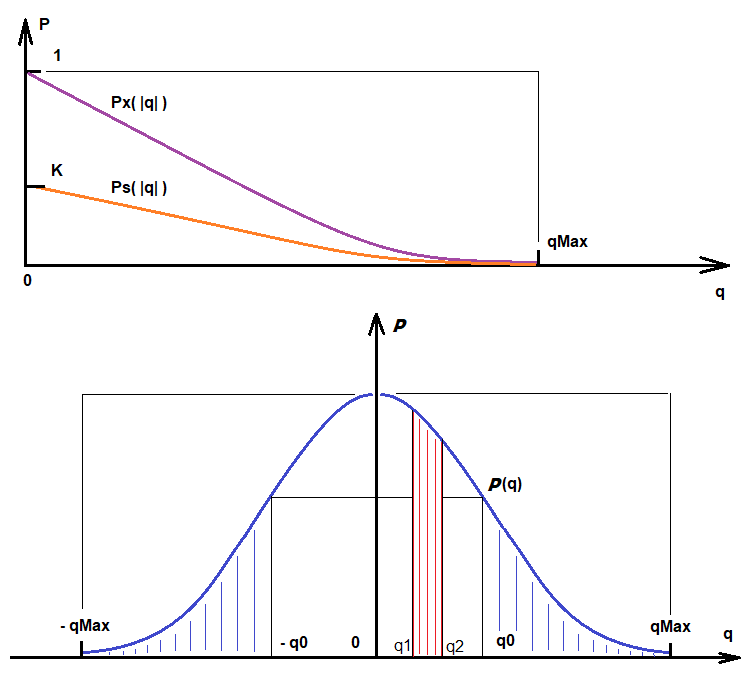
これらの図に基づきます。

  • Integral(q0,qMax) [P(q)] = Integral(-qMax,-q0) [P(q)] =  K*Px(|q|) = Ps(|q|)  - |q|がq0とqMaxの間のバリアントが現在の反復中に見つかる確率
  • Integral(q1,q2) [P(q)] - 反復の結果としてq1とq2の間の品質値が取得される確率(これは、確率変数分布関数を解釈する方法の例です)

したがって、必要な品質が高ければ高いほど、より多くの時間を費やす必要があり、検出されるバリアントは少なくなります。さらに、どのメソッドにも品質値の上限があります。これは、分析するデータとメソッドの完成度の両方に依存します。

2番目のタブでの最適化

2番目のタブの最適化プロセスは、プライマリ検索プロセスとは少し異なりますが、それでも反復と、要件を満たすバリアントを取得する確率を使用します。このタブにははるかに多くのフィルタがあるため、良好な結果が得られる可能性は低くなります。ただし、2番目のタブではすでに処理されたバリアントを改善するため、最初のタブにあるオプションが優れているほどここでより良い結果が得られます。特定のバリアントが改善される最終的な式は、ベルヌーイの式にいくぶん似ています。ここで興味があるのは、フィルタに該当する少なくとも1つのバリアントを取得する確率です。説明は次のとおりです。

  • Py = Sum(1...m...n)[ Sum(0... i ... C(n,m)-1) {  Product(0 .. j .. i-1 )[Pk[j]) * Product(i .. j .. m) [1 - Pk[j]] } ] - フィルタ要件を満たす少なくとも1つのバリアントを取得する確率
  • Pk [i] - 2番目のタブのフィルタの要件を満たすバリアントを取得する確率
  • n - 最適化間隔の分割(2番目のタブの[Interval Points](間隔ポイント)値)

最適化はMetaTrader 4およびMetaTrader 5オプティマイザーとまったく同じ方法で実行されますが、買いまたは売りシグナルである1つのパラメータのみを最適化します。最適化手順は、最適化間隔を分割する部分(間隔ポイント)の数に基づいて自動的に計算されます。最適化される数値の最大値は、最初のタブの検索プロセス中に計算されます。最初のタブのプロセスが完了すると、最適化された数値の値の変動の範囲がわかります。したがって、2番目のタブでは、この間隔を分割するためにグリッドの精度を設定するだけで済みます。バリアントは、2番目のタブで1つのスロットを取ります。これは、より良い品質が達成されるたびに更新されます。 

繰り返しになりますが、品質要件のあるバリアントを取得する確率には、上記と同様の分布関数があります。これは、わずかな調整で同じ式を使用できることを意味します。

  • ntegral(q0,qMax) [P(q)] = Integral(-qMax,-q0) [P(q)] =  K*Px(|q|) = Pz(|q|)  - |q|がq0とqMaxの間のバリアントが現在の反復中に見つかる確率
  • K = Py

ここでの唯一の違いは係数「K」です。これは、以前に取得した新しい確率に等しくなります。必要な品質のバリアントを取得する可能性は非常に低いですが、最初のタブにそのようなバリアントがたくさんあるため、取得するバリアントが多いほど良いです。さらに、最初のタブで生成されるバリアントが多いほど、2番目のタブでより良いバリアントを取得できます。計算も同様です。残念ながら、ベルヌーイの公式はここでは適用できませんが、以前に検討された構造を代わりに使用できます。この場合、1つのバリアントの最適化は、個別の反復として解釈されます。したがって、反復の総数は反復の数と等しくなります。前の式が完全である、要件を満たす少なくとも1つのバリアントが必要です。ここで、Pkは Pz [j](| q |)関数のファミリーによって決定されるPzに置き換えられます。これは、最適化バリアントごとにそのような関数が個別に存在するためです。

  • Pb = Sum(1...m...n)[ Sum(0... i ... C(n,m)-1) {  Product(0.. j .. i-1 )[Pz[j]) * Product(i.. j .. m) [1 - Pz[j]] } ]
  • n - 最初のタブで見つかったバリアントの数

したがって、総当たり攻撃が長ければ長いほど、より良い品質が得られます。ただし、すべてのパラメータが確率と結果に影響を与えることを忘れないでください。大量のリソース消費を回避するために、適切な設定を使用してください。最新のコンピュータは非常に強力ですが、計算効率は、合理的な設定とプロセスの詳細に関する知識によって何倍も向上します。


履歴への固執と過剰適合について

多くの自動取引システムの問題は、それらが過剰に訓練され、履歴に適合していることです。月に最大1000パーセントという印象的な結果を示すシステムを作成することが可能です。しかし、そのようなシステムは実際には機能しません。

取引システムが持つ入力パラメータが多くEAロジックの変動性が大きいほど、そのようなEAは履歴に強く固執します。重要なのは、相場を別のデータ形式に変換するプロセス非常に単純であるということです。順方向と逆方向の両方のデータ変換プロセスを提供できる順方向と逆方向の変換関数が常にあります。これは、暗号化および復号化と比較できます。たとえば、WinRarアーカイブは暗号化の一例です。私たちのタスクのコンテキストでは、暗号化アルゴリズムは、最適化プロセスと取引ロジックの存在を組み合わせたものです。オプティマイザでの十分な数のバックテストと特定の柔軟なロジックが奇跡を起こす可能性があります。この場合、取引ロジックは、過去の読み取り値に基づいて将来の価格をデコードするデコーダーとして機能します。

残念ながら、すべてのエキスパートアドバイザーはある程度履歴に固執しています。ただし、将来的に一部の機能を保持する必要がある論理的な部分もあります。このようなアルゴリズムを取得することは非常に困難です。特定のアルゴリズムの公正な予測の最大能力がわからないため、過剰訓練の境界を決定することはできません。次のローソク足の動きを可能な限り高い確率で予測できるようなアルゴリズムが必要です。ここで、価格データの圧縮度が高いほど、アルゴリズムの信頼性は高くなります。関数sin(w*t)を例にとってみましょう。この関数は無限の数[X[i],Y[i]]の点に対応することがわかっています。これは無限の長さのデータ配列であり、1つの短い正弦関数に圧縮されます。これは理想的なデータ圧縮ですが、このような圧縮は実際には不可能であり、常に何らかのデータ圧縮率があります。この係数が高いほど、市場公式の定義の質が高くなります。

私の方法では、一定量の変数データを使用しますが、それにもかかわらず、他の方法と同様に、過剰適合が発生する可能性があります。履歴の過剰訓練を回避する唯一の方法は、圧縮率を上げることです。これは、分析された履歴セクションのサイズを増やすことによってのみ実装できます。あと一つの、数式内の分析されたバーの数を減らす(Bars To Equation)という方法もあります。数式のバーの数を減らすことで「qMax」の上限は増えるのではなく減るため、最初の方法を使用することをお勧めします。要約すると、訓練には大きな標本と十分な「Bars To Equation」を使用するのが最適ですが、同時に、この値を過度に増やすと総当たり攻撃の速度が低下し、必然的に、より高い率が履歴に過剰適合するリスクが生じます。


使用に関する推奨事項

テスト中に、メインプログラムAwaiter.exeを構成するためのいくつかの重要な詳細を特定しました。それらの中で最も重要なものは次のとおりです。

  1. すべてのタブで設定を行ったら、必ず保存します(ボタン設定の保存)。
  2. スプレッドコントロールは2番目のタブで有効にできます。
  3. HistoryWriter EAを介して相場を生成する場合は、できるだけ大きな標本を使用します(少なくとも10年の履歴)。
  4. 最初のタブにはさらに多くのバリアントを保存できます(1000で十分なようです(バリアントメモリ))。
  5. 最適化タブで大きな間隔ポイント値を設定しないでください(20〜100で十分です)。
  6. 実際のティックでバックテストに合格できる適切な設定を取得したい場合は、バリアントで多数の注文を必要としません(最小注文)。
  7. バリアントの検索速度を制御する必要があります(総当たり攻撃が長時間実行されていて、バリアントが見つからない場合は、おそらく設定を変更する必要があります)。
  8. 安定した結果を得るには、偏差を「0.1〜0.2」の範囲に設定します。 0.1が最良のオプションです。
  9. 最適化タブでFOURIERの式を使用する場合は、[スプレッド制御]オプションを有効にします(式はスプレッドノイズに対して非常に敏感です)。


終わりに

この解決策を聖杯と見なさないでください。これは、ただの道具です。MetaTrader 4およびMetaTrader 5ターミナルで追加のプログラミングまたは最適化なしで使用できる効率的でユーザーフレンドリーなソリューションを実装することは困難です。このソリューションはまさにこれを成し遂げており、一般的に使用する準備ができています。

この方法がお役に立つことを願っています。もちろん、まだ改善の余地はたくさんありますが、これは、一般的には市場調査と取引の両方に役立つツールです。さらなる結果は、改善ではなく、計算能力に依存しますが、将来的には改善されると思います。

もっと時間が必要な未実現のアイデアをまとめました。それらの1つは、ボリンジャーバンドや移動平均などの最も有名なオシレーター指標と価格指標に基づく論理多項式の構築です。しかし、この概念はもう少し複雑です。「指標交差点での取引」ではなく、もっと役立つアイデアを実装したいと思います。また、本稿が読者に何か新しい一般的な有用な情報を提供することを願っています。


これまでの連載記事へのリンク

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8845

添付されたファイル |
ZIPをダウンロード
Awaiter_Project.zip (5961.38 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
ニューラルネットワークが簡単に(第11部): GPTについて ニューラルネットワークが簡単に(第11部): GPTについて
GPT-3は現在存在する言語ニューラルネットワークの中でおそらく最も高度なモデルの1つであり、その最大バリアントには1,750億個のパラメータが含まれています。もちろん、家庭にあるようなPCでそのような怪物を作成するつもりはありませんが、どのアーキテクチャソリューションを作業に使用し、それらからどのように利益を得ることができるかは確認することができます。
グリッドおよびマーチンゲール取引システムでの機械学習 - あなたはそれに賭けますか グリッドおよびマーチンゲール取引システムでの機械学習 - あなたはそれに賭けますか
本稿では、グリッドおよびマーチンゲール取引に適用される機械学習手法について説明します。驚いたことに、世界中のネットではこのアプローチはほとんどまたはまったくカバーされていません。記事を読んだ後は、自分自身の自動売買ボットを作成することができるでしょう。
DoEasyライブラリでのその他のクラス(第67部): チャットオブジェクトクラス DoEasyライブラリでのその他のクラス(第67部): チャットオブジェクトクラス
本稿では、(単一の取引製品チャートの)チャートオブジェクトクラスを作成し、MQL5シグナルオブジェクトのコレクションクラスを改善して、コレクションに格納されている各シグナルオブジェクトでリストの更新時にすべてのパラメータが更新されるようにします。
多層パーセプトロンとバックプロパゲーションアルゴリズム 多層パーセプトロンとバックプロパゲーションアルゴリズム
これら2つの手法の人気が高まり、Matlab、R、Python、C ++などで多くのライブラリが開発されています。これらのライブラリは、入力として訓練セットを受け取り、問題に適切なネットワークを自動的に作成します。基本的なニューラルネットワークタイプ(単一ニューロンパーセプトロンと多層パーセプトロンを含む)がどのように機能するかを理解してみましょう。ネットワークを訓練するためのエキサイティングなアルゴリズムである勾配降下法とバックプロパゲーションについて検討します。既存の複雑なモデルは、多くの場合、このような単純なネットワークモデルに基づいています。