自動取引のための便利でエキゾチックな技術

目次

• はじめに
• 最後のバーの動きを利用したポジション部分決済アルゴリズム
• ハイブリッドロット変動アルゴリズム
• 平均化の原理
• 取引技術の一貫性の直接的および間接的な兆候
• 残高とエクイティの波の使用
• 終わりに

はじめに

著者や一般人が有益であると考える取引技術はたくさんあります。これらの技術に関する情報はさまざまなリソースに多数あるため、本稿ではこれらの技術については検討しません。これらの手法に関して新しいことや興味深いことを提供することはできません。代わりに、この記事をいくつかの理論的にも実際的にも役立つ、有用で非標準的な技術のコレクションとして作成することにしました。それらの技術のいくつかには馴染みがあるかもしれません。最も興味深い手法を取り上げ、なぜ使用する価値があるのかを説明します。さらに、これらの技術の実際面での傾向を示します。

最後のバーの動きを利用したポジション部分決済アルゴリズム

理論

このアプローチは、ポジションを開き、価格がさらにどちらの方向に移動するかわからない場合に役立つ取引技術として役立つ可能性があります。賢明なポジション部分決済はスプレッドによる損失を補い、適切に最適化されれば利益を生み出すことさえできます。

以下から始めましょう。どこで終了するかわからないが、ポジションをすでに開いたとします。どちらの方向で開いたかは関係ありません。どちらにしても、ポジションはいつか決済する必要があります。もちろん、何年もの間自分のポジションを保持する人もいます。ただし、ロボットは集中的に取引し、高頻度で取引すると想定します。ボリューム全体を終了することも、ポジションを部分決済することによって数段階的に終了することもできます。市場はフラットな構造であることがわかっています。つまり、価格は現在の半波の始まりの位置に戻る傾向があります。つまり、上向きの動きが継続する確率は常に50％未満であるということです。したがって、反対の動きの確率は50％を超えます。ポジション全体を決済すると波の将来の振幅がわからなくなるため、波を完全に逃して利益を逃す可能性があります。部分決済の出番です。将来の波の性質がわからないという事実に基づいて、最大の利益を得ることができます。

波とは何かそして波が市場から決して消えないことがわかったので、ポジション決済の原則から始めます。これにより、エントリが間違っていても、少なくともある程度の利益が得られるはずです。そのようなメカニズムは実際に存在します。

アルゴリズムは多数ありますが、私が最も効率的であると信じている1つだけを提示します。これは、以前の完全に形成されたローソク足の動きが大きくて強いほどかなり強力なロールバックの動きがある可能性が高くなるという仮定を利用しています。一般的に言って、このメカニズムの目的は何でしょうか。これは簡単です。損失を減らしながら利益を増やすことです。インパルスも実際には波ですが、通常の古典的な波よりもはるかに便利です。重要なのは、市場に最も近い波の方が信頼性が高いということです。インパルスが強力で持続時間が短いほど、近い将来のロールバックの可能性が高くなり、予想されるロールバックの大きさが大きくなります。アイデアは、インパルスパワーが増加したときにポジションの部分決済がより強くなるようなメカニズムを配置することです。図で示します。

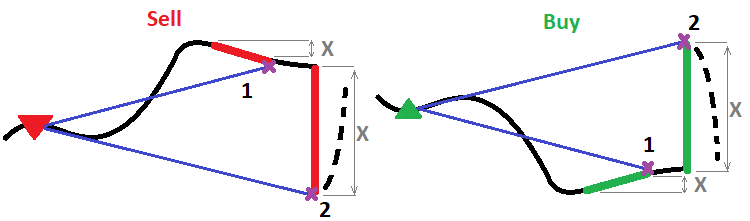
ポジションの決済されるボリュームは任意の関数を使用して計算できますが、そのうちの2つを紹介します。1つは線形関数で、もう1つは累乗関数です。

• { D } - 累乗
• { X } - ポイント単位での前のバーの動き
• { C } - スケール因子
• { Lc(X) = C * Pow(X , D) } - 現在のローソク足で決済されるロットを計算する累乗関数
• { Lc(X) = C * X } - 現在のローソク足で決済されるロットを計算する線形関数

よく見ると、線形関数は累乗関数のD = 1の特殊なケースにすぎません。よって、これは初期思考ロジックの例にすぎないため省略できます。考えるのは最初はいつも簡単ですが、考え直してみると、はるかに用途の広いツールが手に入ります。簡単なことから始めなければならないということだけです。

これらの係数を直接指定してその影響を考慮する必要をなくすために、それらを決定するいくつかの制御パラメータを導入します。

• { StartLotsToOnePoint } - X = 1 の場合、この値でポジションを決済します(入力パラメータ)
• { PointsForEndLots } - 前のローソク足の最終ポジション決済速度の利益方向への移動(入力パラメータ)
• { EndLotsToOnePoint } - X = PointsForEndLotsの場合、この値でポジションを決済します(入力パラメータ)

ここで、係数を計算し、入力パラメータで表される関数の最終形式を取得するために、連立方程式を作成しましょう。この目的のために、考えを数式に変換します。

1. { Lc( 1 ) = StartLotsToOnePoint }
2. { Lc( PointsForEndLots ) = EndLotsToOnePoint }
   

これで、すべての方程式の準備が整いました。次に、それらを拡張形式で記述し、徐々に変換して方程式を解き始めます。

1. { C * Pow(1 , D) = StartLotsToOnePoint }
2. { C * Pow( PointsForEndLots  , D) = EndLotsToOnePoint }
   

最初の方程式では、1がそれ自体と等しい場合、Cをすぐに見つけることができます。

• { C = StartLotsToOnePoint }

2番目の方程式の両辺をCで除算し、方程式の両辺の底PointsForEndLotsに対する対数を求め、次を取得します。

• { log( PointsForEndLots ) [ Pow( PointsForEndLots  , D)] = log( PointsForEndLots ) [  EndLotsToOnePoint / C ] }

底が任意の累乗の対数と同じである対数がこの累乗に等しいことを考慮すると、目的の累乗について方程式を解くことができます。

• { D =  log( PointsForEndLots ) [  EndLotsToOnePoint / C ] }

2番目の未知の係数が見つかりました。しかし、これだけではありません。MQL4とMQL5には、任意の底に対する対数を実装する基本的な関数がなく、あるのは自然対数だけです。したがって、対数の底を自然対数に置き換える必要があります(自然対数は、底がオイラー数で表される対数です)。どんな対数でも自然対数で表すことができるため、言語に他の対数がないことは問題ではありません。これは、少なくとも数学の何かを理解している人にとっては非常に簡単です。底を変更すると、目的の係数の式は次のようになります。

• { D = ln(  EndLotsToOnePoint / C ) /  ln(  PointsForEndLots  ) }

既知のC係数を代入して、次を取得します。

• { D = ln(  EndLotsToOnePoint / StartLotsToOnePoint  ) /  ln(  PointsForEndLots  ) }

両方の係数を関数テンプレートに代入して、最終的な形式を取得します。

• { Lc(X) = StartLotsToOnePoint  * Pow( X ,  ln(  EndLotsToOnePoint / StartLotsToOnePoint  ) /  ln(  PointsForEndLots  )  )  }
  

この関数の利点は、次数を1に等しくすることも、1より大きく、1より小さくすることもできることです。それにより、あらゆる市場や取引手段に適応する際に最大限の柔軟性が提供されます。D = 1の場合、あるのは線形関数です。D > 1の場合、すべての波がスケーラブルであり、特定の振幅の波の数は振幅に反比例するという仮定に合わせて関数が調整されます(つまり、同じ期間の波の数を数える場合、たとえばM5とH1ではH1の波の数は12分の1であることがわかります。これは、1時間ごとのローソク足が5分のローソク足の12分の1であるためです)。D < 1の場合、低振幅の波よりも高振幅の波の方が多いと予想されます。D > 1の場合、主に低振幅の波があると想定します。 

また、必ずしもバーのシーケンスとして離散化された価格系列を使用する必要はありません。ティックやその他の優先価格セグメントを使用できます。ここでバーを使用しているのは、バーがあるからです。

コード:

コードでは、この関数は次のようになります。

double CalcCloseLots(double orderlots0,double X)
   {
   double functionvalue;
   double correctedlots;
   if ( X < 0.0 ) return 0.0;
   functionvalue=StartLotsToOnePoint*MathPow(X ,MathLog(EndLotsToOnePoint/StartLotsToOnePoint)/MathLog(PointsForEndLots));
   correctedlots=GetLotAniError(functionvalue);
   if ( correctedlots > orderlots0 ) return orderlots0;
   else return correctedlots;
   }

ロットが正しい値のみを取るように修正する関数は紫色で強調表示されています(内部を表示しても意味がありません)。関数自体は、緑色で強調表示されている演算子の下で計算されますが、ここで呼び出されるより一般的な関数の一部です。

void PartialCloseType()// close order partially
   {
   bool ord;
   double ValidLot;
   MqlTick TickS;
   SymbolInfoTick(_Symbol,TickS);
            
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == _Symbol )
         {
         if ( OrderType() == OP_BUY )
            {
            ValidLot=CalcCloseLots(OrderLots(),(Open[0]-Open[1])/_Point);
            if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.bid,MathAbs(SlippageMaxClose),Green);
            }
         if ( OrderType() == OP_SELL )
            {
            ValidLot=CalcCloseLots(OrderLots(),(Open[1]-Open[0])/_Point);
            if ( ValidLot > 0.0 ) ord=OrderClose(OrderTicket(),ValidLot,TickS.ask,MathAbs(SlippageMaxClose),Red);
            }         
         break;
         }
      }

MT4Ordersライブラリを使用しているため、このコードはMQL5でコンパイルできます。これらの関数はテストに適していることに注意してください。実際の取引に使用するには、エラーや原因不明のケースに注意して、それらを注意深く調査し、改良する必要があります。とにかく、現バージョンはストラテジーテスターでのテストには非常に適切です。

エキスパートアドバイザーのテスト:

動作を示すためにMetaTrader 4のEAバージョンを作成しました。MetaTrader5でテストすれば、私たちが見たいものはおそらくすべてスプレッドで隠されてしまうからです。代わりに、スプレッドを1に設定し、ランダムな方向に開くポジションを選択しました。

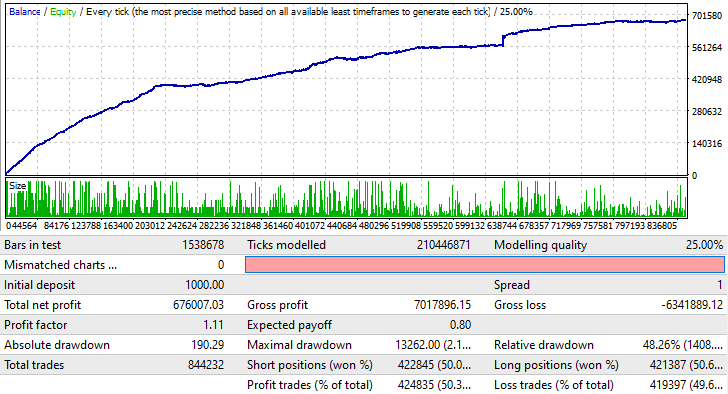
これは、他の通貨ペアでもほぼ同じように機能します。より長い時間枠でも機能しますが、そのためには適切な設定を見つけるために少しの忍耐が必要です。ただし、このテストは、実際の口座でこのEAをすぐに起動できることを意味するものではありません。これは、この技術が適切に使用された場合に役立つ可能性があることの確認としてのみ機能します。とにかく、この時点で、これはこのEAにとってさえ利益のために非常に非常に不十分です。しかし、適切なシグナルと適切なアプローチを組み合わせると、この方法は有益な場合があります。

ハイブリッドロット変動アルゴリズム

市場調査の当初から、すべてのシステムの利益率をプラスにシフトする方法を考えていました。これは、スプレッドにあまり依存しないストラテジーには、他の利益率が1に近いストラテジーと比較して非常に大きなメリットがあるということです。利益率を改善する必要があるのは正確に言って何故なのでしょうか。答えは非常に簡単です。システム全体の相対的なドローダウンとシステムの収益性の両方がこの変数に依存するためです。そのような技術は存在するので紹介しますが、まず、ロット操作を利用する可能性のある最も有名な取引技術について簡単に説明しましょう。利益率を高めるとされている技術には次があります。

• マルチンゲール
• 逆マーチンゲール

実際、すべてはよく議論される2つの手法に要約されますが、これらが失望以外のものをもたらすことはほとんどありません。これは非常に単純な数学的原理に関するものです。グリッドとマルチンゲール - それらは何でありどのように使用するか稿で説明しましたが、この記事では原理自体ではなくすべての原理に何が共通するかついて説明しています。一般的なことはロットはいくつかの条件に応じて減少または増加することです。条件が価格形成の性質とは何の関係もない場合、そのようなシステムは故意に不採算です。

ロット変動を利用するストラテジーには基礎となるシグナルがあり、すべての注文のロットが同じになるように作成することで取得できます。これは、基礎となるシグナルが価格形成の性質に何らかの形で関連しているかどうかを理解するのに役立ちます。ほとんどの場合、そのようなシグナルは数学的な期待値を生成しませんが、このシグナルには、順方向と逆方向の両方のマルチンゲールを同時に使用できるようにするパラメータが1つあります。必要な条件は、多数の低振幅波の存在です。マルチンゲールと逆マルチンゲールの組み合わせを適切に使用すると、それらをハイブリッドメカニズムに変えることができ、数学的な期待値がゼロから正に変わります。これは、次の図で見ることができます。

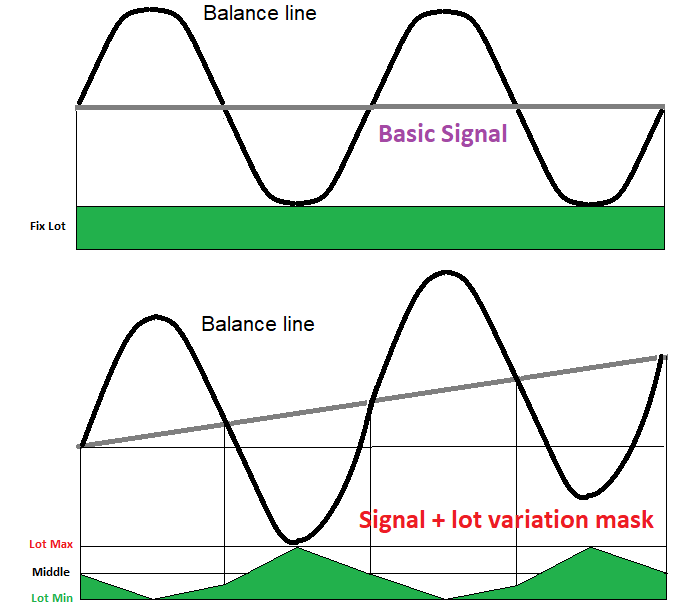
理論

ここでは、スプレッドと手数料を考慮せずに、トレーダーが初期残高に対して正または負の利益で取引を停止することを決定するまで、または、スプレッド、手数料、スワップによって無駄システムがゆっくりと預金を失うまで、常に最初の開始レベルの近くをさまよう特定の初期残高ラインがあると仮定します。これは、任意の取引の残高ラインは、初期残高を中心に変動する波状に似たプロセスであることを意味します。

これに基づいて、残高ライン全体を上昇セクションと下降セクションに分割できます(図は1つの波全体の4分の1を示しています)。波の4分の1が上向きの場合は、ロットを減らす必要があります(逆マルチンゲール)。波が下向きの場合は、ロットを増やす必要があります(マルチンゲール)。無限のロット増加に対する唯一の障害は、口座には最大許容ポジションボリュームがあるという事実です。したがって、そのような状況が可能であったとしても、預金によって追加のポジションが開けなくなります。ロットは明らかに特定の値の回廊で変動する必要があり、それを超えてはなりません。重要な点は波の振幅が大きすぎないようにすることです。できれば、小さな波が多く大きな波が少ないほうが良いです。図と下のロット変動マスクをよく見ると、ハイブリッド変動を使用して、変動が発生する線がどのように上向きの勾配を獲得できるかがわかります。これは、正の数学的期待値とおよび利益率同等です。

この場合、ロットを計算する方法は何でしょうか。一見、状況が不明確に見えるかもしれません。明らかに、ロットはチャネルの境界の1つに到達してそこから出ないかもしれません。このような場合、平均ロット値を中心に安定した変動を得るために、開始ロットに戻るメカニズムを提供する必要があります。このようなシステムの明らかで唯一の欠点は、大振幅波の不耐性です。低振幅の動きでは、メカニズムは完全に機能します。この問題は、関数自体がロットを中央に向かってプッシュするように次のロットを計算する関数によって解決されます。前に決済された注文のロットが境界の1つに近いほど、プッシュが強くなります。これを次の図で示します。

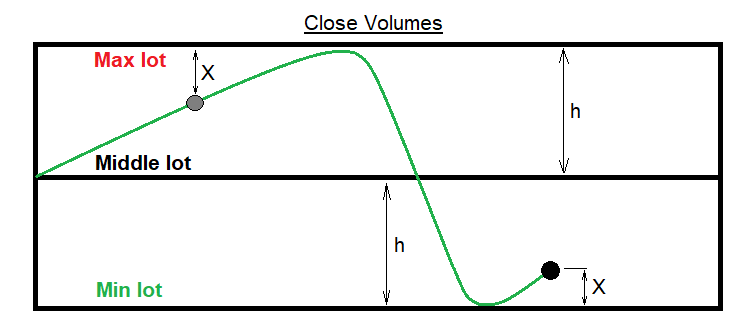
次に、図の表記を使用して、このタスクに適した関数の概要を記述しますが、まず、入力パラメータと補助変数を定義しましょう。

ハイブリッドロット変動を制御するための入力変数

• { MaxLot } - 最大ロット(入力パラメータ)
• { MinLot } - 最小ロット(入力パラメータ)
• { LotForMultiplier } - ボリュームを増減するための参照ロット
• { ProfitForMultiplier } - 参照ロットの損失と利益の増減(ポイント単位)

補助変数

• { MiddleLot = (MaxLot + MinLot)/2 } - 最大ロットと最小ロットの中間
• { h =  (MaxLot - MinLot)/2 } - 半分のチャネル幅(計算に使用)
• { L } - 履歴からの最後の取引のロット
• { X } - 補助変数
• { OrderProfit、OrderComission、OrderSwap、OrderLots } - 手数料、計算された注文スワップ、および履歴からの最後の注文決済ボリュームを除いた利益(既知)
• { TickSize } - ボリュームが1ロットに等しく価格が希望の方向に1ポイント移動した場合のポジション利益の増加
• { PointsProfit = ( OrderProfit + OrderComission + OrderSwap ) / ( OrderLots * TickSize ) } - 履歴の最後の注文の利益(ポイント単位に変換済み)

ロットが中心線より上または下にある場合の機能

• { L  >=  MiddleLot  ?  X = MaxLot - L } - ロットが期間の上部にある場合、Xの値はチャネルの上部境界との差です
• { L  <  MiddleLot  ?  X = L - MinLot } - ロットが期間の上部にある場合、Xの値はチャネルの下部境界との差です
• { L  >=  MiddleLot & PointsProfit < 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) * ( X / h )  } - チャネルの上部境界に近づくと、ロットの増加が減速しました
• { L  <  MiddleLot & PointsProfit >= 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) * ( X / h )  } - チャネルの上部境界に近づくと、ロットの減少が減速しました
• { L  >=  MiddleLot & PointsProfit >= 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) / ( X / h )  )  } - ロットの減少が加速しました 
• { L  <  MiddleLot & PointsProfit < 0   ?  Lo(X) =  OrderLots - LotForMultiplier * (  PointsProfit / ProfitForMultiplier ) / ( X / h )  } - ロットの増加が加速しました

これらの関係は読みにくいため、すべてを理解することは非常に困難です。すべてを連続関数に結合しようとすると、操作が不可能なほど複雑な構造になります。さらにコードで示して、より明確にしてみます。ここでは、MQL4スタイルのコード実装を示します。便利で有名なMT4Ordersライブラリを使用すると、コードをMQL5で簡単に実行できます。

コード:

double CalcMultiplierLot()
   {
   bool ord;
   double templot=(MaxLot+MinLot)/2.0;
   for ( int i=OrdersHistoryTotal()-1; i>=0; i-- )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_HISTORY );
      if ( ord && OrderSymbol() == CurrentSymbol &&  OrderMagicNumber() == MagicF )
         {
         double PointsProfit=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*MarketInfo(CurrentSymbol,MODE_TICKVALUE));
         if ( OrderLots() >= (MaxLot+MinLot)/2.0 )
            {
            if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0));
            if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((MaxLot-OrderLots())/((MaxLot-MinLot)/2.0)) ;
            if ( PointsProfit == 0.0 ) templot=OrderLots();
            break;
            }
         else
            {
            if ( PointsProfit > 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))*((OrderLots()-MinLot)/((MaxLot-MinLot)/2.0));
            if ( PointsProfit < 0.0 ) templot=OrderLots()-(LotForMultiplier*(PointsProfit/ProfitForMultiplier))/((Orderlots()-MinLot)/((MaxLot-MinLot)/2.0));
            if ( PointsProfit == 0.0 ) templot=OrderLots();
            break;
            }
         }
      }
   if ( templot <= MinLot ) templot=(MaxLot+MinLot)/2.0;
   if ( templot >= MaxLot ) templot=(MaxLot+MinLot)/2.0;
         
   return templot;
   }

このライブラリは、各未処理注文を管理する必要がある場合に特に役立ちます。これがアプローチ全体です。アルゴリズムの入力変数は黄色で強調表示されています。

エキスパートアドバイザーのテスト:

利益率の改善が見やすくなるため、このEAは以前のEAと同じ理由でMetaTrader 4も対象としています。

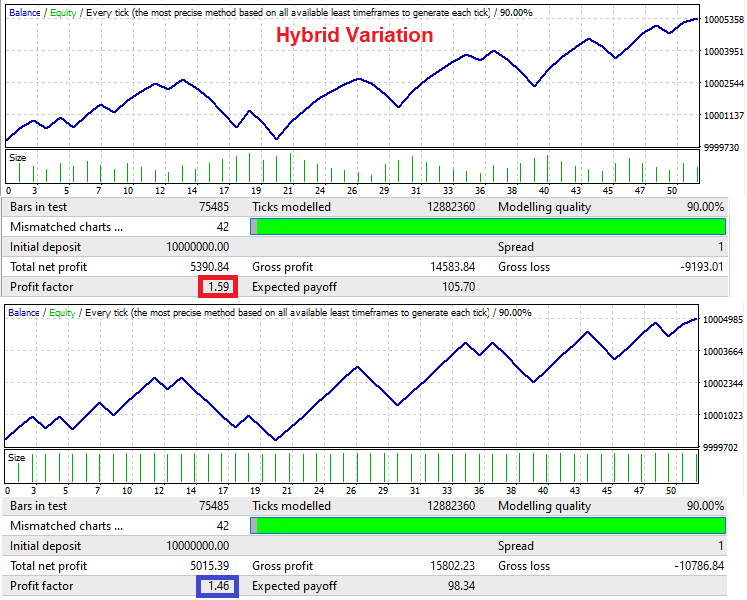
このエキスパートアドバイザーのシグナルは順番に生成されます。買いの後に売りが続き、売りの後に買いが続きます。これは、メカニズムの本質を示すために行われます。2番目のテストでは固定ロットを使用し、最初のテストではハイブリッドロット変動を使用します。元のシグナルの残高変動が最小限である場合にのみ、システムが利益率の改善を提供できることがわかります。システムは大きな波に耐えられません。

平均化の原理

平均化の原則はかなり興味深いアルゴリズムです。マーチンゲールグリッドやピラミッド同様不採算ですが、波の取引に役立つ非常に興味深い機能が1つあります。動きが一定のレベルまで継続し、必然的に一定のポイント数だけロールバックすることがわかっている場合は、マーチンゲールによる平均化を適用できます。この技術は、マーチンゲールで特にうまく機能します。マーチンゲールを使用すると、利益率を1.0より大きく保ちながら、必要なロールバックを減らすことができるからです。 

この原則は、価格がポジションの方向に動かない場合、しばらくすると、間違いなくこの動きの一部によってロールバックするという仮定を利用しています。ただし、このアルゴリズムは波の性質を調べることで多くの銘柄に対して微調整できますが、これは実際には常に発生するとは限りません。このプルバックで利益を生み出すためには、それを予測するか、経験的に決定する必要があります。

これは強いレベルでも機能します。なぜなら、レベルが発生すると、市場はそれを反転についてテストしようとすることが非常に多いからです。最初の取引の方向性を正しく推測し、利益が必要な値に達した場合、取引を終了し、より魅力的と思われる方向に新しい取引を開始します。価格が間違った方向に進んだ場合は、特定の手順を実行することで、ポジションのボリュームを増やすことができます。ポジションを増やすときは、これを非常に注意深く行う必要があります。予想されるロールバックに基づいた正確さが必要です。以下は2つの可能な例です。

一連の買い注文の例:

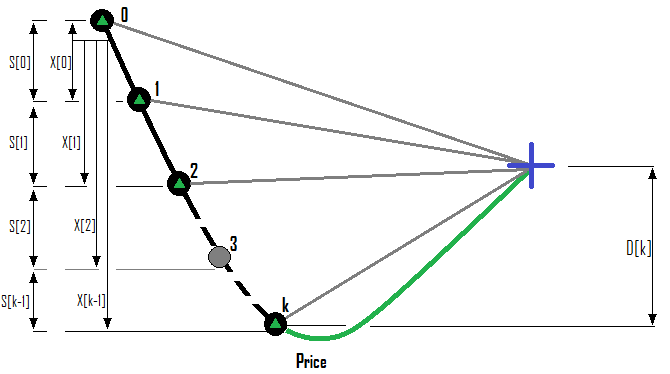
一連の売り注文の例:

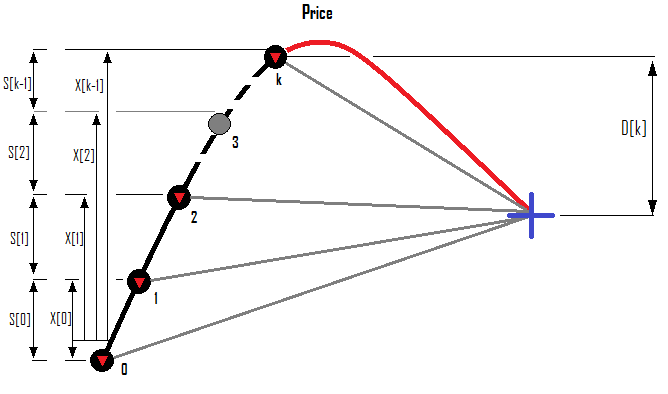
次に、すべての注文の利益または損失を計算する方法と、現在の状況に基づいて、必要なロールバックに基づいて次の注文のロットを計算する方法を示します。ポジションのファンを閉じるには、なぜこのファンを構築する必要があるのか、そしてどの条件でファンが役立つのかを知る必要があります。私だったら利益率を使用します。ファンがプラスならば、その利益率もプラスです。サーバの価格変動やスリッページによって利益がマイナス方向にシフトする可能性があるため、すべての注文の総利益がプラスになってすぐにファンを閉じるのは愚かです。そのようなファンはそのような状況では役に立たないように見えるかもしれません。さらに、サイクルの利益率は、平均化の積極性をさらに調整する機会を提供します。これは、自動化されたストラテジーを最適化するときや設定を手動で検索するときに使用できます。

一連の注文の最大数に制限があるとします。次に、すでにk個の注文を開いている未知の状況にあると仮定します。他のコレクションや配列と同様に、それらのインデックスは0から始まるため、シリーズの最後の注文のインデックスは「k-1」になります。次の注文を開くと、そのインデックスはkになり、注文数は「k +1」になります。これらの理想を問題の入力データに形式化してみましょう。

• { MaxOrders } - シリーズの最大許容注文数
• {  k = 0 ... 1 ... 2 ...  (MaxOrders-1)  } - 前のアプローチから利益が得られない場合に出す、シリーズの次の注文のインデックス
• {  ProfitFactorMax } - 決済の許容利益係数
• {  i = 1 ... 1 ... 2 ... k  } - ファンの既存の注文と、出したい次の注文のインデックス
• {  S[i-1]  } - 前の注文から現在の注文までのポイント単位の距離
• {  X[i-1]  } - シリーズの注文0から現在の注文までのポイント単位の距離
• {  D[k]  } - シリーズの最後の注文の始値に対して予測される希望する方向へのロールバック

さらに、MQL4およびMQL5言語は、特定の注文を参照するときに次のデータを提供すると言うことができます。すべての計算オプションを説明する必要があります。

• {P[i] } - 手数料とスワップを除外しない特定の注文の利益
• {С[i]} - 選択した注文の手数料
  
• {S[i]} - 0:00のロールオーバー中の計算された注文スワップ
  
• {L[i]} - 注文量
  
• {Sp[i]} - 買いポジションを開くときのスプレッド/売りポジションの現在のスプレッド
• {TickSize} - ポジションの利益の増加(ボリュームが1ロットに等しく、価格が目的の方向に1ポイント移動した場合)

これらの値のすべてが自動取引で実際に使用するために必要になるわけではありませんが、これらの値を計算するためのすべての可能なオプションをハイライトすることができます。これらの値のうち、関連性があって価格に関連して表すことができるものを、上の図に示しています。コードで使用する最も単純な計算方法から始めましょう。

最初の注文がプラスの結果で決済された-場合は、何もしません。適切と思われる場合はいつでも、希望する方向に新しい注文を開始します。価格が目標に到達せず、反対方向に進んだ場合、次の注文を開くために、価格が赤字方向にいくつのポイントを移動するかを決定する必要があります(S[k-1] )。価格がこのレベルに達した場合、適切なロールバックを決定する必要があります(D[k])。その後、注文のロットを決定する必要があります。これにより、計画されたロールバックで、選択した値(ProfitFactorMax)よりも大きいすべての注文に必要な利益率が得られます。これを行うには、最初に、現在開いている注文によって生成される利益と損失、およびそれらの合計値を計算する必要があります。目的は、対応する式を書いた後で説明します。

まず、特定の注文ごとの将来の利益値を紹介しましょう。必要なロールバックが発生する場合、これは現在の利益と注文が受け取る増分に等しくなります。

• {  j = 0 ... 1 ... 2 ... k-1 }
  
• {PF[j] = P[j] + С[j] + S[j] + (D[k] * L[j] * TickSize)} - 特定の注文の利益は、必要なロールバックが発生したときにこの値に等しくなります
• {PF[k] = { ( D[k] - Spread[k] ) * L[k] * TickSize} - この値には、開きたいポジションの必要なロットが含まれているため、計算できませんが、この式は後で必要になります
  

前者の場合、P[i]の値は既知であり、組み込みの言語関数を使用して取得でき、自分で計算することもできます。この計算方法は、すべてが標準言語の手段を使用して見つけることができるため、追加として記事の最後に示されます。シリーズの最後に出す注文については、手数料とスワップも必要ですが、これらの値はすでに出した注文に対してのみ取得できます。さらに、ポジションが0:00まで切り替わるかどうかわからないため、スワップ値を決定することはできません。常に不正確な値があります。プラスのスワップを持つ通貨ペアのみを選択することが可能です。 

その後、この予測利益を使用して、利益のある注文と損失のある注文を分割し、結果の利益係数を計算できます。

• {i = 0 ... 1 ... 2 ... k} - すでに開いているインデックスの注文
• { Pr[i] > = 0、Ls[i] > = 0 } - 符号に応じて注文の利益または損失を受け入れる2つの配列を導入します(「+」は利益に使用され、利益係数の計算に必要です)
• { PF[i] < 0 ? Pr[i] = 0 &Ls[i] = - PF[i] } - 注文利益がマイナスの場合、利益を「0」と記入し、利益値は、損失の変数に逆符号で書き込みます
• { PF[i]> 0 ? Ls[i] = 0 & Pr[i] = PF[i]  } - 注文利益がプラスの場合は、適切な配列に書き込み、損失配列にゼロ値を設定します
  

これらの配列に入力した後、総利益と損失、およびそれらの結果を計算する式を書くことができます。

• { SummProfit = Summ[0,k]( PF[i] ) } - すべての勝ち注文の総利益モジュール
• { SummLoss = Summ[0,k]( Ls [i] ) } - すべての負け注文の総損失モジュール
  

次に、ループを閉じる条件を記述する必要があります。

• { SummLoss > 0 ?  SummProfit/SummLoss  = ProfitFactorMax }

この方程式をさらに使用するには、ポジションファンが閉じているとき、シリーズの最後の注文の利益が常にプラスであることを理解する必要があります。これに基づいて、次のように書くことができます。

• { SummProfit = Summ[0,k-1]( PF[j] )  +  PF[k] }
  

この値を方程式に代入すると、次のようになります。

• {  ( Summ[0,k-1]( PF[j] )  +  PF[k] ) /  SummLoss  =  ProfitFactorMax }
  

ここで、この方程式をPF[k]について解くと、次のようになります。

• { PF[k]  =  ProfitFactorMax * SummLoss  -  Summ[0,k-1]( PF[j] ) }
  

PF[k]値の式がすでにあることを考慮して、ここでこの式を代入すると、次のようになります。

• { ( D[k] - Spread[k] ) * L[k] * TickSize = ProfitFactorMax * SummLoss  -  Summ[0,k-1]( PF[j] ) }
  

これで、L[k]についてこの方程式を解くことができます。最終的に、開くのに必要なポジションボリュームを計算するための式が得られます。

• { L[k] =  ( ProfitFactorMax * SummLoss  -  Summ[0,k-1]( PF[j] ) )  /  ( ( D[k] - Spread[k] ) *  TickSize ) }
  

以上です。次に、組み込み関数を使用せずにP[i]値を計算する方法を考えてみましょう。

• { P[i] = ( X[i-1] - Spread[i] ) * L[i] * TickSize + С[j] + S[j] }
  

ロールバック値の計算

次に、ロールバックの計算方法を見てみましょう。私は2つの方法を使用します。多数あるかもしれませんが、私が最も役立つと思う2つの方法だけを提示します。ロールバックは、価格が間違った方向に進んだ量に関連して計算されるもので、D[i]とX[i]が、正のX軸全体で正である任意の関数によって接続できることを意味します。

• { D=D(X) }
• { D[k] = D( X[k-1] ) }

ロールバックの計算には2つの関数を使用します。1番目は線形関数で、2番目は累乗関数です。後者はより難しいですが、より興味深いものです。関数は次のとおりです。

• { D = K * X }
• { D = DMin + C * Pow(S , X) }

検出される係数が強調表示されています。関数の動作はこれらの係数に基づいて異なるため、特定の通貨ペアまたは時間枠に合わせてストラテジーを柔軟に調整できます。

1. { K } - 線形関数のロールバック係数(自動システムの入力パラメータとしても使用されます) 
   
2. {DMin} - 許容される最小ロールバック(D> = DMin、累乗関数の場合)
   
3. {C} - 累乗関数のスケーリング係数
4. {S} - 累乗の底

厳密に言えば、Cを次数に追加することもできますが、この形式の方が読みやすく使いやすいと思います。また、値KおよびDMinは入力パラメータであるため、これらの係数はすでにわかっていることに注意してください。残りの2つの係数を計算する方法は明確ではないので、今明確にしましょう。2つの未知の値を見つけるには、少なくとも2つの連立方程式が必要です。係数は、連立方程式を解くことによって見つけることができます。このような連立方程式を作成するには、まず関数形式をどのように制御するかを決定する必要があります。実際、現在の形式の累乗関数を選択しました。これは、ロールバックを滑らかに減少させる方が簡単で便利なためです。これが、累乗関数を選択した理由です。考慮事項は次のとおりです。

1. {HalfX} - 追加のロールバックの半分の価格変動(関数を制御するための追加の入力パラメータ)
2. { D(0) = DMin + K*DMin }
3. { D(HalfX) = DMin + K*DMin/2 }

したがって、必要な連立方程式を取得し、これを解きます。言い換えると、ロールバックへの追加が開始時の値の半分である最初の未決済注文に対して、価格の動きを損失に向けて設定します。この追加は、開始時に最大値を持ちます。その結果、最小ロールバック未満の値をとることができない関数が得られ、Xが無限大に向かうと、関数は最小ロールバックに向かいます。数学的には、次のように表されます。

• { D >= DMin }
  
• { Lim( X -> +infinity ) = DMin }

これで、この連立方程式を解き始められますが、まず全体を書き直してみましょう。

1. { DMin + C * Pow(S , 0) = DMin + K*DMin } 
2. { DMin + C * Pow(S , HalfX) =  DMin + K*DMin/2 }

最初の方程式では、すべての数の0乗は1である事実を考慮して、Cをすぐに見つけることができます。S変数を除外します。ここで行う必要があるのは、C変数について方程式を解くことだけです。

• { С = K * DMin }
  

Cがわかったので、C変数を前の式に代入するだけで、残りの未知のSを見つけることができます。

• { Pow(S , HalfX) = 0.5 }

次数を削除するには、方程式の両方の部分をHalfXの逆数乗する必要があります。その結果、次の簡単な式が得られます。これが目的の係数になります。

• { S = Pow(0.5  , 1/HalfX) }

係数を代入することで累乗関数を書くことができます。このストラテジーを実装するのに必要なのはこれですべてです。

• { D(X) = DMin + K *  DMin * Pow( Pow(0.5  , 1/HalfX)  , X ) }

この関数はコードではこのように見えます。

コード:

double D(double D0,double K0,double H0,double X)
   {
   return D0+(D0*K0)*MathPow(MathPow(0.5,1.0/H0),X);
   }

理論をテストするためにEAで使用されるいくつかの重要な関数を次に示します。1つ目は、価格からシリーズ内の最も近い未決済注文までのポイント単位の距離を決定する関数です。

double CalculateTranslation()
   {
   bool ord;
   bool bStartDirection;
   bool bFind;
   double ExtremumPrice=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL ) bStartDirection=false;
         if ( OrderType() == OP_BUY ) bStartDirection=true;
         ExtremumPrice=OrderOpenPrice();
         bFind=true;
         break;
         }
      }      
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                        
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         if ( OrderType() == OP_BUY && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         }
      }
   if ( bFind )
      {
      if ( bStartDirection ) return (ExtremumPrice-Close[0])/_Point;
      else return (Close[0]-ExtremumPrice)/_Point;      
      }   
   else return -1.0;
   }

この関数は、シリーズの注文間で必要な手順に準拠するために必要です。この手順は固定されます。「Close []」配列はMQL5に実装されていないので、以前の記事で示したように、実装する必要があります。この手順は非常に明確だと思います。

現在のXとDを計算するために、他のすべての関数と同様に、戻り値を持たない次の関数を使用します。結果をグローバル変数に書き込みます。注文へのアクセスを最小限に抑え、履歴を処理する関数の不要な呼び出しを回避することをお勧めします。

double Xx;//shift of X
double Dd;//desired rollback of D
void CalcXD()//calculate current X and D
   {
   bool ord;
   bool bStartDirection=false;
   bool bFind=false;
   double ExtremumPrice=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL ) bStartDirection=false;
         if ( OrderType() == OP_BUY ) bStartDirection=true;
         ExtremumPrice=OrderOpenPrice();
         bFind=true;
         break;
         }
      }   
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                        
      if ( OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         if ( OrderType() == OP_SELL && OrderOpenPrice() < ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         if ( OrderType() == OP_BUY && OrderOpenPrice() > ExtremumPrice ) ExtremumPrice=OrderOpenPrice();
         }
      }
   Xx=0.0;
   Dd=0.0;   
   if ( bFind )
      {
      if ( !bStartDirection ) Xx=(Close[0]-ExtremumPrice)/_Point;
      if ( bStartDirection ) Xx=(ExtremumPrice-Close[0])/_Point;
      if ( MODEE==MODE_SINGULARITY ) Dd=D(DE,KE,XE,Xx);
      else Dd=Xx*KE;
      }      
   }

このコードはMT4Ordersライブラリと完全に互換性があるため、MQL5でコンパイルできます。これは、後に説明する関数についても同じです。アルゴリズムの入力変数は黄色で強調表示されています。

現在の利益と予測される利益を計算するには、次の3つの変数を使用します。

double TotalProfitPoints=0.0;   
double TotalProfit=0;
double TotalLoss=0;   

戻り値はこれらの変数に追加されますが、関数自体には戻り値がありません。これにより、毎回注文の反復が回避されます。反復すれば、コード操作が数回遅くなります。

次の2つの関数の1つは決済条件に使用され、2番目の関数は現在開いているポジションの予測利益を計算するために使用されます。

void CalcLP()//calculate losses and profits of all open orders
   {
   bool ord;
   double TempProfit=0.0;
   TotalProfit=0.0;   
   TotalLoss=0.0;    
   TotalProfitPoints=0.0;
   
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         TempProfit=OrderProfit()+OrderCommission()+OrderSwap();
         TotalProfitPoints+=(OrderProfit()+OrderCommission()+OrderSwap())/(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE));
         if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit;
         else TotalLoss-=TempProfit;
         }
      }
   }
   
void CalcLPFuture()//calculate losses and profits of all existing orders in the future
   {
   bool ord;
   double TempProfit=0;
   TotalProfit=0;   
   TotalLoss=0;    
    
   for ( int i=0; i<OrdersTotal(); i++ )
      {
      ord=OrderSelect( i, SELECT_BY_POS, MODE_TRADES );
                            
      if ( ord && OrderMagicNumber() == MagicF && OrderSymbol() == Symbol() )
         {
         TempProfit=OrderProfit()+OrderCommission()+OrderSwap()+(OrderLots()*SymbolInfoDouble(Symbol(),SYMBOL_TRADE_TICK_VALUE)*Dd);
         if ( TempProfit >= 0.0 ) TotalProfit+=TempProfit;
         else TotalLoss-=TempProfit;
         }
      }
   }

また、注文シリーズの決済条件の述語関数は次のとおりです。

bool bClose()
   {
   CalcLP();
   if ( TotalLoss != 0.0 && TotalProfit/TotalLoss >= ProfitFactorMin ) return true;
   if ( TotalLoss == 0.0 && TotalProfitPoints >= DE*KE ) return true;
   return false;
   }

エキスパートアドバイザーのテスト:

このメソッドを適切に適用すると、ほとんどすべてのスプレッド、手数料、スワップを克服できるため、説明した原則を使用してMetaTrader5のエキスパートアドバイザーを作成しました。平均化を利用したEAのテスト結果は次のとおりです。

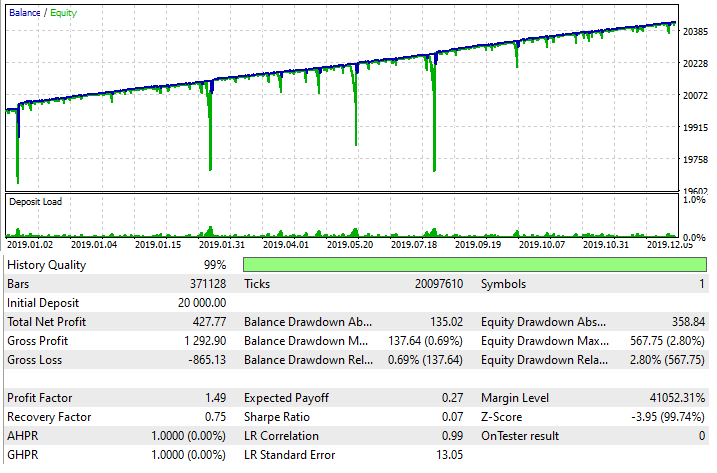
ただし、これは非常に注意深く使用する必要がある取引技術にすぎないことに注意してください。それにもかかわらず、柔軟性は非常に高く、さまざまなストラテジーと組み合わせて使用できます。繰り返しになりますが、ご注意ください。

取引技術の一貫性の直接的および間接的な兆候

本稿の枠組みの中では、どの数学的バックテスト変数が、使用された技術がストラテジーを強化したり負けストラテジーを有益に変えたりすることを証明できるかを考えることは有用です。この質問は非常に重要です。バックテストの結果を誤って解釈すると、実際に機能する技術を除外したり、間違った技術を利用したりする可能性があるためです。新しい取引技術を開発するとき、私は常に2つのルールに従います。これらのルールは、作業技術を検出する可能性と誤った技術を拒否する可能性が最高になるための必要十分条件を作成します。

1. データサンプルのサイズとバックテストでの取引数は、統計的評価のために最大化する必要があります。
2. バックテスト値のわずかな変化でさえ、プラスの変化を示している可能性があります。

多くの場合、すべてのプラスの変化は、増幅して取引に役立てることができます。否定できないメリットがあります。

1. このような取引技術は、あらゆる取引手段で機能します。
2. 技術を組み合わせてハイブリッドに変えることができます。
3. 正しく使用すると、スプレッドがあっても、損失を出すよりも利益を生み出す可能性が高くなります。

次に、取引技術を使用するときに分析する必要のある変数を示します。本稿で説明した最後の取引技術の例を使用してみましょう。バックテスト指標から始めて、それらを使用して合成指標を作成し、改善を検出する方法を見てみましょう。

まず、次の変数に注意してください。

• 最終的なバックテストの利益
• 最大残高ドローダウン
• 最大エクイティドローダウン

役立つ可能性があるが、ストラテジーテスターレポートでは利用できない、追加のより正確な変数がいくつかあります。

• 平均残高ドローダウン
• 平均エクイティドローダウン

これらの指標がシステムの安全性と収益性を正確に示しているのはなぜでしょうか。重要なのは、デモ口座やリアル口座で取引する取引システムのように、バックテストには次の数学的アイデンティティがあるということです。

• { i = 0 ... 1 ... 2 ... m } - 半波の数(半波は1つの上昇しているエクイティまたは残高セグメントで、その後に下降するセグメントが続きます)
• {j = 0 ... 1 ... 2 ... k} - 負の半波セグメント(残高セグメントは、ポジションの開始点と決済点で開始および終了し 、エクイティセグメントは他のポイントで終了および開始します)
• { OrderProfit[j]-OrderComission[j]-OrderSwap[j] < 0 !  Lim( m --> +infinity ) [ Summ(i) [Summ(j) [ OrderProfit[j]-OrderComission[j]-OrderSwap[j] ]] / m  ] = 手数料スプレッドとスワップを除く総利益 } - バックテストまたは取引残高の平均ドローダウン
• { SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] < 0 !  Lim( m --> +infinity ) [ Summ(i) [Summ(j) [ SegmentEquity[j]-SegmentComission[j]-SegmentSwap[j] ]] / m  ] = 手数料スプレッドとスワップを除く総利益   } - バックテストまたは取引残高の平均ドローダウン

言い換えれば、取引手数料がゼロの場合、デモ口座またはリアル口座でのストラテジーの無限のバックテストまたは無限の使用を伴う平均ドローダウンは、残高とエクイティの両方の観点から、最終的な残高の額にになりがちです。もちろん、これはストラテジーに明白なプラスの利益があるる場合にのみ当てはまります。総利益がマイナスの場合は、ミラー式を試すことができます。この式では、マイナスのセグメントではなくプラスのセグメントを合計します。ただし、既知のプラスのバックテストを使用して操作し、それにいくつかの技術を適用するのが最も便利です。ただし、これはグローバルバックテストが利益を示すことを意味するものではありません。ストラテジーが利益を示している履歴間隔(できればいくつかのそのような間隔)を見つけてから、アプローチを適用します。 

ここで、単純なマーチンゲールを使用して、安定性を強化し、パフォーマンスをわずかに利益にシフトする方法を見てみましょう。上記の式に基づいて、そのような合成指標を作成することができます。これに従って、いくつかの小さなセグメントに基づいて、取引全体に対する取引技術の影響を評価することができます。

合成指標の入力データ:

• { Tp } - 最終的なバックテストまたは取引利益
• { BdM } -  平均残高ドローダウン
• { EdM } - 平均エクイティドローダウン
• { BdMax } - 最大残高ドローダウン
• { EdMax } - 最大エクイティドローダウン

バックテストから利用できないデータは色で強調表示されています。ただし、このデータはコードで計算して、取引またはバックテストの最後に表示できます。しかし、私は利用可能な他のデータを使用することを好みます。重要なのは、ほとんどの場合、平均ドローダウンが小さいほど、両方の値からの最大ドローダウンが小さくなるということです。これらの値は確率と非常に密接に関連しており、ある指標の変化は通常、別の指標のほぼ比例した変化を伴います。 

合成指標:

• { A = Tp/BdM } - ストラテジーが将来を予測できない場合は1に等しく、ストラテジーが予測して利益を生み出す方法を知っている場合は複数になります(これは 収益性に関する質問に答える事と同じです)
• { B = Tp/EdM } - 前の値と同じ
• { C = Tp / BdMax } - この指標が増加した場合、この技術はメソッドの有効性を高めると結論付けることができます(減少はマイナスの効果を意味します)
• { D = Tp / EdMax } - 前の値と同じ

これらの4つの基準のいずれかを使用できます。最初の2つはより正確ですが、バックテストではそれらを計算するために必要なデータを提供できないため、入力データを読み取る必要があります。他の2つは、バックテストの値を使用して計算できます。最後の2つの指標は利用可能であり、簡単に見つけることができるため、個人的には使用しています。ここで、ストップ注文で閉じる単純なマーチンゲールの例を使用して、この手法のアプリケーションを見てみましょう。最後のエキゾチックなアプローチを使用して、その変数を強化しようとします。

残高とエクイティの波の使用

理論

実際、この技術はマーチンゲールだけでなく、取引頻度が十分に高い他のストラテジーにも使用できます。この例では、残高のドローダウンに基づく指標を使用します。残高に関連するすべてがより簡単であると考えられているからです。残高チャートを上昇セグメントと下降セグメントに分割しましょう。2つの隣接するセグメントが半波を形成します。取引数が無限大に向かうと、半波の数は無限大に向かいます。マーチンゲールの収益性を少し高めるには、有限のサンプルで十分です。次の図でアイデアを説明します。

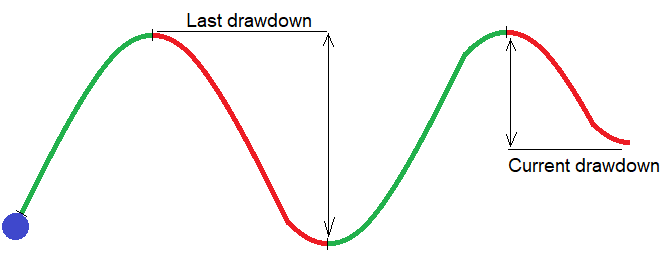
この図は、形成された半波と始まったばかりの半波を示しています。残高グラフは、このような半波で構成されています。これらの半波のサイズは絶えず変動し、チャート上ではそのような半波のグループを常に区別することができます。これらの半波のサイズは、一方の波では小さく、もう一方の波では大きくなります。したがって、ロットを徐々に下げることで、現在のグループに主要ドローダウンのある半波が現れるまで待つことができます。この重要なドローダウンの多くはシリーズ内で最小限になるため、これにより、すべての波のグループの全体的な平均指標が増加し、その結果、元のテストの同じパフォーマンス変数も増加するはずです。

実装するには、マーチンゲール用に2つの追加の入力パラメータが必要です。

• { DealsMinusToBreak } - 前のサイクルで負けた取引の数で、これに達すると、サイクルの開始ロットが開始値にリセットされます
• {LotDecrease} - 取引履歴に新しいサイクルが表示されたときにサイクルの開始ロットを減らすための手順

これらの2つのパラメータにより、安全な半波グループのロットを増やし、危険な半波グループのロットを減らすことができます。これにより、理論的には、上記のパフォーマンス指標が増加します。

次のコードがマーチンゲールEAに追加されます。次のサイクルの開始ロットを計算し、必要に応じてリセットします。

コード:

double DecreasedLot=Lot;//lot to decrease
double CalcSmartLot()//calculate previous cycle
   {
   bool ord;
   int PrevCycleDeals=0;
   HistorySelect(TimeCurrent()-HistoryDaysLoadI*86400,TimeCurrent());
   for ( int i=HistoryDealsTotal()-1; i>=0; i-- )
      {
      ulong ticket=HistoryDealGetTicket(i);
      ord=HistoryDealSelect(ticket);
      if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
      && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
      && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
         {
         if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) > 0 )
            {
            for ( int j=i+1; j>=0; j-- )//found a profitable deal followed by losing (count them)
                {
                ticket=HistoryDealGetTicket(j);
                ord=HistoryDealSelect(ticket);
                if ( ord && HistoryDealGetString(ticket,DEAL_SYMBOL) == _Symbol 
                && HistoryDealGetInteger(ticket,DEAL_MAGIC) == MagicC 
                && HistoryDealGetInteger(ticket,DEAL_ENTRY) == DEAL_ENTRY_OUT )
                   {
                   if ( HistoryDealGetDouble(ticket,DEAL_PROFIT) < 0 )
                      {
                      PrevCycleDeals++;
                      }
                   else
                      {
                      break;
                      }
                   }                
                }
            break;    
            }
         else
            {
            break;
            }
         }
      }
      
   if ( PrevCycleDeals < DealsMinusToBreak ) DecreasedLot-=LotDecrease;
   else DecreasedLot=Lot;
   if ( DecreasedLot <= 0.0 ) DecreasedLot=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);

   return DecreasedLot;
   }

入力パラメータは黄色で強調表示されます。これはテスト関数であり、この形式でストラテジーテスターでのテストにのみ適していることに注意してください。ただし、この仮定の最初の大まかな簡単なテストを実行するだけで十分です。この記事では、アイデアを理解するために必要な最小限のコードのみを提供しています。読者の気を散らさないように、残りのEAコードは提示しません。記事の執筆中に作成された他のEAについても同じです。次に、通常のマーチンゲールをテストしてから、新しいモードをオンにして、パフォーマンス変数にどのように影響するかを確認します。このエキスパートアドバイザーはMetaTrader5用にも設計されています。これは、最初のシグナルが通常のマーチンゲールであり、異なるスプレッドでも同じように機能するためです。

エキスパートアドバイザーのテスト:

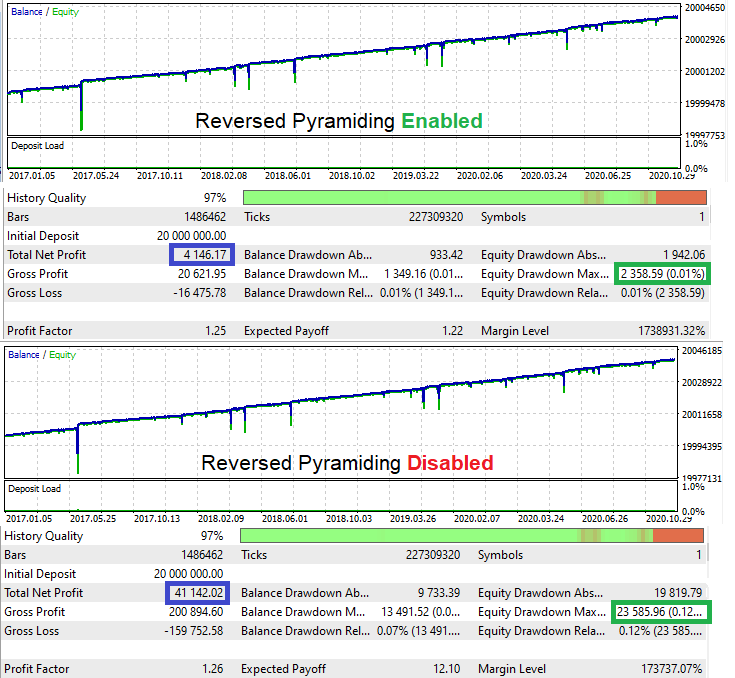
元のテストのDを計算すると、1.744の値になります。新しいモードを有効にすると、この値は1.758になります。収益性はわずかに正しい方向にシフトしています。もちろん、この値はさらにいくつかのテストを実行すると下がる可能性がありますが、平均して増加するはずです。厳密に言えば、デモンストレーションにはロジックで十分です。

終わりに

本稿では、自動取引システムの開発者に役立つような最も興味深く有用な技術を収集しようとしました。適切な調査と研究を経て、これらのいくつかは利益を改善するのに役立ちます。この資料がおもしろくて役立つことを願っています。これらの技術はツールボックスとして見なすことができますが、聖杯を構築する方法のガイドではありません。そのような技術に精通しているだけでも、無茶な投資や重大な損失からは救われるでしょう。より多くの時間と労力を投資することによって、2つの指標の交差に基づく従来の取引システムよりも興味深く安定したシステムの作成を試みることができます。