デニス、 私はこの記事についてこうコメントしている。
理論に関しては、何の疑問もなく、すべてが詳細に示されている。
実践に関しては、経験的ヒストグラムを示した図、特に図2に注目していただきたい。 ポイントは、あなたの分析において2つの非常に重大な誤りがあったということです。
第一に、ヒストグラムを生成するスクリプトのクラス数が9と少なすぎます。もちろんサンプル・サイズが許せば(許しますが)、間違いはないでしょう。もしそうしていれば、対数正規分布の検定も、ハイパーセカンのリターンの検定も、否定的な結果になることを確認できただろう。ちなみに、このような2つの分布が同時にある値とそのモジュラスを表すことができないことを確認するのは非常に簡単で、ハイパーセカンスの「半分」を取ってそれ自身と畳み込めばよいのです(確率変数からモジュラスを取るのと同じです):対数正規分布は間違いなく得られません。
2つ目の不正確さは、リターン分布の頂点(別名期待値)は正確に0でなければならないという先験的知識を使用していないことです(そうでなければ、私たちはとっくに億万長者になっているはずです)。図2のヒストグラムが右にシフトしているように見えるのはそのためです。繰り返しになるが、ヒストグラムをプロットする 際にこの点を考慮すれば、テストの信頼性が高まるだろう。
P.S.私はモデリングの基本について記事を書いている。あなたの記事をありがとうございました。ありがとうございました。
...まず、ヒストグラムを生成するスクリプトのクラス数が少なすぎます - たった9クラスです。もちろんサンプル・サイズが許せば(許しますが)、間違いはないでしょう。この方法でやっていれば、対数正規分布の検定が否定的な結果になることも、ハイパーセカンのリターンの検定が否定的な結果になることも確認できただろう。ちなみに、このような2つの分布がある値とそのモジュラスを同時に表すことができないことを確認するのは非常に簡単です。ハイパーセカンスの「半分」を取って、それ自身と畳み込む(ランダムな値からモジュラスを取ることの類似)だけです:対数正規分布は間違いなく得られません。
alsu 様、ご意見ありがとうございます!
順を追って説明しましょう。
クラス数は任意に設定するのではなく、何らかの公式に従って 設定します。私の場合は スタージス式です。最もポピュラーなルールのひとつだ。それは完璧ではない。でも、それでも......。
どんなルールに従って200~300クラスを取るんだ?
2つ目の不正確さは、リターンの分布の頂点(別名期待値)は正確に0でなければならないという先験的知識を使わなかったことです(そうでなければ、私たちはとっくに億万長者になっているはずです)。図2のヒストグラムが右にシフトしているように見えるのはそのためです。繰り返しになるが、ヒストグラムを作成する際にこの点を考慮すれば、テストの信頼性が高まるだろう。
私は事実に基づいてサンプルを分析する。私は自分が持っているものを分析する。そして、どのような根拠に基づいて歩留まり分布の頂点が正確に0点になるべきなのか?何か誤解しているのかもしれないが...。
それに、フィッティングが実施された分布(X~HS(-0.00, 1.00))を見れば、最初のパラメータ(シフト・パラメータ)が正確に0であることは簡単にわかる。実際、これは期待値と等しい。
こちらも標準値のサンプリングに関するhtmlレポートである。多少なりとも読みやすい図になっていれば幸いである。しかし、記事のものと同一ではない。今、最新のデータを取ってきたところだ。
ご覧の通り、平均は0である。そして最もフィットするのは双曲線セカント分布です:X~HS(0.00, 1.00)。
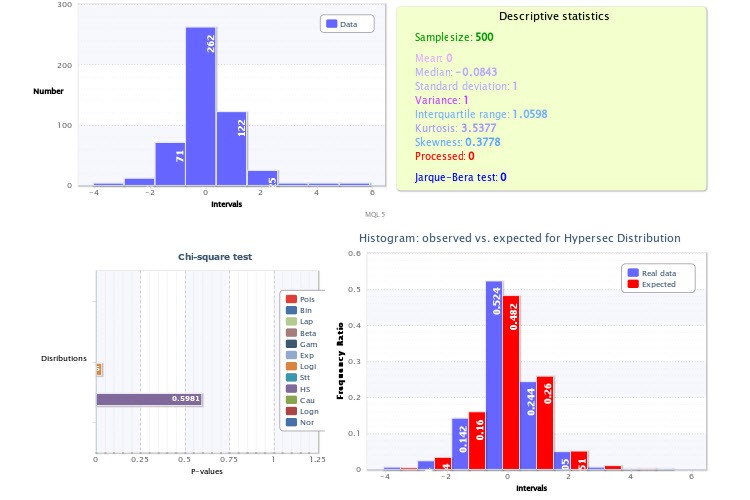
その通り、スタージェスの公式は正確に9クラスを与えたが、これはむしろサンプルサイズを増やすことを考える理由である(公式を逆にすると、あなたは256ぐらいになるのですね?)
その上、この公式は正規分布(この公式が導き出された)の一般的な母集団に対してのみうまく機能し、考えられるように、サンプル・サイズは200値以上ではありません。DiakonisやScottなどの別の公式を使うこともできます。
一般的に、スタージェスは自分の公式を論理的に正当化することはしていない。それがクラス数の選択効率の問題にどう影響するのか?最適性の基準は著者によって定義されたことはなく、式自体も適当に書かれたものである。しかし重要なのは、長い間スタージェスのアプローチが唯一何らかの形で公式化されたものであり、すべての統計パッケージに自動的に(そして私に言わせれば非常に軽率に!)含まれていたということである。
繰り返しになりますが、代替の計算式もありますが、パソコンがあるからこそ、逆説的ですが、自分の頭を装置、つまり、この特定の標本に最適なクラス数を多かれ少なかれ決定する視覚的な方法として使う機会が得られるのです。ちなみにこの方法は、どんな計算式よりも優れていて速いことが多い。
私はいつもみんなに言う--数式に数字を入れる前に、それが何を意味し、どのように(そして適用するかどうか)尋ねるように。要するに、私はスタージェスの公式を使うことには反対である。)
平均について。リターンの期待値は0であるべきだ。そうでなければ、このMOの符号に対応する一方向に常に賭けることができ、あらかじめ決められた大きさのリターンを得ることが保証されるからだ。グラフの左半分は右半分の鏡像であるべきであり(増加率と減少率は統計的に等しく、両者の間に差はないはずである)、対称性の中心は中心に一致する。
したがって、HS(0.00, 1.00)を取るので、クラスを中央に置くべきです - つまり、ゼロクラスはある対称 区間(-x0;x0)のインデックス値を含むべきです。あなたの点0はゼロクラスの真ん中ではない。
実際、離散データでどのようにクラスを対称にするかという問題は非常に非自明であり、繰り返しになりますが、各特定の標本について個別に非常に注意深く解くのがよいでしょう。
alsu、 私の記事のテーマではないが、非常に興味深いトピックに触れてくれた。できる限り、この問題をさらに研究するつもりだ。
建設的なご批判をありがとうございました!
トレーディングにおける科学的知識の適用可能性についてのあなたの意見が気に入りました。
確率論や数理統計に詳しい人にお勧めの本を教えていただけますか?
デニス、こんにちは。トレーディングにおける科学的知識の適用可能性についてのあなたのご意見が好きです。確率論や数理統計に詳しい人にお勧めの本を教えてください。
ご意見ありがとうございます!
初心者向けの本がいいと思います。その本の本文が、その本を読む意欲をそがないものでなければなりません :-))).
私はガイディシェフが好きだったし、ブラシェフも好きだった。
ここに 興味深いスレッドがある。
- rsdn.org
つ目の不正確さは、リターンの分布の頂点(別名期待値)は正確に0でなければならないという先験的知識を用いていないことだ(そうでなければ、とっくの昔に全員が億万長者になっているはずだ)。
そうではありません。分布の頂点が0から相対的にずれる(商品の成長/衰退)ことは、それが将来も同じであることを意味しない。だから、ほとんどのトレーダーは億万長者ではないのだ。
ありがとう。
...分布の頂点が0(上昇/下降する楽器)に対して相対的にずれることは、それが将来もそうであることを必ずしも意味しない...
同感です。
alsu さんに質問です。ゼロ・ポイントというのは市場効率のことですか?
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事 トレーダーの作業における統計的分布の役割 はパブリッシュされました:
本稿は、理論的統計的分布に連携するクラスについて述べた拙著『MQL5 における投擲的可能性』の続編です。われわれには理論的基盤があるので、現実のデータ設定に進み、こ基盤を情報的に利用していきたいと思います。
作者: Dennis Kirichenko