知っておくべきMQL5ウィザードのテクニック（第74回）： 教師あり学習で一目均衡表とADX Wilderのパターンを利用する

はじめに

前回の記事では、一目均衡表とADX Wilderのインジケーターペアを、サポート/レジスタンスとトレンドを補完するツールとして紹介しました。いつものように、これらをウィザードで組み立てたエキスパートアドバイザー(EA)でテストし、10種類のシグナルパターンを検証しました。このインジケーターペアに関しては、ほとんどのパターンが前年度のテスト・最適化を経て、1年間のフォワードウォークでも収益を上げることができました。しかし、Pattern_0、Pattern_1、Pattern_5の3つは満足いく結果が得られませんでした。そこで今回の記事では、教師あり学習がこれらのパターンのパフォーマンス向上にどの程度寄与するかを検証します。具体的には、各パターンのシグナルを単純な入力ベクトルとしてニューラルネットワークに再構築し、ニューラルネットワークを追加のフィルタとして機能させるアプローチを採用します。

ネットワーク

今回の教師あり学習モデルとしては、スペクトル混合カーネルに基づくニューラルネットワークを採用します。このカーネルは、以下の数式で定義されます。

ここで

• τ (\tau)：2点間の時間差
• Q：スペクトル成分の数
• wi​：i番目の成分の重み（振幅）
• li​：i番目の成分の長さスケール（減衰を制御）
• fi​：i番目の成分の周波数（振動の速さ）

本記事では、このスペクトル混合カーネルを用いて、単純なニューラルネットワークの入力層を定義しています。その後に続く層として、PyTorchのLinear層を使用しています。私たちが作成し使用している層は、スペクトル混合層と呼ばれるものです。この層と、それに続く回帰ネットワークは、以下に示すようにPythonで実装しています。

class DeepSpectralMixtureRegressor(nn.Module):
    def __init__(self, input_dim=2, num_components=96):
        super().__init__()
        self.smk = DeepSpectralMixtureLayer(input_dim, num_components)
        feature_dim = input_dim * num_components  # 2 * 96 = 192

        self.head = nn.Sequential(
            nn.Linear(feature_dim, 1024),
            nn.ReLU(),
            nn.Linear(1024, 512),
            nn.ReLU(),
            nn.Linear(512, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, 1)  # <--- Removed sigmoid!
        )

    def forward(self, x):
        features = self.smk(x)
        output = self.head(features)
        return output

一部の研究では、入力層でスペクトル混合カーネルを使用することで、入力データから特徴量を抽出できることが示唆されています。また、その後の層の回帰ヘッドは、モデルが回帰タスクの場合に適しており、私たちのSigmoidの使用例でも確認できます。私たちが実装したスペクトル混合カーネルでは、最初の層が周期的なデータのモデリングをおこない、その後の回帰層/ヘッド層がネットワークの周波数、分散、重みを学習します。この実装アプローチは、入力データに振動パターンを含む回帰タスクに最適です。また、ニューラルネットワークの柔軟性とガウス過程の概念を統合しています。

私たちのネットワークは「DeepSpectralMixtureRegressor」と名付けています。また、モジュラー構造を採用しており、大きく2つの部分に分かれています：特徴抽出と回帰です。特徴抽出の最初の部分は、特にDeepSpectralMixtureLayer関数によって処理されます。以下にそのコードを示します。

class DeepSpectralMixtureLayer(nn.Module):
    def __init__(self, input_dim, num_components):
        super().__init__()
        self.num_components = num_components
        hidden = 512  # Wider hidden layers

        # Go deeper with 4 layers
        def make_subnet():
            return nn.Sequential(
                nn.Linear(input_dim, hidden),
                nn.ReLU(),
                nn.Linear(hidden, hidden),
                nn.ReLU(),
                nn.Linear(hidden, hidden),
                nn.ReLU(),
                nn.Linear(hidden, num_components),
            )

        self.freq_net = make_subnet()
        self.var_net = nn.Sequential(*make_subnet(), nn.Softplus())
        self.weight_net = nn.Sequential(*make_subnet(), nn.Softplus())

    def forward(self, x):
        mu = self.freq_net(x)
        v = self.var_net(x)
        w = self.weight_net(x)

        expanded = x.unsqueeze(2)
        mu = mu.unsqueeze(1)
        v = v.unsqueeze(1)
        w = w.unsqueeze(1)

        x_cos = torch.cos(2 * np.pi * expanded * mu)
        x_exp = torch.exp(-v * expanded**2)
        features = w * x_exp * x_cos

        return features.flatten(start_dim=1)

上記の関数は、周波数・分散・重みをニューラルネットワークを用いて学習します。分散と重みにSoftplus活性化関数を用いることで、常に正の値が保証されます。回帰ヘッドは抽出された特徴を単一の出力にマッピングし、バウンディングされた回帰や二値分類にはSigmoid活性化を使用します。このアーキテクチャの利点はその適応性にあり、モデルはさまざまなデータパターンに対応できます。これにより、特に周期成分を含む時系列予測などのタスクに適しています。ニューラルネットワークとカーネルベースのアプローチの両方を活用できる点が特徴です。

Wilson et al.(2013)では、スペクトル混合カーネルは、スペクトル密度を複数の成分の混合として表現する場合に、周期的パターンをモデル化するガウス過程で使用する共分散関数として、GPyTorchなどのライブラリで実装可能であることが指摘されています。本記事でのアプローチでは、周波数、分散、重みというカーネル成分をニューラルネットワークでパラメータ化することで、この概念をニューラルネットワークに応用しています。これにより、データ駆動型の特徴抽出が可能になり、特に周期的・振動的パターンを持つ時系列データの問題に適しています。この点は、Sebastian Callhのブログ記事でもスペクトル混合カーネルについて強調されています。また、このカーネルの適用方法に関しては、GPyTorchのドキュメントも参考にしています。 

要するに、固定パラメータのカーネルを使う代わりに、私たちのモデルはニューラルネットワークを用いて学習可能な周波数(μ)、分散(v)、重み(w)を生成します。このアプローチにより、さまざまなデータパターンへの適応が可能です。最初の特徴抽出層では、式「w⋅exp(−v⋅x2)⋅cos(2πμx)」を用いて特徴量を計算します。これは、コサインによる周期性のモジュレーションと指数関数的減衰の滑らかさを捉えるものです。DeepSpectralMixtureLayerとして特徴量抽出を一つの層にまとめ、回帰ヘッドを別のコンポーネントとして設計するモジュラー設計により、柔軟性が向上します。回帰ヘッドは、抽出された特徴量を単一出力にマッピングする深い全結合ネットワークで、シグモイド活性化を用いることで、前述したようにバウンディングされた回帰や二値分類に適しています。

コードを詳しく見ていくと、まずPyTorchや関連ライブラリの標準インポートから始まります。これらのインポートにより、テンソル操作、ニューラルネットワークの構築、最適化、データ処理、学習済みモデルのONNX形式へのエクスポート（第三者プラットフォームでの推論用）が可能になります。これは、モデルの構築、学習、デプロイを実現する上で重要です。当然のことながら、これはPyTorchベースの開発だけでなく、機械学習全般においても基盤となる内容です。ガイダンスとして、PyTorchとONNXのバージョン互換性を確保することは、学習時の効率的なデータ読み込みのために重要です。

次に、DeepSpectralMixtureLayer の初期化を設定します。この層では、周波数ネットワーク、分散ネットワーク、重みネットワークの3つのニューラルネットワークを定義します。各ネットワークは入力を成分数（コンポーネント数）にマッピングし、分散と重みがカーネルの定式化上正の値を維持するようにSoftplus活性化関数を使用します。これは重要です。なぜなら、これらのネットワークが個別にスペクトル混合カーネルをパラメータ化することで、ガウス過程を用いたデータ駆動型の特徴抽出を可能にするからです。パラメータnum_componentsは「特徴量の豊かさ」を制御します。このnum_componentsは、タスクの複雑さに応じて調整可能です。Softplus活性化を用いることで、数値的不安定性を引き起こす負の値を回避できます。

次に、ネットワークのフォワードパス関数を設定します。この関数は、前述の式に基づいてスペクトル混合特徴量を計算します。入力やパラメータをリシェイプし、回帰ヘッドにブロードキャストできる形にします。コサイン関数と指数関数の適用により、回帰層向けに出力をフラット化します。この基本的な変換は、スペクトル混合カーネルを模倣しています。入力xの形状は(batch_size, input_dim)に従う必要があります。また、指数関数の数値安定性を確認するために、分散vをクランプする必要がある場合があります。パラメータ「num_components」は、希望する特徴次元数に応じて調整可能です。

上記で特徴抽出層を扱ったので、次に回帰器に移ります。回帰器はモデル定義時に呼び出されるクラスであり、その主な目的は、上で説明したスペクトル混合層と全結合のヘッドを組み合わせることです。このヘッドは、カーネル特徴を単一出力にマッピングし、Sigmoidを用いて0–1の範囲に変換します。ヘッドのアーキテクチャは、層の数やサイズを増やすことでタスクの複雑さに応じて調整可能です。非バウンディング回帰の場合は、Sigmoidを削除することもできます。フォワード関数も、スペクトル層の関数と同様に定義されており、入力をスペクトル混合層で特徴抽出した後、ヘッドを通して最終出力を得ます。このフォワード関数により、エンドツーエンドの学習と推論が可能になります。

入力xのサイズはinput_dimと一致する必要があります。Sigmoid活性化を使用する場合、BCEなどの適切な損失関数が使用できます。パラメータ「num_components」はネットワーク性能に非常に敏感であり、スペクトル成分の総数を決定します。値を大きくすると表現力は高まりますが、過学習のリスクも増加します。最初は64程度から始め、データの複雑さに応じて調整するのが妥当です。スペクトル混合層は表現力が非常に高いため、学習時の過学習監視が重要です。正則化や早期停止を活用することで過学習を抑制できます。

学習されたμ、v、wの解析により、GPyTorchの例で示されるような周期パターンを理解することができます。従来のガウス過程モデルと比較すると、本アプローチには不確実性推定がありません。必要に応じて、これを定量化する追加手法を補うことが可能です。最後に、フォワードパスは計算コストが高くなる場合があります。特にnum_componentsが非常に大きい場合や高次元入力を使用する場合は、モデルのファインチューニングや最適化時に考慮すべき点です。

インジケーターの実装

前回の記事でテストしたシグナルパターンについては、ほとんどがフォワードウォークでまずまずの結果を示しましたが、Pattern_0、Pattern_1、Pattern_5は例外でした。振り返ると、2023年のGBP/USDを対象に10種類のシグナルパターンをテストし、最適化しました。通常の4時間足ではなく30分足を使用したのは、一般に一目均衡表のシグナルは大きな時間足ではそれほど頻繁に出現しないためです。フォワードウォークは、これまで通り2024年を対象におこないました。10パターンのうち7つは2025年でもフォワードウォークで利益を上げることができましたが、テスト期間はわずか2年のみであったため、ここで示す結果を実際の取引環境に持ち込む前には、より長期間の過去データでの追加テストと慎重な検証を読者に強く推奨します。

この前提を踏まえ、次に一目均衡表とADX Wilderのインジケーター関数がPythonでどのように実装されているか、またPattern_0、Pattern_1、Pattern_5の特徴量抽出関数について見ていきましょう。

Pythonでの一目均衡表

Ichimoku関数をPythonで次のように実装します。

def Ichimoku(df, tenkan_period: int = 9, kijun_period: int = 26, senkou_span_b_period: int = 52, displacement: int = 26) -> pd.DataFrame:
    """
    Calculate Ichimoku Kinko Hyo components and append them to the input DataFrame.

    The components are:
        - Tenkan-sen (Conversion Line)
        - Kijun-sen (Base Line)
        - Senkou Span A (Leading Span A)
        - Senkou Span B (Leading Span B)
        - Chikou Span (Lagging Span)

    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', and 'close' columns.
        tenkan_period (int): Lookback period for Tenkan-sen (default 9).
        kijun_period (int): Lookback period for Kijun-sen (default 26).
        senkou_span_b_period (int): Lookback period for Senkou Span B (default 52).
        displacement (int): Forward displacement of Senkou spans and backward shift of Chikou span (default 26).
        
    Returns:
        pd.DataFrame: Input DataFrame with added Ichimoku columns.
    """
    # Input validation
    required_cols = {'high', 'low', 'close'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high', 'low', and 'close' columns")
    if not all(p > 0 for p in [tenkan_period, kijun_period, senkou_span_b_period, displacement]):
        raise ValueError("All period values must be positive integers")

    result_df = df.copy()

    # Tenkan-sen (Conversion Line)
    high_tenkan = result_df['high'].rolling(window=tenkan_period).max()
    low_tenkan = result_df['low'].rolling(window=tenkan_period).min()
    result_df['Tenkan_sen'] = (high_tenkan + low_tenkan) / 2

    # Kijun-sen (Base Line)
    high_kijun = result_df['high'].rolling(window=kijun_period).max()
    low_kijun = result_df['low'].rolling(window=kijun_period).min()
    result_df['Kijun_sen'] = (high_kijun + low_kijun) / 2

    # Senkou Span A (Leading Span A)
    result_df['Senkou_Span_A'] = ((result_df['Tenkan_sen'] + result_df['Kijun_sen']) / 2).shift(displacement)

    # Senkou Span B (Leading Span B)
    high_span_b = result_df['high'].rolling(window=senkou_span_b_period).max()
    low_span_b = result_df['low'].rolling(window=senkou_span_b_period).min()
    result_df['Senkou_Span_B'] = ((high_span_b + low_span_b) / 2).shift(displacement)

    # Chikou Span (Lagging Span)
    result_df['Chikou_Span'] = result_df['close'].shift(-displacement)

    return result_df

上記で作成した関数は、各種インジケーターコンポーネントを計算し、入力のデータフレームに追加します。デフォルトでは、転換線は期間9、基準線は期間26、シフトは26、先行スパンBは期間52が設定されています。コードの冒頭部分では、まず入力データの検証をおこなっています。これにより、データフレームに必要な価格列が存在すること、また期間パラメータが正の値であることを確認し、計算エラーを防止しています。このステップは、データの整合性を保ち、実行時エラーを回避する上で非常に重要です。インジケーター関数は有効な実行時データで動作する必要があるため、処理前に入力を検証し、欠損データや不正なパラメータを適切に処理することが最良の実践となります。

検証が完了した後、まず転換線の計算をおこないます。本コードでは、過去「転換期間」における最高値と最安値の平均を算出しています。通常、期間は9とし、短期的なトレンドを示すインジケーターとして機能します。このバッファは、基準線との交差時に反転の可能性を示すシグナルとして有用であり、最近の価格動向を反映するため、短期売買の意思決定に役立ちます。また、転換期間を調整することで、短期価格変動に対する感度を変更することができます。期間を短くすると感度は高くなり、長くすると低くなります。

次に、基準線バッファを計算します。転換線と同様に、長めの期間（通常26）で算出され、中期的なトレンドを示すインジケーターとして機能します。基準線は、トレンド方向の確認やサポート/レジスタンスとして重要です。転換線と比較すると、やや安定した市場の見通しを提供し、中期分析に役立ちます。さらに、転換線とのクロスは売買シグナルとして活用されることがあります。

続いて先行スパンAを計算します。これは、転換線と基準線の平均値を計算し、先行シフト期間（通常26）だけ先行させた値です。このバッファは、雲の一方の境界を形成します。先行スパンAは将来のサポート/レジスタンスを示すため、こちらで議論されているように、トレンド分析において先見的な視点を提供します。価格と雲の相対的な位置関係を確認することが重要で、価格が雲の上にある場合は強気、下にある場合は弱気の見通しを示します。

次に先行スパンBの計算をおこないます。これは通常52期間の最高値と最安値の平均を算出し、先行させて雲のもう一方の境界を形成します。先行スパンBは長期的なサポート/レジスタンスを示し、特に長い時間軸でのトレンド識別を強化します。参考として、先行AとBの間隔（雲の厚さ）はボラティリティのインジケーターとして利用可能で、厚い雲は強いサポート/レジスタンスを示唆します。

最後に、遅行Spanの計算をおこないます。このバッファは、終値を先行シフト期間（通常26）だけ過去にずらした値であり、現在の価格と過去の価格を比較するために用います。これにより、現在の価格が過去の価格より上にあるか下にあるかを確認し、トレンドの確認・検証に役立ちます。遅行の主目的はトレンドの確認であり、先行シフト期間や長期平均期間を使用するため、十分な履歴データが必要となります。

PythonでのADX Wilder

Pythonで一目均衡表を定義した後は、ADX Wilderに取り組みます。本関数は、ワイルダーの手法を用いてADXを計算します。一目均衡表と同様に、入力の価格データフレームにADX、+DI、-DIの追加バッファを付加します。このインジケーターはデフォルトで期間14を使用しますが、一目均衡表との整合性を取るためや、価格変動への感度を高めるために調整することも可能です。それでも、ここではデフォルトの14を使用します。Pythonでの実装は次のとおりです。

def ADX_Wilder(df, period: int = 14) -> pd.DataFrame:
    """
    Calculate the Average Directional Index (ADX) using Wilder's method and 
    append the ADX, +DI, and -DI columns to the input DataFrame.

    ADX measures trend strength, while +DI and -DI measure trend direction.
    
    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', and 'close' columns.
        period (int): The lookback period to use. Default is 14.
        
    Returns:
        pd.DataFrame: Input DataFrame with 'ADX', '+DI', and '-DI' columns.
    """
    if not all(col in df.columns for col in ['high', 'low', 'close']):
        raise ValueError("DataFrame must contain 'high', 'low', and 'close' columns")
    if period <= 0:
        raise ValueError("Period must be a positive integer")

    result_df = df.copy()

    # Calculate directional movements
    up_move = result_df['high'].diff()
    down_move = result_df['low'].diff()

    plus_dm = np.where((up_move > down_move) & (up_move > 0), up_move, 0)
    minus_dm = np.where((down_move > up_move) & (down_move > 0), down_move, 0)

    # Calculate True Range (TR)
    high_low = result_df['high'] - result_df['low']
    high_close = np.abs(result_df['high'] - result_df['close'].shift(1))
    low_close = np.abs(result_df['low'] - result_df['close'].shift(1))
    tr = np.maximum(high_low, np.maximum(high_close, low_close))

    # Apply Wilder's smoothing
    atr = pd.Series(tr).rolling(window=period).mean()
    plus_di = 100 * pd.Series(plus_dm).rolling(window=period).sum() / atr
    minus_di = 100 * pd.Series(minus_dm).rolling(window=period).sum() / atr
    dx = 100 * np.abs(plus_di - minus_di) / (plus_di + minus_di)
    adx = dx.rolling(window=period).mean()

    result_df['+DI'] = plus_di
    result_df['-DI'] = minus_di
    result_df['ADX'] = adx

    return result_df

まず最初におこなうのは、関数への入力データの検証です。これにより、必要な価格列が存在すること、インジケーター期間が有効であることを確認し、計算エラーを回避します。これは、データの整合性を保ち、有効なデータ上で処理をおこなうために非常に重要です。また、欠損データが存在する場合には適切に処理する必要があります。検証が完了した後におこなうのは、方向性移動の計算です。これは、過去高値・安値の差分から「+DM」および「-DM」の動きを算出するもので、上昇・下降トレンドの強さを示します。この情報は、トレンドの方向性の評価や分析において重要です。正確な方向性差分を計算するためには、十分な履歴データが必要であり、データに欠落やギャップがないかも監視する必要があります。

実際の値幅(True Range)を計算します。これは、当日の高値−安値、当日の高値−前日終値、当日の安値−前日終値の中で最も大きい値を採用します。計算の一貫性を保つため、これらの差分は絶対値として扱います。この範囲により、方向性移動が異なる資産間でも比較可能な形に正規化され、ADXの計算要件に適合します。入力データフレームに欠損値が存在すると計算中にNaNエラーが発生するため、欠損がないことを確認することが重要です。

次に、実際の値幅を移動平均で平滑化します。同様に、「+DM」および「-DM」のバッファも平滑化し、正方向・負方向の指標を100スケールで表現できるよう正規化します。方向性指数「DX」は、「+DM」と「-DM」の絶対差を合計で正規化したもので、トレンドの強さを示すインジケーターです。最終的に、主要インジケーターバッファであるADXは、このDXをインジケーター期間（本記事では14）で平滑化したものとなります。この最終出力が、現在のトレンドの強さを測るインジケーターとして機能します。

前回の記事を振り返ると、ADXは0〜100の範囲でトレンド強度を表し、25以上であれば強いトレンドを示すことが多く、20以下であれば弱い、あるいは発生途上のトレンドであると考えられます。プラス方向性指数(+DI)およびマイナス方向性指数(-DI)は、それぞれ強気・弱気トレンドの強さを定量化し、両者の差はエントリーの売買シグナルとして活用できる可能性があります。使用する期間14も、必要に応じて感度を調整可能で、短い期間はシグナルやフラクタルポイントの早期検出に有利ですが、長い期間は変動が抑えられます。

前述のスペクトル混合カーネルを回帰ネットワークで適用する際、入力としてこれら2つのインジケーターからの情報を、単純な2次元ベクトルの形で取り込みます。過去の記事では、各パターンの様々なシグナルを0または1のブール値に分解し、入力ベクトルの次元を増やす手法も検討・実験しました。この手法は、学習・最適化では良好な結果を示しましたが、フォワードウォークでは期待通りの成果を得られませんでした。現在は、各インジケーターのシグナルやパターンをその一部に分解せず、単一のブール値に統合して使用しています。2次元ベクトルの各次元には、2つのインジケーターからの信号が組み合わされます。第1次元は強気シグナルの確認に、第2次元は弱気シグナルの確認に専念しています。

Feature_0

3つのパフォーマンスの低い特徴量（ラガード特徴量）を、Feature_0、Feature_1、Feature_5のネットワークに適用しています。PythonでFeature_0を次のように実装します。

def feature_0(df):
    """
    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['close'].shift(1) < df['Senkou_Span_A'].shift(1)) &
                     (df['close'] > df['Senkou_Span_A']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    feature[:, 1] = ((df['close'].shift(1) > df['Senkou_Span_A'].shift(1)) &
                     (df['close'] < df['Senkou_Span_A']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

この関数は、まず空のNumPy配列を作成することから始まります。この特徴量配列は、入力データフレームの行数に合わせてサイズを設定していますが、列は2列に固定しています。これにより、シグナル生成のためのクリーンスレートが確保され、前回の残留値が出力に影響することを防ぎます。次に、配列の1列目に値を代入します。これは強気シグナルを確認するための列であり、前回の記事で示した条件に従い、前日の終値が先行スパンAより下にあり、当日の終値が当日の先行スパンAを上回り、ADXが25以上の場合に各行に1を代入します。価格が先行スパンAを上抜ける強気クロスオーバーを検知することで、上昇トレンドの可能性を示唆します。ADXが25以上であることにより、弱いトレンド時の偽シグナルを減らすことができます。

この代入処理はNumPy配列を用いることで、複数行に対して同時に実行されます。これが、Pythonでモデルを開発・学習する際の大きな利点の一つです。続いて、配列の2列目には弱気シグナルの値を代入します。ここでは、前日の終値が前日の先行スパンAより上にあり、当日の終値が当日の先行スパンAを下回り、ADXが25以上の場合に1を設定します。これにより弱気クロスオーバーを検知し、下落トレンドの可能性を示します。ADXフィルタにより、トレンドの強さがシグナルを支持することが確認できます。

強気および弱気の値を代入した後、配列の最初の2行は値が存在せずNaNとなるため、これらを強制的に0に設定します。このパターンのみを用いてネットワークを学習させ、74_0.onnxとしてエクスポートし、MQL5 EAのカスタムシグナルクラスにインポートしました。前回の記事では、この特定のパターンはフォワードウォークで有意な成果を示しませんでした。しかし、今回ネットワークをインジケーター入力シグナルへの追加フィルタとして使用した場合、以下のような結果が得られました。

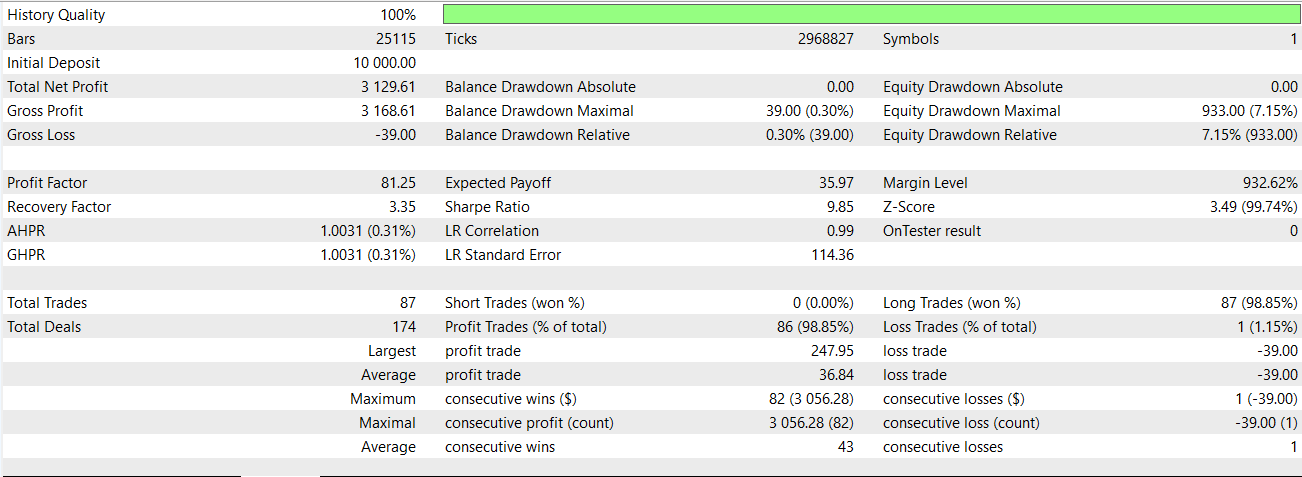
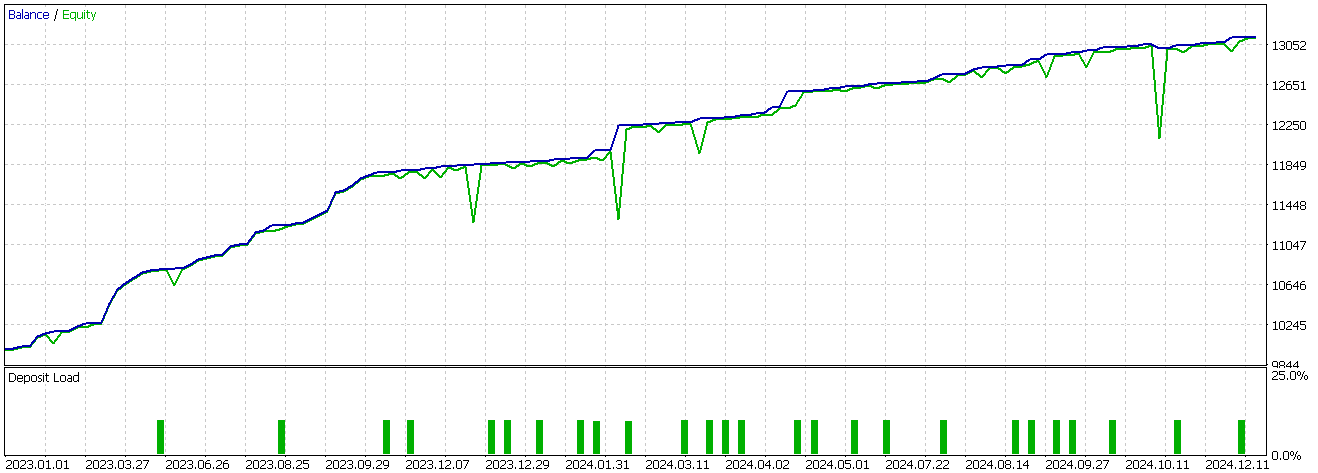
運用の状況は好転しているように見えますが、今回はロングポジションのみを対象としており、テストデータの範囲も限られているため、あくまで探索的な結果に留まります。Feature-0の買いシグナルは、チャート上で以下のように確認できます。

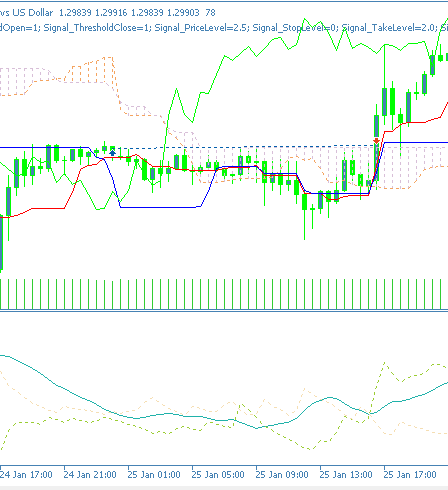
Feature_1

前回の記事でパフォーマンスが低迷したもう一つの特徴量（パターン）はFeature-1です。Pythonでの実装は次のとおりです。

def feature_1(df):
    """

    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['Tenkan_sen'].shift(1) < df['Kijun_sen'].shift(1)) &
                     (df['Tenkan_sen'] > df['Kijun_sen']) &
                     (df['ADX'] >= 20.0)).astype(int)
    
    feature[:, 1] = ((df['Tenkan_sen'].shift(1) > df['Kijun_sen'].shift(1)) &
                     (df['Tenkan_sen'] < df['Kijun_sen']) &
                     (df['ADX'] >= 20.0)).astype(int)    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

再び、出力用配列（ここではfeatureと命名）をゼロで初期化し、入力データフレームの行数に合わせてサイズを設定します。各行には2列を持たせ、強気および弱気のシグナルを記録できるようにしています。1列目には、強気シグナルが確認された場合に1を代入します。条件は、前回の転換線が前回の基準線より下にあり、かつ現在の転換線が現在の基準線を上回り、ADXが20以上であるということです。このシグナルは、転換線と基準線の強気クロスオーバーを捉えます。中期的なシグナルであり、主要トレンドの開始を予測するため、ADXは25である必要はなく、20で十分です。

弱気シグナルは、NumPy配列の各行の2列目に入力され、強気シグナルと鏡像となる条件で1が設定されます。すなわち、前回の転換線が基準線より上にあり、現在の転換線が現在の基準線を下回り、ADXが20以上かつ上昇している場合に、弱気シグナルとして1が代入されます。この手法では、非ゼロの値を代入する前に複数のシグナル条件を満たす必要があり、これにより厳密な判定がおこなわれます。これは、先に述べたような、個々のインジケーターシグナルをビットとして大きな配列に取り込み、ネットワークの入力とする方法とは明確に対照的です。最後に、シフト比較をおこなっているため、最初の2行にはNaNが含まれる可能性があることから、NumPy配列の最初の2行にはゼロを代入して終了します。GBP/USDの30分足チャートにおいて、過去2年間の学習データおよびテストデータでのFeature-1パターンのテスト結果は以下の通りです。

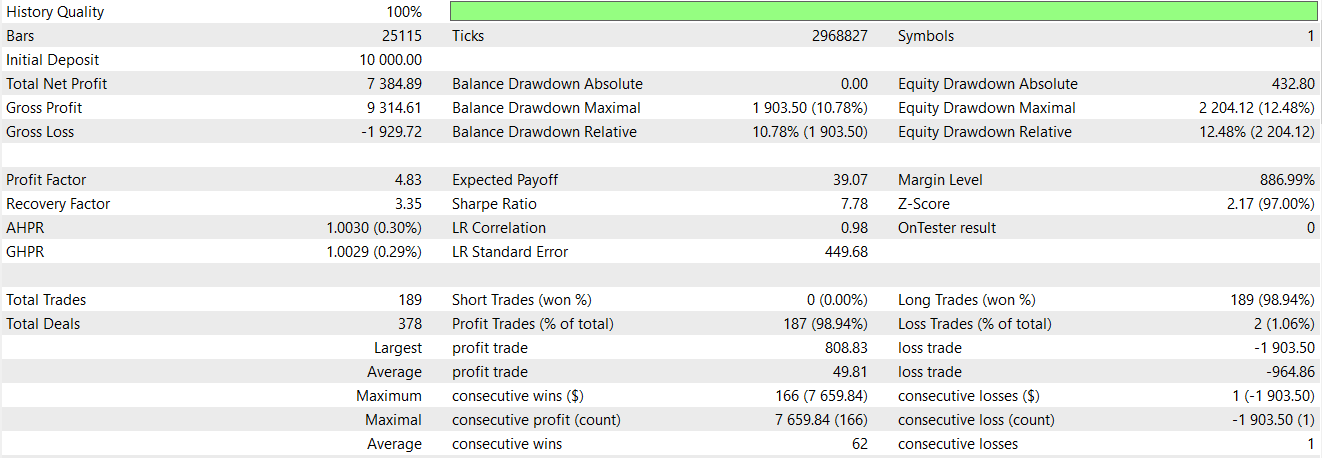
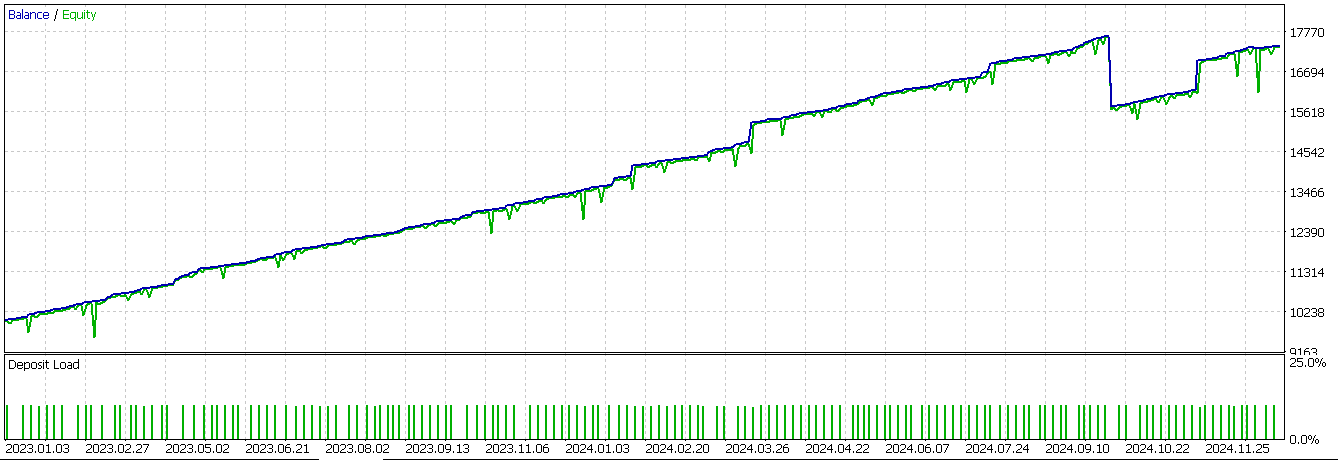
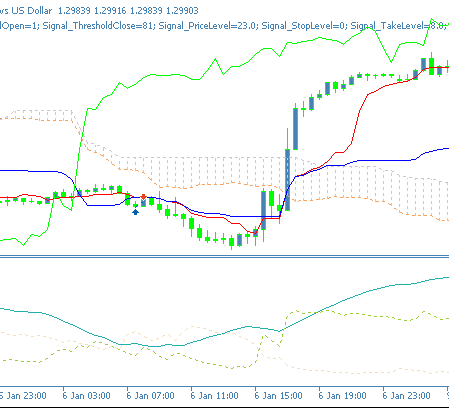
前回の記事で示したシグナル処理をフィルタとして重ね合わせたネットワークは、今回もEAのパフォーマンス改善に寄与しているようです。チャート上でのFeature_1の強気パターンは、以下のように確認できます。

Feature_5

最後に再テストするパターンは、6番目のPattern_5です。Pythonでの実装は以下の通りです。

def feature_5(df):
    """

    """
    feature = np.zeros((len(df), 2))
    
    feature[:, 0] = ((df['close'].shift(2) > df['close'].shift(1)) &
                     (df['close'].shift(1) < df['close']) &
                     (df['close'].shift(2) > df['Tenkan_sen'].shift(2)) &
                     (df['close'] > df['Tenkan_sen']) &
                     (df['close'].shift(1) <= df['Tenkan_sen'].shift(1)) &
                     (df['+DI'] > df['-DI']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    feature[:, 1] = ((df['close'].shift(2) < df['close'].shift(1)) &
                     (df['close'].shift(1) > df['close']) &
                     (df['close'].shift(2) < df['Tenkan_sen'].shift(2)) &
                     (df['close'] < df['Tenkan_sen']) &
                     (df['close'].shift(1) >= df['Tenkan_sen'].shift(1)) &
                     (df['+DI'] < df['-DI']) &
                     (df['ADX'] >= 25.0)).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

私たちの形式は、上記のPattern_0およびPattern_1と類似しています。出力用のNumPy配列も同様に初期化し、サイズを入力データフレームに合わせて設定します。1列目に1を代入して強気シグナルを示すためには、終値バッファが転換線上でUターンするように反発していることが必要です。加えて、プラス方向性移動(+DM)がマイナス方向性移動(-DM)より上回っており、ADXが25以上であることも条件となります。この価格の動きはトレンドの継続を示すことが多く、ADXの符号付き方向性移動バッファの相対的な大きさやその値も考慮したうえで、強気シグナルと判断されます。

2列目には、デフォルトの0に代えて1を代入します。条件は、終値が転換線下から反発して現在の終値が転換線を下回っており、かつADXが25以上で、マイナス方向性移動がプラス方向性移動より大きい場合に、最終的なシグナル確認として1を設定します。最後に、シフト計算によってNaNが生じる可能性があるため、配列の最初の2行はゼロに設定して終了します。このパターンも、上記の2つのパターンと同様の条件下でテストをおこなったところ、以下の結果が得られました。

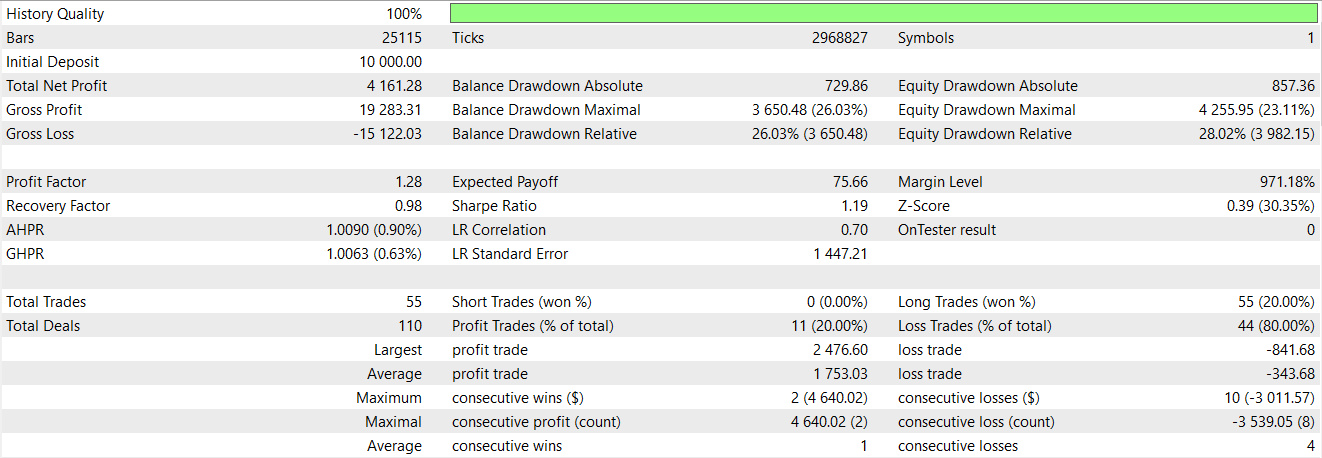
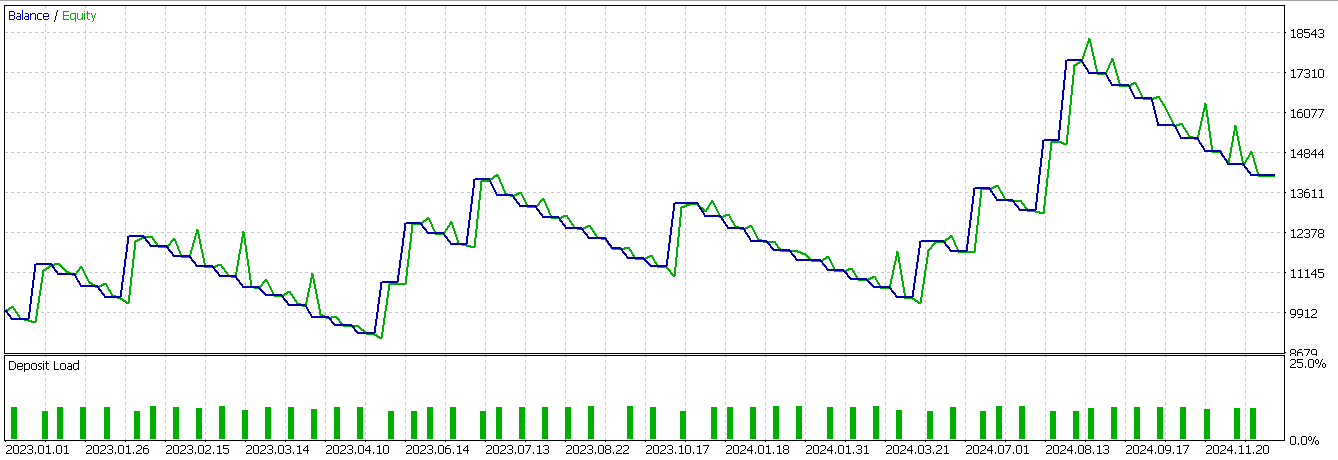
モデル自体は利益を生むものの、エクイティの推移は非常に変動が激しい状況です。そのため、機械学習に典型的なインジケーターシグナルを補助的に組み合わせる余地があります。結果は理想的とは言えず、テストデータも限定的ですが、インジケーターシグナルにスペクトル混合カーネルネットワークを追加フィルタとして組み合わせることで、売買エントリーをより鋭くし、パフォーマンスを改善できる可能性があると言えます。

結論

スペクトル混合カーネルを基に設計されたニューラルネットワークを用いて、一目均衡表とADX Wilderの組み合わせによるインジケーターの生の取引シグナルをファインチューニングする手法を検討しました。採用した特別なネットワークは一定の有望性を示しており、前回の記事でインジケーターシグナルのみを用いて取引をおこなった場合と比べて、確かにパフォーマンスに差が見られました。本稿で提示する結果も、読者がそのまま採用したり既存の取引システムに組み込んだりする前には、さらなる慎重な検証が必要です。特にテスト段階での組み込みに関しては、MQL5ウィザードで組み立てられたEAであれば、複数のカスタムシグナルを選択して組み込むことが可能です。

名前	説明
WZ-74.mq5	ヘッダにインクルードファイルを示すウィザード組み立てEA
SignalWZ-74.mqh	カスタムシグナルクラスファイル
74-5.onnx	シグナルPattern_5用のONNXネットワーク
74-1.onnx	シグナルPattern_1用のONNXネットワーク
74-0.onnx	シグナルPattern_0用のONNXネットワーク