取引システムの構築（第1回）：定量的なアプローチ

はじめに

安定して利益を上げる取引システムは、次の3つの主要な柱の相互作用に基づいています。

1. 勝率
2. リスクリワードレシオ(RRR)
3. リスク量（ポジションサイズによる）

これら3つの変数は、プロフィットファクター、リカバリーファクター、ドローダウンといった主要なパフォーマンス指標の根本的な要因となります。しかし、多くのトレーダーは勝率にばかり注目し、RRRやポジションサイジングの重要性を見落としたまま、自身の（自動）取引システムの有効性を評価してしまいます。

長期的に市場で生き残り、最終的に成功するためには、自分の取引優位性の構造、すなわち「勝率」「RRR」「それらに対応する最適なポジションサイズ」の関係性を理解することが不可欠です。

本記事では、トレーダーがバックテストの統計結果をモンテカルロシミュレーションに取り入れることで、戦略を長期的な観点から評価する方法を解説します。このアプローチにより、幅広い結果のシナリオを生成し、システムを「継続すべきか」「改良すべきか」「破棄すべきか」を判断するための信頼性を高めることができます。

期待値：収益性を支える数学的基盤

収益性は「期待値」によって定量化されます。これは勝率とRRRの関数です。期待値がプラスであれば、そのシステムは利益を生む可能性がありますが、マイナスであれば、どれほど勝率が高く見えても長期的には必ず破綻します。ただし、期待値がプラスであっても、ポジションサイジングが不適切であれば、ドローダウンが回復不可能なレベルに拡大することもあります。

本記事の内容

• 収益性のある取引システムの数学的基礎
• 収益性を達成するために必要な最小限の条件
• Pythonを用いたモンテカルロシミュレーションによる戦略パフォーマンスの検証

本記事の目的は、トレーダーがシステムの統計的な有効性を判断するための評価フレームワークを提供することです。たとえば、あるトレーダーの勝率が特定のRRRに対して必要な最低水準を下回っている場合、バックテストの結果がいかに良好に見えても、長期的な収益性は期待できません。

モンテカルロシミュレーションを利用することで、トレーダーは勝率、RRR、ポジションサイズのさまざまな組み合わせに基づいて数千通りの仮想的な結果をモデル化できます。これにより、実際の取引やバックテストをおこなう前から、より効果的な戦略最適化をおこなうことが可能になります。

すでにバックテストの結果を持っているトレーダーは、実際の勝率、RRR、ポジションサイズを入力して、将来的なパフォーマンスを一定の取引回数にわたってシミュレーションすることができます。こうした統計的な洞察により、そのシステムを信頼すべきかどうかをより明確かつ自信を持って判断できるようになります。

定義と数学的概念

1. 勝率

勝率とは、一定期間における全取引数に対する勝ち取引の割合を指します。パーセンテージ、または勝ち取引の確率として表されます。本記事では、勝率をPで表します。 

例：100回の取引のうち40回が勝ちであった場合、勝率は40％となります。

2. リスクリワードレシオ(RRR)

RRRとは、リワード（テイクプロフィット）とリスク（ストップロス）の比率を表します。

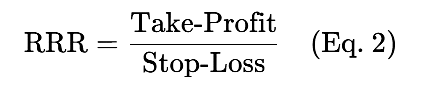
例：テイクプロフィットが100ピップス、ストップロスが50ピップスの場合、RRR = 2となります。

3. ポジションサイジング

ポジションサイジングとは、1回の取引でどの程度の資金をリスクにさらすかを示す指標です。次の式で計算することができます。

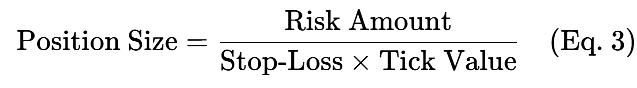
例：ストップロスが50ピップス、1ピップあたりの価値が10ドルで、200ドルをリスクに取る場合、ポジションサイズ = 0.4ロットとなります。

ポジションサイズ = 0.4ロット

4. 期待値

期待値(Ev)とは、1回の取引あたりの平均的な期待リターンを表します。次の式で計算されます。

Ev > 0：長期的に見て利益を生むシステム

Ev < 0：長期的に見て損失を生むシステム

利益を上げるために必要な最小勝率またはRRRの閾値

数学的な事実として、勝率とRRRは相互に依存しています。特定の勝率が与えられた場合、そのシステムが利益を上げるためには最低限必要なRRRが存在します。 逆に、RRRがわかっている場合には、利益を出すために必要な最低勝率が決まります。 高い勝率のみでは、RRRが適切に定義されていない限り、システムの有効性を保証することはできません。

ストップロスとテイクプロフィットがあらかじめ設定されているシステムでは、RRRは固定されています。このとき、対応する勝率が必要最低限を下回る場合、短期的には利益を出していても、長期的には収益性を維持できず、最終的に口座が破綻する可能性があります。これは多くのトレーダーが経験する典型的なパターンです。

利益条件の導出

次に、数学的な考え方を通じてこの関係を詳しく見ていきましょう。

期待値の式は次のように表されます。 

Ev = (勝率*報酬) - (1 - 勝率)*リスク

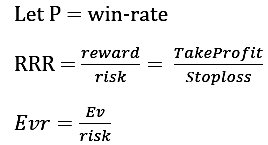
システムが利益を上げるための条件は、Ev > 0であることです。

式5から、次のことがわかります。

RRRが既知の場合、利益を上げるために必要な最小勝率(P)は次の式で求められます。

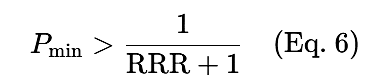
勝率(P)が既知の場合、利益を上げるために必要な最小RRRは次の式で求められます。

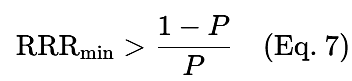
表1：特定のRRRに対する最小勝率

RRR	最小P
1.0	>50.00%
1.5	>40.00%
2.0	>33.33%
2.5	>28.57%
3.0	>25.00%

表1からわかるように、RRR = 1のシステムは、長期的に利益を上げるために50％以上の勝率が必要です。一方で、RRR = 3.0のシステムであれば、25％以上の勝率で長期的に利益を得ることができます。 この表から、RRRが高くなるほど、必要な最小勝率は低くなることが確認できます。したがって、システムのRRRがその最小勝率に対応する基準を上回っていれば、長期的には利益を上げる可能性が高いと言えます。

表2：特定の勝率に対する最小RRR

P	最小RRR
30%	>2.333
40%	>1.50
50%	>1.00
60%	>0.667
70%	>0.429

システムの勝率は、実際にバックテストをおこない、定義済みのRRRを設定しなければ正確にはわかりません。表2は、各勝率において長期的に利益を上げるために必要な最小RRRの目安を示しています。たとえば、勝率が30％である場合、RRRは2.333を超える必要があります。同様に、勝率が70％であれば、RRRは0.429を超える必要があります。このように、勝率が高くなるほど、求められるRRRの最小値は低下します。

このことから、トレーダーは高い勝率（またはRRR）だけを盲目的に追い求めるべきではなく、RRR（または高い勝率）とのバランスを考慮する必要があることがわかります。

勝率とは、単純に「総取引数に対する勝ち取引数の割合」です。したがって、システムの真の勝率を判断するには、十分な取引データを収集する必要があります。例として、ある自動売買システムが6か月間で30回の取引をおこない、そのうち20回が勝ちだった場合、勝率は60％となります。しかし、同じシステムを設定を変えずに18か月間稼働させ、200回の取引で90回の勝ちとなった場合、勝率は45％まで下がります。このように、取引回数が増えるほど、勝率はより信頼性が高く、実際のシステム特性を反映するようになります。

ポジションサイジングとリスク管理

ポジションサイジングを決定する際に使用する金額は、一般的に口座残高に対するパーセンテージで表されます。この割合は非常に重要です。なぜなら、それによってトレーディングシステムが最大ドローダウンの期間を耐え抜けるか、口座破綻を防げるか、そして最終的に取引目標を達成できるかが決まるからです。

多くのトレーダーは、短期間での利益を追求するあまり、口座残高に対して過剰なリスクを取ってしまう傾向があります。このような場合、たとえ収益性の高いシステムであっても、最終的に口座が失われてしまうことがあります。そうなると、トレーダーはしばしばシステム開発者を非難し、詐欺だと決めつけてしまいます。しかし、真実は、どれほど優れたシステムであっても、勝率が100%でない限り損失は必ず発生するということです。もし自分の口座が許容範囲を超えるリスクを取れば、マージンコールや口座全損に至る可能性があります。

ここでは、安全なリスクゾーン内での適切なポジションサイジングの方法について解説します。この手法を理解することで、損失の連続に耐えつつ、長期的な利益目標に向かって進むことができます。これこそが、健全なリスク管理やマネーマネジメントの本質です。それでは、数式を使って考えてみましょう。

定義

•  f：1回の取引で口座全体のうちリスクにさらす固定割合
•  RRRmin = 1.50：最低限必要なリスクリワードレシオ
•  P = 0.40：勝率（40％）

勝ち取引の結果 

勝った場合、得られる利益は次のようになります。

新しい残高 = 現在の残高 + 1.50*(f*現在の残高)

簡素化：

負け取引の結果

負けた場合、失う金額はリスクにさらした金額そのものです。

1取引あたりの期待成長係数

式8と式9を組み合わせると、1回の取引に対する期待成長係数(E[factor])は次のように表されます。

P=0.4を代入して簡略化すると次のようになります。

解釈：RRRmin = 1.50の場合、期待成長率はちょうど1になります。これは、長期的には資金が増えも減りもしない（損益分岐点）であることを意味します。

成長条件

RRR> RRRmin：  RRR =1.70の場合

正の成長(Ef >1)を得るためには、fが次の条件を満たす必要があります。 

 

最適リスク割合(f)の計算

たとえば、目標Ef = 1.002を達成するためには

この結果から、目標を達成するには口座残高の少なくとも2.5%をリスクにさらす必要があることがわかります。2.5%より小さいリスク割合であれば、口座はより安定して時間の経過とともに成長します。このことは、次の重要な概念を示しています。すなわち、任意の勝率、RRR、利益目標の組み合わせに対して、常に対応する最適な1取引あたりのリスク割合が存在するということです。

期待成長係数

期待成長係数(Ef)を求めるためには、トレーダーはまず次の3つの主要なパラメータを定義する必要があります。

1. 利益目標(P_target)
2. 目標達成に必要な取引回数(x)
3. 初期口座残高(Ini_bal)

Efは次の複利成長方程式から導かれます。

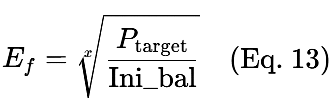
たとえば、次のような場合を考えます。

• 利益目標(P_target) = $10,000
• 取引回数(x) = 300
• 初期残高 (Ini_bal) = $1,000

数字を代入すると次のようになります。

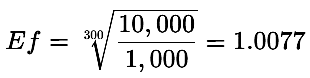
期待成長係数(Ef)は、トレーダーの取引スタイル（保守的か積極的か）を反映します。なぜなら、Efは目標を達成するために必要な1取引あたりのリスク量を決定するからです。

例：

次のような取引システムを考えます。

勝率 = 40%

RRR = 1.7

トレーダーまたは自動売買システムが$1,000を300回の取引で$10,000に増やすことを目標とする場合、式12から求められる1取引あたりの必要リスク割合(f)は次の通りです。

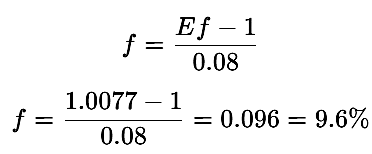
この場合、トレーダーまたは自動売買システムは、1取引あたり少なくとも9.6%をリスクにさらす必要があります。これは非常に積極的なアプローチです。

もし目標達成までの取引回数をx = 700に増やした場合

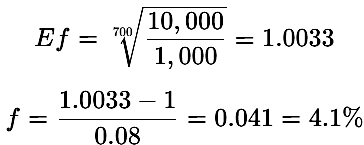
700回の取引では、システムまたはトレーダーはより保守的なアプローチを取ることができ、同じ目標を達成するために必要なリスク割合は取引あたり4.1%に減少します。

勝率が高く、さらに高いRRRを持つ場合には、目標達成はより容易になります。

例として、RRR = 2.0（勝率 = 40%）の場合、Ef = 1 + 0.2*fで、Ef = 1.0077の場合、必要なfは1.54%となります。

この数学モデルから、収益性のあるシステムであっても、期待値とポジションサイジングの両方を最適化する必要があることがわかります。次のセクションでは、これらの概念をモンテカルロシミュレーションを用いて説明し、システムの長期的な可能性を評価していきます。

モンテカルロシミュレーション

取引システムの長期的な安定性を検証するためには、最適化されたRRR、勝率、ポジションサイジングが重要です。モンテカルロシミュレーションでは、数千回のランダム化された取引シーケンスに基づき、可能な結果の範囲をモデル化します。最適化対象となるパラメータは次の通りです。

1. 勝率
2. RRR 
3. ポジションサイジング  

このシミュレーションによって、以下の要素を考慮することができます。

• 連敗
• 最大ドローダウン
• 期待収益の推移
• 口座が維持される確率

しかし、このシミュレーションの目的は、あくまで異なるシナリオ下での期待収益および口座維持確率を確認することです。 

シミュレーションはPythonプログラミングで構築されます。

import numpy as np
import matplotlib.pyplot as plt

# Parameters
win_rate = 0.40
reward_risk_ratio = 1.5  # 1.5:1
risk_per_trade = 1  # Risk $1 per trade (normalized)
num_trades = 1000  # Total number of trades to simulate
num_simulations = 1000  # Number of Monte Carlo simulations

# Monte Carlo simulation
equity_curves = []

計算に必要な数学関数、多次元配列、行列を扱うためにNumPyライブラリをインポートし、npという名前で使用できるようにします。

また、シミュレーション結果を可視化するために、Matplotlibのpyplotモジュールをインポートし、pltという別名で使用できるようにします。

その後、勝率、RRR、1取引あたりのリスク、各シミュレーションの取引回数、シミュレーションの繰り返し回数を初期化します。シミュレーション結果は資産曲線に格納されます。反復回数は、ユーザーの希望に応じて増減させることができます。

for _ in range(num_simulations):
    equity = 0
    curve = [equity] # Start curve with initial equity (0)
    peak = equity # Track peak equity for drawdown calculation
   # max_drawdown = 0 # Track max drawdown for this simulation

    for _ in range(num_trades):
        if np.random.rand() < win_rate:
            pnl = risk_per_trade * reward_risk_ratio
        else:
            pnl = -risk_per_trade
        equity += pnl
        curve.append(equity)

    equity_curves.append(curve)

# Convert to numpy array for easier analysis
equity_curves = np.array(equity_curves)

シミュレーションは1,000回の反復（各100回の取引）を実行し、結果を資産曲線に保存し、分析のためにNumPy配列に変換します。

# Plot results
plt.figure(figsize=(12, 6))
for i in range(min(num_simulations, 100)):
    # Adjust indexing if plotting against trade number (starts from 0)
    plt.plot(range(num_trades + 1), equity_curves[i], alpha=0.2, color='blue')

各シミュレーションの結果はプロットされ、青色で表示されます。

# Plot mean curve
mean_curve = equity_curves.mean(axis=0)
plt.plot(range(num_trades + 1), mean_curve, color='red', linewidth=2, label='Mean Equity Curve')

赤い線はシミュレーション結果の平均を示します。

plt.title(f'Monte Carlo Simulation: {num_simulations} Simulations, {num_trades} Trades Each\nWin Rate = {win_rate*100:.1f}%, 
R:R = {reward_risk_ratio}:1')
plt.xlabel('Number of Trades')
plt.ylabel('Equity (P&L)')
plt.legend()
plt.grid(True)
plt.tight_layout() 
plt.show()

このセグメントは、プロットの書式設定（タイトル、軸ラベル（xラベル、yラベル）、グリッドのアクティブ化(grid=True)を処理します。

# Summary statistics
# Final equity is now the last element of the curve, which has num_trades + 1 points
final_equity = equity_curves[:, -1]
mean_final_equity = final_equity.mean()
median_final_equity = np.median(final_equity)
std_final_equity = final_equity.std()
percent_profitable = np.mean(final_equity > 0) * 100

print('mean_final_equity:',mean_final_equity, '\nmedian_final_equity:', median_final_equity,
 '\nstd_final_equity:', std_final_equity,'\npercent_profitable:', percent_profitable,'%')

最後のコードセクションでは、最終口座残高の平均値、中央値、標準偏差、および利益が出たシミュレーションの割合を計算して表示します。

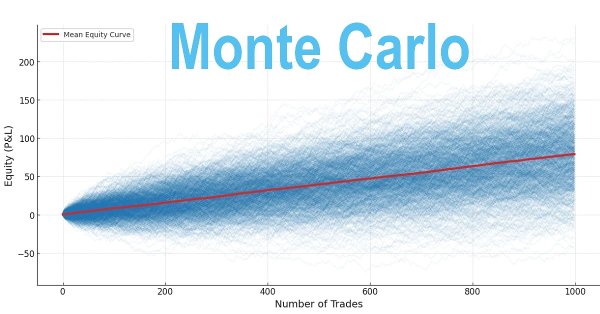
シナリオA：勝率40％、RRR1.5の戦略を1,000シミュレーションで検証

このシナリオでは、勝率40％、RRR1.5の取引戦略を、1回のシミュレーションにつき1,000取引で評価しました。合計1,000回の独立したシミュレーションを実施し、戦略のパフォーマンスおよびリスク特性を確認しました。結果は次の通りです（図1）

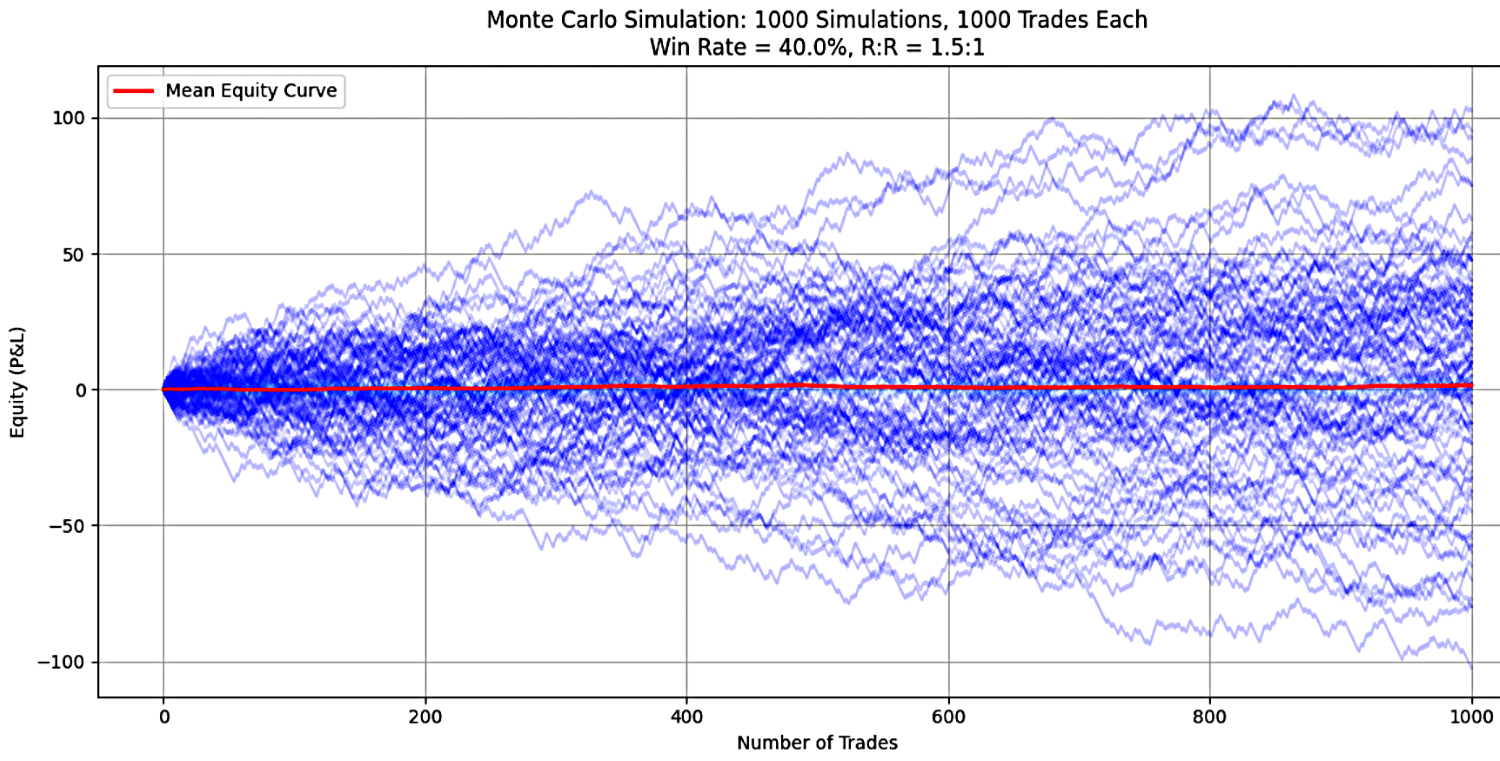
図1

勝率40%、RRR1.5のシミュレーション結果は次のとおりです。

指標	値
最終口座残高の平均値	1.44
最終口座残高の中央値	0.0
最終純資産の標準偏差	37.91
利益が出たシミュレーションの割合	49.0%

結果の解釈

1. 最終口座残高の平均値：全シミュレーションの平均最終口座残高は1.44倍となり、戦略は平均的には小幅な利益を上げたことを示しています。ただし、この平均値は一部の極端に良い結果によって大きく影響されており（図1）、実際には多くのシナリオで損失が発生しています。

2. 最終口座残高の中央値：中央値は0.0で、シミュレーションの半数以上で口座がゼロになったことを示しています。つまり、50％以上のケースで口座破綻が発生しており（おそらく残高が0になるか、マージンコールに達した）、戦略には非常に高い破綻リスクがあります。シナリオの半分は資本を全て失い、残りの半分は利益を出しましたが、その利益が平均値を1.44まで引き上げるほど偏っています。これは、ほとんどの結果が悪く、持続可能なリスク管理ができていないことの警告を示しています。

3. 標準偏差：標準偏差37.91は、結果の極端な変動性と予測困難性を示しています。標準偏差は平均値に比べて大きく、ほとんどのシナリオはほぼ全損（平均=0付近）に集中しています。一部のシナリオでは大きな利益が発生して平均値を押し上げていますが、多くは壊滅的な結果に終わっています。

4. 利益が出たシミュレーションの割合：利益が出たシミュレーションはわずか49％であり、最終口座残高が初期残高を上回ったのはこのケースのみです。残りの51％のシナリオではシステムが損失を出しました。これは中央値が0.0であることと一致しており、損失が発生した場合は壊滅的であることを確認しています。

これらの統計値は、この取引システムのパフォーマンスに関するいくつかの重要な特徴を示しています。 

• 不安定なシステム：

平均最終口座残高はプラス（1.44倍）であっても、これは一部の「幸運な」高利益シナリオによって引き上げられています。中央値が0であることは、ほとんどのシナリオが非常に悪い結果となり、少なくとも50％は口座破綻に至ったことを明確に示しています。 平均値と中央値の大きな差は、システムが根本的に不安定であることを示しており、多くのシナリオは非常に悪く、わずかなシナリオだけが非常に良好な結果を出しています。

• 高い破綻リスク：

中央値が0であることから、この戦略は非常に高い確率で口座を破綻させる可能性があることが示されています。非常に厳格なリスク管理をおこなわなければ、資金が吹き飛ぶリスクが高いです。

• 高い変動性：

標準偏差が大きい（約37.9）ことは、平均（約1.44）に比べて結果のばらつきが極めて大きいことを示しています。一部は非常に良い結果、一部は壊滅的な結果となっており、 この不均一性により安定したリターンを期待してこの戦略を使うことは困難です。

• 弱い収益性：

平均値はプラスであっても、利益が出たシナリオはわずか49％です。平均がプラスであるにもかかわらず、このシステムは信頼性があるとは言えません。安定的でスケーラブルなシステムであれば、利益が出るシナリオの割合はもっと高くなるはずです。

シナリオB：勝率40％、RRR1.7の戦略を1,000シミュレーションで検証

シナリオBでは、勝率は40％のまま、RRRを1.7に引き上げました。  1回のシミュレーションにつき1,000取引、合計1,000回の独立したシミュレーションで評価しました。結果は次の通りです（図2）。

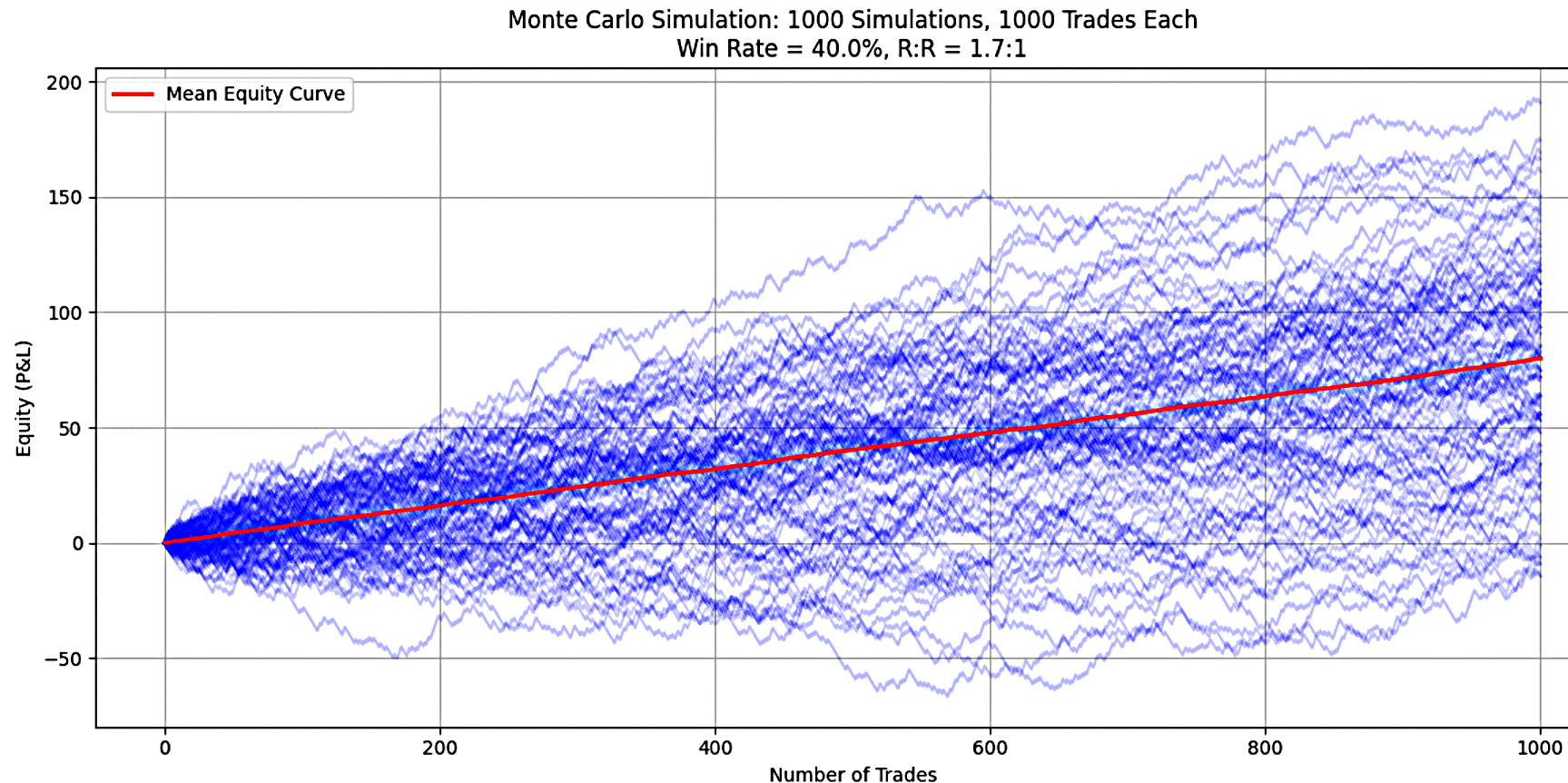
図2

RRR 1.7で勝率40%のシミュレーション結果は次のとおりです。

指標	値
最終口座残高の平均値	80.0
最終口座残高の中央値	80.0
最終純資産の標準偏差	45.82
利益が出たシミュレーションの割合	96.7%

結果の解釈

1. 最終口座残高の平均値：平均では、戦略は初期資金を80倍に増加させました。これは並外れた複利効果を示しており、条件下で戦略の高い収益性を確認できます。初期残高の80倍という平均リターンは非常に優れた結果であり、このシステムが大きな利益を生み出せる能力を持っていることを示しています。

2.  最終口座残高の中央値：中央値も同様に初期資金の80倍であり、少なくとも50％のシナリオでこの水準以上のリターンが達成されています。平均値と中央値が近いことは、結果の分布が対称的で、多くのシミュレーションが80倍付近に集中していることを示しています。この結果は、高い収益性とシミュレーション間の優れた一貫性の両方を示しています。 

3.  最終口座残高の標準偏差： 標準偏差45.82は結果にある程度のばらつきを示していますが、この水準の変動性は平均値と比較すると比較的穏やかであるといえます。標準偏差は平均値の約57％に相当し、個々の結果には（たとえば40倍や120倍といった）差があるものの、大多数の結果は平均80倍付近に集中していることを示しています。これは、ボラティリティが適切に制御され、安定したパフォーマンスを発揮しているシステムであることを意味します。

4. 利益を上げたシミュレーションの割合：全体の96.7％という非常に高い割合のシミュレーションが利益で終了し、損失となったのはわずか3.3％でした。この非常に高い成功率は、システムの信頼性が極めて高く、破綻リスクが非常に低いことを示しています。大多数の取引結果が利益を生み出しており、シミュレーション条件下での戦略の堅牢性を裏付けています。

これらの統計値は、この取引システムのパフォーマンスに関するいくつかの重要な特徴を示しています。 

• 高い収益性：

平均値と中央値がともに80倍で整合しており、結果が密集していることから、このシステムは非常に高い収益性と一貫性を持つことが示されています。

• 高い破綻リスク：

利益を出せなかったシミュレーションはわずか3.3％であり、RRR1.5の以前のシナリオと比べて信頼性が劇的に向上しています。破滅リスクは非常に低い水準に抑えられています。

• 制御されたボラティリティ：

標準偏差の絶対値は大きく見えるものの、非常に高いリターンと比較すれば妥当な範囲です。結果は、一定の変動が見られるものの、システムが一貫して強力な成果を上げていることを示唆しています。

• RRRへの感度：

最も注目すべき点は、勝率を40％に保ったまま、RRRを1.5から1.7にわずかに引き上げただけでパフォーマンスが大幅に改善したことです。これは、特に勝率が低めの戦略において、RRRの最適化がいかに重要であるかを示しており、わずかな調整でもシステムの安定性と収益性を大きく向上させることができることを強調しています。

結論

この分析では、数学的検証およびモンテカルロシミュレーションの両面から、特定の勝率に対してRRRを最適化することが、取引システムの収益性と安定性を劇的に向上させることを明確に示しました。シナリオで示されたように、勝率を40％に固定したままRRRを1.5から1.7に引き上げるだけで、システムは高い不安定性と大きな破綻リスクを伴う状態から、安定した利益と低い口座破綻確率を実現する状態へと変化しました。

重要な点として、勝率とRRRは本質的に相互依存の関係にあります（本記事の式6および式7を参照）。RRRを最適化する努力は自然と実効勝率に影響を与え、逆もまた然りです。特に重要なのは、すべての勝率には、長期的に利益を上げるために超えなければならない対応する最低RRR値が存在するという点です。たとえば、勝率が40％の場合、システムが持続的に利益を上げるためには、RRRが少なくとも1.5を超える必要があります。

この関係は期待値によってさらに明確に説明できます。

RRR=1.5の場合、期待値 = (0.4 × 1.50) − (0.6 × 1) = 0。これは損益分岐点を示しています。このとき平均値と中央値の大きな乖離が生じる理由が説明されます。

RRR=1.7の場合、期待値 = (0.4 × 1.70) − (0.6 × 1) = 0.08。これは正の期待値を示し、96.7％という高い利益確率につながっています。

結論として、勝率とRRRのバランスを適切に取ることで、多くの取引システムは一貫して利益を上げる戦略へと変化させることが可能です。重要なのは単に高い勝率を目指すことではなく、時間をかけて正の期待値を生み出すために、RRRが最低必要水準を確実に上回るよう設計することです。

トレーダーがストップロスとテイクプロフィットを定義した時点で、システムのRRRは固定されます。そのため、バックテストにおいてシステムを利益あるものにするためには、そのRRRに対して必要最低限の勝率を上回らなければなりません。本記事では、複数のRRR値とそれに対応する最低勝率を提示しました。その他の組み合わせについては、式6および式7を用いることで、必要な利益率の閾値を計算することができます。

長期的な有効性を評価するために、トレーダーはモンテカルロシミュレーションを活用し、バックテスト結果に基づいてパフォーマンスをモデル化することができます。 バックテストの統計（勝率、RRR、ポジションサイズ）を用いて数千回の取引シーケンスをシミュレートすることで、モンテカルロ分析は以下の点を明らかにします：

• 長期的な成功/失敗の確率を予測する
• 結果が運に依存しているのか、統計的優位性に基づいているのかを判断する
• 実際に資金をリスクにさらす前に、戦略を信頼できるか、または修正すべきかを見極める

シミュレーションで一貫して良好な結果を示すシステムは、トレーダーに高い信頼感を与え、戦略を信じて規律を保つことを可能にします。

最後に、本記事では期待値とRRRの最適化に焦点を当てましたが、ポジションサイズの管理も同様にシステムパフォーマンスの重要な柱であることを強調しておきます。健全なリスク管理がなければ、たとえ正の期待値を持つシステムであっても失敗する可能性があります。次回の記事では、最適なポジションサイジングを適用し、システムの耐久性を高め、持続的な取引の成功を実現する方法について詳しく解説いたします。