Datenwissenschaft und ML (Teil 40): Verwendung von Fibonacci-Retracements in Daten des maschinellen Lernens
69
0
Inhalt
- Der Ursprung der Fibonacci-Zahlen
- Das Verständnis der Fibonacci-Retracement-Levels unter Handelsaspekten
- Erstellen einer Zielvariablen mit Fibonacci-Retracements
- Training eines Klassifizierungsmodells auf der Grundlage einer Fibonacci-basierten Zielvariable
- Training eines Regressor-Modells auf der Grundlage einer Fibonacci-basierten Zielvariable
- Testen von Fibonacci-basierten maschinellen Lernmodellen mit dem Strategietester
- Abschließende Überlegungen
Der Ursprung der Fibonacci-Zahlen
Die Fibonacci-Zahlen gehen auf den antiken Mathematiker Leonardo von Pisa zurück, der auch als Fibonacci bekannt ist.
In seinem 1202 veröffentlichten Buch „Liber Abaci“ stellte Fibonacci die Zahlenfolge vor, die heute als Fibonacci-Folge bekannt ist. Die Folge, die mit 0 und 1 beginnt, und jede folgende Zahl in der Reihe ist die Summe der beiden vorangegangenen Zahlen.
Diese Sequenz ist sehr aussagekräftig, da sie in vielen Naturphänomenen vorkommt, darunter auch in den Wachstumsmustern von Pflanzen und Tieren.
In der Biologie ähnelt die logarithmische Spirale, die man bei einigen Tier- und Insektenschalen beobachten kann, den Fibonacci-Zahlen, auch wenn sie nicht perfekt ist.
Fibonacci-ähnliche Wachstumsannahmen sind auch in der Kaninchenpopulation und den Bienenstammbäumen zu erkennen.
Fibonacci-Zahlen sind auch in der DNA einiger Säugetiere und Menschen zu finden.
Diese Zahlen sind allgemeingültig, da sie fast überall gesichtet wurden. Im Folgenden finden Sie einige der gebräuchlichen Begriffe, auf die Sie bei der Arbeit mit Fibonacci-Zahlen stoßen werden.
Fibonacci-Folge
In der Mathematik ist eine Fibonacci-Folge eine Folge, in der jedes Element die Summe der beiden vorangehenden Elemente ist. Zahlen, die in einer Fibonacci-Folge eine Rolle spielen, werden als Fibonacci-Zahlen bezeichnet.
Die Fibonacci-Folge kann durch die folgende Gleichung ausgedrückt werden.
Wenn n größer als 1 (n>1) ist.
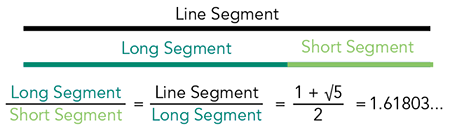
Der Goldene Schnitt
Dies ist ein mathematisches Konzept, das das Verhältnis zwischen zwei Mengen beschreibt, wobei das Verhältnis der kleineren Menge zur größeren dasselbe ist wie das Verhältnis der größeren Menge zur Summe beider.
Der Goldene Schnitt ist ungefähr gleich 1,6180339887 und wird mit dem griechischen Buchstaben Phi (φ) bezeichnet.
Der Goldene Schnitt ist nicht dasselbe wie Phi, aber er ist nahe dran! Es ist eine Beziehung zwischen zwei Zahlen, die in der Fibonacci-Folge nebeneinander stehen.
Wenn man den größeren durch den kleineren Wert teilt, ergibt sich ein Wert, der ungefähr Phi entspricht. Je weiter man in der Fibonacci-Folge geht, desto näher liegen die Antworten bei Phi. Aber die Antwort wird nie genau Phi entsprechen. Das liegt daran, dass Phi nicht als Bruch geschrieben werden kann. Phi ist irrational!
Diese Zahl wurde in verschiedenen natürlichen und vom Menschen geschaffenen Strukturen beobachtet, sie gilt als universelles Prinzip der Schönheit und Harmonie.
Das Verständnis der Fibonacci-Retracement-Levels aus der Sicht des Handels
Fibonacci-Retracement-Levels sind horizontale Linien, die die möglichen Unterstützungs- und Widerstandsniveaus anzeigen, auf denen der Preis möglicherweise seine Richtung umkehren könnte. Sie werden anhand der oben beschriebenen Prinzipien der Fibonacci-Zahlen erstellt.
Dies ist ein gängiges Tool, das Händler im MetaTrader 5 für verschiedene Zwecke verwenden, z. B. zum Festlegen von Handelszielen (Stop-Loss und Take-Profit) und zum Aufspüren von Unterstützungs- und Widerstandslinien, mit denen sich feststellen lässt, wo die Kurse am ehesten umkehren werden.
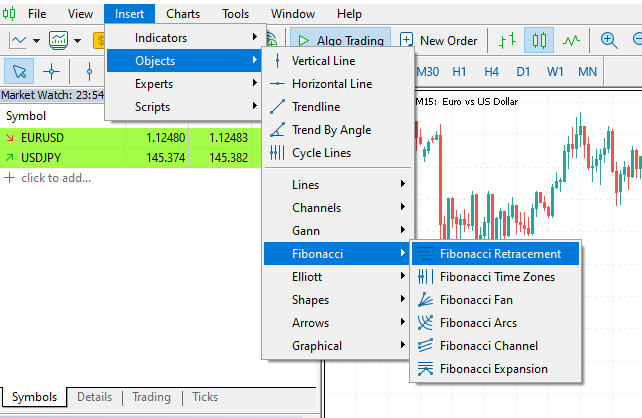
Im MetaTrader 5 finden Sie es unter der Registerkarte Einfügen>Objekte>Fibonacci.
Unten sehen Sie das Fibonacci-Retracement-Tool für das Symbol EURUSD im 1-Stunden-Chart.
Während das Fibonacci-Retracement-Tool zuverlässig zu sein scheint, wenn es um die Bereitstellung von Handelsniveaus geht, die bei der Erkennung von Marktumkehrungen und der Festlegung von Handelszielen nützlich sind, wollen wir die Wirksamkeit der Fibonacci-Niveaus unter dem Aspekt des maschinellen Lernens und der künstlichen Intelligenz (KI) untersuchen, genauer gesagt den Goldenen Schnitt (61,8 oder 0,618).
Im Folgenden werden verschiedene Möglichkeiten zur mathematischen Erstellung von Fibonacci-Levels und deren Verwendung bei der Erstellung einer Zielvariablen untersucht, die von maschinellen Lernmodellen für das Verständnis und die Vorhersage der Marktrichtung verwendet werden kann.
Erstellen einer Zielvariablen mit Fibonacci-Retracements
Um ein Modell zu trainieren, mit dem wir die Beziehungen in unseren Daten mithilfe von überwachtem maschinellem Lernen verstehen können, benötigen wir eine gut formulierte Zielvariable. Da ein Fibonacci-Level nur eine Zahl ist, die ein bestimmtes Preisniveau repräsentiert, können wir den Marktpreis auf dem von uns benötigten Fibonacci-Level erfassen und als Zielvariable für ein Regressionsproblem verwenden.
Für ein Klassifizierungsproblem erstellen wir die Klassenbezeichnungen auf der Grundlage der Marktbewegungen gemäß den Fibonacci-Linien. Wenn sich der Markt also einige Balken vorwärts bewegt und dabei das berechnete Fibonacci-Niveau in einem Aufwärtstrend überschreitet, können wir dies als Aufwärtssignal betrachten (angezeigt durch 1), und wenn sich der Markt andernfalls abwärts bewegt und dabei das von uns festgelegte Fibonacci-Niveau überschreitet, können wir dies als Abwärtssignal betrachten (angezeigt durch 0). Alle anderen Signale können wir als Keine (gekennzeichnet durch -1) zuordnen.
Für ein Klassifizierungsproblem
Imports.
import pandas as pd import numpy as np
Funktionen.
def create_fib_clftargetvar(price: pd.Series, lookback_window: int=10, lookahead_window: int=10, fib_level: float=0.618): """ Creates a target variable based on Fibonacci breakthroughs in price data. Parameters: - price: pd.Series of price data (close, open, high, or low) - lookback_window: int - number of past periods to calculate high/low - lookahead_window: int - number of future periods to assess breakout - fib_level: float - Fibonacci retracement level (e.g. 0.618) Returns: - pd.Series: with values 1 => Bullish fib level reached 0 => Bearish fib level reached -1 => False breakthrough or no fib hit """ high = price.rolling(lookback_window).max() low = price.rolling(lookback_window).min() fib_level_value = high - (high - low) * fib_level # calculate the Fibonacci level in market price price_ahead = price.shift(-lookahead_window) # future price values target_var = [] for i in range(len(price)): if np.isnan(price_ahead.iloc[i]) or np.isnan(fib_level_value.iloc[i]) or np.isnan(price.iloc[i]): target_var.append(np.nan) continue # let's detect bull and bearish movement afterwards if price_ahead.iloc[i] > price.iloc[i]: # The market went bullish if price_ahead.iloc[i] >= fib_level_value.iloc[i]: target_var.append(1) # bullish Fibonacci target reached else: target_var.append(-1) # false breakthrough else: # The market went bearish if price_ahead.iloc[i] <= fib_level_value.iloc[i]: target_var.append(0) # bearish Fibonacci target reached else: target_var.append(-1) # false breakthrough return target_var
Das Fibonacci-Niveau des Marktes wird nach der folgenden Formel berechnet.
fib_level_value = high - (high - low) * fib_level
Da es sich um ein Klassifizierungsproblem handelt, bei dem wir die Marktreaktion auf der Grundlage des vorherigen Fibonacci-Levels vorhersagen wollen, müssen wir in die Zukunft blicken und einen Trend erkennen. Danach prüfen wir, ob der zukünftige Preis auf der Grundlage des lookahead_window das Fibonacci-Level (für einen Aufwärtstrend) oder das Fibonacci-Level (für einen Abwärtstrend) überschritten hat, um Kauf- bzw. Verkaufssignale zu generieren. Ein Haltesignal wird zugewiesen, wenn der Preis das Fibonacci-Niveau in beiden Richtungen nicht erreicht hat.
Erstellen wir die Zielvariable mit dieser Funktion und fügen wir das Ergebnis dem Datafame hinzu.
df["Fib signals"] = create_fib_clftargetvar(price=df["Close"], lookback_window=10, lookahead_window=5, fib_level=0.618) df.dropna(inplace=True) # drop nan(s) caused by the shifting operation df
Das Ergebnis:
| Open | High | Low | Close | Fib-Signale | |
|---|---|---|---|---|---|
| 9 | 1.3492 | 1.3495 | 1.3361 | 1.3362 | 0.0 |
| 10 | 1.3364 | 1.3405 | 1.3350 | 1.3371 | 0.0 |
| 11 | 1.3370 | 1.3376 | 1.3277 | 1.3300 | 0.0 |
| 12 | 1.3302 | 1.3313 | 1.3248 | 1.3279 | -1.0 |
| 13 | 1.3279 | 1.3293 | 1.3260 | 1.3266 | 0.0 |
Für ein Regressionsproblem
def create_fib_regtargetvar(price: pd.Series, lookback_window: int=10, fib_level: float=0.618): """ This function helps us in calculating the target variable based on fibonacci breakthroughs given a price price: Can be close, open, high, low """ high = price.rolling(lookback_window).max() low = price.rolling(lookback_window).min() return high - (high - low) * fib_level
Bei einem Regressionsproblem brauchen wir die Werte nicht zu verschieben, um Informationen über die Zukunft zu erhalten, denn beim manuellen Handel wird das im vorherigen Fenster (lookback_window) berechnete Fibonacci-Level verwendet, um zu vergleichen, ob die zukünftigen Kurse es über- oder unterschritten haben.
Unser Ziel ist es, das Regressor-Modell so zu trainieren, dass es in der Lage ist, den nächsten Fibonacci-Level-Wert auf der Grundlage des lookback_window vorherzusagen.
df["Fibonacci Level"] = create_fib_regtargetvar(price=df["Close"], lookback_window=10, fib_level=0.618) df.dropna(inplace=True) df.head(5)
Nachfolgend sehen Sie den resultierenden Datenrahmen, nachdem die Spalte mit dem Fibonacci-Level hinzugefügt wurde.
| Open | High | Low | Close | Fibonacci-Niveau | |
|---|---|---|---|---|---|
| 9 | 1.3492 | 1.3495 | 1.3361 | 1.3362 | 1.343840 |
| 10 | 1.3364 | 1.3405 | 1.3350 | 1.3371 | 1.342923 |
| 11 | 1.3370 | 1.3376 | 1.3277 | 1.3300 | 1.339015 |
| 12 | 1.3302 | 1.3313 | 1.3248 | 1.3279 | 1.337717 |
| 13 | 1.3279 | 1.3293 | 1.3260 | 1.3266 | 1.335195 |
Training eines Klassifizierungsmodells auf der Grundlage der Fibonacci-basierten Zielvariable
Beginnen wir mit der Klassifizierungszielvariable „Fib-Signale“ und trainieren wir diese Daten mit einem einfachen RandomForestClassifier Modell.
Imports.
from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import train_test_split from sklearn.metrics import classification_report from sklearn.utils.class_weight import compute_class_weight from sklearn.pipeline import Pipeline from sklearn.preprocessing import RobustScaler
Aufteilung von Training und Test.
X = df.drop(columns=[ "Fib signals" ]) y = df["Fib signals"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, shuffle=False)
Das Modell.
class_weights = compute_class_weight('balanced', classes=np.unique(y_train), y=y_train) weight_dict = dict(zip(np.unique(y_train), class_weights)) model = RandomForestClassifier(n_estimators=100, min_samples_split=2, max_depth=10, class_weight=weight_dict, random_state=42 ) clf_pipeline = Pipeline(steps=[ ("scaler", RobustScaler()), ("rfc", model) ]) clf_pipeline.fit(X_train, y_train)
Das Random-Forest-Modell, bei dem es sich um ein auf Entscheidungsbäumen basierendes Modell handelt, benötigt nicht unbedingt eine Skalierungstechnik, aber da es sich bei den Open-, High-, Low- und Close-Werten (OHLC) um kontinuierliche Variablen handelt, die sich im Laufe der Zeit zwangsläufig ändern und Ausreißer in das Modell einbringen, könnte der RobustScaler helfen, dieses Problem in unseren Daten zu unterdrücken.
Schließlich können wir dieses Klassifizierungsmodell sowohl mit den Trainings- als auch mit den Testproben testen.
y_train_pred = clf_pipeline.predict(X_train) print("Train Classification report\n",classification_report(y_train, y_train_pred)) y_test_pred = clf_pipeline.predict(X_test) print("Test Classification report\n",classification_report(y_test, y_test_pred))
Das Ergebnis:
Train Classification report precision recall f1-score support -1.0 0.53 0.55 0.54 4403 0.0 0.59 0.64 0.61 7122 1.0 0.67 0.60 0.64 8294 accuracy 0.61 19819 macro avg 0.60 0.60 0.60 19819 weighted avg 0.61 0.61 0.61 19819 Test Classification report precision recall f1-score support -1.0 0.22 0.22 0.22 1810 0.0 0.38 0.60 0.46 3181 1.0 0.42 0.20 0.27 3504 accuracy 0.35 8495 macro avg 0.34 0.34 0.32 8495 weighted avg 0.36 0.35 0.33 8495
Das Ergebnis sieht bei der Trainingsstichprobe beeindruckend aus, aber bei der Teststichprobe ist es schrecklich. Dies bedeutet, dass das Modell die Muster in einer anderen als der trainierten Stichprobe nicht verstehen kann.
Dies könnte auf verschiedene Faktoren zurückzuführen sein, wie z. B. das Fehlen von Merkmalen zur Erfassung aussagekräftiger Muster auf dem Markt (nur OHLC-Merkmale könnten unzureichend sein), oder vielleicht ist die grobe Art der Erkennung eines Trends auf der Grundlage des nächsten lookahead_window-Balkens, der bei der Erstellung der Zielvariablen verwendet wird, schlecht, was dazu führt, dass das Modell Zwischenbalken übersieht, bei denen der Preis das Fibonacci-Niveau überschritten haben könnte.
Da dieser Prozess darauf abzielte, ein Modell zu trainieren, das vorhersagt, ob der künftige Kurs das Fibonacci-Niveau überschreiten wird, könnte dieses Ergebnis des Klassifizierungsberichts irreführend sein, da es nicht perfekt sein muss. Wir fahren damit vorerst fort, da wir die Ergebnisse der Testdaten in der tatsächlichen Handelsumgebung analysieren werden.
Speichern wir dieses trainierte Modell im ONNX-Format zur externen Verwendung in der Programmiersprache MQL5.
import skl2onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
# Define the initial type of the model’s input initial_type = [('input', FloatTensorType([None, X_train.shape[1]]))] # Convert the pipeline to ONNX onnx_model = convert_sklearn(clf_pipeline, initial_types=initial_type, target_opset=13) # Save the ONNX model to a file with open(f"{symbol}.{timeframe}.Fibonnacitarg-RFC.onnx", "wb") as f: f.write(onnx_model.SerializeToString())
Training eines Regressor-Modells auf die Fibonacci-basierte Zielvariable
Beim Training eines Regressormodells können die gleichen Grundsätze befolgt werden, nur die Art des Modells und die Zielvariable sind in diesem Fall anders.
Imports.
from sklearn.ensemble import RandomForestRegressor from sklearn.metrics import r2_score
Aufteilung von Training und Test.
X = df.drop(columns=[ "Fibonacci Level" ]) y = df["Fibonacci Level"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, shuffle=False)
Das Random-Forest-Regressor-Modell.
model = RandomForestRegressor(n_estimators=100, min_samples_split=2, max_depth=10, random_state=42 ) reg_pipeline = Pipeline(steps=[ ("scaler", RobustScaler()), ("rfr", model) ]) reg_pipeline.fit(X_train, y_train)
Schließlich können wir das Regressor-Modell sowohl an Trainings- als auch an Teststichproben testen.
y_train_pred = reg_pipeline.predict(X_train) print("Train accuracy score:",r2_score(y_train, y_train_pred)) y_test_pred = reg_pipeline.predict(X_test) print("Test accuracy score:",r2_score(y_test, y_test_pred))
Das Ergebnis:
Train accuracy score: 0.9990321734526452 Test accuracy score: 0.9565827587164671
Aus einem Regressionsmodell lässt sich nicht viel über dieses beobachtete R2-Ergebnis ableiten, aber ein Wert von 0,9565 in der Teststichprobe ist ein guter Wert.
Speichern wir dieses trainierte Modell im ONNX-Format zur externen Verwendung in der Programmiersprache MQL5.
# Define the initial type of the model’s input initial_type = [('input', FloatTensorType([None, X_train.shape[1]]))] # Convert the pipeline to ONNX onnx_model = convert_sklearn(reg_pipeline, initial_types=initial_type, target_opset=13) # Save the ONNX model to a file with open(f"{symbol}.{timeframe}.Fibonnacitarg-RFR.onnx", "wb") as f: f.write(onnx_model.SerializeToString())
Testen wir nun die Vorhersagekraft dieser beiden Modelle in einem realen Handelsumfeld.
Testen von Fibonacci-basierten maschinellen Lernmodellen mit dem Strategy Tester
Wir beginnen mit dem Hinzufügen von Random-Forest-Modellen im ONNX-Format als Ressourcen zu unserem Expert Advisor (EA).
#resource "\\Files\\EURUSD.PERIOD_H4.Fibonnacitarg-RFC.onnx" as uchar rfc_onnx[] #resource "\\Files\\EURUSD.PERIOD_H4.Fibonnacitarg-RFR.onnx" as uchar rfr_onnx[]
Anschließend importieren wir eine Bibliothek, die uns beim Laden des Random-Forest-Klassifikators und eines Regressor-Modells im ONNX-Format hilft.
#include <Random Forest.mqh>
CRandomForestClassifier rfc;
CRandomForestRegressor rfr; Wir benötigen dieselben Werte für das Lookahead- und das Lookback-Fenster, die wir auch für die Trainingsdaten verwendet haben. Diese Werte sind nützlich, um zu bestimmen, wie lange man den Handel halten und wann man ihn schließen sollte.
input group "Models configs"; input target_var_type fib_target = CLASSIFIER; //Model type input int lookahead_window = 5; input int lookback_window = 10;
Die Variable fib_target input hilft uns bei der Auswahl des zu verwendenden Modelltyps.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Setting the symbol and timeframe if (!MQLInfoInteger(MQL_TESTER) && !MQLInfoInteger(MQL_DEBUG)) if (!ChartSetSymbolPeriod(0, symbol_, timeframe_)) { printf("%s failed to set symbol %s and timeframe %s",__FUNCTION__,symbol_,EnumToString(timeframe_)); return INIT_FAILED; } //--- m_trade.SetExpertMagicNumber(magic_number); m_trade.SetDeviationInPoints(slippage); m_trade.SetMarginMode(); m_trade.SetTypeFillingBySymbol(Symbol()); //--- switch(fib_target) { case REGRESSOR: if (!rfr.Init(rfr_onnx)) { printf("%s failed to initialize the random forest regressor",__FUNCTION__); return INIT_FAILED; } break; case CLASSIFIER: if (!rfc.Init(rfc_onnx)) { printf("%s failed to initialize the random forest classifier",__FUNCTION__); return INIT_FAILED; } break; } //--- return(INIT_SUCCEEDED); }
In der Funktion OnTick erhalten wir Signale vom Modell, nachdem wir OHLC-Werte übergeben haben, wie sie in den Trainingsdaten verwendet wurden.
Diese Signale werden dann zur Eröffnung von Kauf- und Verkaufstransaktionen verwendet.
void OnTick() { //--- Getting signals from the model if (!isNewBar()) return; vector x = { iOpen(Symbol(), Period(), 1), iHigh(Symbol(), Period(), 1), iLow(Symbol(), Period(), 1), iClose(Symbol(), Period(), 1) }; long signal = 0; switch(fib_target) { case REGRESSOR: { double pred_fib = rfr.predict(x); signal = pred_fib>iClose(Symbol(), Period(), 0)?1:0; //If the predicted fibonacci is greater than the current close price, thats bullish otherwise thats bearish signal } break; case CLASSIFIER: signal = rfc.predict(x).cls; break; } //--- Trading based on the signals received from the model MqlTick ticks; if (!SymbolInfoTick(Symbol(), ticks)) { printf("Failed to obtain ticks information, Error = %d",GetLastError()); return; } double volume_ = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN); if (signal == 1) { if (!PosExists(POSITION_TYPE_BUY) && !PosExists(POSITION_TYPE_SELL)) m_trade.Buy(volume_, Symbol(), ticks.ask); } if (signal == 0) { if (!PosExists(POSITION_TYPE_SELL) && !PosExists(POSITION_TYPE_BUY)) m_trade.Sell(volume_, Symbol(), ticks.bid); } //--- Closing trades switch(fib_target) { case CLASSIFIER: CloseTradeAfterTime((Timeframe2Minutes(Period())*lookahead_window)*60); //Close the trade after a certain lookahead and according the the trained timeframe break; case REGRESSOR: CloseTradeAfterTime((Timeframe2Minutes(Period())*lookback_window)*60); //Close the trade after a certain lookahead and according the the trained timeframe break; } }
Das Schließen von Handelsgeschäften, abhängig vom gewählten Modelltyp, den lookahead_window- und lookback_window-Werten.
Wenn es sich bei dem ausgewählten Modell um einen Klassifikator handelt, werden die Handelsgeschäfte geschlossen, nachdem die Anzahl der Balken, die lookahead_window entspricht, im aktuellen Zeitrahmen verstrichen ist.
Wenn es sich bei dem gewählten Modell um einen Regressor handelt, werden die Handelsgeschäfte geschlossen, nachdem die Anzahl der Balken, die dem lookback_window entspricht, im aktuellen Zeitrahmen verstrichen ist.
Dies entspricht der Art und Weise, wie wir die Zielvariablen im Python-Skript erstellt haben.
Schließlich können wir diese beiden Modelle mit dem Strategietestgerät testen.
Da die Trainingsdaten vom 01.01.2005 bis zum 01.01.2023 erhoben wurden, testen wir die Ergebnisse des Modells vom 01.01.2023 bis zum 31.12.2023 (Daten außerhalb der Stichprobe).
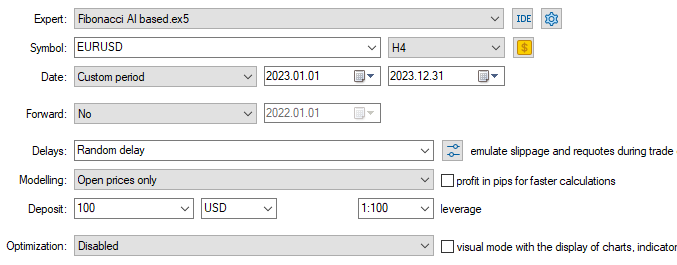
Modell-Typ: Klassifikator
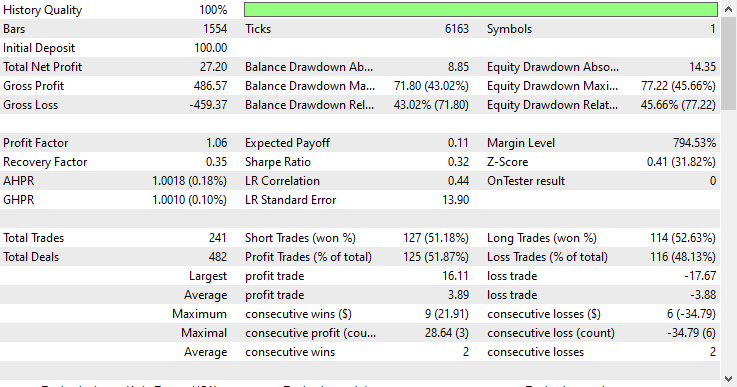
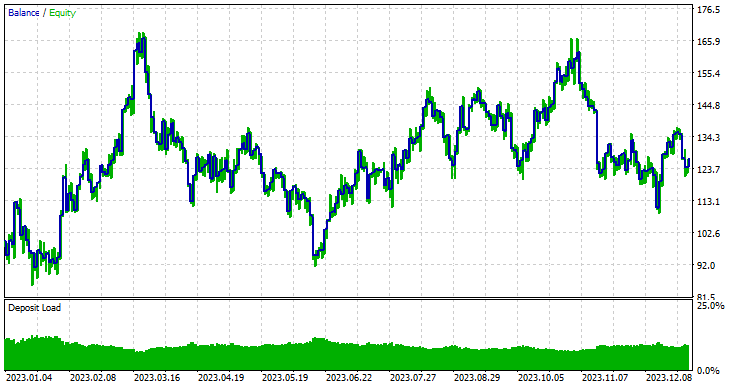
Modell-Typ: Regressor
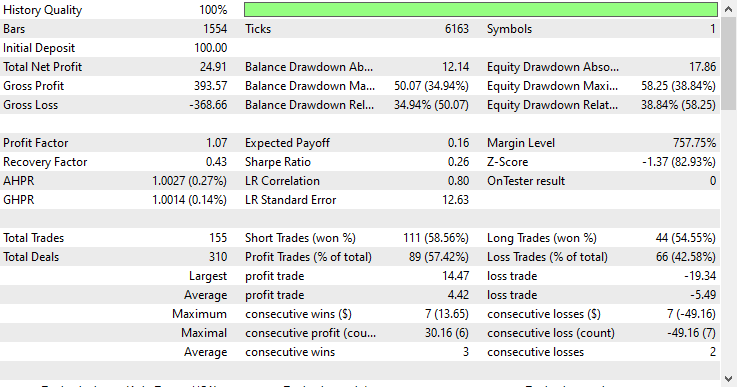
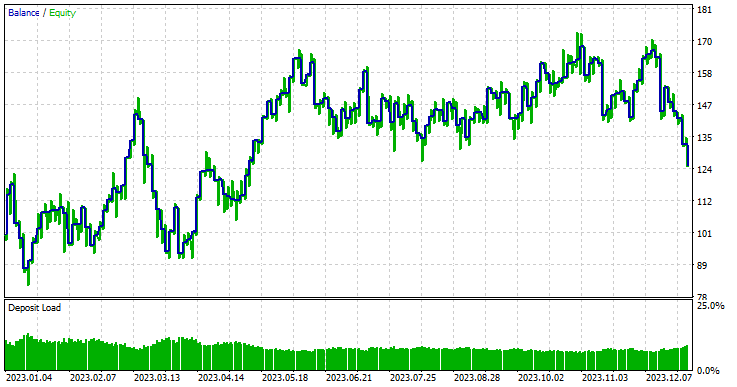
Wenn man bedenkt, dass es sich um Daten außerhalb der Stichprobe handelt, schnitt das Regressormodell mit einer Gewinnrate von 57,42 % außergewöhnlich gut ab.
Um die Sache zu vereinfachen und ein Regressor-Modell nützlich zu machen, habe ich innerhalb des Handelsroboters das kontinuierliche Ergebnis, das von einem Random-Forest-Regressor-Modell geliefert wird, in eine binäre Lösung umgewandelt.
signal = pred_fib>iClose(Symbol(), Period(), 0)?1:0; //If the predicted Fibonacci is greater than the current close price, that's bullish otherwise that's bearish signal
Dies ändert die Art und Weise, wie wir das vorhergesagte Fibonacci-Niveau interpretieren, völlig, denn im Gegensatz zu dem, was wir normalerweise beim manuellen Handel tun, wo wir einen Handel am Ende des Trends eröffnen, sobald wir ein Trendbestätigungssignal oder ähnliches erhalten. Wir setzen unsere Handelsziele auf ein bestimmtes Fibonacci-Niveau (in der Regel 61,8%).
Bei diesem Ansatz gehen wir davon aus, dass unsere maschinellen Lernmodelle dieses Muster über ein bestimmtes Lookback- und Lookahead-Fenster, das für die Trainingsdaten verwendet wurde, bereits verstanden haben, sodass wir nur einige Trades eröffnen und sie entsprechend der angegebenen Anzahl von Balken halten müssen.
Der Schlüssel liegt hier in den Werten des Lookahead- und des Lookback-Fensters, vor allem weil wir bei der Verwendung des Fibonacci-Tools im manuellen Handel die Anzahl der für die Berechnungen zu verwendenden Balken (Tiefst- und Höchstwerte) nicht berücksichtigen, sondern das Tool in der Regel dort einsetzen, wo wir es für richtig halten.
Während das Tool beim manuellen Handel gut funktioniert, gaukelt es uns vor, dass wir das Tool an der richtigen Stelle platziert haben, obwohl wir es nur dort platzieren, wo wir es haben wollen, ohne klare Regeln im Kopf.
Diese beiden Werte (Lookahead- und Lookback-Fenster) sind diejenigen, die wir optimieren müssen, wenn wir die Effektivität der Fibonacci-Levels bei der Erstellung der Zielvariablen und bei der Nutzung des maschinellen Lernens im Allgemeinen untersuchen wollen.
Abschließende Überlegungen
Fibonacci-Retracements und -Levels sind leistungsstarke Techniken zur Erstellung der Zielvariablen für das maschinelle Lernen, wie der obige Bericht des Strategietesters zeigt, der vom Regressor-Modell erstellt wurde. Selbst mit so wenigen Prädiktoren wie Eröffnungs-, Höchst-, Tiefst- und Schlusskursen, die nicht viele Muster bieten, konnten die Modelle einige wertvolle Muster erkennen und im Vergleich zum zufälligen Raten auf der Grundlage der gelernten Informationen aus den Fibonacci-Stufen gute Ergebnisse erzielen.
Wie auch immer man die Ergebnisse betrachtet, sie sind meiner Meinung nach beeindruckend.
Im Moment ist diese Idee noch nicht ausgefeilt genug. Wir müssen unseren Daten noch weitere Funktionen hinzufügen, z. B. Indikatorwerte und Bestätigungen von Handelsstrategien, damit unser auf Fibonacci basierendes Modell komplexe Muster auf dem Markt erfassen kann. Sie können auch gerne andere Fibonacci-Levels erkunden.
Wenn diese Idee weiter verbessert wird, glaube ich, dass sie an den Aktien- und Indexmärkten sehr effektiv sein wird, wo die Rücksetzer regelmäßig in einigen langfristigen Aufwärtstrends auftreten, auch in höheren Zeitrahmen wie dem täglichen Zeitrahmen, wo die Daten „weniger verrauscht“ sind.
Tabelle der Anhänge
| Dateiname & Pfad | Beschreibung und Verwendung |
|---|---|
| Experts\Fibonacci AI based.mq5 | Der wichtigste Expertenratgeber für das Testen von Modellen des maschinellen Lernens. |
| Include\Random Forest.mqh | Enthält Klassen zum Laden und Bereitstellen des Random-Forest-Klassifikators und des Regressors im .ONNX-Format. |
| Files\*.onnx | Modelle für maschinelles Lernen im ONNX-Format. |
| Files\*.csv | CSV-Dateien mit Datensätzen, die für das Training von Modellen für maschinelles Lernen verwendet werden sollen. |
| Python\fibbonanci-in-ml.ipynb | Python-Skript zur Verarbeitung der Daten und zum Training der Random-Forest-Modelle. |
Quellen und Referenzen
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/18078
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
Nutzerdefinierte Debugging- und Profiling-Tools für die MQL5-Entwicklung (Teil I): Erweiterte Protokollierung
Eine alternative Log-datei mit der Verwendung der HTML und CSS
Handel mit dem MQL5 Wirtschaftskalender (Teil 9): Bessere Interaktion mit Nachrichten durch eine dynamische Bildlaufleiste und eine optimierte Anzeige
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.