知っておくべきMQL5ウィザードのテクニック（第79回）：教師あり学習でのゲーターオシレーターとA/Dオシレーターの使用

はじめに

前回および前々回の記事では、ゲーターオシレーターとA/Dオシレーターを組み合わせた場合に、10種類のシグナルパターンをテストしました。その中で、これまでの実績通り、Pattern_0、Pattern_3、Pattern_4が一貫して遅れを取る傾向が見られました。これらのパターンを単に破棄するのではなく、本記事では教師あり学習によってパフォーマンスを改善できるかを検証します。具体的には、カーネル回帰とドット積類似度を組み込んだCNNを用い、初期状態では弱く見えるシグナルパターンから潜在的な価値を抽出できるかを確認します。前回までと同様に、テストはGBP/JPYペアの30分足でおこなっています。

カーネル回帰とドット積類似度

今回、教師あり学習モデルとして選択したのは、カーネル回帰とドット積類似度を用いるCNNです。カーネル回帰は、CNNの各層の出力を、特定のクエリ点に対する入力の類似度に応じて重み付けすることで推定します。この類似度は、カーネル関数としてドット積類似度を用いて定量化されます。本モデルでは、次のセクションでコードを共有する通り、_dot_product_kernel_regressionメソッドにより、特徴量マップ内のすべての時間位置間の類似度をtorch.bmm(x, x.T)を用いて計算し、さらに自己アテンションに近いsoftmax正規化を加えています。

ドット積はデータ適応型の類似度尺度として機能します。ドット積の値が高い場合、2つの位置はチャンネルにわたる活性化パターンが一致していることを示し、重み付き和においてより大きな影響を与えます。別の見方をすると、各位置がクエリ位置との一致度に比例して「投票」をおこなうようなイメージです。CNNの層は、行が時間ステップ、列が特徴量のスプレッドシートとして考えることができます。この場合、単一の行が「位置」を表し、更新対象となる行が「クエリ位置」となります。更新の過程では、このクエリ位置と他のすべての位置を比較して、類似度を定量化します。これらの更新はバックプロパゲーション時におこなわれます。

数学的には、新しい重みは次のように定義できます。特徴ベクトルxiとxjが与えられた場合、 重みwijは次のようになります。

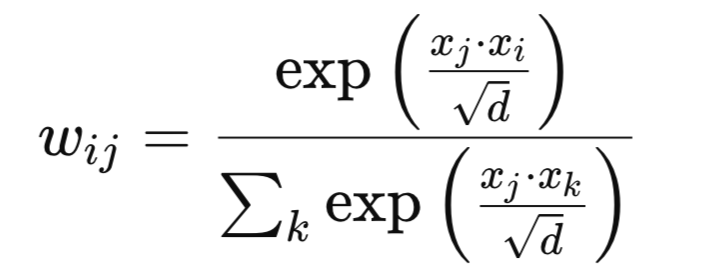
ここで

• d：チャンネル次元
• exp：自然対数の指数関数

私たちの重み行列は、畳み込みのように局所的な近傍に限定されない非局所平滑化をシーケンス全体にわたって実施します。この効果により、特徴空間内の長距離依存関係や相関を捉えることができ、時系列データや構造化データタスクにおける性能向上が期待できます。ドット積類似度は、非隣接の特徴間に意味のある相関が存在するタスクで特に有効です。また、Query、Key、Value投影を追加せずに注意メカニズムのような挙動を導入できる点もメリットです。これは、CNNが捉える局所的な特徴量と、カーネル回帰による大域的な文脈の追加が、非常に相性の良い組み合わせであることを示しています。

ドット積によるCNNカーネルチャネルサイズのガイド

ドット積カーネル回帰は、どの位置でどの解像度において相関が最も強いかを明らかにします。この相似構造に沿ってCNNのカーネルサイズやチャネル深さを調整することで、2つの効果が期待できます。まず第一に、受容野を相関の長さに合わせることができます。これは特に、大きなカーネルで高い類似度が広範囲にわたって持続する場合に有効です。第二に、チャネル数を相関の複雑性に応じて配分することができます。類似度パターンが大きく変化する場合にはより多くのチャネルが割り当てられ、より均一な場合には少なくすることが可能です。このことにより、固定的なヒューリスティックではなく、データ駆動かつタスク特化型のアーキテクチャを設計する可能性が生まれます。

この実装では、次のセクションで示すソースコードの通り、カーネルサイズは3、5、7、9の順でサイクルし、チャネル深さも32から320まで増加します。隔層ごとにドット積回帰を適用しており、これにより各層は大域的相関マップを「見る」ことができます。相似度マップが大きなカーネルで広いピークを示す場合は、それを活用することが可能です。逆にマップが鋭いピークを示す場合は小さなカーネルで十分であり、微細な調整に注力することができます。この手法は、大域的な相関信号に導かれた適応的受容野のチューニングに例えることができます。

CNNで使用する場合は、事前に小規模CNNとドット積カーネルブロックを用いたデータ解析をおこない、相関長を評価することが推奨されます。この解析結果は、メインCNNのカーネルおよびチャネル設計の基礎として利用できます。また、局所的なエッジやパターンを検出する初期層では小さなカーネルを使用し、後続層のカーネルサイズは観測された類似度分布に基づいて調整することが望ましいです。

考えられる欠点と代替手法

ドット積カーネルをこのように使用する際の最大の欠点は驚くことではなく、計算コストです。ドット積類似度は、シーケンス長Lに対して、O(L2)のスケーリングを持ちます。長い信号や大きな特徴量入力の場合、計算負荷が非常に高くなる可能性があります。もう一つの懸念は過平滑化(oversmoothing)です。重みが広がりすぎると特徴量が均質化しすぎ、一部の微細な情報が失われる可能性があります。また、学習の不安定性も問題となる場合があります。類似度が大きい場合に正規化をおこなわないと、重みが爆発するケースが生じることがあります。さらに、完全な類似度行列を保持するためのメモリオーバーヘッドも大きなコストとなる可能性があります。 

しかし、これらの懸念にはいくつかの対策があります。その一つが局所アテンションウィンドウの使用です。先に示した計算複雑性に基づく全位置の類似度計算の代わりに、各クエリ位置の周囲に固定されたウィンドウ内のみで比較をおこないます。これにより、計算量やメモリを削減し、近傍の関連する文脈に重点を置くことができます。加えて、Temperature Scalingを採用することも可能です。ここでは単に、類似度スコアに温度1/τを掛けます。温度が低い場合、少数の位置や層行が支配的になるような、より鋭く選択的な重みが得られます。温度が高い場合、層グリッド全体にわたって重みが滑らかで均等に分布します。この温度は追加のハイパーパラメータとして扱われます。

さらに、カーネル回帰の前にダウンサンプリングをおこなうことも可能です。これには、プーリングやストライド付き畳み込みを用いて入力データのシーケンス長Lを短縮してからドット積を計算する方法が含まれます。シーケンス長を短くすることで、類似度計算を高速化し、メモリ使用量を削減しつつ、依然として大規模な相関を捉えることができます。

ドット積を用いたCNNの代替強化手法

ドット積カーネル回帰に加えて、自己アテンションハイブリッドCNNを適用することも可能です。この場合、標準的なアテンション層ではなく、CNN層と並行して非局所ブロックとしてドット積回帰を使用します。これは、次のセクションで示すソースコードの実装とは異なり、私たちのモデルでは畳み込みスタック内で周期的にカーネル回帰を適用しています。ハイブリッドでは、並列ブランチに挿入して出力を融合します。また、マルチスケール特徴融合によってカーネルを適用することも可能です。この場合、複数のCNN層から取得した特徴量にカーネル回帰を適用し、それらを結合します。これに対して私たちの実装では、カーネル回帰は一度に一つの層にのみ適用しています。マルチスケール融合では、異なる層・解像度からの大域的文脈を統合することができます。 

さらに、事前タスクを用いた正則化としてカーネルを利用することも可能です。この場合、カーネル回帰の出力を補助タスクの学習に使用し、たとえば次ステップの埋め込みを予測するなど、本来のタスクに加えて学習させます。これは私たちの手法とは異なり、単純に特徴の洗練にカーネルを用いるのではなく、正則化の役割も担います。最後に、過去の記事で扱った動的カーネルサイズを用いることも考えられます。この手法では、カーネル回帰から得られた類似度統計を用いて、学習や推論中に畳み込みカーネルサイズを調整します。以下の実装では、カーネルサイズは事前に固定しています。

ネットワーク

ドット積カーネルを回帰で実装するネットワーククラスのコードは次のとおりです。

class DotProductKernelRegressionConv1D(nn.Module):
    def __init__(self, input_length=100):
        super().__init__()
        self.input_length = input_length

        self.kernel_sizes, self.channels = self._design_architecture()

        self.conv_layers = nn.ModuleList()
        self.use_kernel_regression = []  # <-- Python list for markers

        in_channels = 1
        for i, (out_channels, kernel_size) in enumerate(zip(self.channels, self.kernel_sizes)):
            conv_layer = nn.Sequential(
                nn.Conv1d(in_channels, out_channels, kernel_size=kernel_size, padding=kernel_size // 2),
                nn.BatchNorm1d(out_channels),
                nn.ReLU(),
                nn.Dropout(0.2))
            self.conv_layers.append(conv_layer)

            self.use_kernel_regression.append(i % 2 == 0)
            in_channels = out_channels

        self.head = nn.Sequential(
            nn.AdaptiveAvgPool1d(1),
            nn.Flatten(),
            nn.Linear(in_channels, 128),
            nn.ReLU(),
            nn.Dropout(0.2),
            nn.Linear(128, 64),
            nn.ReLU(),
            nn.Linear(64, 1),
            nn.Sigmoid()
        )

    def _dot_product_kernel_regression(self, x):
        """
        Dot product kernel regression.
        For each time position, outputs a weighted sum of all positions using dot product similarity as weights.
        """
        # x: (B, C, L)
        x_ = x.permute(0, 2, 1)  # (B, L, C)
        # Dot product similarity
        sim = torch.bmm(x_, x_.transpose(1, 2))  # (B, L, L)
        # Optionally normalize for stability (like attention)
        weights = F.softmax(sim / (x_.size(-1) ** 0.5), dim=-1)  # (B, L, L)
        out = torch.bmm(weights, x_)  # (B, L, C)
        return out.permute(0, 2, 1)  # (B, C, L)

    def _design_architecture(self):
        num_layers = 10
        kernel_sizes = [3 + (i % 4) * 2 for i in range(num_layers)]
        channels = [32 * (i + 1) for i in range(num_layers)]
        return kernel_sizes, channels

    def forward(self, x):
        x = x.unsqueeze(1)  # (B, 1, L)
        for conv_layer, use_kr in zip(self.conv_layers, self.use_kernel_regression):
            x = conv_layer(x)
            if use_kr:
                x = self._dot_product_kernel_regression(x)
        return self.head(x)

上記のコードの最初の行は、クラスのスケルトンとコンストラクタです。このクラスはnn.Moduleを継承しており、PyTorchのパラメータ追跡、.to(device)や.eval()などの機能が使用可能になります。input_lengthの値は保存されます。畳み込み自体は長さに依存しませんが、この値を保持することで、サニティチェックやONNXへのエクスポート、後に長さ依存のロジックを構築する際に役立ちます。これに続き、アーキテクチャの設計を設定します。ここではカーネルサイズとチャネル数を定義します。これは受容野の計画（カーネルサイズ）やモデル容量の計画（チャネル数）を集中管理するため重要です。一箇所にまとめることで、2つの利点があります。まず第一に、カーネルサイズを整合させる際、カーネル回帰から得られる類似度の観測結果を反映できます。第二に、類似度パターンがより複雑な場合にスケーリングが容易になります。

使用上の指針として、_design_architecture関数はデータ駆動型であるべきです。データバッチを用いて回帰ブロックからの類似度減衰を測定し、それに基づいてカーネルサイズを拡張できます。また、チャネル数を類似度分布のエントロピーに結びつけることも考えられます。この場合、エントロピーが高いほど、モデルの多様性を助けるためにより多くのチャネルが割り当てられます。

次に、畳み込みスタックとカーネル回帰を適用する位置のマーカーを定義します。ModuleList関数を使用することで、各層が登録され、その重みが必要に応じて保存や読み込みされます。パディングをカーネルサイズの半分に設定することで、畳み込みの出力長さがほぼ同じになるか、長さが維持されます。これは、後でカーネル回帰が一貫した長さを前提に計算されるため重要です。

バッチ正規化、ReLU活性化、ドロップアウトの使用も堅牢な手法です。バッチ正規化は学習の安定化、ReLUは非線形性の導入、ドロップアウトは正則化を提供します。use_kernel_regressionのブール値により、計算負荷の高いカーネル回帰をすべての層から切り離し、必要な箇所にのみ適用することが可能です。追加の使用指針として、カーネル回帰が強力な場合は、conv_layerブロック周りに残差スキップを入れることで最適化が容易になります。

次に、予測ヘッドを定義します。このスタッキングは重要で、いくつかの主要コンポーネントを含みます。まず、AdaptiveAvgPool1d(1)により、各チャネルごとに入力長に依存しないグローバルサマリーが生成されます。これは入力の可変性に対応するため重要です。言い換えると、各チャネルの可変長時系列を単一の平均値に圧縮し、固定サイズのサマリーベクトルを生成します。これにより、ネットワークの出力は入力シーケンス長に依存しなくなります。これは、サンプル間で時間ステップ数が異なる場合に特に重要です。

MLPは特徴量サマリーをスカラー出力にマッピングします。出力範囲は0.0から1.0の回帰なので、シグモイド活性化が実用的です。制約のない回帰出力にはIdentity、マルチクラス出力にはLog-SoftMaxを検討できます。方向性の中立性（ロング/ショートの判断など）が懸念される場合、シグモイドを2ヘッドに置き換えることも可能です。第一のヘッドは確率分布としてシグモイドを使用し、第二のヘッドは大きさに焦点を当て、活性化関数としてソフトプラスを使用します。説明可能性が必要な場合は、プールされたベクトルを露出させ、各チャネルの重要度を計算できます。

次に、カーネル回帰のコア関数を定義します。まず入力データxを（バッチサイズ、チャネル数、長さ）に転置します。これにより、ドット積は各位置でチャネル埋め込みに対して計算されます。そのため、チャンネル数Cが内部次元になります。その後、全位置にわたる非局所的なアフィニティ行列を構築し、計算コストは長さの二乗です。これがsim行列です。次に、このsim行列をチャンネル数の平方根でスケーリングし、チャンネル次元が増加してもロジットが安定するようにします。ソフトマックス活性化により、類似度を確率単体(probability simplex)に変換します。各層の行は、すべての行の凸結合として表現されます。カーネル回帰は次のステップで実行され、これらの重みを転置・入れ替え済みの入力ベクトルxに掛けます。各層の行/位置は、ウィンドウ全体の類似位置から情報を借用します。

使用上の指針として、長いシーケンスには局所ウィンドウやブロック対角注意を使用し、NystromやLinformerなどの低ランク操作を実装することが推奨されます。また、カーネル回帰前にダウンサンプリングし、その後アップサンプリングする方法もあります。予測やカジュアルタスクでは、ソフトマックス活性化前にカジュアルマスキングを追加すると、データリークや未来情報へのアクセスを防げます。過平滑化が見られる場合は、温度ハイパーパラメータを次のように導入できます。

weights = F.softmax(sim / (tau * x_.size(-1) ** 0.5), dim=-1)

x = x + alpha * self._dot_product_kernel_regression(x)

次の関数では、モデルアーキテクチャを定義、生成します。この関数は、3から9の範囲でマルチスケールを繰り返しカバーするため、各ステージがカーネル回帰の大域的文脈に応答できます。線形チャネルの増加により、ネットワーク深部でより抽象的な特徴量に対応可能です。測定された類似度幅に応じてサイクルを調整し、広い類似度では層に沿って大きなカーネルに偏るようにするのがベストプラクティスです。チャネルも盲目的に増やすのではなく、活性化のスパース性やカーネル回帰のエントロピーを監視し、必要な箇所に適切に割り当てる必要があります。

ネットワーククラスの最後の関数は、フォワードパス関数です。ここでは、まずバッチ-チャネル-長さフォーマットを強制するために次元を追加します。1次元CNNでは、初期チャネルは1です。  局所畳み込みと大域的カーネル回帰を交互に適用することで強力なパターンを形成します。局所的なモチーフを検出すると、学習された類似度に応じて情報が伝播されます。その後、次の畳み込みで局所的に精緻化されます。self.head()を返すことで、ONNXエクスポートやデプロイ時にフォワードグラフをクリーンに保つことができます。

勾配フローをより強化する必要がある場合は、カーネル回帰や残差周りに層の正規化を補助的に追加することも可能です。

インジケーターの翻訳

前回および前々回の記事で扱ったシグナルパターンを、上記で解説したCNNカーネル回帰モデルの入力として使用するには、Pythonで同等のインジケーターを用意する必要があります。Pythonにはいくつか既製のインジケーターモジュールがありますが、ゼロから独自に実装することも、意外と手間がかからず、計算過程における判断を適切に管理できるという利点があります。そのため、過去の記事と同様に、インジケーターの読み取り値はブルまたはベアを示す2次元ベクトルとしてエンコードし、値は0か1のどちらかのみを取るようにしています。ここでカーネル回帰が有効です。取得した特徴量は、構造的なローソク足やオシレーターのパターンを符号化しており、遠く離れた位置でも「似たように見える」またはドット積類似度の高い埋め込みが互いに補強し合います。カーネル回帰(KR)を用いることで、モデルは時間にわたって統計的な強さを借用できるため、各パターンが単独では比較的まれで弱い場合でも有効です。

また、カーネル回帰をどの層で適用するかを早期に決めることは、原始的なモチーフの伝播に寄与します。後期にKRを適用すると、より高次のモチーフが統合されます。初期段階では浅いKRと小さめのチャネルサイズ、後期段階では深いKRと大きなチャネル数を組み合わせて試すというアプローチは、合理的で効果的です。

ゲーターオシレーター

この関数は、ビル・ウィリアムズのアリゲーターコンポーネントを構築します。ミディアン価格の平滑移動平均(SMMA)を用い、顎、歯、唇の各ラインを前方にシフトさせます。この内容は前回の記事でも扱いました。関数の出力として、顎と歯の差の大きさを表すバッファをGator_Upとして、歯と唇の差の負の値をGator_Downとして作成します。また、拡張/収縮の挙動を示す色の状態も追加しています。以下のPython実装で説明します。

def Gator_Oscillator(df: pd.DataFrame,
                     jaw_period: int = 13, jaw_shift: int = 8,
                     teeth_period: int = 8, teeth_shift: int = 5,
                     lips_period: int = 5, lips_shift: int = 3) -> pd.DataFrame:
    """
    Calculate the Bill Williams Gator Oscillator and append the columns to the input DataFrame.

    Adds color columns for each bar:
    - Gator_Up_Color: 'green' for increasing, 'red' for decreasing, else previous color.
    - Gator_Down_Color: 'green' for increasing (less negative), 'red' for decreasing (more negative), else previous color.

    Args:
        df (pd.DataFrame): DataFrame with 'high' and 'low' columns.
        jaw_period (int): Jaw period (default 13).
        jaw_shift (int): Jaw shift (default 8).
        teeth_period (int): Teeth period (default 8).
        teeth_shift (int): Teeth shift (default 5).
        lips_period (int): Lips period (default 5).
        lips_shift (int): Lips shift (default 3).

    Returns:
        pd.DataFrame: Input DataFrame with 'Gator_Up', 'Gator_Down', 'Gator_Up_Color', 'Gator_Down_Color'.
    """
    required_cols = {'high', 'low'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high' and 'low' columns")
    if not all(p > 0 for p in [jaw_period, jaw_shift, teeth_period, teeth_shift, lips_period, lips_shift]):
        raise ValueError("Period and shift values must be positive integers")

    result_df = df.copy()
    median_price = (result_df['high'] + result_df['low']) / 2

    def smma(series, period):
        smma_vals = []
        smma_prev = series.iloc[0]
        smma_vals.append(smma_prev)
        for price in series.iloc[1:]:
            smma_new = (smma_prev * (period - 1) + price) / period
            smma_vals.append(smma_new)
            smma_prev = smma_new
        return pd.Series(smma_vals, index=series.index)

    jaw = smma(median_price, jaw_period).shift(jaw_shift)
    teeth = smma(median_price, teeth_period).shift(teeth_shift)
    lips = smma(median_price, lips_period).shift(lips_shift)

    result_df['Gator_Up'] = (jaw - teeth).abs()
    result_df['Gator_Down'] = -(teeth - lips).abs()

    # Color logic
    up_vals = result_df['Gator_Up'].values
    down_vals = result_df['Gator_Down'].values

    up_colors = ['green']  # Start with green (or change to None/'grey' if you want)
    for i in range(1, len(up_vals)):
        if pd.isna(up_vals[i]) or pd.isna(up_vals[i-1]):
            up_colors.append(up_colors[-1])
        elif up_vals[i] > up_vals[i-1]:
            up_colors.append('green')
        elif up_vals[i] < up_vals[i-1]:
            up_colors.append('red')
        else:
            up_colors.append(up_colors[-1])

    down_colors = ['green']  # Start with green for "less negative" (getting closer to zero is "increasing")
    for i in range(1, len(down_vals)):
        if pd.isna(down_vals[i]) or pd.isna(down_vals[i-1]):
            down_colors.append(down_colors[-1])
        elif down_vals[i] > down_vals[i-1]:
            down_colors.append('green')  # "less negative" = "up"
        elif down_vals[i] < down_vals[i-1]:
            down_colors.append('red')    # "more negative" = "down"
        else:
            down_colors.append(down_colors[-1])

    result_df['Gator_Up_Color'] = up_colors
    result_df['Gator_Down_Color'] = down_colors

    return result_df

コードを行ごとに見ていくと、まず関数内でおこなう最初の処理は、不正な入力や意味のないハイパーパラメータから保護することです。シフト値は正である必要があります。なぜなら、アリゲーターのラインは意図的に前方にずらされており、視覚的に価格を「先導」させるためです。次に、入力DataFrameの作業コピーとミディアン価格のバッファ/ベクトルを取得します。これにより元の入力データは保持され、ミディアン価格を用いることで終値のみを使う場合よりもノイズが低減されます。この手法は一般的なアリゲーターの慣習に沿ったものです。

続いて、平滑移動平均(SMMA)の実装を定義します。SMMAは再帰的な平滑化をおこなう移動平均で、通常のEMAより反応が遅いため、値動きが不安定な場面でのノイズ除去に適しています。最初の値をseries.iloc[0]で初期化することで、長いウォームアップ期間を避けています。その後、アリゲーターの各ラインと前方へのシフトを設定します。期間は顎から歯、歯から唇へと順に短くなります。すべて前方にシフトされているため、インジケーターの口（顎、歯、唇のライン）が、現在のバーより先行して開閉します。

これが完了すると、次にターゲット出力データバッファGator_UpとGator_Downを定義する準備が整います。これらは絶対値を用いており、アリゲーターの顎がどれだけ広がっているか、すなわちスプレッドの大きさを測定します。バーの正負の符号はプロット用の慣習です。最後に、カラーロジックを実装します。ここではスプレッドの傾向、つまり拡大傾向か縮小傾向かに注目します。下向きのバーはゼロ以下にプロットされるため、その値は負になります。バーが上向きに見えても値そのものは負で、絶対値が小さくなっているだけです。NaNの処理では、開始直後の不規則な動きによるちらつきを避けるために、前の状態を保持します。

A/Dオシレーター

このオシレーターの目的は、マネーフロー乗数と出来高の積から累積/分配線(ADL: Accumulation/Distribution Line)を計算することです。これは、出来高やティックボリュームでスケーリングされた終値のバー範囲を通じて、買い圧力と売り圧力を捉えます。Pythonでの実装は以下の通りです。

def AD_Oscillator(df: pd.DataFrame, fast_period: int = 5, slow_period: int = 13) -> pd.DataFrame:
    """
    Calculate the Accumulation/Distribution Oscillator (A/D Oscillator) and append it to the input DataFrame.

    A/D Oscillator = EMA(ADL, fast_period) - EMA(ADL, slow_period)

    ADL (Accumulation/Distribution Line) is calculated as:
    Money Flow Multiplier = [(Close - Low) - (High - Close)] / (High - Low)
    Money Flow Volume = Money Flow Multiplier * Volume
    ADL = cumulative sum of Money Flow Volume

    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', 'close', 'volume' columns.
        fast_period (int): Fast EMA period (default 3).
        slow_period (int): Slow EMA period (default 10).

    Returns:
        pd.DataFrame: Input DataFrame with 'ADL' and 'AD_Oscillator' columns added.
    """
    required_cols = {'high', 'low', 'close', 'tick_volume'}
    if not required_cols.issubset(df.columns):
        raise ValueError("DataFrame must contain 'high', 'low', 'close', 'tick_volume' columns")
    if not all(p > 0 for p in [fast_period, slow_period]):
        raise ValueError("Period values must be positive integers")
    if fast_period >= slow_period:
        raise ValueError("fast_period must be less than slow_period")

    result_df = df.copy()
    high = result_df['high']
    low = result_df['low']
    close = result_df['close']
    volume = result_df['tick_volume']

    # Avoid divide by zero, replace zero ranges with np.nan
    range_ = high - low
    range_ = range_.replace(0, pd.NA)

    mfm = ((close - low) - (high - close)) / range_
    mfv = mfm * volume
    result_df['ADL'] = mfv.cumsum()

    fast_ema = result_df['ADL'].ewm(span=fast_period, adjust=False).mean()
    slow_ema = result_df['ADL'].ewm(span=slow_period, adjust=False).mean()
    result_df['AD_Oscillator'] = fast_ema - slow_ema

    return result_df

コードの流れを上記のゲーターと同様に見ていくと、まず最初におこなうのは、入力DataFrameに価格と出来高の4つの列が存在するかを確認することです。今回テスト対象としているのは為替ペアであり、過去の記事でも扱った通り、出来高は実出来高ではなくティックボリュームを使用します。次に、この関数が「真のオシレーター」となるように、遅い期間が速い期間よりも長いことを確認します。次に範囲計算用の列を抽出し、ゼロ除算を回避します。高値と安値が同じ場合（たとえば十字線や市場外の見値など）、範囲がゼロになり、乗数が異常に大きくなる可能性があるためです。 

範囲の準備が整ったら、マネーフロー乗数(mfm)とマネーフローボリューム(mfv)を計算します。乗数は-1から+1の範囲に収まります。mfvはその出来高加重版です。cumsum関数により、この出来高圧力を時間的に積分し、ADLが得られます。次に、ADLバッファに対して高速EMAと低速EMAを計算します。adjust=Falseとすることで、標準的な再帰EMAが得られ、ほとんどのトレーダーの期待に沿った動作になります。これらのバッファの差を取ることで、信号が鋭くなり、短期的な蓄積が長期トレンドを上回っている場合にポジティブな値として強調されます。

選択されたシグナルパターン

今回対象とするシグナルパターン、Pattern_0、Pattern_3、Pattern_4の各関数は、入力DataFrameの行数 × 2の形状を持つNumPy配列を返します。過去の記事と同様に、[:, 0]はロング（強気）シグナルをエンコードします。前回の記事で定義したインジケーター値をチェックしたうえで、パターンが強気の場合は1が記録され、そうでなければ0となります。一方、[:, 1]はショート（弱気）シグナルをエンコードし、パターンが存在する場合は1、何も検出されない場合は0です。これら3つのシグナルパターンは、ゲーターオシレーターの色（上向き/下向き）、プライスアクションの制約（高値/安値/終値との比較とshift関数による調整）、そしてモメンタムやボリューム圧力（A/Dオシレーターと同様にshift比較を適用）を組み合わせて構成されています。また、すべてのパターンでは、比較範囲に応じて最初の数行を0に設定し、誤検出を避ける処理が施されています。

Feature_0

前々回の記事で紹介したこのシグナルパターンは、ゲーターの発散とブレイクアウト、さらにA/Dオシレーターでの確認から構成されます。Pythonによるこの特徴量の実装は以下の通りです。

def feature_0(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 0.                                             |
//+------------------------------------------------------------------+

    """
    feature = np.zeros((len(df), 2))
    
    cond_1 = df['Gator_Up_Color'] == 'red'
    cond_2 = df['Gator_Down_Color'] == 'green'

    feature[:, 0] = (cond_1 &
                     cond_2 &
                     (df['high'].shift(2) > df['high'].shift(3)) &
                     (df['high'].shift(1) >= df['high'].shift(2)) &
                     (df['close'] > df['high'].shift(1)) &
                     (df['AD_Oscillator'].shift(1) > df['AD_Oscillator'].shift(2)) &
                     (df['AD_Oscillator'] <= df['AD_Oscillator'].shift(1))).astype(int)
    
    feature[:, 1] = (cond_1 &
                     cond_2 &
                     (df['low'].shift(2) < df['low'].shift(3)) &
                     (df['low'].shift(1) <= df['low'].shift(2)) &
                     (df['close'] < df['low'].shift(1)) &
                     (df['AD_Oscillator'].shift(1) < df['AD_Oscillator'].shift(2)) &
                     (df['AD_Oscillator'] >= df['AD_Oscillator'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

上記のコードでは、まずロング/ショートのフラグを示す2列のバイナリ行列を作成しています。その後、コアとなるゲーターの色のフィルタを定義します。具体的には、上向きのラインは縮小している状態、すなわち赤であることを要求し、下向きのラインは拡張している状態、すなわち緑であることを要求します。続いて、[:, 0]列に対してロング側のルールを正式に定義します。ここでは、ゲーターの状態をエンコードし、事前に設定された色の条件に基づきレジームを構築します。ロング条件では、高値更新を確認して蓄積の存在を担保し、さらにA/Dオシレーターの上昇によるブレイクアウト確認を組み合わせます。これらの指標は、上昇を確認するうえで重要です。すなわち、「レジーム + 蓄積 + ブレイクアウト + コントロールされたモメンタム」というシナリオを狙う構造化された、弱いものの、一定の持続性を期待できるシグナルとなります。

ショート側では、上記と同様のロジックを反転させ、下方向へのブレイクアウトと、その後の分配減速を確認します。最後に、この関数では、shiftによって未割り当てとなった値をすべて0に設定することで、誤検出を防止しています。このパターンのみを対象として、ネットワークをONNX経由で出力し、ウィザードで組み立てたエキスパートアドバイザー(EA)上でテストした結果、以下のレポートが得られました。

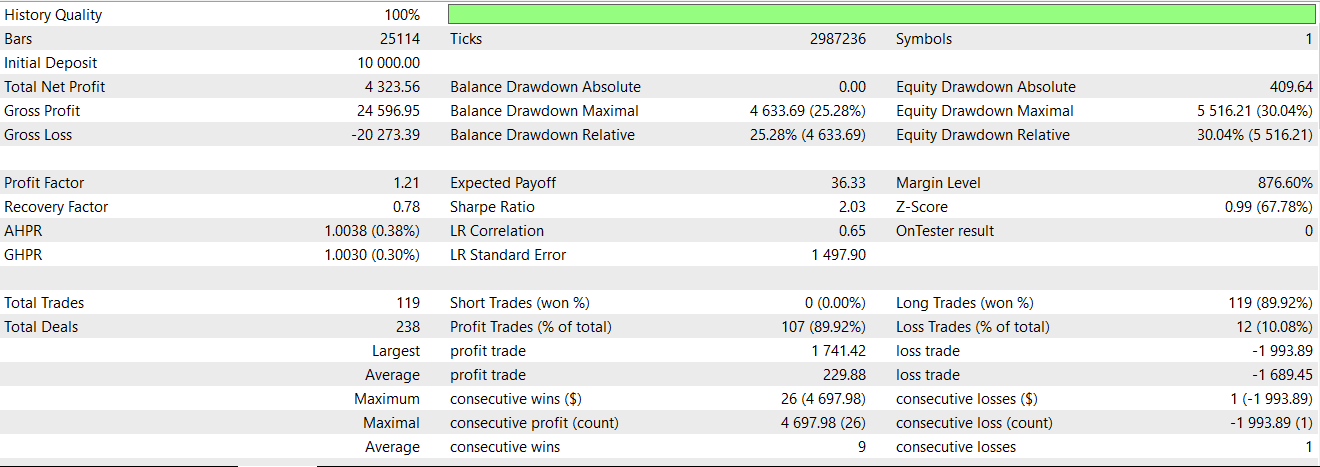
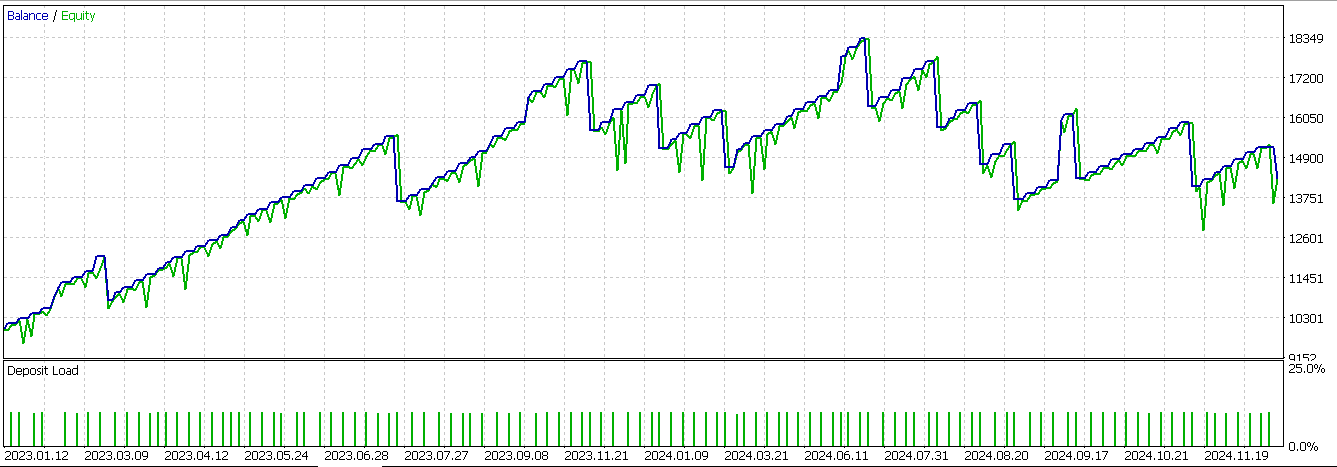
利益の出たエントリーは多いものの、このシグナルは依然として2024年のフォワードウォークでは収益性が確保できていないことが分かります。

Feature_3

2番目のシグナルパターンは、収縮から拡張への移行とバー内での推進に基づいています。Pythonでの実装は次のとおりです。

def feature_3(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 3.                                             |
//+------------------------------------------------------------------+
    """
    feature = np.zeros((len(df), 2))
    
    cond_1 = df['Gator_Up_Color'].shift(1) == 'red'
    cond_2 = df['Gator_Down_Color'].shift(1) == 'red'
    cond_3 = df['Gator_Up_Color'] == 'red'
    cond_4 = df['Gator_Down_Color'] == 'green'
    
    feature[:, 0] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['close']-df['low'].shift(1) > 0.5*(df['high'].shift(1)-df['low'].shift(1))) &
                     (df['AD_Oscillator'].shift(2) > df['AD_Oscillator']) &
                     (df['AD_Oscillator'] > df['AD_Oscillator'].shift(1))).astype(int)
    
    feature[:, 1] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['high'].shift(1)-df['close'] < 0.5*(df['high'].shift(1)-df['low'].shift(1))) &
                     (df['AD_Oscillator'].shift(2) < df['AD_Oscillator']) &
                     (df['AD_Oscillator'] < df['AD_Oscillator'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

ここでの基本条件は、直前のゲーターのヒストグラムバーが上下とも赤であり、その後いずれかが緑に変化することです。これは前々回の記事で、トランジションのサインとして解説しました。このパターンの詳しい説明はその記事で扱ったため、ここでは省略し、同じパターンをニューラルネットワークでフィルタとして適用した際のテスト結果に移ります。得られたレポートは以下の通りです。

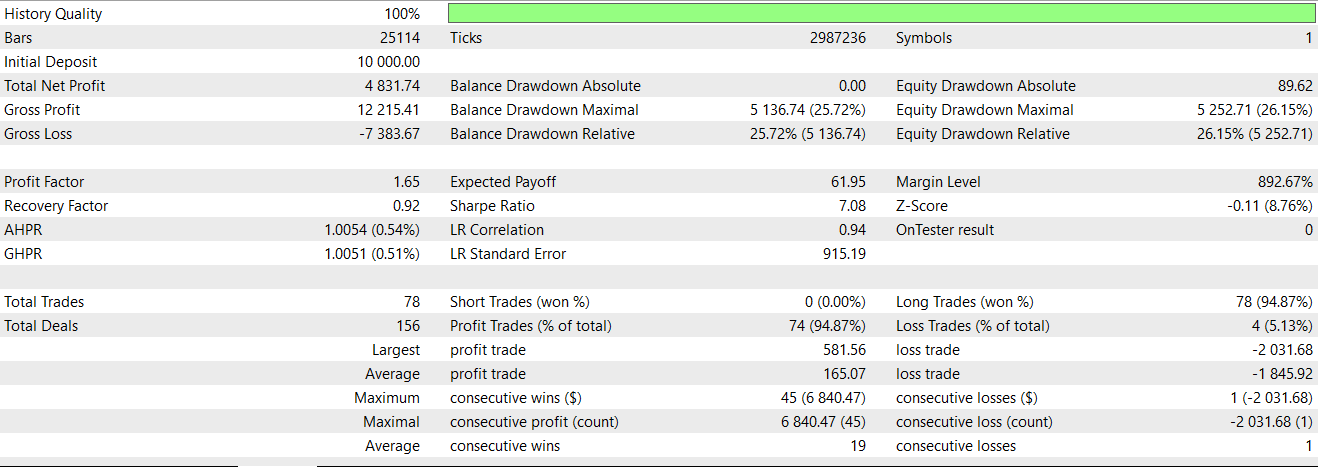
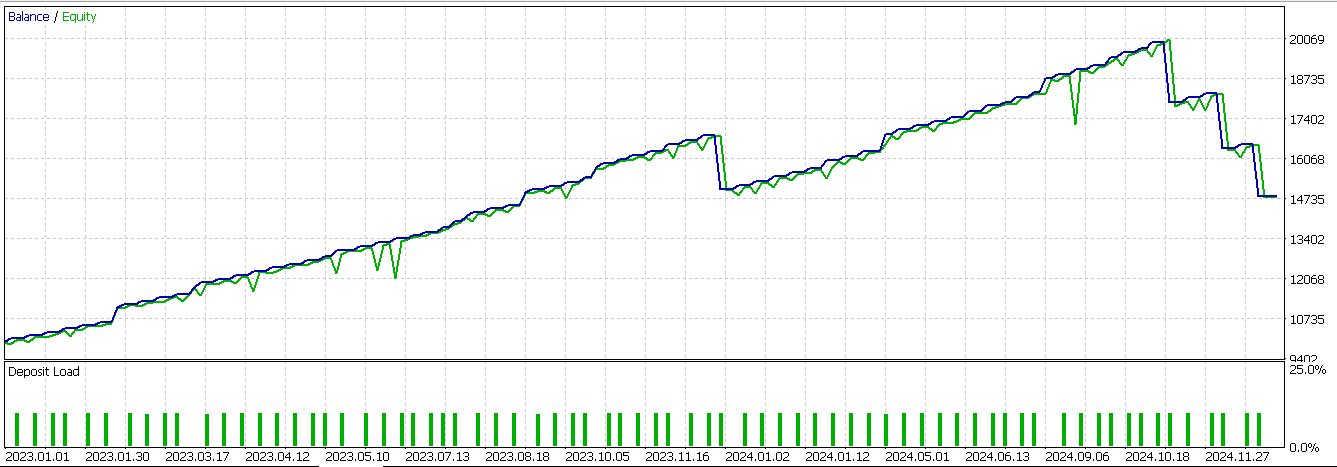
フォワードウォークはほぼ成功しましたが、最後の一連の負け取引により利益が確保できませんでした。私たちのシステムは常にストップロスなしで利確ターゲットのみを使用しているため、これはシグナル反転で決済する方式のため、損失が大きくなったことによります。

Feature_4

最後に確認するシグナルパターンは、色の反転の継続と簡単なモメンタム確認に基づいています。具体的には、前のバーが上向きかつ拡張しており、上側のヒストグラムが緑、下側が赤であった場合、その後のバーで上側ヒストグラムが収縮を示して赤、下側が緑となると、ゲーターオシレーターのレジーム変化を示す可能性があります。加えて、価格の拒否やA/Dオシレーターによるモメンタム確認も適用されます。これらの確認手順については、前回の記事で既に述べた通りです。

def feature_4(df):
    """
//+------------------------------------------------------------------+
//| Check for Pattern 4.                                             |
//+------------------------------------------------------------------+
    """
    feature = np.zeros((len(df), 2))
    
    cond_1 = df['Gator_Up_Color'].shift(1) == 'green'
    cond_2 = df['Gator_Down_Color'].shift(1) == 'red'
    cond_3 = df['Gator_Up_Color'] == 'red'
    cond_4 = df['Gator_Down_Color'] == 'green'
    
    feature[:, 0] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['close'] > df['close'].shift(1)) &
                     (df['low'].shift(1) > df['low']) &
                     (df['AD_Oscillator'] > df['AD_Oscillator'].shift(1))).astype(int)
    
    feature[:, 1] = (cond_1 &
                     cond_2 &
                     cond_3 &
                     cond_4 &
                     (df['close'] < df['close'].shift(1)) &
                     (df['high'].shift(1) < df['high']) &
                     (df['AD_Oscillator'] < df['AD_Oscillator'].shift(1))).astype(int)
    
    
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

このシグナルをテストした結果、ニューラルネットワークを追加のフィルタとして、前回の記事で構築したEAに組み込んだ場合、得られたレポートは以下の通りです。

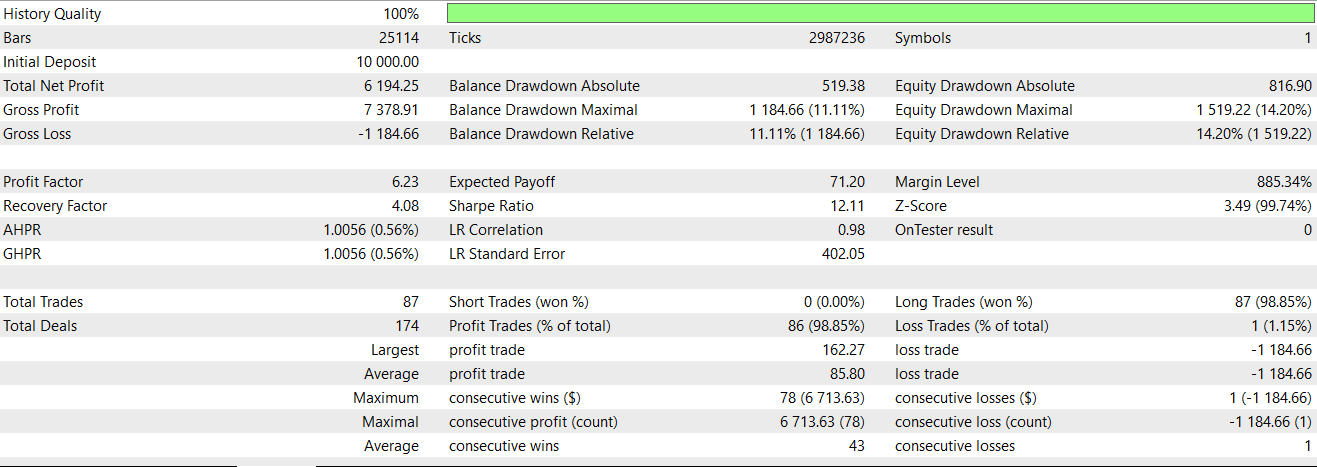
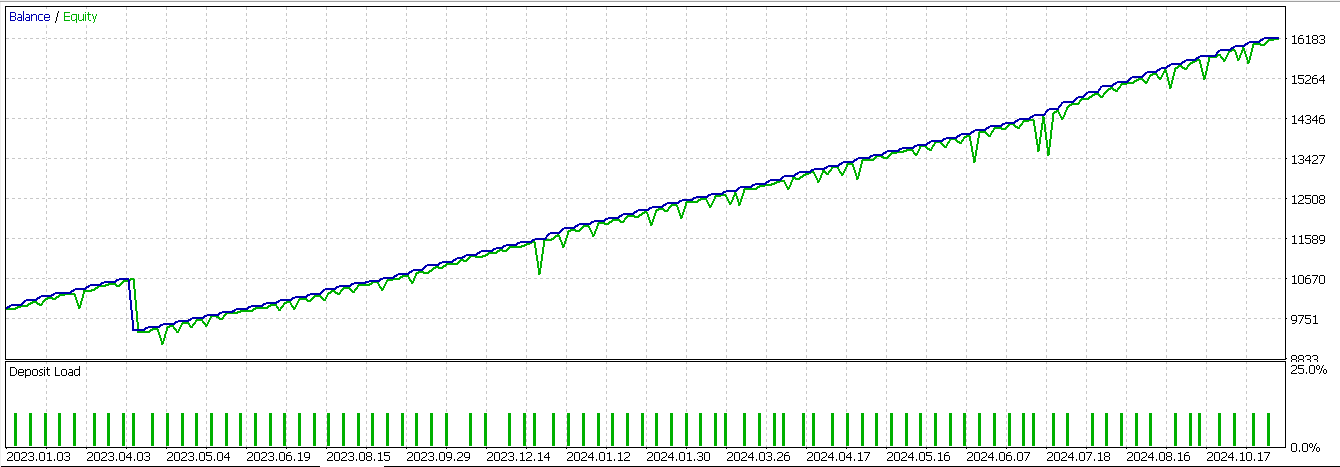
本記事で再検討した3つのシグナルのうち、最初にテストした際から明確に運用成績を反転させたのは、このシグナルのみでした。繰り返しになりますが、テスト期間はわずか2年に限定しているため、このシグナルをさらに開発しようとする場合は、各自で独立した検証をおこなうことが常に求められます。Feature_4のショートシグナルパターンは、価格チャート上で次のように現れる可能性があります。

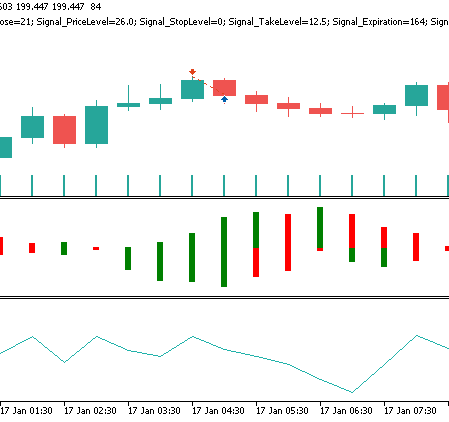
結論

本記事で検討したCNNを用いた教師あり学習モデルは、カーネル回帰とドット積類似度によって強化することで、弱いシグナルパターンを改善できる可能性を示しました。すべてのテスト対象パターンが均等に恩恵を受けたわけではありませんが、Feature_4は明確な反転を示し、このアプローチがEAにおける適切なフィルタとして機能する可能性を示唆しています。とはいえ、テスト期間が限定されているため結論には慎重さが必要です。しかし、この手法は過去の信頼性が低いシグナルからでも、適応的なアーキテクチャにより価値を引き出せる可能性があることを示しています。

名前	説明
WZ-79.mq5	ヘッダに使用ファイルを示すウィザード組み立てEA（ウィザードガイドはこちら）
SignalWZ-79.mqh	ウィザードアセンブリで使用されるカスタムシグナルクラスファイル
79_0.onnx	Pattern_0シグナルのエクスポート済みニューラルネットワーク
79_3.onnx	Pattern_3シグナルのエクスポート済みニューラルネットワーク
79_4.onnx	Pattern_4シグナルのエクスポート済みニューラルネットワーク