知っておくべきMQL5ウィザードのテクニック（第85回）：ストキャスティクスとFrAMAのパターンを用いたβ-VAEによる推論

はじめに

MetaTrader 5のエコシステム内において、MQL5ウィザードは、トレーダーが新しい取引アイデアを迅速にプロトタイプ化し展開できる非常に有用なツールです。これまでの記事で説明した通り、このプロセスは低レベルのコーディングに踏み込むことなく実現されます。ウィザードはモジュール式のフレームワークを基盤としており、トレーダーはあらかじめ用意されたシグナルクラス、マネーマネジメント戦略、トレーリングストップ機能などから自由に選択可能です。このプラグアンドプレイ方式により、エキスパートアドバイザー(EA)を迅速に組み立てることができます。この利便性は、アルゴリズム取引を個人でも利用できるようにするという副次的効果を持ち、結果として市場流動性の向上に寄与する可能性があります。 

第85回では、これまでの記事同様、ウィザードの拡張的な応用として機械学習を統合します。具体的には、前回の記事で考察したβ変分オートエンコーダ(β-VAE: Beta-Variational Auto-Encoder)アルゴリズムを使用し、前回の記事で扱ったストキャスティクスとFrAMAのインジケーターペアから生成したバイナリ信号を処理します。β-VAEは教師なし学習モデルとして、高次元の入力データを潜在空間に圧縮します。これにより、従来のルールベースシステムでは見落とされがちなデータの潜在的構造や関係性を捉えることが可能です。この自動化プロセスは、パターン認識を向上させるだけでなく、カスタムシグナルクラスにおける推論に基づく意思決定を支援することを目的としています。

前回の記事では、ストキャスティクスとFrAMAから導出した10種類の主要パターン、Pattern_0からPattern_9までを考察しました。ウォークフォワードテストの結果、これらのパターンのパフォーマンスには大きな差がありました。具体的には、Pattern_0からPattern_4およびPattern_7とPattern_8は、異なる市場環境を活かすことを目的として選定した複数の資産において一貫して利益を上げることができ、一定の堅牢性を示しました。しかし、Pattern_5、Pattern_6、Pattern_9は明らかに低調で、アウトオブサンプルのウォークフォワード期間において利益を示すことができませんでした。

ここで重要なのは、テストウィンドウが非常に限られていることです。したがって、これらの結果はあくまでどのパターンをさらに検証すべきかの指針であり、信頼可能なパターンを決定するものではありません。低調なパターンは、次の通り定義されます。Pattern_5はFrAMAがフラットでストキャスティクスが上方向にクロスするパターン、Pattern_6はストキャスティクスが買われ過ぎ/売られすぎのフックを形成し、FrAMA傾斜が上向きになるパターン、Pattern_9はストキャスティクスが極端なレベルにありFrAMA傾斜が逆方向の場合です。

これらの失敗は、パターン自体の柔軟性が不足していることが原因である可能性があります。または、テスト範囲が狭すぎたため、長期的には堅牢なパターンが見過ごされた可能性も考えられます。この議論は、読者自身による独自の検証を通じて判断するのが最適です。本記事では、機械学習を用いてPattern_5、Pattern_6、Pattern_9の低調なパフォーマンスを改善できるかどうかを検証します。

買いシグナル(Pattern_5)： FrAMA横這い + ストキャスティクスが30未満で上方向にクロス

売りシグナル(Pattern_6)： ストキャスティクスが80以上で「M」型のピークを形成 + FrAMAの傾きが上向き

売りシグナル(Pattern_9)： FrAMA上向き + ストキャスティクスが90を上回りかつ下降中

本記事の仮説は、β-VAEがバイナリ化されたインジケーター値（ベクトル化された信号）を意味のある潜在表現に変換できるというものです。βパラメータ(beta)により潜在空間内の特徴の分離を重視することで、モデルは隠れた取引パターンや構造を抽出することが可能です。XAU/USD、SPX500、USD/JPYの履歴データで学習をおこない、学習後にONNX形式でモデルをエクスポートし、MQL5ウィザードで使用可能なカスタムシグナルクラスに統合します。ウォークフォワードテストでは、XAU/USDにおいてわずかながら利益が確認され、推論フェーズでの学習結果の活用によって低調なシグナルパターンのパフォーマンスを改善する可能性が示されました。

パターン検出

予測に用いられる機械学習モデルにおいて、パターン認識ではなく予測を目的とする場合、正規化された価格やインジケーター値を含む連続値のベクトル化入力が、機械学習統合への第一歩となります。これにより、大量の時系列データを手作業による分岐なしでモデルに入力できます。この構造により、アルゴリズムはストキャスティクスの振動やFrAMAの形状、さらには価格変動のボラティリティとの関係を、すべて自律的に推論できます。

この構造は自然にスケーリング可能です。インジケーターベクトルが整列しウィンドウ処理されれば、Pythonでは複数のローソク足を同時に数ミリ秒で処理できます。MQL5にエクスポートした場合、ストラテジーテスターのon-new-barメソッドでは同様の性能は得られません。しかし、このアプローチでは、たとえば「ストキャスティクス%Kが%Dを上抜けたか」「FrAMAが横這いか」といった判断のためのif文を使用する必要はありません。これらの情報はすべて浮動小数点テンソルに格納されます。GPU上で学習するシステムでは、これらのテンソルは入力のバッファリングだけでなく、勾配差分（デルタ）の保存にも優れたコンパクト性を提供します。これにより、出力とターゲットの差分を連続的に計算する必要がなくなります。 

しかしながら、この優雅な構造には脆弱性も存在します。連続値入力ベクトルは決して純粋ではなく、市場ノイズ、インジケーターの遅延、丸め誤差を含み、偽の相関を生みやすいという性質があります。この文脈では、スケーリングの誤りが1つあるだけでも平均値をずらし、学習勾配を破壊し、見かけ上の精度を生むことがあります。特に、入力データがボラティリティの高い市場環境で取得される場合、モデルは学習中には予測的に見える変動を学習するかもしれませんが、実際の取引では役に立たなくなることがあります。さらに、連続値の入力は論理的境界を曖昧にします。たとえば、ストキャスティクスの%Kが69.8と70.1の場合、トレンドに意味のある変化がないにもかかわらず分類が反転してしまうことがあります。連続値データの使用は、最近の記事でも強調した通り、シミュレーション上では良好に動作しても、市場環境が変わると性能が揺らぐことがあります。これは、浮動小数点の滑らかさが市場の離散的な挙動を覆い隠してしまうためです。場合によっては、モデルは「幻覚」を見ているかのように、ランダムなデータに対しても予測を示すことがあります。

この問題に対する実務的な「中庸の道」として、本記事では浮動小数点入力データをブール値/バイナリベクトルに蒸留する方法を検討します。これにより、特定の事象に対する「指紋」として入力を扱うことができます。モデルに数値範囲を網羅的に入力する代わりに、たとえばストキャスティクスの%Kが%Dを上抜けるパターンやFrAMAの横這い化などのパターンを、存在する場合は1、存在しない場合は0に変換します。生成されるベクトルの各ビットは、前処理関数内に含まれた小さなif文によってすでに検証済みの条件を表します。低次元かつノイズ耐性の高い入力が、これらのバイナリパターンによって形成され、値の大きさよりも構造を重視する学習が可能になります。β-VAEモデルは、揺らぐ数値ではなく、事象の組み合わせに潜む関係性を学習できます。これを潜在空間に圧縮することで、市場モードをより信頼性高く反映できる可能性があります。

したがって、連続値ベクトル化はスケールと計算性能を提供し、if文を完全に回避できる利点がありますが、バイナリベクトル化は意思決定の明確性をもたらします。生の数値の「混沌」を1や0に変換することで「象徴的秩序」として扱えるようになり、推論も単に脆弱な閾値に依存するのではなく、事前にコーディングされた重要なif文ロジックにも依存できるようになります。

ストキャスティクスの欠点

ストキャスティクスはGeorge Laneによって開発され、基本的にモメンタム指標です。直近の価格幅に対する終値の位置を測ることで、反転の可能性を示す指標となります。復習すると、メインのKバッファは次の式で算出されます。

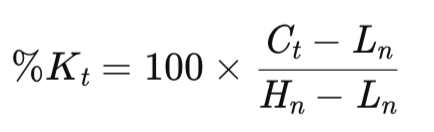
ここで

• Ct​ = 現在の終値
• Hn = 過去n期間における最高値
• Ln​ = 過去n期間における最安値

ルックバック期間nは多くの場合デフォルトで20に設定されますが、前回の2記事でこのインジケーターの組合せを紹介した際には、ハイパーパラメータとして調整可能な形にしていました。これは必ずしも最適な手法ではなく、曲線あてはめを引き起こす可能性があります。しかし、使用したルックバック期間はm期間で平滑化されます。このmは通常3に設定されており、今回も同様に維持しています。平滑化により、より滑らかで変動の少ないK値が得られます。Dバッファは第83回で説明した通り、Kバッファの平滑移動平均として遅延して追従します。デフォルトで期間は3に設定されており、今回も維持しています。Dバッファは、クロスオーバーを用いることでKバッファのピークを特定する役割を持ちます。本記事では、組み込みクラスCiStochasticを用いてこのインジケーターを使用しており、他のストキャスティクスと同様に0〜100の範囲で値を出力します。重要な閾値は80と20です。

非常にシンプルなインジケーターではありますが、重大な弱点も存在します。市場がトレンド状態にある場合、著しく遅れる傾向があります。たとえば上昇トレンドでは、Kバッファはクロスオーバーがこの価格幅内で反転しても、80以上の上位レベルに長時間張り付くことがあります。この状態では、モメンタムが持続するために、継続的な誤った売りシグナルが生成されます。逆に下降トレンドでは、Kバッファが20未満の水準に張り付くため、買いシグナルが遅延することになります。このため、いわゆる「壊れた時計症候群」のように、多くの誤ったシグナルが生成され、ようやく正しいシグナルが出ることになります。

この遅れは、終値を極値に対して正規化する価格幅ベースの計算式に起因すると考えられます。この計算式はトレンドの持続性を無視するため、「張り付き読み（stuck-readings）」が発生します。私たちのPython実装では、KおよびDバッファをベクトル化された系列として取得可能です。さらに、ローソク足ごとの変化を検出するcross-up-seriesなどの関数を備えたカスタムクラスSignalFrAMAStochasticも実装しました。しかしながら、実際の市場ノイズがあるライブテストでは、トレンドが続いている場合、誤ったクロスオーバーのノイズが増幅される傾向があります。私たちはこのインジケーターをPythonで次のように実装しています。

def Stochastic(
    df: pd.DataFrame,
    k_period: int = 20,
    d_period: int = 3,
    smooth_k: int = 3,
    source_col: str = "close",
    only_stochastic: bool = False
) -> pd.DataFrame:
    """
    Compute Stochastic Oscillator (%K and %D) and append columns to the DataFrame.

    Parameters
    ----------
    df : pd.DataFrame
        Input DataFrame; must include columns 'high', 'low', and the `source_col` (default 'close').
    k_period : int
        Lookback period for %K (highest high / lowest low). Default 14.
    d_period : int
        Period for %D (moving average of %K). Default 3.
    smooth_k : int
        Smoothing window applied to raw %K before computing %D. Default 3.
    source_col : str
        Price column to use for close values (default 'close').
    only_stochastic : bool
        If True, return only the Stochastic columns.

    Returns
    -------
    pd.DataFrame
        DataFrame with appended columns: 'Stoch_%K', 'Stoch_%K_smooth', 'Stoch_%D'
    """
    required_cols = {"high", "low", source_col}
    if not required_cols.issubset(df.columns):
        raise ValueError(f"DataFrame must contain columns: {required_cols}")
    if not all(isinstance(p, int) and p > 0 for p in (k_period, d_period, smooth_k)):
        raise ValueError("k_period, d_period, and smooth_k must be positive integers")

    out = df.copy()

    low_k = out["low"].rolling(window=k_period, min_periods=k_period).min()
    high_k = out["high"].rolling(window=k_period, min_periods=k_period).max()

    # Raw %K (0-100)
    raw_k = (out[source_col] - low_k) / (high_k - low_k)
    raw_k = raw_k * 100.0

    # Smoothed %K (optional smoothing)
    stoch_k = raw_k.rolling(window=smooth_k, min_periods=smooth_k).mean()
    # %D is SMA of smoothed %K
    stoch_d = stoch_k.rolling(window=d_period, min_periods=d_period).mean()

    out['raw_k'] = raw_k
    out["k"] = stoch_k
    out["d"] = stoch_d

    if only_stochastic:
        return out[["raw_k", "k", "d"]].copy()
    return out

class SignalFrAMAStochastic:
    # constructor unchanged — can accept pandas Series too
    def __init__(
        self,
        frama: Sequence[float],
        close: Sequence[float],
        high: Sequence[float],
        low: Sequence[float],
        k: Sequence[float],           # Stochastic %K series
        pips: float,
        point: float,
        past: int,
        x_index: int = 0
    ):
        # store as pandas.Series if possible to help with vectorized operations
        if isinstance(frama, pd.Series): self.frama = frama
        else: self.frama = pd.Series(frama) 
        if isinstance(close, pd.Series): self.close = close
        else: self.close = pd.Series(close)
        if isinstance(high, pd.Series): self.high = high
        else: self.high = pd.Series(high)
        if isinstance(low, pd.Series): self.low = low
        else: self.low = pd.Series(low)
        if isinstance(k, pd.Series): self.k = k
        else: self.k = pd.Series(k)

        self.m_pips = pips
        self.point = point
        self.m_past = past
        self._x = x_index

    # ------------------------
    # Small helpers (vectorized)
    # ------------------------
    @staticmethod
    def cross_up_series(a: pd.Series, b: pd.Series) -> pd.Series:
        """
        Vectorized CrossUp: True where a crossed up b between previous and current bar.
        Equivalent MQL: (a1 <= b1) && (a0 > b0)
        In pandas chronological order: a.shift(1) = previous a, a = current a
        """
        a_prev = a.shift(1)
        b_prev = b.shift(1)
        return (a_prev <= b_prev) & (a > b)

    
    # Trimmed code... 


    # ------------------------
    # Vectorized divergence detection
    # ------------------------
    def bullish_divergence_series(self) -> pd.Series:
        """
        Vectorized detection of bullish divergence:
        - Find local lows (low < low.shift(1) & low < low.shift(-1))
        - For consecutive pairs of local lows (older -> newer), mark the time of the *second*
          low True when:
            low_old < low_new  (price makes lower low)
            K_old   > K_new    (oscillator makes higher low)
        This mirrors the MQL routine that finds two local lows within a lookback and checks them.
        """
        low = self.low
        k = self.k
        # boolean mask of local minima
        is_local_min = (low < low.shift(1)) & (low < low.shift(-1))
        local_idx = np.flatnonzero(is_local_min.to_numpy(copy=False))
        # prepare result array
        res = np.zeros(len(low), dtype=bool)

        # We will iterate adjacent pairs of local extrema (sparse).
        # Only consider pairs where the two minima are not more than (m_past+? ) apart is optional;
        # Here we mimic original by not imposing an explicit global window; user can post-filter if needed.
        for i in range(1, len(local_idx)):
            older = local_idx[i - 1]
            newer = local_idx[i]
            # compare values (note: these are numpy indices; preserve pandas indexing by assigning by position)
            if low.iat[older] < low.iat[newer] and k.iat[older] > k.iat[newer]:
                # mark the time of the newer local low
                res[newer] = True

        return pd.Series(res, index=low.index)

    def bearish_divergence_series(self) -> pd.Series:
        """
        Vectorized detection of bearish divergence:
        - Find local highs (high > high.shift(1) & high > high.shift(-1))
        - For consecutive pairs of local highs (older -> newer), mark the time of the *second*
          high True when:
            high_old > high_new (price makes higher high)
            K_old   < K_new   (oscillator makes lower high)
        """
        high = self.high
        k = self.k
        is_local_max = (high > high.shift(1)) & (high > high.shift(-1))
        local_idx = np.flatnonzero(is_local_max.to_numpy(copy=False))
        res = np.zeros(len(high), dtype=bool)

        for i in range(1, len(local_idx)):
            older = local_idx[i - 1]
            newer = local_idx[i]
            if high.iat[older] > high.iat[newer] and k.iat[older] < k.iat[newer]:
                res[newer] = True

        return pd.Series(res, index=high.index)

    # ------------------------
    # Convenience wrappers for CrossUp/Down using stored Series
    # ------------------------
    def cross_up(self, a_col: pd.Series, b_col: pd.Series) -> pd.Series:
        return self.cross_up_series(a_col, b_col)

    def cross_down(self, a_col: pd.Series, b_col: pd.Series) -> pd.Series:
        return self.cross_down_series(a_col, b_col)

このインジケーターのパフォーマンスは、市場環境によって大きく異なることもあります。たとえば、平均回帰が優勢な環境、つまりUSD/JPYなどの外国為替ペアが低ボラティリティの局面にある場合、ストキャスティクスは有効に機能します。売られ過ぎ状態からの反発や買われ過ぎ状態からの反落が頻繁に発生し、価格が均衡点に戻る動きとよく一致するためです。しかし、モメンタム駆動型の環境、たとえばXAU/USDのまれなブレイクアウトが含まれる場合には、加速を反転と誤認することが多く、大きく失敗する傾向があります。前回の記事でおこなったバックテストでは、Pattern_5やPattern_9は、特に10未満および90以上といった極端なレベルに依存していました。クロスは低調で、フォワードウォークで利益が出なかった原因は市場環境との不一致、つまりレンジ相場ではなくトレンド相場であったことに起因します。今年のSPX500の上昇傾向、特に4月の安値以降の上昇は、この問題をさらに悪化させました。これは、短期的にストキャスティクスが市場ノイズに敏感であるため、広範な市場の勢いを無視してしまうことがあるからです。 

これらの欠点を補うためには、FrAMAの文脈的フィルターが重要です。私たちのフラクタル次元に基づくαを用いた適応平均インジケーターは、市場構造に合わせて平滑化度合いを変更します。トレンドが滑らかな場合には平均化期間を短くし、市場が荒れている場合には期間を長くして、市場全体の動きを捉えます。FrAMAの傾きや横這い状態を重ねることで、ストキャスティクスのシグナル、たとえばPattern_5の検証においては、FrAMAが横這いのときのみクロスが有効となるようにしています。これにより、ボラティリティによるノイズを事実上フィルタリングしています。この相互補完的関係は、β-VAEモデルへの入力形成にも影響します。バイナリフラグは「市場環境を意識した」相互作用をエンコードし、その結果、潜在的に学習されるパターンは、真のトレンドの端点間の遅れを分離して捉えることができます。理論上、この手法によってエキスパートアドバイザーはより堅牢に動作することが期待できます。

PythonにおけるFrAMA

私たちの適応型移動平均は、従来の静的な平滑化から動的でより反応性の高い平滑化へのパラダイムシフトを提供します。このインジケーターはカオス理論に着想を得ており、フラクタル次元を組み込むことで、市場ノイズの量と市場構造の比率に数値を与えます。具体的には、nローソク足のウィンドウに対して、デフォルト値はストキャスティクス同様に通常20ですが、FrAMAはこの期間を2つに分割します。これにより、サブウィンドウごとの価格幅比率N1およびN2、さらに全ウィンドウに対するN(1+2)を計算できます。前回の記事を振り返ると、Dは次のように定義されます。

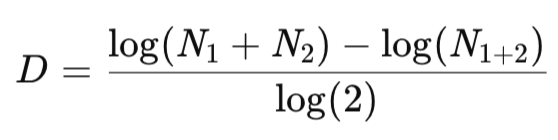
ここで、N1とN2は前述の価格幅比率です。Dの値は、滑らかなトレンドの場合は1に、ノイズのみの場合は2に制限されます。適応重みであるαも0.01から1.0の範囲に制限されており、価格平均バッファと組み合わせることで、適応平均を出力します。これは、前回および前々回の記事で強調した通りです（なお、前々回の記事は執筆時点ではまだ公開待ちです）。MQL5では、この複雑な計算式を意識せず、組み込みインジケータークラスCiFrAMAを使用して実装しました。一方、Pythonにおける私たちのアプローチは以下の通りです。

def FrAMA(
    df: pd.DataFrame,
    period: int = 20,
    price_col: str = "close",
    min_alpha: float = 0.01,
    max_alpha: float = 1.0,
    only_frama: bool = False
) -> pd.DataFrame:
    """
    Compute Fractal Adaptive Moving Average (FRAMA) per John Ehlers' formulation.

    Parameters
    ----------
    df : pd.DataFrame
        Input DataFrame; must include 'high', 'low', and price_col (default 'close').
    period : int
        Window length used to compute fractal dimension (commonly 16). Must be >= 4.
    price_col : str
        Column name to use as price (commonly 'close').
    min_alpha : float
        Minimum alpha clamp (commonly 0.01).
    max_alpha : float
        Maximum alpha clamp (commonly 1.0).
    only_frama : bool
        If True, return only the FRAMA column.

    Returns
    -------
    pd.DataFrame
        DataFrame with appended column: 'FRAMA'
    """
    required_cols = {"high", "low", price_col}
    if not required_cols.issubset(df.columns):
        raise ValueError(f"DataFrame must contain columns: {required_cols}")
    if not (isinstance(period, int) and period >= 4):
        raise ValueError("period must be an integer >= 4")
    if not (0.0 < min_alpha <= max_alpha <= 1.0):
        raise ValueError("min_alpha and max_alpha must satisfy 0 < min_alpha <= max_alpha <= 1")

    out = df.copy()
    n = period
    half = n // 2

    price = out[price_col].to_numpy(dtype=float)
    high = out["high"].to_numpy(dtype=float)
    low = out["low"].to_numpy(dtype=float)
    length = len(out)

    frama = np.full(length, np.nan, dtype=float)

    # Seed: before we have enough bars, set FRAMA to price (common practice)
    # We'll start the loop at index 0 and set initial FRAMA to price[0].
    if length == 0:
        out["frama"] = frama
        return out if not only_frama else out[["frama"]].copy()

    frama[0] = price[0]

    # iterate; we need at least 'n' bars to compute a fractal dimension
    for i in range(1, length):
        if i < n:
            # not enough history to compute full fractal measure -> fallback to price
            frama[i] = price[i]
            continue

        start = i - n + 1
        # first half window: start .. start+half-1
        fh_start = start
        fh_end = start + half - 1
        # second half window: start+half .. i
        sh_start = fh_end + 1
        sh_end = i

        # compute ranges per sub-window (using highs and lows)
        mH = np.max(high[fh_start: fh_end + 1])   # max high in first half
        mL = np.min(low[fh_start: fh_end + 1])    # min low in first half
        N1 = (mH - mL) / float(max(1, half))

        HH = np.max(high[sh_start: sh_end + 1])   # max high in second half
        LL = np.min(low[sh_start: sh_end + 1])    # min low in second half
        N2 = (HH - LL) / float(max(1, half))

        # entire window:
        Mx = np.max(high[start: i + 1])
        Mn = np.min(low[start: i + 1])
        N3 = (Mx - Mn) / float(max(1, n))

        # compute fractal dimension D according to Ehlers:
        # D = (log(N1 + N2) - log(N3)) / log(2)
        # Use guard clauses when N1, N2, N3 are zero or negative
        if (N1 > 0.0) and (N2 > 0.0) and (N3 > 0.0):
            D = (np.log(N1 + N2) - np.log(N3)) / np.log(2.0)
        else:
            # fallback to D = 1 (line-like) when not computable
            D = 1.0

        # alpha conversion using Ehlers' exponential mapping (clamped)
        alpha = np.exp(-4.6 * (D - 1.0))
        if alpha < min_alpha:
            alpha = min_alpha
        if alpha > max_alpha:
            alpha = max_alpha

        # EMA-like update
        frama[i] = alpha * price[i] + (1.0 - alpha) * frama[i - 1]

    out["frama"] = frama
    if only_frama:
        return out[["frama"]].copy()
    return out

FrAMAの最大の強みは、トレンドに対するカメレオンのような適応力にあると言えます。効率的なトレンドでは、Dが低く、αが0.01に近づくため、FrAMAは長期間の単純移動平均(SMA)のように動き、遅延を抑えた追従が可能になります。一方で、フラクタル的な混沌状態において%Dが高値に達すると、αは1.0に近づき、FrAMAは事実上、価格にぴったり追従する高速な指数移動平均(EMA)のように振る舞います。これにより、価格の急変動や逆行を回避しやすくなります。この特性により、FrAMAは固定期間の移動平均よりも、相場環境が変化する場合に優れたパフォーマンスを発揮する傾向があります。たとえば、今年のXAU/USDにおけるボラティリティの高い急騰、すなわちゴールドの上昇局面が始まった局面に着目すると、FrAMAの高いα値により応答性が向上し、前述のストキャスティクスの遅れや「壊れた時計症候群」を容易に補うことができます。これをPythonで次のように実装します。

class SignalFrAMAStochastic:
    # constructor unchanged — can accept pandas Series too
    def __init__(
        self,
        frama: Sequence[float],
        close: Sequence[float],
        high: Sequence[float],
        low: Sequence[float],
        k: Sequence[float],           # Stochastic %K series
        pips: float,
        point: float,
        past: int,
        x_index: int = 0
    ):
        # store as pandas.Series if possible to help with vectorized operations
        if isinstance(frama, pd.Series): self.frama = frama
        else: self.frama = pd.Series(frama) 
        if isinstance(close, pd.Series): self.close = close
        else: self.close = pd.Series(close)
        if isinstance(high, pd.Series): self.high = high
        else: self.high = pd.Series(high)
        if isinstance(low, pd.Series): self.low = low
        else: self.low = pd.Series(low)
        if isinstance(k, pd.Series): self.k = k
        else: self.k = pd.Series(k)

        self.m_pips = pips
        self.point = point
        self.m_past = past
        self._x = x_index

    # Trimmed Code...

    @staticmethod
    def frama_slope_series(frama: pd.Series) -> pd.Series:
        """
        Vectorized FrAMASlope: FrAMA(t) - FrAMA(t-1)  (maps MQL FrAMA(ind) - FrAMA(ind+1))
        Note: first value will be NaN because shift(1) yields NaN at the start.
        """
        return frama - frama.shift(1)

    def flat_frama_series(self, window: Optional[int] = None) -> pd.Series:
        """
        Return boolean Series: True where absolute FRAMA slope stayed <= tol
        for `window` bars including current bar and previous (window-1) bars.
        - window default: self.m_past
        - tol = self.m_pips * self.point
        """
        if window is None:
            window = self.m_past
        tol = self.m_pips * self.point
        slope = self.frama_slope_series(self.frama).abs()
        # rolling max over the last `window` bars (includes current and previous window-1)
        # need min_periods=window to mimic MQL conservative behavior
        rolling_max = slope.rolling(window=window, min_periods=window).max()
        return rolling_max <= tol

    def far_above_series(self, mult: float) -> pd.Series:
        """
        Vectorized FarAboveFrama for every row:
        dist = abs(close - frama)
        atr = high.shift(1) - low.shift(1)   (previous bar's range, matching MQL's ind+1)
        condition: close > frama AND dist > mult * point * atr / 4
        """
        dist = (self.close - self.frama).abs()
        atr = (self.high.shift(1) - self.low.shift(1))
        # avoid divide-by-zero; treat atr<=0 as False
        cond = (self.close > self.frama) & (atr > 0) & (dist > (mult * self.point * atr / 4.0))
        # fill NaNs with False
        return cond.fillna(False)

    def far_below_series(self, mult: float) -> pd.Series:
        """
        Vectorized FarBelowFrama for every row:
        condition: close < frama AND dist > mult * point * atr / 4
        """
        dist = (self.close - self.frama).abs()
        atr = (self.high.shift(1) - self.low.shift(1))
        cond = (self.close < self.frama) & (atr > 0) & (dist > (mult * self.point * atr / 4.0))
        return cond.fillna(False)

    # ------------------------
    # Vectorized divergence detection
    # ------------------------
  
    # Trimmed code...

前回の記事および本記事で取り上げているシグナルパターンにおいて、ユーティリティ関数であるflat_frama_seriesおよびframa_slope_seriesは、それぞれPattern_5の価格幅を特定するため、Pattern_9の傾きを特定するために役立ちます。

市場のアーキタイプ

市場が示す挙動は、多様な分類体系に分けることができます。前回の2つの記事および本記事においては、原則としてトレンド vs. 平均回帰、自己相関 vs. 分離、高ボラティリティ vs. 低ボラティリティの3つのタイプに焦点を当てています。トレンド相場では、FrAMAの正の傾きなどが支配的な特徴として現れ、モメンタム型の取引に適合しますが、ストキャスティクスによる誤反転シグナルには対応できません。一方、平均回帰相場では価格が均衡点の周りで振動するため、FrAMAがほぼ横這いの場合、ストキャスティクスの買われ過ぎ/売られ過ぎが有効に機能します。

相関関係は資産間の依存関係を示します。たとえば、株式とビットコインの間に見られる奇妙な相関について多く議論があります。学術的にはビットコインは米国経済や「財政の無責任性」に対するヘッジとされますが、実際には両者が同じ方向に動くことが多く、分離されているとは言えません。もし両者が本当に非連動であれば、両方を保有することで実質的な分散投資となります。SPX500内には時折、負の相関を持つセクターも含まれます。こうした変化が、前回の記事でPattern_2、Pattern_3、Pattern_9の自己相関パターンにSPX500を用いた理由の一つです。  

市場タイプの多様性は、β-VAEのパターン学習をテストして検証するために広範なテスト環境が必要であることを示しています。各市場タイプが特定の資産に適していると考え、確立された資産クラスから3つの資産を選びました。選定したのはXAU/USD、SPX500、USD/JPYです。XAU/USD（ゴールド） はコモディティバスケットから選びました。ゴールドは安全資産フローや地政学リスク、インフレによる高ボラティリティの影響を受けやすく、その記憶効果は長期に及ぶことがあります。これは、β-VAEが市場環境の持続性を潜在空間で捉える能力をテストするのに適しています。 

SPX500 は株式市場の動向を反映する確立された指標として選びました。リスクセンチメントに応じた相関トレンドフォローの性質を示し、モメンタムフェーズでのストキャスティクス遅延を浮き彫りにしました。これはPattern_9が失敗した局面です。最後に、USD/JPYは外国為替市場の代表として選びました。金利差や中央銀行の介入によるボラティリティを活用する目的です。特にPattern_5におけるflat-FrAMAフィルタの検証に役立ちます。

AEモデルでは、3つの遅延パターン（Pattern_5、Pattern_6、Pattern_9）を同時に実装し、信号パターン間の潜在的な共通パターンを捉える潜在モデルを開発します。各資産は独立してテストしますが、各資産で3つの遅延パターンを同時に検証します。複数パターンの同時テストは、信号の統合が適切でない場合、問題を引き起こすことがあります。本記事で用いる機械学習アプローチにおいても、異なるパターンが互いのポジションを打ち消す危険性があります。前回の記事でも触れた通り、適切に統合されない学習は、しばしば曲線当てはめに陥る可能性があります。今回のアプローチでは、すべてのシグナルを統合し、長短ポジションの判断を1つの信号として生成します。独立して判断するのではなく、これによりPattern_5、Pattern_6、Pattern_9の組み合わせをβ-VAEモデルに投入することで、「全体の合計が部分の総和を上回る」効果が期待できます。

β-VAEモデル

私たちの信号統合モデルの中核には、β-VAEがあります。これは生成モデルであり、教師なし学習で動作します。標準のVAEに比べて、潜在表現を分離した特徴量に焦点を当てている点がアップグレードポイントです。構造としては、エンコーダとデコーダのペアから成り、隠れ空間は通常、高次元であり、入力空間よりもはるかに大きな次元数を持ちます。エンコーダはニューラルネットワークで構成され、低次元入力空間から高次元の潜在空間へのフィードフォワードとして機能します。

本記事において、入力は6次元で、潜在空間は2048次元に設定しています。6次元の入力は、3つのシグナルパターン（Pattern_5、Pattern_6、Pattern_9）に対応しています。復習すると、各パターンは2次元ベクトルを出力し、それぞれのインデックスは1または0の値に正規化されます。2つのインデックスは、それぞれ該当するシグナルパターンの強気と弱気を追跡します。私たちはPythonにおいて、β-VAEモデルを以下のように実装しています。

# ----------------------------- β-VAE (inference simplified to VAE-only) -----------------------------
class BetaVAEUnsupervised(nn.Module):
    """
    Encoder: features -> (mu, logvar)
    Decoder: z -> x_hat
    **Inference (now VAE-only):** latent z is mapped to y via an internal head.
    All former infer modes (ridge/knn/kernel/lwlr/mlp) are bypassed.
    """
    def __init__(self, feature_dim, latent_dim, k_neighbors=5, beta=4.0, recon='bce',
                 infer_mode='vae', ridge_alpha=1e-2, kernel_bandwidth=1.0):
        super().__init__()
        self.latent_dim = latent_dim
        self.k_neighbors = k_neighbors
        self.beta = beta
        self.recon = recon
        self.infer_mode = 'vae'  # force VAE-only
        self.ridge_alpha = float(ridge_alpha)
        self.kernel_bandwidth = float(kernel_bandwidth)

        # Encoder
        self.feature_encoder = nn.Sequential(
            nn.Linear(feature_dim, 256), nn.ReLU(),
            nn.Linear(256, 128), nn.ReLU(),
            nn.Linear(128, latent_dim * 2)
        )
        # Decoder
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, 256), nn.ReLU(),
            nn.Linear(256, feature_dim)
        )
        # New: latent→y head (supervised head trained with MSE)
        self.y_head = nn.Sequential(
            nn.Linear(latent_dim, 128), nn.ReLU(),
            nn.Linear(128, 1)
        )

    def encode(self, features):
        h = self.feature_encoder(features)
        z_mean, z_logvar = torch.chunk(h, 2, dim=1)
        return z_mean, z_logvar

    def reparameterize(self, mean, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mean + eps * std

    def decode(self, z):
        return self.decoder(z)

    def predict_from_latent(self, z):
        # VAE-only mapping
        return self.y_head(z)

    def forward(self, features, y=None):
        mu, logvar = self.encode(features)
        z = self.reparameterize(mu, logvar)
        x_logits = self.decode(z)
        y_hat = self.predict_from_latent(z)
        if y is not None:
            return {'z': z, 'z_mean': mu, 'z_logvar': logvar, 'x_logits': x_logits, 'y_hat': y_hat}
        else:
            return {'y': y_hat}

6次元のバイナリ入力を2048次元の潜在層にマッピングする際は、線形ReLU層を使い、6⇾256⇾128⇾4096の構成で処理します。  最終的に4096とするのは、2048次元のセットを2つ保持するためです。ここから分岐し、一方は平均に、もう一方は分散の対数に接続され、それぞれ2048次元となります。この確率的エンコーディングでは再パラメータ化を用いてzをサンプリングし、再生成された入力をネットワーク出力に供給します。これにより、逆伝播が可能になります。デコーディングは上記構成を逆順でおこない、2048 ⇾ 128 ⇾ 256 ⇾ 6の順で処理されます。この入力バイナリの再構成により、まずロジットが出力され、その後シグモイド活性化関数を通じて確率値が生成されます。 

前回のβ-VAE実装では、学習時にインジケーター入力値とペアリングされていたため、フォワードパスのみで価格変動を推定していました。将来の価格変動を予測するために入力されるデータには、ニュートラルなプレースホルダー値を与えていました。当時の価格変動範囲は0.0〜1.0だったため、プレースホルダー値は0.5です。今回実装したβ-VAEは同様に柔軟なフォワードパス機能を持っていますが、新たに「潜在空間 z → y」のヘッドサイズを 2048 ⇾ 128 ⇾ 1 に設定し、次の価格変動を -1〜+1 の範囲で予測します。これにより、-1は弱気、+1は強気を表すことになります。入力はzであり、これにより教師なし学習と教師あり学習の融合が可能となります。 

このVAEで使用する βパラメータ は、潜在空間内で変数の簡潔さや独立性をどの程度強くモデルに課すかを決めます。変分オートエンコーダでは、入力データの再構成精度、潜在空間が標準正規分布などの既知のメトリックにどれだけ近づくかの正則化の2つの要素のバランスが必要です。

βが1の場合、これは「正規」変分オートエンコーダと呼ばれます。名前の由来は正規分布であり、この場合カルバック・ライブラー情報量により潜在空間の値が概ね正規分布に従うように調整されます。しかしβを増加させ、たとえば4に設定すると、正則化の重要度が相対的に高くなります。具体的には、潜在空間の値をできるだけ疎に（多くを0に近づけ）、変数間の独立性を高め、相関を減らす方向に押し出されます。実務上、この操作により潜在空間内のさまざまな隠れた特徴量やパターンをより良く分離できるようになります。

より明確に分離された潜在空間は、VAEがアウトオブサンプルでもパターンを一般化し、正確に識別するのに役立ちます。私たちのβ-VAE損失関数は、このカルバック・ライブラー項を計算するよう設計しており、Pythonで以下のように実装しています。

def beta_vae_loss(features, x_logits, mu, logvar, beta=4.0, recon='bce'):
    if recon == 'bce':
        recon_loss = F.binary_cross_entropy_with_logits(x_logits, features, reduction='sum') / features.size(0)
    else:
        recon_loss = F.mse_loss(torch.sigmoid(x_logits), features, reduction='mean') * features.size(1)
    kl = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp()) / features.size(0)
    loss = recon_loss + beta * kl
    return loss, recon_loss.detach(), kl.detach()

KLは-0.5∑(1 + logvar - μ² - exp(logvar))として計算され、その後バッチごとに平均化され、さらにβによって重み付けされます。これは前述したとおり、再構成精度と潜在空間の可変性をトレードオフさせる仕組みであり、インジケーターの隠れ階層構造を浮き彫りにします。損失関数の分解(loss decomposition)は複数段階のプロセスで構成されており、入力データの再構成にはロジット付きバイナリクロスエントロピーを用います。最終的な総損失はハイブリッドな目的関数となっており、モデルが入力パターンを再構成できることを保証するだけでなく、潜在空間が特化し、入力特徴量データの異なる側面を捉えられるようにします。たとえば、ある潜在変数はクロスオーバーの強度を記録し、別の変数は傾きの方向を表す、といった具合です。このように多様な特徴量を内部的に記録できる能力は、前述のとおりβ係数によって制御されます。

MQL5での実装

Pythonの機械学習エコシステムとMQL5のトレーディングフレームワークを橋渡しするために、MQL5で使用するONNXファイルを書き出すまでに至るPython側の主要な手順を扱います。これらの手順は、前述のとおり、データ処理、モデル学習、そしてデプロイメントを一体化したシームレスなパイプラインを構築するものです。書き出されたONNXモデルは資産ごとに1つずつ初期化されており、各モデルは3つすべてのパターンを相互に補完し合う形で使用しつつ、注文のクロスや競合が発生しないよう設計されています。過去の記事ではONNXモデルはパターン別でしたが、ここで扱うモデルは資産別である点が異なります。そのため、クラスのコンストラクタおよび検証処理は次のような構成になります。

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CSignalIL_Stochastic_FrAMA::CSignalIL_Stochastic_FrAMA(void) : m_pattern_6(50),
   m_pattern_9(50),
   m_pattern_5(50),
   m_model_type(0)
//m_patterns_usage(255)
{
//--- initialization of protected data
   m_used_series = USE_SERIES_CLOSE + USE_SERIES_TIME;
   PatternsUsage(m_patterns_usage);
//--- create model from static buffer
   m_handles[0] = OnnxCreateFromBuffer(__84_USDJPY, ONNX_DEFAULT);
   m_handles[1] = OnnxCreateFromBuffer(__84_XAU, ONNX_DEFAULT);
   m_handles[2] = OnnxCreateFromBuffer(__84_SPY, ONNX_DEFAULT);
}

//+------------------------------------------------------------------+
//| Validation settings protected data.                              |
//+------------------------------------------------------------------+
bool CSignalIL_Stochastic_FrAMA::ValidationSettings(void)
{
//--- validation settings of additional filters
   if(!CExpertSignal::ValidationSettings())
      return(false);
//--- initial data checks
   // Set input shapes
   const long _in_shape[] = {1, 6};
   const long _out_shape[] = {1, 1};
   if(!OnnxSetInputShape(m_handles[m_model_type], ONNX_DEFAULT, _in_shape))
   {  Print("OnnxSetInputShape error ", GetLastError());
      return(false);
   }
   // Set output shapes
   if(!OnnxSetOutputShape(m_handles[m_model_type], 0, _out_shape))
   {  Print("OnnxSetOutputShape error ", GetLastError());
      return(false);
   }
//--- ok
   return(true);
}

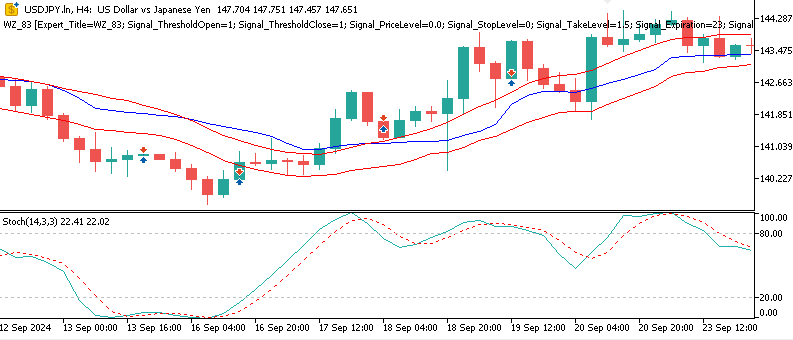
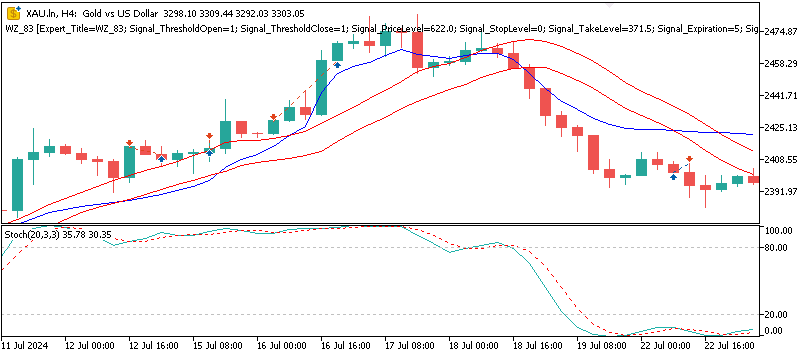
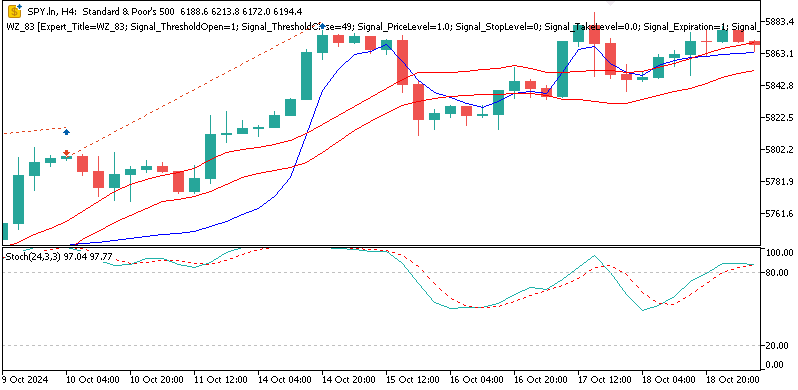
テストは異なる「モデルタイプ」にわたって実施しました。このパラメータは、3つすべてのシグナルパターンを同時に動作させた状態で検証する、今回テスト対象とした3種類の資産を表す略号です。したがって、この整数値が0の場合はUSDJPYを、1の場合はXAUUSDを、2の場合はSPX500をテストしていることを意味します。本テストの目的は、シグナルパターン5、6、9のパフォーマンスを改善できるかどうかを検証することでした。通常は1つのパターンを個別にテストする方が直接的ですが、今回は3つの異なる資産に対して3つすべてのパターンを統合して検証しています。特定の市場タイプに適した異なるテスト資産を用いることで、これらをまとめてテストユニバースとしています。

学習および最適化には、前回の記事で使用した2023年7月から2024年7月までと同様のテストウィンドウを用いました。調整した基準は、カスタムシグナルにおけるオープンおよびクローズの閾値、指値注文の距離を設定するエントリープライスのpips、そして各新バーごとにチェックされる際に、パターンが存在していれば累積されるシグナルパターンの閾値です。フォワードウォークの結果は次のとおりです。

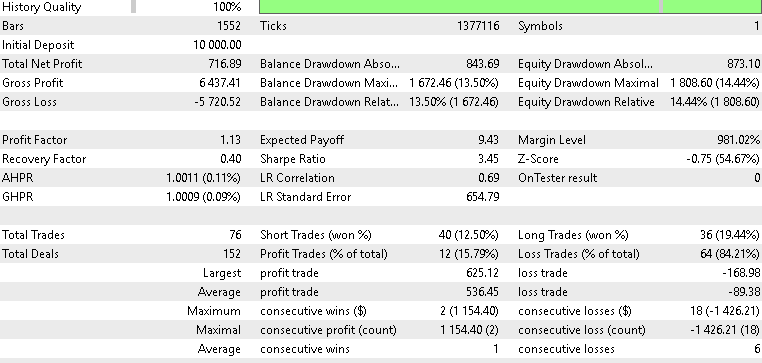
XAU/USD

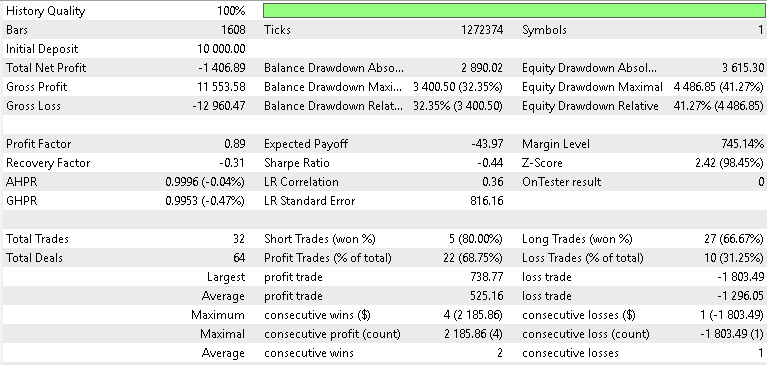
USD/JPY

SPX 500

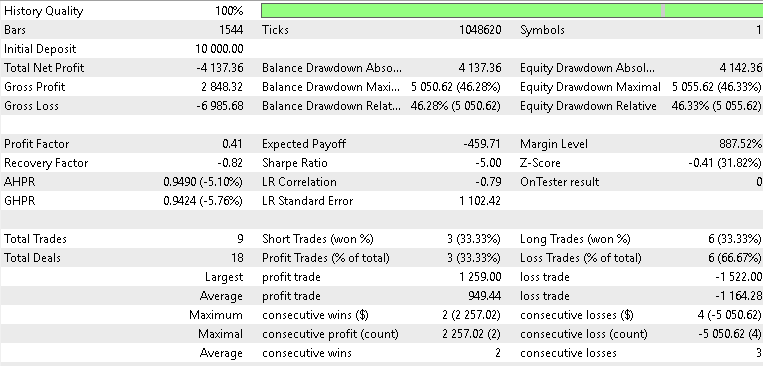
フォワードテストの結果はまちまちでしたが、それでも示唆に富むものでした。ゴールドでテストした場合、4時間足において、β-VAEモデルは年間で約2.1％という緩やかながらも収益性を示しました。潜在層の変数を分解して、どの変数がどのシグナルパターンに特化しているかを正確に特定することはできませんが、Pattern_5のフラットクロスに関する埋め込みが、ゴールドの急騰局面の中でボラティリティ主導の反転を捉えていた可能性は推測できます。SPX500についてもテストをおこないましたが、フォワードウォークでの年間リターンはマイナス0.8％でした。同様にUSDJPYも良好な結果とはならず、3つの中で最も悪い成績となるマイナス1.4％のリターンを記録しました。総合すると、損益分岐点を超えられたのはXAUのみであり、今回のテスト結果は、VAEがXAUUSDにおいてわずかな改善しかもたらさなかったという点で、前回の記事である第84回の結果を概ね踏襲するものとなりました。

結論

まとめると、β-VAE推論モデルと、ストキャスティクスおよびフラクタル適応移動平均線のインジケーターの組み合わせは、ある程度ではあるものの実用性を示した分離された潜在特徴量を提供します。ONNXからMQL5への「パイプライン」は、前回の記事からの改善、特にXAUUSDにおける若干の利益を示しましたが、同時に限界も浮き彫りにしました。USD/JPYおよびSPX500でのフォワードテストは、良くても精彩を欠く結果でした。そのため、慎重な特徴量エンジニアリング、相場レジームを考慮したテスト、そして保守的な運用が求められます。ここに示したすべての結果は、これまでと同様に実験的なものであり、今後の検討に進む前には、必ず独立した検証と十分な注意が必要です。

名前	説明
WZ-84.mq5	ヘッダに参照ファイルの名前と場所をリストするウィザード組み立てEA
SignalWZ-84.mqh	カスタムシグナルクラスファイル
84-XAU.onnx	ゴールドで学習したONNXモデル
84-USDJPY.onnx	USD/JPYで学習したONNXモデル
84-SPY.onnx	SPX 500で学習したONNXモデル