価格変動モデルとその主な規定（第3回）：証券取引所の投機の最適なパラメータを計算する

はじめに

前回の記事（第1回、第2回）では、価格ダイナミクスを生み出す基本的な原理と潜在的なメカニズムを紹介しましたが、それは純粋に理論的なものであり、観測された範囲を超えたものでさえありました（しかし、その基礎となるものではありました）。今回と次回の記事では、（多くの計算が評価的な性質を持つ）新しい工学的学問の基礎を築き、ユーザーが観察された価格ダイナミクスから実際的に有用な結論を導き出し、それを直接取引に応用できるようにしようと思います。この記事では、一般的に、持続可能な利益を提供できる工学的アプローチとアルゴリズム、および最大平均利益を達成できる最適な利食いと損切りの値の確率的計算についてお話します。

1.モデル

前回（第２回）では価格確率フローの(II.3)方程式を取得しました（簡潔にするため、以下では、第R部の方程式Nには「R.N」と番号が付けられます。Rはローマ数字です）。このような確率の流れは、縮小された形、あるいは観測された形では、「上昇」と「下降」の値動きの確率で表されます。このような確率を実際に評価するためのアプローチを定式化してみましょう。

 

離散時間表現（バーの概念に基づく）では、の価格履歴セグメント（始値、終値、高値または安値）がシリーズとして表示される場合（ここでの番号付けの順序は、後続のバーの番号が前のバーの番号よりも高くなるようにする）、価格は離散的なステップで移動します。スケールが大きい場合、あるいは が非常に大きい場合、このような価格跳躍の確率を、上向きの値動きの確率を（ここではのセットメンバーの数）、あるいは下向きの値動きの確率を（ここではのセットメンバーの数）として評価し、議論することができます。  同時に、平均的な飛躍の寿命を計算することも可能です。 

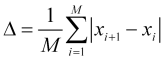                                                                                                    (1.1)

（価格）。実際には、機関でカオス的に動く価格は、ランダムウォークによって現在の平均値（このような確率で定義される）から乖離していることがわかります。その偏差は、以下のオーダーです。

                                                                                                                    (1.2)

（これは、、または期間の移動平均からの乖離(1.2)をチャネルラインとするCasual Channel指標によって確認される）。

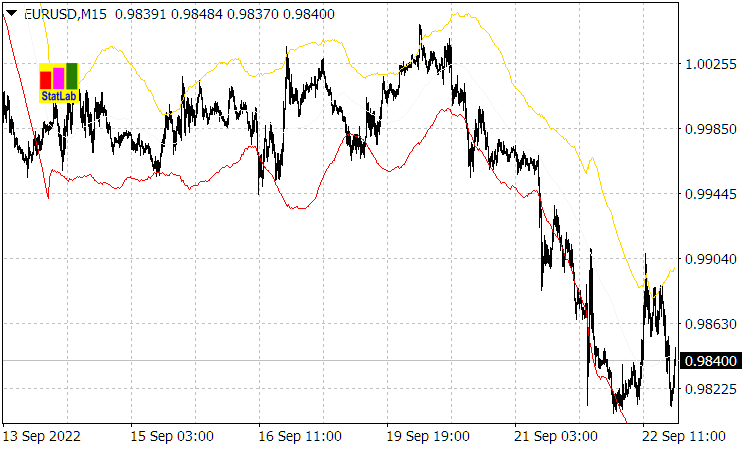
図1：カジュアルチャンネル指標

明らかに、オーダーがのランダムな価格偏差の特徴的な時間（ここで、は、適切な時間枠の一時的なバーの長さです）は、  とまったく同じように価格がランダムに変動した場合、平均価格からの乖離（1.2）は同じになります。

 

したがって、ここで提供するモデルの簡略化では、価格は同様の飛躍で動くと仮定し、その方向の確率は と とします。 

 

上記の方法を使用して計算された飛躍と確率は、さまざまな飛躍の影響下で形成された現在の価格変動ではなく、以前の区間全体（つまり、値の範囲の平均）にすでに関連していました。そして最も重要なのは、との確率がまだ予測されていないことです。

 

第2回で述べたように 従来の統計手法とその数学的装置は、かなりの誤差を使用して確率波caを重ね合わせて形成される価格ダイナミクスの場合には適していません。従って、観測データを応用した分析、および適切な確率論的統計学的計算には、近似的な性質があります。

2.以前の操作確率と正規化された価格速度の実用的な決定：将来の価格分布を計算するためにこれらのパラメータを使用する原理

平均区間における値動きの平均速度は、以下のようになります。

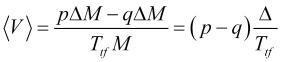                                                                                  (2.1)

これは移動平均変化率（ここで はバーインデックス）を適切な平均周期で表示し、何らかの速度変動は示しません。したがって、平均速度は実用的に計算可能な量です。

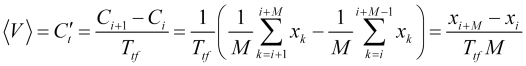                        (2.2)

(2.1)を(2.2)に当てはめると、経験的に決定されたパラメータが得られます。

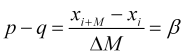                                                                                                         (2.3)

であるので、これを正規化価格速度と呼びます。一方. を示すのは簡単です。例えば、(1.1)から次の不等式が成り立ちます。

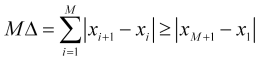                                                                                        (2.4)

(2.3)にが伴います。また、 と仮定することもできます。確率はであるので、です。(2.3)とを使って確率 

               および                                                                        (2.5)

を求めます。同様に、正規化された速度を表す別の式は

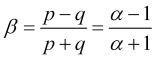                                                                                                    (2.6)                               

となります。ここで、パラメータ

                                                                                  (2.7)

です。さらなる計算では、パラメータ  

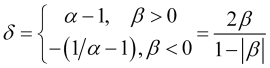                                                                          (2.8)

も必要となります。これを通して、正規化された速度自体は以下のように表されます。

                                                                                                          (2.9)

 

価格区間で計算された飛躍の確率(2.5)は、その区間の平均的なものであり、最後価格の形成に関与します。したがって、（価格が判明している現時点で）これらの平均確率が分かれば、将来のでの価格を予測することができます。より正確には、価格の確率分布を予測することができます。 の価格チャートとの正規化された速度（ここからとが計算される）を比較すると、（頂点の位置の一致によって）その強い類似性をたどることができ、この速度（より正確には、それに対応する確率）がの現在の価格を形成していることがわかります。

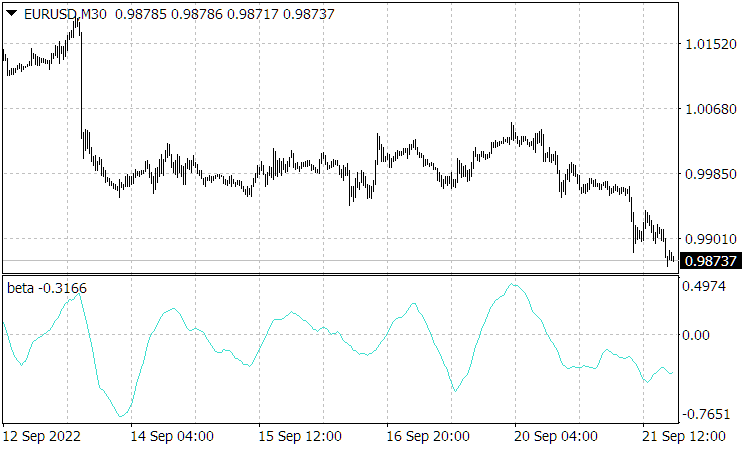
図2：図は正規化された速度のグラフです。

 

実際、(2.3)から、 が成り立ちます。つまり、 の価格は、 の価格から、 の将来の速度の配列、またはその平均値によって形成されます。

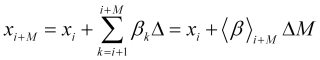                           (2.10)                                                              

ここで、グラフの点に表示される、将来の区間における正規化された速度の平均は、

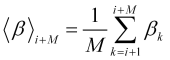                                                                 (2.11)

一方、確率区間との平均は、を式(2.5)に代入して求められます（明らかに、(2.10)においてのメンバーがの周辺にある場合、とのようなグラフになる）。そして、のバーで十分に滑らかな関数を予測し、必要な確率 とを計算します。これにより、（ の時点で)将来価格の確率分布と、取引に必要なパラメータ（ポジションの開始方向と逆指値注文の位置）を計算することができます。

 

ここで使われる正規化速度予測の本質は以下の通りです。正規化速度の一時関数は、ゼロに等しい数学的期待値に近いの範囲内で変動します（または、対象地域全体をカバーする場合は、グローバルトレンドの速度を示す小さな値 ）。この場合、例えば、の形をとる条件付き数学的期待に基づく最も単純な統計的予測は、 に従って予測関数をゼロまたはに近づけます。言い換えれば、対応するプロセスの自己相関関数 が減少するにつれて、 のような条件によって開かれるポジションの数が急激に減少し、最後の値に基づく些細な予測によるゲームよりも、さらに収益性の低いゲームとなります。一方、価格ダイナミクスは振動過程によってよくモデル化され、予測されます。その背景には、以前の記事で明らかにした考え方があります。この理論構築の段階では、バーの関数（振動的な性質を持つ）の予測は、経験的な過去のデータに基づいて計算されたフーリエ外挿に基づいておこなわれました。この場合、以前の記事で提案されたウェーブレット外挿の使用はまだ目立った利点を提供していないためです。

3.トレンドの質：現在と将来のトレンドの程度を見極め、適切な仕事の地平を見据える

トレンドが の平均化時間より長く続く場合、（(2.1)と(2.3)に従って）平均化時間中の価格の自然な上昇は、以下のオーダーとなります。

               .                                    (3.1)

インクリメントの不確実性 

                                                                                                              (3.2)

また、Casual Channel指標チャンネルのある境界から別の境界に移動し、同時に正規化された速度で平均的にドリフトするときの価格変動の全範囲（図1）は次のように推定されます。

                                                                               (3.3)

ここで

                                                                                                 (3.4)         

です。トレンドに従うなら、シフト(3.1)の値が、このシフト

                                                                              (3.5)

の不確かさ(3.2)よりも有意に大きいままであることが望ましくなります。(2.6)と(2.9)から、必要な平均化時間の下限推定値が得られます。

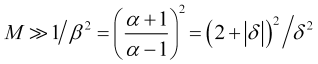                                                                (3.6)

満たされた場合、(3.4)に従って、平均化時間（棒グラフ）は次のように計算されます。 

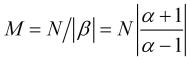                                                                                               (3.7)

不確実性の価格増分を無視できない場合、平均化時間は二次方程式(3.4)の正根とみなされます。

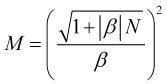                                                                                                      (3.7.1)

 

トレンドの質の定義

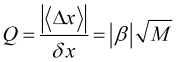                                                                                                      (3.8)

を、その自然増分と不確かさまたはノイズの比として表します。安定した収益を上げるトレンドフォロー戦略には、の品質の高さが必要であることは明らかです。しかし、品質を計算する品質トレンド指標（図3）は、せいぜい1通貨で数単位の値に達します。さらに、質の高いトレンドを見極めたとしても、市場の力学を乱し、トレンドを終わらせたり、あるいは逆行させたりするような強力な外部イベントの出現は予測不可能であるため、そのトレンドがいつ終わるかを判断することはできません。したがって、収益性の高い戦略は、トレンドの方向の比較的小さな変動で利益を取ることにのみ基づくことができます。

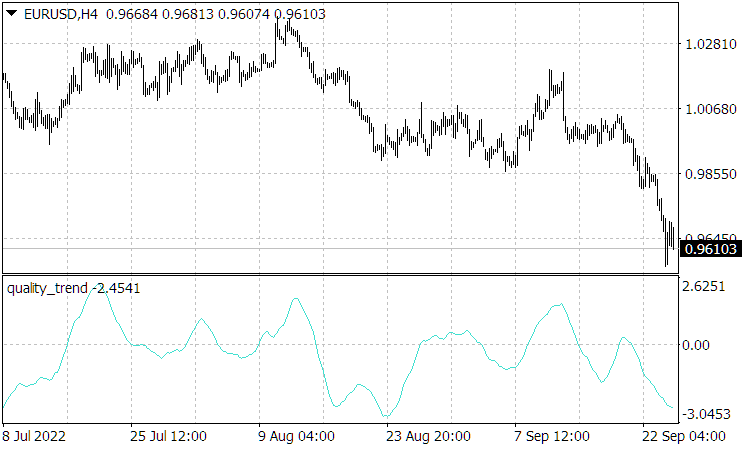
図3：価格増分がモジュロで取得されない品質トレンド指標（指標の符号はトレンドの方向を示す）

品質トレンド指標の値は、(2.10)の比率で示されたように、正規化された速度に比例し、そのピークの位置において価格履歴と類似していることが判明し、それに応じて、クオリティトレンドの読みは遅れないことが判明したことに注意してください。さらに、トレンドが変化する前であっても、それに対応する値動き（上昇トレンドの場合は上昇、下降トレンドの場合は下降）の速度が低下するため、指標の数値が値動きを上回ることがあります（しばしばそうなります）。しかし、この指標がこのような予測行動をとるのは、市場自体の動きを乱すような強い影響が市場にない場合に限られます。このような影響を受けた後、その緩和時間の間、品質トレンドの測定値は、平均化期間によって決定されるラグを持つ「通常の」ラグを持つ測定値となります。

 

市場に対するサードパーティの強い影響がない場合に、関数の動作を分析し、考えられる傾向の範囲を評価してみましょう。平均周期の減少に伴い、正規化された速度の計算値 は増加する可能性があります（結局のところ、常に変化する市場におけるその「瞬間的な」値は、平均的な値よりも大きな振幅で変化し、平均化が大きいほど、そのような変動は小さくなります）。つまり、Q値比では、 およびその逆が乗算されるメンバーでは、関数が最大値を持つことが可能になります。しかし、非常に小さな区間では、との跳躍の真の確率が一定であるとき、それに関する市場状況の小さな変化により、この短い平均期間におけるそれらの統計的に計算された値 と は、ほとんどの場合、真の確率とは大きく異なります。なぜなら、不確実性期間が減少するにつれて、その上で計算された確率の とは増加するからです。したがって、信頼できる確率の計算を提供する平均化期間（）については、 のタイプ比を満たす必要があり、その最小値が決定されます。そうでない場合、（ただしこれは、小さな平均化間隔で瞬時の正規化速度が大きく変動する場合よりも広いケースであり、このような比率は、真の確率の急激な変化を伴う大きな間隔でも起こりうるため）、統計的に計算された確率値を使用することはできません。正規化速度の変動が強い場合、それに基づく関数もその最大値付近で強く変動することに注意してください。したがって、市場の状況を分析するために使用される最大値は、それが滑らかに形成されるように選択されるべきであり、上記から導かれるように、十分に大きな平均化期間で達成されます。条件が満たされる場合、これはさらなる理論で満たされると想定され、推定確率およびは、動作するおよびの確率と識別できます。これは、およびとも書きます。

 

との確率が一定である領域では、安定したトレンドが形成されます。一方、（すなわち、）の確率が低下すると、の増分の成長率が低下し、（逆相関のが達成されると）トレンドが逆転する可能性さえあります。これは、計算されたQ値の低下にもつながります。逆に、高いQ値とその成長は、一般的な確率がよりも強い優位性を持つだけでなく、その不変性、さらには増加さえも示しています。したがって、トレンドの質（3.8）が高ければ高いほど、そこにトレンドが存在する確率、すなわち期間全体にわたってトレンドが存在する確率が高くなり、一方、質の低い値は横ばいを示します。また、トレンド（長さ）だけでなく、横ばいや、さらに逆向きのトレンドを持つ価格履歴の区間をカバーする平均化期間を長くすると、Q値が急激に低下することも明らかです。したがって、トレンドの長さ は、ピークQ値によって特定されます。

 

期間を長くして、 よりも大きなスケールの一方向のトレンドをカバーするようにすると、の長さによる小さなトレンドセクションのスケールよりも、トレンドの質は逆に増加します。異なる時間軸のチャートの類似性（を条件とする）により、(3.8)の正規化された速度のスケールは、の増加によってほとんど変化しないが、は増加します。さらに（これには、品質方程式(3.8)に現れる、値計算補正がすでに必要）、トレンドのノイズ汚染は、との確率を持つ「標準的な」跳躍（検討中のモデルに対応）によって形成される統計的分布を超える、大小のカオス的な価格跳躍によって、急激に増幅されます。このような非標準的なジャンプはすべてのスケールで同じであり、トレンドに「追加的な」ノイズを発生させるため、トレンドが特定されるスケールが大きくなるほど、この追加ノイズの重みは減少します。上記はすべて、関数を使用することで、グローバルな一方向のトレンドの場合、いくつかのクオリティピークを定義できることを意味しています。このクオリティピークは、の増加、または特定されたトレンドエリアの規模の増加に伴って上昇します。

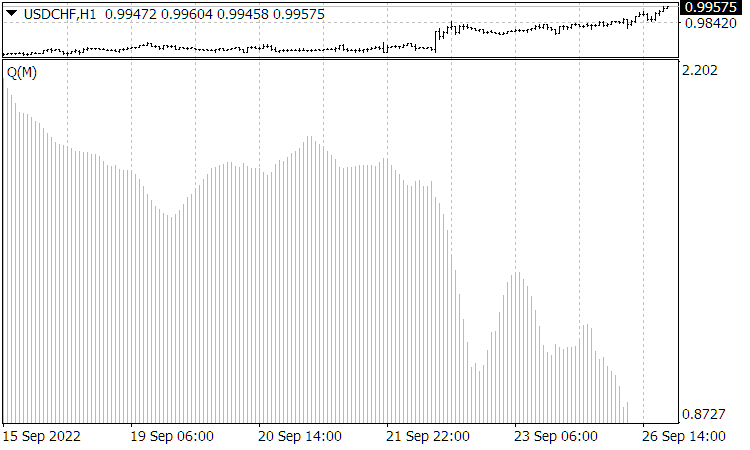
図4：現在の関数（X軸は、時間ではなく、品質トレンドの平均期間を10から160まで表示）

  

最後に、このゲームはすでに形成された履歴に基づいているのではなく、リアルタイムで、正規化された速度予測値のセット に基づく、いくつかの予測の知識が必要です。したがって、新たに出現したトレンドの可能な長さ を評価するためには、平均化期間の全スペクトルを調べ、予測が現在のバーからバーで進むとき、つまり次のように計算されたとき、予測品質の最大値をいくつか特定する必要があります。

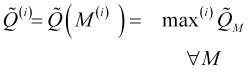                                                                               (3.9)                 

ここで、 は番目の最大値の識別関数です。この場合、最大ピーク

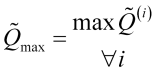                                                                                                     (3.10) 

とそれに対応する平均化スケール上の点を設定する必要があります。  

 

より小さな平均化区間（）において、予測品質が最大ピーク（ ）に向かうが、これらの区間においても品質が有意であり、単調に成長するか、増加する（これも増加するバックログに基づく）ピークの連続である場合には、対応する一方向の傾向（品質の各ピークの後にロールバックがある）が存在することは明らかです。品質の最大ピークのの後、それが対応する平均のスケールで下がり始めると、トレンドに減速が生じ、やがて反転につながる可能性があります。後者は、検討中の為替商品のQ値がよりも大きな値になることはめったにないという意味で、ピーク値が非常に大きい場合に最も可能性が高くなります。いずれにせよ、上昇トレンドはに達するまで続き、その前にこのトレンドに従って建てたポジションを決済する必要があります。   

 

ここで、取引に有望なトレンドセグメントの長さを推定してみましょう。この長さは、 トレンドの予測長さと必ずしも等しい必要はありません。第一に、予測数学の仕事自体の信頼性が低いため（これは、ニューラルネットワークやARIMAなどを含む、様々な周波数や他の外挿装置であっても、そのすべてのタイプに適用されます）、利益は、識別された将来のトレンドの、トレンドが形成される可能性が高い比較的小さなセグメント上に取られるべきです。したがって、前項から導かれるように、の不等式は必然的に満たされるはずです。第二に、本モデルでは、将来の確率値 との推定値を使用します。また、平均の跳躍は一定であると仮定しています。なぜなら、市場が惰性で独自の法則に従って発展するときに機能する予測があるからです。しかし、連載第1回に示したように、予測可能な市場展開の間隔は、最後の強力な外部イベントから始まり、次のそのようなイベントの発生まで続きます。従って、ここで開発されている数学的装置全体には適切な作業範囲 があり、その量は現在のバーから強い外部イベントが始まる将来のバーまでのバーの数に等しくなります。このような数学的装置（これは非常に重要です）をある地平線を越えて使おうとすれば、その操作に誤りが生じ、必然的に損失が生じます。このような数学的装置を適切に作動させるための可能な地平を決定するためには、現在および将来のあらゆる政治・経済的出来事が市場の状態に及ぼす影響の強さを評価するファンダメンタル分析または専門家による研究を基礎とする必要があります。したがって、取引に有望な予測トレンド区間の長さは、上記の比率によって推定されます。

                                                                                     (3.11)   

そして、その下からは、確率そのものと比較した確率の不確かさ（揺らぎ）の小ささの、以前に確立された比率に基づいて推定されるべきです。

                                                                                                  (3.12)

このグラフは、予測Q値グラフからも決定され、このグラフが非常に滑らかに変化する部分に対応します。トレンドのこのセクションで予想される自然価格の変化は以下の通りです。

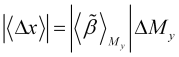                                                                                                  (3.13)

これは、純粋なトレンドフォロー戦略で得られる利益のオーダーに相当します。

 

第三に、トレンドセグメントの長さの選択も、以下に示す計算に基づいておこなう必要があります。この計算により、基本的に、所定の市場条件下で平均的な統計的利益を得ることが可能な区間（ 値）、すなわち を設定することができます。これに加えて、トレーダーは自分で時間枠を選択し、その非モデル（すべての時間枠で同一）の飛躍によるすべての時間枠での価格ノイズのため、真の（式（3.8）で計算されるモデルではなく）品質は、時間枠が減少すると減少します。従って、トレーダーは、大きな時間枠の場合、トレンドの質は高いが、利益を得るまでに長い待ち時間がかかるオプション、あるいは、小さな時間枠の典型的なケースである、低い質のトレンドで素早く利益を得る（従って、リスクも大きくなる）オプションのいずれかを選択することになります。

4.一定の運用確率で最大の利益をもたらす利食い値と損切り値を確率論的に計算し、後者を表現する

タスクを設定します。 

価格はゼロのマークから垂直方向にジャンプして動きます。上方への価格ジャンプの確率、下方への価格ジャンプの確率、それぞれです。もちろん、と という予測平均がありますが、これは重要ではありません。上部にはaの距離に利食いがあり、下部にはゼロマークからｂの距離に損切りがあります（座標軸で見た場合）。最大の利益を確保する証券取引所のゲームのパラメータを見つけます。

 

解決策

              価格は、座標nのポイントに行くことも、n-1のポイントから下に行くことも、n+1のポイントから上に行くこともできます。したがって、ポイントnで価格が見つかる確率は、次のようになります。 

                                                                                                   (4.1)

(4.1)から、次の有限差分方程式が得られます。 

                                                                                (4.2)

 

装備可能なジャンプ。 

              まず、等可換ジャンプの場合を考えてみましょう 。 ここで、(4.2)から次のようになります。

                                                         (4.3)

ここで、 は定数です。そこから、次のようになります。

                                                                                                               (4.4)

              したがって、価格が動き出した瞬間にゼロである確率はとなります。よって、 

                                                                                                                    (4.5)

              損切りbが利食いaが、平均化（および動き）の期間にわたる動きの特性（ここでは (3.4) で平均価格ジャンプで推定）価格範囲を構成すると仮定しましょう。とは確率の一定性に基づいています。が利食いがゼロになる損切りポイントに価格がすでに到達している確率は です。(4.5)を代入すると、次のようになります。

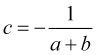                                                                                                                       (4.6)

(4.5)と合わせると、利食いを達成する確率は次のようになります。

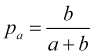                                                                                                                        (4.7)

一方、損切りが発動される確率は

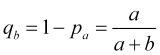                                                                                                       (4.8)

です。従って、同じ確率で異なる方向に価格がジャンプする場合、ジャンプ回数の平均利益

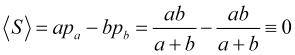                                                                          (4.9)

は、利食いと損切りの位置に関係なく、常にゼロになります（もちろん、スプレッドによってマイナスになる）。 

 

利食いに向かう傾向があります。

 

（より正確には）として、すべての式（4.2）を掛け合わせると、次のようになります。

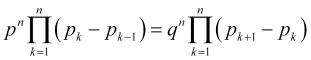                                                                    (4.10)

(4.10)の同一係数を減少させ、(2.7)の表記を用い、を考慮すると、次のようになります。 

                                                                                                (4.11)

さらなる関係式(4.11)と幾何級数の和の式を用いて、確率級数の隣り合う項の差の和としてを表示してみましょう。

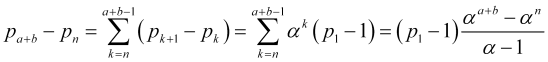             (4.12)

、よって

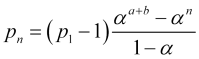                                                                                                   (4.13)

、従って

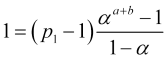                                                                                                        (4.14)

(4.13)を(4.14)で割ると、利食い達成確率aが得られます。               

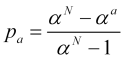                                                                                                                   (4.15)

したがって、損切りがトリガーされる確率はに等しくなります。そうすると、価格ジャンプのポジションあたりの平均利益は次のようになります。

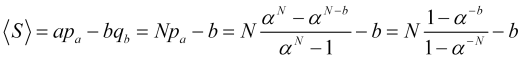                       (4.16)

これは(4.16)の表現では損切り値bの関数であり、この表現では単にジャンプの数ですが、実際にはの値があります。利益はです。 オープンポジションに向かう価格変動の確率が高まると、平均利益（4.16）が増加することは明らかです。これは、がの値をとるとき、すなわちはからの成長関数です。

 

Nとの指定された値に従って、平均統計的利益(4.16)の最大値を見つけてみましょう。そのために、微分をゼロに等しくしてみましょう。

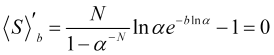                                                                             (4.17)

ここから、価格飛躍で、希望の損切りの値を求めます。 

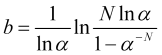                                                                                                      (4.18)

 

なので、 の対数は正であり、です。したがって、対数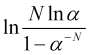 の値は正でなければなりません。この条件は、以下の場合に満たされます。

                                                                                                             (4.19)

または   

                                                           (4.20)                                                                                      

ここでです。(4.20) の不等式は、任意のに対して厳密に満たされます。なぜなら、の指数は、直線の上方を通過し、でのみ直線に接するからです。 

関数(4.16)の二次微分

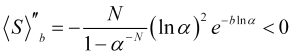                                                                            (4.21)

すなわち、関数の曲率は下向きであり、(4.18)で最大となります。 N=100とにおける関数(4.16)を図5に示します。 

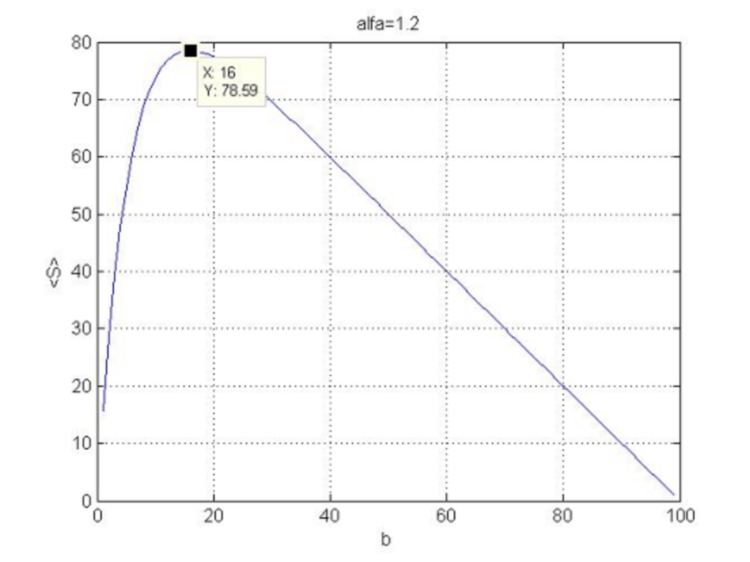
図5：利益関数の損切り依存性。

平均利益が正になるためには、率が1を大幅に上回る必要があることに留意してください。実際に、()とし、展開の第2項を無視し、第1項 だけを残すと、取引ごとの平均利益 

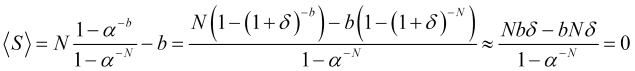    (4.22)

はゼロに等しくなります（反対のジャンプの確率が等しい場合と同じ）。展開の第2項を無視できない場合、ジャンプの回数 が十分大きいか を考慮すると、

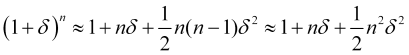                                             (4.23)

となります。これは、平均利益(4.16)に正の値を与えます

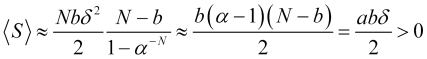                                        (4.24)

、（したがって、）のためです。

              の引数に対する近似平均利益(4.24)は、（損切りと利食いが等しい）で最大となる逆二次放物線であり、です。

 

ここで非常に重要なポイントがあります。上記の理論では、平均利益は平均価格に基づいて計算されていますが、実際には平均価格は大きく変動し、その変動幅は対応する平均シフトを大きく上回ることさえあります。しかし、逆指値注文（利食いと損切り）は平均価格ではなく、変動幅の端で決済されます。したがって、（平均値に基づく）数学的装置が機能するためには、損切りは価格の不確実性 （その変動トリガーが平均値から見てモデルトリガーとほとんど変わらず、これらの変動が無視できるように）、すなわち（1.2）に従って、 を大きく上回る必要があります、 

                                                                                                                        (4.25)

この場合、平均化期間の(3.7.1)式を用い、(4.25)から以下の不等式を満たす関数を得ます。

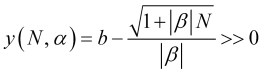                                                                               (4.26)

これは価格変動の小ささの基準であり、 は(2.6)の比率から求められます。(4.26)に(4.18)の損切りを代入すると、関数グラフ(図6)が得られますが、このような関数はゼロよりはるかに大きいことはなく、それどころか、基本的に負であること、すなわち、比率(4.25)が最適な損切り(4.18)を満たすことはないことが明らかです。

 

MATLABコード

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> y=b-s;
>> plot3(N,a,y)
>> grid on

   

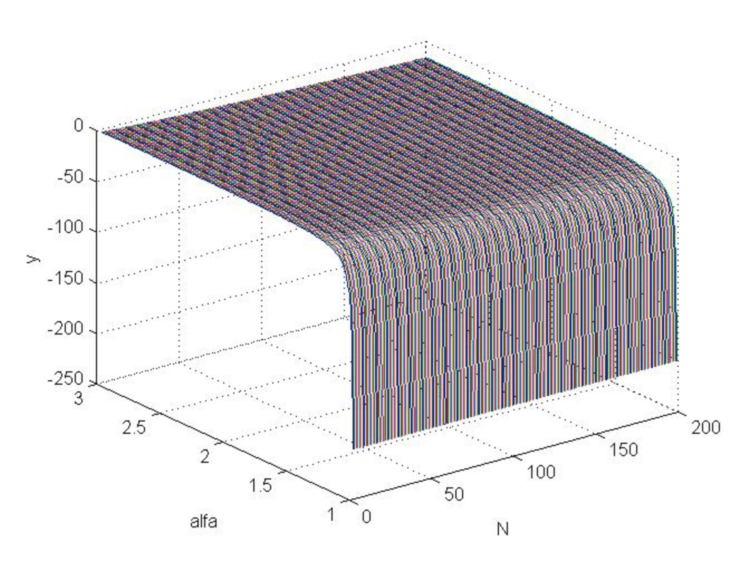
図6：αを1から3に、Nを3から200に変化させたときのy関数グラフ

 

 

したがって、上記で計算された逆指値注文の値を使用すると、価格の変動がその平均的な逆指値損失の動きのモデルにおける最適なものよりも基本的に大きいことが判明するため、平均的な統計上の損失が発生します。

                                                                                                                            (4.27)

これは、最適な損切り(4.18)を相対的に小さく(4.25)する平均期間を探すのではなく、損切りの大きさ自体を変える必要があることを意味します（この課題には解がないため）。もちろん、これによって利益も変わってきます。

 

平均値動きモデルの最適な利食いは、現在のバーからバー先に位置する予測移動平均価格のポイントと一致します。しかし、逆指値注文が決済される平均からの強い価格乖離を考慮に入れると、（図1のCasual Channel指標のグラフでわかるように）利益を確保するために、このような最適な利食いは、平均乖離よりも大きい量だけ減少させる必要があります。

                                                                                                               (4.28)

ここで、率は、弱いトレンド（ほとんど利益がない）の場合は1より少し大きく、強いトレンドの場合はおよそです。ここではまさに最適化によって正確な値を求めるべきパラメータであり、損切りは同じ量だけ増やすべきです、すなわち 

                                                                                                                (4.29)

です。そして、損切りは、オープンポジションに対する可能な価格乖離の平均値（ 未来バーの場合）から だけ離れた値として、より低い確率でより頻繁にトリガーされず、一方、利食いは、より高い確率でより頻繁にトリガーされます。したがって、最大利益については、次のような見積もりが得られます。

              (4.30)

ここで、 は(4.16)の値、あるいは(3.7.1)を考慮すると

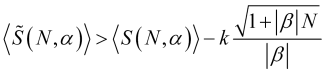                                                                    (4.31)

その関数（最適なb(4.18)から）を構築することができます。 それを最大化するN値に加えて平均期間を求めることができます。 

 

k=3MATLABコード

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> s0=N.*(1-a.^(-b))./(1-a.^(-N))-b;
>> Profit=s0-3*s;
>> plot3(N , a, Profit)
>> grid on 

 

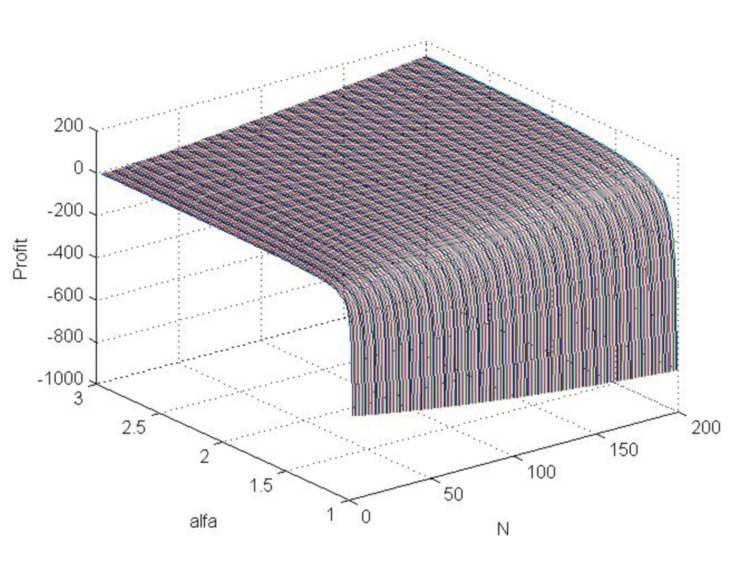
図7：αが1から3に、Nが3から200に変化したときの利益関数グラフ（モデル価格のジャンプ）

グラフは、数学的期待値が正になる利益が一般的に可能であり、αとNが大きくなるにつれて増加することを示しています。 

 

最も有望な平均化期間 を見つけるためには、予測Q値関数 を構築する必要があります。このため、CalculateScientificTradePeriodスクリプトが開発されました。最も有望な期間をの最大位置で定義する必要があります（ここで）、この最大値にスムーズに到達し ((3.12) 比率が満たされている)、適切な作業期間よりも遠くに位置しないを定義します。このようにして見つけたの値が、正の（少なくとも2、3のスプレッドを超えるだけでなく）利益値（4.31）と十分に高い勝率（4.15）を提供し、それが区間 を設定するのであれば、取引決定はここに基づいておこなわれるべきです。最適な（平均利益を最大化する）利食いと損切りを計算し、さらなる価格トレンドを判断するために、ScientificTrade指標を開発しました。そのアルゴリズムは、上で示した理論全体に基づいています。

 

CalculateScientificTradePeriodスクリプトアルゴリズムは、非常にリソースを消費するため、指標ではなくスクリプトを使用します。これにより、ティックごとにこのアルゴリズムが実行され、コンピューターがフリーズしてしまいます。FindScientificTradePeriod指標は、スクリプトによって計算されたデー タを表示するために使用します。  

 

 

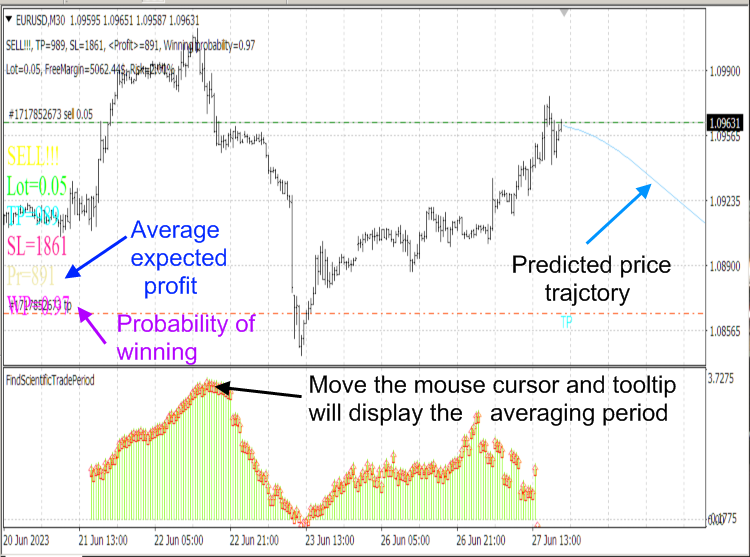
図8： ScientificTrade指標およびFindScientificTradePeriod指標 

 

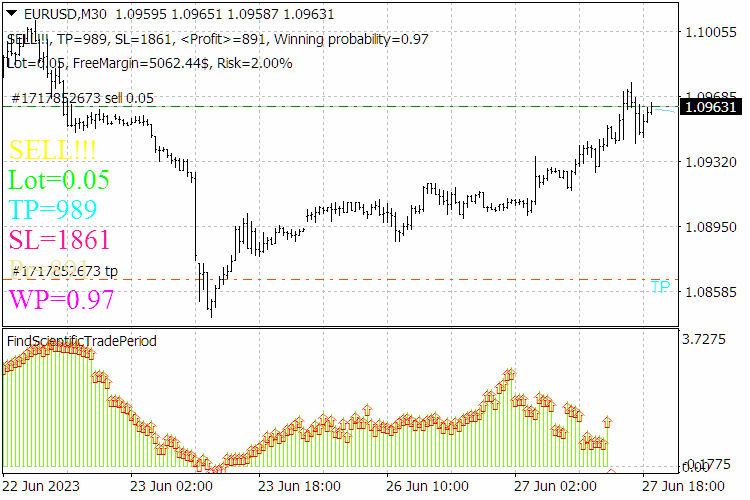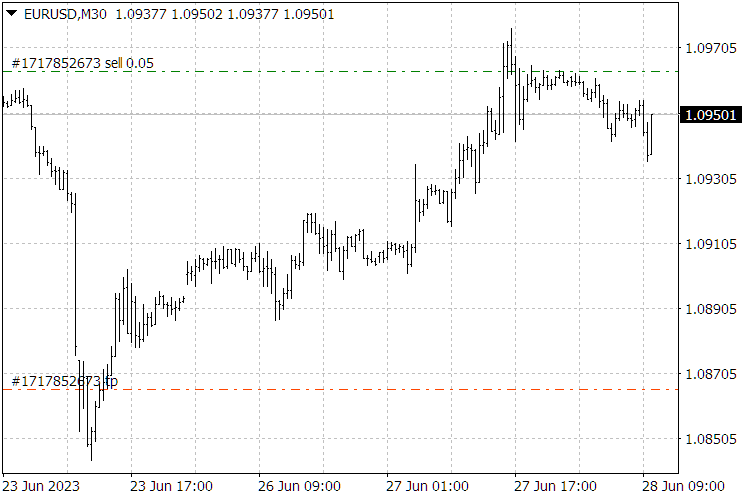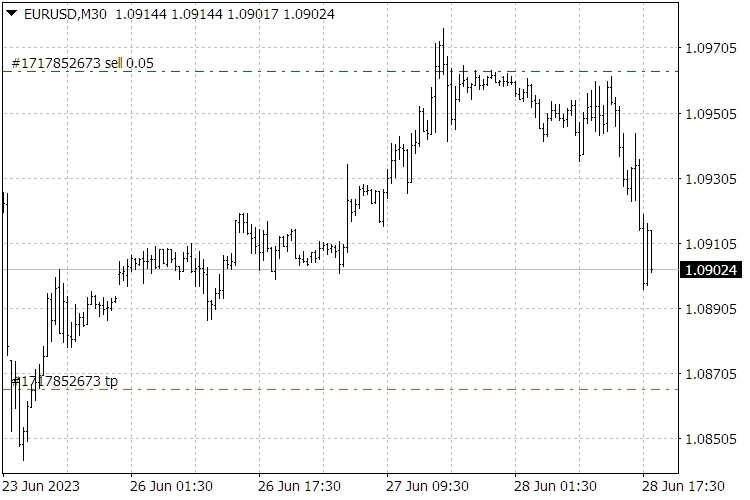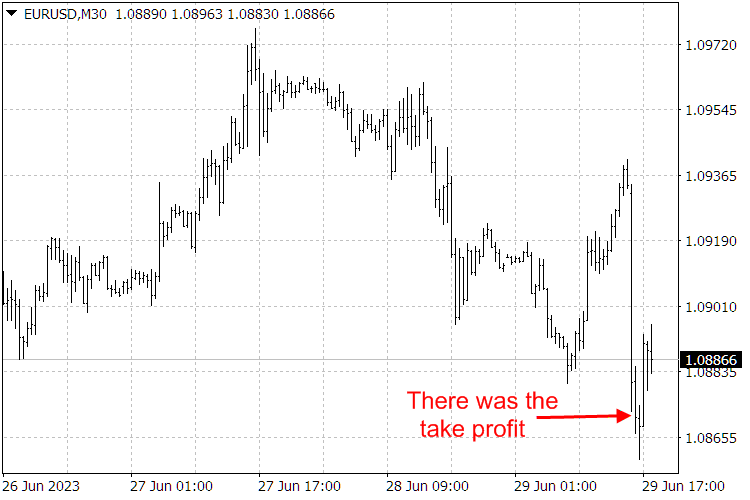
図9： ScientificTrade指標の結果 

5.数学的装置そのものの枠組みの中で、適用された計算の取り返しのつかない誤差：自然に発生する価格の反発と反転の瞬間を見極めるアプローチ

前述したように、ScientificTrade指標によって予測され、損切りおよび利食いの場所の指標によって計算されたトレンドは、 およびの予測値に基づいています。この予測値は、（フーリエ外挿指標における）予測装置自体の信頼性が低いため、誤っていることが判明する可能性があります。したがって、そのような予測は、上で示したすべての数学的装置の適切な作業範囲内で誤りであることが判明する可能性があります。

誤った数学的予測の少なくともいくつかのケースを除外するために、CalculateScientificTradePeriodスクリプトによって決定された間隔でScientificTrade指標によって計算されたトレンドは、与えられた間隔で権威のあるファンダメンタル分析の専門家によって提供された予測トレンドと一致する必要があります。ScientificTradeと専門家の両方が同じ誤った予想（私たちが知ることはできない）を提供すれば、損失も避けられないことは明らかです。私の主観的な観察によると、専門家はCalculateScientificTradePeriodスクリプトと組み合わせたScientificTrade指標よりも間違いを犯す可能性が高いようです。これは、専門家が判断できないトレンドの変化を引き起こすほとんどの外部イベントよりも、市場発展の内部法則の方が強い影響を与えるためだと私は考えています。さらに、このような内的理由による市場の反転は、強力な外的イベントが発生する前に起こることが多く、またそのようなイベントよりも頻繁に起こります。適切なメカニズムについては後述します。        

上記の問題の本質を表現するには、まず、市場が独自の法則に従って発展しているとき（価格が外部からの強い事象に押されていないとき）でも、価格が常に等距離のジャンプで動くとは限らないことに留意すべきです。この概念は単純化されたモデルであり、少なくとも何かを理解し、市場の混乱の中で計算することを可能にします。現実には、価格は平均的な静的トレンドに反して短期的に（古典的な統計の範囲を超えて）強い動きをすることがあり、それによると、一定の方向にゆっくりと（大きな変動を伴って）漂います。さらに、このような強い動きが、市場に対する外部からの影響によるものではなく、市場の内部プロセスに由来するものであれば、それは通常、統計的なトレンドに反するものです。したがって、このような強い動きは損切りを打ちのめし、ほとんどの小口トレーダーにとって最大の損失となります。

実際（取引サービスや相場を提供する業者が意図的に損切りを叩き出すことを除外すれば）、ルシャトリエの原理は、量から質への移行という弁証法的な法則と連動して、ここでも働いています。特定の市場手段の特定の（市場にも依存する）成長（または下落）レベルに達すると、品質の急激な上昇が発生します。ルシャトリエの原理（その作用は、ほとんどの場合、近い準平衡状態を経て進化する経済を含む、平衡状態にあるあらゆる複雑なシステムにまで及びます）によれば、これは上記の量の増加に抵抗し、急激に（ジャンプによって）減少させる傾向があります。システムとしての市場は、その単調な発展とともに、徐々に近い準平衡状態を通過するため、ルシャトリエの原理はその小さな変化には反応せず、あるシステムにすでに大きな量的変化が蓄積されているときに突然作用します。市場波動モデル（第1回）の観点からは、このようなジャンプは、対応する市場商品の部分的な確率波の位相が前進的に接近する（または等しくなる）ことで説明できます。

理論的には、自然価格ジャンプのアプローチは、比率(II.17)を使って特定することができます。しかし実際には、予測されたQ値のグラフを使う方が、ジャンプが近づいていることを検知しやすくなります。特に、将来のある時点（現在のバーからバーだけ離れている）で予測されるQ値が、対応する時間枠、すなわち（現在の状況を考慮し、予測状況を考慮しない場合は、単に）で、与えられた市場商品に関するある限界値を超えるか、またはそれに近づく場合、この時点でグローバルトレンドの変化が可能です。

一般に，自然な価格ジャンプ（大小を問わず）は，その分布の確率振幅のレベルでは，非対称ウェーブレットによって記述される（第1部）、比（I.17)）によって記述されます。その場合，その全確率振幅が構成されるすべての部分的な価格の波の位相が近接し，均等であることを実現した後，対応するウェーブレットの非対称性によって，後者の位相が反転し，実際のとの確率の急激な変化につながり，その結果，予測確率と とは根本的に異なるようになります。市場独自の法則によって品質が跳ね上がるような危機的状況は、取引から除外されるべきなのは明らかです。このような部分的な価格波の非対称性によって、部分的な価格波がフェルミオンと類似していることが保証され、それが価格水準を変えたいという不変の欲求と、（価格変動の結果として解釈される）著しい幅を決定します。したがって、通常の統計ではなく、フェルミ-ディラック統計によって市場商品の進化を記述する方がより正しくなります。  

その動きの最も激しい局面（その確率の振幅の最大係数）における価格波の反転（第1回）の記述された効果により、最高Q値に基づく最も最適な取引パラメータは、また、最大の利益を確保するはずであることに注意することも面白いです。しかし、ほとんどのトレーダーが（直感的または数学的に）プロセスの単調さとその慣性に関する習慣的な考え（物理的大宇宙で観察されるすべてのものの特徴）に基づいて特定したこれらの取引パラメータは、実際には、最大の損失を引き起こします。

その結果、日常的な「法則」がここでも当てはまることが判明しました。金が金を生み、その大部分は銀行に貯蔵されるため、市場は小口取引業者から資金を引き揚げます。結局のところ、市場は、上記の理由から、突然（それは定期的におこなわれる）大多数のトレーダーが予測したトレンドに反して展開し始めます。このプロセスには人間の「悪意」はありません。市場は、物理的なマクロプロセスに特徴的な一定の慣性（小口トレーダーが一定期間利益を得るために利用する）を持たず、ある瞬間（適切な理論武装をしていない専門家やトレーダーには予測不可能）には、創発的なレベルで動作する内部法則の影響下（強力な外部イベントの影響さえ凌駕する）で、さまざまな市場参加者が発する個々の部分的な価格波のすべての位相を容易に反転させます。 

全体として、市場は混沌に支配されています。だからこそ、市場秩序が最大限に特定されれば、それは必ず破られるのであり、これはかなりよく観察された市場の法則といえます。それを知らずに安定した利益を得ることは不可能です。

結論

この記事では、収益性の高い取引戦略を構築するための工学的アプローチを紹介しました。このアプローチは、市場で、正の期待利益が得られるゲームが提供される可能性があるようなポジションをトレーダーが開始および終了するための条件は極めて厳しいことを示しました。このセットは古典的な方法では特定できません。このことは、この工学的アプローチに基づくScientificTrade指標を個人的に使用し、予測にフーリエ外挿を使用することで、ある程度確認することができます（統計は今のところ十分とは言えませんが）。もちろん、この指標はまだ改善する必要があります。現時点での主な欠点は、精度が不十分な数学的予測装置を使用していることです。