O modelo de movimento de preços e suas principais disposições (Parte 3): Cálculo dos parâmetros ótimos para negociação em bolsa

Introdução

Se nos artigos anteriores (Parte 1 e Parte 2) foram apresentados os princípios fundamentais e os mecanismos subjacentes à geração da dinâmica de preços, o que tinha um caráter estritamente teórico e até ultrapassava os limites da observação (ainda que tenha servido como base para ela), neste artigo e nos seguintes, tentarei estabelecer as bases de uma nova disciplina de engenharia (onde muitos cálculos serão, portanto, de natureza estimativa), que permitiria tirar conclusões praticamente úteis da dinâmica de preços observada e aplicá-las diretamente na negociação. Neste artigo, falaremos sobre abordagens de engenharia e algoritmos que, em geral, são capazes de garantir lucro consistente, bem como cálculos probabilísticos dos valores ótimos de take profit e stop loss que permitiriam alcançar o máximo de lucro médio.

1. Modelo.

No artigo anterior (Parte 2), obtive a equação (II.3) para o fluxo de probabilidade de preços (para brevidade, a equação (N) do artigo Parte R será numerada como (R.N), onde R é um número romano). Um fluxo de probabilidade desse tipo, em forma reduzida ou observada, é expresso em probabilidades de movimento de preço "para cima" e "para baixo", ou, para ser mais preciso, cria tais probabilidades. Vamos formular a abordagem para a avaliação prática dessas probabilidades.

 

Na representação de tempo discreto (com base no conceito de barras), quando o segmento do histórico de preços (Abertura, Fechamento, Máxima ou Mínima) é apresentado como a série (a ordem de numeração aqui é tal que as barras subsequentes têm números mais altos do que as anteriores), o preço se move em etapas discretas. Em escalas grandes ou no caso de um tamanho bastante grande , isso nos permite discutir as probabilidades desses saltos de preço avaliados para a probabilidade de movimento de preço para cima, como , onde - número de membros do conjunto , ou para a probabilidade de movimento para baixo , onde - número de membros.  Ao mesmo tempo, é possível calcular a duração do salto médio 

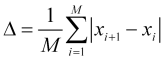                                                                                                    (1.1)

do preço .  Na prática, podemos descobrir que um preço que se move de forma caótica durante o período se afasta de sua média atual (definida por tais probabilidades) devido a um movimento aleatório. O desvio é da ordem de

              ,                                                                                                      (1.2)

(isso é confirmado pelo indicador Casual Channel, cujas linhas de canal são ou desvios (1.2) da média móvel do período ).

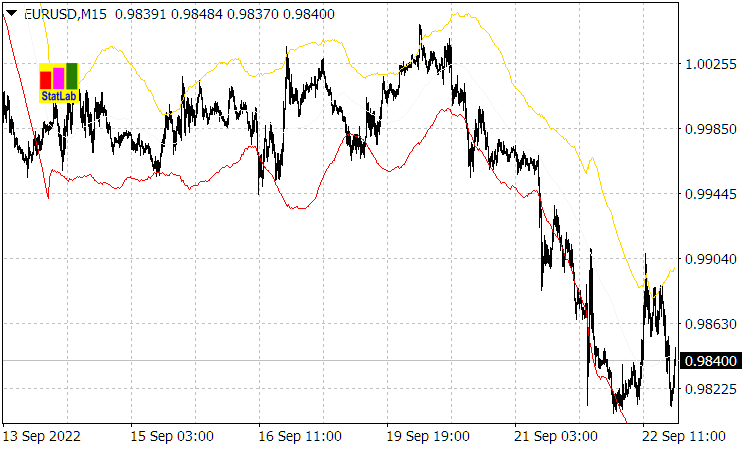
Fig. 1.  Indicador Casual Channel

Obviamente, o tempo característico do desvio aleatório de preço por da ordem de , onde é o comprimento temporário de uma barra do período apropriado.  Veríamos o mesmo desvio (1.2) do preço em relação à média, se o preço se movesse aleatoriamente por saltos semelhantes exatamente iguais a .    

 

Portanto, na simplificação do modelo fornecida aqui, vamos assumir que o preço se move em saltos semelhantes , com probabilidades de suas direções de e . 

 

O salto , calculado usando os métodos descritos anteriormente, bem como as probabilidades, já eram relevantes para o intervalo anterior como um todo, ou seja, como médias para a faixa de valores, em vez dos movimentos de preço atuais formados sob a influência de diferentes saltos e, o mais importante, das probabilidades e que ainda estão por serem previstas.

 

Como mencionei na Parte 2, os métodos da estatística convencional e seu aparato matemático não são adequados no caso da dinâmica de preços formada por superposições de ondas de probabilidade que causam erros consideráveis. Assim, a análise baseada na aplicação de dados observados e nos cálculos probabilísticos e estatísticos apropriados possui natureza aproximada.   

2. Determinação prática das probabilidades previamente operacionais e da velocidade de preço normalizada. O princípio de usar esses parâmetros para calcular a distribuição futura de preços.

A velocidade média de movimento de preço ao longo do intervalo de média é igual a

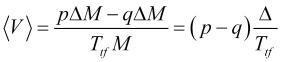                                                                                  (2.1)

e mostra a taxa de mudança da média móvel (onde é um índice de barra) com o período de média apropriado, e não algum tipo de flutuações de velocidade. Portanto, a velocidade média é uma quantidade praticamente calculável

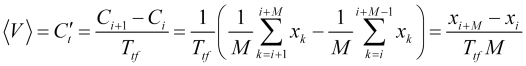                .         (2.2)

Igualando (2.1) a (2.2), obtemos um parâmetro empiricamente determinado

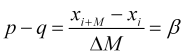               ,                                                                                           (2.3)

Vamos chamar isso de velocidade de preço normalizada, uma vez que , enquanto . É fácil demonstrar . Na verdade, por exemplo, a partir de (1.1) segue a desigualdade

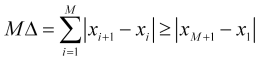              ,                                                                           (2.4)

implicando (2.3) juntamente com . Também podemos assumir , e como a probabilidade é , então . Use (2.3) e para encontrar as probabilidades 

                 e  ,                                                                        (2.5)

bem como outra expressão para a velocidade normalizada

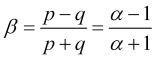                 ,                                                                                    (2.6)                               

onde o parâmetro

                .                                                                   (2.7)

Em cálculos futuros, também precisaremos do parâmetro  

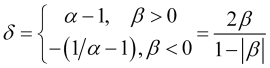               ,                                                            (2.8)

através do qual a própria velocidade normalizada é expressa da seguinte forma

                .                                                                                            (2.9)

 

As probabilidades (2.5) de saltos calculados no intervalo de preço são as médias para o intervalo e participam na formação do preço final . Assim, se conhecemos (no momento atual ou antecipadamente quando o preço é conhecido) essas probabilidades médias, podemos prever o preço no futuro , ou, para ser mais preciso, a distribuição de probabilidade do preço.  Ao comparar os gráficos de preços e a velocidade normalizada (a partir da qual são calculados e ), podemos observar sua forte semelhança (pela coincidência das localizações de seus vértices), mostrando que foi essa velocidade (mais precisamente, as probabilidades correspondentes a ela) que formaram o preço atual de .

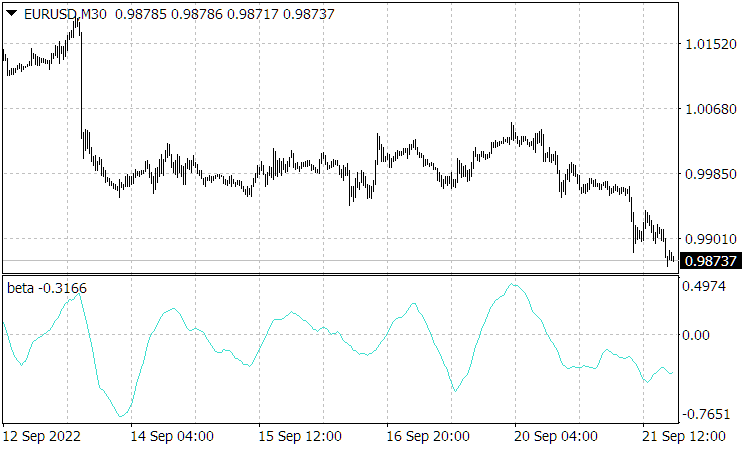
Fig. 2. A figura mostra o gráfico de velocidade normalizada.

 

Isso é compreensível. De fato, a partir de (2.3) segue . Isso significa que o preço é formado a partir do preço pelo array de velocidades futuras ou suas médias pelo intervalo

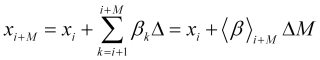  ,                         (2.10)                                                              

onde a velocidade normalizada média sobre o intervalo futuro, exibida em seu gráfico no ponto

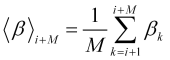            ,                                                     (2.11)

enquanto as médias do intervalo de probabilidade e são encontradas substituindo nas equações (2.5) (obviamente, se em (2.10) o membro estiver em torno de , então temos gráficos semelhantes a e ). Em seguida, tendo previsto funções suficientemente suaves em barras à frente, calculamos as probabilidades necessárias e , o que nos permite calcular (no momento de ) a distribuição de probabilidade do preço futuro e seus parâmetros necessários para a negociação (direção de abertura de posição e posição da ordem de stop).

 

A essência da previsão de velocidade normalizada usada aqui é a seguinte. A função temporária de velocidade normalizada flutua dentro da faixa de próxima à sua expectativa matemática igual a zero (ou ao pequeno valor que exibe a velocidade da tendência global, se cobrir toda a área em consideração). Nesse caso, por exemplo, a previsão estatística mais simples baseada na expectativa matemática condicional, tomando a forma de , aproximará a função de previsão de zero ou  de acordo com . Em outras palavras, à medida que a função de autocorrelação do processo correspondente diminui rapidamente, reduzindo o número de posições abertas por uma condição como  e tornando o jogo ainda menos lucrativo do que um jogo com uma previsão trivial baseada no último valor . Por outro lado, a dinâmica de preços é bem modelada e prevista por processos oscilatórios. A ideia por trás disso foi apresentada em artigos anteriores. Nesta etapa do desenvolvimento da teoria, a previsão da função (que tem natureza oscilatória) em barras à frente foi feita com base na extrapolação de Fourier calculada com base em dados históricos empíricos , uma vez que o uso da extrapolação wavelet proposta em artigos anteriores neste caso ainda não proporcionou vantagens perceptíveis.

3. Qualidade da tendência. Avaliando a extensão das tendências atuais e futuras, horizonte de trabalho adequado.

Se a tendência durar mais do que o tempo de média , então o aumento natural no preço durante o tempo de média (de acordo com (2.1) e (2.3)) é da ordem de

               .                                    (3.1)

Incerteza desse incremento 

                ,                                                                                               (3.2)

então a faixa completa de movimento de preço (veja a Fig. 1), quando ele se move de uma borda do canal do indicador Casual Channel para outra e ao mesmo tempo deriva em média na velocidade normalizada , é estimada como

                 ,                                                               (3.3)

onde

                 .                                                                                 (3.4)         

Se seguirmos a tendência, então é desejável que o valor do deslocamento (3.1) permaneça significativamente maior do que a incerteza (3.2) desse deslocamento

               ,                                                                (3.5)

a partir dele e de (2.6) e (2.9), obtemos uma estimativa inferior para o tempo de média necessário

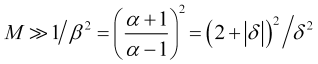              ,                                                   (3.6)

quando cumprido, de acordo com (3.4), o tempo de média (em barras) é calculado como 

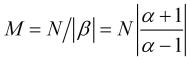              .                                                                                  (3.7)

Se o incremento de preço da incerteza não puder ser negligenciado, então o tempo de média é considerado como a raiz positiva da equação quadrática (3.4).

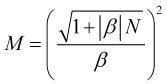               .                                                                                        (3.7.1)

 

Define a qualidade da tendência

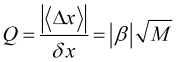               ,                                                                                        (3.8)

como a razão entre o seu incremento natural e sua incerteza ou ruído. É bastante claro que uma estratégia de seguimento de tendência lucrativa e estável requer alta qualidade . Mas o indicador de Quality Trend, que calcula a qualidade (Fig. 3), atinge o valor de apenas algumas unidades no máximo para uma moeda. Além disso, mesmo identificando uma tendência de alta qualidade, não é possível determinar quando ela terminará devido à imprevisibilidade do surgimento de eventos externos fortes que podem perturbar a dinâmica do mercado e encerrar a tendência ou até mesmo revertê-la. Por isso, uma estratégia lucrativa só pode ser baseada em obter lucros com flutuações relativamente pequenas na direção da tendência.

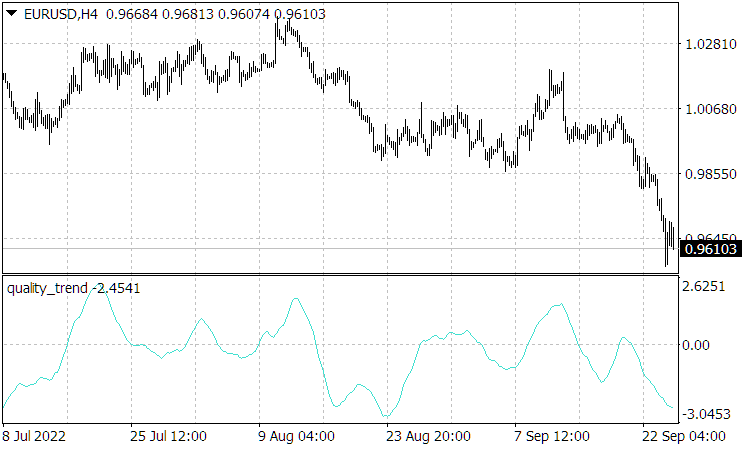
Fig. 3. O indicador Quality Trend, onde o incremento de preço não é calculado em módulo, ou seja, o sinal do indicador indica a direção da tendência.

Observa-se que as leituras do indicador Quality Trend, sendo proporcionais à velocidade normalizada, conforme demonstrado na relação (2.10) para a mesma, são semelhantes à ação do histórico de preços e, portanto, as leituras do Quality Trend não ficam para trás. Além disso, as leituras deste indicador podem até mesmo antecipar (e frequentemente antecipam) os movimentos de preços, uma vez que antes da mudança de tendência, a velocidade correspondente do movimento dos preços (ascendente para uma tendência de alta ou descendente para uma tendência de baixa) diminui. No entanto, esse comportamento de previsão do indicador ocorre apenas na ausência de influências significativas no mercado que perturbem seu movimento natural. E após tais influências, durante o período de sua relaxação, as leituras do indicador Quality Trend se tornam "normais" e ficam para trás, com o atraso determinado pelo seu período de suavização.

 

Vamos analisar o comportamento da função e avaliar a possível extensão das tendências, desde que não haja influências externas fortes no mercado. Com a diminuição do período médio , os valores calculados da velocidade normalizada podem aumentar (afinal, seus valores "instantâneos" em um mercado em constante mudança mudam com uma amplitude maior do que os valores médios e quanto maior a média, menor tais variações), ou seja, na relação do fator de qualidade, os membros para os quais e vice-versa são multiplicados, o que permite que a função tenha máximos. No entanto, em um intervalo muito pequeno, quando as verdadeiras probabilidades de saltos e são constantes, devido às pequenas mudanças na situação de mercado nele, seus valores calculados estatisticamente e ao longo deste curto período de média, provavelmente diferirão muito das probabilidades verdadeiras, porque com a diminuição do período de incerteza, as e das probabilidades calculadas nele aumentam. Assim, para o período de média que fornece o cálculo de probabilidades mais ou menos confiáveis, as relações de tipo devem ser satisfeitas, o que determinará seu valor mínimo. Caso contrário, quando  (embora esse seja um caso mais amplo do que o caso de grandes flutuações na velocidade normalizada instantânea em intervalos de média pequenos, já que essa relação também pode ocorrer em intervalos grandes com uma rápida mudança na probabilidade verdadeira ), os valores de probabilidade calculados estatisticamente não podem ser usados. Observe que em casos de fortes flutuações na velocidade normalizada, a função  baseada nela também flutua fortemente perto de seu máximo, portanto, o máximo usado para analisar a situação de mercado deve ser escolhido de forma que ele se forme suavemente, o que, como segue do exposto acima, é alcançado com períodos de média suficientemente grandes. Se a condição  for atendida, o que se supõe ser cumprido na teoria subsequente, as probabilidades estimadas  e  podem ser identificadas com as probabilidades atuantes  e  , que então também escreveremos como  e .

 

Precisamente nas áreas em que as probabilidades  e constantes, uma tendência estável é formada, enquanto a queda na probabilidade predominante  (ou seja,  ) reduzirá a taxa de crescimento do incremento  e talvez até mesmo (quando a relação inversa  é alcançada ) reverterá a tendência, o que também leva a uma redução no fator de qualidade calculado. Por outro lado, um alto fator de qualidade e seu crescimento indicam não apenas uma forte predominância da probabilidade predominante  sobre , mas também sobre sua constância e até aumento. Portanto, quanto maior a qualidade da tendência (3.8), maior a probabilidade de que ela esteja presente ali, ou seja, durante todo o intervalo , enquanto o baixo valor de qualidade  indica um mercado lateral. Também é claro que se aumentarmos o período de média , abrangendo não apenas uma tendência (com comprimento de  ) mas também um mercado lateral e, além disso, uma seção do histórico de preços com uma tendência oposta, então o fator de qualidade diminuirá rapidamente; portanto, o comprimento  da tendência é identificado pelo fator de qualidade de pico.

 

Se aumentarmos o período de forma a cobrir com ele uma tendência unidirecional de maior escala , do que a escala de uma seção de tendência menor com comprimento de , a qualidade da tendência, pelo contrário, aumenta, uma vez que devido à semelhança de gráficos em diferentes intervalos de tempo (desde que ), a escala das velocidades normalizadas em (3.8) permanece quase inalterada com o aumento de , enquanto  aumentará. Além disso (isso já requer a correção do cálculo do valor , que aparece na equação de qualidade (3.8)), a contaminação por ruído da tendência é amplificada acentuadamente por saltos de preços caóticos grandes e pequenos que vão além da distribuição estatística formada pelos saltos "padrão" (correspondendo ao modelo em consideração) com as probabilidades  e . Tais saltos não padrão são iguais para todas as escalas e criam "ruído adicional" para a tendência, de modo que o peso desse ruído adicional diminui com o aumento das escalas em que a tendência é identificada. Tudo o que foi mencionado acima implica o fato de que a função  pode ser usada para definir vários picos de qualidade no caso de uma tendência global unidirecional, que aumentarão com o aumento de  ou o aumento da escala das áreas de tendência identificadas.

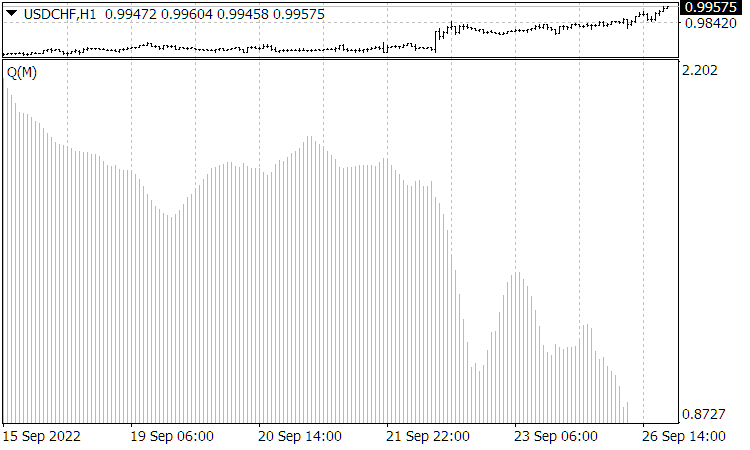
Fig. 4. Função atual. O eixo X aqui exibe o período de média para Quality Trend de 10 a 160, em vez do tempo.

  

Finalmente, o jogo não se baseia em um histórico já formado, mas em tempo real, o conhecimento de uma série de previsões , baseadas no conjunto de valores de previsão de velocidade normalizada, é necessário. Portanto, para avaliar o possível comprimento  de uma tendência recém-formada, precisamos percorrer todo o espectro de períodos de média e identificar um número de máximos da qualidade de previsão , quando sua previsão avança por  barras a partir da barra atual, ou seja, calculado

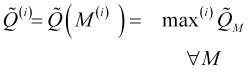               ,                                                                 (3.9)                 

onde  é uma função de identificação do º máximo. Nesse caso, também precisamos definir o pico máximo

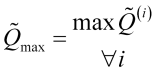                 ,                                                                                    (3.10) 

e seu ponto correspondente na escala de média.  

 

É óbvio que em intervalos de média menores  indo para o pico máximo  da qualidade de previsão, desde que nesses intervalos a qualidade também seja significativa e cresça de forma monótona ou em uma sequência de picos crescentes (também com base em um crescente atraso), haverá uma tendência unidirecional correspondente (com recuos após cada pico de qualidade). Após  do pico máximo  de qualidade, quando ele começa a cair na escala de média correspondente , ocorre uma desaceleração na tendência, o que pode levar em breve a uma reversão. Isso é mais provável quando o valor do pico é muito significativo no sentido de que o fator de qualidade para o instrumento de bolsa em questão raramente atinge valores maiores que  . Em qualquer caso, uma tendência de alta continuará até atingir um nível no qual você deve fechar a posição aberta de acordo com essa tendência.   

 

Vamos agora tentar estimar os comprimentos  dos segmentos de tendência que são promissores para negociação, que não precisam necessariamente ser iguais ao comprimento previsto da tendência. Em primeiro lugar, devido à baixa confiabilidade do trabalho da matemática preditiva em si (o que se aplica a todos os seus tipos, incluindo vários extrapoladores de frequência e outros, incluindo redes neurais e ARIMA, etc.), o lucro deve ser obtido em segmentos relativamente pequenos  da futura tendência identificada , a tendência é mais provável de se formar. Assim, como segue do parágrafo anterior, a desigualdade deve necessariamente ser cumprida .  Em segundo lugar, o modelo apresentado utiliza estimativas dos valores futuros de probabilidade  e , bem como os saltos médios são assumidos como constantes, uma vez que existem previsões que funcionam quando o mercado se desenvolve por inércia e de acordo com suas próprias leis. No entanto, como mostrado no primeiro artigo (Parte 1), o intervalo de desenvolvimento previsível do mercado começa a partir do último evento externo forte e continua até o próximo evento desse tipo. Portanto, existe o horizonte de trabalho adequado  de todo o aparato matemático sendo desenvolvido aqui, onde a quantidade  é igual ao número de barras da barra atual até a barra futura do início de um evento externo forte. Se tentarmos usar esse aparato matemático (o que é extremamente importante) além do horizonte dado, isso causará erros em seu funcionamento e perdas inevitáveis. Para determinar o horizonte possível para o funcionamento adequado de tal aparato matemático, é necessário se basear em análises fundamentais ou pesquisas de especialistas que avaliam a influência de todos os eventos políticos e econômicos atuais e futuros sobre o estado do mercado.  Portanto, o comprimento do segmento de tendência previsto como promissor para negociação é estimado por cima pela razão

              ,                                                                        (3.11)   

e por baixo deve ser estimado com base na razão previamente estabelecida da pequenez da incerteza de probabilidade (flutuações) em comparação com a própria probabilidade

               ,                                                                                    (3.12)

que também é determinada a partir do gráfico do fator de qualidade previsto e corresponde às áreas onde esse gráfico muda de forma bastante suave. A mudança de preço natural esperada nesta seção da tendência é

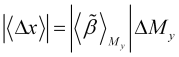               ,                                                                                    (3.13)

o que corresponde à ordem do lucro obtido com uma estratégia puramente de acompanhamento de tendência.

 

Em terceiro lugar, a seleção do comprimento do segmento de tendência também deve ser baseada nos cálculos apresentados abaixo, o que essencialmente nos permite definir os valores do intervalo  , nos quais é possível obter um lucro estatístico médio nas condições de mercado dadas, ou seja, . Além de tudo isso, os traders escolhem o período por conta própria, e a qualidade real (e não o modelo, calculado pela fórmula (3.8)) diminui com a diminuição do período devido ao ruído de preço em todos os períodos devido aos seus saltos não-modelados (idênticos em todos os períodos). Portanto, os traders têm a opção de escolher opções com alta qualidade de tendência, mas com uma espera longa por lucro, o que ocorre em grandes períodos; ou fazer um lucro rapidamente em tendências de menor qualidade (e, consequentemente, maiores riscos), que é típico para períodos menores.

4. Cálculo probabilístico dos valores de take profit e stop loss que proporcionam o lucro máximo com probabilidades de operação constantes e a expressão destas últimas.

Definindo uma tarefa. 

O preço se move em saltos na dimensão vertical a partir da marca zero. A probabilidade de um salto de preço para cima , a probabilidade de um salto de preço para baixo , respectivamente, . Claro, aqui existem médias previstas e , o que não é importante agora.  No topo, há o take profit à distância de "a", enquanto na parte inferior, há o stop loss à distância de "b" a partir da marca zero (quando visto nos eixos de coordenadas ).  Encontre os parâmetros da negociação em bolsa que garantem o lucro máximo.

 

Solução.

              O preço pode ir até o ponto com coordenada "n" ou de baixo a partir do ponto "n-1" ou de cima a partir do ponto "n+1". Logo, a probabilidade de encontrar o preço no ponto "n" é igual a 

               .                                                                                     (4.1)

A partir de (4.1), obtemos a equação de diferenças finitas 

                                                                                (4.2)

 

Saltos equiprováveis. 

              Vamos primeiro considerar o caso de saltos equiprováveis Aqui, obtemos o seguinte a partir de (4.2):

               ,                                           (4.3)

onde é uma constante, a partir da qual encontramos

               .                                                                                                 (4.4)

              A probabilidade de o preço estar em zero no momento inicial de seu movimento é , portanto, 

               .                                                                                                      (4.5)

              Vamos assumir que o stop loss "b" juntamente com o take profit "a" constituem a faixa de preço característica (estimada aqui (3.4) em saltos médios de preço ) do movimento ao longo do período de sua média (e movimento) em que se baseia a constância de probabilidades e . A probabilidade de o preço já estar no ponto de stop loss onde atinge um take profit de zero é . Substituindo (4.5), obtemos

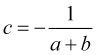                                                                                                                       (4.6)

juntamente com (4.5), isso nos fornece a probabilidade de atingir o take profit igual a

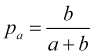                                                                                                                        (4.7)

enquanto a probabilidade de acionamento do stop loss

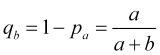               .                                                                                         (4.8)

Portanto, com saltos de preço igualmente prováveis em diferentes direções, o lucro médio no número de salto

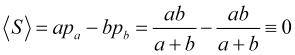                                                                          (4.9)

sé sempre zero (o spread, é claro, o torna negativo) independentemente da posição do take profit e stop loss, que podem ser quaisquer. 

 

Há uma tendência a se mover em direção ao take profit.

 

Se  (ou, para ser mais preciso, ) então, multiplicando todas as equações (4.2), encontramos

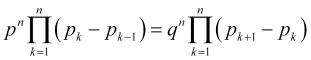               ,                                                      (4.10)

reduzindo fatores idênticos em (4.10), usando a notação (2.7) e considerando que , obtemos 

                .                                                                                 (4.11)

Vamos exibir como a soma das diferenças dos termos adjacentes da série de probabilidades usando relações adicionais (4.11) e a equação para somar a progressão geométrica

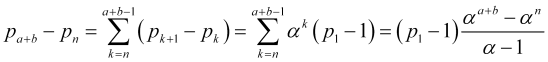 ,             (4.12)

 , portanto,

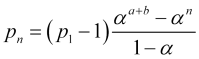                                                                                                   (4.13)

 , logo,

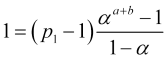              ,                                                                                           (4.14)

dividindo (4.13) por (4.14), obtemos a probabilidade de alcançar o take profit "a"               

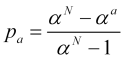              .                                                                                                      (4.15)

A probabilidade de acionamento do stop loss, respectivamente, é igual a , então o lucro médio por posição em saltos de preço é igual a

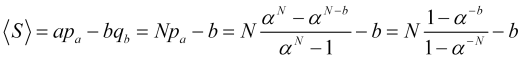               ,         (4.16)

que na representação (4.16) é uma função do valor do stop loss "b", que nesta representação é simplesmente o número de saltos, mas na verdade há um valor de . O lucro é .  É claro que com o aumento da probabilidade de movimento do preço em direção a uma posição aberta, o lucro médio (4.16) aumenta. Quando  assume o valor de , ou seja,  é uma função crescente de .

 

Vamos encontrar o máximo do lucro estatístico médio (4.16) sujeito aos valores dados de N e . Para alcançar isso, vamos igualar sua derivada a zero

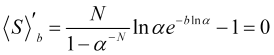                ,                                                             (4.17)

de onde encontramos o valor desejado de stop loss em saltos de preço 

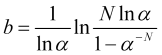               .                                                                                        (4.18)

 

Como , o logaritmo é positivo e . De forma correspondente, o valor do logaritmo 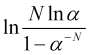deve ser positivo. Essa condição é satisfeita se

               ,                                                                                               (4.19)

ou   

      ,                                                      (4.20)                                                                                      

onde  . A desigualdade (4.20) é estritamente satisfeita para qualquer , já que o expoente passa acima da linha reta , tocando-a apenas em . 

A segunda derivada da função (4.16)

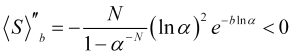                                                                            (4.21)

é sempre negativa nessas condições, ou seja, a curvatura da função é direcionada para baixo e temos o máximo em (4.18).  A função (4.16) em N=100 e  é exibida na Figura 5. 

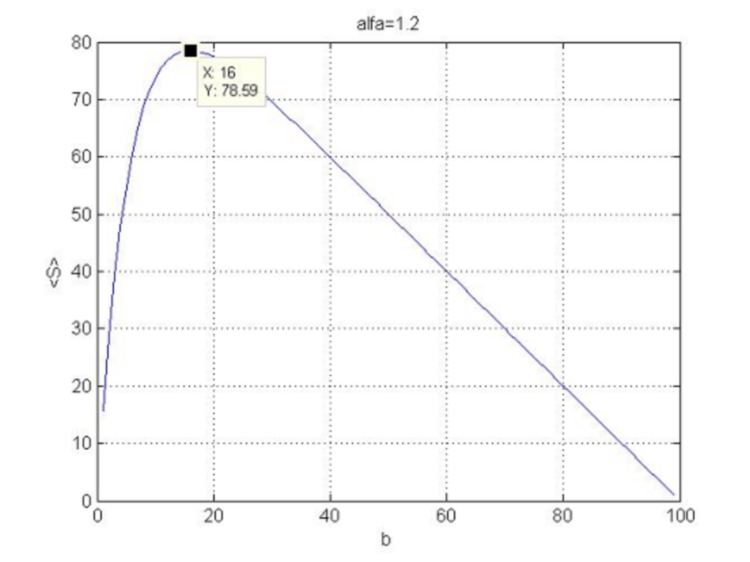
Fig.5. Dependência da função de lucro do stop loss.

Tenha em mente que, para que o lucro médio seja positivo, a razão deve ser significativamente superior a um. Na verdade, se , onde  e podemos negligenciar o segundo termo da expansão, deixando apenas o primeiro termo , então o lucro médio por negociação 

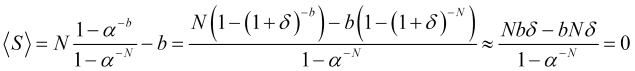    (4.22)

será igual a zero (como no caso de probabilidades iguais de saltos opostos). Se o segundo termo da expansão não puder ser negligenciado, então, levando em consideração que o número de saltos  é grande o suficiente ou , temos

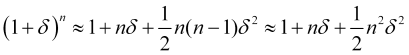               ,                               (4.23)

o que fornecerá um valor positivo para o lucro médio (4.16)

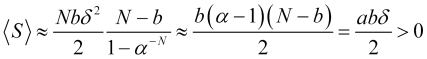               ,                          (4.24)

já que   ,     (e, portanto,  ).

              O lucro médio aproximado (4.24) em relação ao argumento é uma parábola quadrática invertida cujo máximo é atingido em  (que é a igualdade de stop loss e take profit), quando .

 

Aqui está um ponto muito importante. Na teoria apresentada acima, o lucro médio foi calculado apenas com base nos valores médios de preço, que, na verdade, flutua muito e até pode exceder muito os deslocamentos médios correspondentes na faixa de suas flutuações. No entanto, as ordens de stop (take profit e stop loss) não são fechadas nos valores médios de preço, mas precisamente nas extremidades da faixa de suas flutuações. Portanto, para que o aparato matemático apresentado (baseado em valores médios) funcione, o stop loss deve exceder significativamente a da incerteza do preço (para que sua flutuação de acionamento difira pouco do acionamento do modelo em termos da média e essas flutuações possam ser negligenciadas), ou seja, de acordo com (1.2), 

                .                                                                                                         (4.25)

Nesse caso, usando as expressões (3.7.1) para o período de média, obtemos de (4.25) a função a seguinte desigualdade deve ser satisfeita para

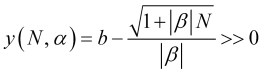               ,                                                                 (4.26)

que é um critério para a pequenez das flutuações de preço, onde  é encontrado a partir da proporção (2.6). Substituindo o stop loss (4.18) em (4.26), obtemos o gráfico da função (Fig. 6), o que torna claro que essa função não é muito maior que zero, mas, pelo contrário, é fundamentalmente negativa, ou seja, a relação (4.25) nunca é satisfeita com o stop loss ideal (4.18).

 

Código MATLAB

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> y=b-s;
>> plot3(N,a,y)
>> grid on

   

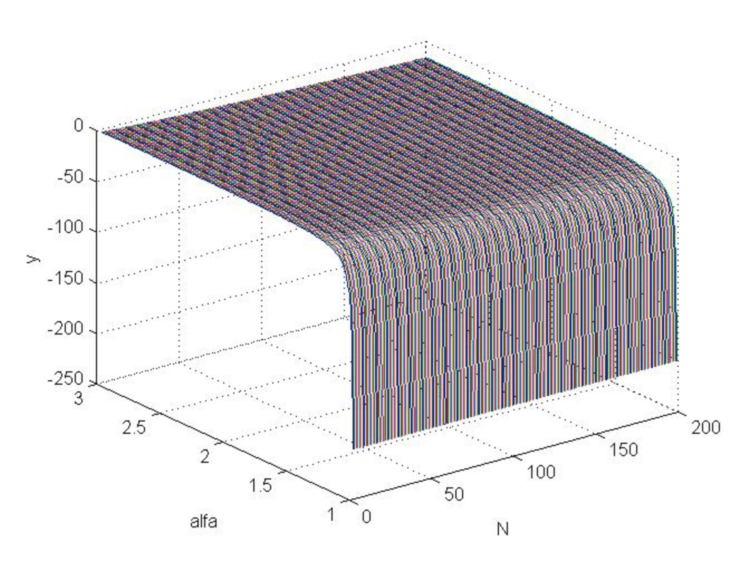
Fig.6. Gráfico da função "y" ao variar Alpha de 1 a 3 e N de 3 a 200.

 

 

Assim, o uso dos valores das ordens de stop calculados acima levará a perdas estatísticas médias, já que as flutuações de preço acabam sendo fundamentalmente maiores do que as previstas no modelo de movimento médio do stop loss

               .                                                                                                              (4.27)

Isso significa que precisamos mudar o tamanho do próprio stop loss, em vez de procurar pelo período de média que torna o stop loss ideal (4.18) relativamente pequeno (4.25) (já que essa tarefa não tem solução).Isso, é claro, também mudará o lucro.

 

O take profit ideal para o modelo de movimento médio de preço médio coincide com o ponto do preço médio móvel de previsão, que está localizado a barras à frente da barra atual. Mas se levarmos em conta desvios de preço acentuados em relação à média, nos quais as ordens de stop são fechadas, então (conforme pode ser visto no gráfico do indicador Casual Channel na Figura 1), para garantir um jogo lucrativo, esse take profit ideal deve ser reduzido em uma quantia maior do que o desvio médio

              ,                                                                                                  (4.28)

onde a razão  deve ser ligeiramente maior que um para tendências fracas (com quase nenhum lucro) e aproximadamente  para tendências fortes, sendo aqui exatamente o parâmetro cujo valor exato deve ser buscado por meio de otimização, e o stop loss deve ser aumentado pela mesma quantia, ou seja, 

               .                                                                                                  (4.29)

Então, um stop loss, como um valor separado do valor médio da possível variação de preço (para barras futuras) em relação a uma posição aberta por , será acionado com muito menos frequência com uma probabilidade menor do que , enquanto o take profit será acionado com mais frequência com uma probabilidade maior que . Consequentemente, para obter o lucro máximo, obtemos a estimativa

               , (4.30)

onde    é um valor de (4.16),   ou, considerando   (3.7.1)

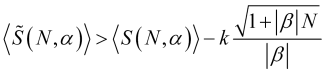                                                                    (4.31)

cuja função (no caso do ótimo b a partir de (4.18)) pode ser construída, de modo que somos capazes de encontrar o valor de N que a maximize, bem como o período de média. 

 

Código MATLAB para k=3

>> [N,a]=meshgrid([3:200],[1.01:0.01:3]);
>> b=log(N.*log(a)./(1-a.^(-N)))./log(a);
>> beta=(a-1)./(a+1);
>> s=(N.*beta+1).^(1/2)./beta;
>> s0=N.*(1-a.^(-b))./(1-a.^(-N))-b;
>> Profit=s0-3*s;
>> plot3(N , a, Profit)
>> grid on 

 

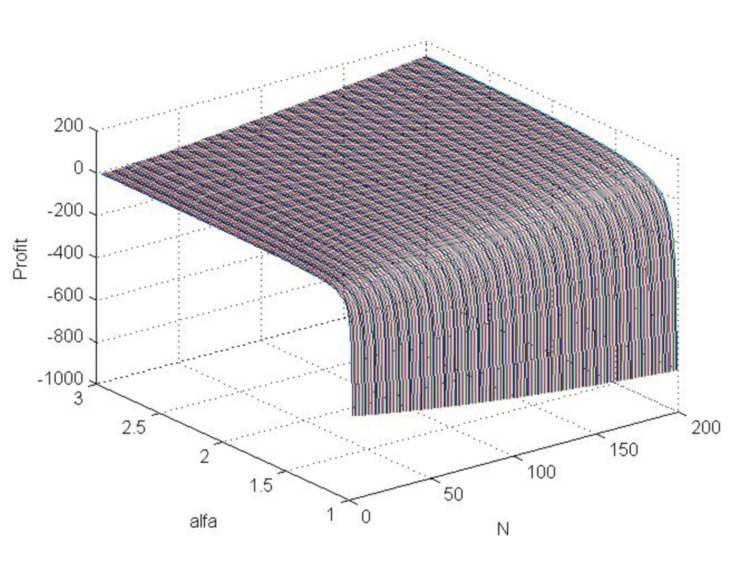
Fig.7. Gráfico da função de lucro (em saltos de preço do modelo) à medida que Alpha varia de 1 a 3 e N de 3 a 200.

O gráfico mostra que o lucro com uma expectativa matemática positiva é geralmente possível e aumenta com o aumento de Alpha e N. 

 

Para encontrar o período de média mais promissor, precisamos construir uma função de fator de qualidade preditiva . É por isso que o script CalculateScientificTradePeriod foi desenvolvido. Precisamos definir o período mais promissor pela localização do máximo , onde quando esse máximo é atingido suavemente (a relação (3.12) é cumprida) e não está localizado além do horizonte de trabalho adequado. Se o valor encontrado dessa maneira fornecer um valor de lucro positivo (bem como superior a pelo menos um par de spreads) (4.31) e uma probabilidade suficientemente alta de vitória (4.15), que define o intervalo , então a decisão de negociação deve ser baseada nela aqui. Para calcular o take profit e stop loss ótimos (maximizando o lucro médio), bem como para determinar a tendência de preço futura, desenvolvi o indicador ScientificTrade, cujos algoritmos são baseados na teoria apresentada acima.

 

Observe que o algoritmo do script CalculateScientificTradePeriod consome muitos recursos, portanto, usamos o script, não o indicador, que executaria esse algoritmo a cada tick e congelaria o computador. O indicador FindScientificTradePeriod é usado para exibir os dados calculados pelo script.  

 

 

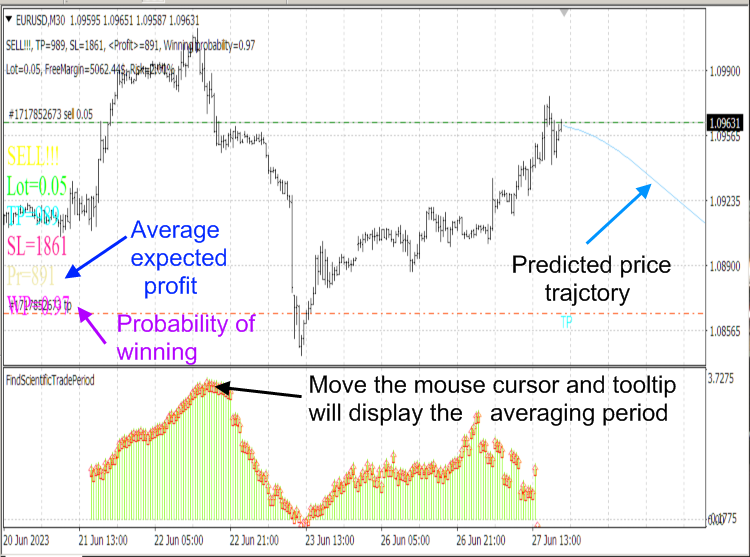
Fig.8.  Indicadores ScientificTrade e FindScientificTradePeriod. 

 

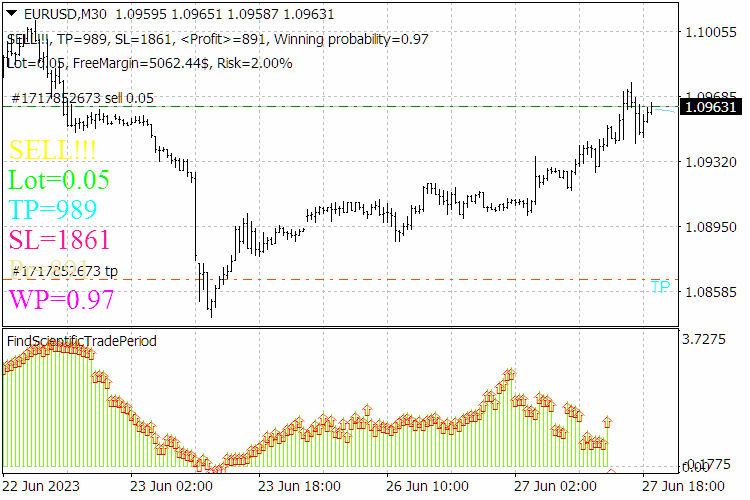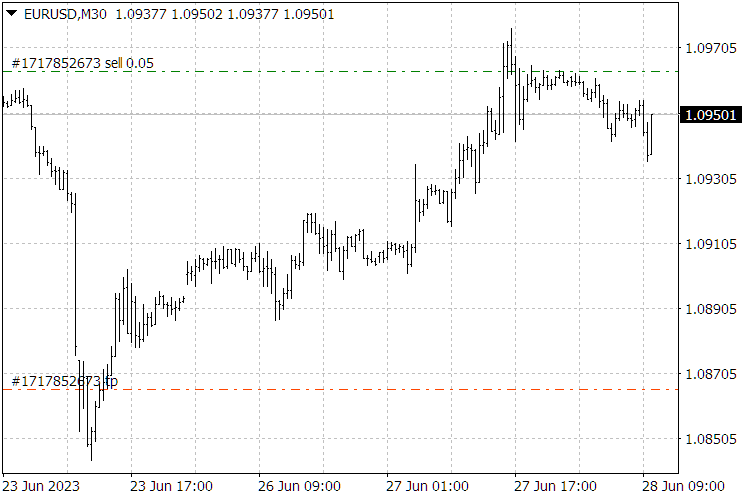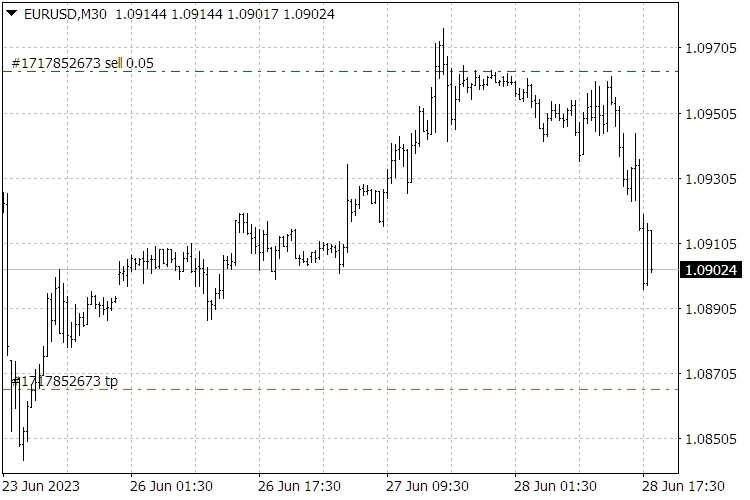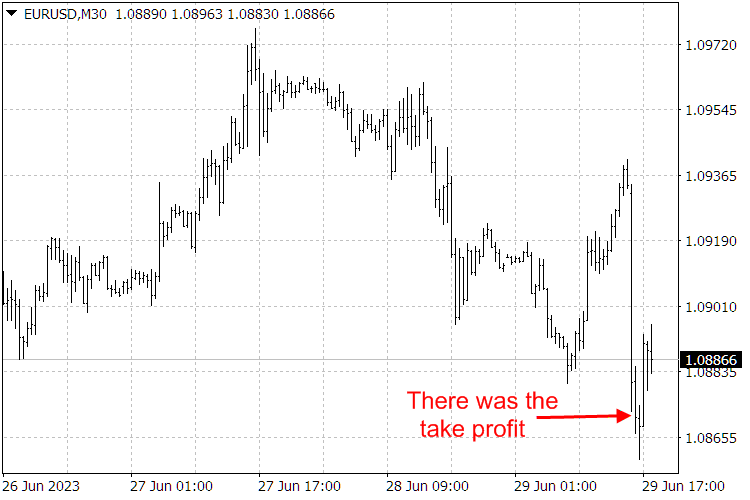
Fig.9.  Resultados do indicador ScientificTrade. 

5. Erro irreversível dos cálculos aplicados no âmbito do próprio aparato matemático. A abordagem para identificar momentos de reversões e reversões de preços que ocorrem naturalmente.

Como mencionado anteriormente, as tendências previstas pelo indicador ScientificTrade e calculadas pelo indicador de localização de stop loss e take profit são baseadas nos valores de previsão  e  , que podem se revelar incorretos devido à falta de confiabilidade do aparato de previsão em si (no indicador Fourier extrapolator). Portanto, tais previsões podem se revelar falsas dentro do horizonte de trabalho adequado de todo o aparato matemático apresentado acima.

Para excluir pelo menos alguns casos de previsões matemáticas falsas, as tendências calculadas pelo indicador ScientificTrade no intervalo determinado pelo script CalculateScientificTradePeriod devem coincidir com as tendências previstas por especialistas em análise fundamental autorizados para um determinado intervalo. É claro que se tanto o ScientificTrade quanto os especialistas fornecerem a mesma previsão falsa (o que não podemos saber), então as perdas também são inevitáveis. De acordo com minhas observações subjetivas, os especialistas são mais propensos a cometer erros do que o indicador ScientificTrade em combinação com o script CalculateScientificTradePeriod, o que, na minha opinião, se deve ao fato de que as leis internas do desenvolvimento do mercado têm um impacto mais forte do que a maioria dos eventos externos que causam mudanças nas tendências que os especialistas não conseguem determinar. Além disso, tais reversões de mercado causadas por motivos internos frequentemente ocorrem antes do início de eventos externos fortes, bem como com mais frequência do que esses eventos. Os mecanismos apropriados serão discutidos abaixo.        

Para expressar a essência do problema acima, deve-se primeiro notar que o preço nem sempre se move em saltos equidistantes, mesmo quando o mercado se desenvolve de acordo com suas próprias leis (quando o preço não é impulsionado por eventos externos fortes). Esse conceito é um modelo simplificado, que nos permite entender pelo menos alguma coisa e fazer cálculos no caos do mercado. Na realidade, o preço ocasionalmente faz movimentos fortes de curto prazo (além do escopo da estatística clássica) contrários às tendências estáticas médias, de acordo com as quais ele se move lentamente (com grandes flutuações) em uma direção específica. Além disso, se tais movimentos fortes não forem causados por influências externas no mercado, mas se originarem de seus processos internos, geralmente são direcionados contra as tendências estatísticas. Portanto, tais movimentos fortes derrubam as ordens de stop loss e criam perdas máximas para a maioria dos pequenos traders.

Na verdade (se excluirmos a derrubada intencional de ordens de stop loss por parte dos fornecedores de serviços de negociação e cotações), o princípio de Le Chatelier funciona aqui em conjunto com a lei dialética da transição da quantidade para a qualidade. Ao atingir um nível específico de crescimento (ou queda), também dependente do mercado, de um determinado instrumento de mercado, ocorre um salto acentuado na qualidade, que, de acordo com o princípio de Le Chatelier (cuja ação se estende a qualquer sistema complexo em equilíbrio, incluindo a economia, que na maior parte do tempo evolui passando por estados de quase-equilíbrio próximos), tende a resistir ao crescimento da quantidade mencionada acima, reduzindo-a abruptamente (em um salto). Como o mercado, como sistema, com seu desenvolvimento monótono, passa gradualmente por estados de quase-equilíbrio próximos, o princípio de Le Chatelier não reage às suas pequenas mudanças, mas age abruptamente quando grandes mudanças quantitativas já estão se acumulando em um determinado sistema. Do ponto de vista do modelo de ondas do mercado (Parte 1), tais saltos podem ser explicados pela proximidade avançada (ou igualdade) das fases de ondas de probabilidade parcial do instrumento de mercado correspondente.

Teoricamente, a abordagem de um salto de preço natural pode ser identificada usando a relação (II. 17). No entanto, na prática, é muito mais fácil detectar a aproximação de um salto usando o gráfico de fator de qualidade previsto. Em particular, se o fator de qualidade previsto em algum momento futuro (distante do bar atual por barras) exceder ou se aproximar de um valor crítico específico para um determinado instrumento de mercado no intervalo de tempo correspondente , ou seja, (se considerarmos a situação atual e não a previsão, então simplesmente ), então neste momento uma mudança na tendência global é possível.

Em geral, os saltos de preço naturais (de qualquer natureza, tanto globais quanto pequenos) no nível das amplitudes de probabilidade de sua distribuição são descritos por wavelets antissimétricos (Parte 1, relação (I. 17)), quando, após perceber a proximidade e até a igualdade das fases de todas as ondas de preço parciais, a partir das quais sua amplitude de probabilidade total é composta, a fase desta última, devido à antissimetria dos wavelets correspondentes, é invertida, o que leva a uma mudança brusca nas probabilidades reais e , que serão então fundamentalmente diferentes das probabilidades previstas e .  É claro que tais situações críticas, quando ocorrem saltos na qualidade devido às próprias leis do mercado, devem ser excluídas da negociação. Essa antissimetria das ondas parciais de preço garante sua semelhança com férmions, o que determina o desejo constante de mudar os níveis de preço e sua largura significativa (que é interpretada como resultado das flutuações de preço). Portanto, é mais correto descrever a evolução dos instrumentos de mercado não por estatísticas comuns, mas por estatísticas de Fermi-Dirac.  

Devido ao efeito descrito da inversão das ondas de preço (Parte 1) na fase mais intensa de seu movimento (o módulo máximo da amplitude de sua probabilidade), também é curioso notar que, aparentemente, os parâmetros de negociação mais ideais com base no fator de qualidade mais alto também deveriam garantir o lucro máximo. No entanto, esses parâmetros de negociação identificados pela maioria dos traders (intuitiva ou matematicamente) com base em ideias habituais (características de tudo observado no macrocosmo físico) sobre a monotonia dos processos e sua inércia, na verdade, causam perdas máximas.

Como resultado, a "lei" cotidiana acaba sendo verdadeira aqui também: dinheiro gera dinheiro, a maior parte do qual está armazenada nos bancos, então o mercado retira dinheiro dos pequenos traders. Afinal, o mercado, pelas razões mencionadas acima, de repente (o que faz regularmente) começa a se desenvolver contrariamente às tendências previstas pela maioria dos traders que jogam contra elas. Esse processo não tem a intenção "má" humana. O mercado não possui inércia constante (usada por pequenos traders para obter lucro por algum período de tempo) característica dos macroprocessos físicos e, em certos momentos (imprevisíveis para especialistas e traders não armados com a teoria apropriada), ele facilmente reverte as fases de todas as ondas de preço parciais individuais emitidas por diferentes participantes do mercado sob a influência de suas leis internas que operam em seu nível emergente (superando a influência de até eventos externos fortes). 

Em geral, o mercado é regido pelo caos. É por isso que, se alguma ordem de mercado é identificada ao máximo, ela deve ser violada, o que pode ser considerado uma lei bastante observada do mercado. É impossível obter lucro estável sem conhecê-la.

Considerações finais

O artigo apresenta uma abordagem de engenharia que desenvolvi para criar uma estratégia lucrativa de negociação na bolsa. Essa abordagem demonstra que o mercado oferece aos traders um conjunto extremamente restrito de condições para abrir e fechar posições que poderiam resultar em um investimento com expectativa matemática de lucro positivo. E esse conjunto de condições não pode ser identificado por métodos clássicos. No entanto, um investimento com expectativa matemática de lucro positivo é, em princípio, possível, como é parcialmente confirmado pelo meu uso pessoal (embora a estatística seja limitada) do indicador "ScientificTrade", que se baseia nessa abordagem de engenharia e utiliza a extrapolação de Fourier para previsões. Claro, este indicador ainda precisa de aperfeiçoamento, e no momento seu principal defeito está relacionado ao uso de um aparato matemático de previsão não suficientemente preciso.