外国為替平均回帰戦略のためのカルマンフィルター

はじめに

カルマンフィルターは、価格変動のノイズを除去して金融時系列の真の状態を推定するために、アルゴリズム取引で用いられる再帰的なアルゴリズムです。新しい市場データに基づいて予測を動的に更新するため、平均回帰のような適応型戦略において非常に有用です。本記事ではまず、カルマンフィルターの計算方法と実装について紹介します。次に、このフィルターをクラシックな平均回帰型の外国為替(FX)戦略に適用する例を示します。最後に、異なる通貨ペアにおいてカルマンフィルターと移動平均を比較し、さまざまな統計分析をおこないます。

カルマンフィルター

カルマンフィルターは、1960年にルドルフ・E・カルマンによって提唱された最適な再帰推定器であり、動的システムの追跡と予測に用いられます。元々は航空宇宙や制御システム向けに開発されましたが、現在では金融、ロボティクス、信号処理など幅広い分野で応用されています。このフィルターは、システムの次状態を推定する「予測ステップ」と、新しい観測値に基づいて推定を更新しノイズを最小化する「更新ステップ」の2段階で動作します。 

アルゴリズム取引の分野では、移動平均や線形回帰モデルと同様に、トレーダーが通常使用する一般的なレジームフィルターとして理解できます。カルマンフィルターは新しいデータに動的に適応し、ノイズを低減しながらリアルタイムで効率的に推定値を更新できるため、市場のレジームシフト検出に効果的です。ただし、線形ダイナミクスを前提としており、パラメータの慎重な調整が必要で、急激な変化の検出に遅れが生じる場合や、移動平均などの単純なフィルターに比べて計算負荷が高いという欠点もあります。

アルゴリズム取引でのカルマンフィルターの主な用途例は以下の通りです。

• 平均回帰取引： 推定価格と現在価格の差をエントリーフィルターとして利用
• ペアトレード： 相関のある資産間のスプレッドを動的に推定し、市場状況の変化に応じてヘッジ比率を調整
• トレンドフォロー： 短期的なノイズを除去し、長期的な価格トレンドをより正確に検出
• ボラティリティ推定： リスク管理やポジションサイズ決定のために、市場ボラティリティの適応的な推定を提供

カルマンフィルターの計算式は以下の通りです。

複雑な計算式を簡単に理解するために、まずは視覚的な例を見てみましょう。

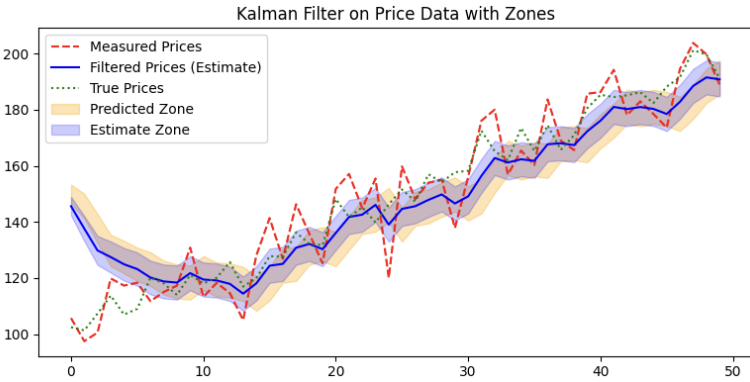
カルマンフィルターは、ノイズを含む観測値と予測値に基づいて、真の価格の推定値を更新する仕組みで、通常は以下の3つのステップで動作します。

1. 予想：フィルターは最初に価格の初期推定値（予測価格）とその不確実性（予測共分散）を設定します。これはオレンジ色の「予測ゾーン」として示され、前回の推定値とプロセスノイズを考慮したうえで、真の価格が存在すると予想される範囲を表しています。

2. 更新：新しい価格データ（観測価格）が得られた時、カルマンフィルターはそれを予測価格と比較します。次に「カルマンゲイン」（紫色の線）を計算し、新しい観測値と予測値のどちらにどれだけの重みを置くかを決定します。観測データが非常にノイズが多い場合は、予測値をより信頼します。 

3. 推定：フィルターは新しい観測値を取り入れて予測価格を更新します。更新後の価格は「推定ゾーン」（青色）で示され、予測時よりも不確実性が減少しています。このゾーンは推定が精緻になるにつれて狭くなります。 

ここで、予測の不確実性は観測値と予測値の共分散で表されます。 共分散が大きいほど推定の信頼度が低く、小さいほど高いことを意味します。観測データが信頼できる場合、カルマンゲインは高くなり、新しいデータをより重視して不確実性が縮小します。一方、ノイズが多い観測の場合はカルマンゲインが低くなり、前回の予測に依存します。

ノイズの大きさは分散で定義され、具体的には観測分散とプロセス分散があります。これらは共分散のように自動調整されるものではなく、カルマンフィルターの滑らかさの度合いを決めるためにあらかじめ設定します。

以下に、分散の値が曲線の滑らかさに与える影響の例を示します。

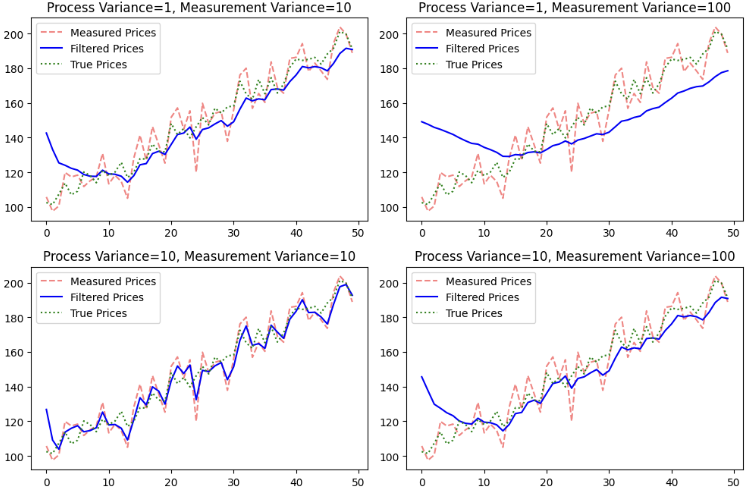
一般的に、プロセス分散(Q)はモデルが時間経過に伴って真の状態がどれだけ変化すると予想しているかを表し、観測分散(R)は得られたデータの信頼度を示します。 Qが大きいとフィルターは急激な変化に対して敏感に反応しますが、その分変動が大きくなります。 Rが大きいと過去の推定値をより信頼して予測を滑らかにしますが、その代わりに調整が遅れる傾向があります。低いQと適度なRの組み合わせは安定した予測をもたらし、高いQと低いRの組み合わせは反応性が高いもののノイズが多くなります。

戦略の実装

平均回帰戦略は、一般的に「売られ過ぎで買い、買われ過ぎで売り、価格が平均に戻ったら決済する」というアプローチを取ります。この戦略は、価格データが基本的に安定しており、極端な水準に長時間留まらないという前提に基づいています。価格が一方の極端な状態にある場合、最終的には均衡点に戻ると期待されます。この理論は特に外国為替のような準定常的データに当てはまり、長年にわたり平均回帰戦略で利益を上げてきました。

今回のアプローチは、100期間のボリンジャーバンド（偏差2.0）を使って以下のルールで定量化します。詳細な計画は次のとおりです。

• 最終の終値が下部バンドを下回ったら買い（ロングエントリー）
• 最終の終値が上部バンドを上回ったら売り（ショートエントリー）
• 価格が中間バンドを横切ったらポジションをクローズ（決済）
• オーバートレードを避けるため、同時に保有するポジションは1つのみ
• 平均回帰戦略でよく見られるファットテールリスク（英語）を回避するため、ストップロス幅は価格の1%に設定

取引対象は15分足のFX通貨ペアを想定しています。これは、十分な取引頻度と質を両立できる一般的な時間枠です。

まずは必要な関数を定義してから、取引ロジックを組むのが効率的です。今回は買い・売りの関数を以下のように実装します。

#include <Trade/Trade.mqh>
CTrade trade;
//+------------------------------------------------------------------+
//| Buy Function                                                     |
//+------------------------------------------------------------------+
void executeBuy(string symbol) {
       double ask = SymbolInfoDouble(symbol, SYMBOL_ASK);
       double lots=0.01;
       double sl = ask*(1-0.01);
       trade.Buy(lots,symbol,ask,sl);
}

//+------------------------------------------------------------------+
//| Sell Function                                                    |
//+------------------------------------------------------------------+
void executeSell(string symbol) {      
       double bid = SymbolInfoDouble(symbol, SYMBOL_BID);
       double lots=0.01;
       double sl = bid*(1+0.01);
       trade.Sell(lots,symbol,bid,sl);     
}

次に、グローバル変数と初期化関数をここで定義します。これにより、EAのマジックナンバーと、後で使用するボリンジャーバンドのハンドルが初期化されます。

input int Magic = 0;
input int bbPeriod = 100;
input double d = 2.0;

int barsTotal = 0;
int handleMa;

//+------------------------------------------------------------------+
//| Initialization                                                   |
//+------------------------------------------------------------------+
int OnInit()
{   handleBb = iBands(_Symbol,PERIOD_CURRENT,bbPeriod,0,d,PRICE_CLOSE);  
    trade.SetExpertMagicNumber(Magic);
    return INIT_SUCCEEDED;
}

最後に、OnTick()関数内で以下のようにして、取引ロジックをティックごとではなくバーごとにのみ処理するようにします。

int bars = iBars(_Symbol,PERIOD_CURRENT);
  
if (barsTotal!= bars){
   barsTotal = bars;

ボリンジャーバンドの現在値を取得するために、ハンドルから値をコピーして格納できるバッファ配列を作成します。

double bbLower[], bbUpper[], bbMiddle[];
CopyBuffer(handleBb,UPPER_BAND,1,1,bbUpper);
CopyBuffer(handleBb,LOWER_BAND,1,1,bbLower);
CopyBuffer(handleBb,0,1,1,bbMiddle);

このチェックは、取引口座内のすべての現在保有中のポジションをループして、この特定のEAによって開かれたポジションかどうかを確認します。もし既にこのEAが開いたポジションが存在する場合、NotInPosition 変数をfalseに設定します。また、中間バンドに価格が戻ったポジションについては、すべて決済します。

bool NotInPosition = true;
for(int i = 0; i<PositionsTotal(); i++){
    ulong pos = PositionGetTicket(i);
    string symboll = PositionGetSymbol(i);
    if(PositionGetInteger(POSITION_MAGIC) == Magic&&symboll== _Symbol){
       NotInPosition = false;
       if((PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY&&price>bbMiddle[0])
       ||(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL&&price<bbMiddle[0]))trade.PositionClose(pos);  
  }
}  

最終的な取引ロジックは次のように実行されます。

if(price<bbLower[0]&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&NotInPosition) executeSell(_Symbol);

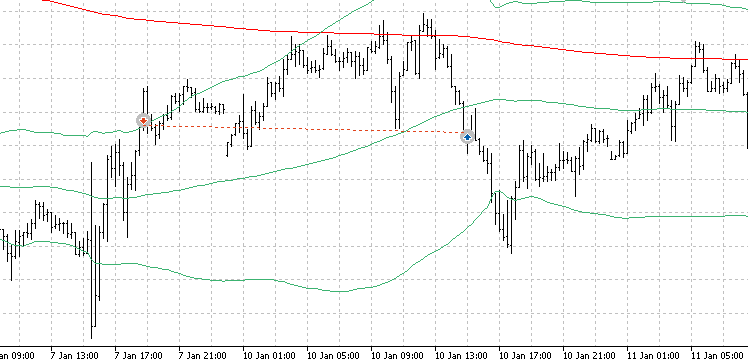
EAをコンパイルし、ストラテジーテスタービジュアライザーに移動して、EAが期待どおりに動作しているかどうかを確認します。

ビジュアライザーでの典型的な取引は次のようになります。

次に、MetaEditorに戻り、レジームフィルターを実装します。

まず、500期間のEMAについては、エントリー時に平均回帰戦略がトレンドと一致するように、追加の確認として以下のコードを元のEAに追加します。

int handleMa;
handleMa = iMA(_Symbol,PERIOD_CURRENT,maPeriod,0,MODE_EMA,PRICE_CLOSE);
 
double ma[];
CopyBuffer(handleMa,0,1,1,ma);
    
if(price<bbLower[0]&&price>ma[0]&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&price<ma[0]&&NotInPosition) executeSell(_Symbol);

 その後、カルマンフィルターの値を取得するための関数を実装します。

//+------------------------------------------------------------------+
//| Kalman Filter Function                                           |
//+------------------------------------------------------------------+
double KalmanFilter(double price,double measurement_variance,double process_variance)
{
    // Prediction step (state does not change)
    double predicted_state = prev_state;
    double predicted_covariance = prev_covariance + process_variance;

    // Kalman gain calculation
    double kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance);

    // Update step (incorporate new price observation)
    double updated_state = predicted_state + kalman_gain * (price - predicted_state);
    double updated_covariance = (1 - kalman_gain) * predicted_covariance;

    // Store updated values for next iteration
    prev_state = updated_state;
    prev_covariance = updated_covariance;

    return updated_state;
}

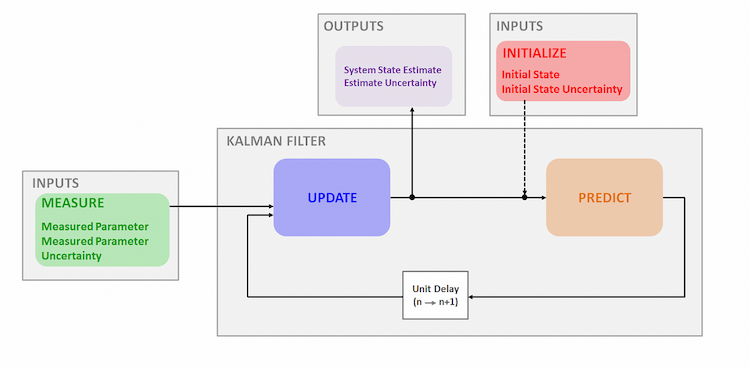
この関数は、こちらの図のような再帰手順に従います。

EAにカルマンレジームフィルターを実装するには、OnTick()関数に次の行を追加します。

double kalman = KalmanFilter(price,mv,pv);
if(price<bbLower[0]&&price>kalman&&NotInPosition) executeBuy(_Symbol);
if(price>bbUpper[0]&&price<kalman&&NotInPosition) executeSell(_Symbol);

カルマンフィルターは、真の価格の推定値を継続的に更新し、ノイズを平滑化しながら価格変動に適応していく仕組みで、基本的には価格予測器として機能します。価格がボリンジャーバンドの下部バンドを下回った場合、市場が売られ過ぎであり平均回帰が期待されるシグナルとなります。ここでは、カルマンフィルターを反転の確認として利用します。売られ過ぎの局面で、価格がカルマン推定値を上回っていれば、すでに価格に上昇の兆しが現れていると判断します。売りのシナリオでは逆の判断となります。

一方、移動平均も一般的なレジームフィルターですが、その役割はカルマンフィルターとはやや異なります。移動平均はトレンドの指標として機能し、価格の移動平均に対する位置関係が現在のトレンド方向を示します。

完全なコードは次のとおりです。

#include <Trade/Trade.mqh>
CTrade trade;

input double mv = 10;
input double pv = 1.0;
input int Magic = 0;
input int bbPeriod = 100;
input double d = 2.0;
input int maPeriod = 500;

double prev_state;       // Previous estimated price
double prev_covariance = 1;  // Previous covariance (uncertainty)
int barsTotal = 0;
int handleMa;
int handleBb;

//+------------------------------------------------------------------+
//| Initialization                                                   |
//+------------------------------------------------------------------+
int OnInit()
{   handleMa = iMA(_Symbol,PERIOD_CURRENT,maPeriod,0,MODE_EMA,PRICE_CLOSE);
    handleBb = iBands(_Symbol,PERIOD_CURRENT,bbPeriod,0,d,PRICE_CLOSE);
    prev_state = iClose(_Symbol,PERIOD_CURRENT,1);  
    trade.SetExpertMagicNumber(Magic);
    return INIT_SUCCEEDED;
}

//+------------------------------------------------------------------+
//| Deinitializer function                                           |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }

//+------------------------------------------------------------------+
//| OnTick Function                                                  |
//+------------------------------------------------------------------+
void OnTick()
{
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
     bool NotInPosition = true;
     double price = iClose(_Symbol,PERIOD_CURRENT,1); 
     double bbLower[], bbUpper[], bbMiddle[];
     double ma[];
     double kalman = KalmanFilter(price,mv,pv);
     
     CopyBuffer(handleMa,0,1,1,ma);
     CopyBuffer(handleBb,UPPER_BAND,1,1,bbUpper);
     CopyBuffer(handleBb,LOWER_BAND,1,1,bbLower);
     CopyBuffer(handleBb,0,1,1,bbMiddle);
     
     for(int i = 0; i<PositionsTotal(); i++){
         ulong pos = PositionGetTicket(i);
         string symboll = PositionGetSymbol(i);
         if(PositionGetInteger(POSITION_MAGIC) == Magic&&symboll== _Symbol){
            NotInPosition = false;
            if((PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_BUY&&price>bbMiddle[0])
            ||(PositionGetInteger(POSITION_TYPE) == POSITION_TYPE_SELL&&price<bbMiddle[0]))trade.PositionClose(pos);  
      }
    }  
    
     if(price<bbLower[0]&&price>kalman&&NotInPosition) executeBuy(_Symbol);
     if(price>bbUpper[0]&&price<kalman&&NotInPosition) executeSell(_Symbol);
    }
}

//+------------------------------------------------------------------+
//| Kalman Filter Function                                           |
//+------------------------------------------------------------------+
double KalmanFilter(double price,double measurement_variance,double process_variance)
{
    // Prediction step (state does not change)
    double predicted_state = prev_state;
    double predicted_covariance = prev_covariance + process_variance;

    // Kalman gain calculation
    double kalman_gain = predicted_covariance / (predicted_covariance + measurement_variance);

    // Update step (incorporate new price observation)
    double updated_state = predicted_state + kalman_gain * (price - predicted_state);
    double updated_covariance = (1 - kalman_gain) * predicted_covariance;

    // Store updated values for next iteration
    prev_state = updated_state;
    prev_covariance = updated_covariance;

    return updated_state;
}

//+------------------------------------------------------------------+
//| Buy Function                                                     |
//+------------------------------------------------------------------+
void executeBuy(string symbol) {
       double ask = SymbolInfoDouble(symbol, SYMBOL_ASK);
       double lots=0.01;
       double sl = ask*(1-0.01);
       trade.Buy(lots,symbol,ask,sl);
}

//+------------------------------------------------------------------+
//| Sell Function                                                    |
//+------------------------------------------------------------------+
void executeSell(string symbol) {      
       double bid = SymbolInfoDouble(symbol, SYMBOL_BID);
       double lots=0.01;
       double sl = bid*(1+0.01);
       trade.Sell(lots,symbol,bid,sl);     
} 

レジームフィルターを変更するには、最終的な売買基準を調整するだけです。

統計分析

EAをコンパイルし、MetaTrader5ターミナルに移動します。左上で[表示]->[銘柄]->[Forex]をクリックし、すべてのメジャーペアとマイナーペアに対して[銘柄を表示する]を選択します。これにより、それらが気配値表示リストに追加され、後のマーケットスキャンに使用されます。

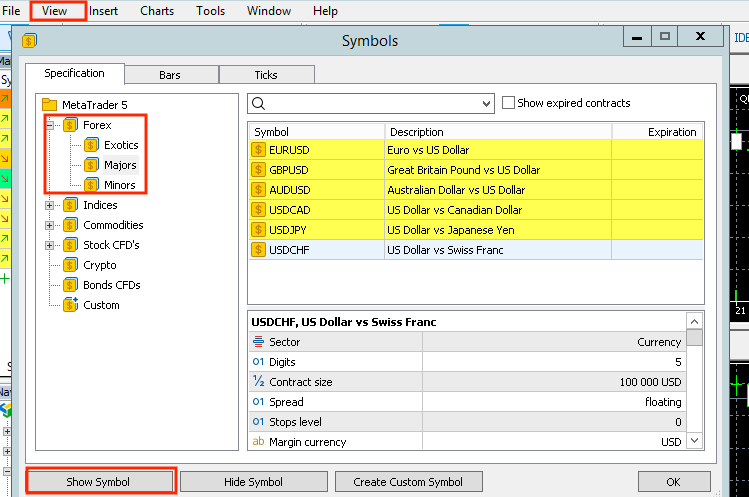
次に、ストラテジーテスターセクションのマーケットスキャナーに移動し、過去3年間のデータを使用して戦略をバックテストします。これにより、レジームフィルターによって、取引する可能性のあるほとんどの外国為替ペアの収益性が向上するかどうかを把握できるようになります。

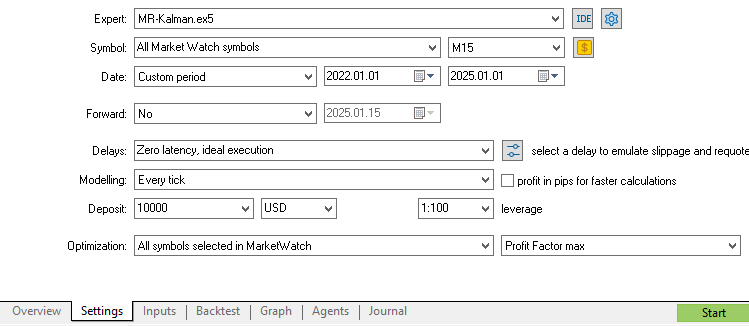
もちろん、フィルタリングされる取引の数は、インジケーターのパラメータによって異なります。本研究では、一般的に用いられるパラメータ値を使用しており、ほぼ同じ数の取引がフィルターされるように設定しています。具体的には、500期間の指数移動平均(EMA)と、カルマンフィルターの観測分散を10、プロセス分散を1としています。より効果的な結果を得るために、読者の皆様にはパラメータの微調整を推奨します。

まず、レジームフィルターを一切使用しない場合の結果をベースラインとしてテストします。平均的には、レジームフィルターを搭載したEAがベースラインの大多数の結果を上回ることが期待されます。

上位のパフォーマンスを示したFX通貨ペアの結果は以下のようになります。

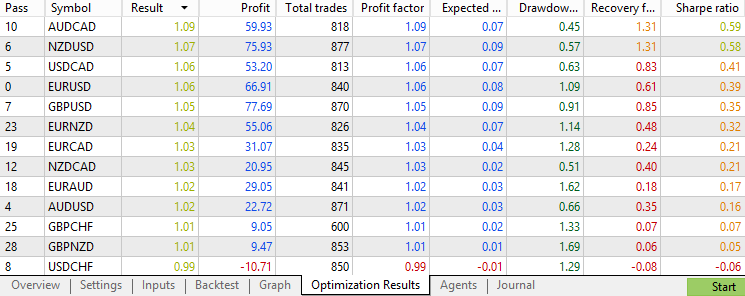
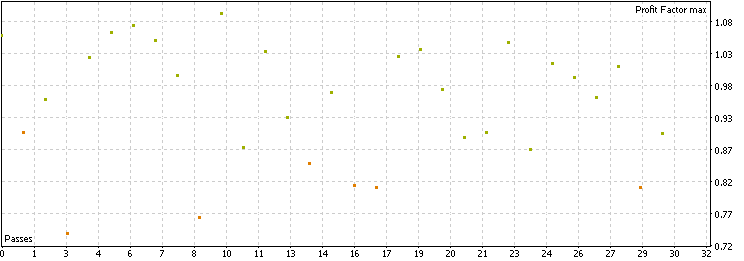
過去3年間で各通貨ペアごとに平均して800回以上の取引が実行されており、十分なサンプル数が得られているため、結論の一般性を示唆しています。プロフィットファクターは主に0.8〜1.1の範囲に分布しており、一定の水準ではあるものの、1.1を超えるペアやシャープレシオが1を超えるペアはありませんでした。全体として、この素の戦略は近年多くのFX通貨ペアで機能しているものの、収益性は特に優れているとは言えません。この点を念頭に置きつつ、フィルターを適用した際のパフォーマンスと比較していきます。

次に、移動平均フィルターを適用した戦略のバックテストをおこないます。結果は次のとおりです。

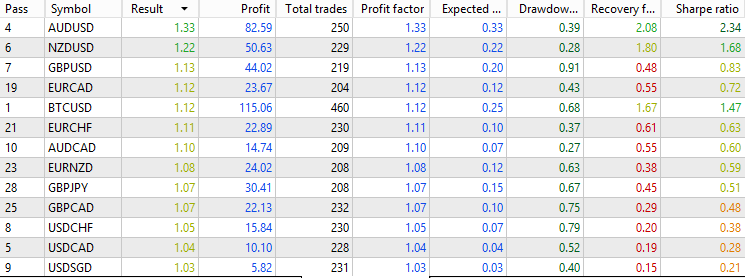
移動平均フィルターを使用することで、元の取引の約70％が除外され、各通貨ペアあたり約250件の取引に絞られました。さらに、フィルター後の取引はベースラインと比較して平均的に質が向上しています。ほとんどのFX通貨ペアは0.9〜1.2のプロフィットファクターの範囲に収まり、最も成績の良いペアはプロフィットファクター1.33、シャープレシオ2.34を記録しました。これは、移動平均をフィルターとして使うことで、この古典的な平均回帰戦略の収益性が全体的に改善されたことを示唆しています。

さて、最も気になるところですが、カルマンフィルターを用いた場合の戦略パフォーマンスを見てみましょう。

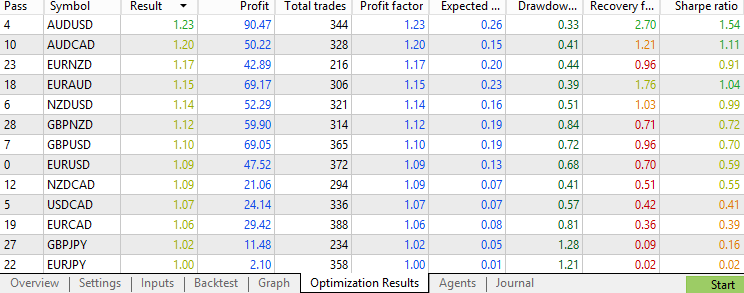
カルマンフィルターは元の取引の約60％を除外し、各通貨ペアあたり約350件の取引を残しました。分布を見ると、ほとんどのプロフィットファクターは0.85〜1.2の範囲に収まっており、移動平均のパフォーマンスに近く、ベースラインの成績よりも優れています。さらに、1.0以上および1.2以上のプロフィットファクターを持つ通貨ペアの数を考慮すると、この戦略において移動平均とカルマンフィルターは平均的な取引の質を向上させる点でほぼ同等であると結論づけられます。今回のケースではカルマンフィルターが移動平均を上回る結果にはならず、複雑さが必ずしもより良いパフォーマンスにつながるわけではないことを示唆しています。

前述したように、カルマンフィルターの使用方法は移動平均とは若干異なるフィルタリングロジックを持っていますが、今回の結果を見る限り、どちらも悪質な取引を除外する点で似た効果を示しています。そこで、それぞれが除外している取引が類似しているかどうかを分析し、カルマンフィルターの効果が単にEMAと同じものなのかを検証します。

参考として、上記2つの条件で最もパフォーマンスが良かったAUDUSD通貨ペアを選択します。

以下はベースラインのバックテスト結果です。

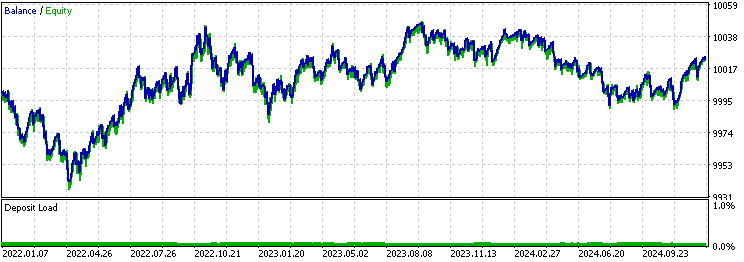
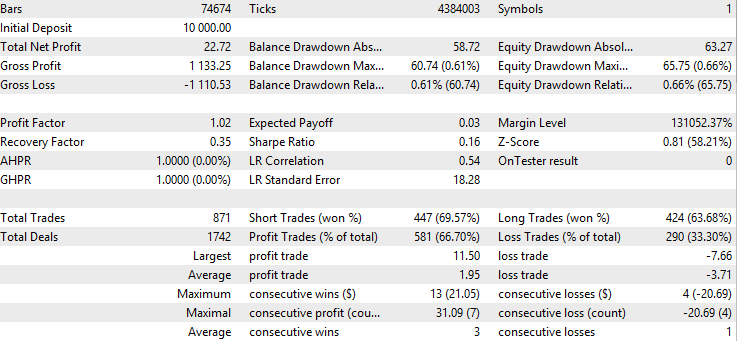
以下は、指数移動平均フィルターのバックテスト結果です。

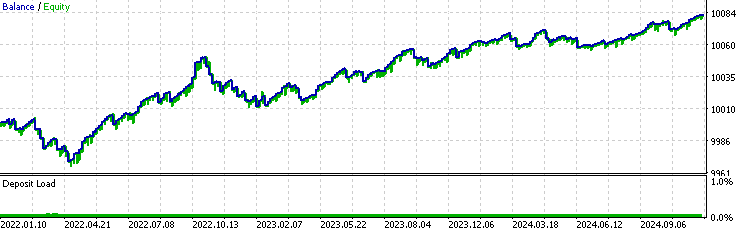
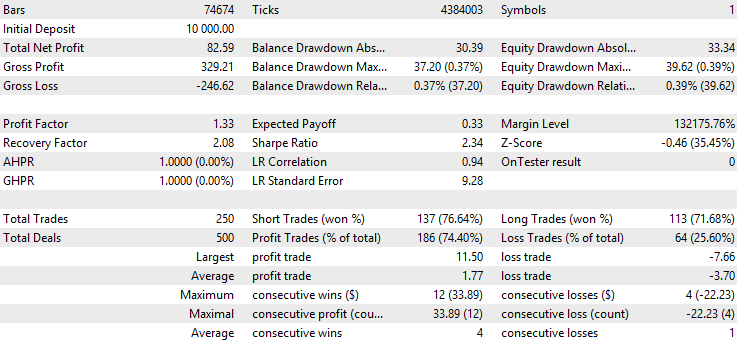
以下は、カルマンフィルターの結果です。

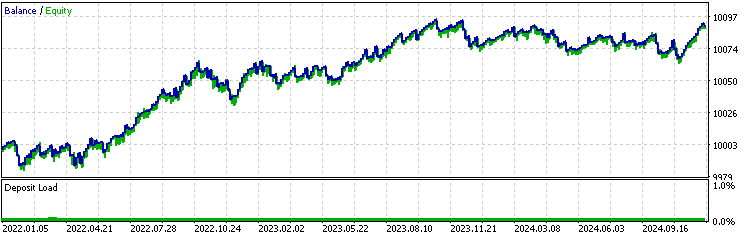
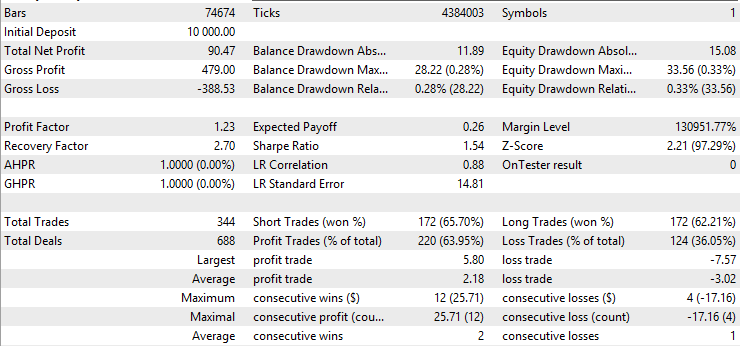
注目すべき点は、移動平均バージョンの勝率が、ベースラインおよびカルマンフィルターバージョンに比べて明らかに高いということです。一方で、平均利益が低く、平均損失が他のバージョンよりも大きいことも確認できます。これはすでに、移動平均を用いたバージョンが、カルマンフィルターとはまったく異なる種類の取引を選択していることを示唆しています。この違いをさらに詳しく分析するために、バックテスト結果ページを右クリックしてバックテストのExcelレポートを取得します。

各レポートでは、Deals記号の行番号を記録します。

次に、PythonまたはJupyter Notebookに入ります。次のコードをコピーして貼り付け、skiprow番号を各ExcelレポートのDeals行番号に変更すれば完了です。

import pandas as pd
import matplotlib.pyplot as plt
from matplotlib_venn import venn3
df1 = pd.read_excel("baseline.xlsx", skiprows=1805)
df2 = pd.read_excel("ma.xlsx", skiprows =563 )
df3 = pd.read_excel("kalman.xlsx",skiprows = 751)
df1 = df1[['Time']][1:-1]
df1 = df1[df1.index % 2 == 0]  # Filter for rows with odd indices
df2 = df2[['Time']][1:-1]
df2 = df2[df2.index % 2 == 0]
df3 = df3[['Time']][1:-1]
df3 = df3[df3.index % 2 == 0]

# Convert "Time" columns to datetime
df1['Time'] = pd.to_datetime(df1['Time'])
df2['Time'] = pd.to_datetime(df2['Time'])
df3['Time'] = pd.to_datetime(df3['Time'])

# Find intersections
set1 = set(df1['Time'])
set2 = set(df2['Time'])
set3 = set(df3['Time'])

# Create the Venn diagram
venn_labels = {
    '100': len(set1 - set2 - set3),  # Only in df1
    '010': len(set2 - set1 - set3),  # Only in df2
    '001': len(set3 - set1 - set2),  # Only in df3
    '110': len(set1 & set2 - set3),  # In df1 and df2
    '011': len(set2 & set3 - set1),  # In df2 and df3
    '101': len(set1 & set3 - set2),  # In df1 and df3
    '111': len(set1 & set2 & set3)   # In all three
}

# Plot the Venn diagram
plt.figure(figsize=(8, 8))
venn3(subsets=venn_labels, set_labels=('Baseline', 'EMA', 'Kalman'))
plt.title("Venn Diagram of Time Overlap")
plt.show()

このコードのロジックは本質的に、行をスキップして偶数インデックスの行を選択することで、各バージョンのポジション終了時刻を3つのデータフレームに保存するというものです。その後、それぞれのデータフレームを集合に変換し、時間が重複しているかどうかを比較することでベン図を作成します。グラフには、各領域における取引数が異なる色で分けて表示されます。なお、戦略が一度に1つのポジションしか持てないように設定されているため、ベースラインにはEMA版やカルマン版が持っているすべての取引が含まれているわけではなく、他のバージョンが持っている一部の取引を逃していることがあります。

出力されたベン図は次の通りです。

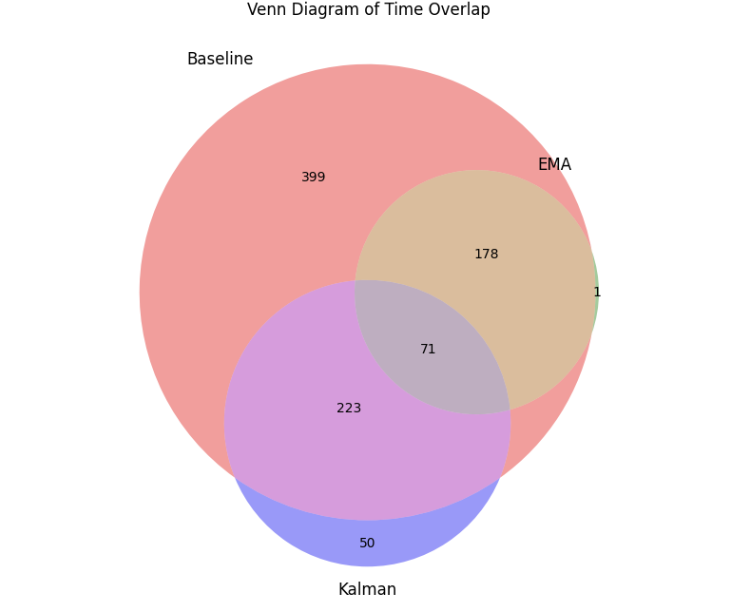
カルマンフィルターと移動平均が重なる領域を観察すると、両バージョンがそれぞれ数百回の取引を行った中で、共通していた取引はわずか71件であることがわかります。これは、両者が元の戦略から同程度の取引を除外しているにもかかわらず、そのフィルタリング効果が非常に異なっていることを示しています。このことから、カルマンフィルターは一般的なトレンドフィルターとは異なる独自のフィルター手法を提供するものであり、その研究と活用の重要性があらためて強調されます。

結論

本記事では、アルゴリズム取引における高度な再帰的アルゴリズム「カルマンフィルター」を紹介しました。まず、その仕組みと実装方法を解説し、視覚的な例や数式を用いて理解を深めました。続いて、FXの平均回帰戦略を開発するプロセスを段階的に示し、MQL5でのカルマンフィルターの実装方法を説明しました。最後に、マーケットスキャン、バックテスト、取引の重複比較といった各種統計的分析を通じて、そのフィルタリング能力を移動平均およびベースライン戦略と比較しながら評価しました。

実際の取引において、カルマンフィルターは大手クオンツ系の取引機関で広く活用されていますが、個人トレーダーの間ではまだあまり知られていません。本記事は、MQL5コミュニティに向けて、カルマンフィルターの実用的な導入方法とその評価手法を提供することを目的としました。今後の戦略開発において、カルマンフィルターをより有効に活用するための一助となれば幸いです。読者の皆様には、ぜひこのフレームワークを実際に試していただき、ご自身の取引手法に取り入れてみることをおすすめします。

ファイルの表

ファイル名	説明
Kalman visualizations.ipynb	この記事で使用した視覚化用のPythonコード
MR-Kalman.mq5	EAコード