Станиславу больше спасибо! Наконец-то написана статья про нейросети с использованием нативных матриц...
К слову. Буквально сегодня обнаружил, что в Документации появился новый блок, касающийся ML.

- www.mql5.com
"Те вещи, которые я забыл, ты еще даже не знаешь" - так мог бы ответить автор на подобную критику.
Там два аспекта и это важно:
1. Исполнение, техническая часть, универсальность, похвалили даже матёрые программисты. И здесь действительно, я не могу и не буду и не пытался критиковать код. Я ведь о другом:
2. Тестирование. Автор указал на работоспособность всех своих моделей. На деле же при нажатии кнопки "Старт" в тестере появляется рандомная картинка на форвард в 2 недели, из 10 нажатий 5 - слив, 5 - прибыль. Естественно, если поставить такое на реал - 50 на 50 жизнеспособность твоего депо. Это не дело. На мои вопросы о том, что это такое и как исправить, автор сказал, что так должно быть, это принцип работы модели. Ну тут я выпал просто, нет слов.
Два месяца пытался завести эти сети, никак не хотели работать на NVIDIA, спасибо Aleksey Vyazmikin, переписал код автора и всё заработало на 3080. А в итоге - неработоспособные модели. Вдвойне обидно.
Но если обидел/задел, прошу извинить, не имел такой цели.
matrix temp; if(!outputs[n].Derivative(temp, of))
При обратном распространении производные функции ожидают получить x, а не активацию x (если только они не изменили это недавно для функций активации, к которым это относится).
Вот пример:
#property version "1.00" int OnInit() { //--- double values[]; matrix vValues; int total=20; double start=-1.0; double step=0.1; ArrayResize(values,total,0); vValues.Init(20,1); for(int i=0;i<total;i++){ values[i]=sigmoid(start); vValues[i][0]=start; start+=step; } matrix activations; vValues.Activation(activations,AF_SIGMOID); //напечатать сигмоид for(int i=0;i<total;i++){ Print("sigmoidDV("+values[i]+")sigmoidVV("+activations[i][0]+")"); } // деривативы matrix derivatives; activations.Derivative(derivatives,AF_SIGMOID); for(int i=0;i<total;i++){ values[i]=sigmoid_derivative(values[i]); Print("dDV("+values[i]+")dVV("+derivatives[i][0]+")"); } //--- return(INIT_SUCCEEDED); } double sigmoid(double of){ return((1.0/(1.0+MathExp((-1.0*of))))); } double sigmoid_derivative(double output){ return(output*(1-output)); }
Также существуют функции активации, для которых вы можете послать больше входов как в активации, так и в деривации, как, например, для elu
Derivative(output,AF_ELU,alpha); Activation(output,AF_ELU,alpha);
В обратном распространении производные функции ожидают получить x, а не активацию x (если только они не изменили это недавно для функций активации, к которым это относится).
Я не совсем понимаю, что вы имеете в виду. В статье есть формулы, которые в точности преобразуются в строки исходного кода. Выходы получаются с помощью Activation call на этапе feedforward, а затем мы берем их производные на backpropagation. Возможно, вы упустили, что индексация выходных массивов в классах происходит со смещением +1 к индексации весов слоев.
Я не совсем понимаю, что вы имеете в виду. В статье есть формулы, которые в точности преобразуются в строки исходного кода. Выходы получаются с помощью вызова Activation на этапе feedforward, а затем мы берем их производные на backpropagation. Возможно, вы упустили, что индексация выходных массивов в классах происходит со смещением +1 к индексации весов слоев.
Да, матрица temp умножается на веса, а затем output[] содержит значения активации.
В заднем реквизите вы получаете производные от этих значений активации, в то время как функция производной MatrixVector ожидает, что вы отправите временные значения
Вот разница в производных
Позвольте мне упростить это:
#property version "1.00" int OnInit() { //--- //предположим, что x - это выход предыдущего слоя (*) весов узла //значение, которое входит в активацию . double x=3; //мы получаем сигмоид по формуле ниже double activation_of_x=sigmoid(x); //и для производной мы делаем double derivative_of_activation_of_x=sigmoid_derivative(activation_of_x); //мы делаем это с помощью matrixvector vector vX; vX.Init(1); vX[0]=3; //мы создаем вектор активаций vector vActivation_of_x; vX.Activation(vActivation_of_x,AF_SIGMOID); //мы создаем вектор для производных vector vDerivative_of_activation_of_x,vDerivative_of_x; vActivation_of_x.Derivative(vDerivative_of_activation_of_x,AF_SIGMOID); vX.Derivative(vDerivative_of_x,AF_SIGMOID); Print("NormalActivation("+activation_of_x+")"); Print("vector Activation("+vActivation_of_x[0]+")"); Print("NormalDerivative("+derivative_of_activation_of_x+")"); Print("vector Derivative Of Activation Of X ("+vDerivative_of_activation_of_x[0]+")"); Print("vector Derivative Of X ("+vDerivative_of_x[0]+")"); //вы выполняете векторную производную от активации x, которая возвращает неверное значение //vectorMatrix ожидает, что вы отправите x, а не активацию(x). //--- return(INIT_SUCCEEDED); } double sigmoid(double of){ return((1.0/(1.0+MathExp((-1.0*of))))); } double sigmoid_derivative(double output){ return(output*(1-output)); }
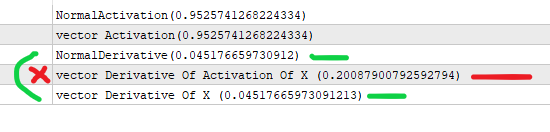
Я понял вашу мысль. Действительно, сигмоидальная производная формулируется через 'y', то есть через сигмоидальное значение в точке x, то есть y(x): y'(x) = y(x)*(1-y(x)). Именно так и реализованы коды в статье.
Ваш тестовый скрипт вычисляет "производную", принимая в качестве входных данных x, а не y, поэтому значения отличаются.
Я понял вашу мысль. Действительно, сигмоидальная производная формулируется через 'y', то есть через сигмоидальное значение в точке x, то есть y(x): y'(x) = y(x)*(1-y(x)). Именно так и реализованы коды в статье.
Ваш тестовый скрипт вычисляет "производную", принимая в качестве входных данных x, а не y, поэтому значения отличаются.
Да, но значения активации передаются в функцию деривации, в то время как она ожидает значения до активации. Вот о чем я говорю.
И вы упустили момент, правильное значение - с x в качестве входа. (правильное значение согласно самой функции mq).
Вы не храните где-то (я думаю) значения весов output_of_previous *, которые должны быть отправлены в функции деривации (согласно самой функции mq, я подчеркну это).
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования

Опубликована статья Нейронные сети обратного распространения ошибки на матрицах MQL5:
Статья описывает теорию и практику применения алгоритма обратного распространения ошибки на MQL5 с помощью матриц. Прилагаются готовые классы и примеры скрипта, индикатора и эксперта.
Как мы увидим далее, MQL5 предоставляет большой набор встроенных активационных функций. Выбор конкретной функции следует делать на основе специфики задачи (регрессия, классификация). Как правило, для любой задачи можно подобрать несколько функций и далее экспериментальным путем найти оптимальную из них.
Популярные функции активации
Активационные функции могут иметь различные диапазоны значений — ограниченные или неограниченные. В частности, сигмоида (3) отображает данные в диапазон [0,+1] (лучше подходит для задач классификации), а гиперболический тангенс — в диапазон [-1,+1] (лучше подходит для задач регрессии и прогнозирования).
Автор: Stanislav Korotky