記事「MQL5行列を使用した誤差逆伝播法によるニューラルネットワーク」についてのディスカッション

新しいコメント
 

新しい記事「MQL5行列を使用した誤差逆伝播法によるニューラルネットワーク」はパブリッシュされました:

この記事では、行列を使用してMQL5で誤差逆伝播法（バックプロパゲーション）アルゴリズムを適用する理論と実践について説明します。スクリプト、インジケータ、エキスパートアドバイザー(EA)の例とともに、既製のクラスが提示されます。

以下で説明するように、MQL5には組み込み活性化関数の大規模なセットがあります。関数は、特定の問題（回帰、分類）に基づいて選択する必要があります。通常、いくつかの関数を選択し、実験的に最適なものを見つけることができます。

良く知られている活性化関数

良く知られている活性化関数

活性化関数は、制限付きまたは無制限のさまざまな値の範囲を持つことができます。特に、シグモイド(3)はデータを範囲[0,+1]にマッピングするもので、分類問題に適しています。双曲線正接はデータを範囲[-1,+1]にマッピングするもので、回帰と予測の問題により適していると考えられます。

作者: Stanislav Korotky

 
詳細な記事と正直な結論に感謝する。
以前のニューラル・ネットワーカーは35の記事で聖杯の写真を載せていたが、実際はコインの裏返しだった。

西側では、誰かが強化学習に基づいて、一貫して利益を上げるニューラルネットワークを作ることに成功したという記事を読んだ。
 

スタニスラフにもっと感謝を！ついにネイティブ行列を使ったニューラルネットワークについての記事が書かれた...。

ところで。ちょうど今日、MLに関するドキュメントに新しいブロックが あることを知りました。

Документация по MQL5: ONNX модели
Документация по MQL5: ONNX модели
  • www.mql5.com
ONNX модели - Справочник MQL5 - Справочник по языку алгоритмического/автоматического трейдинга для MetaTrader 5
 
Ivan Butko #:
詳細な記事と正直な結論に感謝する。
以前のニューラル・ネットワーカーの35本の記事には聖杯の写真が掲載されていたが、実際はコイン・フリップだった。

「私が忘れていること、あなたはまだ知らないこと」-著者はこのような批判にこう答えることができた。

 
Rashid Umarov #:

「私が忘れてしまったことは、あなたがまだ知らないことだ」というのが、このような批判に対する著者の答えかもしれない。



1.実行、技術的な部分、普遍性、成熟したプログラマーにさえ賞賛される。そしてここで、私はコードを批判することはできないし、するつもりもないし、したこともない。

2.テスト。著者は、彼のモデルはすべて動くと指摘している。実際、テスターで「スタート」ボタンを押すと、2週間先までのランダムな画像が表示され、10回押したうち5回がプラム、5回が利益となる。当然ながら、このようなものを実際のデポに置けば、デポの実行可能性は半々だ。これはそうではありません。これは何なのか、どうすれば直るのか、という私の質問に、著者は「こうあるべきだ、これがモデルの原則だ」と言った。
。 2ヶ月間、私はこれらのネットワークを開始しようとしましたが、彼らはNVIDIA上で動作したくなかった、おかげでAleksey Vyazmikinは、著者のコードを書き直し、すべてが3080上で動作しました。そして最後に - 操作できないモデル。それは二重に不快です。

だから、権威に訴えるのは不適切だ。私は彼のプロフェッショナリズムを批判していない。

しかし、もし私があなたを怒らせたなら、謝罪する。そのような意図はなかった。
  
matrix temp;
if(!outputs[n].Derivative(temp, of))

バックプロパゲーションでは、微分関数はxを 受け取ることを期待し、xの活性化は 期待しない（適用する活性化関数が最近変更されたのでなければ）。

以下はその例である：

#property version   "1.00"

int OnInit()
  {
//---
  double values[];
  matrix vValues;
  int total=20;
  double start=-1.0;
  double step=0.1;
  ArrayResize(values,total,0);
  vValues.Init(20,1);
  for(int i=0;i<total;i++){
  values[i]=sigmoid(start);
  vValues[i][0]=start;
  start+=step;
  }
  matrix activations;
  vValues.Activation(activations,AF_SIGMOID);
  //シグモイドを印刷する
  for(int i=0;i<total;i++){
  Print("sigmoidDV("+values[i]+")sigmoidVV("+activations[i][0]+")");
  }
  //デリバティブ
  matrix derivatives;
  activations.Derivative(derivatives,AF_SIGMOID);
  for(int i=0;i<total;i++){
  values[i]=sigmoid_derivative(values[i]);
  Print("dDV("+values[i]+")dVV("+derivatives[i][0]+")");
  }
//---
   return(INIT_SUCCEEDED);
  }

double sigmoid(double of){
return((1.0/(1.0+MathExp((-1.0*of)))));
}

double sigmoid_derivative(double output){
return(output*(1-output));
}

また、例えばeluのように、活性化と導出の両方でより多くの入力を送ることができる活性化関数もあります。

Derivative(output,AF_ELU,alpha);
Activation(output,AF_ELU,alpha);
 
Lorentzos Roussos #:

バックプロパゲーションでは、微分関数はxを 受け取ることを想定しており、xの活性化は 想定していない（適用する活性化関数が最近変更されたのでなければ）。

おっしゃっている意味がよくわかりません。記事の中に数式があり、それが正確にソースコードの行に変換されています。出力はフィードフォワード段階で活性化コールを使って得られ、バックプロパゲーションでその微分を取ります。おそらく、クラス内の出力配列のインデックス付けが、レイヤーの重みのインデックス付けに+1のバイアスがかかっていることを見逃しているのだろう。

 
Stanislav Korotky #:

おっしゃっている意味がよくわかりません。記事の中に数式がありますが、それを正確にソースコードの行に変換しています。出力はフィードフォワード段階でActivationコールを使って得られ、バックプロパゲーションでその微分を取ります。おそらく、クラス内の出力配列のインデックス付けが、レイヤーの重みのインデックス付けに+1のバイアスがかかっていることを見逃しているのだろう。

そうです、temp 行列に重みが掛けられ、output[]に活性化値が格納されます。

MatrixVectorの微分関数はtempの 値を送ることを期待しているのに対して、バックプロップではこれらの活性化値の 微分を取っています。

導関数の違いは以下の通りです

 

簡単に説明しよう：

#property version   "1.00"

int OnInit()
  {
//---
  //xを前のレイヤーの出力と仮定する (*) ノードの重み 
  //アクティベーションに入る値。 
    double x=3;
  //以下の式でシグモイドを求める。 
    double activation_of_x=sigmoid(x);
  //そして微分には次のようにする。 
    double derivative_of_activation_of_x=sigmoid_derivative(activation_of_x);
  //これはmatrixvectorで行う。
    vector vX;
    vX.Init(1);
    vX[0]=3;
    //アクティベーションのベクトルを作成する
    vector vActivation_of_x;
    vX.Activation(vActivation_of_x,AF_SIGMOID);
    // 派生用のベクトルを作成する
    vector vDerivative_of_activation_of_x,vDerivative_of_x;
    vActivation_of_x.Derivative(vDerivative_of_activation_of_x,AF_SIGMOID);
    vX.Derivative(vDerivative_of_x,AF_SIGMOID);
    
    Print("NormalActivation("+activation_of_x+")");
    Print("vector Activation("+vActivation_of_x[0]+")");
    Print("NormalDerivative("+derivative_of_activation_of_x+")");
    Print("vector Derivative Of Activation Of X ("+vDerivative_of_activation_of_x[0]+")");
    Print("vector Derivative Of X ("+vDerivative_of_x[0]+")");
    //xの活性化をベクトル微分しているが、これは間違った値を返す
    //vectorMatrix は、activation(x) ではなく x を送信することを期待する。
//---
   return(INIT_SUCCEEDED);
  }

double sigmoid(double of){
return((1.0/(1.0+MathExp((-1.0*of)))));
}

double sigmoid_derivative(double output){
return(output*(1-output));
}


 
Lorentzos Roussos #:

簡単に説明しよう：

言いたいことはわかった。確かにシグモイド微分はy'を介して、つまり点xにおけるシグモイド値、つまりy(x)を介して定式化されます： y'(x) = y(x)*(1-y(x)).これは記事のコードが実装している方法と同じである。

あなたのテストスクリプトはyではなくxを入力として "微分 "を計算している。

 
Stanislav Korotky #:

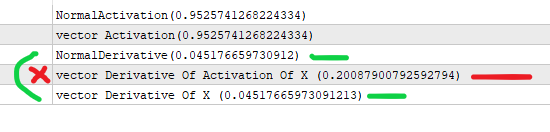
おっしゃるとおりです。確かに、シグモイド微分は「y」を介して、つまり点xにおけるシグモイド値、つまりy(x)を介して定式化されます： y'(x) = y(x)*(1-y(x)).この記事のコードはまさにこのように実装されている。

あなたのテストスクリプトは yではなくxを入力として "微分 "を計算している。

はい、しかし導出関数には活性化値が渡され、導出関数には活性化前の値が渡されます。それが私の言いたいことです。

そして、あなたはそこを見逃している、正しい値はxを入力とするものである。 mqの関数自体によれば正しい値である

あなたはoutput_of_previous * weightsをどこかに保存していない（と思う）。

123
新しいコメント