
El comercio en fórex y sus matemáticas básicas
Introducción
El autor del presente artículo es un desarrollador de estrategias automáticas con más de 5 años de experiencia en el mencionado campo y otro software adicional. En este artículo, trataremos de desvelar aunque sea parcialmente algunos secretos para aquellos que acaban de comenzar a comerciar en Fórex o en cualquier otra bolsa, y también intentaremos responder a las preguntas más emocionantes que cualquier comerciante empieza a plantearse, si es que ha decidio probar finalmente suerte en esta esfera.
Esperamos que este artículo resulte de utilidad para todos, y no solo para los principiantes. Además, no pretendemos enunciar la verdad última, sino más bien exponer la historia real y las consecuencias reales de nuestra investigación.
Algunos de los robots e indicadores descritos se encuentran entre los productos del autor. Pero son solo una pequeña parte. Hemos escrito una amplia variedad de robots usando multitud de estrategias. Trataremos de mostrar cómo este enfoque, con la debida persistencia, nos permitirá entender la verdadera naturaleza del mercado, descubriendo qué estrategias son dignas de atención y cuáles no.
¿Por qué resulta tan difícil comprender dónde entrar y dónde salir?
Dónde entrar y dónde salir: estas son las dos preguntas más importantes. Si recibimos respuesta a estas, ya no necesitaremos saber nada más. ¡Pero, claro, nunca existe una respuesta simple para dichas preguntas! A primera vista, siempre podemos identificar un patrón y seguirlo durante un cierto tiempo, pero ¿cómo podemos distinguirlo sin disponer de herramientas e indicadores especiales? Los patrones más simples que siempre aparecen son TENDENCIA y FLAT. Una tendencia es un movimiento prolongado en una dirección, mientras que el flat supone virajes más frecuentes.
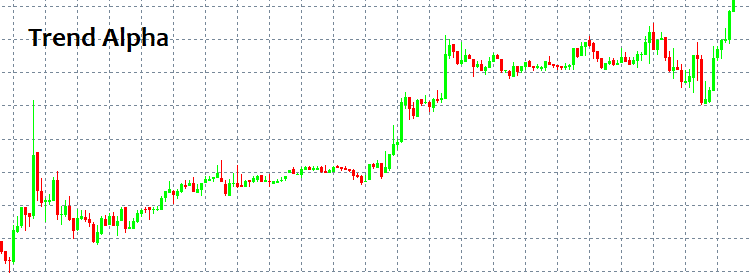
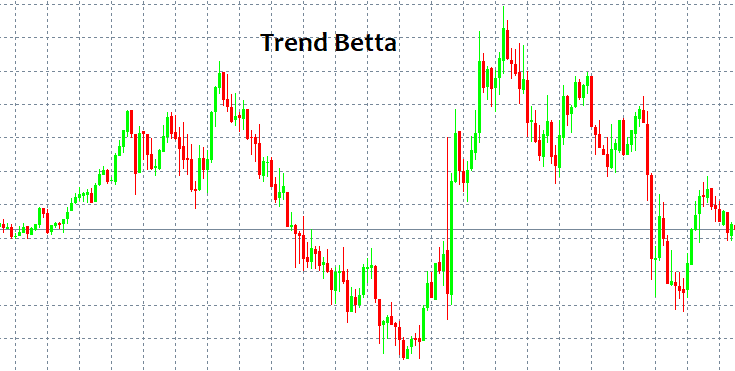

Los seres humanos pueden distinguir estos patrones de inmediato, porque el ojo humano identifica fácilmente todo ello, incluso sin el uso de indicadores. El problema surge cuando un modelo empieza a funcionar, porque solo entonces es visible; pero una vez se pone en marcha, ya no existen garantías de que sea algún tipo de modelo o de que siga desarrollándose. En otras palabras, tras detectar un cierto patrón de comportamiento, no existen garantías de que en la próxima vela el mercado no vaya a desplazarse en la dirección opuesta a la seleccionada, dejando a cero todo nuestro depósito. Esto puede ocurrir con casi cualquier estrategia en la que el lector pueda estar (ingenuamente) seguro al 100%. Trataremos de explicar por qué sucede así usando el lenguaje matemático, como veremos a continuación.
Mecanismos y niveles de mercado
Vamos a hablar un poco sobre los precios y, en general, sobre cómo se mueve el precio. Existen 2 fuerzas en el mercado, la de mercado y la limitada. De la misma forma que existen 2 tipos de órdenes, de mercado y limitadas. Los compradores y vendedores limitados llenan la profundidad de mercado, mientras que los compradores del mercado lo vacían. La profundidad de mercado es simplemente una escala vertical con los precios a los que alguien quiere comprar algo y alguien quiere vender algo. Siempre existe un intervalo entre los vendedores y los compradores limitados, conocido como spread. El spread es la distancia que hay entre el mejor precio de compra y el mejor precio de venta, medido por el número de movimientos mínimos de precio. Los compradores quieren comprar más barato y los vendedores quieren vender más caro. Por este motivo, las órdenes límite de los compradores siempre se encuentran en la parte inferior y los pedidos de los vendedores siempre están en la parte superior. Cuando los compradores y vendedores en el mercado entran en la profundidad de mercado, se vinculan dos pedidos: el limitado y el de mercado, y solo cuando se destruye el pedido limitado, el mercado se mueve.
Cuando en el mercado aparece una orden de mercado abierta, en la mayoría de los casos contiene Stop Loss y Take Profit. Al igual que las órdenes limitadas, estos stops se extienden por el mercado y representan, como resultado, los niveles de aceleración de los precios o su viraje. Todo depende del número y el tipo de los stops, así como del volumen de las transacciones. Conociendo estos niveles, podemos saber dónde y cuánto alcanzará o recuperará el precio.
Las órdenes límite también pueden provocar fluctuaciones y acumulaciones bastante difíciles de superar. La mayoría de las veces aparecen en puntos de precio importantes, como la apertura del día o la apertura de la semana. Cuando comerciamos partiendo de niveles, en la mayoría de las ocasiones significará que comerciaremos desde niveles de orden limitados. A continuación, trataremos de describir brevemente lo que hemos mencionado.
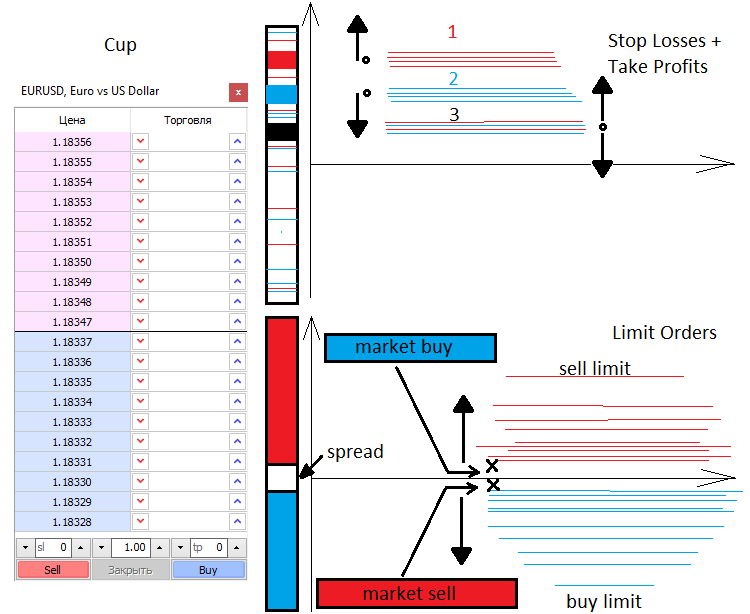
Descripción matemática del mercado
Lo que vemos en la ventana de MetaTrader es una función discreta del argumento t, donde t es el tiempo. La función es discreta porque el número de tics es finito. En el caso actual, los ticks son puntos entre los cuales no existe nada en absoluto. Los ticks son los elementos más pequeños de posible discretización de los precios, los elementos más grandes son las barras, las velas M1, M5, M15, etcétera. En el mercado existen tanto el elemento aleatorio como los patrones. Los patrones pueden poseer varias escalas y duración. No obstante, el mercado, en su mayor parte, es un entorno probabilístico, caótico y casi impredecible. Para entender el mercado, debemos analizarlo usando el prisma de los conceptos de la teoría de probabilidad. Precisamente se necesita la discretización para introducir los conceptos de probabilidad y densidad de la probabilidad.
Para introducir el concepto de esperanza matemática, primero debemos introducir el concepto de evento y grupo completo de eventos:
- Evento C1 — Beneficio, su valor es igual a tp
- Evento C2 — Pérdida, su valor es sl
- P1 — probabilidad del evento C1
- P2 — probabilidad del evento C2
Los eventos C1 y C2 forman un grupo completo de eventos incompatibles (es decir, algunos de estos eventos ocurrirán en cualquier caso), y, por consiguiente, la suma de estas probabilidades será igual a la unidad P2(tp,sl) + P2(tp,sl) = 1. Esta fórmula puede sernos de utilidad.
Poniendo a prueba un asesor experto o una estrategia manual con una apertura aleatoria y usando StopLoss y TakeProfit seleccionados completamente al azar, no obstante, siempre obtendremos un resultado no aleatorio, obtendremos una esperanza matemática igual a "-(Spread)", que indicaría "0" si el margen pudiera establecerse como cero. Lo cual nos lleva a concluir que, sea como sea que coloquemos los stops, obtendremos una expectativa cero en un mercado aleatorio, y no un beneficio o pérdidas accidentales sujetos a la aparición de patrones relacionados. Podemos llegar a la misma conclusión suponiendo que la expectativa (Tick[0].Bid - Tick[1].Bid) también sea igual a cero. Estas son conclusiones bastante simples a las que podemos llegar de muchas maneras.
- M=P1*tp-P2*sl= P1*tp-(1- P1)*sl — para cualquier mercado
- P1*tp-P2*sl= 0 — para un mercado caótico
Esta es la fórmula principal de un mercado caótico que describe la expectativa de un cierre y apertura caóticos de órdenes que se encuentran cubiertas por stops. Una vez resuelta la última ecuación, obtendremos todas las probabilidades que nos interesan, tanto para la aleatoriedad completa como para el caso contrario, siempre que conozcamos los valores de los stops.
Aquí hay solo una fórmula para el caso más simple, cuyo uso podremos extender a cualquier estrategia; eso precisamente vamos a hacer ahora para conseguir que el lector comprenda por completo lo que constituye la esperanza matemática final, de la cual pretendemos lograr que no sea igual a cero. También introduciremos el concepto de factor de beneficio y escribiremos las fórmulas correspondientes.
Ahora supongamos que nuestra estrategia conlleva cerrar no solo con stops, sino también con algunas señales. Para ello, introducimos un nuevo espacio de eventos C3, C4, en el que el primer evento se cerrará con stops, y el segundo, con señales. Estos también forman un grupo completo de eventos inconsistentes, que podemos escribir por analogía:
M=P3*M3+P4*M4=P3*M3+(1-P3)*M4, donde M3=P1*tp-(1- P1)*sl, y M4=Suma(P0[i]*pr[i]) - Suma(P01[j]*ls[j]); Suma( P0[i] )+ Suma( P01[j] ) =1
- M3: esperanza matemática del valor del beneficio al cerrar con una orden stop.
- M4 — esperanza matemática del valor del beneficio al cerrar con una señal.
- P1 , P2 — probabilidad de activación de los stops, siempre que algunos de ellos se active en cualquier caso.
- P0[i] — probabilidad de cerrar una transacción con pr[i] beneficios, siempre que la transacción no haya tocado el stop. i — número de la opción de cierre
- P01[j] — probabilidad de cerrar una transacción con ls[j] pérdidas, siempre que la transacción no haya tocado los stops. j — número de la opción de cierre
es decir, tenemos 2 eventos incompatibles, cuyos resultados se usan para compilar 2 espacios de eventos independientes más, en los que también seleccionamos un grupo completo. Solo que ahora las probabilidades P1, P2, P0 [i], P01 [j] son probabilidades condicionales. Y P3, P4 son probabilidades de hipótesis. La probabilidad condicional representa la probabilidad de que ocurra un evento, siempre que se haya dado una hipótesis. Todo está en rigurosa consonancia con la fórmula de probabilidad total (fórmula de Bayes). Si el lector no está familiarizado, le recomendamos que la lea y estudie detenidamente. En este caso, además, para un comercio completamente incoherente y caótico, M=0.
Ahora nuestra fórmula es mucho más clara y amplia, y tiene en cuenta tanto los stops próximos como las señales cercanas. Pero podemos ir un poco más allá siguiendo esta analogía y escribir una fórmula general que abarque cualquier estrategia que considere incluso los stops dinámicos. Eso precisamente vamos a hacer. Introducimos N eventos más que forman un grupo completo, y que indican la apertura de transacciones abiertas con el mismo StopLoss y TakeProfit. CS[1] .. CS[2] .. CS[3] ....... CS[N] . En este caso, además, exactamente igual PS[1] + PS[2] + PS[3] + ....... +PS[N] = 1.
M = PS[1]*MS[1]+PS[2]*MS[2]+ ... + PS[k]*MS[k] ... +PS[N]*MS[N] , MS[k] = P3[k]*M3[k]+(1- P3[k])*M4[k], M3[k] = P1[k] *tp[k] -(1- P1[k] )*sl[k], M4[k] = Suma(i)(P0[i][k]*pr[i][k]) - Suma(j)(P01[j][k] *ls[j][k] ); Suma(i)( P0[i][k] )+ Suma(j)( P01[j][k] ) =1.
- PS[k] — probabilidad de colocar la k-ésima opción de stop.
- MS[k] — esperanza matemática de transacciones cerradas con k stops.
- M3[k] — esperanza matemática del valor del beneficio al cerrar una orden stop con k stops.
- M4[k] — esperanza matemática del valor del beneficio al cerrar con una señal con k stops.
- P1[k] , P2[k] — probabilidad de activación de los stops, siempre que algunos de ellos se active en cualquier caso.
- P0[i][k] — probabilidad de cerrar una transacción con pr[i][k] beneficios con una señal con k stops. i — número de la opción de cierre
- P01[j][k] — probabilidad de cerrar una transacción con ls[j][k] pérdidas con una señal con k paradas. j — número de la opción de cierre
De la misma manera que en las fórmulas anteriores, más sencillas, M=0 cuando comerciamos sin sentido y sin spread. Lo máximo que puede hacer el lector es modificar la estrategia en sí, pero si esta carece de sentido, simplemente cambiará el equilibrio de todas estas variables, obteniendo aún así "0". Para introducir en este equilibrio un desequilibrio, debemos conocer lo principal: la probabilidad de que el mercado se desplace en una dirección concreta en un segmento fijo de movimiento de precios en puntos o la expectativa de movimiento de precios en un periodo fijo. Precisamentemente por este motivo se seleccionan los puntos de entrada y salida. Si encontramos estos, tendremos una estrategia rentable.
Ahora, vamos a crear una fórmula para el factor de beneficio. PF = Profit/Loss. Por definición, el factor de beneficio es la relación entre beneficios y pérdidas. Si el número es superior a 1, la estrategia será rentable; de lo contrario, no lo será. Esto se puede redefinir utilizando la esperanza matemática. PrF=Mp/Ml. ¿Qué indica la relación entre el beneficio neto esperado y la pérdida neta esperada? Vamos a escribir sus fórmulas.
- Mp = PS[1]*MSp[1]+PS[2]*MSp[2]+ ... + PS[k]*MSp[k] ... +PS[N]*MSp[N] , MSp[k] = P3[k]*M3p[k]+(1- P3[k])*M4p[k] , M3p[k] = P1[k] *tp[k], M4p[k] = Suma(i)(P0[i][k]*pr[i][k])
- Ml = PS[1]*MSl[1]+PS[2]*MSl[2]+ ... + PS[k]*MSl[k] ... +PS[N]*MSl[N] , MSl[k] = P3[k]*M3l[k]+(1- P3[k])*M4l[k] , M3l[k] = (1- P1[k] )*sl[k], M4l[k] = Suma(j)(P01[j][k]*ls[j][k])
Suma(i)( P0[i][k] ) + Suma(j)( P01[j][k] ) =1.
- MSp[k] — esperanza matemática de transacciones cerradas con k stops.
- MSl[k] — esperanza matemática de transacciones cerradas con k stops.
- M3p[k] — esperanza matemática del valor del beneficio al cerrar utilizando una orden stop con k stops.
- M4p[k] — esperanza matemática del valor del beneficio al cerrar con una señal con k paradas.
- M3l[k] — esperanza matemática del valor del beneficio al cerrar utilizando una orden stop con k stops.
- M4l[k] — esperanza matemática del valor del beneficio al cerrar con una señal con k paradas.
Para que el lector lo entienda mejor, describiremos todos los eventos anidados:
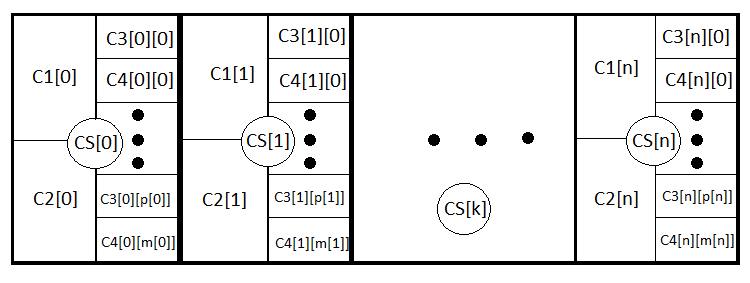
En esencia, son las mismas ecuaciones, aunque a la primera le falta la parte relacionada con las pérdidas, mientras que a la segunda le falta la parte relacionada con los beneficios. En caso de comercio incoherente, PrF = 1 De nuevo con la condición de que el margen sea igual a cero. M, PrF son dos valores totalmente adecuados para valorar la estrategia desde cualquier punto de vista.
En concreto, disponemos de la capacidad de evaluar la tendencia o la naturaleza plana de un determinado instrumento utilizando la propia teoría de probabilidad y combinatoria. Además, también podemos encontrar algunas diferencias de aleatoriedad usando las densidades de distribución de la probabilidad.
Vamos a construir un gráfico de densidad de probabilidad de la distribución de un valor aleatorio para un precio discretizado en un salto H fijo en puntos. Supondremos que si el precio se mueve H en cualquier dirección, se habrá dado un salto. El eje X muestra un valor aleatorio como un movimiento del gráfico de precios vertical medido en el número de saltos. En este caso, es imprescindible que se den n saltos, ya que esta es la única forma de valorar el movimiento general del precio.
- n es el número total de saltos, siempre es constante
- d es el número de saltos para una caída de precio
- u es el número de saltos para aumentar el precio
- s es el movimiento ascendente total en saltos
Tras definir estos valores, calculamos u y d:
Para posibilitar la existencia de los "s" saltos finales hacia arriba (el valor puede ser negativo, lo que indicaría saltos hacia abajo), debemos ofrecer un cierto número de saltos hacia arriba y hacia abajo: "u", "d". En este caso, el movimiento "s" resultante hacia arriba o hacia abajo dependerá de todos los saltos en general:
n=u+d;
s=u-d;
Se trata de un sistema de 2 ecuaciones. Tras resolverlo, obtenemos u y d:
u=(s+n)/2, d=n-u.
No obstante, no todos los valores de "s" son adecuados para un determinado valor de "n". El salto entre los posibles valores de s es siempre igual a 2. Esto se hace para posibilitar "u" y "d" con valores naturales, ya que se usan para combinatoria, o mejor dicho, para calcular combinaciones. Si estos números son fraccionarios, entonces no podremos calcular el factorial, que es la piedra angular de toda combinatoria. A continuación, mostramos todos los posibles escenarios de desarrollo para 18 saltos. El gráfico nos ayuda a percibir visualmente la amplitud de las variantes de los eventos.
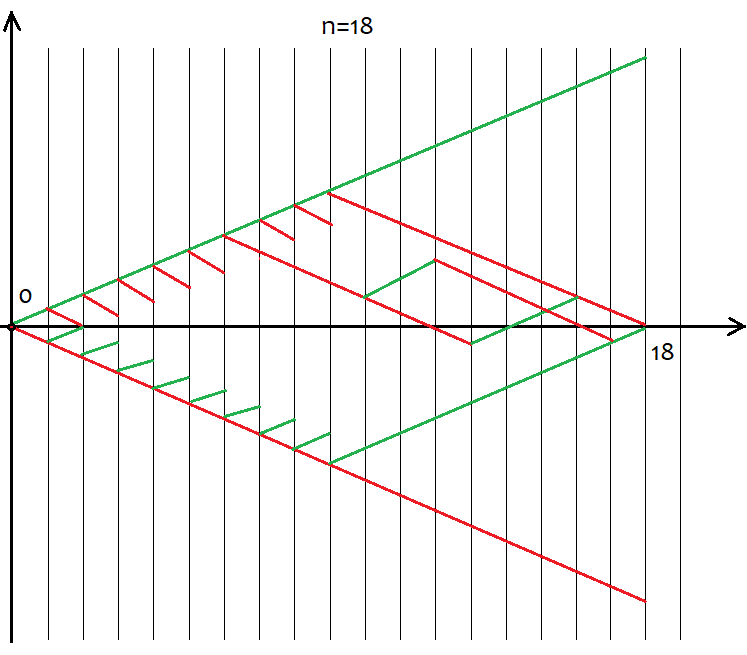
Resulta fácil calcular que, para todas las variantes de formación de los precios, tendremos 2^n de estas, ya que después de cada salto solo hay 2 opciones de movimiento, hacia arriba o hacia abajo. No vamos a tratar de comprender cada una de estas variantes, es imposible. Solo necesitamos saber que tenemos n celdas únicas, de las cuales u y d deben estar arriba y abajo, respectivamente. Además, las variantes en las que existen los mismos números u y d redundan, después de todo, en los mismos s. Para calcular el número total de variantes que darán el mismo "s", podemos usar la fórmula de combinación de la combinatoria С=n!/(u!*(n-u)!), así como su fórmula equivalente С=n!/(d!*(n-d)!). Para diferentes u,d, obtenemos el mismo valor de C. Como se pueden hacer combinaciones tanto en el segmento ascendente como en el descendente, entonces nos planteamos para qué segmentos hacer las combinaciones. Respuesta: para cualquiera de ellos. Porque, a pesar de sus diferencias, estas combinaciones son equivalentes, cosa que demostraremos a continuación utilizando un programa basado en MathCad 15.
Ahora que hemos determinado el número de combinaciones para cada escenario, podemos determinar la probabilidad de una combinación particular (o evento, al gusto de cada uno). P = С/(2^n). Podemos calcular este valor para todos los "s", y la suma de estas probabilidades siempre será igual a 1, ya que una de estas variantes sucederá de todos modos. Usando como base esta matriz de probabilidad, podemos construir el gráfico de densidad de la probabilidad relativa al valor aleatorio "s", considerando que el salto s es 2. En este caso, la densidad en un salto particular se puede obtener simplemente dividiendo la probabilidad por el tamaño del salto s, es decir, por 2. El motivo de ello es que no podemos construir una función continua para valores discretos. Esta densidad sigue siendo relevante medio salto hacia la izquierda y hacia la derecha, es decir, en 1. Esto nos ayuda a encontrar de forma visual los nodos y nos permite realizar la integración numérica. Para los valores negativos de "s", simplemente mostraremos de forma inversa el gráfico en relación con el eje de densidad de la probabilidad. Para n valores pares, la numeración de nodos comienza desde 0, para los impares, desde 1. En el caso de n valores pares, no podemos ofrece valores impares, mientras que en el caso de n valores impares, no podemos ofrecer valores pares. Para aclarar la situación, adjuntamos una captura de pantalla de la aplicación del cálculo:
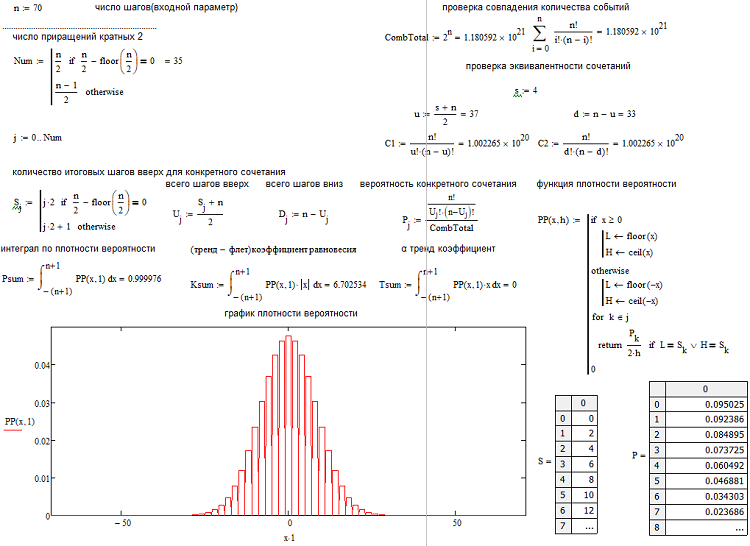
Aquí se muestra todo lo que tenemos que entender. Este programa se adjuntará al artículo como archivo, así que el lector podrá jugar con los parámetros. Al mismo tiempo, muchas personas están interesadas en cómo determinar si ahora hay tendencia o flat. Pensamos en fórmulas propias para cuantificar la tendencia de un instrumento, o su planitud, respectivamente. Al mismo tiempo, la tendencia es diferente: Alpha y Betta. Las dividimos en 2 grupos, alpha para una tendencia de compra o venta; mientras que betta indica solo el deseo de continuar desplazándose sin un movimiento pronunciado hacia la compra o la venta, e indica el esfuerzo por volver al precio inicial.
En general, para muchos, la definición de tendencia y flat es diferente. Vamos a intentar dar una definición más rigurosa a todos estos fenómenos. Y es que una comprensión básica sobre estas cosas y cómo cuantificarlas es suficiente para avivar muchas estrategias que antes se consideraban muertas o vulgares. Tomemos estas fórmulas básicas:
K=Integral(p*|x|)
o
K=Summ(P[i]*|s[i]|)
La primera de ellas es para una variable aleatoria continua, y la segunda, para una discreta. En nuestro caso, para mayor claridad, haremos que el valor discreto sea continuo, y por consiguiente, usaremos la primera fórmula. La integral va de menos a más infinito. Este es el coeficiente de equilibrio o coeficiente de tendencia. Cuando lo calculamos para una variable aleatoria, obtenemos un punto de equilibrio en relación al cual podemos comparar la distribución real de la cotización con la referencia. Si Кp > K, el mercado puede considerarse en tendencia, y si Кp < K, el mercado será lateral.
Asimismo, podemos calcular el valor máximo de este coeficiente. Será igual a KMax=1*Max(|x|) o KMax=1*Max(|s[i]|). También podemos calcular el valor mínimo de este coeficiente. Será igual a KMin=1*Min(|x|) = 0 o KMin=1*Min(|s[i]|) = 0. Los puntos medio, mínimo y máximo de KMid son todo lo que necesitamos para valorar la tendencia o el flat del área analizada en tanto por ciento.
if ( K >= KMid ) KTrendPercent=((K-KMid)/(KMax-KMid))*100 else KFletPercent=((KMid-K)/KMid)*100.
Pero esto resulta todavía insuficiente para caracterizar por completo la situación. Aquí es donde acude en nuestra ayuda el segundo coeficiente T=Integral(p*x), T=Summ(P[i]*s[i]). Básicamente, muestra la esperanza matemática de los saltos ascendentes y, al mismo tiempo, es un indicador de la tendencia alfa. Tp> 0 indica una tendencia de compra, mientras que Tp < 0 indica una tendencia de venta, es decir, T=0 es para el paseo aleatorio.
Encontramos el valor máximo y mínimo del coeficiente: TMax=1*Max(x) o TMax=1*Max(s[i]); el mínimo en valor absoluto es igual al máximo, pero es simplemente negativo TMin= - TMax. Si medimos el porcentaje de la tendencia alfa de 100 a -100, podemos escribir ecuaciones para calcular un valor similar al anterior:
APercent=( T /TMax)*100.
Si el porcentaje es positivo, la tendencia será alcista; si es negativo, la tendencia será bajista. En general, pueden darse casos mixtos. Pueden existir tanto alfa flat como alfa de tendencia, pero no una tendencia y un flat simultáneamente. O lo uno, o lo otro. A continuación, mostramos una ilustración gráfica de lo anteriormente mencionado, así como ejemplos de gráficos de densidad construidos para varios saltos.
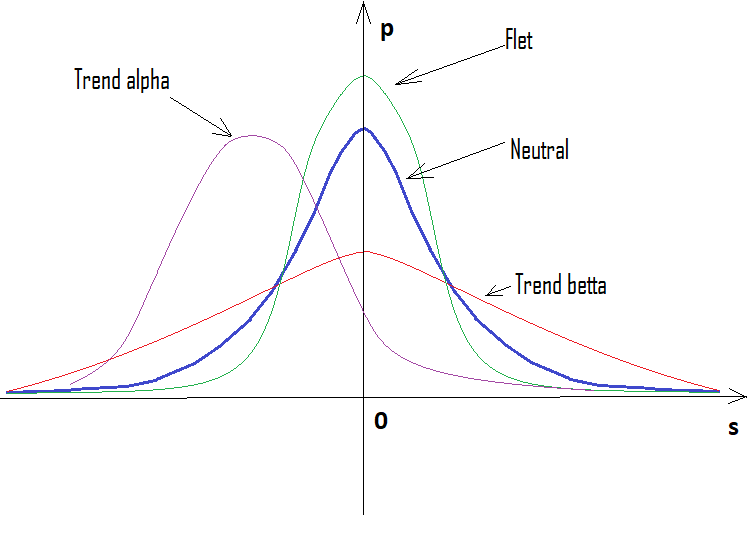
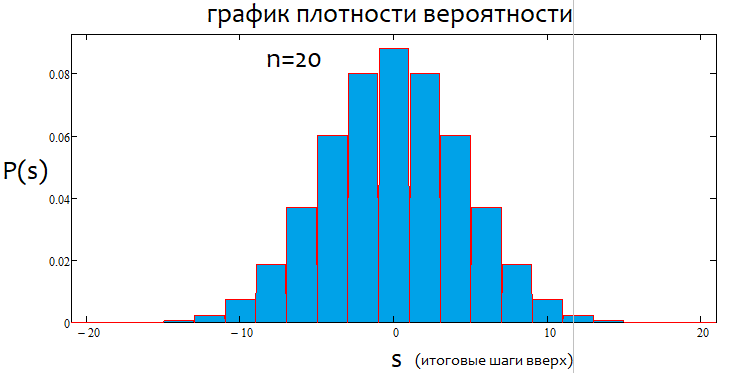
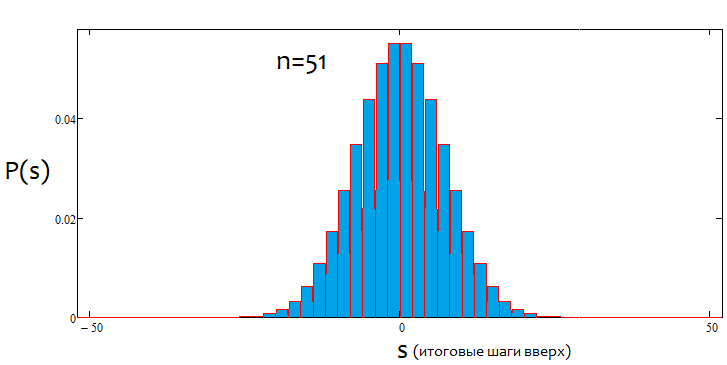
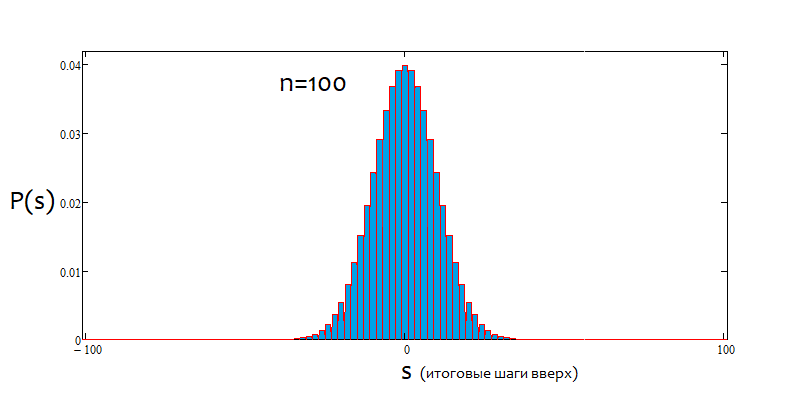
Como podemos ver, a medida que aumenta el número de saltos, el gráfico se vuelve más estrecho y alto. Para cada número de saltos, los valores alfa y beta correspondientes serán diferentes, al igual que el patrón de distribución en sí mismo. Al modificar el número de pasos, debemos volver a calcular la distribución de referencia.
Podemos usar todas estas fórmulas para construir sistemas comerciales automatizados; también podemos crear indicadores basados en estos algoritmos. Algunos tráders ya han implementado estas cosas en sus asesores. Además, es mejor usar este análisis que no hacerlo. Los lectores familiarizados con las matemáticas tendrán inmediatamente ideas sobre cómo aplicar esto. Y aquellos a quienes, por alguna razón, las matemáticas les resulten difíciles, no importa: siempre podrán leer materiales, entenderlos e intentar implementarlos. Todo saldrá bien.
Escribimos un indicador simple
En esta parte del artículo, convertiremos nuestra investigación matemática más sencilla en un indicador que nos ayudará con la selección de los puntos de entrada al mercado, y que también servirá de base para la redacción de asesores. Escribiremos nuestro indicador en MQL5. El autor sigue siendo de la opinión que el viejo MT4 es mucho mejor que su descendiente. Por consiguiente, el código se adaptará al máximo para la migración a MQL4. En general, creemos lógico usar un enfoque sin problemas innecesarios. Para ello, recurrimos a la POO en el último momento, si vemos que el código se vuelve innecesariamente engorroso e ilegible. Pero en el 90% de los casos, esto se puede evitar. Los pequeños paneles, los botones, la información excesiva en el gráfico, a juicio del autor, todo ello está destinado al consumidor final. Siempre resulta mejor escribir el mínimo requerido. Al igual que en las matemáticas: lo necesario y suficiente.
Vamos a comenzar por los parámetros de entrada del indicador.
input uint BarsI=990;//Bars TO Analyse ( start calc. & drawing ) input uint StepsMemoryI=2000;//Steps In Memory input uint StepsI=40;//Formula Steps input uint StepPoints=30;//Step Value input bool bDrawE=true;//Draw Steps
Cuando el indicador está cargado, podemos efectuar el cálculo inicial de un cierto número de saltos usando como base algunas de las últimas velas del gráfico. También necesitaremos un búfer para guardar los datos sobre nuestros últimos saltos. Los nuevos datos sustituirán a los antiguos. Su tamaño debe ser limitado. Se usará el mismo tamaño para dibujar los saltos en el gráfico. También debemos especificar el número de saltos para los que vamos a construir la distribución y calcular los valores necesarios. Luego tenemos que informar al sistema del tamaño del salto en puntos, y, finalmente, si necesitamos visualizar los pasos. Los saltos se visualizarán con la ayuda de un gráfico.
En cuanto al estilo del indicador, hemos elegido una ventana separada, donde se dibujará la distribución neutral y la situación actual, así como dos líneas, pero con otra línea más en el gráfico. Desafortunadamente, las capacidades de los indicadores no presuponen dibujar en una ventana principal aparte, por lo que hemos tenido que recurrir al dibujado.
Para poder acceder a los datos de las barras, al igual que en MQL4, hemos usado un pequeño truco:
//variable to be moved in MQL5 double Close[]; double Open[]; double High[]; double Low[]; long Volume[]; datetime Time[]; double Bid; double Ask; double Point=_Point; int Bars=1000; MqlTick TickAlphaPsi; void DimensionAllMQL5Values()//set the necessary array size { ArrayResize(Close,BarsI,0); ArrayResize(Open,BarsI,0); ArrayResize(Time,BarsI,0); ArrayResize(High,BarsI,0); ArrayResize(Low,BarsI,0); ArrayResize(Volume,BarsI,0); } void CalcAllMQL5Values()//recalculate all arrays { ArraySetAsSeries(Close,false); ArraySetAsSeries(Open,false); ArraySetAsSeries(High,false); ArraySetAsSeries(Low,false); ArraySetAsSeries(Volume,false); ArraySetAsSeries(Time,false); if( Bars >= int(BarsI) ) { CopyClose(_Symbol,_Period,0,BarsI,Close); CopyOpen(_Symbol,_Period,0,BarsI,Open); CopyHigh(_Symbol,_Period,0,BarsI,High); CopyLow(_Symbol,_Period,0,BarsI,Low); CopyTickVolume(_Symbol,_Period,0,BarsI,Volume); CopyTime(_Symbol,_Period,0,BarsI,Time); } ArraySetAsSeries(Close,true); ArraySetAsSeries(Open,true); ArraySetAsSeries(High,true); ArraySetAsSeries(Low,true); ArraySetAsSeries(Volume,true); ArraySetAsSeries(Time,true); SymbolInfoTick(Symbol(),TickAlphaPsi); Bid=TickAlphaPsi.bid; Ask=TickAlphaPsi.ask; } ////////////////////////////////////////////////////////////
Ahora nuestro código es totalmente compatible con MQL4, así que podremos hacer un análogo de MQL4 a partir de él sin mucha dificultad y con mucha rapidez.
Continuemos. Para describir los saltos, primero necesitamos describir los nodos.
struct Target//structure for storing node data { double Price0;//node price datetime Time0;//node price bool Direction;//direction of a step ending at the current node bool bActive;//whether the node is active }; double StartTick;//initial tick price Target Targets[];//destination point ticks (points located from the previous one by StepPoints)
Además, necesitamos un punto desde el que contar el siguiente salto. El nodo almacena información sobre sí mismo y el salto que termina en él; también existe un componente booleano que dice si el nodo está activo. Solo cuando toda la memoria de la matriz de nodos esté llena de nodos reales, comenzará a calcularse la distribución real, porque se calcula en saltos. Si no hay saltos, significa que no se dará ningún cálculo.
Además, debemos poder actualizar el estado de los saltos en cada tick, y también realizar un cálculo aproximado por barras cuando se inicialice el indicador.
bool UpdatePoints(double Price00,datetime Time00)//update the node array and return 'true' in case of a new node { if ( MathAbs(Price00-StartTick)/Point >= StepPoints )//if the step size reaches the required one, write it and shift the array back { for(int i=ArraySize(Targets)-1;i>0;i--)//fist move everything back { Targets[i]=Targets[i-1]; } //after that, generate a new node Targets[0].bActive=true; Targets[0].Time0=Time00; Targets[0].Price0=Price00; Targets[0].Direction= Price00 > StartTick ? true : false; //finally, redefine the initial tick to track the next node StartTick=Price00; return true; } else return false; } void StartCalculations()//approximate initial calculations (by bar closing prices) { for(int j=int(BarsI)-2;j>0;j--) { UpdatePoints(Close[j],Time[j]); } }
A continuación, vamos a describir los métodos y variables necesarios para calcular todos los parámetros de la línea neutra. Su ordenada representará la probabilidad de una combinación o resultado particular, lo que deseemos. Diremos abiertamente que no es del gusto del autor llamar a esto distribución normal, porque la distribución normal es una cantidad continua y, en este caso, estamos trazando una cantidad discreta. Además, la distribución normal supone la densidad de la probabilidad, no la probabilidad, como en el caso de nuestro indicador. Aquí resulta más conveniente para nosotros construir el gráfico de probabilidad, en lugar del gráfico de densidad.
int S[];//array of final upward steps int U[];//array of upward steps int D[];//array of downward steps double P[];//array of particular outcome probabilities double KBettaMid;//neutral Betta ratio value double KBettaMax;//maximum Betta ratio value //minimum Betta = 0, there is no point in setting it double KAlphaMax;//maximum Alpha ratio value double KAlphaMin;//minimum Alpha ratio value //average Alpha = 0, there is no point in setting it int CalcNumSteps(int Steps0)//calculate the number of steps { if ( Steps0/2.0-MathFloor(Steps0/2.0) == 0 ) return int(Steps0/2.0); else return int((Steps0-1)/2.0); } void ReadyArrays(int Size0,int Steps0)//prepare the arrays { int Size=CalcNumSteps(Steps0); ArrayResize(S,Size); ArrayResize(U,Size); ArrayResize(D,Size); ArrayResize(P,Size); ArrayFill(S,0,ArraySize(S),0);//clear ArrayFill(U,0,ArraySize(U),0); ArrayFill(D,0,ArraySize(D),0); ArrayFill(P,0,ArraySize(P),0.0); } void CalculateAllArrays(int Size0,int Steps0)//calculate all arrays { ReadyArrays(Size0,Steps0); double CT=CombTotal(Steps0);//number of combinations for(int i=0;i<ArraySize(S);i++) { S[i]=Steps0/2.0-MathFloor(Steps0/2.0) == 0 ? i*2 : i*2+1 ; U[i]=int((S[i]+Steps0)/2.0); D[i]=Steps0-U[i]; P[i]=C(Steps0,U[i])/CT; } } void CalculateBettaNeutral()//calculate all Alpha and Betta ratios { KBettaMid=0.0; if ( S[0]==0 ) { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=1;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } else { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } KBettaMax=S[ArraySize(S)-1]; KAlphaMax=S[ArraySize(S)-1]; KAlphaMin=-KAlphaMax; } double Factorial(int n)//factorial of n value { double Rez=1.0; for(int i=1;i<=n;i++) { Rez*=double(i); } return Rez; } double C(int n,int k)//combinations from n by k { return Factorial(n)/(Factorial(k)*Factorial(n-k)); } double CombTotal(int n)//number of combinations in total { return MathPow(2.0,n); }
Todas estas funciones deben llamarse en el lugar correcto. Salvo las dos primeras, todas las funciones aquí están pensadas para calcular los valores de las matrices o implementar algunas funciones matemáticas auxiliares. Las funciones se llaman durante la inicialización junto con el cálculo de la distribución neutra y sirven para establecer los tamaños de nuestras matrices.
A continuación, por analogía, vamos a crear un bloque de código para calcular la distribución real y sus principales parámetros.
double AlphaPercent;//alpha trend percentage double BettaPercent;//betta trend percentage int ActionsTotal;//total number of unique cases in the Array of steps considering the number of steps for checking the option int Np[];//number of actual profitable outcomes of a specific case int Nm[];//number of actual losing outcomes of a specific case double Pp[];//probability of a specific profitable step double Pm[];//probability of a specific losing step int Sm[];//number of losing steps void ReadyMainArrays()//prepare the main arrays { if ( S[0]==0 ) { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)-1); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)-1); ArrayResize(Sm,ArraySize(S)-1); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i+1]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } else { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)); ArrayResize(Sm,ArraySize(S)); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } } void CalculateActionsTotal(int Size0,int Steps0)//total number of possible outcomes made up of the array of steps { ActionsTotal=(Size0-1)-(Steps0-1); } bool CalculateMainArrays(int Steps0)//count the main arrays { int U0;//upward steps int D0;//downward steps int S0;//total number of upward steps if ( Targets[ArraySize(Targets)-1].bActive ) { ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); for(int i=1;i<=ActionsTotal;i++) { U0=0; D0=0; S0=0; for(int j=0;j<Steps0;j++) { if ( Targets[ArraySize(Targets)-1-i-j].Direction ) U0++; else D0++; } S0=U0-D0; for(int k=0;k<ArraySize(S);k++) { if ( S[k] == S0 ) { Np[k]++; break; } } for(int k=0;k<ArraySize(Sm);k++) { if ( Sm[k] == S0 ) { Nm[k]++; break; } } } for(int k=0;k<ArraySize(S);k++) { Pp[k]=Np[k]/double(ActionsTotal); } for(int k=0;k<ArraySize(Sm);k++) { Pm[k]=Nm[k]/double(ActionsTotal); } AlphaPercent=0.0; BettaPercent=0.0; for(int k=0;k<ArraySize(S);k++) { AlphaPercent+=S[k]*Pp[k]; BettaPercent+=MathAbs(S[k])*Pp[k]; } for(int k=0;k<ArraySize(Sm);k++) { AlphaPercent+=Sm[k]*Pm[k]; BettaPercent+=MathAbs(Sm[k])*Pm[k]; } AlphaPercent= (AlphaPercent/KAlphaMax)*100; BettaPercent= (BettaPercent-KBettaMid) >= 0.0 ? ((BettaPercent-KBettaMid)/(KBettaMax-KBettaMid))*100 : ((BettaPercent-KBettaMid)/KBettaMid)*100; Comment(StringFormat("Alpha = %.f %%\nBetta = %.f %%",AlphaPercent,BettaPercent));//display these numbers on the screen return true; } else return false; }
Aquí todo es parecido, pero hay muchas más matrices, ya que el gráfico no siempre se mostrará en el eje vertical. Para eso, necesitamos matrices y variables adicionales, pero en general la lógica resulta simple: calculamos el número de resultados en un caso particular, y luego dividimos por el número total de resultados. Así, obtenemos todas las probabilidades (ordenadas) y las abscisas correspondientes. No vamos a profundizar y analizar cada ciclo, cada variable. Todas estas dificultades, en esencia, son para que luego no haya problemas con la transferencia de valores a los búferes sin trucos innecesarios. Aquí todo es prácticamente igual: determinamos el tamaño de las matrices, y luego las calculamos. Luego calculamos el tanto por ciento de la tendencia alfa y la tendencia beta y lo mostramos en la esquina superior izquierda de la pantalla.
Queda por determinar cómo y dónde lo llamamos.
int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,NeutralBuffer,INDICATOR_DATA); SetIndexBuffer(1,CurrentBuffer,INDICATOR_DATA); CleanAll(); DimensionAllMQL5Values(); CalcAllMQL5Values(); StartTick=Close[BarsI-1]; ArrayResize(Targets,StepsMemoryI);//maximum number of nodes CalculateAllArrays(StepsMemoryI,StepsI); CalculateBettaNeutral(); StartCalculations(); ReadyMainArrays(); CalculateActionsTotal(StepsMemoryI,StepsI); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { CalcAllMQL5Values(); if ( UpdatePoints(Close[0],TimeCurrent()) ) { if ( CalculateMainArrays(StepsI) ) { if ( bDrawE ) RedrawAll(); } } int iterator=rates_total-(ArraySize(Sm)+ArraySize(S))-1; for(int i=0;i<ArraySize(Sm);i++) { iterator++; NeutralBuffer[iterator]=P[ArraySize(S)-1-i]; CurrentBuffer[iterator]=Pm[ArraySize(Sm)-1-i]; } for(int i=0;i<ArraySize(S);i++) { iterator++; NeutralBuffer[iterator]=P[i]; CurrentBuffer[iterator]=Pp[i]; } return(rates_total); }
Como búferes, aquí se usan CurrentBuffer, NeutralBuffer. Para mayor simplicidad, hemos implementado la representación en las velas más cercanas al mercado. Cada probabilidad se encuentra en una barra por separado. Esto nos ha permitido deshacernos de complicaciones innecesarias. Solo tendrá que ampliar o reducir el gráfico y podrá ver todo. No hemos representado las funciones CleanAll() y RedrawAll(). En general, podemos comentarlas y todo funcionará bien, solo que sin dibujado. No hemos incluido aquí el bloque de dibujado. Si el lector así lo desea, podrá consultar el código fuente. No hay nada interesante ahí. El indicador se adjuntará al artículo. El indicador se adjuntará en 2 versiones: para MetaTrader 4 y para MetaTrader 5.
Este será el aspecto que tendrá.
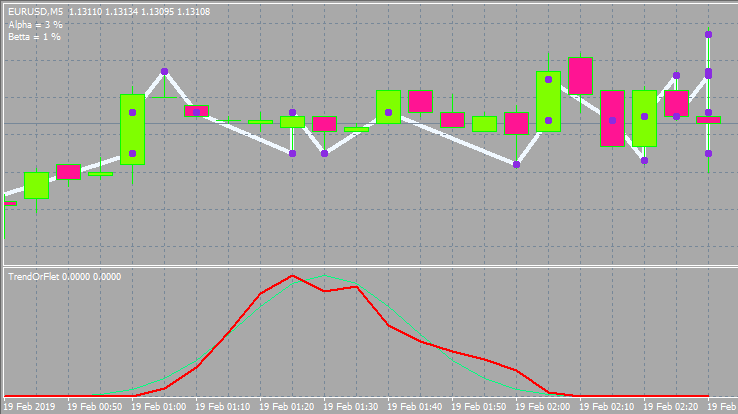
Bueno, y una variante con los diferentes parámetros de entrada y el estilo de la ventana.
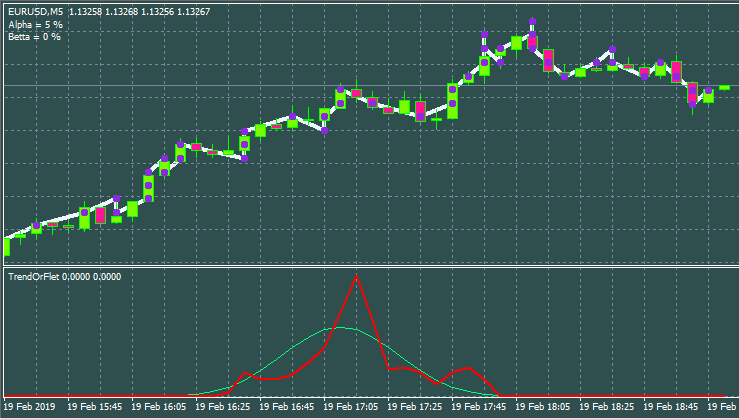
Revisión de las estrategias más interesantes según nuestra versión
Hemos creado los asesores y analizado los de otros programadores. Según nuestra experiencia, sucede algo interesante al utilizar una cuadrícula o un martingale, o ambos. Pero hablando con rigor, tanto el martingale como la cuadrícula tienen una expectativa igual a "0". No se deje engañar por los gráficos al alza, ya que algún día podría sufrir una pérdida estrepitosa. No le recomendamos que se arriesgue. Hay cuadrículas que funcionan y se venden en el Mercado. Funcionan bien e incluso muestran un factor de beneficio de alrededor de 3-6. Parece una figura muy bonita, y además, todo funciona para cualquier pareja de divisas. Pero no resulta fácil crear filtros que permitan ganar. Usando el método descrito anteriormente, simplemente puede filtrar estas señales. Para la cuadrícula, necesitará una tendencia, sin importar la dirección de esta.
El martingale y la cuadrícula son un ejemplo de las estrategias más simples que todos tenemos a la vista y todos conocemos, debido a su sencillez y disponibilidad. Pero no todo el mundo puede usarlos correctamente. Los siguientes en cuanto a dificultad, son los asesores expertos adaptativos. Pueden adaptarse a cualquier cosa, como el flat, una tendencia, o cualquier otro patrón de comportamiento. Toman una parte del mercado, buscan patrones en él y luego comercian durante un corto periodo temporal con la esperanza de que el patrón se mantenga por algún tiempo.
Un grupo aparte está formado por sistemas exóticos con algoritmos misteriosos y poco convencionales que tratan de sacar provecho de la naturaleza caótica del mercado. Dichos sistemas se basan en matemáticas puras y pueden generar beneficios en cualquier instrumento y segmento temporal. Este beneficio no es grande, pero sí estable. Últimamente nos hemos ocupado de estos sistemas. Este grupo también incluye robots basados en la fuerza bruta. La fuerza bruta se puede ejecutar mediante software adicional. En el próximo artículo, mostraremos una versión propia de dicho programa.
El nicho superior lo ocupan los robots basados en redes neuronales y software similar. Estos robots muestran resultados muy diversos y cuentan con el más alto nivel de sofisticación, ya que la red neuronal es un prototipo de inteligencia artificial. Si una red neuronal se ha desarrollado y entrenado de la forma adecuada, puede mostrar una eficacia no igualable por ninguna otra estrategia.
En cuanto al arbitraje, en opinión del autor, sus posibilidades ahora son casi iguales a cero. Tenemos los asesores adecuados, pero su utilidad es nula.
¿Vale la pena el juego?
Alguna gente juega en la bolsa de valores movida por la emoción, otra busca dinero fácil y rápido, y otra solo se interesa por estudiar el mercado, los procesos que comprende, construir fórmulas y teorías. Hay cierta gente que simplemente no tiene otra opción porque no hay vuelta atrás. El autor pertenece más bien a la última categoría. Con todo su conocimiento y experiencia, de momento no ha logrado tener una cuenta estable rentable. Tiene asesores, el simulador respalda su trabajo... Pero no todo es tan sencillo.
Los que creen poder enriquecerse rápidamente, probablemente se vean en la situación opuesta. Después de todo, el mercado no se creó para que gane un simple tráder. Fue creado con el propósito opuesto, y para aquellos que aún no lo han entendido, es hora de ir comprendiéndolo. Pero si usted decide a pesar de todo que puede conseguir su meta, haga acopio de tiempo y paciencia. No verá un resultado rápido. Y si encima no sabe programar o escribir asesores, entonces no tiene prácticamente ninguna posibilidad. Son muchos los pseudo-tráders de todo tipo que afirman algo después de haber realizado entre 20 y 30 transacciones. Entre tanto, los tráders serios escriben un asesor, lo ponen a prueba, y sí, funciona durante un año o dos, vale, pero luego indagan un poco en la historia, y resulta que todo es al revés... Eso, en el mejor de los casos.
Y por lo general, luego nada funciona. En realidad, comerciar manualmente puede ser algo bueno, pero tiene más de arte que de sistema simple y comprensible. Básicamente, toda la información al respecto es solo una especulación desastrosa. Un galimatías contradictorio, en el que algunas cosas tienen sentido, y otras no. Así que no hay motivos para intentar resolver este lío... Patrones, niveles, fibonacci, patrones de velas, otras tonterías... Es posible ganar dinero en el mercado, pero pasará mucho tiempo antes de que eso suceda. En opinión del autor, no vale la pena. Sería mejor trabajar como programador y llevar una vida tranquila. Desde el punto de vista de las matemáticas, el mercado es solo una curvatura, una bidimensional poco interesante. Mejor no mirar estas tristes velas toda la vida ).
¿Existe el Grial y dónde buscarlo?
Creo que el Grial es más que posible. Hay asesores relativamente simples que lo demuestran. Desafortunadamente, la esperanza matemática apenas cubre el spread. Casi todos los desarrolladores tienen estrategias que lo confirman. En el mercado hay muchos robots que pueden llamarse griales en todos los sentidos. Pero ganar dinero con estos sistemas es muy complicado, ya que debemos luchar por cada pip, y también habilitar programas de asociación y retorno del spread. Los griales que ofrecen beneficios considerables y cargas bajas sobre el depósito son raros.
Si desea desarrollar un grial por su cuenta, entonces será mejor fijarse en las redes neuronales. Tienen mucho potencial en términos de beneficio. Por supuesto, puede intentar combinar varios enfoques exóticos y fuerza bruta, pero le recomendamos profundizar directamente en las redes neuronales.
Curiosamente, la respuesta a las preguntas sobre si existe un Grial y dónde buscarlo es bastante sencilla y obvia para el autor después de la tonelada de asesores que ha desarrollado.
Consejos para los tráders sencillos
Todo el mundo quiere tres cosas:
- Conseguir una esperanza matemática positiva
- Incrementar los beneficios si se logra una posición rentable
- Reducir las pérdidas en caso meterse en una posición no rentable
De hecho, el primer punto es la piedra angular. Si el lector tiene una estrategia rentable (da igual si comercia con sus propias manos o con un asesor experto), siempre existe el deseo de intervenir en una transacción de forma que todo salga de forma inesperada. No debe permitir eso. Las situaciones en las que hay muchas menos transacciones ganadoras que perdedoras tienen un impacto psicológico muy significativo. Esto ejerce presión sobre el tráder y reduce todo el sistema a la nada. Lo más importante es no intentar obtener ganancias cuando se encuentre en números rojos. Eso no le dará absolutamente nada salvo ansiedad y pérdidas innecesarias. Debe acordarse de la esperanza matemática independientemente de las pérdidas de la posición actual: lo que importa es cuántas de esas posiciones quedarán al final y cuántas rentables les contrapondremos.
El segundo punto importante es el lote que utilizamos. Si ganamos, reduciremos gradualmente el lote, si perdemos, por el contrario, aumentaremos gradualmente el mismo. Pero solo podemos aumentarlo hasta un valor extremo. Hablamos de un martingale directo e inverso. Si lo piensa bien, podría escribir su propio asesor experto para que comercie solo conforme a las variaciones del lote; un asesor que no pueda ser una cuadrícula o un martingale, sino algo más grande y, además, seguro. Lo más importante es que funcione con todas las parejas de divisas de la historia completa de cotizaciones. Este principio funciona incluso en mercados caóticos, sin importar dónde y cómo entremos. Si le damos el uso adecuado, compensaremos todos los spreads y las comisiones, mientras que con un uso magistral, obtendremos beneficios, incluso si por lo general abrimos posiciones en lugares aleatorios y en una dirección aleatoria.
El tercer punto también es importante. Para reducir las pérdidas y aumentar los beneficios, debemos intentar abrir una posición de compra dentro de una media onda negativa y vender dentro de una media onda positiva. Resulta que una media onda en la mayoría de los casos indica que los vendedores o compradores estaban activos en dicha área, lo que a su vez significa que un cierto porcentaje de ellos estaba en el mercado para abrir posiciones, y las posiciones que estaban abiertas tarde o temprano serán cerradas, moviendo el precio en la dirección opuesta. Por eso el mercado tiene una estructura de onda. Vemos estas ondas por todas partes. Una compra va seguida de una venta, y viceversa. Además, cada tráder cierra las posiciones según los mismos criterios.
Conclusión
Para concluir, debemos decir que, obviamente, todo es subjetivo, y que cada cual analiza el tema desde su punto de vista. Al final, todo depende de cada uno de nosotros, de una forma u otra. Pero, con todas las desventajas y la pérdida de tiempo que sufrimos, también queremos crear nuestro propio súper sistema y recoger los frutos de nuestro tesón. De lo contrario, no tendría en absoluto sentido recurrir a fórex. La experiencia es inestimable, y el dinero, muy poco. Pero hay algo atractivo en esto que no nos permite abandonar esta esfera. Todo el mundo sabe a qué nos referimos, pero pronunciarlo en voz alta sonaría pueril. Por ello, probablemente no lo expresaremos, para no trollear).
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8274
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aproximación por fuerza bruta a la búsqueda de patrones
Aproximación por fuerza bruta a la búsqueda de patrones
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Gracias por este artículo. Nunca se me han dado bien las matemáticas, pero seguiré intentando entenderlas para convertirme en un mejor trader.
¡Gran artículo! Muchas gracias.
Gracias, he escrito un montón de otros artículos desde éste, echar un vistazo y ver si encuentra algo más útil.