外国為替取引の背後にある基本的な数学

はじめに

私は5年以上の経験を持つ自動ストラテジーおよびソフトウェアの開発者です。この記事では、外国為替やその他の取引所で取引を始めたばかりの人に秘密を開かすとともに、最も人気のある取引の質問に答えてみようと思います。

この記事が初心者と経験豊富なトレーダーの両方に役立つことを願っています。また、これは純粋に実際の経験と研究に基づく私のビジョンであることに注意してください。

言及されたロボットとインディケーターのいくつかは私の製品にあります。しかし、これはほんの一部です。私は、さまざまなストラテジーを適用するさまざまなロボットを開発しました。説明されたアプローチがどのように市場の本質への洞察を得ることができるか、そしてどのストラテジーが注意を払う価値があるかを示すことを試みます。

入口と出口を見つけるのがとても難しいのはなぜでしょうか。

市場に出入りする場所がわかれば、おそらく他に何も知る必要はありません。残念ながら、入口/出口ポイントの問題はとらえどころのないものです。一見すると、いつでもパターンを識別して、しばらくそれに従うことができます。しかし、洗練されたツールやインディケーターなしでそれを検出する方法は？最も単純で常に繰り返されるパターンは「トレンド」と「フラット」です。トレンドは一方向への長期的な動きですが、フラットはより頻繁な反転を意味します。

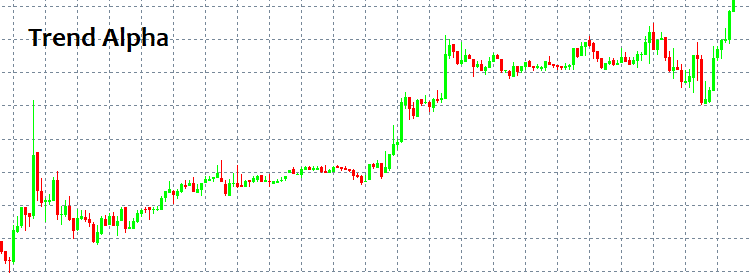
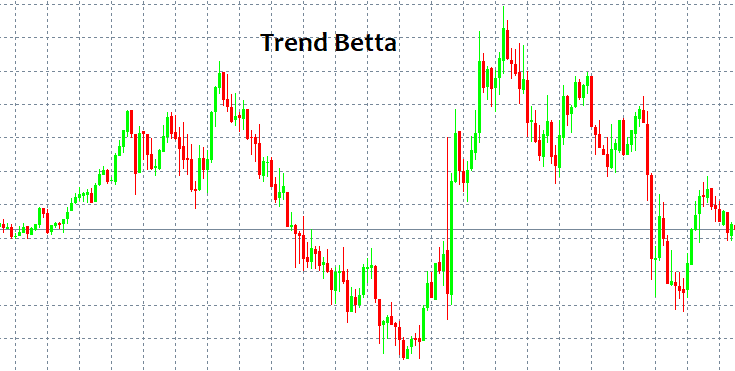
これらのパターンは、インディケーターなしで人間の目にいおって見つけることができるため、簡単に検出できます。ここでの主な問題は、パターンがトリガーされた後にのみパターンを表示できることです。さらに、パターンがあったことを保証することはできません。ストラテジーに関係なく、どのパターンも預金を破壊から救うことはできません。私は数学の言語を使用して考えられる理由を提供しようとします。

市場のメカニズムとレベル

価格設定と市場価格を動かす力について少しお話ししましょう。市場には、成行と指値という2つの力があります。同様に、注文には成行と指値の2種類があります。指値注文の買い手と売り手は市場の深さを狭めますが、成行注文の買い手と売り手はそれを広めます。市場の深さとは基本的に、何かを売買する意思がある人を示す垂直価格スケールです。指値注文の売り手と買い手の間には常にギャップがあります。このギャップはスプレッドと呼ばれます。スプレッドは、最小価格変動の数で測定されたベストの売りと買いの価格間の距離です。買い手は最も安い価格で買いたいのに対し、売り手は最も高い価格で売りたいと考えます。したがって、買い手の指値注文は常に一番下にあり、売り手のものは常に一番上にあります。成行注文の買い手と売り手が市場の深さに入り、2つの注文(指値注文と成行注文)がリンクされます。指値注文がトリガーされると、市場の動きが発生します。

アクティブな注文が表示されると、通常は決済逆指値(S/L)と決済指値(T/P)があります。指値注文と同様に、これらの決済逆指値は市場全体に散らばっており、価格の加速または逆転レベルを形成します。すべては、決済逆指値の量とタイプ、および取引量に依存します。これらのレベルを知ることで、価格がどこで加速または逆転する可能性があるかがわかります。

指値注文は、通過するのが難しい変動やクラスターを形成することもあります。それらは通常、1日または1週間の開始など、価格の重要な点で出現します。レベルベースの取引について議論するとき、トレーダーは通常、指値注文レベルを使用することを意味します。これはすべて、次のように簡単に表示できます。.

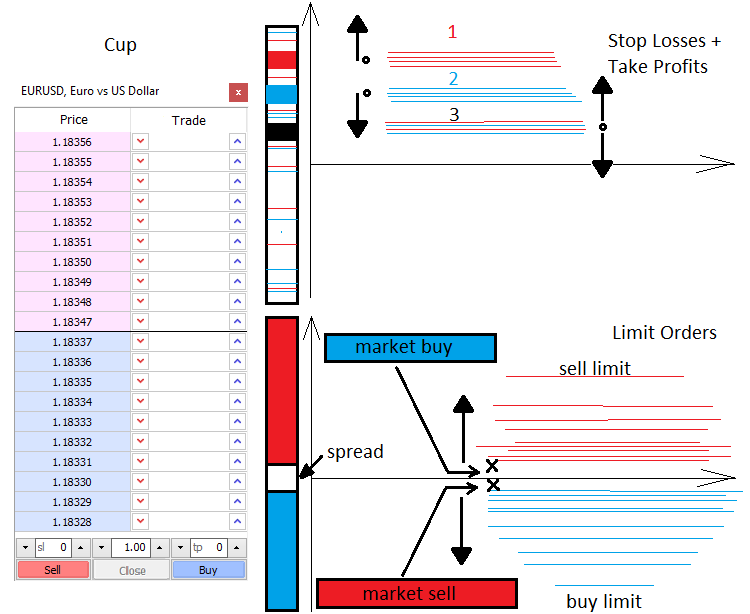
市場の数学的な説明

MetaTraderウィンドウに表示されるのは、t引数の離散関数です。ここでtは時間です。ティック数が有限であるため、関数は離散的です。現在の場合、ティックは間に何も含まれていないポイントです。ティックは可能な価格離散化の最小要素であり、より大きな要素はバー、M1、M5、M15ローソク足などです。市場はランダムとパターンの両方の要素を備えています。パターンは、さまざまなスケールと期間にすることができます。ただし、市場はほとんどの場合、確率的で混沌とした、ほとんど予測不可能な環境です。市場を理解するには、確率論の概念を通して市場を見る必要があります。確率と確率密度の概念を導入するには、離散化が必要です。 

予想される見返りの概念を導入するには、最初に「イベント」および「網羅的イベント」という用語を検討する必要があります。

• C1イベント - 利益、tpに等しい
• C2イベント - 損失、slに等しい
• P1 - C1イベントの確率
• P2 - C2イベントの確率

С1イベントとС2イベントは、対称的なイベントの網羅的なグループを形成します(つまり、これらのイベントの1つはいずれの場合にも発生します)。したがって、これらの確率の合計は1(P2(tp,sl) +  P2(tp,sl) = 1)に等しくなります。この方程式は後で便利になるかもしれません。

EAまたはランダムなオープニング、およびランダムな決済逆指値(S/L)と決済指値(T/P)を使用した手動ストラテジーをテストしている間も、ランダムではない結果が1つ得られ、予想される見返りは「-(スプレッド)」に等しくなります。スプレッドをゼロに設定できる場合、これは0です。これは、決済逆指値に関係なく、ランダム市場で常にゼロの期待見返りが得られることを示唆しています。非ランダム市場では、市場が関連するパターンを特徴としている限り、常に利益または損失を受け取ります。予想される見返り(Tick [0] .Bid- Tick [1] .Bid)もゼロに等しいと仮定することで、同じ結論に達することができます。これらは、多くの方法で到達できるかなり単純な結論です。

• M=P1*tp-P2*sl= P1*tp-(1- P1)*sl  — 任意の市場
  
  
• P1*tp-P2*sl= 0 — カオス的市場
  

これは、決済逆指値を使用してカオス注文の開始と終了の予想される見返りを説明する主要なカオス的市場の方程式です。最後の方程式を解いた後、決済逆指値がわかっている場合、完全なランダム性とその逆の場合の両方で、関心のあるすべての確率を取得します。 

ここで提供される方程式は、任意のストラテジーに一般化できる最も単純なケースのみを対象としています。これはまさに、ゼロ以外にするために必要な最終的な期待見返りを構成するものを完全に理解するために私がやろうとしていることです。また、利益率の概念を紹介し、適切な方程式を書きましょう。

ストラテジーが決済逆指値および他のいくつかのシグナルの両方によって決済することを含むと仮定します。これを行うために、最初のイベントが決済逆指値で終了し、2番目のイベントがシグナルで終了するС3、С4イベント空間を紹介します。それらはまた、反対のイベントの完全なグループを形成するので、類推を使用して次のように書くことができます。

M=P3*M3+P4*M4=P3*M3+(1-P3)*M4, where  M3=P1*tp-(1- P1)*sl, while  M4=Sum(P0[i]*pr[i]) - Sum(P01[j]*ls[j]);  Sum( P0[i] )+  Sum( P01[j] ) =1

• M3 - 逆指値注文として決済したときに予想される見返り。
• M4 - シグナルで決済したときに予想される見返り。
• P1 , P2 — いずれの場合でも、決済逆指値の1つがトリガーされた場合の、決済逆指値アクティブ化の確率。
  
• P0[i] - 決済逆指値がトリガーされていない場合、pr[i] の利益で取引を成立させる確率。i — 決済オプション番号
  
• P01[j] — 決済逆指値がトリガーされていない場合、ls[j]の損失で取引を成立させる確率( j - 決済オプション番号)
  

言い換えれば、2つの反対のイベントがあります。それらの結果は、グループ全体を定義する別の2つの独立したイベント空間を形成します。ただし、確率P1、P2、P0[i]、P01[j]は条件付きであり、P3およびP4は仮説の確率です。条件付き確率は、仮説が発生したときのイベントの確率です。すべてが、全確率の公式(ベイズの公式)に厳密に従っています。よく調べて把握することを強くお勧めします。完全にカオス的な取引の場合、M= 0です。

決済逆指値とシグナルの両方での決済を考慮すると、方程式はより明確で広範になりました。このアナロジーをさらにたどって、動的な決済逆指値さえも考慮に入れるストラテジーの一般式を書くことができます。これが私がやろうとしていることです。完全なグループを形成するN個の新しいイベントを紹介しましょう。つまり、同様の決済逆指値と決済指値を持つ取引を開始します。CS[1] .. CS[2] .. CS[3] ....... CS[N] . 同様に、PS[1] + PS[2] + PS[3] + ....... +PS[N] = 1.

M = PS[1]*MS[1]+PS[2]*MS[2]+ ... + PS[k]*MS[k] ... +PS[N]*MS[N] , MS[k] = P3[k]*M3[k]+(1- P3[k])*M4[k],  M3[k] =  P1[k] *tp[k] -(1- P1[k] )*sl[k], M4[k] =  Sum(i)(P0[i][k]*pr[i][k]) - Sum(j)(P01[j][k] *ls[j][k] );  Sum(i)( P0[i][k]  )+  Sum(j)( P01[j][k]  ) =1.

• PS[k] — k番目の決済逆指値オプションを設定する確率
  
• MS[k]  —  k番目の決済逆指値での成約済み取引の予想される見返り
  
• M3 [k] — k番目の決済逆指値で逆指値注文として決済したときに予想される見返り
• M4[k] — k番目の決済逆指値のシグナルで決済したときに予想される見返り
• P1[k]、P2[k] — いずれの場合でも、いずれかの決済逆指値がトリガーされた場合の決済逆指値アクティブ化の確率
  
• P0[i][k]  — k番目の決済逆指値のシグナルによってpr[i][k]の利益で取引を成立させる確率(i — 決済オプション番号)
  
• P01[j][k]  — k番目の決済逆指値のシグナルによってls[j][k] の損失で取引を成立させる確率(j — 決済オプション番号)

前の(より単純な)方程式同様、カオス的取引とスプレッドがない場合はM=0です。できることのほとんどはストラテジーを変更することですが、合理的な根拠が含まれていない場合は、これらの変数のバランスを変更するだけで、0を取得できます。この望ましくない均衡を破るために、ポイント単位の固定移動セグメント内の任意の方向への市場移動の確率、または特定の期間内の予想価格移動の見返りを知る必要があります。それに応じて出入口が選択されます。出入口を見つけることができれば、有益なストラテジーを持っていることになります。

それでは、利益係数の方程式を作成しましょう。PF = 利益/損失。利益率は、損失に対する利益の比率です。数が1を超える場合、ストラテジーは有益です。超えない場合は、有益ではありません。これは、予想される見返りを使用して再定義できます。PrF=Mp/Ml。これは、予想純損失に対する予想純利益の見返りの比率を意味します。方程式を書いてみましょう。

• Mp = PS[1]*MSp[1]+PS[2]*MSp[2]+ ... + PS[k]*MSp[k] ... +PS[N]*MSp[N] , MSp[k] = P3[k]*M3p[k]+(1- P3[k])*M4p[k] ,  M3p[k] =  P1[k] *tp[k], M4p[k] =  Sum(i)(P0[i][k]*pr[i][k])
  
  
• Ml = PS[1]*MSl[1]+PS[2]*MSl[2]+ ... + PS[k]*MSl[k] ... +PS[N]*MSl[N] , MSl[k] = P3[k]*M3l[k]+(1- P3[k])*M4l[k] ,  M3l[k] =   (1- P1[k] )*sl[k], M4l[k] =  Sum(j)(P01[j][k]*ls[j][k])
  

Sum(i)( P0[i][k] ) +  Sum(j)( P01[j][k]  ) =1.

• MSp [k] — k番目の決済逆指値で成約した取引の予想される見返り
• MSl[k] - k番目の決済逆指値での成約済み取引の予想される見返り
  
• M3p[k] — k番目の決済逆指値で逆指値注文として決済したときに予想される見返り
• M4p[k] — k番目の決済逆指値のシグナで決済したときに予想される見返り
• M3l [k] - k番目の決済逆指値の逆指値注文で決済したときに予想される損失
• M4l [k] — k番目の決済逆指値のシグナルで決済したときに予想される損失

より深く理解するために、ネストされたすべてのイベントについて説明します。

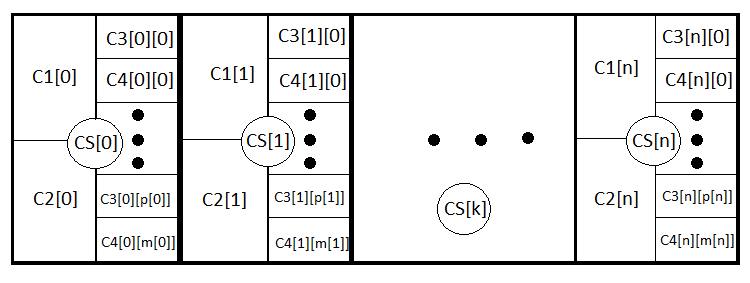
実際、これらは同じ方程式ですが、最初の方程式には損失に関連する部分がなく、2番目の方程式には利益に関連する部分がありません。カオス的取引の場合、スプレッドが再びゼロに等しい場合、PrF = 1です。MとPrFは、あらゆる側面からストラテジーを評価するのに十分な2つの値です。

特に、同じ確率論と組み合わせ論を使用して、特定の商品の傾向またはフラットな性質を評価する機能があります。また、確率分布密度を使用して、ランダム性との違いを見つけることもできます。

ポイント単位の固定Hステップで離散化された価格のランダム値分布確率密度グラフを作成します。価格がHをいずれかの方向に移動した場合、ステップが実行されたと仮定します。X軸は、ステップの数で測定された垂直価格チャートの動きの形式でランダムな値を表示するためのものです。この場合、これが全体的な価格変動を評価する唯一の方法であるため、nステップが不可欠です。

• n — 総ステップ数(定数値)
• d — 値下げのステップ数
• u — 値上げのステップ数
• s — 段階的に上向きに移動する合計

これらの値を定義した後、uとdを計算します。

「s」ステップの合計を上向きに指定するには(値は負の場合、下向きのステップを意味します)、特定の数の上下ステップ(「u」、「d」)を指定する必要があります。最後の「 s 」の上下の動きは、合計ですべてのステップに依存します。

n=u+d;

s=u-d;

これは2つの方程式のシステムです。それを解くと、uとdが得られます。

u=(s+n)/2, d=n-u.

ただし、すべての「s」値が特定の「n」値に適しているわけではありません。可能なs値間のステップは常に2に等しくなります。これは、「u」と「d」が組み合わせ論、またはむしろ組み合わせの計算に使用されるため、自然な値を提供するために行われます。これらの数値が分数である場合、すべての組み合わせ論の基礎である階乗を計算することはできません。以下は、18ステップで考えられるすべてのシナリオです。グラフは、イベントオプションの広さを示しています。

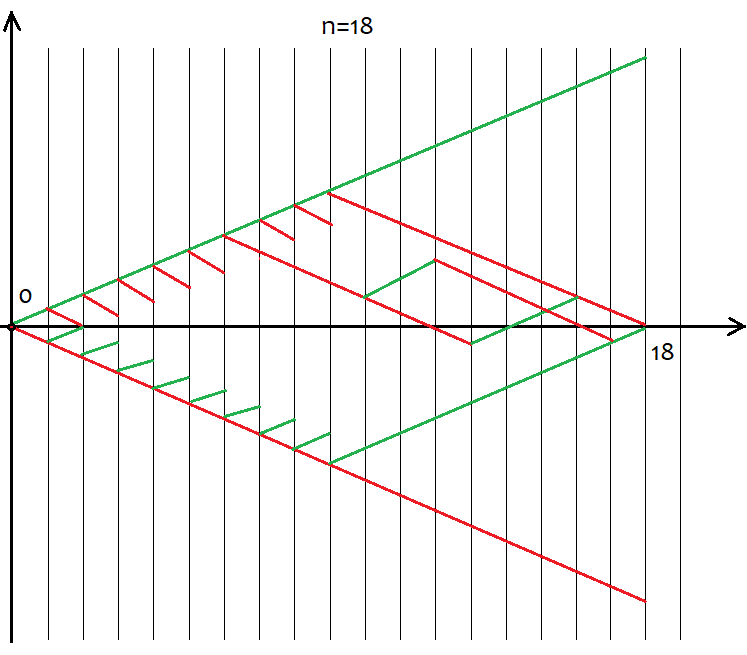
各ステップの後に可能な移動方向は上または下の2つしかないため、さまざまな価格設定オプションのオプション数が2^nであると定義するのは簡単です。不可能なので、これらのオプションのそれぞれを把握するのは不可能なので、試みる必要はありません。代わりに、n個の一意のセルがあり、そのうちuとdがそれぞれ上と下にあることを知っておく必要があります。同じuとdを持つオプションは、最終的に同じsを提供します。同じ「s」を提供するオプションの総数を計算するために、組み合わせ論С=n!/(u!*(n-u)!)からの組み合わせ方程式、および同等の方程式С=n!/(d!*(n-d)!)を使用できます。 uとdが異なる場合、Cの値は同じになります。セグメントの昇順と降順の両方で組み合わせを行うことができるため、必然的に既視感になります。では、組み合わせを形成するためにどのセグメントを使用する必要があるのでしょうか。これらの組み合わせは違いはあるものの同等であるため、答えは「任意」です。 MathCad15ベースのアプリケーションを使用して以下で証明を試みます。

各シナリオの組み合わせの数を決定したので、特定の組み合わせ(またはイベントなど)の確率を決定できます。P =  С/(2^n). この値はすべての「s」に対して計算でき、これらのオプションの1つがとにかく発生するため、これらの確率の合計は常に1に等しくなります。この確率配列に基づいて、sステップが2であることを考慮して、「s」ランダム値に関連する確率密度グラフを作成できます。この場合、特定のステップでの密度は、確率をsステップサイズ(つまり2)で割るだけで取得できます。これは、離散値の連続関数を作成できないためです。この密度は、左右に半ステップ(つまり1)だけ関連性があります。これでノードを見つけて、数値積分が可能になります。負の「s」値の場合、確率密度軸を基準にしてグラフを単純にミラーリングします。偶数のn値の場合、ノードの番号付けは0から始まり、奇数の場合は1から始まります。偶数のn値の場合は奇数のs値を提供することはできず、奇数のn値の場合は偶数のs値を提供することはできません。以下の計算アプリケーションのスクリーンショットは、これを明確にしています。

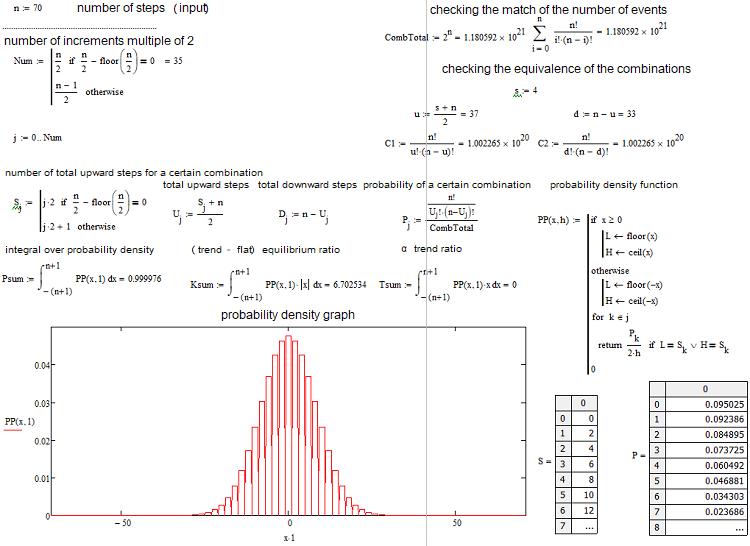
必要なものはすべてリストされています。アプリケーションは以下に添付されているので、パラメータを試してみてください。最も一般的な質問の1つは、現在の市場状況がトレンドであるかフラットベースであるかをどのように定義するかです。商品のトレンドやフラットな性質を定量化するための独自の方程式を考え出しました。私はトレンドをアルファとベータに分けました。アルファは売買する傾向を意味しますが、ベータは明確に定義された買い手または売り手の普及なしに動きを続ける傾向です。最後に、フラットは初期価格に戻る傾向を意味します。

トレンドとフラットの定義はトレーダーによって大きく異なります。これらすべての現象をより厳密に定義しようとしています。なぜなら、これらの問題とその定量化の基本的な理解でさえ、以前は生命がないまたは単純すぎると考えられていた多くのストラテジーを適用できるからです。これらの主な方程式は 

K=Integral(p*|x|)

または

K=Summ(P[i]*|s[i]|)

です。最初のオプションは連続確率変数用で、2番目のオプションは離散変数用です。より明確にするために離散値を連続にし、最初の式を使用しました。積分はマイナスからプラスの無限大に及びます。これは均衡またはトレンド比率です。ランダムな値で計算した後、相場の実際の分布を参照分布と比較するために使用される均衡点を取得します。Кp>Kの場合、市場はトレンドと見なすことができます。Кp<Kの場合、市場は横ばいです。

比率の最大値を計算できます。これは、KMax=1*Max(|x|) or KMax=1*Max(|s[i]|)に等しくなります。比率の最小値を計算することもできます。これは、KMin=1*Min(|x|) = 0 or KMin=1*Min(|s[i]|) = 0に等しくなります。分析された領域の傾向または平坦な性質をパーセンテージで評価するために必要なのは、KMidの中点、最小値、および最大値だけです。

( K >= KMid )の場合は、KTrendPercent=((K-KMid)/(KMax-KMid))*100、その他の場合はKFletPercent=((KMid-K)/KMid)*100です。 

しかし、これは状況を完全に特徴づけるにはまだ十分ではありません。ここで、2番目の比率T=Integral(p*x)、T=Summ(P[i]*s[i])が役に立ちます。これは基本的に、上昇ステップ数の予想される見返りを示し、同時にアルファトレンドの指標でもあります。Tp>0は買いトレンドを意味し、Tp<0は売りトレンドを意味します。つまり、T = 0はランダムウォーク用です。

比率の最大値と最小値を見つけましょう。TMax=1*Max(x)またはTMax=1*Max(s[i])。絶対値の最小値は最大値と同じですが、単純に負の値です(TMin= - TMax)。100から-100までのアルファトレンドのパーセンテージを測定する場合、前の値と同様の値を計算するための方程式を書くことができます。

APercent=( T /TMax)*100.

トレンドは、パーセンテージが正の場合は強気であり、負の場合は弱気です。ケースは混在している可能性があります。アルファフラットとアルファトレンドがあるかもしれませんが、トレンドとフラットが同時にあるわけではありません。以下は、上記のステートメントの図解と、さまざまなステップ数で作成された密度グラフの例です。

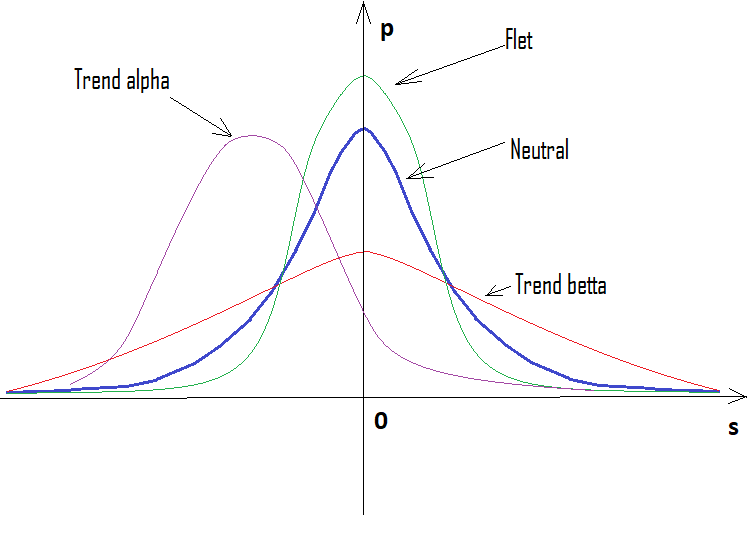
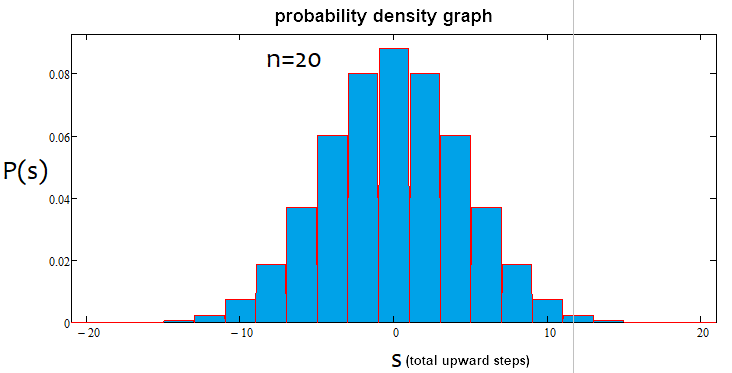
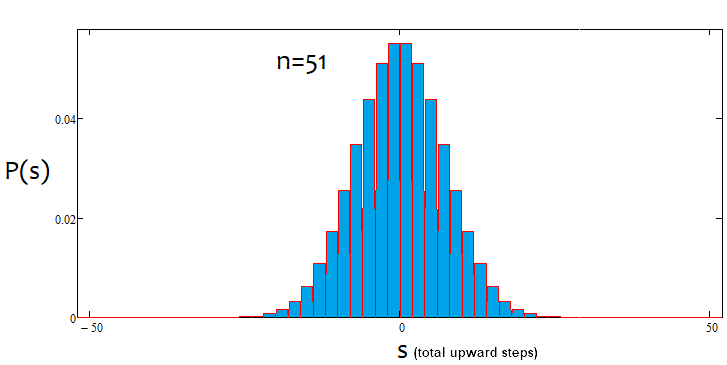
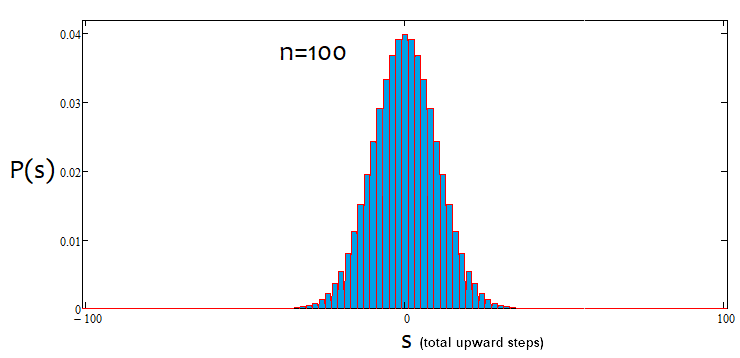
ご覧のとおり、ステップ数が増えると、グラフは狭くなり、高くなります。分布自体と同様に、ステップ数ごとに対応するアルファ値とベータ値が異なります。ステップ数を変更する場合は、参照分布を再計算する必要があります。

これらの方程式はすべて、自動取引システムの構築に適用できます。これらのアルゴリズムは、インディケーターの開発にも使用できます。一部のトレーダーはすでにこれらのことをEAに実装しています。私が1つ確信しているのは、この分析を避けるよりも適用する方が良いということです。数学に精通している人はすぐにそれを適用する方法についていくつかの新しいアイデアを思い付くでしょう。そうでない人には努力が必要です。

簡単なインディケーターを書く

ここでは、私の単純な数学的研究を、市場のエントリポイントを検出し、EAを作成するための基礎として機能するインディケーターに変換します。インディケーターはMQL5で開発します。ただし、コードは、可能な限りMQL4に移植できるように適合させる必要があります。一般的に、コードが不必要に面倒で読めなくなった場合にのみOOPに頼り、可能な限り単純なメソッドの使用を試みます。ただし、これは90%の場合に回避できます。チャートに表示される不必要にカラフルなパネル、ボタン、および大量のデータは、視覚を妨げるだけです。代わりに、私は常にできるだけ少ないビジュアルツールを使用することにしています。

インディケーター入力から始めましょう。

input uint BarsI=990;//Bars TO Analyse ( start calc. & drawing )
input uint StepsMemoryI=2000;//Steps In Memory
input uint StepsI=40;//Formula Steps
input uint StepPoints=30;//Step Value
input bool bDrawE=true;//Draw Steps

インディケーターが読み込まれると、特定の最後のローソク足を基準として、特定のステップ数の初期計算を実行できます。最後のステップに関するデータを格納するためのバッファも必要になります。新しいデータは古いデータを置き換えます。そのサイズは制限されます。同じサイズを使用して、チャートにステップを描画します。分布を構築し、必要な値を計算するためのステップ数を指定する必要があります。次に、ポイント単位のステップサイズと、ステップの視覚化が必要かどうかをシステムに通知する必要があります。ステップはチャートに描くことによって視覚化されます。

ニュートラル分布と現在の状況を表示する別のウィンドウでインディケータースタイルを選択しました。2つのラインがありますが、3番目のラインがあるとよいでしょう。残念ながら、インディケーター機能は個別のメインウィンドウでの描画を意味しないため、描画に頼らざるを得ませんでした。

MQL4のようにバーデータにアクセスできるようにするには、常に次の小さなトリックを使用します。

//variable to be moved in MQL5
double Close[];
double Open[];
double High[];
double Low[];
long Volume[];
datetime Time[];
double Bid;
double Ask;
double Point=_Point;
int Bars=1000;
MqlTick TickAlphaPsi;

void DimensionAllMQL5Values()//set the necessary array size
   {
   ArrayResize(Close,BarsI,0);
   ArrayResize(Open,BarsI,0);   
   ArrayResize(Time,BarsI,0);
   ArrayResize(High,BarsI,0);
   ArrayResize(Low,BarsI,0);
   ArrayResize(Volume,BarsI,0);
   }

void CalcAllMQL5Values()//recalculate all arrays
   {
   ArraySetAsSeries(Close,false);                        
   ArraySetAsSeries(Open,false);                           
   ArraySetAsSeries(High,false);                        
   ArraySetAsSeries(Low,false);                              
   ArraySetAsSeries(Volume,false);
   ArraySetAsSeries(Time,false);                                                            
   if( Bars >= int(BarsI) ) 
      {
      CopyClose(_Symbol,_Period,0,BarsI,Close);
      CopyOpen(_Symbol,_Period,0,BarsI,Open);   
      CopyHigh(_Symbol,_Period,0,BarsI,High);
      CopyLow(_Symbol,_Period,0,BarsI,Low);
      CopyTickVolume(_Symbol,_Period,0,BarsI,Volume); 
      CopyTime(_Symbol,_Period,0,BarsI,Time);      
      }
   ArraySetAsSeries(Close,true);
   ArraySetAsSeries(Open,true);
   ArraySetAsSeries(High,true);                        
   ArraySetAsSeries(Low,true);
   ArraySetAsSeries(Volume,true);                                                                                                
   ArraySetAsSeries(Time,true);
   SymbolInfoTick(Symbol(),TickAlphaPsi);
   Bid=TickAlphaPsi.bid;
   Ask=TickAlphaPsi.ask;
   }
////////////////////////////////////////////////////////////

これで、コードは可能な限りMQL4と互換性があり、MQL4アナログにすばやく簡単に変換できます。

手順を説明するには、最初にノードを説明する必要があります。

struct Target//structure for storing node data
   {
   double Price0;//node price
   datetime Time0;//node price
   bool Direction;//direction of a step ending at the current node
   bool bActive;//whether the node is active
   };
   
double StartTick;//initial tick price
Target Targets[];//destination point ticks (points located from the previous one by StepPoints)

さらに、次のステップを数えるためのポイントが必要になります。ノードには、ノード自体とノードで終了したステップに関するデータ、およびノードがアクティブかどうかを示すブールコンポーネントが格納されます。ノード配列のメモリ全体が実際のノードでいっぱいになった場合にのみ、実際の分布は段階的に計算されるため計算されます。ステップがなければ、計算もありません。

さらに、各ティックでステップのステータスを更新し、インディケーターを初期化するときにバーによる概算計算を実行する機能が必要です。

bool UpdatePoints(double Price00,datetime Time00)//update the node array and return 'true' in case of a new node
   {
   if ( MathAbs(Price00-StartTick)/Point >= StepPoints )//if the step size reaches the required one, write it and 
shift the array back
      {
      for(int i=ArraySize(Targets)-1;i>0;i--)//first move everything back
         {
         Targets[i]=Targets[i-1];
         }
      //after that, generate a new node  
      Targets[0].bActive=true;
      Targets[0].Time0=Time00;
      Targets[0].Price0=Price00;
      Targets[0].Direction= Price00 > StartTick ? true : false;
      //finally, redefine the initial tick to track the next node
      StartTick=Price00;
      return true;
      }
   else return false;
   }

void StartCalculations()//approximate initial calculations (by bar closing prices)
   {
   for(int j=int(BarsI)-2;j>0;j--) 
      {
      UpdatePoints(Close[j],Time[j]);
      }  
   }

次に、すべての中立的なラインパラメータを計算するために必要なメソッドと変数について説明します。その縦座標は、特定の組み合わせまたは結果の確率を表します。離散値のグラフを作成している間、正規分布は連続量であるため、これを正規分布と呼ぶのは好きではありません。また、正規分布は、指標の場合のように確率ではなく確率密度です。密度よりも確率グラフを作成する方が便利です。

int S[];//array of final upward steps
int U[];//array of upward steps
int D[];//array of downward steps
double P[];//array of particular outcome probabilities

double KBettaMid;//neutral Betta ratio value
double KBettaMax;//maximum Betta ratio value
//minimum Betta = 0, there is no point in setting it
double KAlphaMax;//maximum Alpha ratio value
double KAlphaMin;//minimum Alpha ratio value
//average Alpha = 0, there is no point in setting it

int CalcNumSteps(int Steps0)//calculate the number of steps
   {
   if ( Steps0/2.0-MathFloor(Steps0/2.0) == 0 ) return int(Steps0/2.0);
   else return int((Steps0-1)/2.0);
   }

void ReadyArrays(int Size0,int Steps0)//prepare the arrays
   {
   int Size=CalcNumSteps(Steps0);
   ArrayResize(S,Size);
   ArrayResize(U,Size);
   ArrayResize(D,Size);
   ArrayResize(P,Size);
   ArrayFill(S,0,ArraySize(S),0);//clear
   ArrayFill(U,0,ArraySize(U),0);
   ArrayFill(D,0,ArraySize(D),0);
   ArrayFill(P,0,ArraySize(P),0.0);
   }

void CalculateAllArrays(int Size0,int Steps0)//calculate all arrays
   {
   ReadyArrays(Size0,Steps0);
   double CT=CombTotal(Steps0);//number of combinations
   for(int i=0;i<ArraySize(S);i++)
      {
      S[i]=Steps0/2.0-MathFloor(Steps0/2.0) == 0 ? i*2 : i*2+1 ;
      U[i]=int((S[i]+Steps0)/2.0);
      D[i]=Steps0-U[i];
      P[i]=C(Steps0,U[i])/CT;
      }
   }

void CalculateBettaNeutral()//calculate all Alpha and Betta ratios
   {
   KBettaMid=0.0;
   if ( S[0]==0 )
      {
      for(int i=0;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(S[i])*P[i];
         }
      for(int i=1;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(-S[i])*P[i];
         }
      }
   else
      {
      for(int i=0;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(S[i])*P[i];
         }
      for(int i=0;i<ArraySize(S);i++)
         {
         KBettaMid+=MathAbs(-S[i])*P[i];
         }
      }
   KBettaMax=S[ArraySize(S)-1];
   KAlphaMax=S[ArraySize(S)-1];
   KAlphaMin=-KAlphaMax;
   }
   
double Factorial(int n)//factorial of n value
   {
   double Rez=1.0;
   for(int i=1;i<=n;i++)
      {
      Rez*=double(i);
      }
   return Rez;
   }
   
double C(int n,int k)//combinations from n by k
   {
   return Factorial(n)/(Factorial(k)*Factorial(n-k));
   }
   
double CombTotal(int n)//number of combinations in total
   {
   return MathPow(2.0,n);
   }

これらの関数はすべて、適切な場所で呼び出す必要があります。ここでのすべての関数は、配列の値を計算することを目的としているか、最初の2つを除いていくつかの補助的な数学関数を実装しています。これらは、中立的分布の計算とともに初期化中に呼び出され、配列のサイズを設定するために使用されます。

次に、同じ方法で実際の分布とその主なパラメータを計算するためのコードブロックを作成します。

double AlphaPercent;//alpha trend percentage
double BettaPercent;//betta trend percentage
int ActionsTotal;//total number of unique cases in the Array of steps considering the number of steps for checking the option
int Np[];//number of actual profitable outcomes of a specific case
int Nm[];//number of actual losing outcomes of a specific case
double Pp[];//probability of a specific profitable step
double Pm[];//probability of a specific losing step
int Sm[];//number of losing steps

void ReadyMainArrays()//prepare the main arrays
   {
   if ( S[0]==0 )
      {
      ArrayResize(Np,ArraySize(S));
      ArrayResize(Nm,ArraySize(S)-1);
      ArrayResize(Pp,ArraySize(S));
      ArrayResize(Pm,ArraySize(S)-1);      
      ArrayResize(Sm,ArraySize(S)-1);
      for(int i=0;i<ArraySize(Sm);i++)
         {
         Sm[i]=-S[i+1];
         }
      ArrayFill(Np,0,ArraySize(Np),0);//clear
      ArrayFill(Nm,0,ArraySize(Nm),0);
      ArrayFill(Pp,0,ArraySize(Pp),0);
      ArrayFill(Pm,0,ArraySize(Pm),0);      
      }
   else
      {
      ArrayResize(Np,ArraySize(S));
      ArrayResize(Nm,ArraySize(S));
      ArrayResize(Pp,ArraySize(S));
      ArrayResize(Pm,ArraySize(S));      
      ArrayResize(Sm,ArraySize(S));
      for(int i=0;i<ArraySize(Sm);i++)
         {
         Sm[i]=-S[i];
         }
      ArrayFill(Np,0,ArraySize(Np),0);//clear
      ArrayFill(Nm,0,ArraySize(Nm),0);
      ArrayFill(Pp,0,ArraySize(Pp),0);
      ArrayFill(Pm,0,ArraySize(Pm),0);            
      }   
   }

void CalculateActionsTotal(int Size0,int Steps0)//total number of possible outcomes made up of the array of steps
   {
   ActionsTotal=(Size0-1)-(Steps0-1);
   }

bool CalculateMainArrays(int Steps0)//count the main arrays
   {
   int U0;//upward steps
   int D0;//downward steps
   int S0;//total number of upward steps
   if ( Targets[ArraySize(Targets)-1].bActive )
      {
      ArrayFill(Np,0,ArraySize(Np),0);//clear
      ArrayFill(Nm,0,ArraySize(Nm),0);
      ArrayFill(Pp,0,ArraySize(Pp),0);
      ArrayFill(Pm,0,ArraySize(Pm),0);      
      for(int i=1;i<=ActionsTotal;i++)
         {
         U0=0;
         D0=0;
         S0=0;
         for(int j=0;j<Steps0;j++)
            {
            if ( Targets[ArraySize(Targets)-1-i-j].Direction ) U0++;
            else D0++;
            }
         S0=U0-D0;
         
         for(int k=0;k<ArraySize(S);k++)
            {
            if ( S[k] == S0 )
               {
               Np[k]++;
               break;
               }
            }
         for(int k=0;k<ArraySize(Sm);k++)
            {
            if ( Sm[k] == S0 )
               {
               Nm[k]++;
               break;
               }
            }
         }
         
      for(int k=0;k<ArraySize(S);k++)
         {
         Pp[k]=Np[k]/double(ActionsTotal);
         }
      for(int k=0;k<ArraySize(Sm);k++)
         {
         Pm[k]=Nm[k]/double(ActionsTotal);
         }         
         
      AlphaPercent=0.0;
      BettaPercent=0.0;
      for(int k=0;k<ArraySize(S);k++)
         {
         AlphaPercent+=S[k]*Pp[k];
         BettaPercent+=MathAbs(S[k])*Pp[k];
         }
      for(int k=0;k<ArraySize(Sm);k++)
         {
         AlphaPercent+=Sm[k]*Pm[k];
         BettaPercent+=MathAbs(Sm[k])*Pm[k];
         }
      AlphaPercent= (AlphaPercent/KAlphaMax)*100;
      BettaPercent= (BettaPercent-KBettaMid) >= 0.0 ? ((BettaPercent-KBettaMid)/(KBettaMax-KBettaMid))*100 : ((BettaPercent-KBettaMid)/KBettaMid)*100;
      
      Comment(StringFormat("Alpha = %.f %%\nBetta = %.f %%",AlphaPercent,BettaPercent));//display these numbers on the screen
      return true;
      }
   else return false;
   }

ここではすべてが単純ですが、グラフが垂直軸に対して常にミラーリングされているとは限らないため、配列ははるかに多くなります。これを実現するには、追加の配列と変数が必要ですが、一般的なロジックは単純です。特定のケースの結果の数を計算し、それをすべての結果の総数で割ります。これは、すべての確率(縦座標)と対応する横座標を取得する方法です。各ループと変数については詳しく説明しません。値をバッファに移動する際の問題を回避するには、これらすべての複雑さが必要です。ここではすべてがほぼ同じです。配列のサイズを定義し、それらを数えます。次に、アルファとベータの傾向のパーセンテージを計算し、画面の左上隅に表示します。

残っているのは、何をどこに呼び出すかを定義することです。

int OnInit()
  {
   //--- indicator buffers mapping
   SetIndexBuffer(0,NeutralBuffer,INDICATOR_DATA);
   SetIndexBuffer(1,CurrentBuffer,INDICATOR_DATA);
   CleanAll();
   DimensionAllMQL5Values();
   CalcAllMQL5Values();
   StartTick=Close[BarsI-1];
   ArrayResize(Targets,StepsMemoryI);//maximum number of nodes
   CalculateAllArrays(StepsMemoryI,StepsI);
   CalculateBettaNeutral();
   StartCalculations();
   ReadyMainArrays();
   CalculateActionsTotal(StepsMemoryI,StepsI);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  CalcAllMQL5Values();
  
  if ( UpdatePoints(Close[0],TimeCurrent()) )
     {
     if ( CalculateMainArrays(StepsI) )
        {
        if ( bDrawE ) RedrawAll();
        }
     }
      
  int iterator=rates_total-(ArraySize(Sm)+ArraySize(S))-1;
  for(int i=0;i<ArraySize(Sm);i++)
     {
     iterator++;
     NeutralBuffer[iterator]=P[ArraySize(S)-1-i];
     CurrentBuffer[iterator]=Pm[ArraySize(Sm)-1-i];
     }
  for(int i=0;i<ArraySize(S);i++)
     {
     iterator++;
     NeutralBuffer[iterator]=P[i];
     CurrentBuffer[iterator]=Pp[i];
     }

   return(rates_total);
  }

CurrentBufferとNeutralBufferは、ここではバッファとして使用されます。より明確にするために、市場に最も近いローソク足を表示することにします。各確率は別々のバーにあります。これにより、不要な複雑さを取り除くことができました。チャートをズームインおよびズームアウトするだけで、すべてが表示されます。CleanAll()およびRedrawAll()関数はここには示されていません。コメントアウトすれば、レンダリングなしですべてが正常に機能します。また、ここには描画ブロックは含まれていません。添付ファイルをご覧ください。特筆すべきことは何もありません。インディケーターは、MetaTrader4とMetaTrader5の2つのバージョンで以下にも添付されています。

これは次のようになります。

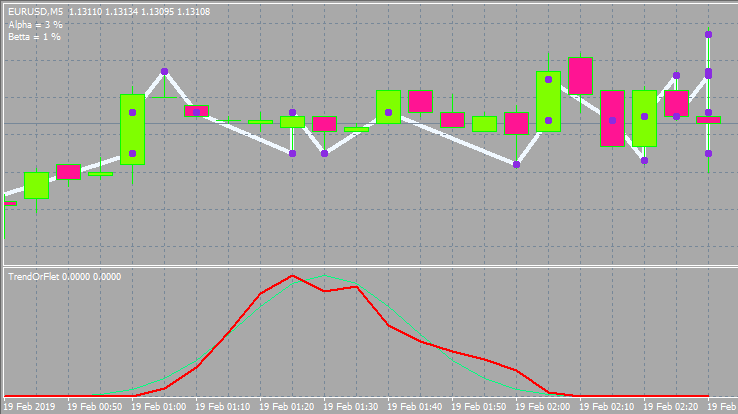
以下は、他の入力とウィンドウスタイルのオプションです。

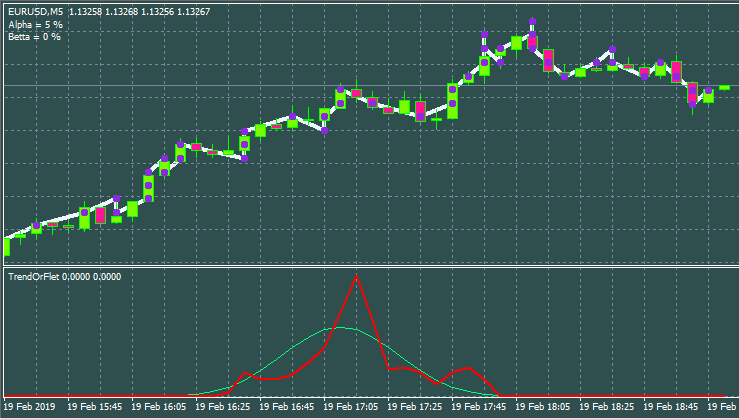
最も興味深いストラテジーのレビュー

私はたくさんのストラテジーを開発し、見てきました。私の謙虚な経験では、グリッドまたはマーチンゲール、あるいはその両方を使用すると、最も注目すべきことが起こります。厳密に言えば、マーチンゲールとグリッドの両方の予想される見返りは0です。上向きのチャートにだまされないでください。いつか莫大な損失を被ることになります。起動するグリッドは存在し、それらは市場で見つけることができます。それらはかなりうまく機能し、3-6の利益率さえ示しています。これはかなり高い値で、さらに、それらはどの通貨ペアでも安定しています。しかし、勝つことを可能にするフィルターを思い付くのは簡単ではありません。上記の方法では、これらの信号を分類できます。グリッドにはトレンドが必要ですが、方向は重要ではありません。 

マーチンゲールとグリッドは、最も単純で人気のあるストラテジーの例です。ただし、すべての人が適切な方法でそれらを適用できるわけではありません。自己適応型エキスパートアドバイザーはもう少し複雑です。これえらは、フラット、トレンドまたは他のパターンであるかどうかにかかわらず何にでも適応することができます。通常、パターンを探し、パターンがしばらく残ることを期待して短期間取引するために市場の特定の部分を取ることを含みます。

別のグループは、市場の混沌とした性質で利益を得ようとする神秘的で型破りなアルゴリズムを備えたエキゾチックなシステムによって形成されます。このようなシステムは純粋数学に基づいており、あらゆる手段と期間で利益を上げることができます。利益は大きくはないが安定しています。私は最近そのようなシステムを扱っています。このグループには、総当たり攻撃ベースのロボットも含まれます。総当たり攻撃は、追加のソフトウェアを使用して実行できます。次の記事では、そのようなプログラムの私のバージョンを紹介します。

一番上のニッチは、ニューラルネットワークや同様のソフトウェアに基づくロボットによって占められています。ニューラルネットワークはAIのプロトタイプであるため、これらのロボットは非常に異なる結果を示し、最高レベルの洗練された機能を備えています。ニューラルネットワークが適切に開発およびトレーニングされている場合、他のストラテジーでは比類のない最高の効率を示すことができます。

仲裁に関しては、私の意見では、その可能性はほぼゼロになりました。適切なEAがあり、結果は得られません。

わざわざ苦労する価値はあるのでしょうか。

市場での取引にときめきを見出す人や簡単に手早く収入を得たい人がいる一方、方程式と理論を介して市場プロセスを研究したいと思う人もいます。その上、後戻りできないために、単に他の選択肢がないトレーダーがいます。私は主に後者のカテゴリーに属しています。すべての知識と経験をもっても、私には現在、収益性の高い安定した口座がありません。EAのテストランは良好ですが、すべてが思ったほど簡単ではありません)。

すぐに金持ちになろうと努力している人は、おそらく反対の結果に直面するでしょう。結局のところ、市場は一般的なトレーダーが勝つようにはできていません。それは全く反対の目的を持っています。ただし、このトピックに挑戦する勇気がある場合は、十分な時間と忍耐力があることを確認してください。結果はすぐには現れません。プログラミングのスキルがない場合、実質的にチャンスはまったくありません。二三十の取引を行った後に結果について自慢する多くの疑似トレーダーを見てきました。私の場合、まともなEAを開発した後、1、2年は機能するかもしれませんが、必然的に失敗します。多くの場合、最初から機能しません。

もちろん、手作業などもありますが、芸術に似ていると思います。全体として、市場でお金を稼ぐことは可能ですが、それには多くの時間がかかります。個人的には、それだけの価値はないと思います。数学的な観点からは、市場は退屈な2次元曲線にすぎません。私は確かに私の人生全体でローソク足を見たくありません)。

「聖杯」は存在し、どこでそれを探すべきですか。

聖杯は可能以上のものだと思います。私はそれを証明する比較的単純なEAを持っています。残念ながら、予想される見返りはスプレッドをほとんどカバーしていません。ほとんどすべての開発者がこれを確認するストラテジーを持っていると思います。市場には、あらゆる点で聖杯と呼ぶことができるロボットがたくさんあります。しかし、そのようなシステムでお金を稼ぐことは、ピップごとに戦う必要があるだけでなく、スプレッドリターンとパートナーシッププログラムを可能にする必要があるため、非常に困難です。かなりの利益と低い預金負荷を特徴とする聖杯はまれです。

自分で聖杯を開発したい場合は、ニューラルネットワークに目を向けたほうがよいでしょう。ニューラルネットワークは利益の面で多くの可能性を秘めています。もちろん、さまざまなエキゾチックなアプローチと総当たり攻撃を組み合わせることができますが、すぐにニューラルネットワークを調べることをお勧めします。

奇妙なことに、聖杯が存在するかどうか、そしてどこで聖杯を探すべきかという質問への答えは、たくさんのEAを開発した後で、非常に単純で明白になりました。

一般的なトレーダーのためのヒント

すべてのトレーダーは3つのことを望んでいます。

• プラスの予想される見返りを達成する
• 収益性の高いポジションの場合は利益を増やす
• ポジションに損失がある場合は損失を減らす

ここで最も重要なのは最初のポイントです。収益性の高いストラテジーがある場合(手動かアルゴリズムかに関係なく)、常に介入する必要があります。これは許可されるべきではありません。利益のある取引損失を伴う取引よりも少ないという状況は、取引システムを台無しにするかなりの心理的影響を及ぼします。最も重要なことは、赤字のときに急いで損失を取り戻そうとしないことです。そうしないと、さらに多くの損失が発生する可能性があります。予想される見返りについて覚えておいてください。現在のポジションの株式損失が何であるかは問題ではありません。本当に重要なのは、ポジションの総数と損益比率です。

次に重要なことは、取引に適用するロットサイズです。現在利益を上げている場合は、徐々にロットを減らします。それ以外の場合は、増やします。ただし、特定のしきい値までしか増やす必要はありません。これは順方向と逆方向のマーチンゲールです。慎重に考えると、純粋にロットのバリエーションに基づいて独自のEAを開発できます。これはもはやグリッドやマーチンゲールではなく、より複雑で安全なものになります。さらに、そのようなEAは、相場の履歴を通じてすべての通貨ペアで機能する可能性があります。この原則は混沌とした市場でも機能し、どこにどのようにエントリするかは問題ではありません。適切に使用すれば、すべてのスプレッドと手数料を補うことができ、巧みに使用すれば、ランダムなポイントとランダムな方向で市場にエントリしても利益が得られます。

損失を減らして利益を増やすには、マイナスの半波で買い、プラスの半波で売ります。中間点は通常、現在の市場エリアでの買い手または売り手の以前の活動を示します。これは、それらの一部が市場のものであったことを意味しますが、ポジションは遅かれ早かれ反対方向に価格を押し上げます。それが市場に波の構造がある理由です。これらの波はどこでも見ることができます。買いの後に売りが続き、その逆も同様です。また、同じ基準を使用してポジションを決済します。

終わりに

視点は誰のものでも主観的です。結局のところ、それはどちらにしてもすべてあなた次第です。不利な点と無駄にされた時間にかかわらず、誰もが独自のスーパーシステムを作成し、決意の成果を享受したいと考えています。そうでなければ、私には外国為替取引を掘り下げる意味がまったくわかりません。この活動は、私を含む多くのトレーダーにとって魅力的なままです。この気持ちがどのように呼ばれるかは誰もが知っていますが、子供っぽく聞こえます。したがって、トローリングを避けるために名指しにはしません。)