
Negociação Forex e sua matemática básica
Introdução
Sou um programador de estratégias automáticas com mais de 5 anos de experiência em desenvolvimento, bem como de outros softwares adicionais. Neste artigo, tentarei desvendar o mistério para aqueles que estão apenas começando a operar Forex, ou em qualquer outro mercado, e também me esforçarei para responder ao leitor às questões mais inquietantes que qualquer trader começa a pensar quando, apesar de tudo, decide tentar a sorte nesta área.
Espero que este artigo seja útil para todos, e não apenas para iniciantes. Além disso, não venho fingir ter a verdade, eu só relatarei uma história real e as consequências reais de minha pesquisa.
Alguns dos robôs e indicadores que escrevi estão dentro da minha carteira de produtos. Mas é apenas uma pequena parte. Eu escrevi uma grande variedade de robôs usando um amplo leque de estratégias. Tentarei mostrar como dada abordagem, com a devida persistência, permite entender a verdadeira natureza do mercado e em quais estratégias vale a pena prestar atenção e em quais não.
Por que é tão confuso onde entrar e onde sair?
Onde entrar e onde sair são duas questões importantíssimas cuja resposta não é simples! À primeira vista, sempre podemos identificar um padrão e segui-lo por um tempo, mas como identificá-lo sem ter ferramentas e indicadores especiais? Os padrões mais simples que sempre aparecem são a TENDÊNCIA e a LATERALIZAÇÃO. Uma tendência é um movimento prolongado numa direção, e uma lateralização consiste em reversões frequentes.
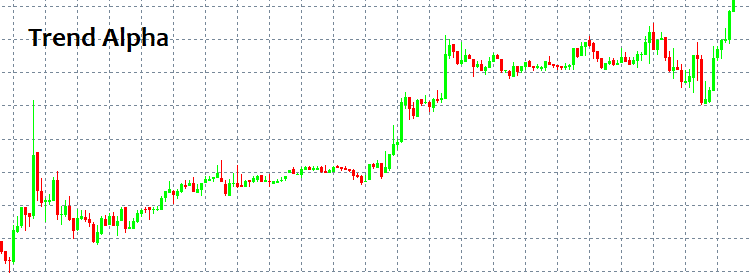
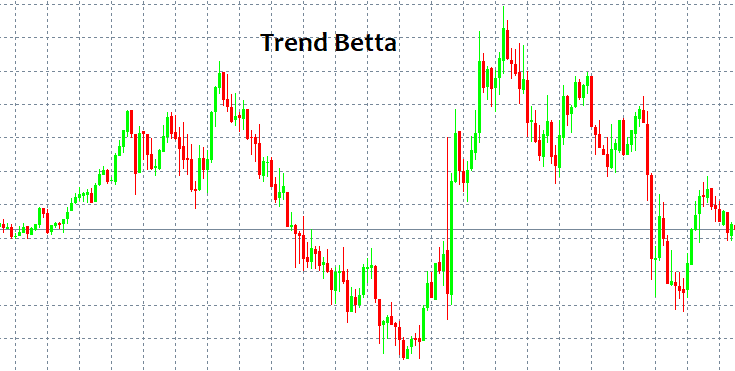

As pessoas conseguem ver esses padrões imediatamente, porque o olho humano identifica facilmente tudo isso mesmo sem indicadores. Mas o problema é que quando algum modelo começa a funcionar, só então fica visível, mas já tendo funcionado não há garantia de que seja algum tipo de modelo ou que continue a se desenvolver. Em outras palavras, após detectar um padrão de comportamento, não há garantia de que no próximo candle o mercado não irá na direção oposta à escolhida e não zerará todo o seu depósito. Isso pode acontecer com quase qualquer estratégia em que você esteja ingenuamente 100% seguro. Por meio da linguagem da matemática a seguir, eu tentarei explicar por que isso acontece.
Mecanismos e níveis de mercado
Vou falar um pouco sobre formação de preços e, em geral, sobre como o preço se move. Existem 2 forças no mercado, a de mercado e a limitada. Da mesma forma que existem 2 tipos de ordens, a mercado e limitadas. Compradores e vendedores limitados preenchem o livro de ofertas, enquanto os de mercado o esvaziam. O livro de ofertas é simplesmente uma escala vertical com preços pelos quais alguém deseja comprar algo e alguém deseja vender algo. Sempre há um espaço entre os vendedores e compradores limitados, chamado de spread. Spread é a distância entre o melhor preço de compra e o melhor preço de venda, medida pelo número de movimentos mínimos do preço. Os compradores querem comprar mais barato e os vendedores querem vender mais caro. Por esse motivo, as ordens limitadas dos compradores estão sempre no fundo e as dos vendedores estão sempre no topo. Quando os compradores e vendedores a mercado entram no livro de ofertas, duas ordens são vinculadas - limitada e a mercado, e só quando a ordem limitada é destruída, o mercado se move.
Quando uma ordem a mercado aberta aparece no mercado, na maioria dos casos ela tem Stop Loss e Take Profit. Assim como as ordens limitadas, esses stops estão espalhados por todo o mercado e representam, como resultado, níveis de aceleração ou reversão de preços. Tudo depende do número e do tipo de stops, bem como do volume de transações. Conhecendo esses níveis, podemos saber onde e quanto o preço atingirá ou se recuperará.
As ordens limitadas também podem formar flutuações e acúmulos que são bastante difíceis de ultrapassar. Na maioria das vezes, ocorrem em faixas de preço importantes, como na abertura do dia ou na abertura da semana. Ao negociar a partir de níveis, na maioria das vezes significa operar a partir dos níveis de ordens limitadas. Abaixo, tentarei descrever brevemente o que disse.
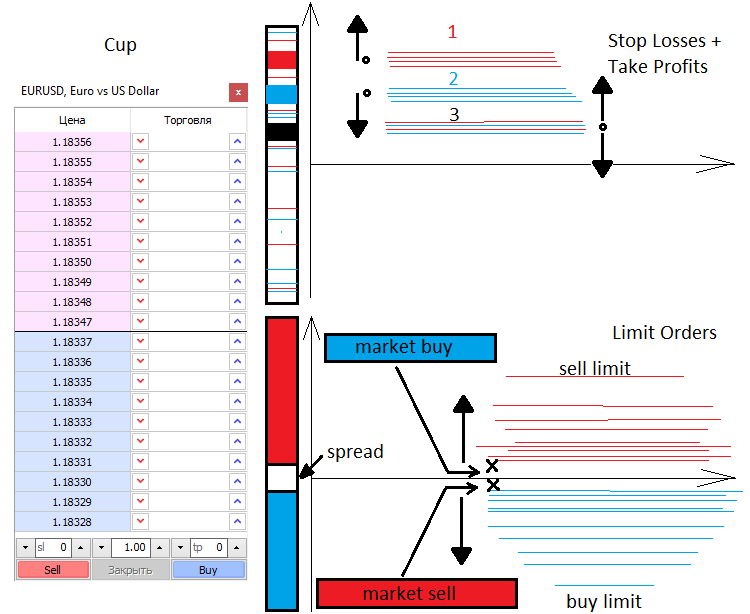
Descrição matemática do mercado
O que vemos na janela MetaTrader é uma função discreta do argumento t, onde t é o tempo. É discreta, uma vez que há um número finito de ticks, ticks em nosso caso são pontos entre os quais não há absolutamente nada. Os ticks são o menor elemento de possível discretização do preço, enquanto as barras ou candles M1 já são o maior, etc. No mercado existe um componente aleatório e existem padrões. Os padrões de comportamento são de diferentes escalas e durações. Mas, na maior parte, o mercado é uma espuma probabilística, caótica, quase imprevisível. Para entender o mercado, é melhor analisá-lo por meio da teoria da probabilidade. A discretização é apenas necessária para ser capaz de introduzir o conceito de probabilidade, densidade de probabilidade.
Para introduzir o conceito de expectância, primeiro precisamos apresentar o de evento e o de grupo completo de eventos:
- Evento C1 — lucro, seu valor é igual a tp
- Evento C2 — perda, seu valor é igual a sl
- P1 — probabilidade do evento C1
- P2 — probabilidade do evento C2
Os eventos C1 e C2 formam um grupo completo de eventos incompatíveis (ou seja, alguns desses eventos ocorrerão em qualquer caso), e, portanto, a soma dessas probabilidades será igual a um P2(tp,sl) + P2(tp,sl) = 1. Esta fórmula pode ser útil.
Ao testar um Expert Advisor ou uma estratégia manual com uma abertura aleatória e usando StopLoss e TakeProfit, escolhidos completamente aleatoriamente, no entanto, sempre obteremos um resultado não aleatório, obteremos uma expectância de "-(Spread)", o que significaria "0" se o spread pudesse ser definido zero. O que nos leva à conclusão de que, não importa como colocarmos stops, obteremos expectativa zero se o mercado for aleatório. Já se não for aleatório, teremos lucro ou perda caso apareçam padrões de comportamento relacionados a cada um destes. Podemos concluir o mesmo se assumirmos que a expectância (Tick[0].Bid - Tick[1].Bid) também é zero. Estas são conclusões bastante simples que podem ser tiradas de várias maneiras.
- M=P1*tp-P2*sl= P1*tp-(1- P1)*sl — para qualquer mercado
- P1*tp-P2*sl= 0 — para um mercado caótico
Esta é a fórmula básica - para um mercado caótico - que descreve a expectância de um fechamento e abertura caóticos de ordens que são cobertas por stops. Resolvida a última equação, obtemos todas as probabilidades que nos interessam, tanto para o caso de aleatoriedade total quanto para o caso oposto, desde que conheçamos os valores dos stops.
Aqui temos apenas uma fórmula para o caso mais simples, que pode ser generalizada para qualquer estratégia, o que faremos agora para compreender completamente o que constitui a expectância total, que no final precisamos tornar diferente de zero. Também apresentaremos o conceito de fator de lucro e escreveremos as fórmulas correspondentes.
Agora vamos supor que nossa estratégia envolve o fechamento não apenas com base em stops, mas também de acordo com sinais. Para isso, introduzimos um novo espaço de eventos C3, C4, em que o primeiro evento é um fechamento baseado em stops e o segundo, em sinais. Eles também formam um grupo completo de eventos inconsistentes, que podemos escrever por analogia:
M=P3*M3+P4*M4=P3*M3+(1-P3)*M4, onde M3=P1*tp-(1- P1)*sl, a M4=Soma(P0[i]*pr[i]) - Soma(P01[j]*ls[j]); Soma( P0[i] )+ Soma( P01[j] ) =1
- M3 — expectância do valor do lucro ao fechar com ordem stop.
- M4 — expectância do valor do lucro ao fechar com base num sinal.
- P1 , P2 — probabilidade de os stops serem acionados, desde que algum deles seja disparado de qualquer maneira.
- P0[i] — probabilidade de fechar uma transação com lucro pr[i], desde que a transação não atinja os stops. Onde i é o número da opção de fechamento
- P01[j] — probabilidade de fechar uma transação com perda ls[j] , desde que a transação não atinja os stops. Onde j é o número da opção de fechamento
T. temos 2 eventos incompatíveis, de cujos resultados são compilados mais 2 espaços de eventos independentes em que também selecionamos um grupo completo. Somente agora as probabilidades P1, P2, P0[i], P01[j] são probabilidades condicionadas. E P3, P4 são as probabilidades das hipóteses. A probabilidade condicional é a probabilidade de um evento ocorrer, desde que uma hipótese tenha ocorrido. Tudo está estritamente de acordo com a fórmula da probabilidade total (teorema de Bayes). Se alguém não a conhece, aconselho que leia e estude bem. Além disso, para negociação completamente insensata e caótica, M=0.
Agora nossa fórmula se tornou muito mais clara e ampla, agora levamos em consideração os fechamentos com base em stops e aqueles segundo sinais. Na verdade, podemos ir mais longe seguindo essa analogia e escrever uma fórmula geral para qualquer estratégia que leve em consideração até mesmo stops dinâmicos. Isso é o que faremos. Vamos introduzir mais N eventos que formam um grupo completo, o que significa a abertura de transações abertas com o mesmo StopLoss e TakeProfit. CS[1] .. CS[2] .. CS[3] ....... CS[N] . Além disso, da mesma forma PS[1] + PS[2] + PS[3] + ....... +PS[N] = 1.
M = PS[1]*MS[1]+PS[2]*MS[2]+ ... + PS[k]*MS[k] ... +PS[N]*MS[N] , MS[k] = P3[k]*M3[k]+(1- P3[k])*M4[k], M3[k] = P1[k] *tp[k] -(1- P1[k] )*sl[k], M4[k] = Soma(i)(P0[i][k]*pr[i][k]) - Soma(j)(P01[j][k] *ls[j][k] ); Soma(i)( P0[i][k] )+ Soma(j)( P01[j][k] ) =1.
- PS[k] — probabilidade de colocar a k-ésima opção de stops.
- MS[k] — expectância de transações fechadas com k stops.
- M3[k] — expectância do valor do lucro ao fechar com ordem stop com k stops.
- M4[k] — expectância do valor do lucro ao fechar segundo sinal com k stops.
- P1[k] , P2[k] — probabilidade de os stops serem acionados, desde que algum deles seja disparado de qualquer maneira.
- P0[i][k] — probabilidade de fechar uma transação com lucro pr[i][k], segundo sinal com k stops. Onde i é o número da opção de fechamento
- P01[j][k] — probabilidade de fechar uma transação com perda ls[j][k] , segundo sinal com k de stops. Onde j é o número da opção de fechamento
Da mesma forma que nas fórmulas anteriores mais simples, M=0 ao negociar de forma insensata e sem spread. O máximo que você pode fazer é mudar a estratégia em si, e se esta não fazer sentido, você simplesmente mudará o equilíbrio de todas essas variáveis, porém ainda obterá "0". Já para introduzir um desequilíbrio nesse equilíbrio, você precisa saber o principal - a probabilidade de o mercado se mover em determinada direção em certo segmento fixo de movimento de preço em pontos ou a expectância de movimento de preço num período fixo. Os pontos de entrada e de saída são escolhidos exatamente por esse motivo. Se você encontrar isso, terá uma estratégia lucrativa.
Agora vamos criar uma fórmula para o fator de lucro. PF = Profit/Loss. Por definição, o fator de lucro é a relação entre lucro e perda. Se o número for maior do que 1, a estratégia será lucrativa; caso contrário, não será lucrativa. Isso pode ser redefinido usando expectativa. PrF=Mp/Ml. O que significa a relação entre o lucro líquido esperado e a perda líquida esperada? Vamos escrever suas fórmulas.
- Mp = PS[1]*MSp[1]+PS[2]*MSp[2]+ ... + PS[k]*MSp[k] ... +PS[N]*MSp[N] , MSp[k] = P3[k]*M3p[k]+(1- P3[k])*M4p[k] , M3p[k] = P1[k] *tp[k], M4p[k] = Soma(i)(P0[i][k]*pr[i][k])
- Ml = PS[1]*MSl[1]+PS[2]*MSl[2]+ ... + PS[k]*MSl[k] ... +PS[N]*MSl[N] , MSl[k] = P3[k]*M3l[k]+(1- P3[k])*M4l[k] , M3l[k] = (1- P1[k] )*sl[k], M4l[k] = Soma(j)(P01[j][k]*ls[j][k])
Soma(i)( P0[i][k] ) + Soma(j)( P01[j][k] ) =1.
- MSp[k] — expectância de transações fechadas com k stops.
- MSl[k] — expectância de transações fechadas com k stops.
- M3p[k] — expectância do valor do lucro ao fechar usando uma ordem stop com k stops.
- M4p[k] — expectância do valor do lucro ao fechar segundo sinal com k stops.
- M3l[k] — expectância do valor do lucro ao fechar usando uma ordem stop com k stops.
- M4l[k] — expectância do valor da perda ao fechar segundo sinal com k stops.
Para uma compreensão mais profunda, apresentarei um esquema de todos os eventos anexados:
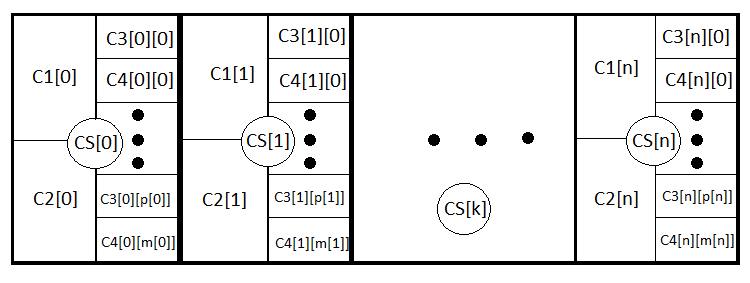
Na verdade, as mesmas fórmulas, apenas na primeira são eliminados os termos relativos ao prejuízo e, na segunda, ao lucro. Quando a negociação for insensata PrF = 1. Novamente, caso o spread seja zero. M, PrF são dois valores suficientes para avaliar a estratégia de todos os ângulos.
Pode-se avaliar se um instrumento é adequado para buscar tendências ou movimentos laterias, usando a mesma teoria de probabilidade e combinatória, ou ver algumas diferenças de aleatoriedade usando as densidades de distribuição de probabilidade.
Construiremos um gráfico da densidade de probabilidade da distribuição de uma variável aleatória para um preço discretizado para um passo fixo H em pontos. Assumiremos que, se o preço ultrapassar H em qualquer direção é porque ocorreu um passo. Como uma variável aleatória ao longo do eixo X, adiaremos o movimento vertical do gráfico ao longo do eixo do preço, medido no número de passos. Nesse caso, é imperativo que ocorram n passos, só então podemos estimar o movimento geral do preço.
- n — número total de passos, é sempre constante
- d — número de passos para uma queda do preço
- u — número de passos para uma subida do preço
- s — movimento ascendente total em passos
Após determinar esses valores, calculamos u e d:
Para fornecer os passos finais "s" ascendentes (neste caso, o valor pode ser negativo, o que significa passos descendentes), é necessário dar um certo número de passos para cima e para baixo: "u", "d". Nesse caso, o movimento final para cima ou para baixo "s" dependerá de todos os passos em geral:
n=u+d;
s=u-d;
Este é um sistema de 2 equações, que permite obter u e d:
u=(s+n)/2, d=n-u.
No entanto, nem todos os valores de "s" são adequados para um valor específico de "n". O passo entre os valores possíveis de s é sempre 2. Isso é necessário para fornecer "u" e "d" com valores naturais, pois os usaremos para análise combinatória. Se esses números forem fracionários, não podemos calcular o fatorial. E o fatorial é a pedra angular de todos os cálculos de combinações. Abaixo está esquema de todos os cenários possíveis para 18 passos. Deve ajudá-lo a compreender visualmente como são abrangentes as variações de eventos.
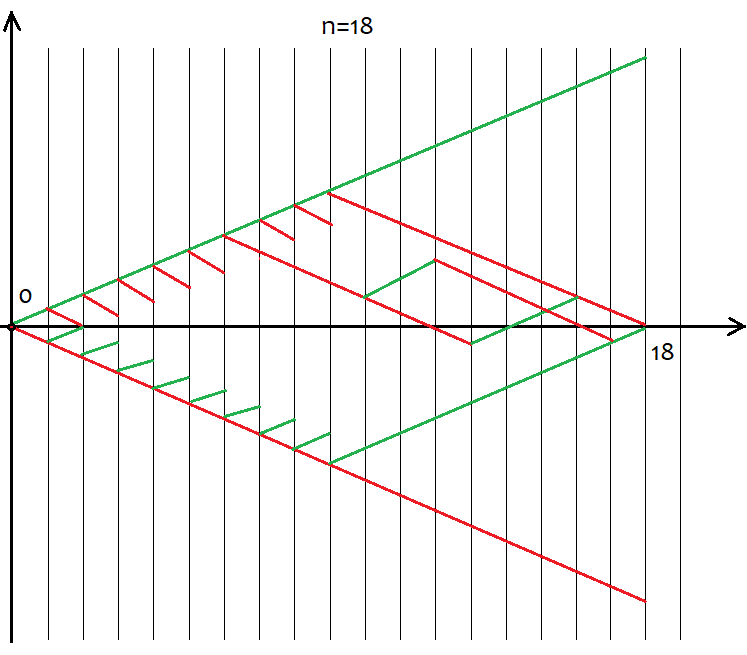
É fácil calcular que, para todas as variações de formação de preços, haverá 2^n dessas variações, já que após cada passo existem apenas 2 variações de movimento, para cima ou para baixo. Dispensamos a tentativa de entender cada uma dessas variações, é impossível. Só precisamos saber que temos n células exclusivas, das quais u e d devem estar para cima e para baixo, respectivamente. Além disso, as variações em que existem os mesmos números u e d resultam, afinal, nos mesmos s. Para calcular o número total de variações que darão o mesmo "s" podemos usar a fórmula de combinação a partir da combinatória C=n!/(u!*(n-u)!), bem como sua fórmula equivalente C=n!/(d!*(n-d)!). Para diferentes u, d, obtemos o mesmo valor de C. Uma vez que as combinações podem ser feitas tanto nos segmentos ascendentes quanto nos descendentes, certamente é levantada a questão de para que segmentos fazer as combinações. Resposta: tanto faz. Pois essas combinações são equivalentes, apesar de suas diferenças, o que demostrarei a seguir usando um programa baseado em MathCad 15.
Agora que determinamos o número de combinações para cada cenário, podemos determinar a probabilidade de uma combinação particular (ou evento, o que você quiser). P = С/(2^n). Este valor pode ser calculado para todos os "s", e a soma dessas probabilidades sempre será igual a 1, pois qualquer uma dessas variações acontecerá de qualquer maneira. Com base nessa matriz de probabilidades, podemos representar graficamente a densidade de probabilidade em relação à variável aleatória "s", ao mesmo tempo que consideramos o passo s como igual a 2. Assim, a densidade num determinado passo pode ser obtido simplesmente dividindo a probabilidade pelo tamanho do passo s, ou seja, em 2. Tudo isso se deve ao fato de que não podemos construir uma função contínua para quantidades discretas. Essa densidade será relevante meio passo à esquerda e à direita, ou seja, por 1. Ela permitirá compreender visualmente onde estão os nós e facilitará a integração numérica. Mas também precisamos lembrar que também existem "s" negativos e, para eles, simplesmente espelharemos o gráfico sobre o eixo de densidade de probabilidade. Para n pares, a numeração dos nós começa em 0, para n ímpares, em 1. Isso porque para n pares não podemos fornecer s ímpares, e para n ímpar não podemos fornecer s pares. Para esclarecer a situação, apresento uma captura de tela do programa de cálculo:
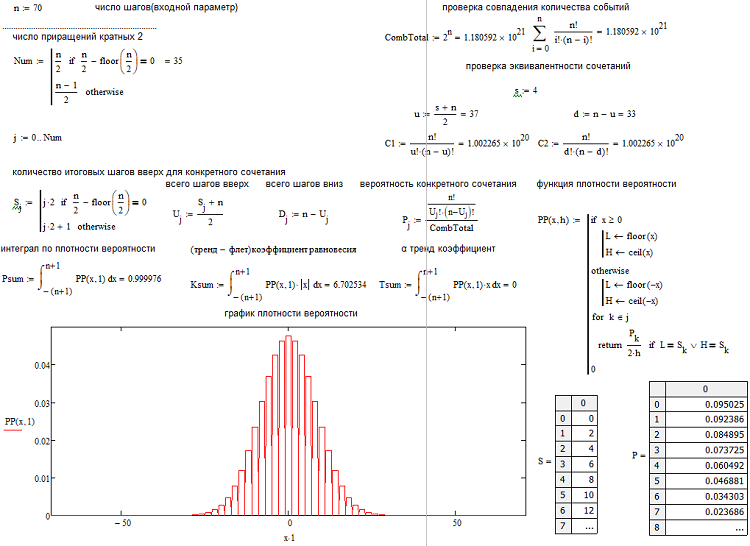
Aqui está tudo que precisamos entender. Este programa será anexado como um arquivo ao artigo e todos os interessados podem brincar com os parâmetros. Além disso, muitas pessoas estão interessadas em saber como determinar se é tendência ou lateralização. Eu criei minhas próprias fórmulas para avaliar quantitativamente a existência de uma tendência ou uma lateralização. Ao mesmo tempo, há diferentes tendências, Alpha e Betta. Eu as divide em dois grupos, alfa (tendência de compra ou de venda), beta (é apenas a tentativa de continuar o movimento sem um deslocamento pronunciado na direção de compra ou de venda), já uma lateralização é a tentativa de voltar ao preço inicial.
De modo geral, para muitos, a definição de tendência e lateralização é diferente. Estou tentando dar uma definição mais rigorosa a todos esses fenômenos. Afinal, basta uma compreensão básica dessas coisas e como quantificá-las para podermos dar vida a muitas estratégias que antes eram consideradas mortas ou vulgares. Vou mostrar essas fórmulas básicas:
K=Integral(p*|x|)
ou
K=Summ(P[i]*|s[i]|)
A primeira variação é para uma variável aleatória contínua e a segunda, para uma discreta. Em nosso caso, para maior clareza, tornamos o valor discreto contínuo, respectivamente, usamos a primeira fórmula. A integral vai de menos a mais infinito. Este é o coeficiente de equilíbrio ou coeficiente de tendência. Quando o calculamos para uma variável aleatória, obtemos um ponto de equilíbrio em relação ao qual podemos comparar a distribuição real da cotação com a de referência. Se Кp > K, o mercado pode ser considerado tendência, e se kp < k, o mercado é lateral.
Neste caso, também podemos calcular o valor máximo deste coeficiente, ele será igual a KMax=1*Max(|x|) ou KMax=1*Max(|s[i]|). Também podemos calcular o valor mínimo deste coeficiente, será igual a KMin=1*Min(|x|) = 0 ou KMin=1*Min(|s[i]|) = 0. O ponto médio KMid, mínimo e máximo, é tudo o que é necessário para avaliar se a área analisada é uma tendência ou uma lateralização, em porcentagem.
if ( K >= KMid ) KTrendPercent=((K-KMid)/(KMax-KMid))*100 else KFletPercent=((KMid-K)/KMid)*100.
Mas isso ainda não é suficiente para caracterizar completamente a situação. Para isso, usamos o segundo coeficiente T=Integral(p*x), T=Summ(P[i]*s[i]), que na verdade reflete o número esperado de passos ascendentes, mas ao mesmo tempo é um indicador da tendência alfa. Se Tp > 0, a tendência será de compra, já se Tp < 0, ela será de venda, uma vez que T=0 para passeio aleatório.
Encontramos o valor máximo e mínimo deste coeficiente: TMax=1*Max(x) ou TMax=1*Max(s[i]), enquanto o mínimo em valor absoluto é igual ao máximo, mas apenas negativo TMin= - TMax. Se medirmos a porcentagem da tendência alfa de 100 a -100, poderemos escrever fórmulas para calcular dado valor, da mesma forma que para o valor anterior:
APercent=( T /TMax)*100.
Se a porcentagem for positiva, teremos uma tendência de alta; se for negativa, uma de baixa. De modo geral, as situações podem ser mistas. Pode haver tendência alfa lateral e tendência alfa, mas tendência e lateralização, não. Ou uma coisa ou a outra. Abaixo você verá uma ilustração gráfica do que foi dito e exemplos de gráficos de densidade para diferente número de passos.
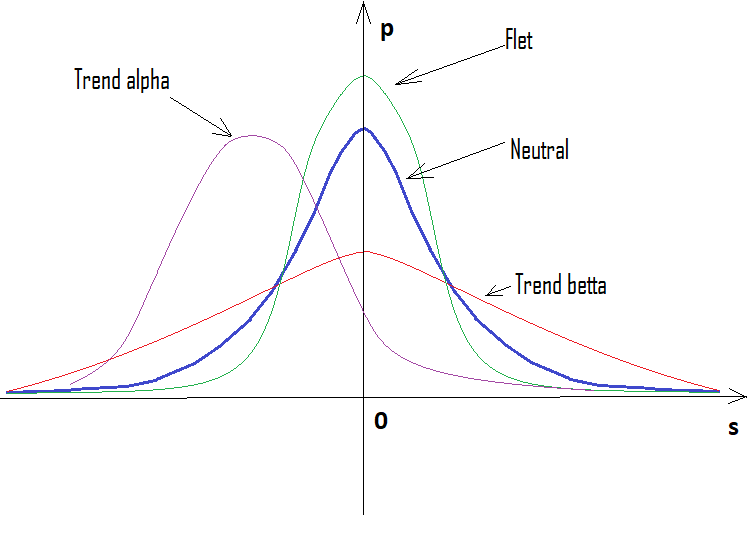
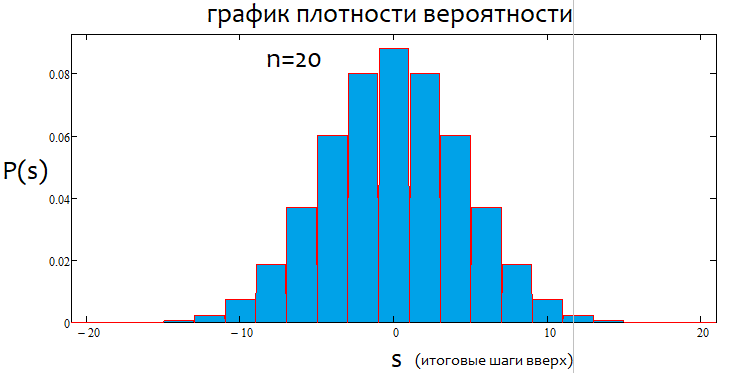
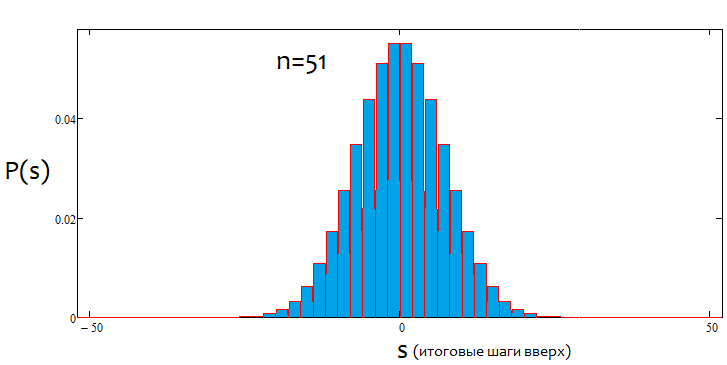
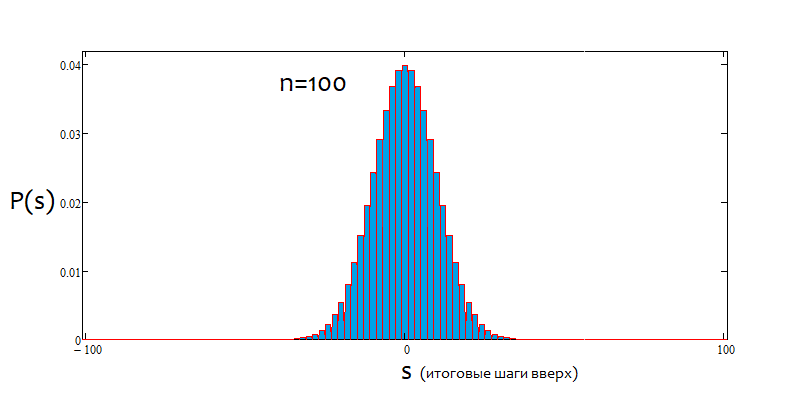
Como podemos ver, com o aumento do número de passos, o gráfico fica mais estreito e alto. Para cada número de passos, os valores alfa e beta correspondentes serão diferentes, assim como o próprio padrão de distribuição. Ao alterar o número de passos, a distribuição de referência deve ser recalculada.
Todas essas fórmulas podem ser usadas para construir sistemas de negociação automatizados; você também pode criar indicadores com base nesses algoritmos. Muitos já implementaram essas coisas em seus EAs. Uma coisa é certa, é melhor usar essa análise do que não. Uma pessoa familiarizada com a matemática terá imediatamente ideias sobre como aplicá-la. Por outra parte, aqueles que, por algum motivo, acham difícil, não importa, lemos, analisamos, tentamos. Tudo vai dar certo.
Escrevemos um indicador simples
Nesta parte do artigo, vamos transformar nossa pesquisa matemática mais simples num indicador que nos ajudará nos pontos de entrada no mercado, além de servir de base para a programação de EAs. Vamos escrever nosso indicador em MQL5. Mas ainda acho que o bom e velho MT4 é muito melhor que seu descendente. Por isso, o código será adaptado ao máximo para portar para MQL4. Em geral, eu mesmo defendo e uso uma abordagem descomplicada. Eu recorro à POO no último momento, se vejo que o código se torna desnecessariamente pesado e ilegível. Mas em 90% dos casos, isso pode ser evitado. Se me perguntarem, ter painéis e botões bonitinhos e fofinhos, bem como muitas informações no gráfico é para mim pura música pop. Isso é feito apenas para o consumidor final. Sempre tento escrever o mínimo exigido. Como em matemática: o necessário e suficiente.
Vamos começar com os parâmetros de entrada do indicador.
input uint BarsI=990;//Bars TO Analyse ( start calc. & drawing ) input uint StepsMemoryI=2000;//Steps In Memory input uint StepsI=40;//Formula Steps input uint StepPoints=30;//Step Value input bool bDrawE=true;//Draw Steps
Quando o indicador é carregado, podemos realizar um cálculo inicial de alguns passos, tomando como base alguns dos últimos candles do gráfico. Também precisamos de um buffer que armazene informações sobre nossos últimos passos e, à medida que chegarem, exclua os antigos e escreva novos em seu lugar. Também terá um tamanho limitado. Usaremos o mesmo tamanho para desenhar passos no gráfico. A nível de indicador, devemos definir quantos passos vamos usar ao construir a distribuição e calcular os valores necessários. A seguir, precisamos informar ao sistema quantos pontos são o tamanho do nosso passo. E, finalmente, precisamos da visualização desses passos. Os passos serão visualizados a partir de um gráfico.
Em geral, escolhi o estilo do indicador numa janela separada, onde a distribuição neutra e a situação atual serão desenhadas. Duas linhas, mas eu queria mais outra linha no gráfico. Infelizmente, como as capacidades dos indicadores não implicam desenhar na janela separada e principal simultaneamente, tive que recorrer ao desenho.
Para poder acessar os dados das barras, como em MQL4, sempre recorro a um pequeno truque:
//variable to be moved in MQL5 double Close[]; double Open[]; double High[]; double Low[]; long Volume[]; datetime Time[]; double Bid; double Ask; double Point=_Point; int Bars=1000; MqlTick TickAlphaPsi; void DimensionAllMQL5Values()//set the necessary array size { ArrayResize(Close,BarsI,0); ArrayResize(Open,BarsI,0); ArrayResize(Time,BarsI,0); ArrayResize(High,BarsI,0); ArrayResize(Low,BarsI,0); ArrayResize(Volume,BarsI,0); } void CalcAllMQL5Values()//recalculate all arrays { ArraySetAsSeries(Close,false); ArraySetAsSeries(Open,false); ArraySetAsSeries(High,false); ArraySetAsSeries(Low,false); ArraySetAsSeries(Volume,false); ArraySetAsSeries(Time,false); if( Bars >= int(BarsI) ) { CopyClose(_Symbol,_Period,0,BarsI,Close); CopyOpen(_Symbol,_Period,0,BarsI,Open); CopyHigh(_Symbol,_Period,0,BarsI,High); CopyLow(_Symbol,_Period,0,BarsI,Low); CopyTickVolume(_Symbol,_Period,0,BarsI,Volume); CopyTime(_Symbol,_Period,0,BarsI,Time); } ArraySetAsSeries(Close,true); ArraySetAsSeries(Open,true); ArraySetAsSeries(High,true); ArraySetAsSeries(Low,true); ArraySetAsSeries(Volume,true); ArraySetAsSeries(Time,true); SymbolInfoTick(Symbol(),TickAlphaPsi); Bid=TickAlphaPsi.bid; Ask=TickAlphaPsi.ask; } ////////////////////////////////////////////////////////////
Agora nosso código é compatível ao máximo com MQL4, e sem muita dificuldade e muito rapidamente você pode fazer um análogo MQL4 a partir dele.
Vamos continuar. Para descrever os passos, primeiro precisamos descrever os nós.
struct Target//structure for storing node data { double Price0;//node price datetime Time0;//node price bool Direction;//direction of a step ending at the current node bool bActive;//whether the node is active }; double StartTick;//initial tick price Target Targets[];//destination point ticks (points located from the previous one by StepPoints)
Além disso, precisamos de um ponto a partir do qual contar o próximo passo. O nó armazena informações sobre si mesmo e o passo que termina nele, também há um componente booleano que diz se o nó está ativo. Somente quando toda a memória da matriz de nós for preenchida com nós reais, começará a ser calculada a distribuição real, porque esta é calculada em passos. Se não houver passos, significa que não haverá nenhum cálculo.
Além disso, devemos conseguir atualizar o estado dos passos a cada tick, bem como realizar um cálculo aproximado por barras quando o indicador é inicializado.
bool UpdatePoints(double Price00,datetime Time00)//update the node array and return 'true' in case of a new node { if ( MathAbs(Price00-StartTick)/Point >= StepPoints )//if the step size reaches the required one, write it and shift the array back { for(int i=ArraySize(Targets)-1;i>0;i--)//fist move everything back { Targets[i]=Targets[i-1]; } //after that, generate a new node Targets[0].bActive=true; Targets[0].Time0=Time00; Targets[0].Price0=Price00; Targets[0].Direction= Price00 > StartTick ? true : false; //finally, redefine the initial tick to track the next node StartTick=Price00; return true; } else return false; } void StartCalculations()//approximate initial calculations (by bar closing prices) { for(int j=int(BarsI)-2;j>0;j--) { UpdatePoints(Close[j],Time[j]); } }
A seguir, descreveremos os métodos e variáveis necessários para calcular todos os parâmetros da linha neutra. Sua ordenada representará a probabilidade de uma combinação ou resultado particular, o que você quiser. Direi desde já que não gosto de chamar isso de distribuição normal, porque a distribuição normal é uma quantidade contínua e, neste caso, estamos traçando uma quantidade discreta. Além disso, a distribuição normal é a densidade de probabilidade, não a probabilidade, como no caso do nosso indicador. Aqui é mais conveniente para nós traçarmos um gráfico a probabilidade, em vez de do da sua densidade.
int S[];//array of final upward steps int U[];//array of upward steps int D[];//array of downward steps double P[];//array of particular outcome probabilities double KBettaMid;//neutral Betta ratio value double KBettaMax;//maximum Betta ratio value //minimum Betta = 0, there is no point in setting it double KAlphaMax;//maximum Alpha ratio value double KAlphaMin;//minimum Alpha ratio value //average Alpha = 0, there is no point in setting it int CalcNumSteps(int Steps0)//calculate the number of steps { if ( Steps0/2.0-MathFloor(Steps0/2.0) == 0 ) return int(Steps0/2.0); else return int((Steps0-1)/2.0); } void ReadyArrays(int Size0,int Steps0)//prepare the arrays { int Size=CalcNumSteps(Steps0); ArrayResize(S,Size); ArrayResize(U,Size); ArrayResize(D,Size); ArrayResize(P,Size); ArrayFill(S,0,ArraySize(S),0);//clear ArrayFill(U,0,ArraySize(U),0); ArrayFill(D,0,ArraySize(D),0); ArrayFill(P,0,ArraySize(P),0.0); } void CalculateAllArrays(int Size0,int Steps0)//calculate all arrays { ReadyArrays(Size0,Steps0); double CT=CombTotal(Steps0);//number of combinations for(int i=0;i<ArraySize(S);i++) { S[i]=Steps0/2.0-MathFloor(Steps0/2.0) == 0 ? i*2 : i*2+1 ; U[i]=int((S[i]+Steps0)/2.0); D[i]=Steps0-U[i]; P[i]=C(Steps0,U[i])/CT; } } void CalculateBettaNeutral()//calculate all Alpha and Betta ratios { KBettaMid=0.0; if ( S[0]==0 ) { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=1;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } else { for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(S[i])*P[i]; } for(int i=0;i<ArraySize(S);i++) { KBettaMid+=MathAbs(-S[i])*P[i]; } } KBettaMax=S[ArraySize(S)-1]; KAlphaMax=S[ArraySize(S)-1]; KAlphaMin=-KAlphaMax; } double Factorial(int n)//factorial of n value { double Rez=1.0; for(int i=1;i<=n;i++) { Rez*=double(i); } return Rez; } double C(int n,int k)//combinations from n by k { return Factorial(n)/(Factorial(k)*Factorial(n-k)); } double CombTotal(int n)//number of combinations in total { return MathPow(2.0,n); }
Todas essas funções precisam ser chamadas no local certo. Todas as funções aqui se destinam a calcular os valores de matrizes ou a implementar algumas funções matemáticas auxiliares, exceto as duas primeiras. Elas são chamadas durante a inicialização junto com o cálculo da distribuição neutra, e servem para definir os tamanhos das nossas matrizes.
A seguir, da mesma forma, criaremos um bloco de código para calcular a distribuição real e seus principais parâmetros.
double AlphaPercent;//alpha trend percentage double BettaPercent;//betta trend percentage int ActionsTotal;//total number of unique cases in the Array of steps considering the number of steps for checking the option int Np[];//number of actual profitable outcomes of a specific case int Nm[];//number of actual losing outcomes of a specific case double Pp[];//probability of a specific profitable step double Pm[];//probability of a specific losing step int Sm[];//number of losing steps void ReadyMainArrays()//prepare the main arrays { if ( S[0]==0 ) { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)-1); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)-1); ArrayResize(Sm,ArraySize(S)-1); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i+1]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } else { ArrayResize(Np,ArraySize(S)); ArrayResize(Nm,ArraySize(S)); ArrayResize(Pp,ArraySize(S)); ArrayResize(Pm,ArraySize(S)); ArrayResize(Sm,ArraySize(S)); for(int i=0;i<ArraySize(Sm);i++) { Sm[i]=-S[i]; } ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); } } void CalculateActionsTotal(int Size0,int Steps0)//total number of possible outcomes made up of the array of steps { ActionsTotal=(Size0-1)-(Steps0-1); } bool CalculateMainArrays(int Steps0)//count the main arrays { int U0;//upward steps int D0;//downward steps int S0;//total number of upward steps if ( Targets[ArraySize(Targets)-1].bActive ) { ArrayFill(Np,0,ArraySize(Np),0);//clear ArrayFill(Nm,0,ArraySize(Nm),0); ArrayFill(Pp,0,ArraySize(Pp),0); ArrayFill(Pm,0,ArraySize(Pm),0); for(int i=1;i<=ActionsTotal;i++) { U0=0; D0=0; S0=0; for(int j=0;j<Steps0;j++) { if ( Targets[ArraySize(Targets)-1-i-j].Direction ) U0++; else D0++; } S0=U0-D0; for(int k=0;k<ArraySize(S);k++) { if ( S[k] == S0 ) { Np[k]++; break; } } for(int k=0;k<ArraySize(Sm);k++) { if ( Sm[k] == S0 ) { Nm[k]++; break; } } } for(int k=0;k<ArraySize(S);k++) { Pp[k]=Np[k]/double(ActionsTotal); } for(int k=0;k<ArraySize(Sm);k++) { Pm[k]=Nm[k]/double(ActionsTotal); } AlphaPercent=0.0; BettaPercent=0.0; for(int k=0;k<ArraySize(S);k++) { AlphaPercent+=S[k]*Pp[k]; BettaPercent+=MathAbs(S[k])*Pp[k]; } for(int k=0;k<ArraySize(Sm);k++) { AlphaPercent+=Sm[k]*Pm[k]; BettaPercent+=MathAbs(Sm[k])*Pm[k]; } AlphaPercent= (AlphaPercent/KAlphaMax)*100; BettaPercent= (BettaPercent-KBettaMid) >= 0.0 ? ((BettaPercent-KBettaMid)/(KBettaMax-KBettaMid))*100 : ((BettaPercent-KBettaMid)/KBettaMid)*100; Comment(StringFormat("Alpha = %.f %%\nBetta = %.f %%",AlphaPercent,BettaPercent));//display these numbers on the screen return true; } else return false; }
Aqui tudo é semelhante, mas há muitas mais matrizes, pois o gráfico nem sempre será espelhado no eixo vertical. Para isso, precisamos de matrizes e variáveis adicionais, mas em geral a lógica é simples: contamos o número de resultados num caso particular e depois dividimos pelo número total de resultados. Assim, obtemos todas as probabilidades (ordenadas) e as abscissas correspondentes. Não vou me aprofundar e analisar cada loop, cada variável. Todas essas dificuldades, na verdade, são para que não houvesse problemas posteriormente com a transferência de valores para buffers sem truques desnecessários. Aqui tudo é quase igual: determinamos o tamanho das matrizes, nós as contamos. Em seguida, calculamos a porcentagem da tendência alfa e beta da tendência e a exibimos no canto superior esquerdo da tela.
Resta determinar o que e onde chamamos.
int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,NeutralBuffer,INDICATOR_DATA); SetIndexBuffer(1,CurrentBuffer,INDICATOR_DATA); CleanAll(); DimensionAllMQL5Values(); CalcAllMQL5Values(); StartTick=Close[BarsI-1]; ArrayResize(Targets,StepsMemoryI);//maximum number of nodes CalculateAllArrays(StepsMemoryI,StepsI); CalculateBettaNeutral(); StartCalculations(); ReadyMainArrays(); CalculateActionsTotal(StepsMemoryI,StepsI); return(INIT_SUCCEEDED); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { CalcAllMQL5Values(); if ( UpdatePoints(Close[0],TimeCurrent()) ) { if ( CalculateMainArrays(StepsI) ) { if ( bDrawE ) RedrawAll(); } } int iterator=rates_total-(ArraySize(Sm)+ArraySize(S))-1; for(int i=0;i<ArraySize(Sm);i++) { iterator++; NeutralBuffer[iterator]=P[ArraySize(S)-1-i]; CurrentBuffer[iterator]=Pm[ArraySize(Sm)-1-i]; } for(int i=0;i<ArraySize(S);i++) { iterator++; NeutralBuffer[iterator]=P[i]; CurrentBuffer[iterator]=Pp[i]; } return(rates_total); }
CurrentBuffer, NeutralBuffer são usados aqui como buffers. Para simplificar, fiz uma exposição sobre os candles mais próximos do mercado. Cada probabilidade está numa barra separada. Isso nos permitiu livrar-nos de dificuldades desnecessárias. Basta aumentar ou diminuir o zoom no gráfico e ver tudo. Não pus as funções CleanAll() e RedrawAll(). Na verdade, elas podem ser comentadas, e tufo funcionará bem só que sem renderização. Não incluí o bloco para renderização. Quem precisar, pode ir ao código fonte. Não tem nada de interessante. O indicador será anexado ao artigo. O indicador será anexado em 2 versões - para MetaTrader 4 e MetaTrader 5.
Isso ficará assim.
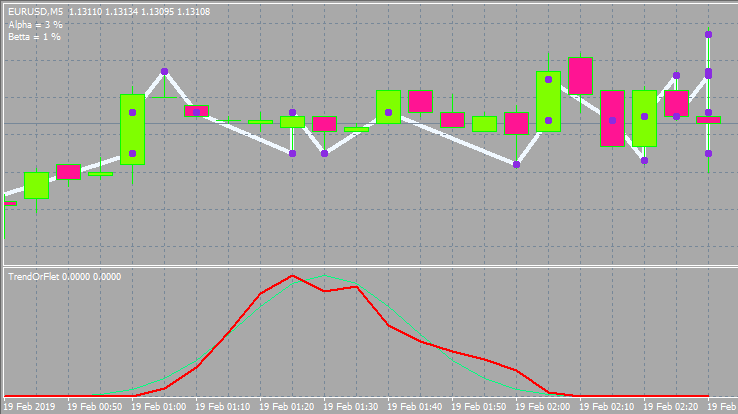
Bem, uma variante com diferentes parâmetros de entrada e estilo de janela.
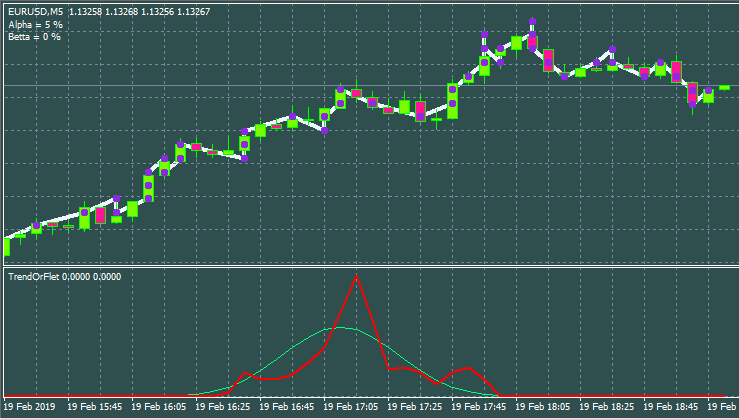
Revisão das estratégias mais interessantes de acordo com minha versão
Eu mesmo fez EAs e vi os de outros programadores. Na minha humilde experiência, algo interessante acontece ao usar uma grade ou ao usar um martingale, ou ambos. Mas, estritamente falando, tanto o martingale quanto a grade têm expectância "0". Não se deixe enganar pelos gráficos ascendentes, pois um dia você poderá apanhar um loss bem gordo. Eu não aconselho você a arriscar. Acredite na minha palavra... Existem grades que funcionam e são vendidas no mercado (marketplace da MQL5). Elas funcionam bem e até mostram um fator de lucro na região de 3-6. Parece um algarismo muito bonito, apesar de tudo isso funcionar para qualquer par de moedas. Mas não é fácil criar filtros que lhe permitam vencer. Usando o método descrito acima, você pode simplesmente filtrar esses sinais. Para a grade, você precisa de uma tendência, sem importar sua direção.
Martingale e grade são um exemplo das estratégias mais simples que estão à vista, todos as conhecem. Tudo pela sua simplicidade e disponibilidade. Mas nem todos podem aplicá-las corretamente. Os Expert Advisors que se adaptam por si só são os seguintes mais difíceis. Eles podem se adaptar a qualquer coisa, como a uma lateralização, a uma tendência, a qualquer outro padrão de comportamento. Eles pegam um pedaço do mercado, procuram padrões e barganham por um curto período de tempo na esperança de que o padrão permaneça por algum tempo.
Um nicho especial é ocupado por sistemas exóticos com algoritmos misteriosos, ao contrário de qualquer outra coisa, abusando apenas do caos do mercado. Esses sistemas funcionam com matemática pura e são capazes de lucrar com base em qualquer instrumento, em qualquer período. Esse lucro não é grande, mas estável. É mesmo com esses sistemas que tenho trabalhado recentemente. Neste nicho também podem ser incluídos robôs baseados em força bruta. A força bruta pode ser executada em software adicional. No próximo artigo, mostrarei minha versão desse software.
O nicho superior é ocupado por robôs baseados em redes neurais e softwares semelhantes. Esses robôs podem apresentar resultados muito diferentes. A complexidade de tais sistemas é máxima. Afinal, uma rede neural é um protótipo de IA. Ao escrever corretamente uma rede neural e treiná-la adequadamente, podemos obter indicadores de lucro que nenhuma outra estratégia pode alcançar.
Quanto à arbitragem, na minha opinião, agora suas possibilidades são praticamente nulas. Eu tenho Expert Advisors. A sua utilidade é "0".
Porém, será isso o que queremos?
Há quem participa da bolsa por entusiasmo, há quem está em busca de dinheiro fácil e rápido, há quem está simplesmente interessado em estudar o mercado, seus processos, construir fórmulas e teorias. E também tem aqueles que simplesmente não tem outra escolha, pois já não há caminho de volta. Eu pertenço mais à última categoria. Com todo o meu conhecimento e experiência, no momento não tenho uma conta estável lucrativa. Tenho EAs, enquanto meu testador diz vá em frente... Mas nem tudo é tão simples 🙂.
Para aqueles que pensam em ficar ricos rapidamente, provavelmente obterão o cenário oposto. Afinal, o mercado não foi criado para que um simples operador ganhe. Foi criado com o propósito oposto e, para quem ainda não entendeu, é hora de entender. Mas se você tem coragem e decide que pode, acumule tempo e paciência. Você não verá um resultado rápido. Se você não sabe programar ou escrever EAs, você não terá praticamente nenhuma chance. Eu vi muitos pseudo traders de todos os tipos que afirmam algo após terem negociado de 20 a 30 trades. Ademais, quando escrevo um EA, primeiro, verifico bem, depois, ele funciona um ou dois anos, depois começo a me aprofundar no histórico, e aí tudo é ao contrário... Isso no melhor dos casos.
Mas, geralmente, nada da certo nesses casos. Na verdade, operar manualmente pode resultar em algo bom, mas isso é mais uma arte do que algum sistema simples e compreensível. Basicamente, todas as informações sobre isso são apenas uma bagunça e especulações. Um contradiz o outro, algo é saudável, algo, não. Tente resolver essa bagunça... Padrões, níveis, fibonacci, padrões de candles, outros disparates... você pode ganhar dinheiro no mercado, mas vai gastar muito tempo antes disso acontecer. Pessoalmente, acho que não vale a pena. Seria melhor se eu fosse trabalhar como programador, agora estaria bebendo um coquetel em algum lugar sem reparar. Já do ponto de vista da matemática, o mercado é apenas uma curvatura, uma bidimensional desinteressante. Eu não gostaria de olhar para esses tristes candles durante toda a minha vida 🙂.
Será que o Santo Graal é possível e onde procurá-lo?
Se chegarmos a esta questão, direi sem hesitar que o Graal é mais do que possível. Eu tenho EAs que provam isso. Embora esses Expert Advisors não sejam tão complicados, os spreads mal interrompem a expectância. Sim, acho que quase todo desenvolvedor tem estratégias que vão confirmar isso. Existem até robôs no mercado, que em todos os aspectos são Santos Grais. Mas ganhar dinheiro com esses sistemas ainda é extremamente difícil, você precisa raspar cada pip, anexar o retorno do spread e os programas para afiliados. Atualmente, Grais com belos lucros e uma pequena carga no depósito podem ser contados com os dedos da mão.
Se você realmente deseja escrever um Graal sozinho, é melhor olhar para as redes neurais. Se houver uma oportunidade de obter lucros superiores, então é só aí. Você também pode combinar qualquer força exótica e bruta. Mas é melhor começar com as redes neurais imediatamente.
Curiosamente, a resposta à questão de onde procurar o Graal e se ele é possível é tão simples e óbvia para mim que não resta dúvida depois de uma tonelada de EAs que fiz.
Dicas para simples traders
Todo mundo quer três coisas:
- Conseguir uma expectância positiva
- Aumentar o lucro no caso de uma posição lucrativa
- Reduzir a perda em caso de uma posição não lucrativa
Na verdade, o primeiro ponto é a pedra angular. Se você tem uma estratégia lucrativa e independentemente de operar manualmente ou com um EA, sempre há o desejo de operar, dando tudo errado. Não podemos permitir isso. Situações em que há muito menos trades vencedores do que perdedores exercem um impacto psicológico muito grande. Isso coloca pressão sobre o operador e anula todo o sistema. O aspeto mais importante é que não há necessidade de tentar obter lucro quando você está no vermelho. Não vai lhe dar absolutamente nada, exceto ansiedade e perdas desnecessárias. Você precisa se lembrar da expectância independentemente da perda da posição atual, o que importa é quantas dessas posições serão no final e quantas lucrativas iremos contrapor a elas.
O segundo ponto importante é o lote usado. Se ganharmos, significa que vamos reduzindo o lote gradativamente, se perdermos, ao contrário, aumentamos gradativamente o lote. Mas só podemos aumentá-lo apenas para algum valor extremo. Isso é um martingale direto e reverso. Se pensar com cuidado, você pode escrever seu próprio Expert Advisor para operar apenas com base nas variações do lote, EA esse que não poderá ser uma grade ou um martingale, senão algo maior e, além disso, mais seguro. O mais importante é que funcione com todos os pares de moedas do histórico de cotações completo. Esse princípio funciona mesmo em mercados caóticos, sem importar onde e como entrar. Com o uso adequado, você compensa todos os spreads e comissões, já com o uso magistral, você lucra, mesmo que você abra geralmente em lugares aleatórios e numa direção aleatória.
O terceiro ponto também é importante. Para reduzir as perdas e aumentar os lucros, tente abrir uma posição de compra dentro de uma meia onda negativa e vender dentro de uma meia onda positiva. Acontece que uma meia onda na maioria dos casos indica que os vendedores ou compradores estavam ativos nesta área, o que por sua vez significa que alguma porcentagem deles eram a mercado para abertura de posição, e as posições que estavam abertas mais cedo ou mais tarde seriam encerradas, movendo o preço na direção oposta. É por isso que o mercado tem uma estrutura ondulatória. Vemos essas ondas em todos os lugares. Uma compra é seguida por uma venda e vice-versa. Além disso, cada um de nós fecha as posições de acordo com o mesmo critério.
Fim do artigo
Claro, no final, direi que tudo é subjetivo e que cada um analisa à sua maneira. No final das contas, tudo depende de você, de uma forma ou de outra. Mas, apesar de todos os contras e tempo perdido, todo mundo também quer criar seu próprio super sistema e colher os benefícios de sua teimosia. De outra forma, não entendo por que operar Forex. A experiência é inestimável e o dinheiro, mínimo. Mas há algo de atraente nisto que não me permite sair desta esfera. Todo mundo sabe como chamá-lo, embora soe infantil. Por isso, provavelmente não vou verbalizá-lo, para não trollar 🙂.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8274
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Uma abordagem científica para o desenvolvimento de algoritmos de negociação
Uma abordagem científica para o desenvolvimento de algoritmos de negociação
 Otimização paralela pelo método de enxame de partículas (Particle Swarm Optimization)
Otimização paralela pelo método de enxame de partículas (Particle Swarm Optimization)
 Abordagem de força bruta para encontrar padrões
Abordagem de força bruta para encontrar padrões
 Símbolos personalizados: Fundamentos práticos
Símbolos personalizados: Fundamentos práticos
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Obrigado por este artigo. Nunca fui muito bom em matemática, mas continuarei tentando entendê-la para poder me tornar um operador melhor.
Ótimo artigo! Obrigado a você!
Obrigado, escrevi muitos outros artigos depois deste, dê uma olhada e veja se encontra algo mais útil.