Construya Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte II): Ajuste de redes neuronales profundas

Introducción

Los miembros de nuestra comunidad están interesados en integrar IA en sus estrategias comerciales, lo que requiere ajustar los modelos de IA para mercados específicos. Cada modelo de IA tiene parámetros ajustables que influyen significativamente en su rendimiento; las configuraciones óptimas para un mercado pueden no funcionar para otro. Este artículo mostrará cómo personalizar los modelos de IA para superar las configuraciones predeterminadas utilizando algoritmos de optimización, específicamente el algoritmo Nelder-Mead. Aplicaremos este algoritmo para ajustar una red neuronal profunda utilizando datos de la terminal MetaTrader 5 y luego exportaremos el modelo optimizado en formato ONNX para su uso en un Asesor Experto. Para aquellos que no estén familiarizados con estos conceptos, proporcionaremos explicaciones detalladas a lo largo del artículo.

Algoritmo de optimización de Nelder-Mead

El algoritmo Nelder-Mead es una opción popular para problemas de optimización multimodales ruidosos, no diferenciables y no lineales. El algoritmo, que debe su nombre a sus inventores John Nelder y Roger Mead, se presentó en el artículo de 1965 titulado "Un método simplex para la minimización de funciones". Se puede utilizar para problemas de optimización tanto univariados como multivariados.

El algoritmo Nelder-Mead no se basa en información derivada; en cambio, es un algoritmo de optimización de búsqueda de patrones. Requiere que el usuario proporcione un punto de partida. Dependiendo del punto de partida elegido, el algoritmo podría quedar atrapado en un óptimo local engañoso. Por lo tanto, puede ser beneficioso realizar la optimización varias veces con diferentes puntos de partida para mejorar las posibilidades de encontrar un óptimo global.

El algoritmo funciona utilizando una forma geométrica llamada simplex. El simplex tiene un vértice para cada variable de entrada más un vértice adicional. Se evalúan los puntos (vértices) del simplex y se utilizan reglas simples para mover los puntos en función de sus evaluaciones. El algoritmo tiene ciertas condiciones de detención, como alcanzar el número máximo de iteraciones o lograr un cambio mínimo en los valores de evaluación. Si no se realizan mejoras o se excede el número permitido de iteraciones, el procedimiento de optimización se detiene.

Figura 1: Roger Mead.

Figura 2: John Nelder.

Empecemos

Comenzamos obteniendo los datos que necesitamos de nuestro terminal MetaTrader 5. Primero, abrimos nuestra terminal MetaTrader 5 y hacemos clic en el ícono Símbolo en el menú contextual. Desde allí, seleccionamos barras y buscamos el símbolo que deseamos utilizar. Una vez que haya solicitado los datos, simplemente haga clic en exportar y los datos estarán disponibles para usted en formato CSV.

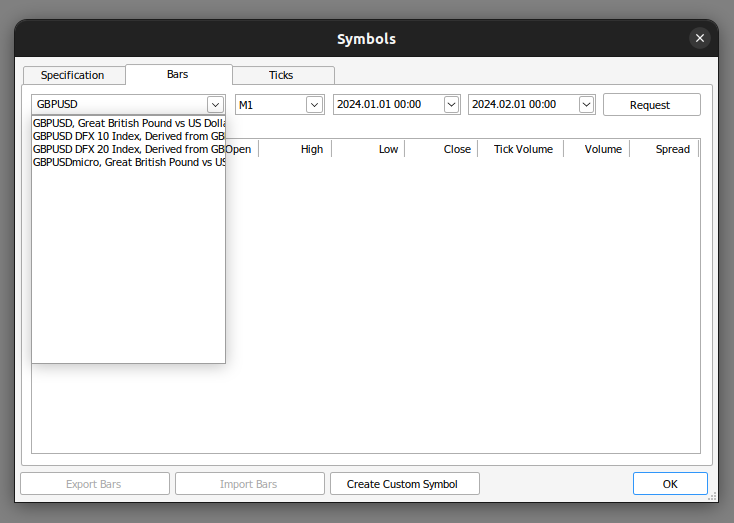
Figura 3: Busque los datos que necesita.

Ahora que nuestros datos están listos, podemos comenzar a importar las bibliotecas que necesitamos.

#import libraries we need
import pandas as pd
import numpy as np
from numpy.random import randn,rand
import seaborn as sns

Luego leemos los datos que preparamos.

#Read in our market data
brent = pd.read_csv("/home/volatily/market_data/Market Data UK Brent Oil.csv", sep="\t")

Necesitamos etiquetar nuestros datos.

#Preparing to label the data
look_ahead = 20

#Defining the target
brent["Target"] = brent["Close"].shift(-look_ahead)

#Drop missing values
brent.dropna(inplace=True)

Importemos las bibliotecas que necesitamos para la optimización.

#In this article we will cover some techniques for hyper-parameter tuning 
from scipy.optimize import minimize
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import root_mean_squared_error
import time

Ahora crearemos nuestro objeto de validación cruzada de series de tiempo.

#Define the time series split parameters
splits = 5
gap = look_ahead

#Create the time series split object
tscv = TimeSeriesSplit(n_splits=splits,gap=gap)

#Create a dataframe to store our accuracy 
current_error_rate = pd.DataFrame(index = np.arange(0,splits),columns=["Current Error"])

Definamos los predictores y objetivos de nuestro modelo.

#Define the predictors and the target
predictors = ["Open","High","Low","Close"]
target = "Target"

Ahora definimos la función que pretendemos minimizar: el error de validación cruzada del modelo. Tenga en cuenta que esto es sólo para fines demostrativos. Lo ideal sería dividir el conjunto de datos en dos, realizar la optimización en una mitad y medir la precisión en la otra mitad. Sin embargo, para esta demostración, estamos optimizando el modelo y midiendo su precisión utilizando el mismo conjunto de datos.

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    model = MLPRegressor(hidden_layer_sizes=(5,2),alpha=x[0],early_stopping=True,shuffle=False,learning_rate_init=x[1],tol=x[2])
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(brent)):
        #The data
        X_train = brent.loc[train[0]:train[-1],predictors]
        y_train = brent.loc[train[0]:train[-1],target]
        X_test  = brent.loc[test[0]:test[-1],predictors]
        y_test  = brent.loc[test[0]:test[-1],target]
        #Train the model
        model.fit(X_train,y_train)
        #Measure the RMSE
        current_error_rate.iloc[i,0] = root_mean_squared_error(y_test,model.predict(X_test))
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Recordemos que el algoritmo Nelder-Mead requiere un punto de partida inicial. Para encontrar un buen punto de partida, realizaremos una búsqueda lineal sobre los parámetros en cuestión. Utilizaremos un bucle for para medir nuestra precisión con parámetros establecidos en 0,1, luego en 0,01, y así sucesivamente. Esto nos ayudará a identificar un punto de partida potencialmente bueno para el algoritmo.

#Let us measure how much time this takes.
start = time.time()

#Create a dataframe to measure the error rates
starting_point_error = pd.DataFrame(index=np.arange(0,21),columns=["Average CV RMSE"])
starting_point_error["Iteration"] = np.arange(0,21)

#Let us first find a good starting point for our optimization algorithm
for i in np.arange(0,21):
    #Set a new starting point
    new_starting_point = (10.0 ** -i)
    #Store error rates
    starting_point_error.iloc[i,0] = objective([new_starting_point,new_starting_point,new_starting_point]) 

#Record the time stamp at the end
stop = time.time()

#Report the amount of time taken
print(f"Completed in {stop - start} seconds")

Completado en 312.29402351379395 segundos.

Observemos ahora nuestros niveles de error.

CV RMSE promedio	Iteración
0.91546	0
0.267167	1
14.846035	2
15.763264	3
56.820397	4
75.202923	5
72.562681	6
64.33746	7
88.980977	8
83.791834	9
82.871215	10
88.031151	11
65.532539	12
78.177191	13
85.063947	14
88.631589	15
74.369735	16
86.133656	17
90.482654	18
102.803612	19
74.636781	20

Como podemos ver, parece que pasamos por una región óptima entre la iteración 0 y 2. A partir de ahí nuestro error fue aumentando. Podemos observar la misma información visualmente.

sns.lineplot(data=starting_point_error,x="Iteration",y="Average CV RMSE")

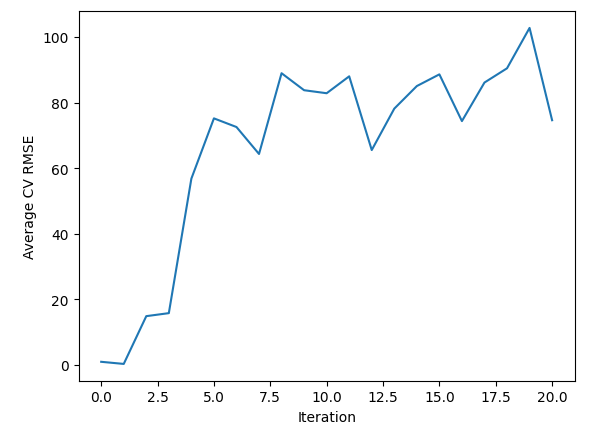
Figura 4: Visualizando los resultados de nuestra búsqueda de línea.

Ahora que tenemos una idea de cuál puede ser un buen punto de partida, definamos una función que nos dé puntos aleatorios dentro del rango en el que creemos que pueden estar los óptimos.

pt = abs(((10 ** -1) + rand(3) * ((10 ** 0) - (10 ** -1))))
pt

array([0.75747551, 0.34066536, 0.26214705])

Tenga en cuenta que estamos obteniendo una matriz de 3 valores aleatorios porque estamos optimizando 3 parámetros diferentes en nuestra red neuronal. Ahora realicemos el ajuste de hiperparámetros.

start = time.time()
result = minimize(objective,pt,method="nelder-mead")
stop = time.time()
print(f"Task completed in {stop - start} seconds")

Tarea completada en 1332,9911317825317 segundos.

Interpretemos el resultado de la optimización.

result

message: Maximum number of function evaluations has been exceeded.
       success: False
        status: 1
           fun: 0.12022686955703668
             x: [ 7.575e-01  3.577e-01  2.621e-01]
           nit: 225
          nfev: 600
 final_simplex: (array([[ 7.575e-01,  3.577e-01,  2.621e-01],
                       [ 7.575e-01,  3.577e-01,  2.621e-01],
                       [ 7.575e-01,  3.577e-01,  2.621e-01],
                       [ 7.575e-01,  3.577e-01,  2.621e-01]]), array([ 1.202e-01,  2.393e-01,  2.625e-01,  8.978e-01])

Primero, observe el mensaje fácil de usar que se muestra en la parte superior. El mensaje indica que el algoritmo ha superado el número máximo de evaluaciones de funciones. Recuerde las condiciones que especificamos anteriormente con respecto a los escenarios que provocarían que se detuviera la optimización. Si bien podemos intentar aumentar la cantidad de iteraciones permitidas, eso no garantiza un mejor rendimiento.

Podemos ver la clave 'fun', que indica el resultado óptimo que el algoritmo logró de la función. A continuación está la clave "x", que muestra los valores de x que dieron como resultado el resultado óptimo.

También podemos observar la tecla ‘nit’, que nos indica el número de iteraciones que realizó la función. Por último, la clave 'nfev' indica el número de veces que el algoritmo llamó a la función objetivo para evaluar su salida. Recuerde que nuestra función objetivo realizó una validación cruzada de cinco veces y devolvió la tasa de error promedio. Esto significa que cada vez que llamamos a la función una vez, ajustamos nuestra red neuronal 5 veces. Por lo tanto, ¡600 evaluaciones de funciones significan que ajustamos nuestra red neuronal 3000 veces!

Comparemos ahora el modelo predeterminado y el modelo personalizado que construimos.

#Let us compare our customised model and the defualt model
custom_model = MLPRegressor(hidden_layer_sizes=(5,2),alpha=result.x[0],early_stopping=True,shuffle=False,learning_rate_init=result.x[1],tol=result.x[2])

#Default model
default_model = MLPRegressor(hidden_layer_sizes=(5,2))

Prepararemos el objeto de división de series de tiempo.

#Define the time series split parameters
splits = 10
gap = look_ahead

#Create the time series split object
tscv = TimeSeriesSplit(n_splits=splits,gap=gap)

#Create a dataframe to store our accuracy 
model_error_rate = pd.DataFrame(index = np.arange(0,splits),columns=["Default Model","Custom Model"])

Ahora validaremos de forma cruzada cada modelo.

#Now we will cross validate the model
for i,(train,test) in enumerate(tscv.split(brent)):
    #The data
    X_train = brent.loc[train[0]:train[-1],predictors]
    y_train = brent.loc[train[0]:train[-1],target]
    X_test  = brent.loc[test[0]:test[-1],predictors]
    y_test  = brent.loc[test[0]:test[-1],target]
    #Our model
    model = MLPRegressor(hidden_layer_sizes=(5,2),alpha=result.x[0],early_stopping=True,shuffle=False,learning_rate_init=result.x[1],tol=result.x[2])
    #Train the model
    model.fit(X_train,y_train)
    #Measure the RMSE
    model_error_rate.iloc[i,1] = root_mean_squared_error(y_test,model.predict(X_test))

Observemos nuestras métricas de error.

model_error_rate

Modelo predeterminado	Modelo personalizado
0.153904	0.550214
0.113818	0.501043
82.188345	0.52897
0.114108	0.117466
0.114718	0.112892
77.508403	0.258558
0.109191	0.304262
0.142143	0.363774
0.163161	0.153202
0.120068	2.20102

Visualicemos también los resultados.

model_error_rate["Default Model"].plot(legend=True)
model_error_rate["Custom Model"].plot(legend=True)

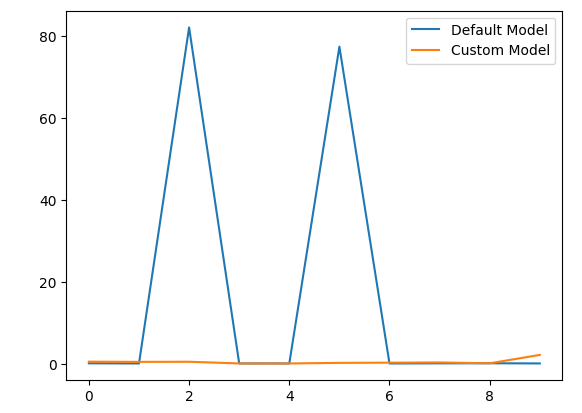
Figura 5: Visualización del rendimiento de nuestro modelo personalizado.

Como podemos observar, el modelo personalizado superó al modelo predeterminado. Sin embargo, nuestra prueba habría sido más convincente si hubiéramos utilizado conjuntos de datos separados para entrenar los modelos y evaluar su precisión. Utilizar el mismo conjunto de datos para ambos propósitos no es el procedimiento ideal.

A continuación, nos prepararemos para convertir nuestra red neuronal profunda en su representación ONNX. ONNX, que significa Open Neural Network Exchange, es un formato estandarizado que permite que los modelos de IA entrenados en cualquier marco compatible se utilicen en diferentes programas. Por ejemplo, ONNX nos permite entrenar un modelo de IA en Python y luego usarlo en MQL5 o incluso en un programa Java (siempre que la API de Java admita ONNX).

Primero, importamos las bibliotecas que necesitamos.

#Now we will prepare to export our neural network into ONNX format
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn
import onnxruntime as ort
import netron

Definamos la forma de entrada para nuestro modelo, recuerde que nuestro modelo toma 4 entradas.

#Define the input types
initial_type = [("float_input",FloatTensorType([1,4]))]

Adaptable a nuestro modelo personalizado.

#Fit our custom model
custom_model.fit(brent.loc[:,["Open","High","Low","Close"]],brent.loc[:,"Target"])

Crear la representación ONNX de nuestra red neuronal profunda es fácil gracias a la biblioteca skl2onnx.

#Create the onnx represantation
onnx = convert_sklearn(custom_model,initial_types=initial_type,target_opset=12)

Define el nombre de nuestro archivo ONNX.

#The name of our ONNX file
onnx_filename = "Brent_M1.onnx"

Ahora escribiremos el archivo ONNX.

#Write out the ONNX file
with open(onnx_filename,"wb") as f:
    f.write(onnx.SerializeToString())

Inspeccionemos los parámetros de nuestro modelo ONNX.

#Now let us inspect our ONNX model
onnx_session = ort.InferenceSession(onnx_filename)
input_name   = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

Veamos la forma de entrada.

for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

1. Name: float_input, Data Type: tensor(float), Shape: [1, 4]

Observe la forma de salida de nuestro modelo.

for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

1. Name: variable, Data Type: tensor(float), Shape: [1, 1]

Ahora podemos ver nuestro modelo visualmente usando Netron. Estos pasos nos ayudan a garantizar que nuestras formas de entrada y salida ONNX se ajusten a nuestras expectativas.

#We can also inspect our model visually using netron.
netron.start(onnx_filename)

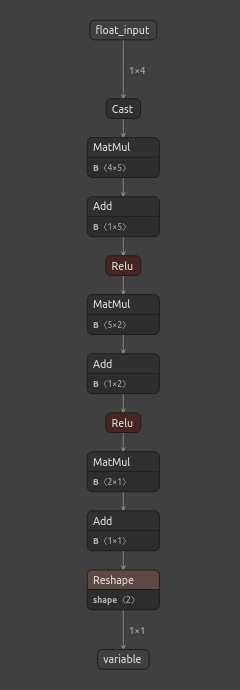
Figura 6: La representación ONNX de nuestra red neuronal.

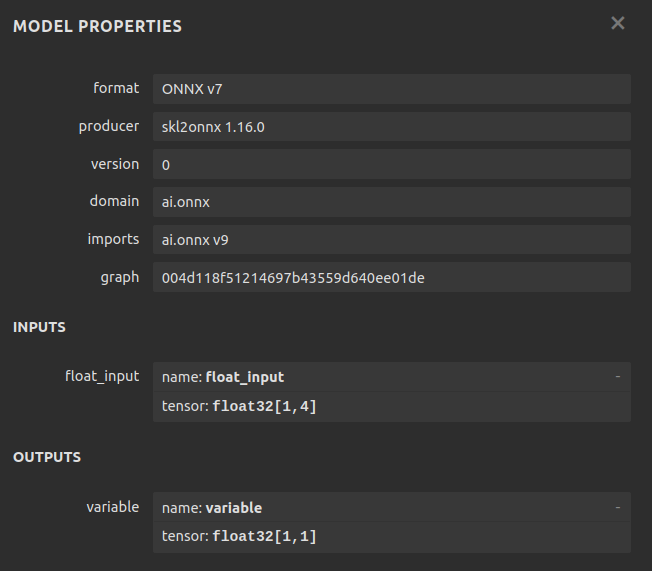
Figura 7: Metadetalles de nuestro modelo ONNX.

Netron es una biblioteca Python de código abierto que nos permite inspeccionar visualmente los modelos ONNX, verificar sus parámetros y revisar metadatos. Para aquellos interesados en aprender más sobre el uso de los modelos ONNX en MetaTrader 5, hay muchos artículos bien escritos disponibles. Uno de mis autores favoritos sobre el tema es Omega.

Implementación en MQL5

Con la configuración de nuestro modelo ONNX finalizada, podemos comenzar a construir nuestro Asesor Experto en MQL5.

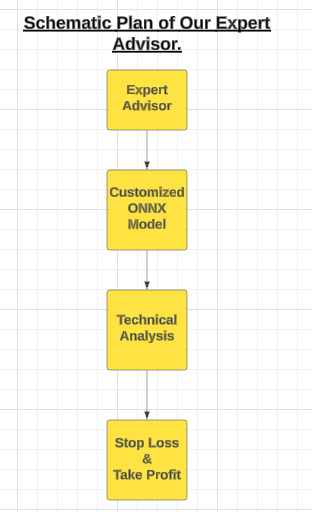
Figura 8: Un plano esquemático de nuestro Asesor Experto.

Nuestro Asesor Experto utilizará el modelo ONNX personalizado para generar señales de entrada. Sin embargo, todos los buenos traders deben tener cuidado de no ejecutar todas las señales de entrada que reciben. Para inculcar esta disciplina en nuestro Asesor Experto, lo programaremos para esperar la confirmación de los indicadores técnicos antes de abrir una posición.

Estos indicadores técnicos nos ayudarán a cronometrar nuestras entradas de manera efectiva. Una vez abiertas las posiciones, los niveles de stop loss definidos por el usuario serán responsables de cerrarlas. El primer paso es especificar el modelo ONNX como recurso para nuestra aplicación.

//+------------------------------------------------------------------+
//|                                   Custom Deep Neural Network.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load the ONNX model                                              |
//+------------------------------------------------------------------+
#resource "\\Files\\Brent_M1.onnx" as const uchar ModelBuffer[];

A continuación, cargaremos la biblioteca de operaciones, que es esencial para gestionar nuestras posiciones.

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh>
CTrade Trade;

Ahora podemos pasar a crear variables globales para nuestro programa.

//+------------------------------------------------------------------+
//| Gloabal variables                                                |
//+------------------------------------------------------------------+
long model; //The handler for our ONNX model
vector forecast = vector::Zeros(1); //Our model's forecast

const int states = 3; //The total number of states the system can be in
vector state = vector::Zeros(states); //The state of our system

int mfi_handler,wpr_handler; //Handlers for our technical indicators
vector mfi_reading,wpr_reading; //The values of our indicators will be kept in vectors

double minimum_volume, trading_volume; //Smallest lot size allowed & our calculated lotsize
double ask_price, bid_price; //Market rates

Definamos las entradas de usuario que nos permiten modificar el comportamiento del Asesor Experto.

//+------------------------------------------------------------------+
//| Inputs                                                           |
//+------------------------------------------------------------------+
input int mfi_period = 20; //Money Flow Index Period
input int wpr_period = 30; //Williams Percent Range Period

input int lot_multiple = 20; //How big should our lot sizes be?
input double sl_width = 2; //How tight should the stop loss be?

input double max_profit = 10; //Close the position when this profit level is reached.
input double max_loss = 10; //Close the position when this loss level is reached.

Nuestra aplicación requiere funciones auxiliares para realizar rutinas específicas. Comenzamos definiendo una función que gestiona el estado de la aplicación. Esta aplicación tendrá tres estados: el estado 0 implica que no tenemos posiciones, mientras que los estados 1 y 2 indican una posición de compra o venta, respectivamente.

Dependiendo del estado actual, la aplicación tendrá acceso a diferentes funciones.

//+------------------------------------------------------------------+
//| This function is responsible for updating the system state       |
//+------------------------------------------------------------------+
void update_state(int index)
  {
//--- Reset the system state
   state = vector::Zeros(states);
//--- Now update the current state
   state[index] = 1;
  }

A continuación, necesitamos una función responsable de validar las entradas del usuario al iniciar la aplicación. Por ejemplo, esta función garantizará que todos los períodos de indicadores técnicos sean mayores que 0.

//+------------------------------------------------------------------+
//| This function will ensure that user inputs are valid             |
//+------------------------------------------------------------------+
bool valid_inputs(void)
  {
//--- Let us validate the inputs the user passed
   return((mfi_period > 0)&&(wpr_period > 0) && (max_profit >= 0) && (max_loss >= 0) && (lot_multiple >= 0) && (sl_width >= 0));
  }

Nuestro Asesor Experto verificará continuamente si los niveles de beneficio cumplen con las entradas especificadas por el usuario. Por ejemplo, si el usuario establece un objetivo de beneficio máximo de $1, la posición se cerrará automáticamente una vez que alcance un beneficio de $1, incluso si aún no ha alcanzado el nivel de toma de beneficios. La misma lógica se aplica al stop loss: la posición se cerrará en función del umbral que se alcance primero, ya sea el nivel de stop loss o el nivel de pérdida máxima. Esta función está diseñada para proporcionar flexibilidad en la definición de niveles de riesgo aceptables.

//+------------------------------------------------------------------+
//| This function will check our profit levels                       |
//+------------------------------------------------------------------+
void check_profit_level(void)
  {
//--- Let us check if the user set a max profit/loss limit
   if(max_loss > 0 || max_profit > 0)
     {
      //--- If true, let us inspect whether we have passed the limit.
      if((PositionGetDouble(POSITION_PROFIT) > max_profit) || (PositionGetDouble(POSITION_PROFIT) < (max_loss * -1)))
        {
         //--- Close the position
         Trade.PositionClose(Symbol());
        }
     }
  }

Dado que tenemos un sistema basado en IA, construyamos una función para verificar si nuestro modelo pronostica un movimiento del mercado que pueda ser adverso para nuestra posición abierta. Estas señales pueden servir como indicaciones tempranas de un cambio en el sentimiento del mercado.

//+------------------------------------------------------------------+
//| If we predict a reversal, let's close our positions              |
//+------------------------------------------------------------------+
void find_reversal(void)
  {
//--- We have a position
   if(((state[1] == 1) && (forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0))) || ((state[2] == 1) && (forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))))
     {
      Trade.PositionClose(Symbol());
     }
  }

A continuación, definiremos una función para comprobar si hay señales de entrada válidas. Una señal de entrada se considera válida si cumple dos condiciones: primero, debe estar respaldada por cambios en el nivel de precios en períodos de tiempo más altos; segundo, nuestro modelo de IA debe pronosticar un movimiento de precios alineado con esta tendencia más alta. Si se cumplen ambas condiciones, comprobaremos nuestros indicadores técnicos para el nivel final de confirmación.

//+------------------------------------------------------------------+
//| This function will determine if we have a valid entry            |
//+------------------------------------------------------------------+
void find_entry(void)
  {
//--- First we want to know if the higher timeframes are moving in the same direction we want to go
   double higher_time_frame_trend = iClose(Symbol(),PERIOD_W1,16) - iClose(Symbol(),PERIOD_W1,0);

//--- If price levels appreciated, the difference will be negative
   if(higher_time_frame_trend < 0)
     {
      //--- We may be better off only taking buy opportunities
      //--- Buy opportunities are triggered when the model's prediction is greater than the current price
      if(forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))
        {
         //--- We will use technical indicators to time our entries
         bullish_sentiment();
        }
     }

//--- If price levels depreciated, the difference will be positive
   if(higher_time_frame_trend > 0)
     {
      //--- We may be better off only taking sell opportunities
      //--- Sell opportunities are triggered when the model's prediction is less than the current price
      if(forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0))
        {
         //--- We will use technical indicators to time our entries
         bearish_sentiment();
        }
     }
  }

Ahora, hemos llegado a la función encargada de interpretar nuestros indicadores técnicos. Hay varias formas de interpretar estos indicadores, sin embargo, prefiero centrarlos alrededor de 50. De esta manera, los valores superiores a 50 confirman un sentimiento alcista, mientras que los valores inferiores a 50 indican un sentimiento bajista. Utilizaremos el índice de flujo de dinero (MFI) como nuestro indicador de volumen y el rango de porcentaje de Williams (WPR) como nuestro indicador de fortaleza de tendencia.

//+------------------------------------------------------------------+
//| This function will interpret our indicators for buy signals      |
//+------------------------------------------------------------------+
void bullish_sentiment(void)
  {
//--- For bullish entries we want strong volume readings from our MFI
//--- And confirmation from our WPR indicator
   wpr_reading.CopyIndicatorBuffer(wpr_handler,0,0,1);
   mfi_reading.CopyIndicatorBuffer(mfi_handler,0,0,1);
   if((wpr_reading[0] > -50) && (mfi_reading[0] > 50))
     {
      //--- Get the ask price
      ask_price = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
      //--- Make sure we have no open positions
      if(PositionsTotal() == 0)
         Trade.Buy(trading_volume,Symbol(),ask_price,(ask_price - sl_width),(ask_price + sl_width),"Custom Deep Neural Network");
      update_state(1);
     }
  }

//+------------------------------------------------------------------+
//| This function will interpret our indicators for sell signals     |
//+------------------------------------------------------------------+
void bearish_sentiment(void)
  {
//--- For bearish entries we want strong volume readings from our MFI
//--- And confirmation from our WPR indicator
   wpr_reading.CopyIndicatorBuffer(wpr_handler,0,0,1);
   mfi_reading.CopyIndicatorBuffer(mfi_handler,0,0,1);
   if((wpr_reading[0] < -50) && (mfi_reading[0] < 50))
     {
      //--- Get the bid price
      bid_price = SymbolInfoDouble(Symbol(),SYMBOL_BID);
      if(PositionsTotal() == 0)
         Trade.Sell(trading_volume,Symbol(),bid_price,(bid_price + sl_width),(bid_price - sl_width),"Custom Deep Neural Network");
      //--- Update the state
      update_state(2);
     }
  }

A continuación, nos centramos en obtener predicciones de nuestro modelo ONNX. Recuerde, nuestro modelo espera entradas de forma [1,4] y devuelve salidas de forma [1,1]. Definimos vectores para almacenar las entradas y salidas en consecuencia, y luego usamos la función OnnxRun para obtener el pronóstico del modelo.

//+------------------------------------------------------------------+
//| This function will fetch forecasts from our model                |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- First we get the input data ready
   vector input_data = {iOpen(_Symbol,PERIOD_CURRENT,0),iHigh(_Symbol,PERIOD_CURRENT,0),iLow(_Symbol,PERIOD_CURRENT,0),iClose(_Symbol,PERIOD_CURRENT,0)};
//--- Now we need to perform inferencing
   if(!OnnxRun(model,ONNX_DATA_TYPE_FLOAT,input_data,forecast))
     {
      Comment("Failed to obtain a forecast from the model: ",GetLastError());
      forecast[0] = 0;
      return;
     }
//--- We succeded!
   Comment("Model forecast: ",forecast[0]);
  }

Ahora podemos comenzar a construir el controlador de eventos para nuestra aplicación, que se invocará tras la inicialización del Asesor Experto. Nuestro procedimiento primero validará las entradas del usuario y luego definirá las formas de entrada y salida de nuestro modelo ONNX. A continuación, configuraremos nuestros indicadores técnicos, obtendremos datos del mercado y, finalmente, estableceremos el estado de nuestro sistema en 0.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Make sure user inputs are valid
   if(!valid_inputs())
     {
      Comment("Invalid inputs were passed to the application.");
      return(INIT_FAILED);
     }

//--- Create the ONNX model from the buffer
   model = OnnxCreateFromBuffer(ModelBuffer,ONNX_DEFAULT);

//--- Check if we were succesfull
   if(model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to create the ONNX model from the buffer: ",GetLastError());
      return(INIT_FAILED);
     }

//--- Set the input shape of the model
   ulong input_shape[] = {1,4};

//--- Check if we were succesfull
   if(!OnnxSetInputShape(model,0,input_shape))
     {
      Comment("[ERROR] Failed to set the ONNX model input shape: ",GetLastError());
      return(INIT_FAILED);
     }

//--- Set the output shape of the model
   ulong output_shape[] = {1,1};

//--- Check if we were succesfull
   if(!OnnxSetOutputShape(model,0,output_shape))
     {
      Comment("[ERROR] Failed to set the ONNX model output shape: ",GetLastError());
      return(INIT_FAILED);
     }

//--- Setup the technical indicators
   wpr_handler = iWPR(Symbol(),PERIOD_CURRENT,wpr_period);
   mfi_handler = iMFI(Symbol(),PERIOD_CURRENT,mfi_period,VOLUME_TICK);

//--- Fetch market data
   minimum_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN);
   trading_volume = minimum_volume * lot_multiple;

//--- Set the system to state 0, indicating we have no open positions
   update_state(0);

//--- Everything went fine
   return(INIT_SUCCEEDED);
  }

Una parte crucial de nuestra aplicación es el procedimiento de desinicialización. En este controlador de eventos, liberaremos cualquier recurso que ya no sea necesario cuando el Asesor Experto no esté en uso.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free the onnx resources
   OnnxRelease(model);

//--- Free the indicator resources
   IndicatorRelease(wpr_handler);
   IndicatorRelease(mfi_handler);

//--- Detach the expert advisor
   ExpertRemove();
  }

Por último, necesitamos definir nuestro controlador de eventos OnTick. Las acciones tomadas dependerán del estado del sistema. Si no tenemos posiciones abiertas (estado 0), nuestra prioridad será obtener un pronóstico de nuestro modelo e identificar una entrada potencial. Si tenemos una posición abierta (estado 1 para largo o estado 2 para corto), nuestro enfoque se desplazará hacia la gestión de la posición. Esto incluye el monitoreo de posibles reversiones y la verificación de los niveles de riesgo, los objetivos de ganancias y los niveles máximos de ganancias.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Which state is the system in?
   if(state[0] == 1)
     {
      //--- Being in this state means we have no open positions, let's analyse the market to try find one
      model_predict();
      find_entry();
     }

   if((state[1] == 1) || (state[2] == 1))
     {
      //--- Being in this state means we have an position open, if our model forecasts a reversal move we will close
      model_predict();
      find_reversal();
      check_profit_level();
     }
  }
//+------------------------------------------------------------------+

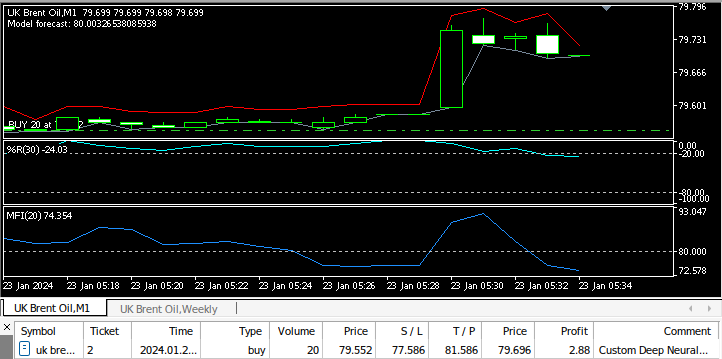
Figura 9: Prueba de nuestro Asesor Experto.

Conclusión

Este artículo proporcionó una introducción suave al uso de algoritmos de optimización para la selección de hiperparámetros del modelo. En futuros artículos, adoptaremos una metodología más sólida, utilizando dos conjuntos de datos dedicados: uno para optimizar el modelo y el otro para realizar una validación cruzada y comparar su rendimiento con un modelo que utiliza configuraciones predeterminadas.