Técnicas do MQL5 Wizard que você deve conhecer (Parte 27): Médias Móveis e o Ângulo de Ataque

Introdução

Continuamos a série sobre setups de negociação e ideias que podem ser rapidamente testadas e refinadas graças ao MQL5 Wizard, considerando o ângulo de ataque. De maneira geral, a expressão “ângulo de ataque” está associada ao ângulo ideal em que um caça deve decolar, quando otimizado para o máximo de sustentação e mínimo consumo de combustível.

Para os traders, no entanto, essa frase geralmente se refere à trajetória do preço de um ativo quando no meio de uma tendência, sendo o consenso geral de que um ângulo íngreme aponta para uma tendência forte. Portanto, iniciamos este artigo explorando não apenas essa visão, mas mais importante ainda, adotando também os meios pelos quais o indicador ou o ângulo de preço poderiam ser medidos. Em seguida, criticamos essa abordagem tentando apontar alguns dos problemas com ela, propomos uma alternativa possivelmente melhor e concluímos, como sempre, com resultados e relatórios de testes. 

Como sempre, usamos uma instância de uma classe de sinal personalizada para testar nossas hipóteses sobre como medir o ângulo de ataque, e medimos esse ângulo não a partir do preço bruto, mas de uma média móvel. Usamos a média móvel decaente como nosso indicador para medir e acompanhar a significância do ângulo de ataque. Preços brutos também podem ser usados para monitorar os ângulos de ataque, no entanto, como eles tendem a ter valores mais voláteis do que o buffer de um indicador, adotamos o último. Qualquer média móvel poderia ter sido usada, mas adotamos a média móvel decaente porque ela é um pouco nova e pode não ser familiar para a maioria dos traders.

Abordagens Atuais para o Uso do Ângulo de Ataque

A abordagem comum para calcular o ângulo de ataque começa identificando dois pontos de preço dentro de um buffer de preços ou indicadores dos quais o ângulo será medido. Esse buffer pode ser os preços brutos do ativo, mas eles tendem a ser muito voláteis, por isso é mais comum usar um buffer suavizado, como o buffer de uma média móvel. Portanto, se estivermos realizando isso no período diário, pegaríamos a média móvel de hoje e a média móvel de N dias atrás.

O que se segue é determinar a mudança na média móvel por período, que, no nosso caso, é os N períodos nos quais os dois valores da média móvel foram obtidos. A primeira coisa que geralmente é determinada é a inclinação, m, que pode ser calculada usando a fórmula apresentada abaixo:

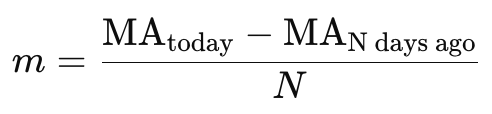
onde:

• MA (hoje) é o valor da média móvel de hoje.
• MA (há N dias) é o valor da média móvel de N dias atrás.
• N é o número de dias entre os dois pontos.

O valor retornado de m pela nossa fórmula acima representa a inclinação e é proporcional ao ângulo de ataque da média móvel. Ele pode ser usado em seu formato atual como um indicador de íngreme e, portanto, do momentum do preço. No entanto, para muitas pessoas, a noção de um ângulo se refere a algo no papel que, para os fins dessa ação de preço, estaria na faixa de 0 – 90 graus.

Se você quiser representar essa inclinação como um ângulo, você usaria a função arcotangente (tangente inversa) para converter a inclinação para graus:

O valor retornado θ é o ângulo em radianos. Para convertê-lo para graus, você multiplicaria por:

Para ver isso em ação, vamos considerar um exemplo de aplicação muito simples. Suponha que você tenha os seguintes dados para um período de 10 dias:

• Há 10 dias, a MA era: 100
• Hoje a MA é: 110

Pela nossa fórmula simples acima, a inclinação, m, seria:

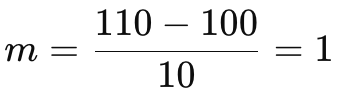
A partir disso, o ângulo θ (theta) em radianos seria:

E se convertermos isso para graus:

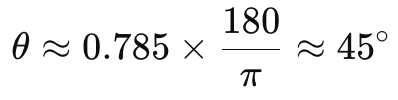
Chegaríamos a um valor que na mente de muitas pessoas está na borda de ser muito íngreme. 45 graus. Se o ativo em questão fosse um par de forex de iene, você poderia justificar ou aceitar a ideia de 45 graus. No entanto, considere uma situação onde o preço é de uma empresa de tecnologia, e ele sobe pela mesma quantidade, mas em um único dia. Se fizermos os mesmos cálculos que fizemos acima, nosso ângulo será de 84 graus, o que é quase 90! No entanto, a interpretação básica do "ângulo de ataque" com essa abordagem, que não é um termo padrão na análise financeira, leva à interpretação da inclinação de uma média móvel como fornecendo insights sobre a força e direção da tendência. Quanto mais íngreme o ângulo (ou inclinação), mais forte é a tendência.

Problemas com a Abordagem Atual e Métodos

Como mencionado acima na aplicação das medições atuais do ângulo de ataque, existem vários problemas, principalmente decorrentes da excessiva sensibilidade à escala de preços e resultados inconsistentes de ângulo em diferentes intervalos de tempo. Para ilustrar esses problemas, vamos começar com a questão da sensibilidade aos preços.

Se o nosso ativo negociado fosse um par de forex que não fosse de iene, como o GBPUSD, então uma mudança de preço comparável de 10 dias, que para esse par seria cerca de 0,10, daria um valor de m de 0,01. Se multiplicarmos isso por 180 e depois dividirmos o resultado por PI, obteremos um ângulo de 0,57 graus. Todos sabemos pelas nossas observações que 45 graus e 0,57 graus estão a milhas de distância em magnitude e ainda assim ambas as moedas, o par de iene e o GBPUSD, tiveram movimentos de 10000 pontos! Você poderia argumentar que essa diferença nos ângulos se deve ao fato de os pares de iene serem mais voláteis, mas a razão entre os dois ângulos é 90x!! Como a maioria dos traders concordaria, o iene não é 90 vezes mais volátil do que pares não iene como o GBPUSD. Isso é obviamente porque, para avaliar corretamente a mudança nos preços dos pares de forex, o valor do ponto de movimento precisa ser levado em consideração. E para isso, de acordo com forex.com, os pares mais voláteis são liderados pelo AUDUSD e NZDUSD em 2023!

O par de iene mais volátil está em terceiro lugar, e isso apesar de ambos AUDUSD e NZDUSD negociarem com decimais de 5 dígitos, o que implica que o nosso movimento de 0,10 pontos acima resultaria no mesmo ângulo de 0,57 graus.

De acordo com a lista do forex.com, o AUDUSD liderou com a maior volatilidade devido a uma média de 1,04% de mudança diária. Com um preço em torno de 0,68150, um movimento de 10 dias com 1,04% por dia resultaria em 0,070876. Isso nos daria um m, ou inclinação, de 0,0070876, e um ângulo, ao longo dos 10 dias, de 0,406 graus. Menos do que os 0,507 que estimamos com o GBPUSD acima, mas o mais importante é que o GBPJPY, que ficou em 7º lugar na lista, foi relatado com uma mudança média de preço de 0,81%. Essa mudança de preço ao longo de 10 dias semelhantes, com um preço base de 147,679, resultaria em um ângulo de 50,1 graus!

Agora, é verdade que o ângulo de ataque não é destinado a medir a volatilidade per se, no entanto, a maioria dos leitores e traders, acredito eu, esperaria que a magnitude de um ângulo estimado de ataque fosse uma medida, de alguma forma, do tamanho do eventual movimento do preço do ativo. O fato de isso claramente não ser o caso coloca essa abordagem em medir esse ângulo em risco. Além dessas inconsistências de sensibilidade ao preço, mudanças em um gráfico/intervalo de tempo de análise podem alterar significativamente o tamanho do ângulo de ataque.

Considere, por exemplo, em nossos casos acima, se mudássemos do período diário para o período de 4 horas. Na primeira ilustração, onde tínhamos o ângulo de 45 graus, esse valor mudaria para 0,95 graus! Isso levanta a questão de por que, ao simplesmente ‘detalharmos’ o período em que estamos medindo o ângulo, sem fazer mudanças na escala de preços, de repente obtemos um ângulo muito plano, inferior a um grau? A resposta bruta para isso é que temos uma base mais longa e, portanto, o ângulo aumenta menos quando comparado à mesma altura, mas como o comprimento da base é realmente o mesmo quando medido em tempo e não em suas unidades, essa distorção não deveria estar presente.

Introduzindo um Método Alternativo

Um exame mais atento dos problemas decorrentes de mudanças no intervalo de tempo, no entanto, apresenta uma possível solução. Em qualquer triângulo, sempre que estamos procurando o tamanho do ângulo, e temos tanto uma altura quanto uma base para esse triângulo retângulo, o arco-tangente da base dividida pela altura deve nos dar um dos ângulos em graus.

fonte

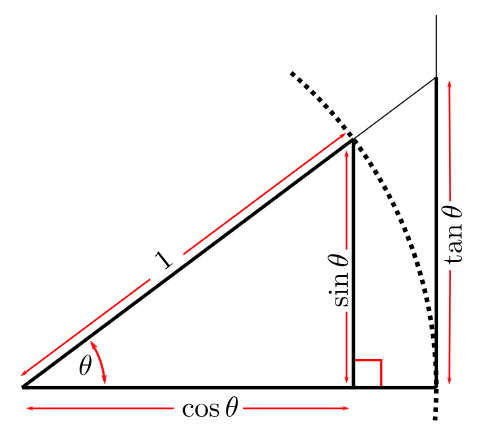
Portanto, a partir da nossa imagem acima, a base do triângulo retângulo maior é na verdade 1 (é mais do que cosθ), razão pela qual nosso lado oposto tem uma altura de tanθ. O ponto chave a ser observado aqui é que as unidades do lado adjacente (a base) são semelhantes às unidades do lado oposto (a altura). Quando isso ocorre, você obtém valores significativos de grau para theta ao encontrar o arco-tangente ou arco-cosseno, conforme o caso do ângulo theta.

O diagrama compartilhado acima, embora forneça ‘informações demais’, enfatiza a definição de tangente como sendo uma razão. Seno para Cosseno. Ou como com como. Você precisa ter o eixo horizontal nas mesmas unidades do eixo vertical para que o ângulo theta seja significativo. Isso então levanta a questão de como os dois eixos de preço e tempo podem ser harmonizados para ter as mesmas unidades?

As escolhas enfrentadas nessa normalização são: ou ambos os eixos de tempo e preço são convertidos para unidades de tempo, ou ambos são convertidos para unidades de preço. Essa noção de conversão pode parecer radical a princípio, mas assim que começamos a visualizar e comparar os resultados, tudo começa a fazer sentido. Porque o preço é o que é crítico, um movimento de preço na direção errada é o que causa drawdowns, teremos ambos os eixos ‘verticais’ e ‘horizontais’ de nossa ação de preço marcados em unidades de preço. Isso então levanta a questão; como podemos redimensionar um eixo de tempo para preço?

Existem várias abordagens que podem ser adotadas para fazer isso, e nosso objetivo com este artigo não é enumerar todas elas ou necessariamente usar a ‘melhor’ delas. O que vamos usar, no entanto, será uma escala variável. Quando apresentados com dois pontos de preço que estão a uma distância D no tempo, a distância D será convertida para as unidades de preço da faixa de preço sobre a distância D anterior. Parece muito simples, mas gera resultados relativamente consistentes para o tamanho do ângulo de ataque. Em MQL5, implementaríamos isso da seguinte forma:

//+------------------------------------------------------------------+
//| Get Angle function
//+------------------------------------------------------------------+
double CSignalAA::Angle(int Index)
{  double _angle = 0.0;
   double _price = DM(Index) - DM(Index+m_length_period);
   double _max = DM(Index+m_length_period+1);
   double _min = DM(Index+m_length_period+1);
   for(int i=Index+m_length_period+2;i<Index+(2*m_length_period);i++)
   {  double _dm = DM(i);
      _max = fmax(_max, _dm);
      _min = fmin(_min, _dm);
   }
   double _time = fmax(m_symbol.Point(), _max - _min);
   _angle = (180.0 / M_PI) * MathArctan(fabs(_price) / _time);
   if(_price < 0.0)
   {  _angle *= -1.0;
   }
   return(_angle);
}

Nossa função simplesmente pega dois espaços de índice e os usa para determinar de onde medir o ângulo de ataque e também, como mencionado acima, até onde devemos retroceder na história para procurar o intervalo de preços, que serve como nossa medida de tempo ou valor do eixo horizontal. O intervalo de preços na história selecionada poderia ser zero, por isso temos um ponto determinado pelo tamanho mínimo do ponto de preço do ativo negociado, servindo como o intervalo mínimo. Os leitores podem alterar esse valor para ser o spread no momento ou qualquer valor, desde que divisões por zero sejam evitadas. Estamos fazendo referência à função da média móvel decaente (DM), que será introduzida abaixo.

Média Móvel Decaente (DMA)

Esta média móvel atribui pesos decaindo exponencialmente, que diminuem mais rapidamente do que nas médias móveis exponenciais tradicionais. Ela é definida pela fórmula apresentada abaixo:

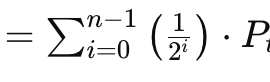
Onde

• n é o tamanho da amostra média
• i é o índice de posição dentro da amostra
• P é o preço no tempo i

Como algumas das médias móveis inovadoras que vimos em artigos recentes desta série, esta pode ser implementada como uma função ou um indicador personalizado se você deseja negociar manualmente com ela. Indicadores personalizados são bons para fazer o buffer, o que pode trazer uma eficiência extra até para um Expert Advisor. No entanto, estamos mantendo a abordagem de função para nossos fins de teste, pois um Indicador Personalizado implica que nosso Expert Advisor compilado terá requisitos adicionais.

Existem várias médias exponenciais que dão mais peso aos preços mais recentes, eu acho que a média móvel decaente faz isso com mais intensidade. Podemos implementá-la em MQL5 da seguinte forma:

//+------------------------------------------------------------------+
//| Decaying Mean                                                   |
//+------------------------------------------------------------------+
double CSignalAA::DM(int Index, int Mask = 8)
{  double _dm = 0.0;
   vector _r;
   if(_r.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_length_period))
   {  //vectors are not series
      double _weight = 0.0;
      for(int i = 0; i < m_length_period; i++)
      {  _dm += (1.0/pow(2.0, m_length_period-i))*_r[i];
         _weight += (1.0/pow(2.0, m_length_period-i));
      }
      if(_weight != 0.0)
      {  _dm /= _weight;
      }
   }
   return(_dm);
}

Estamos simplesmente aplicando um peso a cada preço dentro da amostra que está sendo média, com a principal cautela aqui sendo que vetores não copiam taxas como séries. Isso significa que precisamos estar atentos para que o preço de índice mais alto seja o preço mais recente ou o preço mais próximo do índice a partir do qual começamos nossa cópia. Isso implica que nossa ponderação (o expoente dado ao denominador 2) será invertida enquanto estamos contando em um loop for.

Classe de Sinal

Para juntar tudo isso em uma classe, adicionamos as funções de média decaente e ângulo a uma instância de uma classe de sinal e, claro, fazemos mudanças nas condições de long e short, conforme mostrado abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAA::LongCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle >= m_threshold)
   {  result = int(round(100.0 * ((_angle) / (90.0))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAA::ShortCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle <= -m_threshold)
   {  result = int(round(100.0 * (fabs(_angle) / (90.0))));
   }
   return(result);
}

Nossas condições são realmente simples e tudo o que elas verificam é se o ângulo, conforme medido a partir de uma distância de entrada, excede ou é igual a um valor de limiar de entrada em magnitude. Isso significa que nossas condições são inherentemente de acompanhamento de tendência. A função ‘Ângulo’ retorna um valor positivo ou negativo, portanto, as condições de long e short verificam isso antes de abrir uma posição. A abordagem de acompanhamento de tendência poderia ser invertida em situações onde o ângulo é muito íngreme. Isso é algo que não exploramos neste artigo, mas fica para o leitor investigar e ver se poderia ter algum mérito. Outro ponto de interesse poderia ser como dimensionamos o valor ‘resultado’ nas condições. Como nossa função de ângulo agora retorna valores mais ‘consistentes’, ao contrário dos da abordagem ortodoxa, podemos ter confiança de que não obteremos um ângulo superior ou até mesmo próximo de 90 graus em magnitude.

Por isso, normalizamos o valor absoluto do ângulo dividindo-o por 90 e reescalonando-o para o intervalo de 0 a 100, de modo que ele sirva como o resultado. Abordagens alternativas para normalizar isso, novamente, podem ser exploradas, mas esta é a que tende a dar mais peso ao valor do ângulo de ataque, que é o principal assunto deste artigo.

Testes de Estratégia e Relatórios para Ambas as Abordagens

Se fizermos testes no intervalo de 4 horas para o par GBPCHF ao longo do ano de 2023 (de 01.01.2023 a 01.01.2024), obtemos os seguintes resultados:

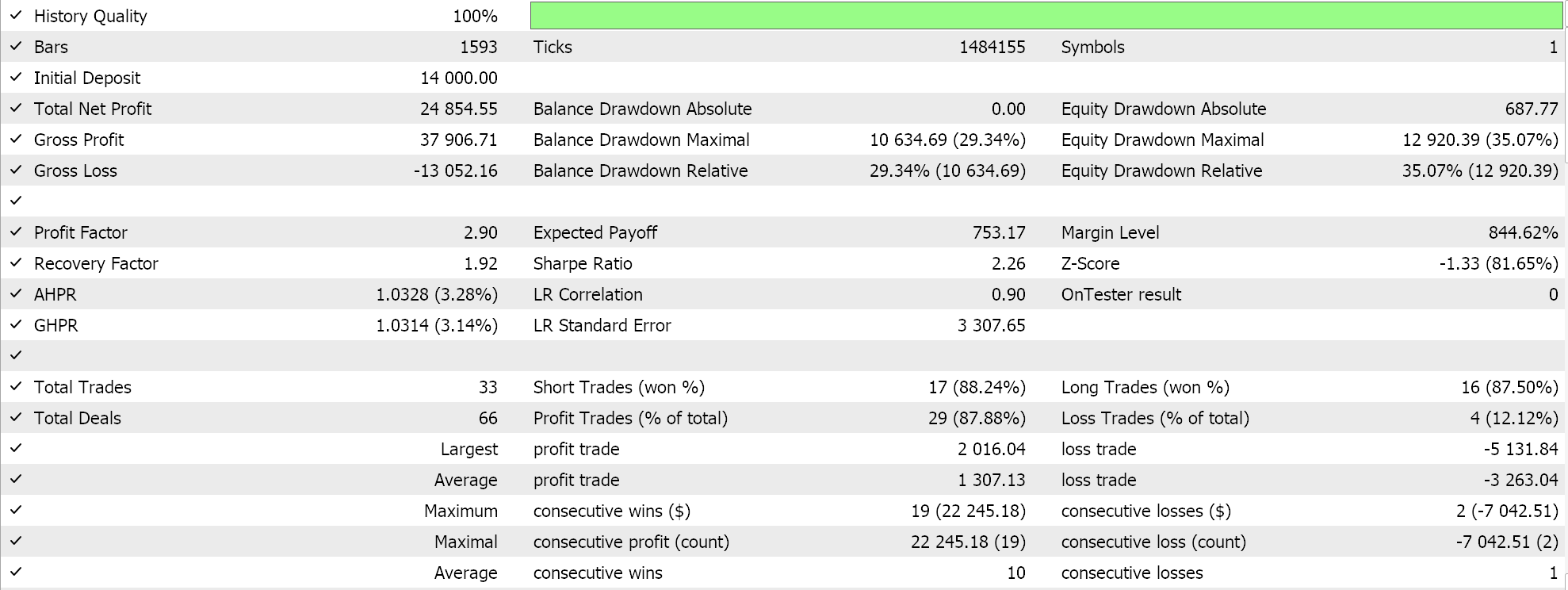
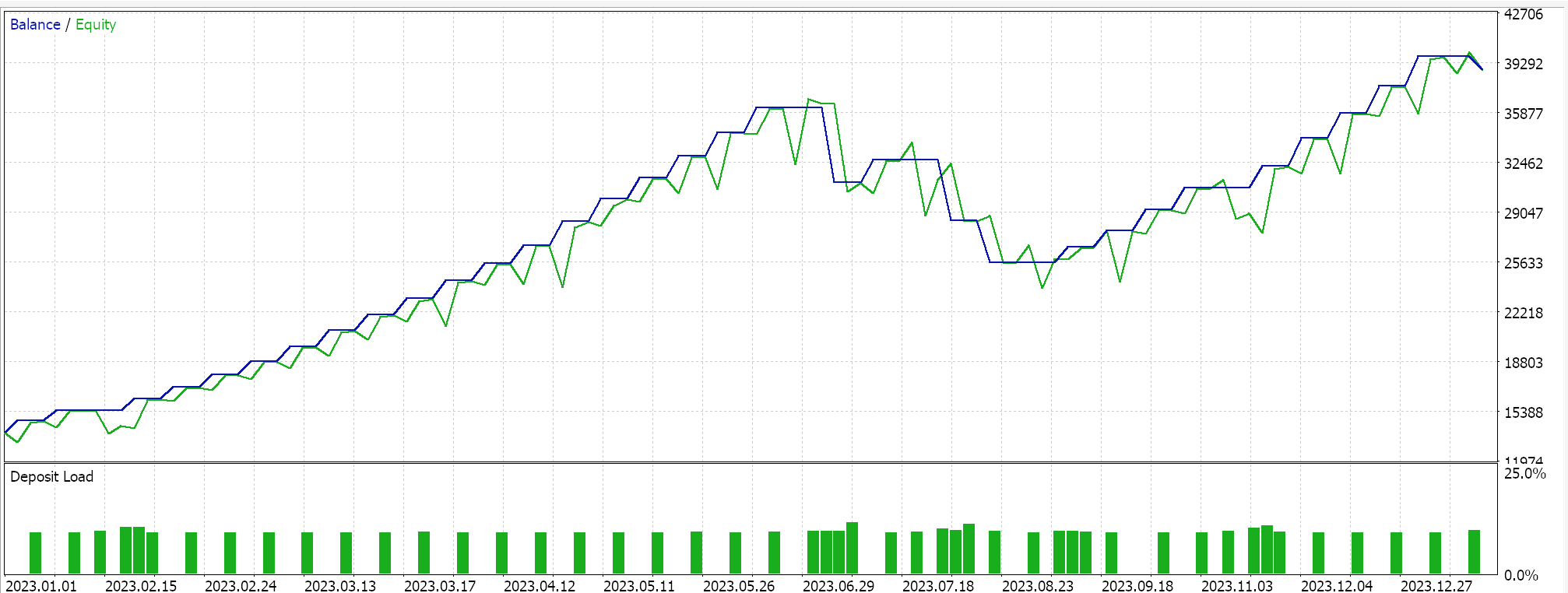
Eles indicam algum potencial, no entanto, pode-se argumentar que não há negociações suficientes sendo realizadas. E, claro, essas execuções, além de estarem limitadas a apenas um ano, não estão utilizando o recurso de walk-forward do testador de estratégias, que pode servir como um filtro rápido para o que funcionará e o que não funcionará. No entanto, usamos a inclinação da média móvel decaente como nosso proxy para a inclinação do preço e, devido ao fato de essa média ser fortemente inclinada para os preços mais recentes, estamos propensos a obter muitos sinais com grandes oscilações.

Ângulo de Ataque Crítico

O ângulo crítico é um conceito que vamos pegar da aerodinâmica. Até aqui, nossa configuração tem procurado condições de long ou short apenas com base na magnitude do ângulo da média móvel decaente. O ângulo crítico de ataque introduz a noção de que esse ângulo, no qual baseamos nossas decisões de abertura, em vez de ser definido por um único valor de limiar, é na verdade melhor definido dentro de uma faixa ou intervalo específico. Para testar e explorar isso, modificamos nossa classe de sinal personalizada, introduzindo um parâmetro extra.

O parâmetro que adicionamos à nossa classe de sinal é o valor do tipo double ‘m_band’, que ajuda a definir o limite superior do intervalo do ângulo de disparo, já que já temos o valor do limiar. Essa modificação seria refletida da seguinte forma nas funções das condições de long e short:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAA::LongCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle >= m_threshold && _angle <= m_threshold+m_band)
   {  result = int(round(100.0 * ((_angle) / (90.0))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAA::ShortCondition(void)
{  int result = 0;
   double _angle = Angle(StartIndex());
   if(_angle <= -m_threshold && _angle >= -(m_threshold+m_band))
   {  result = int(round(100.0 * (fabs(_angle) / (90.0))));
   }
   return(result);
}

A principal mudança é a verificação de que o ângulo é maior do que o limiar, como aconteceu com nosso primeiro sinal, mas também que ele esteja abaixo de um limite superior definido pelo parâmetro da faixa. Se fizermos testes com este arquivo de sinal, uma vez montado em um Expert Advisor (guias para os novatos podem ser encontrados aqui e aqui), obtemos os seguintes resultados de um teste semelhante ao que fizemos acima:

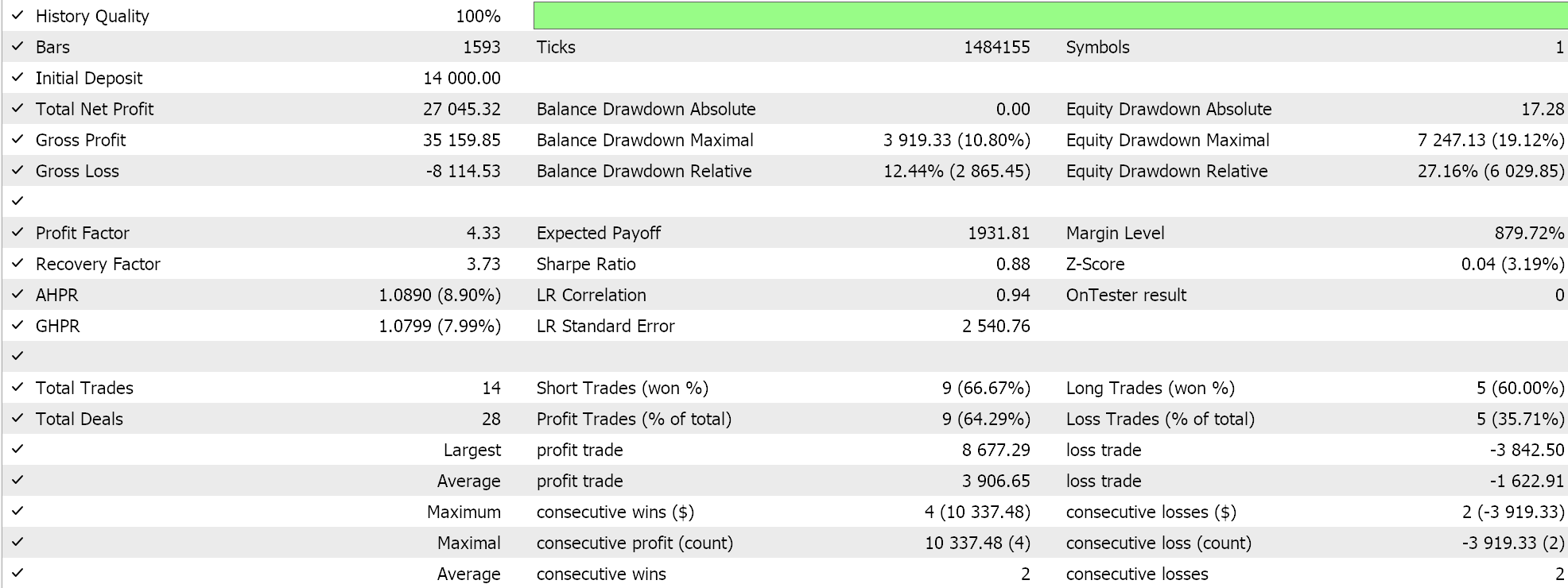
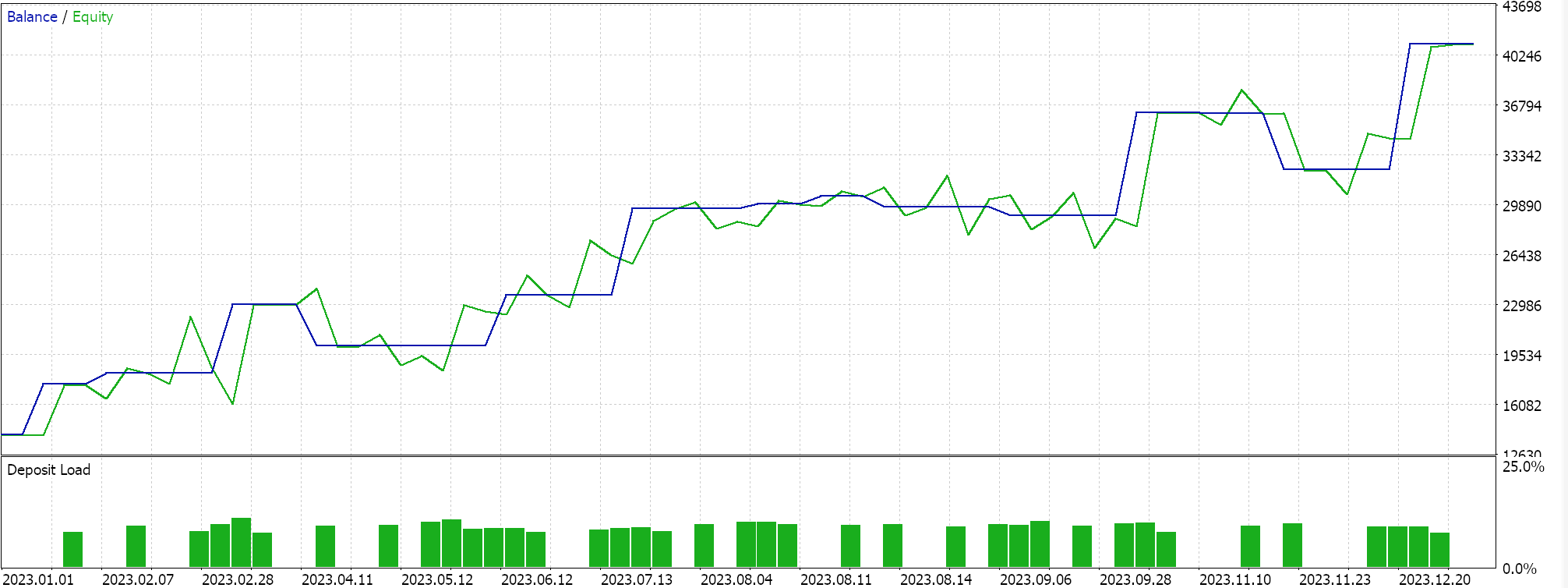
Uma comparação rápida com nossos resultados anteriores mostra claramente que não estamos negociando com tanta frequência e talvez isso fosse esperado, pois agora exigimos que o ângulo não apenas exceda o limiar, mas também permaneça dentro de uma certa faixa. O desempenho geral foi melhor em várias métricas, como fator de lucro, fator de recuperação, percentual de drawdowns, etc. Isso é algo, portanto, que pode ser explorado mais a fundo com testes por períodos mais longos e com dados de tick, antes que conclusões possam ser tiradas sobre sua eficácia.

Conclusão

Portanto, para resumir, analisamos o ângulo de ataque como uma métrica para séries temporais financeiras tanto sob sua visão tradicional de simplesmente calcular o ângulo com base nas mudanças de preço e tempo bruto, quanto sob uma abordagem inovadora de converter o eixo de tempo da série temporal para unidades de preço. Os testes da abordagem anterior não foram apresentados neste artigo porque identificamos muitas inconsistências na forma como o ângulo de ataque é medido, o que parecia inútil e um desperdício de recursos computacionais tentar realizar execuções no testador de estratégias.

No entanto, os testes com nossa abordagem inovadora de ter o eixo horizontal ou de tempo demarcado em unidades de tempo, antes de calcular o ângulo de ataque, geraram alguns resultados promissores. Realizamos testes com essa abordagem em dois modos. Primeiro, simplesmente usamos um limiar de ângulo para filtrar quais posições deveríamos abrir e, em segundo lugar, engajamos o conceito de ângulo crítico onde, para abrir uma posição, o ângulo de ataque não apenas precisava exceder o limiar, mas também estar suficientemente próximo ao limiar, ficando dentro de uma determinada faixa.