ZUP - 派斯温托通用锯齿形调整浪模式。第 2 部分

简介

由于编程语言 MQL4 是 MetaTrader 4 客户终端中的内置语言，因此可以创建各种指标。其中一些指标可能很复杂，另一些则可能非常简单。这完全取决于开发人员的想象力。本文介绍了开发复杂程序的方法。依我看来，它介绍的是一个指标平台 - ZUP。本文还简要描述了 ZUP 中内置的图形工具。ZUP 始终是最新的。本文中我们介绍 ZUP_v63 的图形工具。

派斯温托模式 ( http://www.ensignsoftware.com/tips/tradingtips35.htm#Pesavento )

在下图中，锯齿形中断处用虚线连接起来。每条虚线中间都提供了一个数字。这些附近有数字的虚线代表着一种名为派斯温托模式的工具。此派斯温托模式工具必须与派斯温托模式市场形态区分开来。下文中我们会解释什么是派斯温托模式市场形态。

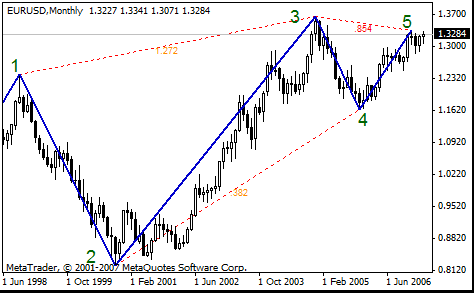
让我们计算23和34 23 和 34 在点中的大小。线 23 的大小= (1.3665-0.8225)*10000=5440.线 23 的大小= (1.3665-1.1638)*10000=2027.再相除：34/23= 2027/5440=0.373.得数与斐波纳奇的 0.382 相差 2.46%。你会看到点2和点 4 2 与 4 之间的虚线旁边的值为 0.382。

用户会注意到，当市场接近一个特定的斐波纳奇位时，斐波纳奇位将开始“工作”。市场通常会在斐波纳奇位附近停止或转向。市场行为在某种特定区域内具有相当高的可预测性。此区域的大小用百分比表示，等于 2*Delta。

在下方的图表中，可看到斐波纳奇的 0.382 在点 42 与 4 之间的虚线旁边的值为 0.382。斐波纳奇位比十一月的最小值低 (1.1638-1.1557)*10000=51 个点.

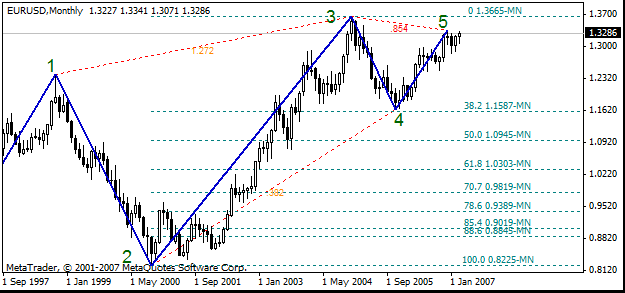
2005 年 11 月，EURUSD 还差一点未达到斐波纳奇 0.382 就转向了。这就是斐波纳奇 0.382 的“工作”方式。一般来说，该虚线旁显示的数字等于下一条线的大小除以上一条锯齿形调整浪线的大小。在上例中，线的比率为34/23。此比率是锯齿形调整浪的点2和4 之间的指定回调率。

那么，为何虚线旁显示的是 0.382，而不是 0.373？我们注意到，市场上“活跃”着一些斐波纳奇位，这一点是非常肯定的。它意味着有一组“有效的”的斐波纳奇位。不同的作者给出不同的斐波纳奇位集合。

派斯温托模式工具操作算法

首先，计算锯齿形调整浪的峰值和谷值之间的回调线。然后将计算得出的值与预定义的斐波纳奇位集合进行比较。如果该值与得自斐波纳奇位集合的数值有差异，但偏离不超过 Delta%，则得自该斐波纳奇位集合的数值将显示在相应虚线旁。此数字是彩色的，因为它是为来自斐波纳奇位集合的数字定义的。（如果该斐波纳奇位集合与拉里·派斯温托开发的数值表相对应，我们将获得名为派斯温托模式的市场形态。）如果得到的值与得自斐波纳奇位集合的数值偏离超过 Delta%，则得到的值将显示在虚线旁，并使用不同的颜色。

如果提供了派斯温托模式工具，则无需计算回调率。如果某个斐波纳奇位涵盖了此价格，则派斯温托模式将用预定义的颜色显示该斐波纳奇位的值。派斯温托模式工具将交付根据回调线计算例程得出的值。

用于处理派斯温托模式的指标输入：

• ExtHidden
  
  0 - 不显示派斯温托模式。但可显示其他工具。
  1 - 显示锯齿形调整浪的峰值或谷值之间的所有回调百分比 >0.1 或 <9.36 的线。
  2 - 仅显示回调百分比等于选定斐波纳奇位集合中某个值的线。
  3 - 显示第 2 条中列示的数字以及锯齿形调整浪的峰值与谷值之间的所有虚线。
  4 - 显示不等于选定斐波纳奇位集合中的值的数字，以及对应的联接线。
  5 - 仅显示锯齿形调整浪。隐藏所有其他工具。（所有工具作业都被隐藏。）

我们将调用连接到锯齿形调整浪“工具作业”的工具。

• ExtFiboZigZag- 允许显示名为“锯齿形斐波纳奇”的工具。
  
  
  
  
  
  
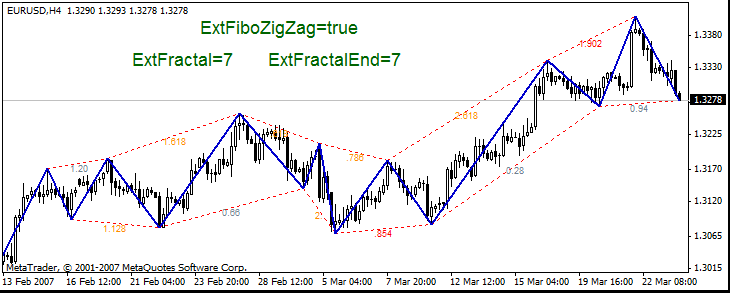
• ExtFractal- 锯齿形调整浪最大值/最小值的数量，线从这些最大值/最小值转到锯齿形调整浪的其他最大值/最小值。
• ExtFractalEnd- 线所到的最大值/最小值的数量。此最大值/最小值之后没有联接线。
  

最大值/最小值是从零柱开始计数的。

• ExtFractalEnd- 如果为零，联接线升/降至最新联接线，包括零柱、锯齿形中断处。ExtFractalEnd 的最小值为 1。
• ExtDelta-（容差或 Delta）计算中的偏差。它还设置一个潜在枢轴区域的值。它必须处于以下值域内：0 < ExtDelta < 1。
• ExtDeltaType- 选择算法以计算容差，即 Delta。
  
  0 - “按原样”显示恢复比例，带两个小数位。
  1 - 根据以下公式计算容差：（回调率 - 选定斐波纳奇位集合中的一个数值）
  2 - 根据以下公式计算容差：（回调率 - 选定斐波纳奇位集合中的一个数值）/（选定斐波纳奇位集合中的一个数值）。
  3 - “按原样”显示恢复比例，带三个小数位。
  
  拉里·派斯温托称，将容差设定在 4% (0.04) 的范围内就足够了。当价格进入容差区域，数值就变成选定斐波纳奇位集合中的数值，并使用选定斐波纳奇位集合中的该数值的颜色。
  
  
• ExtSizeTxt- 选择数值显示的字体大小
• ExtLine - 选择联接线的颜色
• ExtPesavento - 选择选定斐波纳奇位集合中的数值的颜色
• ExtGartley886 - 选择其他数值的颜色
• ExtNotFibo - 选择派斯温托模式中所有其他数值的颜色
• ExtPPWithBars
  
  0 - 显示派斯温托模式中的回调值
  1 - 并在括号中显示该给定回调线的锯齿形调整浪峰值之间的柱数。
  2 - 显示派斯温托模式中的回调值，并在括号中显示单独针对第一条和第二条锯齿形调整浪线的锯齿形调整浪峰值之间的柱数。
  3 - 在括号中显示价格回调率后的时间回调率。时间回调率是第二条锯齿形调整浪线上的柱数与第一条上的柱数之比。
  4 - 在括号中显示时间回调率，即第二条线的开发时间与第一条线的开发时间之比。
  5 - 在括号中显示在两条相邻的锯齿形调整浪线上构建的矩形面积之比。锯齿形调整浪线是这些矩形的对角线。
  6 - 在括号中显示点数和锯齿形中断处的当前价格与选定斐波纳奇位集合（或对应斐波纳奇位）中的数值之间的差异百分比。例如，2.618 (7/2.81%)。括号中的数字 7 表示 2.618 的斐波纳奇位高出柱最大值 7 个点或 2.81%。如果 7 是一个负值，2.618 的斐波纳奇位低于柱最大值 7 个点。
  

派斯温托模式与名为斐波纳奇位的工具拥有相同的功能。

不同交易品种的斐波纳奇位集合

在 ZUP 中，斐波纳奇位集合可分为标准集合和替代集合。我们也将替代数字集合称为派斯温托数字。

你可使用参数 ExtFiboType 选择标准斐波纳奇位集合或是替代斐波纳奇位集合：

• ExtFiboType = false - 显示标准斐波纳奇位集合
• ExtFiboType = true - 显示替代斐波纳奇位集合
• ExtFiboChoice - 指定替代斐波纳奇位集合
  

下文给出了 ZUP 中内置的不同交易品种的斐波纳奇位（数字）完整列表。

• 派斯温托模式
  
  ZUP 版本到版本 58：
  标准斐波纳奇位集合0.146-0.236-0.382-0.5-0.618-0.764-0.854-1.0-1.236-1.618
  派斯温托数字：0.146-0.236-0.382-0.447-0.5-0.618-0.707-0.786-0.841-0.886-1.0-1.128-1.272-1.414-1.5-1.618-1.732-1.902-2.0-2.236-2.414-2.618-3.14-3.618-4.0
  
  版本 59 中有多个替代数字组合可供选择。
  
  
• 标准斐波纳奇位集合
  
  0.146 - 0.236 - 0.382 - 0.5 - 0.618 - 0.764 - 0.854 - 1.0 - 1.236 - 1.618 - 4.236
  
  
• 替代斐波纳奇位集合
  
  ExtFiboChoice= 0 - 拉里·派斯温托的数字集合：0.25 - 0.382 - 0.5 - 0.618 - 0.707 - 0.786 - 0.841 - 1.0 - 1.128 - 1.272 - 1.414 - 1.618 - 2.0 - 2.618 - 4.0
  ExtFiboChoice= 1 - 一组用于构建伽利模式的数字：0.382 - 0.447 - 0.5 - 0.618 - 0.707 - 0.786 - 0.886 - 1.128 - 1.272 - 1.414 - 1。618 - 2.0 - 2.236 - 2.618 - 3.142 - 3.618
  ExtFiboChoice = 2 - 一组用于构建伽利模式的数字以及其他有用数字。可稍后在此处添加数字。现在，此处包括的额外数字如下：0.146 - 0.236 - 0.854 - 1.732 - 1.902
  ExtFiboChoice = 3 - 布莱斯吉尔摩在其《市场几何 2》[5;6] 一书中的数字一览表中指出的最重要的数字集合：0.25 - 0.382 - 0.5 - 0.618 - 0.667 - 0.786 - 1.0 - 1.272 - 1.618 - 1.732 - 1.75 - 2.0 - 2.236 - 2.5 - 2.618 - 3.0 - 3.33 - 4.236 - 6.854
  
  布莱斯吉尔摩在其《市场几何 2》一书中将数字进行了分组。以下是根据 John Edwards 在 Onix 论坛的建议从布莱斯吉尔摩的书中取出的数字集合。
  
  ExtFiboChoice = 4 - 数字集合“几何”0.146 - 0.186 - 0.236 - 0.3 - 0.382 - 0.486 - 0.526 - 0.618 - 0.786 - 1.0 - 1.272 - 1.618 - 1.902 - 2.058 - 2.618 - 3.33 - 4.236 - 5.388 - 6.854
  ExtFiboChoice =5 - 标准斐波纳奇位集合 0.177 - 0.25 - 0.354 - 0.5 - 0.707 - 1.414 - 2.0 - 2.828 - 4.0 - 5.657 - 8.0
  ExtFiboChoice = 6 - 数字集合“几何”0.167 - 0.333 - 0.577 - 0.667 - 1.5 - 1.732 - 3.0 - 6.0
  ExtFiboChoice= 7 - 数字集合“黄金分割”0.236 - 0.30 - 0.486 - 0.618 - 0.786 - 1.272 - 1.618 - 2.058 - 2.618 - 3.33
  ExtFiboChoice = 8 - 数字集合“几何”0.354 - 0.50 - 0.707 - 1.414 - 2.0 - 2.828 - 4.0.
  ExtFiboChoice = 9 - 数字集合“几何”0.192 - 0.333 - 0.577 - 1.732 - 3.0 - 5.2 - 9.0
  ExtFiboChoice= 10 - 数字集合“矩形”（布莱斯吉尔摩的根 5）0.20 - 0.447 - 2.236 - 5.0
  ExtFiboChoice = 11 - 数字集合“额外有用数”1.414 * 1.618 = 2.288, 1.414 * 0.618 = 0.874, 2.618 * 1.272 = 3.330, 2.618 * 1.618 = 4.236, 1.618 / 2 = 0.809, 2.618 / 2 = 1.309, 1.618 * 2 = 3.236, 1.732 * 2 = 3.464, 2.236 * 2 = 4.472
  
  
• Robert Fisher [6] 所述的斐波纳奇位和扩展，但方式略有区别
  
  标准数字：0-0.146-0.236-0.382-0.5-0.618-0.764-0.854-1.0-1.236-1.618-2.618-4.236-6.854
  派斯温托数字：0-0.382-0.5-0.618-0.707-0.786-0.854-0.886-1.0-1.128-1.272-1.414-1.618-2.0-2.414-2.618-4.0
  
  
• MetaTrader 中的斐波纳奇扩展 标准数字：
  
  标准数字：0.236-0.382-0.5-0.618-0.764-0.854-1.0-1.236-1.618-2.0-2.618
  派斯温托数字：0.382-0.5-0.618-0.707-0.786-0.886-1.0-1.272-1.414-1.618-2.0-2.618
  
  
• 斐波纳奇扇。静态的斐波纳奇扇与静态的安德鲁斯干草叉一同显示。动态的斐波纳奇扇显示在第一条线上 标准数字：
  
  标准数字：0.236-0.382-0.5-0.618-0.764-0.854
  派斯温托数字：0.236-0.382-0.5-0.618-0.786-0.886
  
  
• 随机点上以及沿安德鲁斯干草叉中线的斐波纳奇扇
  
  标准数字：0.236-0.236-0.382-0.5-0.618-0.764-0.854-1.0:1.618-2.618
  派斯温托数字：0.382-0.5-0.618-0.707-0.786-0.886-1.0-1.272-1.414-1.618-2.618
  
  
• 反应线 (RL)
  
  标准数字：0.236-0.382-0.5-0.618-0.764-1.0-1.618-2.0-2.618-4.0
  派斯温托数字：0.382-0.5-0.618-0.707-0.786-0.886-1.0-1.128-1.272-1.414-1.618-2.0-2.414-2.618-4.0
  
  
• 警告线（UWL 和 LWL）
  
  标准数字：0.618-1.0-1.618-2.0-2.618
  
  
• 斐波纳奇时间
  
  标准数字：0-1-1.236-1.382-1.5-1.618-1.764-1.854-2.0-2.236-2.618-3.0-2.618
  派斯温托数字：0-1-1.382-1.5-1.618-1.707-1.786-1.886-2.0-2.272-2.414-2.618-3.0-3.414-3.618-4.0
  
  
• Versum 位
  
  Standard numbers - 23.6-38.2-45.5-50.0-54.5-61.8-76.4
  派斯温托数字 -

以后可对此列表进行修改。

锯齿形中断处和线的编号

指标中的很多工具都是以锯齿形调整浪的某条特定线或某个特定中断处为基础的。例如：

• ExtFiboStaticNum- 要在其上构建静态斐波纳奇位的锯齿形调整浪线的编号。
• ExtFiboExpansion - MetaTrader 中的斐波纳奇扩展 - 它指定斐波纳奇扩展的第一个点所在的锯齿形中断处。

下表用红色显示中断处的编号，用蓝绿色显示线的编号。

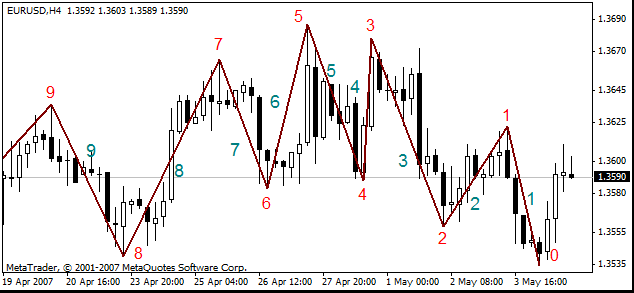
如果在第一条线上或在零 (0) 号中断处绘图，工具将随着当前价格的变化而发生动态变化。如果形态未触及第一条线或零号中断处，工具不会发生变化，工具状态将是相应的静态。ZUP 中的所有图形工具都构建在前九条线或前十个峰值 (0-9) 上。但派斯温托模式不仅可构建在这前十个峰值上，还可构建在所有中断处上。

动态和静态斐波纳奇位。斐波纳奇扩展

ZUP 中内置的图形工具可以是动态或静态的。静态图形工具锚定到已形成的锯齿形中断处，即不会再改变的中断处。动态图形工具锚定到锯齿形调整浪中始终不断变化位置的第一根线的末端。

动态图形工具允许你快速作出决策。如果行情发生变化，我们可通过查看动态图形工具的形态来观测可能的趋势。一旦锯齿形调整浪的第一根线发生变化，动态图形工具也将会自动重新构建。

动态斐波纳奇位构建在锯齿形调整浪的第一条不断变化的线上。

静态斐波纳奇位构建在第 2 到第 9 条线上。

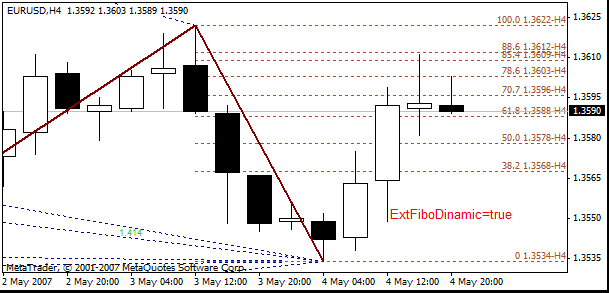
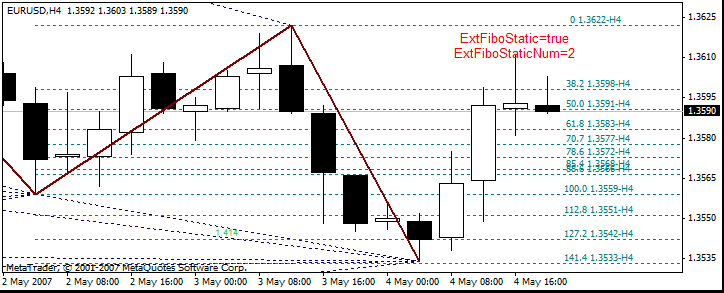
用于处理斐波纳奇位的参数：

• ExtFiboType = true - 带派斯温托数字的斐波纳奇位；false - 标准斐波纳奇位
• ExtFiboDinamic - 允许显示动态斐波纳奇位动态斐波纳奇位将显示在锯齿形调整浪的第一条线上
• ExtFiboStatic - 允许显示静态斐波纳奇位
• ExtFiboStaticNum - 最开始显示静态斐波纳奇位的锯齿形调整浪线的编号
• ExtFiboS和ExtFiboD - 选择静态和动态斐波纳奇位的颜色

到此将显示斐波纳奇位值（例如 61.8），对应斐波纳奇位的价格以及显示该斐波纳奇位所在时间范围的名称。在 DT 模式下工作时，必须知道这个时间范围。动态斐波纳奇位的值较接近图表窗口边框。静态斐波纳奇位的值从窗口边框缩进一段距离。

当静态和动态斐波纳奇位同时显示时，斐波纳奇位的值部分会重叠起来。查看时可能会造成不便。但是，MetaTrader 4 不允许在距图表窗口边框一定距离之处显示静态斐波纳奇位。动态斐波纳奇位将随锯齿形调整浪第一根线的大小或位置的变化而自动变化。

• ExtFiboCorrectionExpansion 切换静态和动态斐波纳奇位，以显示修正或斐波纳奇扩展。

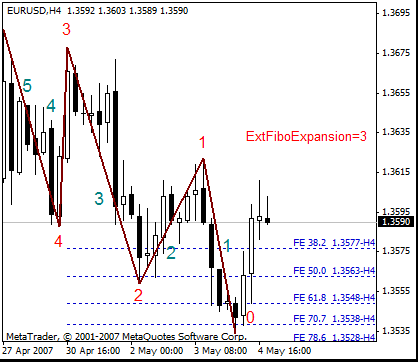
将以 Robert Fisher 的《新斐波纳奇交易者》[6] 中所述的方式显示斐波纳奇扩展。此时，锯齿形调整浪线的大小将被视为依据。扩展看上去似乎延长了这条线。按 Robert Fisher 的说明，扩展数字会加上前缀 Fe。

• ExtFiboExpansion - MetaTrader 4 中的斐波纳奇扩展 - 它设置三个斐波纳奇扩展点中的第一个点所在的锯齿形中断处。
  
  ExtFiboExpansion<2 - 不显示斐波纳奇扩展
  ExtFiboExpansion=2 - 动态斐波纳奇扩展
  ExtFiboExpansion>2 -
  
  
  
  
  

安德鲁斯干草叉 (http://www.trading-naked.com/alan_andrews_course_1.htm)

Patrick Mikula 介绍了安德鲁斯干草叉及其配套战术 (http://www.mikulaforecasting.com/books/aabook.htm)。Putnik 还详细描述了安德鲁斯干草叉的构建方式，具体请访问 ONIX 论坛，网址为：http://onix-trade.net/forum/index.php?showtopic=8249 在 ZUP 中构建安德鲁斯干草叉也是应 Putnik 的请求而实现的。

安德鲁斯干草叉所用完整参数列表如下：

• ExtPitchforkDinamic
  
  > 0 ( = 1) 显示最后两个锯齿形调整浪极值的动态安德鲁斯干草叉
  = 2 - 显示带 50-% 正中线的安德鲁斯干草叉
  = 3 - 显示一个 50-% 的安德鲁斯干草叉（按照 ONIX 论坛的一位参与者 Vinsant 的解释）
  = 4 - 显示希夫线
  
  
• ExtPitchforkStatic
  
  > 0 ( = 1) 显示编号为 ExtPitchforkStaticNum 的锯齿形调整浪极值的静态安德鲁斯干草叉
  = 2 - 显示带 50-% 正中线的安德鲁斯干草叉
  = 3 - 显示一个 50-% 的安德鲁斯干草叉（按照 Vinsant 的解释）
  = 4 - 显示希夫线
  
  
• 3 <=ExtPitchforkStaticNum <= 9 - 静态安德鲁斯干草叉开始时所在锯齿形调整浪峰值的编号。
• ExtLinePitchforkS和ExtLinePitchforkD 指定静态和动态干草叉的颜色。
• ExtPitchforkStaticColor-- 指定静态干草叉填充的颜色，并启用此填充。选择颜色可启用填充，将此参数设为“NONE”可禁用填充。
• ExtFiboFanDinamic - 启用显示动态斐波纳奇扇。
• ExtFiboFanStatic - 启用显示静态斐波纳奇扇。
• ExtFiboFanExp - 斐波纳奇扇的射线数。True=6，false=4。
• ExtFiboFanHidden - 允许显示斐波纳奇扇的射线标记。它仅处理静态和动态斐波纳奇扇。
• ExtFiboFanD - 设置动态斐波纳奇扇的颜色。
• ExtFiboFanS - 设置静态斐波纳奇扇的颜色。
• ExtFiboFanMedianaStaticColor和ExtFiboFanMedianaDinamicColor - 设置静态和动态干草叉的正中线上的斐波纳奇扇的颜色，并启用对应的斐波纳奇扇
• ExtPitchforkStyle - 设置干草叉输出样式：
  
  0 - 实线
  1 - 短划线
  2 - 点线
  3 - 链线
  4 - 点划线
  5-10 - 设置实线的粗度
  
  
• ExtFiboTime1 - 启用斐波纳奇时区 1。
• ExtFiboTime2- 启用斐波纳奇时区 2。
• ExtFiboTime1C - 设置时区 1 的线条颜色。
• ExtFiboTime2C- 设置时区 2 的线条颜色。
• ExtPivotZoneStaticColor - 设置静态枢轴区域的填充色。
• ExtPivotZoneDinamicColor - 设置动态枢轴区域的填充色。
• ExtPivotZoneFramework - 指定将枢轴区域显示为一个框架（默认）或已填充的矩形。
• ExtUTL - 启用安德鲁斯干草叉的上控制线。
• ExtLTL - 启用安德鲁斯干草叉的下控制线。
• ExtUWL - 启用上警告线。
• ExtLWL - 启用下警告线。
• ExtISLDinamic - 启用动态安德鲁斯干草叉的内部信号线。
• ExtISLStatic - 启用静态安德鲁斯干草叉的内部信号线。
• ExtRLine - 启用沿安德鲁斯干草叉显示反应线。
• ExtRLineBase - 隐藏定向反应线。

下图给出了安德鲁斯干草叉的构建示例。

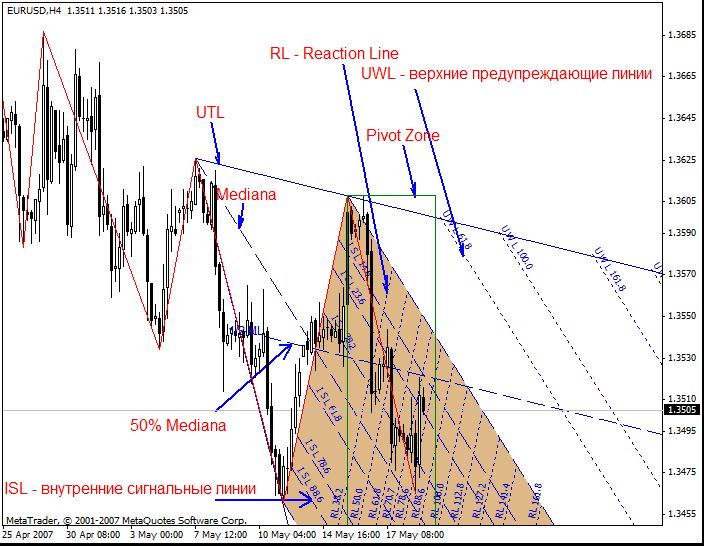
注意：

反应线是使用斐波纳奇通道绘制的。很多情况下，绘制的反应线都是有错误的。虽然都是无关紧要的小错，但日积月累，越来越多。绘制时不可能毫无错误。由于斐波纳奇通道针对烛台的特定锚定，MetaTrader 4 中不可能绘制零错误的标准工具斐波纳奇通道。在我的第一篇文章中 ZUP - 派斯温托通用锯齿形调整浪模式第 1 部分中，我也谈及了这种错误。之所以要慎用当前实现中的反应线，原因就在于此。这种错误仅可由 MetaTrader 4 开发人员修复。

• ExtPitchforkCandle - 包括显示选定烛台中的干草叉集合
• ExtPitchfork_1_HighLow - 当干草叉构建于选定烛台上时，它指定在该烛台的最大值或最小值上构建干草叉的第一个点
• ExtDateTimePitchfork_1、ExtDateTimePitchfork_2、ExtDateTimePitchfork_3 - 指定分别为第一个、第二个和第三个点构建安德鲁斯干草叉时所在烛台的时间和日期。
  

如何显示选定烛台上的干草叉集合

让我们选择要在其上显示干草叉的烛台。将鼠标悬停到这些烛台上。然后将这些烛台的日期和时间写在一张单独的纸上，之后，调用对话框以更改指标参数。在参数 ExtDateTimePitchfork_1、ExtDateTimePitchfork_2、ExtDateTimePitchfork_3 中，输入烛台的日期和时间。使用 ExtPitchfork_1_HighLow 确定是根据最大值还是最小值构建干草叉的第一个点。设置 ExtPitchforkCandle = true。使用 ExtPitchforkCandle 确定是在锯齿形调整浪极值还是在选定烛台的极值上构建干草叉集合。

选择 ExtPitchforkStatic>0 时，将在选定烛台上构建静态干草叉集合，并显示在屏幕上。可保存该干草叉集合。如果干草叉的第三个点位于零柱上，将显示无法保存的动态干草叉。
下例中显示了安德鲁斯干草叉在选定烛台上的构建方式。干草叉锚定到的烛台是 ZUP 中的默认烛台。以下是使用 ZUP_v63 做的屏幕截图。在早期版本中，由于 MetaTrader 4 中斐波纳奇通道的特点，在此图表中构建的反应线 RL*** 是有错误的。反应线是使用斐波纳奇通道构建的。

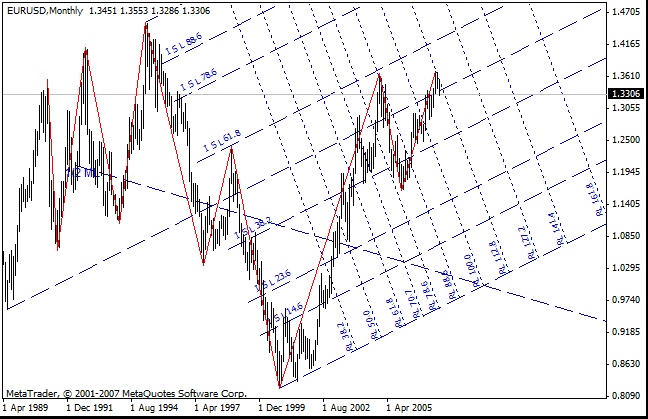
参数 ExtSave 允许保存静态干草叉集合、斐波纳奇时间、斐波纳奇扩展和静态斐波纳奇位。此参数不保存静态干草叉通道的填充。

如何使用 ExtSave：

1. 应构建安德鲁斯干草叉集合和所有辅助线。
2. 打开指标设置面板，将 ExtSave 设置为 true。
3. 关闭设置面板。将在图表上绘制该干草叉集合。
4. 重新打开指标设置面板，将 ExtSave 设置为 false。
5. 关闭面板。保存的干草叉集合将显示在图表上。同一个干草叉集合将显示在上一个集合上，但删除指标时，第二个集合（显示在第一个集合上）也将一起被删除，而第一个集合将留在图表上。
   

如果未执行第 4 和第 5 个步骤，每一次更改指标参数时，实际的干草叉集合与其当前参数都将被保存到图表中。如果指标被删除，大量干草叉集合仍将留在图表中，互相叠加或略有偏移。

工具（干草叉、扇等）应保存在最小的实际时间范围上。如果保存在较大的时间范围上，当你切换到较小时间范围时，将从较小时间范围的第一根烛台开始绘制保存的工具，此烛台是保存工具的较大时间范围内及时包括的烛台。这也是 MetaTrader 4 的特色之一。当切换到另一个时间范围时，保存的工具显示时会有错误。

如果不保存工具，仅使用 ZUP 显示它们，则这些工具将正确构建。在 ZUP 的 DT 模式中，锯齿形中断处会重新计算，且这些中断处构建在更改时间范围时实际最大值和最小值所在的烛台上。这样，这些工具将重新锚定到更精确的点。此时未观察到绘图缺陷。

micmed 的通道

micmed 的通道是 ONIX 论坛的一位参与者 micmed 所开发的一种新的图形工具。这种工具是基于安德鲁斯干草叉开发出来的，不同之处是它采用一种特殊的方式来选择干草叉的锚定点。

以下内容引述自 micmed 在 ONIX 论坛上发表的一些帖子（由 MetaQuotes Software Corp. 翻译成英文）：

...类似于屏幕截图中所示的内容也可被添加到干草叉集合中，我把它们称为“黄金分割”。试着用了一下 VL (*)，我发现这种干草叉保留适当通道的频率最高...

这正解释了这种绘图的好处：根据上述要求构建的黄金分割可以进一步用作一个通道，尽管它在经典通道的边框显示之前就早已构建。这完全与斐波纳奇数字和谐地交融起来...

...实际上这些并不是干草叉，只是用它们构建更容易。关于构建，我将点 1 放在从 B 构建成的垂直线。以下是一些观察所得：

1. 如果对角线 AB 比对角线 BC 短，那么我在距顶点 B 32.8% 之处进行构建。
2. 如果对角线 AB 比对角线 BC 长，就在距顶点 B 61..8% 之处进行构建。
3. 也有 50% 的距离，通常是在枢轴处，而且它们通常一个接一个，2 到 3 个三角形
4. 如果通道被突破，点 38.2 将换成 61.8，反之亦然（屏幕截图）。

* - VL - Versum 位 - 一种新的图形工具，将在后文中介绍。

参数：

• ExtCM_0_1A_2B - 启用绘制 micmed 的通道。可选值为 1-2-3-4。默认值为 0，表示将构建正常的安德鲁斯干草叉。
• ExtCM_Fibo - 设置安德鲁斯干草叉正中线的位置，以绘制 micmed 的通道。值的范围为 0 到 1。
  

参数 ExtCM_0_1A_2B 将所有安德鲁斯干草叉（见上文）锚定到其他点。要绘制 micmed 的通道，首先应构建安德鲁斯干草叉。然后，使用参数 ExtCM_0_1A_2B 选择干草叉的新锚定点。参数 ExtCM_0_1A_2B 的值取决于 AB 和 BC 的长度。

以下是作者关于通道绘制方式的说明：

从 ZUP 55 版本中开始加入的 micmed 的通道是使用名为安德鲁斯干草叉的标准工具在三个点上构建而成的，其中，点 2 和 点 3 如经典干草叉那样选自两个峰值，而点 1 是根据以下两个参数选定的：

• ExtCM_0_1A_2B（可以是 0、1、2、3、4）定义点 1 所在的垂直线
  
  如果值为
  0 - 不绘制 micmed 的通道，而是绘制标准干草叉
  1 - 在从峰值 A 沿斐波纳奇位 AB 所成的垂直线上选择点 1
  2 - 在从峰值 B 沿斐波纳奇位 BC 所成的垂直线上选择点 1
  3 - 在从峰值 A 沿斐波纳奇位 BC 所成的垂直线上选择点 1
  4 -在从峰值 B 沿根据以下算法得出的斐波纳奇位所成的垂直线上选择点 1：如果 AB>BC，则值为 0.618；如果 AB<BC，则值为 0.382
  
  
• ExtCM_Fibo（值的范围为 0.0 到 1.0）定义点 1 的斐波纳奇位的值

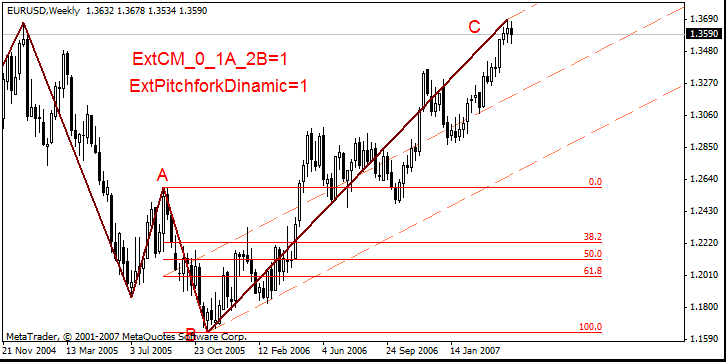
示例图：

• ExtCM_0_1A_2B = 1，ExtCM_Fibo = 0.618

  
  
  
  

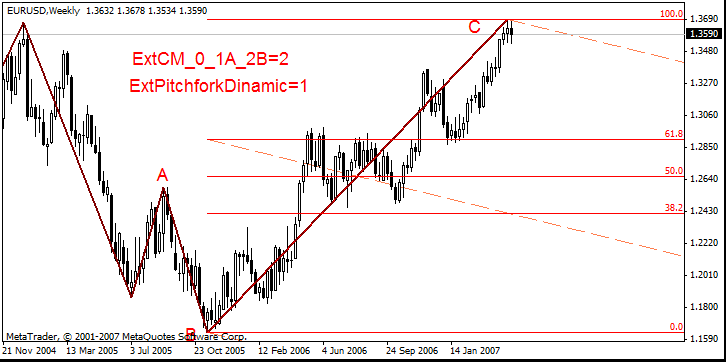
• ExtCM_0_1A_2B = 2，ExtCM_Fibo = 0.618
  

  
  
  
  

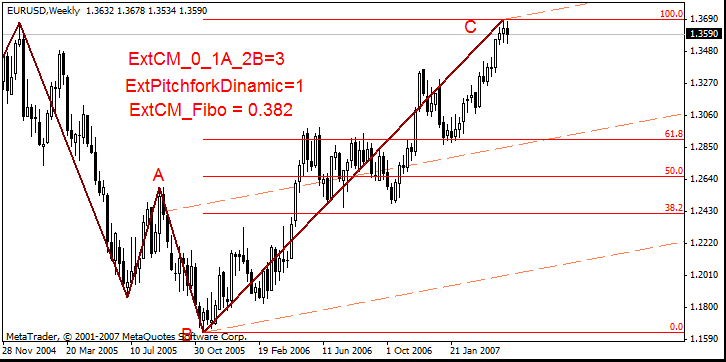
• ExtCM_0_1A_2B = 3，ExtCM_Fibo = 0.382

  
  
  
  

分析从 1989 年开始的 EURUSD 日线图上的历史记录 - ZUP_v54 与参数 Extindicator=6、minBars=25 - 构建有 103 个三角形，其中

• 如果 AB>BC，根据 0.618 的值在峰值 B 的垂直线上选择点 1（31 个三角形）
• 如果 AB<BC，根据 0.382 的值在峰值 B 的垂直线上选择点 1（31 个三角形）

此外还观察到，在突破的通道中，点 1 的斐波纳奇位值从 0.382 更改为 0.618，反之亦然（趋势方向变化），并且在平盘时值为 0.5（40 个三角形）。

模式 3 适用于极快的峰值。否则，通道将形成非常尖锐的角度...

我很乐意分享一个我认为非常重要的发现。在通道构建模式 4 中（也许在其他模式中也有，但这个模式是自动化模式），价格始终(!)会到达 RL 161.8 与通道正中线交叉处的水平的价格，并且几乎总是在 RL 100 - 161.8 的范围内。

以上内容引述自 micmed 的帖子。提供这些内容是为了更好地理解新的图形工具 micmed 的通道的工作方式。斐波纳奇位显示在图表中，以说明通道的构建算法。包含此图形工具的 ZUP 不显示斐波纳奇位。

Versum 位

此图形工具的开发者是 KBPauk 和 ONIX 论坛的一位参与者 versum。当然，很可能有其他人也实施过这个工具。在 ZUP 中，此工具名为 Versum 位。

参数：

• ExtVLStaticColor - 通过选择颜色启用静态 Versum 位
• ExtVLDinamicColor - 通过选择颜色启用动态 Versum 位
• ExtVLStaticNum - 设置显示静态 Versum 位所在波峰的编号。
  

此工具补充安德鲁斯干草叉，类似于斐波纳奇扇。它与安德鲁斯干草叉一样围绕着正中线开展工作。安德鲁斯干草叉正中线与 VL 的 50-% 水平相吻合。以下是绘制动态 VL 的示例。斐波纳奇位显示在图表中，以说明此图形工具的构建方式。包含此图形工具的 ZUP 不显示斐波纳奇位。

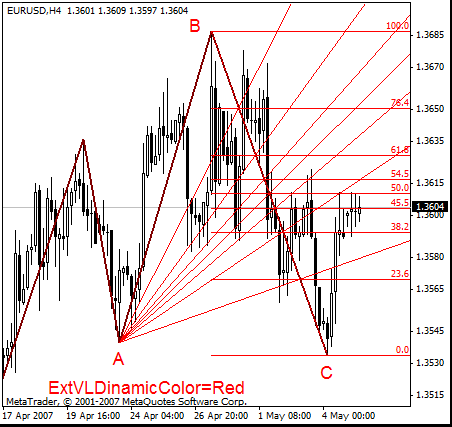
以下内容引述自 versum 的帖子（由 MetaQuotes Software Corp. 翻译成英文）：

这可同时被视为一个扇形（即辐射线）和一个斐波纳奇扇，因为我使用的线段与这些线条相交，并被斐波纳奇位（当时正在使用的工具）划分为多个部分...图 1 中可以看到，线段 BC 被斐波纳奇位分为多个部分。线条从前一个峰值/谷值（即点 A）开始绘制，通过斐波纳奇位与线段 BC 的相交点。这些是预期的价位。

那么我们能得到什么？

1. 随着时间而变化的价位（这是最重要的）
2. 这些是作为伽利模式和其他形态和模型开发依据的变体，但要在“以后”才能看到它们
3. 预期的趋势开发。

如何使用它？

如果价格触及或超过 50-% 线（通过除以 50-% 价位的点）的价位，那么我们就可以说（尽管不是 100-% 肯定），趋势仍保持不变。如果低于 50-% 线，那么我们可以说，当前趋势可能会发生变化...

注意：

1. 我并未严格地使用获取的价位，最高为 1 价格利润点。我认为更应该将其视为一个区域。
2. 我也并未将斐波纳奇位看做万能的措施。线段各个部分之间的其他比率可以变得更好。

独立的斐波纳奇扇

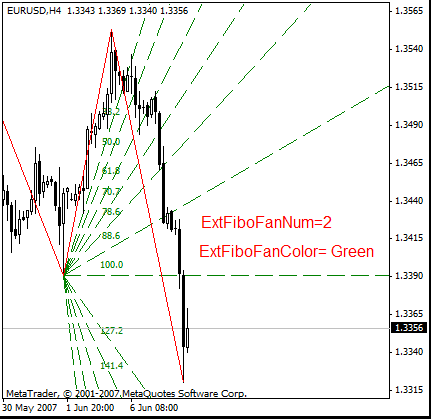
除了与安德鲁斯干草叉配合使用的斐波纳奇扇之外，独立的斐波纳奇扇也有可能启用。这些斐波纳奇扇显示在锯齿形调整浪的前九条线上或锯齿形调整浪的前十个极值上。使用参数 ExtFiboFanColor 选择颜色，便可启用这些独立扇。这些扇由参数 ExtFiboFanNum 管理。

增强模式

当锯齿形调整浪的峰值和谷值属于同一波动水平时，市场分析是最有效的。但情况往往是，锯齿形调整浪的峰值和谷值对于一个波动水平来说“过多”了。在这些“过多”的极值上构建 ZUP 中的内置工具是不可取的。显然，这个主题需要专项研究，并进行公开的讨论...

增强模式专用于在“恰当的”极值上构建工具。以下工具可用于增强模式：

1. 静态干草叉
2. 静态斐波纳奇位
3. 静态斐波纳奇扩展
4. 独立的斐波纳奇扇
5. Versum 位
   
6. Micmed 的通道
   

安德鲁斯干草叉集合以干草叉为中心。干草叉集合的线条锚定到干草叉的特定点。例如，从干草叉的第一个初始点为起点，经过第二和第三个点绘制控制线。在增强模式中，所有线条都将锚定到干草叉的对应点，无论这些点在什么位置。

如果用之前的方式设置可在增强模式下工作的所有五个工具的参数，那么最终结果与之前不会有任何区别。

在增强模式下：

1. 对于静态干草叉，你将必须指定三个要在其上构建干草叉的峰值，而不再只指定一个显示第一个峰值的数字。示例如下：ExtPitchforkStaticNum=741。
   

   
   
   
   

   这里，峰值 7 对应干草叉的第一个点，谷值 4 对应干草叉的第二个点，峰值 1 对应干草叉的第三个点。在此例中，50-% 正中线以连接干草叉的点 1 和点 2（锯齿形调整浪极值 7 和 4）的线段的中点为起点，经过连接干草叉的点 2 和点 3（锯齿形调整浪极值 4 和 1）的线段的中线构建而成。反应线锚定到干草叉的点 2 和点 3。
   
   如果参数 ExtPitchforkStaticNum 中的最后一位数字大于 0，将显示静态干草叉。如果是 0，则将是动态干草叉。但一旦出现新的锯齿形调整浪线，该干草叉就会变成静态干草叉。如果在干草叉从动态转变为静态的过程中更改了指标的任何参数，则会再次显示动态干草叉。
   
   重要事项：位数 (741) 必须是相互交替的峰值与谷值。如果连续指定两个峰值或两个估值，则将无法构建干草叉。这意味着奇数和偶数必须交替出现。
   
   
2. 对于增强模式中的静态斐波纳奇位，应在参数中指定两个要在其上构建斐波纳奇位的锯齿形调整浪极值。例如，ExtFiboStaticNum=72。

   
   
   
   

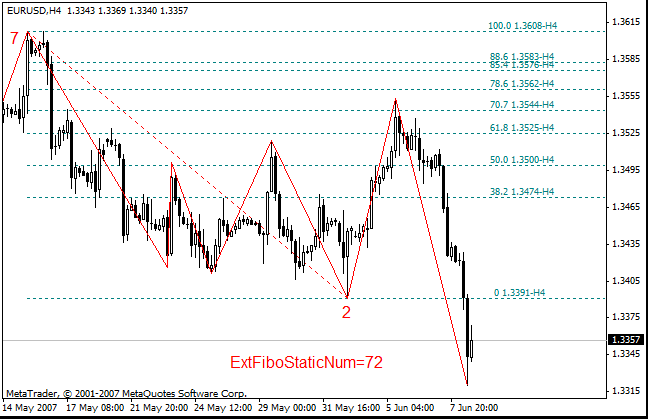
3. 在增强模式中，静态斐波纳奇扩展应构建在三个锯齿形调整浪极值上。示例：ExtFiboExpansion=721。

   
   
   
   
   

   上例中，将根据斐波纳奇扩展在 MetaTrader 4 中的绘制方式构建它们。但如果已显示斐波纳奇位（工具 2）且 ExtFiboCorrectionExpansion = true，则将显示斐波纳奇扩展而非斐波纳奇位。但是，在这种情况下，斐波纳奇扩展将构建在两个点上，与 Robert Fisher 书 [6] 中所述的扩展相对应。
   
   
4. 增强模式下，独立斐波纳奇扇构建在两个极值上。示例：ExtFiboFanNum=74

   
   
   
   
   

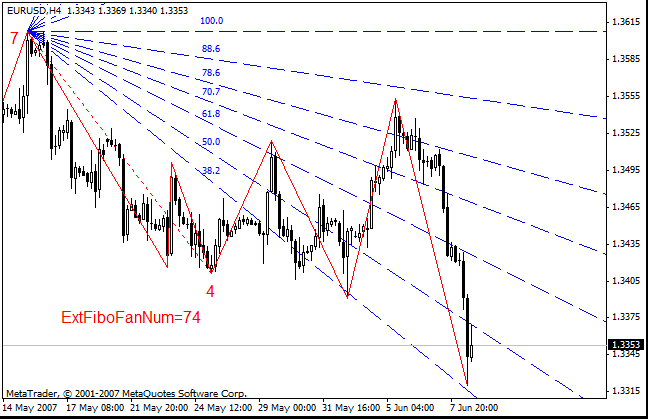
5. Versum 位：

   
   
   
   
   

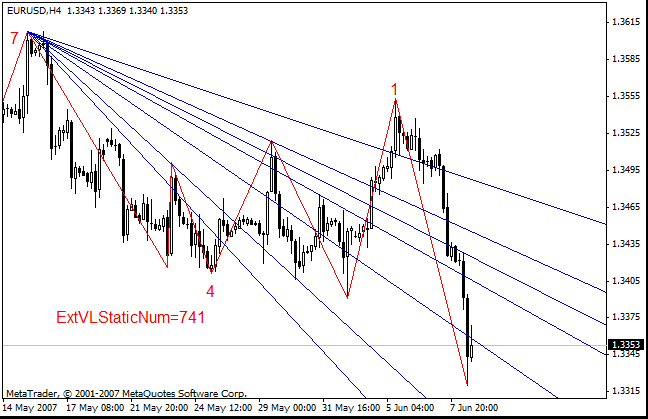
6. Micmed 的通道：

   
   
   
   

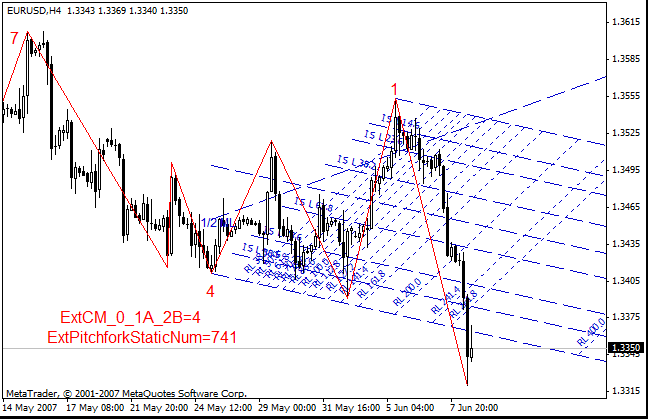
以下是我要再次强调的内容：

对于所有工具，在增强模式下，峰值和谷值都必须交替出现。如果出现两个连续的峰值或谷值，则无法构建工具。这个“连续”表示出现两个连续的、用于定义参数中极值的数位。

增强模式下的所有工具都有静态和动态这两种形态。如果已定义参数中的最后一个数位为 0，则该工具将动态地变化。

斐波纳奇弧

ZUP_v63 中可以构建斐波纳奇弧。下文中的所有参数都是 ZUP_v63 中的参数。

参数：

• ExtArcDinamicNum - 设置将构建动态斐波纳奇弧的锯齿形中断处的编号；
• ExtArcStaticNum - 设置将构建静态斐波纳奇弧的锯齿形中断处的编号；
• ExtArcDinamicColor - 设置动态斐波纳奇弧的颜色；
• ExtArcStaticColor - 设置静态斐波纳奇弧的颜色；
• ExtArcDinamicScale - 设置动态斐波纳奇弧的比例；0 - 自动比例；>0 - 自定义比例；
• ExtArcStaticScale - 设置静态斐波纳奇弧的比例；0 - 自动比例；>0 - 自定义比例。

弧有两个锚定点。

• 对于参数 ExtArcStaticNum=21：
  
  2 - 静态弧的中心点，它显示锯齿形调整浪峰值/谷值的编号
  1 - 弧的 100% 点，它也显示锯齿形调整浪峰值/谷值的编号
  
  
• 对于 ExtArcStaticNum=12 的设置
  
  1 - 中心点
  2 - 100-% 点
  

例如，如果设置 ExtArcStaticNum=3，中心点将在锯齿形调整浪的中断处 3 上，100% 点将在中断处 2 上。

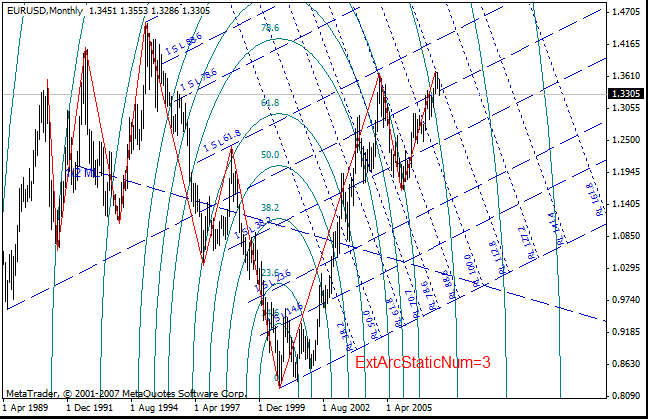
如果设置 ExtArcStaticNum=83，中心点将在中断处 8 上，100% 点将在中断处 3 上。也可在两个峰值或谷值之间定义中心点和 100% 点，例如：ExtArcStaticNum=42。

可在任意两个锯齿形中断处（中断处 1 到 9）之间绘制静态弧。可在“中断处”0 和后续 9 个中断处中的任意一个之间构建动态弧。

如果设置 ExtArcDinamicNum=8，中心点将在锯齿形调整浪的点 0 上，100% 点将在中断处 8 上。如果设置 ExtArcDinamicNum=80，中心点将在中断处 8 上，100% 点将在点 0 上。

此弧是沿着其所在的锯齿形调整浪线进行校准的。此线表示连接中心点与弧的 100% 点的线条，也即弧锚定到的点。它用参数 ExtArcDinamicScale=0 和 ExtArcStaticScale=0 自动进行校准。计算自动执行，方式如下：计算中心点与弧的 100% 点之间的点数，然后除以这些点之间的柱数。得数定义了绘制弧时的比例值。这样就按比例调整了弧。

如果在参数 ExtArcDinamicScale 和 ExtArcStaticScale 中写入一个超过 0 的数字，则将使用此数字校准（缩放）弧。

指标的可选性

可使用 ZigZag ExtIndicator = 1、ExtIndicator = 2 和 ExtIndicator = 3 以及参数 chHL=true 显示图表中的确认位。确认位显示通道。如果价格突破了通道的对侧，锯齿形调整浪将绘制一条新的线。

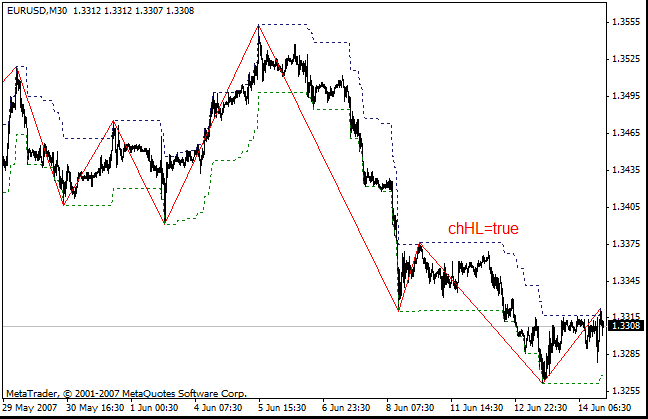
可使用参数 PeakDet = true 显示之前的锯齿形调整浪最小值和最大值的价位。

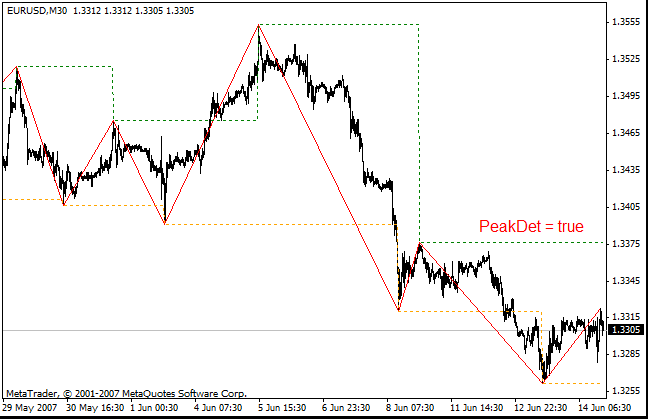
参数 chHL 和 PeakDet 取自原始的 Alex 的锯齿形调整浪。

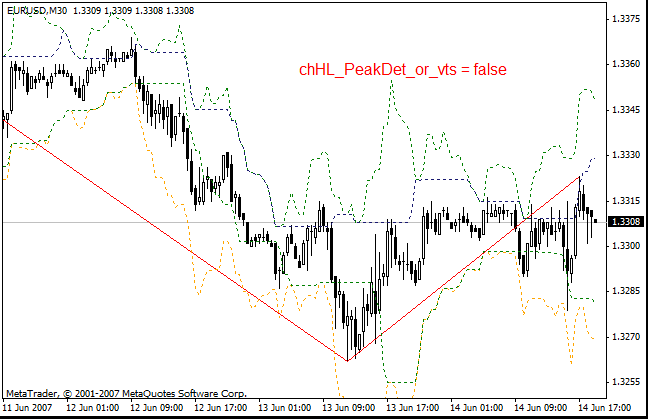
• chHL_PeakDet_or_vts- 如果为 true（默认设置），则允许输出确认线（价格通道）和之前的锯齿形调整浪最大值的价位。如果是 false，将显示指标 i-vts。如果设置为 false，将在屏幕上显示两个使用不同设置的 i-vts 指标副本。
• NumberOfBars - 要为 i-vts 计算的柱数（0 到所有柱）。
• NumberOfVTS - 这是目前为止我能判断出的一个用于 i-vts 的平滑参数。
• NumberOfVTS1 - 第二个 i-vts 副本的平滑参数。

常规选项

• ExtObjectColor - 设置连接图形对象基点的线条的颜色；
• ExtObjectStyle - 设置连接图形对象基点的线条的样式；
• ExtObjectWidth - 设置连接图形对象基点的线条的粗度；

这三个参数都适用于斐波纳奇位、斐波纳奇扩展、斐波纳奇弧和斐波纳奇时区。之前这些对象的基点使用红色虚线连接起来的。这三个参数可同时用于所有上述对象。

• ExtSendMail - 允许发送有关显示的模式的电子邮件消息；
• ExtAlert- 允许在出现新的锯齿形调整浪线时发送消息和发出警报；；
• ExtBack - 设置后台所有对象的显示；
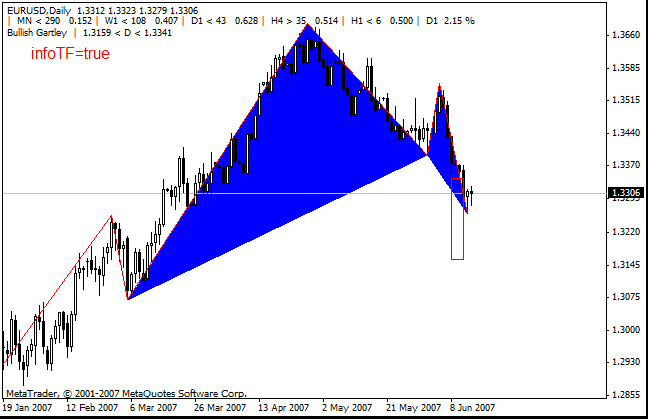
• infoTF - 显示有关 5 个较大时间范围的信息。显示的信息如下：时间范围名称、点中的烛台大小、与最小值相关的价格的当前状态。它还以百分比显示第一条锯齿形调整浪线的高度。它显示伽利模式的名称以及伽利模式可能的 D 点开发区的大小。

总结

本文介绍了 ZUP 中内置工具的主要功能：

1. 派斯温托模式：
2. 与安德鲁斯干草叉配合使用的工具集合；
3. 斐波纳奇扇；
4. 斐波纳奇位；
5. 斐波纳奇弧；
6. 斐波纳奇扩展的两种形态。

本文介绍了以下新工具：Versum 位和 micmed 的通道。斐波纳奇位在各种图形工具中使用的值的完整列表。同时也简要地介绍了 ZUP 参数。

我会继续增强 ZUP 的功能。未来有可能会增强已有的工具功能，并嵌入一些新的工具。后续还将添加新的参数。我还找到并修复了各种错误。ZUP 的进一步开发工作将在 ONIX 论坛上进行，网址为：http://onix-trade.net/forum/index.php?showforum=54

由于我们总在向 ZUP 添加新功能，完成相关功能说明是一项非常困难的工作。截至目前，我们已发布了 ZUP_v64。这个最新版本增强了 micmed 的通道的配套功能，现在可以使用自定义斐波纳奇位等。并且还添加了两个新的锯齿形调整浪：ExtIndicator=12 - Talex 开发的锯齿形调整浪，和 ExtIndicator=13 - Tovaroved 开发的锯齿形调整浪。

文本随附提供 ZUP_v63 和 ZUP_v64。ZUP_v64 还配上一段简短的说明，介绍其新颖之处（ MS Word 文件）。

参考文献列表

1. Larry Pesavento.Fibonacci Ratios with Pattern Recognition
2. Larry Pesavento.Profitable Patterns for Stock Trading
3. Bryce Gilmore.Dynamic Time and Price Analysis of Market Trends
4. Bryce Gilmore.Geometry of Markets
5. Bryce Gilmore.Geometry of Markets 2
6. Robert FisherNovie metodi torgovli po Fibonacci （Robert Fisher.The New Fibonacci Trader，译成俄语)