周波数領域でのフィルタリングと特徴抽出
105
0
はじめに
金融市場の分野では、正確な予測モデルが非常に求められています。信頼できる予測モデルには、意味のある関連情報が必要です。この記事では、特徴抽出のためのツールとして、周波数領域で適用されるさまざまなデジタルフィルタの使用法を探ります。離散フーリエ変換 (DFT)（英語）を用いて周波数領域に変換した時系列を分析することの利点と欠点について見ていきます。同相フィルタ、直交フィルタ、直交ミラーフィルタの、3種類のデジタルフィルタについて説明します。時系列分析における各タイプの有用性を強調します。最後に、各タイプの例を実装したコードを紹介します。
周波数領域でのフィルタリング
「初心者のためのMQL5におけるデジタルフィルタの実践的実装」稿の中で著者は、畳み込みを通して時間領域で適用されるデジタルフィルタを紹介しています。この系列は、フィルタの種類とそのパラメータによって、長さの異なる独自の重みのセットと掛け合わされます。重みの数は、フィルタをデータの範囲に適用する際に、対応する系列値と畳み込まれる移動窓を定義します。移動平均線も同じように機能します。
この記事では、周波数領域のフィルタを適用します。基本的な手順は以下の通りです。
- まず、DFT演算の準備として系列が前処理されます。
- DFTは、 高速フーリエ変換アルゴリズム(FFT)を使用して系列に適用されます。
- 次に、必要と思われる方法で直列の波形を操作します。つまり、フィルタが適用され、それによって直列の元の波形が変更されます。
- 修正された波形に対して逆DFT演算がおこなわれ、おなじみの時間領域に変換されます。
- 最後に、最初の前処理段階でおこなわれた操作によってもたらされた影響を元に戻します。
時間領域の畳み込みと同様に、系列のDFT項は、特定のフィルタを定義する係数と掛けられます。周波数領域でのフィルタリングは、多くの手順を必要とするため、計算コストが高くつくと思われるかもしれません。しかし、必ずしもそうとは限りません。
大規模なデータセットを扱う場合、高速フーリエ変換(FFT)アルゴリズムを採用すると、時間領域で系列を畳み込むよりもはるかに高速になることがあります。これは、あるベストプラクティスを採用した場合に特に当てはまります。これについては別のセクションで説明します。
フィルタの形状と機能
フィルタは関数によって決定され、その出力はフィルタの仕様に従って操作できます。関数の出力を操作すると、フィルタの形状が変化します。フィルタの形状は、フィルタの応答カーブです。フィルタが周波数領域でどのように振る舞うかを支配します。シグナル処理では、さまざまな分野で多くのフィルタ形状が使用されています。時系列分析では、角が丸いフィルタが好まれます。
角が丸いフィルタは、時系列分析に貴重なユニークな特性を持っています。角を丸くすることで、よりスムーズな周波数特性が実現されます。これは、周波数成分間の遷移で明らかになる歪みを最小限に抑えるのに役立ちます。フィルタ形状の丸い角によって、現実世界での実用的な実装が容易になります。その設計は数学的近似に基づいているため、より優れた性能を発揮することが多いです。必要な周波数成分と不要な周波数成分を区別する能力と、歪みの最小化のバランスがうまくとられます。
ガウス関数は、このプレゼンテーションで好まれているフィルタ関数です。 その形状は時間領域に集中する傾向があります。他のフィルタ機能に比べ、持続時間が比較的短いということです。適切なフィルタ機能を選択する際には、多くの取引オフを考慮する必要があります。ここではアプリケーションの要件が優先されます。
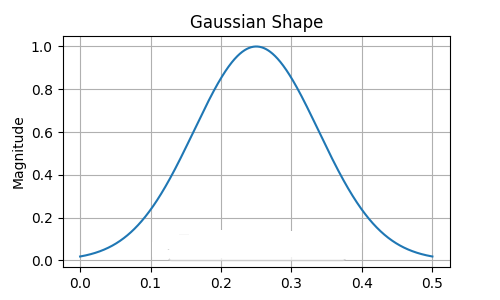
フィルタ仕様
この記事で取り上げるフィルタはすべて、中心周波数と幅の2つのパラメータで指定されます。スケールと呼ばれることもあります。いずれもサンプルあたりの周波数サイクルで示します。中心周波数は、0から0.5の範囲の値を取ることができます。幅のパラメータは、フィルタ機能を比較的そのまま通過させる、通過帯域の中心周波数の上下の周波数範囲を決定します。幅は約0.01以上の値を取るべきです。
同相フィルタ
まず、同相フィルタから始めて、フィルタの種類を探ります。波形の時間的な位置は位相と呼ばれます。同相フィルタは、入力シグナルと出力の位相関係を維持します。つまり、入力シグナルが同相フィルタを通過するとき、フィルタリングされた出力は、許容される周波数範囲内で入力と同じ時間的関係を保持します。
バンドパスフィルタは同相フィルタの一種で、他の多くのフィルタを構成する基本的な構成要素として機能します。フィルタは、特定の範囲の周波数を通過させ、その範囲外の周波数を減衰または拒否します。それは、通過帯域より低い、または高い周波数のシグナルを減衰させることで動作します。
ローパスフィルタとハイパスフィルタは、バンドパスフィルタを変更することで実装されます。ローパスフィルタは、シグナルの低周波を強調します。ほとんどの場合、プロセスの一般的な傾向を検出するために使用されます。中心周波数が低いほど、フィルタ出力は滑らかになります。バンドパスフィルタ機能を使用して、中心周波数以下のすべての周波数に定数1.0を乗じ、それ以上の周波数を適宜減衰させます。
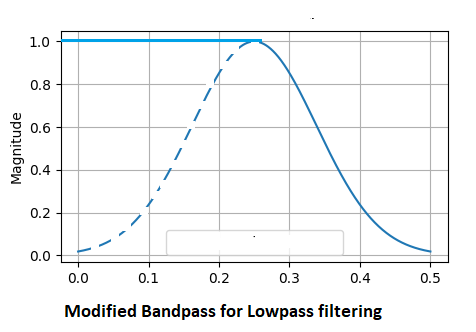
ハイパスフィルタは、シグナルから緩やかな変化をすべて取り除き、急激な変化に関する情報のみを残します。この場合、中心周波数の低域通過帯域より下のすべての周波数が低減されます。より高い帯域の周波数だけが通過します。
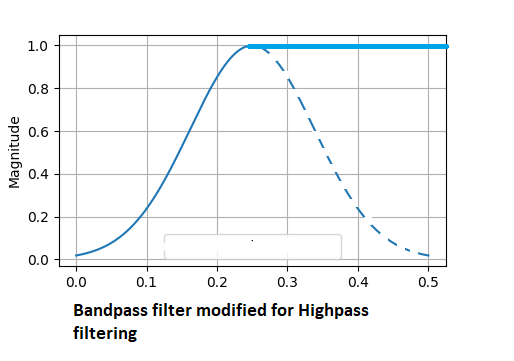
同相フィルタには数多くのバリエーションがあり、これまでに説明したものより優れたものもあるでしょう。ここに挙げたものはすべて、フィルタ形状が適度な丸みを帯びているという第一の特性を共有しており、これは強調してもしきれないほど重要な品質です。
直交フィルタ
これらのフィルタ（In-quadratureまたはquadratureフィルタと呼ばれる）は、入力に対して90度（Pi/2ラジアン）の位相シフトを適用してシグナルを処理するように設計されています。単独で使用した場合はたまにしか役に立たず、同相フィルタと組み合わせて使用するのが一般的です。特定の状況では、時系列内の位相関係を検出するのに有用です。
直交フィルタの価値を理解するには、例を見るのが一番です。以下は、短い周期成分で描かれた系列です。
次のプロットは、上記の系列のバンドパスフィルタ出力です。バンドパスフィルタの同相特性が強調されています。フィルタリングされたシグナルの動きは、元の系列の動きと一致しています。
次のプロットは、バンドパスフィルタの直交バージョンのフィルタ出力を示しています。よく見ると、フィルタされたシグナルのピークは、元のシグナルのゼロクロスに対応しています。基本的に、直交フィルタ出力は、同相バンドパス出力に適用されるシフトと一致します。
これは、直交出力シグナルのピークが入力系列の大きな変化を示していることを意味します。直交フィルタのピークと谷は、入力シグナルに速い変化が起きていることを示します。あるいは、入力シグナルが安定している場合、出力はゼロかゼロに近くなります。つまり、直交フィルタは特定の割合で起こる変化に敏感なのです。
別の例を見てみましょう。以下の系列は、急激な上方への動きが特徴です。
同相コンポーネントと直交コンポーネント（英語）フィルタ付き出力が続きます。ここでも、急激な上昇に対する山と谷の位置にご注目ください。同相出力でその動きを確認するのは難しいですが、直交フィルタ処理された系列は爆発的な動きを検出します。
この2種類のフィルタがどのように使用されたかで、併用時の有用性が浮き彫りになりました。同じパラメータを持つ同相フィルタと直交フィルタが併用された場合、それらは直交ミラーフィルタ（QMフィルタ）と呼ばれます。
直交ミラーフィルタ
QMフィルタは、周期的な成分の局所的なインスタンスの検出に役立ちます。QMフィルタを使用して、同相出力と直交出力を相対的に分析します。特定の周期的イベントが存在しない場合、これらの出力はどちらもゼロになります。同相出力を実数部、同相出力を虚数部として扱うことで、両者の出力を組み合わせることができます。フィルタリングされた波形の振幅と位相を計算できるようになります。
コードの実装を見る前に、まずどのような時系列分析手順でも最も重要な側面の1つを扱わなければなりません。
変換前の系列の前処理
時系列は有限の長さであるため、DFTで周波数領域に変換する際に問題が生じます。 DFTでは、未加工の級数は周期的であり、したがって無限に繰り返されると仮定します。非周期的なシグナルにDFTを適用すると、出力波形に歪みが生じることがあります。
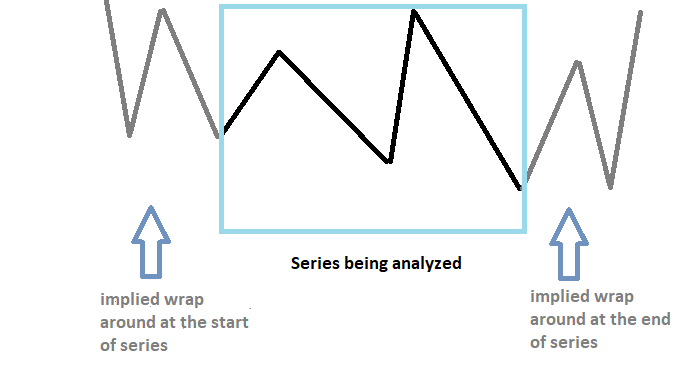
回り込み作用を軽減するためには、定数値を増やして系列の終わりを先細りにする必要があります。系列内のサンプル数を人為的に増やすことで、より細かい周波数分解能を実現し、スペクトルの漏れを減らすことができます。これはパディングと呼ばれる操作です。パディングされた系列はDFTを使用して変換されます。直列に追加された値は、直列のスペクトルの歪みを減らすのに役立ちますが、利点はそれだけではありません。
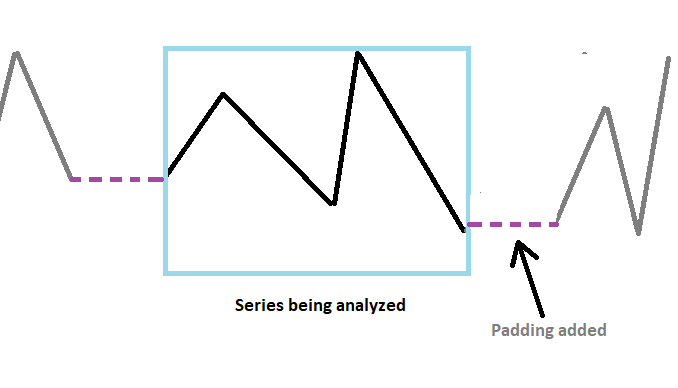
サンプル数の合計が2の累乗になるように系列の長さを長くすると、FFTアルゴリズムの計算効率が大幅に向上します。最初は、意図的に長さを長くすることがパフォーマンスの向上につながるというのは奇妙に思えますが、事実です。よって、パディングは欠かせません。ゼロを使用する以外に、系列の平均値を計算した値で系列をパディングすることもできます。
金融時系列には通常、非定常という厄介な癖があります。系列がパディングされ、その系列にゆっくり変化する成分が含まれている場合です。元の系列の両端の値と、パディングに使用された値の急激なコントラストは、周波数領域で顕著な周波数成分として現れることがあります。汚染が引き起こされます。
このような歪みを防ぐためには、元の系列値をトレンド除去する必要があります。そのため、元の系列値はデトレンドされた値に置き換えられます。系列の元の時間領域に戻る必要があるときは、系列を再トレンドさせればよいのです。これは、次のセクションでコードの実装を説明するときに実証されます。
CFilterクラス
CFilterクラスは、説明した3つのフィルタタイプの基本的な例をカプセル化しています。コードはFilter.mqhに含まれており、ALGLIBライブラリのfasttransforms.mqhをインクルードすることから始まります。
//+------------------------------------------------------------------+ //| CFilter - class implementing select filters in the freq domain | //+------------------------------------------------------------------+ class CFilter { int m_length; //length of original series int m_padded_len; //modified length of series int m_half_padded_len; //half of modded series double m_slope, m_intercept; //slope and intercept of trend in series double m_buffer[]; //general internal buffer bool m_initialized; //initialization flag complex m_dft[]; //general complex buffer public: CFilter(double &series[],uint min_padding=0, bool detrend=true); ~CFilter(void); void Lowpass(double freq,double width,double &out[],bool add_trend); void Highpass(double freq,double width, double &out[]); void Bandpass(double freq,double width, double &out[]); void Qmf(double freq,double width, complex &out[]); bool IsInitialized(void) { return m_initialized; } };
CFilterにはパラメトリックなコンストラクタがあり、ユーザはフィルタリングされる未加工の系列を渡さなければなりません。また、適用されるパディングの量と、DFT変換を適用する前に系列をトレンド除去するかどうかを指定する2つのパラメータも渡さなければなりません。min_paddingにゼロが設定された場合、実際のパディング量はサンプル数によってのみ決定されます。min_paddingは、系列の長さを2のべき乗に近づけるために含まれる余分な値を除いて、系列に追加される値の最小数を決定します。
コンストラクタの内部では、すべての引数が確認された後、パディングされた系列の最終的な長さが計算され、指定されていればデトレンドが適用されます。パディングされた系列は配列m_bufferに書き込まれます。そしてDFTは、複素数の配列であるm_dftに与えられた系列の波形で適用されます。コンストラクタでエラーが発生した場合、m_initializedはfalseに設定されます。
//+------------------------------------------------------------------+ //|constructor | //+------------------------------------------------------------------+ CFilter::CFilter(double &series[],uint min_padding=0,bool detrend=true) { //---local variables m_initialized=false; int i; int npts = ArraySize(series); int pad = (int)MathAbs(min_padding); //--- check size of series if(npts<=0) { Print("Input array is empty"); return ; } //--- m_length = npts ; for(m_padded_len=2 ; m_padded_len<INT_MAX ; m_padded_len*=2) { if(m_padded_len >= npts+pad) break ; } //--- if(m_padded_len<npts+pad) { Print("Warning, calculated length of modified series is too long"); return; } //--- m_half_padded_len = m_padded_len / 2; //--- ArrayResize(m_buffer,m_padded_len); //--- if(m_padded_len > npts) // Any padding needed? { if(detrend) { m_intercept = series[0] ; m_slope = (series[npts-1] - series[0]) / (npts-1) ; } else { m_intercept = m_slope = 0.0 ; for(i=0 ; i<npts ; i++) m_intercept += series[i] ; m_intercept /= npts ; } for(i=0 ; i<npts ; i++) { m_buffer[i]=series[i] - m_intercept - m_slope * i ; } for(i=npts ; i<m_padded_len ; i++) { m_buffer[i]=0.0; } } else { ArrayCopy(m_buffer,series); m_intercept = m_slope = 0.0 ; } //---Compute the Fourier transform of the padded series CFastFourierTransform::FFTR1D(m_buffer,int(m_padded_len),m_dft); //--- m_initialized = true; }
インスタンスが正しく構築されているかどうかは、IsInitialized()を呼び出して確認します。成功すればtrueが返されます。
インスタンス化に成功すると、m_dftに格納されたシグナルに指定されたフィルタを適用する、一般にアクセス可能なメソッドのいずれかを呼び出すことができます。これらのほとんどは同じような入力条件を持っています。まず、freqとwidthパラメータで定義される、フィルタの仕様です。これらは、適用する通過帯域の中心周波数と幅に対応します。ほとんどすべてのメソッドは、フィルタリングの結果が保存される、少なくとも最後の入力配列を期待しています。
Lowpass()は、4番目の入力パラメータを受け付ける唯一のメソッドです。このパラメータは、元のシグナルに最初に適用されたデトレンドを、フィルタの出力で反転させるかどうかを決定します。
//+--------------------------------------------------------------------+ //|Filters series in frequency domain and returns output in time domain| //+--------------------------------------------------------------------+ void CFilter::Lowpass(double freq,double width,double &out[],bool add_trend) { //--- int i ; double f, dist, wt ; complex dft_temp[]; ArrayCopy(dft_temp,m_dft); //--- for(i=0 ; i<=m_half_padded_len ; i++) { f = (double) i / (double) m_padded_len ; // This frequency if(f <= freq) // Flat to here wt = 1.0 ; else { dist = (f - freq) / width ; wt = exp(-dist * dist) ; } dft_temp[i].real*=wt; dft_temp[i].imag*=wt; } //--- double temp[]; //--- CFastFourierTransform::FFTR1DInv(dft_temp,m_padded_len,temp); //--- ArrayResize(out, m_length); //--- for(int i = 0; i<m_length; i++) out[i]=(add_trend)?temp[i] + m_intercept + m_slope*i:temp[i]; }
同相フィルタの実装には2つの手順があります。まず、m_dftに入れられたシグナルの波形に、修正されたフィルタ関数を掛けます。この実装ではガウス関数です。最後に逆DFTをおこない、系列を時間領域に戻します。
QMフィルタ出力を計算するには、波形のDFT項とフィルタ関数の直交バージョンを掛けます。直交フィルタ関数は、単純に90度の位相シフトを適用した同相フィルタ関数です。この位相シフトを実現するために、同相フィルタ関数はi倍され、純粋な虚数になります。その結果、出力がナイキスト周波数に対して対称な関数となります。周波数0.5の両側の出力項は、絶対値では等しいが、符号は逆になります。
Qmf()メソッドは、波形のDFT項と同相および直交フィルタ関数の和を乗算することによって、この事実を利用します。これは、直交フィルタ関数をi倍して純粋実数（直交フィルタ関数は純粋虚数であることを思い出してください）にすることによっておこなわれます。フィルタ機能を足し合わせると、ナイキスト周波数を超えた出力は互いに打ち消し合います。コードでは、0.5以上のDFT項は0に設定されます。ナイキスト周波数以下のフィルタ出力のみを計算する必要があります。波形がフィルタされると、複素逆DFTがおこなわれ、時間領域に戻ります。
//+------------------------------------------------------------------+ //| Implements Quadrature Mirror Filter, output is complex | //+------------------------------------------------------------------+ void CFilter::Qmf(double freq,double width,complex &out[]) { //--- int i ; double f, dist, wt ; complex dft_temp[]; ArrayCopy(dft_temp,m_dft); //--- for(i=1 ; i<m_half_padded_len ; i++) { f = (double) i / (double) m_padded_len ; // This frequency dist = (f - freq) / width ; wt = exp(-dist * dist) ; dft_temp[i].real *= wt ; dft_temp[i].imag *= wt ; dft_temp[m_padded_len-i].real = dft_temp[m_padded_len-i].imag = 0.0 ; // Causes QMF outputs } //--- dft_temp[0].real = 0.0 ; dist = (0.5 - freq) / width ; dft_temp[m_half_padded_len].real = 0.5 * dft_temp[m_half_padded_len].imag * exp(-dist * dist) ; //--- dft_temp[0].imag = dft_temp[m_half_padded_len].imag = 0.0 ; // By definition of real transform //--- CFastFourierTransform::FFTC1DInv(dft_temp,m_padded_len); ArrayResize(out,m_length); //--- for(i=0 ; i<m_length ; i++) { out[i].real = dft_temp[i].real/double(m_half_padded_len) ; out[i].imag = dft_temp[i].imag/double(m_half_padded_len) ; } } //+------------------------------------------------------------------+
AFDプログラム
CFilterの使い方を説明するために、AFD.mq5を紹介しましょう。アプリケーションはエキスパートアドバイザー(EA)として実装されています。指定した長さのランダムなシーケンスを生成することができます。ユーザーは、生成する系列の長さを設定し、使用する乱数のシードも調整できます。上のグラフでは系列は青でプロットされています。生成された系列に選択されたフィルタを適用した結果を、2番目のプロットで観察することができます。フィルタのすべてのパラメータは、プログラムのグラフィカルユーザーインターフェイスから調整できます。アプリケーションを以下に示します。
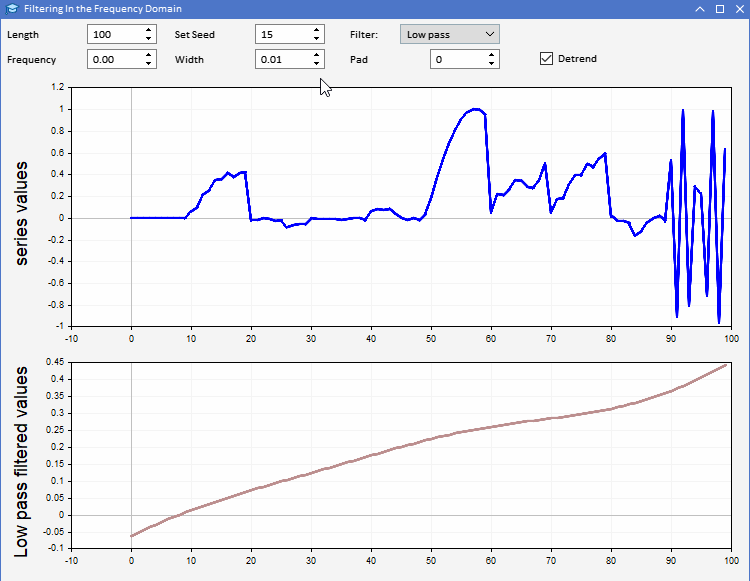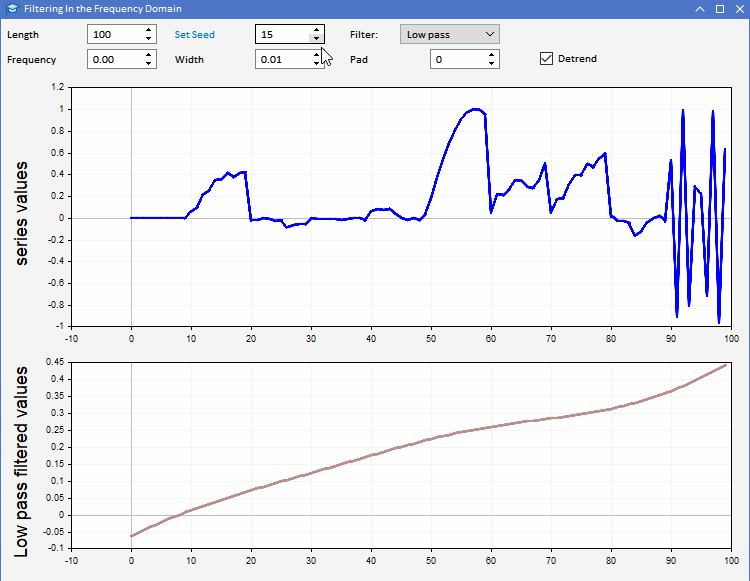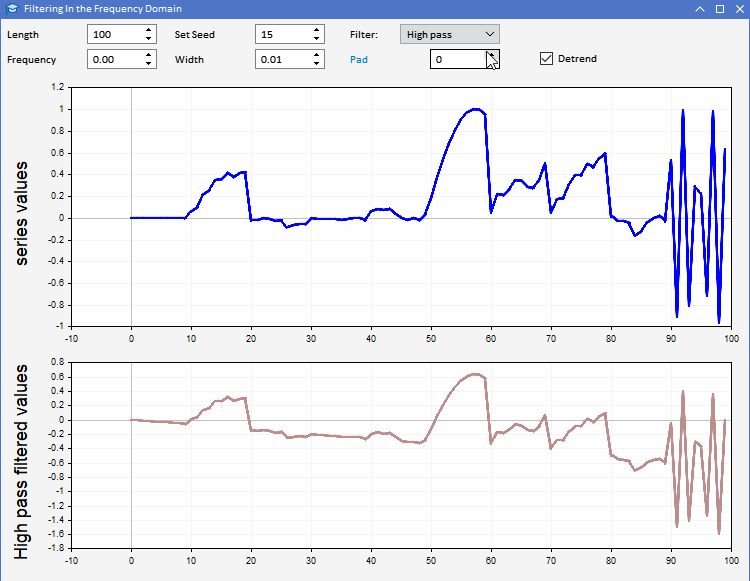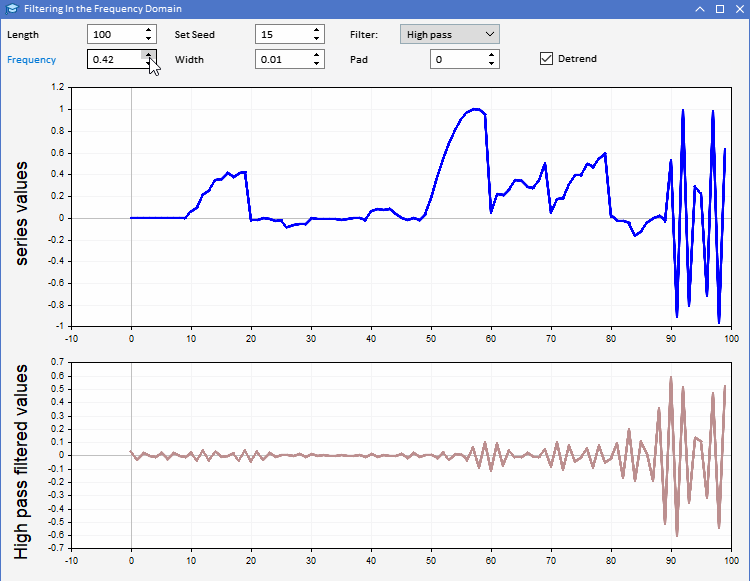
AFDアプリケーションを使用すれば、フィルタ出力によって明らかになるさまざまな種類の情報を、より直感的に理解することができます。同相フィルタからの出力は、2つの方法で使用することができます。ローパスフィルタからの出力は、任意の時点における入力系列の平均値に関する情報を提供するために使用することができます。ハイパスフィルタ出力は、元の系列に時折見られるハイとローを明らかにします。これらの出力は、各時点における入力系列の状態を示します。
バンドパスフィルタの出力は、その関連性があまり明らかではありません。フィルタ出力の意味を観察だけで理解することは、おそらく誰にも不可能でしょう。しかし、このデータが予測モデルに役立つ可能性はあります。もしかしたら、ある通過帯域のバンドパス出力がピークや谷にあることを知ることは、元の系列で何かを意味するのかもしれません。
異なる周波数におけるランダム系列のバンドパス出力を見てみましょう。
出力はもう1つの情報を明らかにします。バンドパス出力のピークは、特定のタイムスロットにおける周期的な変動量を表します。より正確には、変動の振幅を示し、周期的変動の存在を示します。ピークが低いほどばらつきが小さいことを示し、ピークが高いほどばらつきが大きいことを示します。
振幅はQMフィルタ出力のサンプリングによって与えられます。QMフィルタ値を使った振幅と位相の計算は、AFD.mq5から引用した以下のコードに示されています。
case ENUM_QMF_AMPLITUDE: { y_name = "Amplitude"; complex comp[]; filter.Qmf(freq,scale,comp); ArrayResize(m_output1,ArraySize(comp)); for(int i=0; i<ArraySize(m_output); i++) m_output1[i]=MathSqrt(comp[i].real*comp[i].real + comp[i].imag*comp[i].imag); } break; case ENUM_QMF_PHASE: { y_name = "Phase"; complex comp[]; filter.Qmf(freq,scale,comp); ArrayResize(m_output1,ArraySize(comp)); for(int i=0; i<ArraySize(m_output); i++) m_output1[i]=(comp[i].real>=1.e-40 || comp[i].imag>=1.e-40)?atan2(comp[i].imag, comp[i].real):0.0; } break;
周波数ごとのバンドパス出力の違いは、利用可能な情報に多様性があることを示しています。したがって、機械学習アルゴリズムに供給する独自の特徴を構築することができます。このようなデータセットを賢く構築するためには、実務者は特定のフィルタを定義するパラメータをしっかりと把握する必要があります。
幅パラメータ
前述したように、実装されているすべてのフィルタのパラメータは、単位時間あたりの周波数サイクルで表現されています。周波数領域で分析をおこなうことの欠点の1つは、周波数成分と時間領域でのその範囲との関連付けが難しいことです。前節で見たランダム系列を例にとると、バンドパス出力は周波数0.15、0.3、0.45で、すべて同じ幅0.03でサンプリングされました。これらの値が何を意味するのか、特にシリーズの時間領域との関連で理解することが重要です。
周波数が0.15の場合、周期は1/0.15=6.67サンプル/サイクルとなります。幅は周波数領域での分解能を決定します。狭い周波数帯域を分離したい場合は、小さな幅を適用します。通常は0.01が最小ですが、これより低くすることも可能です。もう一度例に戻ります。幅は0.03に設定したので、通過帯域は0.15-0.03から0.15+0.03、つまり0.12から0.18まで広がます。この範囲の周波数は通過し、上下の周波数はほぼ完全に停止します。
この幅は、時間領域での分解能の指標にもなります。周波数領域の分解能と時間領域の分解能の関係は逆です。ある領域で解像度が高くなると、別の領域では解像度が低下します。幅に対する時間領域の広がりを推定するために、以下の式を適用します。0.8/幅
これを使用することで、現在位置から相対的な周波数通過帯域によって影響を受ける時間領域のサンプル数を推定することができます。言い換えれば、観測された出力に影響を与える現在の位置の前後のサンプル数を推定します。例に戻ると、幅が0.03の場合、時間的な広がりは0.8/0.03=27サンプルとなります。つまり、各出力の値は、その前の27のオブザベーションと、その次の27のオブザベーションによって決定されるか、影響を受けるということです。
一般的に言って、フィルタの幅は、調べたい通過帯域の中心周波数に比例すべきです。これは周波数の周期と関係しています。周波数が低いほど周期は長くなり、高いほど周期は短くなります。したがって、低い周波数では、時間領域での分解能を犠牲にし、狭い幅を選ぶ余裕があります。一方、より高い周波数では、より広い幅のパラメータが有効であり、これは時間領域ではより短い範囲に変換されます。
最後に、幅パラメータも予測モデルに供給される値に影響を与えます。 先ほどの例で、暗黙の時間領域を計算すると、約27回の観測となります。タイムスロット番号201の次の値を予測したいとします。200個の既知の値、つまり系列の終わりから27スロットに基づいて計算された、フィルタされた出力の値を提供します。フィルタのパラメータの制約のもとでは、DFTによって引き起こされる回り込み効果の影響を受けることがわかっているからです。
最後の例では、異なる周波数でフィルタリングされた出力をサンプリングしたが、すべて同じ幅です。実際には、可能な限り有用な情報を取り込むために、戦略的に選択された周波数と幅でフィルタリングされた出力をサンプリングする方が有益でしょう。
結論
まとめると、3種類のフィルタを見てきました。
- 同相フィルタは、ノイズの多い系列を異なる成分に分解し、重要な情報を強調し、気を散らす余計な特性を取り除くのに役立ちます。学習アルゴリズムに関連情報を提供することで、より優れた予測モデルを構築することができます。
- 直交フィルタは、系列内の急激なレベル変化の領域を検出するために使用することができます。系列中の重要な動きを目で見るのは簡単かもしれませんが、そのような現象を学習アルゴリズムに伝えるのは難しいかもしれません。これは直交フィルタの値です。
- 同相フィルタと直交フィルタの組み合わせは、周期的な特徴の存在を識別するために協働します。これらのツールは、時系列に一見無作為に現れる特徴を特定し、研究するのに有効です。
周波数領域でのフィルタリングは、FFTアルゴリズムが提供する計算効率を活用します。時間領域での畳み込みの方法と比べれば、勝負になりません。しかし、あるのはバラばかりではありません。直列を周波数領域に変換することには落とし穴があり、不注意なデータの取り扱いによってもたらされる歪みのために、まったく間違った結論になってしまうことがあります。実践する際は用心深くあるべきです。
すべてのツールとプログラムのコードを添付します。AFD.mq5は、定評あるEasy and Fast (EAF)GUIライブラリを使用しています。mql5.comのコードベースで入手できます。余談ですが、ALGLIBとともにEAFライブラリを使用する場合は、必ずアプリケーションの最後にEAFをインクルードしてください。これらのライブラリ間には、コンパイルの成功を妨げる名前の競合がいくつかあります。
| ファイル名 | 詳細 |
|---|---|
| Mql5IncludeFilter.mqh | 基本的なデジタルフィルタを周波数領域で実装するCFilterクラスの定義が含まれる |
| Mql5\Include\RandomStationarySeries.mqh | 様々な特徴を持つランダム系列を生成するためのルーチン（関数）が含まれる（AFD.ex5アプリケーションで使用） |
| Mql5ExpertsAFD.mq5 | AFDアプリケーションのソースコードで、mql5.comcodebaseにあるEasy and Fast GUIライブラリを使用 |
| Mql5ExpertsAFD.ex5 | EAとして実装された、コンパイル済みのAFDアプリケーション |
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/13881
知っておくべきMQL5ウィザードのテクニック（第09回）：K平均法とフラクタル波の組み合わせ
ソフトウェア開発とMQL5におけるデザインパターン（第4回）：振る舞いパターン2
時系列マイニングのためのデータラベル（第4回）：ラベルデータを使用した解釈可能性の分解
データサイエンスと機械学習（第17回）：木の中のお金？外国為替取引におけるランダムフォレストの芸術と科学
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索