Filterung und Merkmalsextraktion von Frequenzen

Einführung

Im Bereich der Finanzmärkte sind genaue Prognosemodelle sehr begehrt. Zuverlässige Prognosemodelle erfordern aussagekräftige und relevante Informationen. In diesem Artikel werden wir die Verwendung verschiedener digitaler Filter, die im Frequenzbereich angewendet werden, als Hilfsmittel für die Merkmalsextraktion untersuchen. Wir werden einige der Vor- und Nachteile der Analyse von in den Frequenzbereich konvertierten Zeitreihen unter Verwendung der Diskrete Fourier-Transformation (DFT) erläutern. Es werden drei Arten von digitalen Filtern besprochen: die Spiegelfilter von In-Phase, In-Quadratur und Quadratur. Ausarbeiten des Nutzens jedes Typs in der Zeitreihenanalyse. Schließlich wird der Code vorgestellt, der Beispiele für jeden Typ implementiert.

Filterung im Frequenzbereich

In dem Artikel „Praktische Implementierung digitaler Filter in MQL5 für Anfänger“ stellt der Autor digitale Filter vor, die im Zeitbereich durch Faltung angewendet werden. Die Reihe wird mit einem einzigartigen Satz von Gewichten unterschiedlicher Länge multipliziert, je nach Filtertyp und seinen Parametern. Die Anzahl der Gewichte definiert ein bewegliches Fenster, das mit den entsprechenden Serienwerten gefaltet wird, wenn der Filter über den Umfang der Daten angewendet wird. Auch gleitende Durchschnitte funktionieren auf die gleiche Weise.

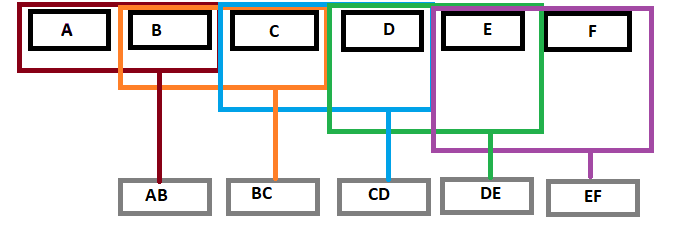
In diesem Artikel werden wir Filter im Frequenzbereich anwenden. Die grundlegenden Schritte sind wie folgt:

1.  Zunächst wird die Reihe zur Vorbereitung einer DFT-Operation vorverarbeitet.
2.  Die DFT wird mit dem Algorithmus Schnelle Fourier-Transformation (FFT) auf die Reihen angewendet.
3.  Als Nächstes manipulieren wir die Wellenform der Reihe in der Weise, die wir für notwendig halten. Das heißt, es wird ein Filter angewandt, wodurch die ursprüngliche Wellenform der Reihe verändert wird.
4.  Die modifizierte Wellenform wird durch eine inverse DFT-Operation in den bekannten Zeitbereich zurückverwandelt.
5. Schließlich werden die Auswirkungen der in der ersten Vorverarbeitungsphase durchgeführten Operationen rückgängig gemacht.

Ähnlich wie bei der Faltung im Zeitbereich werden die DFT-Terme einer Reihe mit Koeffizienten multipliziert, die einen bestimmten Filter definieren. Die zahlreichen Schritte lassen vermuten, dass die Filterung im Frequenzbereich sehr viel rechenintensiver ist. Dies ist jedoch nicht immer der Fall.

Bei großen Datensätzen kann der Algorithmus der Schnellen Fourier-Transformation (FFT) tatsächlich viel schneller sein als die Faltung einer Reihe im Zeitbereich. Dies gilt insbesondere dann, wenn bestimmte bewährte Praktiken angewandt werden, die wir in einem anderen Abschnitt behandeln werden.

Filterformen und -funktionen

Der Filter wird durch eine Funktion bestimmt, deren Ausgang entsprechend der Spezifikation des Filters manipuliert werden kann. Durch Manipulation des Funktionsausgangs wird die Form des Filters verändert. Die Form des Filters ist die Ansprechkurve des Filters. Er bestimmt, wie sich der Filter im Frequenzbereich verhält. Es gibt viele Filterformen, die in der Signalverarbeitung in verschiedenen Fachgebieten verwendet werden. Bei der Zeitreihenanalyse werden Filter mit runden Ecken bevorzugt.

Filter mit runden Ecken haben einzigartige Eigenschaften, die für die Zeitreihenanalyse von unschätzbarem Wert sind. Die runden Ecken sorgen für einen glatteren Frequenzgang. Dies trägt dazu bei, die Verzerrungen an den Übergängen zwischen den Frequenzkomponenten zu minimieren. Runde Ecken in der Form des Filters erleichtern die praktische Umsetzung in der realen Welt. Da ihre Entwürfe auf mathematischen Näherungen beruhen, die oft eine bessere Leistung bieten. Dabei wird ein gutes Gleichgewicht zwischen der Fähigkeit, erwünschte und unerwünschte Frequenzkomponenten zu unterscheiden, und der Minimierung von Verzerrungen erreicht.

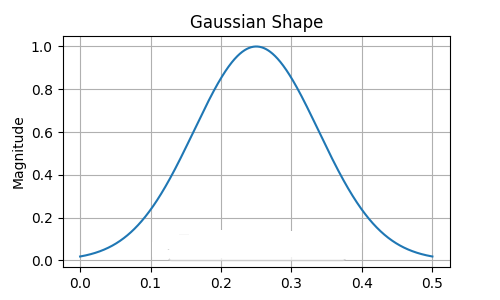
Die Gaußfunktion ist die in dieser Präsentation bevorzugte Filterfunktion.  Ihre Form ist tendenziell stärker auf den Zeitbereich konzentriert. Das bedeutet, dass sie im Vergleich zu anderen Filterfunktionen eine relativ kurze Dauer hat. Bei der Auswahl einer geeigneten Filterfunktion sind viele Kompromisse zu berücksichtigen. Hier haben die Anwendungsanforderungen Vorrang.

Filter-Spezifikation

Die in diesem Artikel vorgestellten Filter werden alle durch zwei Parameter spezifiziert. Die Mittenfrequenz und der Breitenparameter. Manchmal auch Skala genannt. Beide sollten in Form von Frequenzzyklen pro Probe angegeben werden. Die Mittenfrequenz kann Werte im Bereich von 0 bis 0,5 annehmen. Der Parameter width (Breite) bestimmt den Bereich der Frequenzen oberhalb und unterhalb der Mittenfrequenz im Durchlassbereich, der relativ unverändert durch die Filterfunktion geleitet wird. Die Breite sollte Werte von etwa 0,01 und mehr annehmen.

Phasengleiche Filter

Wir beginnen unsere Untersuchung der Filtertypen mit phasengleichen Filtern. Die Position einer Wellenform in der Zeit wird als ihre Phase bezeichnet. Gleichphasige Filter halten die Phasenbeziehung zwischen dem Eingangssignal und dem Ausgangssignal aufrecht. Das bedeutet, wenn ein Eingangssignal einen phasengleichen Filter durchläuft, behält das gefilterte Ausgangssignal innerhalb des zulässigen Frequenzbereichs die gleichen zeitlichen Beziehungen wie das Eingangssignal.

Bandpassfilter sind eine Art phasengleicher Filter, der als grundlegender Baustein dient, aus dem viele andere Filter aufgebaut werden können. Der Filter lässt einen bestimmten Frequenzbereich durch, während er Frequenzen außerhalb dieses Bereichs abschwächt oder unterdrückt. Er reduziert Signale mit Frequenzen, die unter oder über dem Durchlassbereich liegen.

Tiefpass- und Hochpassfilter werden durch Modifikation des Bandpassfilters realisiert. Ein Tiefpassfilter betont die tiefen Frequenzen eines Signals. Wird meist verwendet, um die allgemeine Tendenz eines Prozesses zu erkennen. Je niedriger die Mittenfrequenz ist, desto glatter ist das gefilterte Ergebnis. Mit der Bandpassfilterfunktion werden alle Frequenzen, die kleiner oder gleich der Mittenfrequenz sind, mit der Konstante 1,0 multipliziert und alle darüber liegenden Frequenzen entsprechend abgeschwächt. 

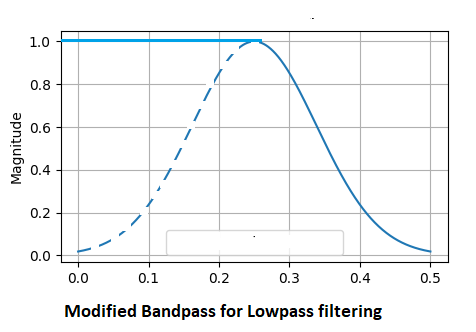
Ein Hochpassfilter entfernt alle langsamen Veränderungen aus dem Signal und lässt nur Informationen über schnelle Veränderungen übrig. In diesem Fall werden alle Frequenzen unterhalb des unteren Durchlassbereichs der Mittenfrequenz reduziert. Nur die Frequenzen in den höheren Bändern werden durchgelassen.

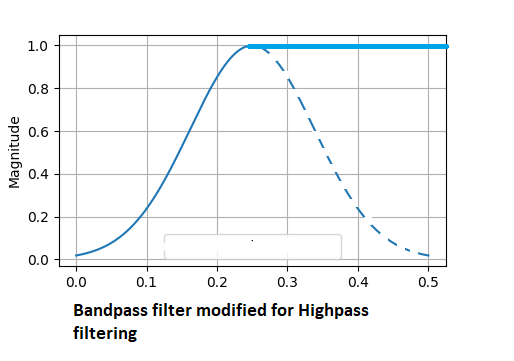
Es gibt zahlreiche Varianten von In-Phase-Filtern, von denen einige möglicherweise besser sind als die bisher beschriebenen. Die hier erwähnten Filter haben alle die Haupteigenschaft, eine ausreichend runde Filterform zu haben, eine wichtige Eigenschaft, die nicht genug betont werden kann.  

In-Quadratur-Filter

Diese Filter (auch als Quadraturfilter bezeichnet) sind so konzipiert, dass sie Signale mit einer Phasenverschiebung von 90 Grad (Pi/2 Radiant) gegenüber dem Eingang verarbeiten. Sie sind nur gelegentlich für sich allein nützlich und werden eher in Kombination mit gleichphasigen Filtern verwendet. In bestimmten Situationen sind sie nützlich, um Phasenbeziehungen innerhalb von Zeitreihen zu erkennen.

Um den Wert eines In-Quadratur-Filters zu verstehen, ist es am besten, ein Beispiel zu betrachten. Im Folgenden wird eine Reihe durch eine kurze periodische Komponente dargestellt.

Das nächste Diagramm ist die bandgefilterte Ausgabe der obigen Reihe. Sie unterstreicht die phasengleiche Natur des Bandpassfilters. Die Bewegungen des gefilterten Signals stimmen mit denen der ursprünglichen Serie überein.

Die folgende Abbildung zeigt das gefilterte Ausgangssignal einer Quadraturversion des Bandpassfilters. Bei genauer Betrachtung ist zu erkennen, dass die Spitzen im gefilterten Signal den Nulldurchgängen im Originalsignal entsprechen. Im Grunde genommen entspricht der in Quadratur gefilterte Ausgang einer Verschiebung, die auf den phasengleichen Bandpassausgang angewendet wird.

Dies bedeutet, dass Spitzen im Quadratur-Ausgangssignal eine signifikante Änderung in der Eingangsreihe anzeigen. Die Spitzen und Senken eines In-Quadratur-Filters geben einen Hinweis auf schnelle Änderungen im Eingangssignal. Wenn das Eingangssignal konstant ist, ist das Ausgangssignal Null oder geht gegen Null. Das bedeutet, dass In-Quadratur-Filter empfindlich auf Änderungen reagieren, die mit bestimmten Raten auftreten.

Schauen wir uns ein anderes Beispiel an. Die nachfolgende Serie ist durch eine starke, abrupte Bewegung nach oben gekennzeichnet.

Es folgen gefilterte Ausgänge dieser Serie mit dem I&Q-Verfahren. Achten Sie auch hier auf die Position der Höchst- und Tiefststände im Verhältnis zur starken Aufwärtsbewegung. Während es schwierig ist, die Bewegung anhand des gleichphasigen Ausgangs festzustellen, kann die in Quadratur gefilterte Reihe die explosive Bewegung erkennen.

Die Art und Weise, in der die beiden Filtertypen verwendet wurden, verdeutlicht ihren Nutzen, wenn sie zusammen eingesetzt werden. Wenn ein In-Phase- und ein In-Quadratur-Filter mit denselben Parametern zusammen verwendet werden, nennt man sie Quadratur-Spiegel-Filter (QM-Filter).

Quadraturspiegelfilter

QM-Filter helfen bei der Erkennung von lokalisierten Instanzen periodischer Komponenten. Mit Hilfe des QM-Filters analysieren wir den In-Phase-Ausgang im Verhältnis zum In-Quadratur-Ausgang. Beide Ausgänge sind auf Null, wenn ein bestimmtes periodisches Ereignis nicht vorhanden ist. Die Ausgangssignale beider Geräte können kombiniert werden, indem das phasengleiche Ausgangssignal als Realteil und das quadraturgleiche Ausgangssignal als Imaginärteil behandelt wird. Das ermöglicht die Berechnung von Amplitude und Phase der gefilterten Wellenform.

Bevor wir uns mit der Implementierung des Codes befassen, müssen wir uns zunächst mit einem der wichtigsten Aspekte eines jeden Verfahrens zur Zeitreihenanalyse befassen.

Vorverarbeitung der Reihen vor der Transformation

Die Tatsache, dass Zeitreihen eine endliche Länge haben, führt zu Problemen bei der Umwandlung in den Frequenzbereich mit der DFT.  Bei der DFT wird davon ausgegangen, dass die Rohreihe periodisch ist und sich daher unendlich oft wiederholt. Die Anwendung der DFT auf ein nicht-periodisches Signal kann zu Verzerrungen in der Wellenform des Ausgangs führen.

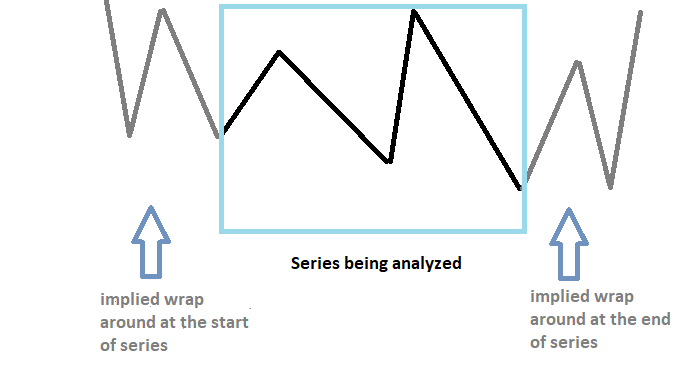
Um die Umhüllungseffekte abzuschwächen, müssen wir das Ende der Reihe mit zusätzlichen konstanten Werten ausdünnen. Durch die künstliche Erhöhung der Anzahl der Abtastwerte in der Reihe kann eine feinere Frequenzauflösung erreicht und der spektrale Leckverlust verringert werden. Dies ist ein Vorgang, der als Auffüllen (padding) bezeichnet wird. Die aufgefüllte Reihe wird mit Hilfe der DFT umgerechnet. Die zusätzlichen Werte, die der Reihe hinzugefügt werden, tragen dazu bei, Verzerrungen im Spektrum der Reihe zu verringern, aber das sind nicht die einzigen Vorteile.

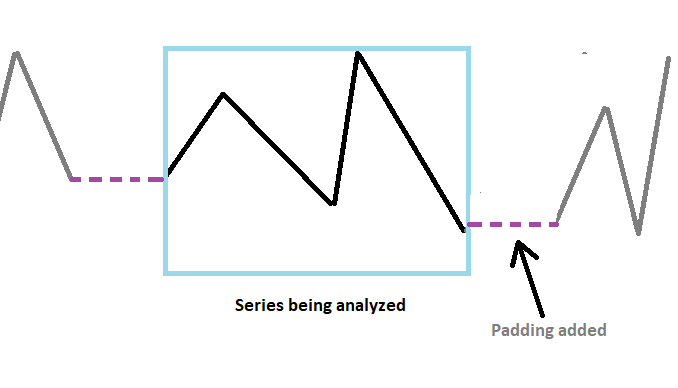
Die Erhöhung der Länge der Reihe, sodass die Gesamtzahl der Abtastwerte eine Potenz von 2 ist, verbessert die Recheneffizienz des FFT-Algorithmus erheblich. Auf den ersten Blick scheint es seltsam, dass eine absichtliche Erhöhung der Länge zu einer besseren Leistung führt, aber es stimmt. Eine Auffüllung ist also unerlässlich. Neben der Verwendung von Nullen kann eine Reihe auch mit dem berechneten Mittelwert der Reihe aufgefüllt werden.

Finanzielle Zeitreihen haben in der Regel die unangenehme Angewohnheit, nicht stationär zu sein. Wenn eine Reihe aufgefüllt wird und die Reihe eine sich langsam verändernde Komponente enthält. Der scharfe Kontrast zwischen den Werten an den beiden Enden der ursprünglichen Reihe und den zum Auffüllen verwendeten Werten kann sich als auffällige Frequenzkomponente im Frequenzbereich manifestieren. Verursachen von Verunreinigungen.

Um dieser Form der Verzerrung vorzubeugen, müssen die ursprünglichen Reihenwerte detrendiert werden. Die ursprünglichen Reihenwerte werden also durch die umgekehrten Werte ersetzt. Wenn wir zum ursprünglichen Zeitbereich der Reihe zurückkehren wollen, müssen wir nur den Trend der Reihe neu bestimmen. Dies wird im nächsten Abschnitt über die Implementierung des Codes gezeigt.

Die Klasse CFilter

Die Klasse CFilter kapselt grundlegende Beispiele für die drei besprochenen Filtertypen. Der Code ist in Filter.mqh enthalten, das mit der Einbindung der Datei fasttransforms.mqh aus der ALGLIB-Bibliothek beginnt.

//+------------------------------------------------------------------+
//|  CFilter - class implementing select filters in the freq domain  |
//+------------------------------------------------------------------+
class CFilter
  {
   int               m_length;                   //length of original series
   int               m_padded_len;                //modified length of series
   int               m_half_padded_len;           //half of modded series
   double            m_slope, m_intercept;     //slope and intercept of trend in series
   double            m_buffer[];               //general internal buffer
   bool              m_initialized;              //initialization flag
   complex           m_dft[];                 //general complex buffer

public:
                     CFilter(double &series[],uint min_padding=0, bool detrend=true);
                    ~CFilter(void);

   void              Lowpass(double freq,double width,double &out[],bool add_trend);
   void              Highpass(double freq,double width, double &out[]);
   void              Bandpass(double freq,double width, double &out[]);
   void              Qmf(double freq,double width, complex &out[]);
   bool              IsInitialized(void) { return m_initialized; }
  };

CFilter verfügt über einen parametrischen Konstruktor, dem der Nutzer die zu filternde Rohreihe sowie zwei weitere Parameter übergeben muss, die angeben, wie viel Auffüllungen angewendet werden soll und ob die Reihe vor Anwendung einer DFT-Transformation detrendiert werden soll. Wenn für „min_padding“ Null eingestellt ist, wird der tatsächliche Umfang des Auffüllens nur durch die Anzahl der Stichproben bestimmt. „min_padding“ legt die Mindestanzahl der Werte fest, die der Reihe hinzugefügt werden, abzüglich aller zusätzlichen Werte, die zur Verlängerung der Reihe auf die nächste Zweierpotenz einbezogen werden.

Innerhalb des Konstruktors wird nach Überprüfung aller Argumente die endgültige Länge der aufgefüllten Reihe berechnet und, falls angegeben, Detrending angewendet. Die aufgefüllte Reihe wird in das Array „m_buffer“ geschrieben. Und die DFT wird mit der Wellenform der in „m_dft“, einem Array komplexer Zahlen, angegebenen Reihe angewendet. Wenn im Konstruktor ein Fehler auftritt, wird „m_initialized“ auf false gesetzt.

//+------------------------------------------------------------------+
//|constructor                                                       |
//+------------------------------------------------------------------+
CFilter::CFilter(double &series[],uint min_padding=0,bool detrend=true)
  {
//---local variables
   m_initialized=false;
   int i;
   int npts = ArraySize(series);
   int pad = (int)MathAbs(min_padding);
//--- check size of series
   if(npts<=0)
     {
      Print("Input array is empty");
      return ;
     }
//---
   m_length = npts ;
   for(m_padded_len=2 ; m_padded_len<INT_MAX ; m_padded_len*=2)
     {
      if(m_padded_len >= npts+pad)
         break ;
     }
//---
   if(m_padded_len<npts+pad)
     {
      Print("Warning, calculated length of modified series is too long");
      return;
     }
//---
   m_half_padded_len = m_padded_len / 2;
//---
   ArrayResize(m_buffer,m_padded_len);
//---
   if(m_padded_len > npts)            // Any padding needed?
     {

      if(detrend)
        {
         m_intercept = series[0] ;
         m_slope = (series[npts-1] - series[0]) / (npts-1) ;
        }
      else
        {
         m_intercept = m_slope = 0.0 ;
         for(i=0 ; i<npts ; i++)
            m_intercept += series[i] ;
         m_intercept /= npts ;
        }

      for(i=0 ; i<npts ; i++)
        {
         m_buffer[i]=series[i] - m_intercept - m_slope * i ;
        }
      for(i=npts ; i<m_padded_len ; i++)
        {
         m_buffer[i]=0.0;
        }
     }

   else
     {
      ArrayCopy(m_buffer,series);
      m_intercept = m_slope = 0.0 ;
     }
//---Compute the Fourier transform of the padded series
   CFastFourierTransform::FFTR1D(m_buffer,int(m_padded_len),m_dft);
//---
   m_initialized = true;

  }

Nutzer sollten überprüfen, ob eine Instanz korrekt erstellt wurde, indem sie „IsInitialized()“ aufrufen. Bei Erfolg sollte sie true zurückgeben.

Nach erfolgreicher Instanziierung kann der Nutzer eine der öffentlich zugänglichen Methoden aufrufen, die einen bestimmten Filter auf das in „m_dft“ gespeicherte Signal anwendet. Die meisten von ihnen haben ähnliche Eingangsvoraussetzungen. Zunächst werden die Spezifikationen des Filters durch die Parameter „freq“ und „width“ festgelegt. Sie entsprechen der Mittenfrequenz und der Breite des zu verwendenden Durchlassbereichs. Fast alle Methoden erwarten mindestens ein letztes Eingabefeld, in dem die Ergebnisse der Filterung gespeichert werden.

„Lowpass()“ ist die einzige Methode, die einen vierten Eingangsparameter akzeptiert, der festlegt, ob ein ursprünglich auf das ursprüngliche Signal angewandtes Detrending am Ausgang des Filters umgekehrt werden soll.

//+--------------------------------------------------------------------+
//|Filters series in frequency domain and returns output in time domain|
//+--------------------------------------------------------------------+
void CFilter::Lowpass(double freq,double width,double &out[],bool add_trend)
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=0 ; i<=m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;  // This frequency
      if(f <= freq)                  // Flat to here
         wt = 1.0 ;
      else
        {
         dist = (f - freq) / width ;
         wt = exp(-dist * dist) ;
        }
      dft_temp[i].real*=wt;
      dft_temp[i].imag*=wt;
     }
//---
   double temp[];
//---
   CFastFourierTransform::FFTR1DInv(dft_temp,m_padded_len,temp);
//---
   ArrayResize(out, m_length);
//---
   for(int i = 0; i<m_length; i++)
      out[i]=(add_trend)?temp[i] + m_intercept + m_slope*i:temp[i];

  }

 Bei der Implementierung von In-Phase-Filtern sind zwei Schritte erforderlich: Zunächst wird die Wellenform des in „m_dft“ abgelegten Signals mit der modifizierten Filterfunktion multipliziert. In dieser Implementierung ist das die Gaußsche Funktion. Schließlich wird eine inverse DFT durchgeführt, die die Reihe in den Zeitbereich zurückführt.  

Zur Berechnung der QM-Filterausgänge werden die DFT-Terme einer Wellenform mit der Quadraturversion einer Filterfunktion multipliziert. Die In-Quadratur-Filterfunktion ist einfach eine In-Phase-Filterfunktion mit einer Phasenverschiebung von 90 Grad. Um diese Phasenverschiebung zu erreichen, wird die phasengleiche Filterfunktion mit i multipliziert, wodurch sie rein imaginär wird. Das Ergebnis ist eine Funktion, deren Ausgänge symmetrisch zur Nyquist-Frequenz sind. Die Ausgangsterme auf beiden Seiten der 0,5-Frequenz sind in absoluten Zahlen gleich, aber mit entgegengesetztem Vorzeichen.

Die Methode „Qmf()“ macht sich diese Tatsache zunutze, indem sie die DFT-Terme der Wellenform mit der Summe der In-Phase- und In-Quadratur-Filterfunktionen multipliziert. Dies geschieht, indem die In-Quadratur-Filterfunktion durch Multiplikation mit i zu einer rein reellen Funktion wird (zur Erinnerung: die In-Quadratur-Filterfunktion ist rein imaginär). Wenn die Filterfunktionen addiert werden, heben sich die Ausgänge jenseits der Nyquist-Frequenz gegenseitig auf. Im Code werden die gefilterten DFT-Terme über 0,5 auf 0 gesetzt. Nur gefilterte Ausgänge unterhalb und gleich der Nyquist-Frequenz müssen berechnet werden. Sobald die Wellenform gefiltert wurde, wird eine komplexe inverse DFT durchgeführt, um in den Zeitbereich zurückzukehren.

//+------------------------------------------------------------------+
//| Implements Quadrature Mirror Filter, output is complex           |
//+------------------------------------------------------------------+
void CFilter::Qmf(double freq,double width,complex &out[])
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=1 ; i<m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;    // This frequency
      dist = (f - freq) / width ;
      wt = exp(-dist * dist) ;
      dft_temp[i].real *= wt ;
      dft_temp[i].imag *= wt ;
      dft_temp[m_padded_len-i].real = dft_temp[m_padded_len-i].imag = 0.0 ;  // Causes QMF outputs
     }

//---
   dft_temp[0].real = 0.0 ;
   dist = (0.5 - freq) / width ;
   dft_temp[m_half_padded_len].real = 0.5 * dft_temp[m_half_padded_len].imag * exp(-dist * dist) ;
//---
   dft_temp[0].imag = dft_temp[m_half_padded_len].imag = 0.0 ;     // By definition of real transform
//---
   CFastFourierTransform::FFTC1DInv(dft_temp,m_padded_len);
   ArrayResize(out,m_length);
//---
   for(i=0 ; i<m_length ; i++)
     {
      out[i].real = dft_temp[i].real/double(m_half_padded_len) ;
      out[i].imag = dft_temp[i].imag/double(m_half_padded_len) ;
     }
  }
//+------------------------------------------------------------------+

Das AFD-Programm

Um die Verwendung von CFilter zu demonstrieren, stellen wir AFD.mq5 vor. Eine Anwendung in Form eines Expert Advisors. Sie ermöglicht es den Nutzern, Zufallsfolgen einer bestimmten Länge zu erzeugen. Die Nutzer können die Länge der zu erzeugenden Reihe festlegen und auch den Seed der verwendeten Zufallszahlen anpassen. Die Reihe ist in der oberen Grafik blau dargestellt. Das Ergebnis der Anwendung eines ausgewählten Filters auf die erzeugten Reihen ist in der zweiten Grafik zu sehen. Alle Parameter des Filters können über die grafische Nutzeroberfläche des Programms eingestellt werden. Die Anwendung ist unten dargestellt.

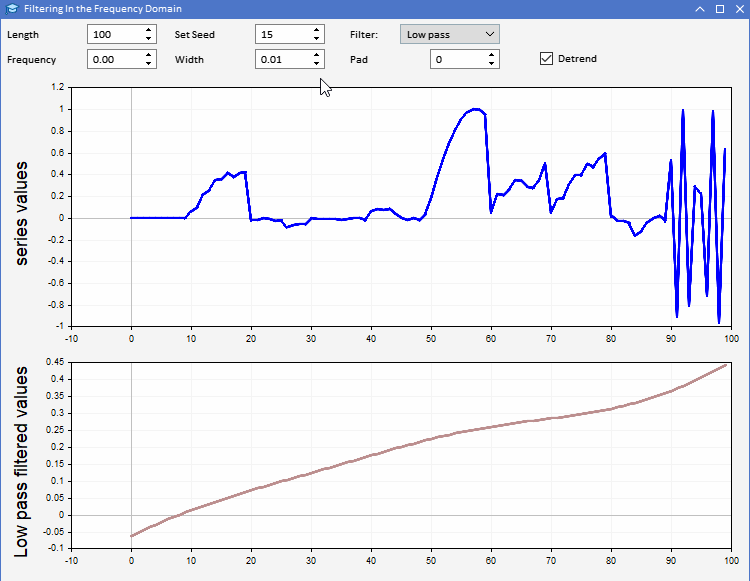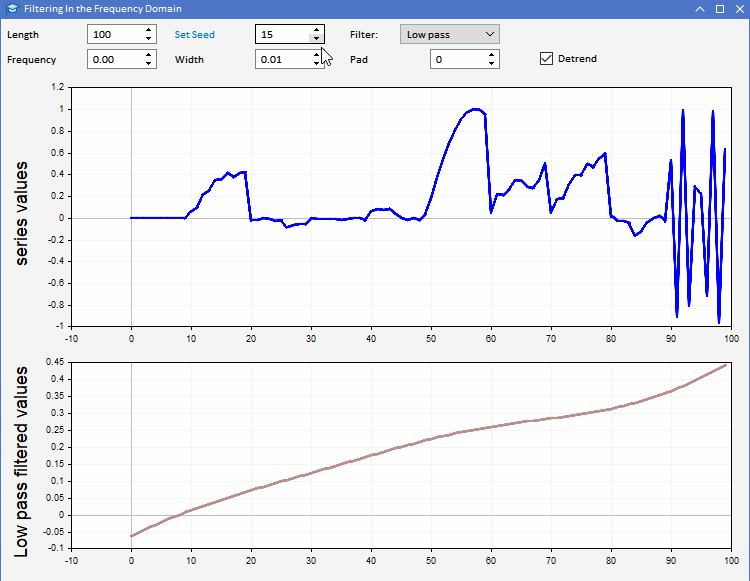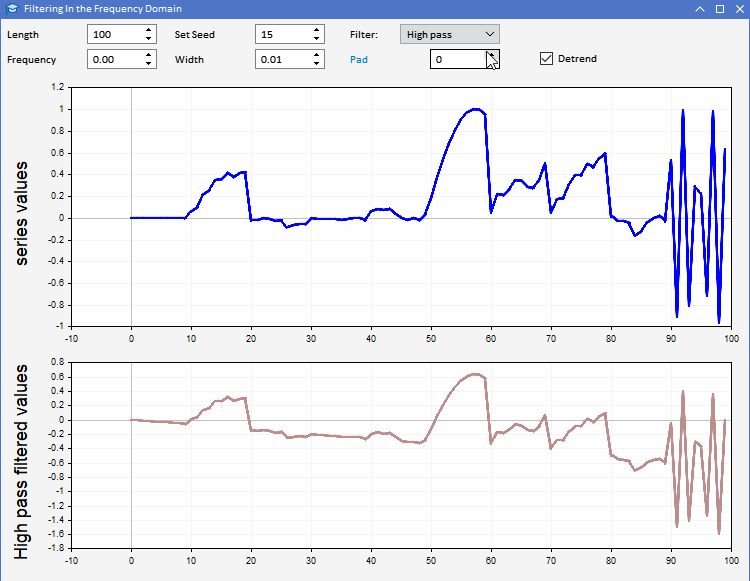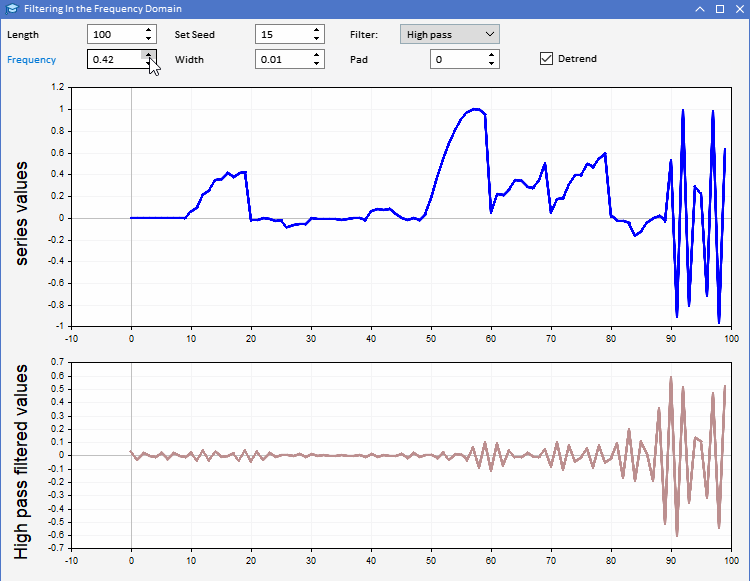
Mit Hilfe der AFD-Anwendung können wir ein intuitiveres Verständnis für die verschiedenen Arten von Informationen entwickeln, die sich aus den Filterausgaben ergeben. Der Ausgang von gleichphasigen Filtern kann auf zwei Arten verwendet werden. Die Ausgabe eines Tiefpassfilters kann verwendet werden, um Informationen über den Durchschnittswert der Eingangsreihe zu einem bestimmten Zeitpunkt zu erhalten. Der Ausgang des Hochpassfilters zeigt die gelegentlichen Höhen und Tiefen, die in der Originalserie zu hören sind. Diese Ausgaben geben einen Eindruck vom Zustand der Eingabeserie zu jedem Zeitpunkt.

Die Bedeutung der Bandpassfilterausgänge ist weniger offensichtlich. Wahrscheinlich ist es unmöglich, die Filterleistung allein durch Beobachtung zu verstehen. Es ist jedoch möglich, dass diese Daten für ein Prognosemodell nützlich sein könnten. Vielleicht bedeutet das Wissen, dass der Bandpassausgang für einen bestimmten Durchlassbereich eine Spitze oder einen Tiefpunkt aufweist, etwas in der ursprünglichen Serie.

Betrachten wir die Bandpassausgabe einer Zufallsreihe bei verschiedenen Frequenzen.

Die Ergebnisse offenbaren eine andere Art von Information. Die Spitzen der Bandpass-Ausgangssignale zeigen den Umfang der periodischen Schwankungen in einem bestimmten Zeitfenster an. Genauer gesagt zeigt sie die Amplitude der Veränderung an, was auf das Vorhandensein einer periodischen Veränderung hinweist. Niedrigere Spitzenwerte signalisieren eine geringere Abweichung, höhere Spitzenwerte das Gegenteil.

Die Amplitude wird durch Abtasten des QM-Filterausgangs ermittelt. Amplituden- und Phasenberechnungen unter Verwendung von QM-Filterwerten sind in dem nachstehenden Codeausschnitt aus AFD.mq5 dargestellt.

 case ENUM_QMF_AMPLITUDE:
        {
         y_name = "Amplitude";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=MathSqrt(comp[i].real*comp[i].real + comp[i].imag*comp[i].imag);
        }
      break;
      case ENUM_QMF_PHASE:
        {
         y_name = "Phase";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=(comp[i].real>=1.e-40 || comp[i].imag>=1.e-40)?atan2(comp[i].imag, comp[i].real):0.0;
        }
      break;

Der Unterschied in der Bandpassleistung bei verschiedenen Frequenzen zeigt, dass eine Vielzahl von Informationen verfügbar ist. Es ist daher möglich, einzigartige Merkmale zu konstruieren, die einem maschinellen Lernalgorithmus zur Verfügung gestellt werden können. Um diese Datensätze auf intelligente Weise zu konstruieren, muss ein Praktiker die Parameter, die einen bestimmten Filter definieren, genau kennen.

Der Parameter Breite

Wie bereits erwähnt, werden die Parameter aller implementierten Filter in Form von Frequenzzyklen pro Zeiteinheit ausgedrückt. Einer der Nachteile bei der Durchführung von Analysen im Frequenzbereich ist die Schwierigkeit, Frequenzkomponenten mit ihrer Ausdehnung im Zeitbereich in Beziehung zu setzen. Am Beispiel der soeben betrachteten Zufallsreihe im letzten Abschnitt wurden die Bandpass-Ausgänge bei den Frequenzen 0,15, 0,3 und 0,45 mit derselben Breite von 0,03 abgetastet. Es ist wichtig zu verstehen, was diese Werte bedeuten, insbesondere in Bezug auf den Zeitbereich der Reihe.

Eine Frequenz von 0,15 hat eine Periode von 1/0,15 = 6,67 Abtastungen pro Zyklus. Die Breite bestimmt die Auflösung im Frequenzbereich. Wenn wir ein schmales Frequenzband isolieren wollen, wenden wir eine geringe Breite an. 0,01 ist in der Regel das Minimum, aber es ist auch möglich, darunter zu gehen. Noch einmal zurück zum Beispiel. Die Breite wurde auf 0,03 eingestellt, sodass sich der Durchlassbereich von 0,15-0,03 bis 0,15+0,03, also 0,12 bis 0,18 erstreckt. Frequenzen in diesem Bereich werden durchgelassen, darüber und darunter liegende Frequenzen werden fast vollständig gestoppt.

Die Breite gibt auch einen Hinweis auf die Auflösung im Zeitbereich. Die Beziehung zwischen Frequenzbereichsauflösung und Zeitbereichsauflösung ist umgekehrt. Eine höhere Auflösung in einem Bereich führt zu einem Verlust an Auflösung in einem anderen Bereich. Um die Ausdehnung des Zeitbereichs im Verhältnis zur Breite abzuschätzen, wenden wir die folgende Formel an: 0.8/width

Damit können wir die Anzahl der Abtastwerte im Zeitbereich abschätzen, die vom Frequenzdurchlassbereich relativ zur aktuellen Position betroffen sind. Mit anderen Worten, sie schätzt die Anzahl der Stichproben vor und nach der aktuellen Position, die sich auf das beobachtete Ergebnis auswirken. Zurück zum Beispiel: Eine Breite von 0,03 bedeutet einen zeitlichen Umfang von 0,8/0,03 = 27 Stichproben. Das bedeutet, dass der Wert an jedem der Ausgänge durch 27 vorangegangene und weitere 27 nachfolgende Beobachtungen bestimmt oder beeinflusst wird.

Im Allgemeinen sollte die Breite eines Filters proportional zur Mittenfrequenz des Durchlassbereichs sein, den wir untersuchen wollen. Dies hängt mit der Periode der Frequenz zusammen. Niedrigere Frequenzen haben längere Perioden, während höhere Frequenzen kürzere Perioden haben. Daher können wir es uns bei niedrigeren Frequenzen leisten, die Auflösung im Zeitbereich zu opfern und uns für eine geringe Breite zu entscheiden. Höhere Frequenzen hingegen profitieren von breiteren Breitenparametern, was sich in einer kürzeren Ausdehnung im Zeitbereich niederschlägt.

Schließlich wirkt sich auch der Breitenparameter auf die Werte aus, die einem Prognosemodell zugeführt werden.  Anhand des vorherigen Beispiels, dessen impliziter Zeitbereich wir auf etwa 27 Beobachtungen berechnet haben. Angenommen, wir wollen den nächsten Wert der Reihe zum Zeitpunkt 201 vorhersagen. Wir würden den Wert des gefilterten Ausgangs angeben, der auf der Grundlage der 200 bekannten Werte berechnet wurde und sich 27 Slots vor dem Ende der Serie befindet. Wir können die gefilterte Ausgabe nicht wissentlich über diesen Punkt hinaus verwenden, weil wir wissen, dass sie unter den Einschränkungen der Filterparameter den durch die DFT induzierten Umhüllungseffekten unterliegen würde.

Im letzten Beispiel wurden die gefilterten Ausgänge mit unterschiedlichen Frequenzen, aber mit derselben Breite abgetastet. In der Praxis wäre es vorteilhafter, gefilterte Ausgänge bei strategisch ausgewählten Frequenzen und Breiten abzutasten, um so viele nützliche Informationen wie möglich zu erfassen.

Schlussfolgerung

Zusammenfassend haben wir uns drei Arten von Filtern angesehen:

• Phasengleiche Filter helfen dabei, eine verrauschte Reihe in verschiedene Komponenten zu zerlegen, wobei wichtige Informationen hervorgehoben und störende überflüssige Merkmale entfernt werden. Durch die Bereitstellung relevanter Informationen für Lernalgorithmen können wir bessere Vorhersagemodelle erstellen.

• In-Quadratur-Filter können verwendet werden, um Bereiche mit schnellen Werteänderungen in einer Serie zu erkennen. Obwohl es einfach sein kann, signifikante Bewegungen in einer Serie zu erkennen, kann es schwierig sein, solche Phänomene einem Lernalgorithmus zu vermitteln. Dies ist der Wert von In-Quadratur-Filtern.

• Die Kombination aus In-Phase- und In-Quadratur-Filtern arbeitet zusammen, um das Vorhandensein eines periodischen Merkmals zu erkennen. Diese Werkzeuge können bei der Identifizierung und Untersuchung von Merkmalen, die sich auf scheinbar zufällige Weise in einer Zeitreihe manifestieren, wirksam sein.

Bei der Filterung im Frequenzbereich wird die vom FFT-Algorithmus gebotene Recheneffizienz genutzt. Verglichen mit der Methode der Faltung im Zeitbereich ist sie unschlagbar. Aber es ist nicht alles rosig. Die Umwandlung von Reihen in den Frequenzbereich birgt viele Fallstricke, die aufgrund von Verzerrungen, die durch unvorsichtige Datenverarbeitung entstehen, zu völlig falschen Schlussfolgerungen führen können. Die Praktiker sollten also wachsam sein.

Der Code für alle Tools und Programme ist beigefügt. Die AFD.mq5 verwendet die bewährte Easy and Fast (EAF) GUI-Bibliothek. Sie ist in der Codebasis von mql5.com verfügbar. Nur eine Randbemerkung: Wenn Sie die EAF-Bibliothek zusammen mit ALGLIB verwenden, stellen Sie immer sicher, dass Sie EAF als letztes in Ihre Anwendung einbinden, da es einige Namenskonflikte zwischen diesen Bibliotheken gibt, die eine erfolgreiche Kompilierung behindern.  

Datei Name	Beschreibung
Mql5\Include\Filter.mqh	Enthält die Definition der Klasse CFilter, die grundlegende digitale Filter im Frequenzbereich implementiert.
Mql5\Include\RandomStationarySeries.mqh	Enthält Routinen (Funktionen) zur Erzeugung von Zufallsreihen mit unterschiedlichen Eigenschaften. Verwendet in der Anwendung AFD.ex5.
Mql5\Experts\AFD.mq5	Dies ist der Quellcode der AFD-Anwendung, sie verwendet die Easy and Fast GUI-Bibliothek, die in der mql5.com-Codebasis aufgeführt ist.
Mql5\Experts\AFD.ex5	Die kompilierte AFD-Anwendung, implementiert als Expert Advisor.