Red neuronal en la práctica: La primera neurona

Introducción

Hola a todos, y bienvenidos a otro artículo sobre redes neuronales. En el artículo anterior Red neuronal en la práctica: Esbozando una neurona, creamos un esquema básico e inicial para la construcción de una simple neurona. Sin embargo, esa simple neurona que construimos no es exactamente lo que necesitamos. Esto se debe a que tiene una pequeña falla, por así decirlo. Pero quiero que tú, mi querido y estimado lector, comprendas el paso a paso de cómo se construye una red neuronal. Esa falla no afecta mucho el funcionamiento de esa sencilla neurona.

Quizás estés pensando: "¿Pero qué falla es esa de la que hablas? No noté nada mal. La neurona funcionó perfectamente en las pruebas que realicé". Bueno, retrocedamos un poco en esta misma serie sobre redes neuronales, para que puedas entender de qué estoy hablando.

En los primeros artículos sobre redes neuronales, mostré cómo podríamos forzar a la máquina a crear una ecuación de línea recta. Inicialmente, la ecuación estaba limitada al origen en los ejes cartesianos, es decir, la línea pasaba obligatoriamente por el punto (0, 0). Esto se debía a que el valor de la constante < b > en la ecuación vista a continuación era cero.

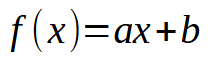
A pesar de que utilizamos el método de mínimos cuadrados para intentar encontrar una ecuación adecuada, de modo que el conjunto de datos o conocimiento previo contenido en la base de datos pudiera ser representado adecuadamente en forma de una ecuación matemática, ese modelado no lograba forzar la búsqueda de una ecuación realmente adecuada. Esto se debe a que, dependiendo de los datos presentes en la base de conocimiento, necesitaríamos que el valor de la constante < b > fuera diferente de cero.

Si estudias con calma esos artículos anteriores, notarás que fue necesario realizar ciertos malabarismos matemáticos para definir el mejor valor posible tanto para la constante < a >, que es el coeficiente angular, como para la constante < b >, que es el punto de intersección. Estas maniobras permitían encontrar la ecuación de línea recta más adecuada, mostrándose dos formas de hacerlo: una mediante cálculos de derivadas y otra mediante cálculos matriciales.

Sin embargo, para lo que necesitamos hacer a partir de este momento, tales cálculos no nos serán útiles, ya que necesitamos modelar otra forma de encontrar las constantes de la ecuación de línea recta. En el artículo anterior, mostré cómo podríamos encontrar la constante que representa el coeficiente angular. Espero que te hayas divertido y hayas experimentado bastante con ese código, porque ahora haremos algo un poco más complicado. Sin embargo, aunque es solo un poco más complicado, de hecho abrirá las puertas a muchas otras cosas. Literalmente, este quizás sea el artículo más interesante que verás en esta serie sobre redes neuronales, ya que después de él, todo será mucho más sencillo y práctico.

Por qué les gusta tanto complicar las cosas

Muy bien, mi querido lector, antes de que veamos la parte del código en sí, me gustaría intentar ayudarte a entender algunas cosas. Normalmente, cuando buscas estudiar sobre redes neuronales, te encontrarás con un montón de términos. Literalmente es una avalancha de conceptos. No sé por qué a las personas que explican sobre redes neuronales les gusta tanto complicar algo que es simple. A mi modo de ver, no hay motivo para ello. Pero no estoy aquí para juzgar ni minimizar. Estoy aquí para explicarte cómo funcionan las cosas detrás de escena.

Para simplificar al máximo, me centraré en algunos términos que suelen aparecer frecuentemente cuando se habla de redes neuronales. Vamos con el primero: Pesos. Este término, pesos, no es más que el coeficiente angular de una ecuación de línea recta. No importa cómo quieran llamarlo, el término peso simplemente se refiere al coeficiente angular. Otro término muy divulgado es: Sesgo. Bueno, este término, que también puedes escuchar como: Bias, no es nada del otro mundo, ni está restringido únicamente a redes neuronales o inteligencia artificial. Nada de eso. Este término no es más que el punto de intersección. Recuerda que estamos lidiando con una recta secante. Por favor, no confundas las cosas.

A partir de estos términos, que aparentemente parecen cosas de otro mundo, surgen un montón de otros conceptos y expresiones. Pero todos ellos, absolutamente todos, no son novedades. De hecho, son solo nombres diferentes para cosas que ya existían. No entraré en el porqué de poner nombres distintos a conceptos conocidos. Sin embargo, si al intentar estudiar redes neuronales o algo relacionado con ellas ves aparecer términos extraños, busca entender cuál es la fórmula matemática detrás de todo eso, y verás que básicamente es mucho más simple de lo que aparenta ser.

Te digo esto porque hay mucha gente que adora complicar las cosas.

Toman algo sencillo y comienzan a inventar una serie de elementos adicionales, simplemente para complicar algo que cualquiera puede entender. Cuando se trata de programación o ciencias exactas, cuanto más simple, mejor. Cuando las cosas empiezan a llenarse de adornos o elementos que desvían nuestra atención, es el momento de detenerse, quitar toda esa parafernalia y maquillaje, para así poder ver la verdadera realidad. Muchos dirán que es complicado, que es necesario ser un experto en el área para entender o implementar una red neuronal, que solo se puede hacer usando tal o cual lenguaje, o con tal o cual recurso. Pero hasta el momento, tú, mi querido y estimado lector, habrás notado que una red neuronal no es complicada. Es simple y no hay razón para el pánico ni la histeria que muchos buscan provocar en las redes sociales.

Muy bien, ahora basta de rodeos y pasemos a un nuevo tema. Veamos cómo podemos añadir el valor de la constante < b >, que es el punto de intersección, o como algunos prefieren llamarlo: Sesgo o Bias. Esto para que podamos forzar la ecuación de la recta a representar de manera más precisa la base de datos que estamos utilizando para entrenar nuestra neurona.

El nacimiento de la primera neurona

Para que nuestra primera neurona cobre vida, y una vez que lo haga, ya no necesitaremos modificarla, como verás más adelante. Primero debemos entender lo que tenemos entre manos. Nuestra neurona actual se comporta como la animación de abajo.

Esta es la misma animación vista en el artículo "Red neuronal en la práctica: Línea Secante". Es decir, acabamos de dar el primer paso para construir una neurona que pueda realizar algo que antes hacíamos manualmente con las teclas de dirección. Sin embargo, habrás notado que esto no es suficiente. De hecho, necesitamos incluir la constante de intersección para que la ecuación obtenida sea aún mejor. Quizás estés pensando que hacer esto será algo extremadamente complicado, pero no lo es. De hecho, hacerlo es tan simple que resulta casi aburrido. Observa cómo añadimos la constante de intersección a la neurona. Esto puede apreciarse en el siguiente fragmento de código.

01. //+------------------------------------------------------------------+
02. double Cost(const double w, const double b)
03. {
04.     double err, fx, x;
05. 
06.     err = 0;
07.     for (uint c = 0; c < nTrain; c++)
08.     {
09.         x = Train[c][0];
10.         fx =  a * w + b;
11.         err += MathPow(fx - Train[c][1], 2);
12.     }
13. 
14.     return err / nTrain;
15. }
16. //+------------------------------------------------------------------+

Me estoy asegurando de dividir el código en fragmentos para que tú, mi querido lector, comprendas en detalle lo que se está haciendo. Y luego dime: ¿Es complicado o no? ¿Realmente necesita toda esa complicación que muchos gustan de añadir cuando hablan de redes neuronales?

Presta mucha atención, porque el nivel de complejidad es casi ridículo. (RISAS). En la línea nueve tomamos nuestro valor de entrenamiento y lo colocamos en la variable X. Luego, en la línea diez, hacemos la factorización. Vaya, qué cuenta más complicada. Pero espera un momento. ¿No es esta justamente la ecuación mostrada al principio? La famosa ecuación de la línea recta. ¡Estás de broma! Esto no va a funcionar como una neurona utilizada en programas de inteligencia artificial.

Calma, mi querido lector. Verás que esto sí funcionará, igual que cualquier otro programa de inteligencia artificial o red neuronal. No importa cuán complicado quieran explicarte el tema. Verás que esto es exactamente lo mismo que se implementa en cualquier tipo de red neuronal. Lo que cambia es el próximo paso, que veremos en breve. Pero el cambio no es tan grande como quizás estés imaginando. Tranquilo, lo veremos paso a paso.

Una vez que el cálculo de error, o coste, se haya actualizado, podemos actualizar el fragmento que ajustará estos dos parámetros en la función de coste. Esto se hará de manera gradual para que puedas entender algunos detalles involucrados. Así que, lo primero que haremos es modificar el código original, presentado en el artículo anterior, por el nuevo código que se muestra a continuación.

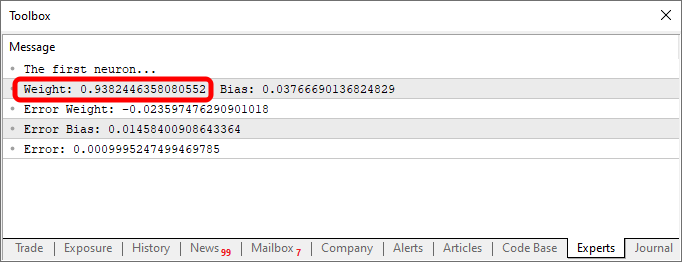
01. //+------------------------------------------------------------------+
02. void OnStart()
03. {
04.     double weight, ew, eb, e1, bias;
05.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
06. 
07.     Print("The first neuron...");
08.     MathSrand(512);
09.     weight = (double)macroRandom;
10.     bias = (double)macroRandom;
11. 
12.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
13.     {
14.         ew = (Cost(weight + eps, bias) - e1) / eps;
15.         eb = (Cost(weight, bias + eps) - e1) / eps;
16.         weight -= (ew * eps);
17.         bias -= (eb * eps);
18.         if (f != INVALID_HANDLE)
19.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
20.     }
21.     if (f != INVALID_HANDLE)
22.         FileClose(f);
23.     Print("Weight: ", weight, "  Bias: ", bias);
24.     Print("Error Weight: ", ew);
25.     Print("Error Bias: ", eb);
26.     Print("Error: ", e1);
27. }
28. //+------------------------------------------------------------------+

Al ejecutar el script después de estas modificaciones, verás algo parecido a la imagen de abajo.

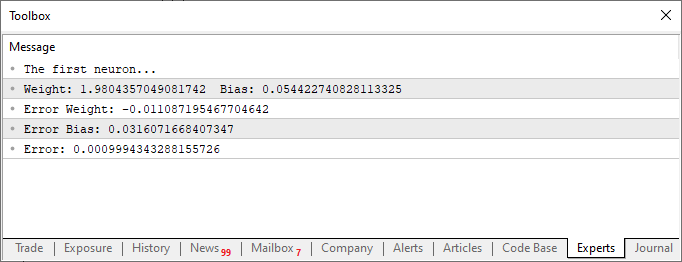
Ahora observemos únicamente este segundo fragmento de código. En la línea cuatro, añadimos y modificamos algunas variables. Algo bastante simple. Ya en la línea diez, le indicamos a la aplicación que defina un valor aleatorio para el sesgo, o nuestra constante de intersección. Ahora, observa que también necesitaremos pasar este valor a la función Cost. Esto se hace en las líneas 12, 14 y 15. Sin embargo, la parte interesante es que estaremos generando dos tipos de errores acumulados: uno para el valor del peso y otro para el valor del sesgo. Debes entender que, aunque ambos forman parte de la misma ecuación, deberán ajustarse de manera diferente. Por lo tanto, necesitamos saber qué error representa cada uno dentro del sistema general.

Sabiendo esto, en las líneas 16 y 17 podemos ajustar adecuadamente los valores para la siguiente iteración del bucle for. Ahora, de la misma manera que se hizo en el artículo anterior, también lanzamos los valores a un archivo CSV. Esto nos permitirá generar un gráfico para estudiar cómo se están ajustando estos valores.

Bien, en este punto, nuestra primera neurona está completamente construida. Pero hay algunos detalles que podrás entender si observas el código completo de esta neurona. El código completo se muestra justo a continuación.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w, const double b)
18. {
19.     double err, fx, a;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.     {
24.         a = Train[c][0];
25.         fx =  a * w + b;
26.         err += MathPow(fx - Train[c][1], 2);
27.     }
28. 
29.     return err / nTrain;
30. }
31. //+------------------------------------------------------------------+
32. void OnStart()
33. {
34.     double weight, ew, eb, e1, bias;
35.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
36. 
37.     Print("The first neuron...");
38.     MathSrand(512);
39.     weight = (double)macroRandom;
40.     bias = (double)macroRandom;
41. 
42.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight, bias)) > eps); c++)
43.     {
44.         ew = (Cost(weight + eps, bias) - e1) / eps;
45.         eb = (Cost(weight, bias + eps) - e1) / eps;
46.         weight -= (ew * eps);
47.         bias -= (eb * eps);
48.         if (f != INVALID_HANDLE)
49.             FileWriteString(f, StringFormat("%I64u;%f;%f;%f;%f;%f\n", c, weight, ew, bias, eb, e1));
50.     }
51.     if (f != INVALID_HANDLE)
52.         FileClose(f);
53.     Print("Weight: ", weight, "  Bias: ", bias);
54.     Print("Error Weight: ", ew);
55.     Print("Error Bias: ", eb);
56.     Print("Error: ", e1);
57. }
58. //+------------------------------------------------------------------+

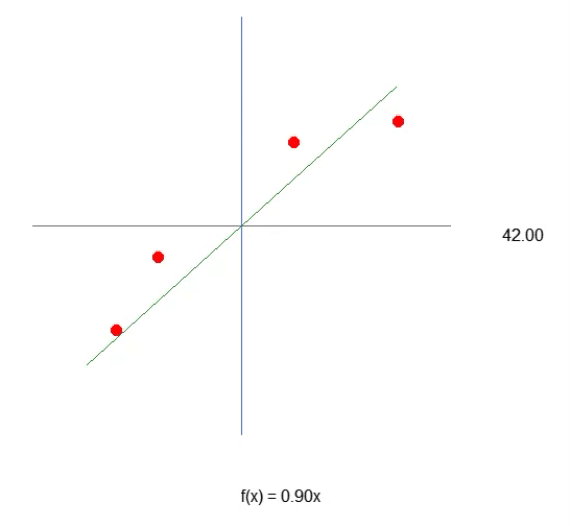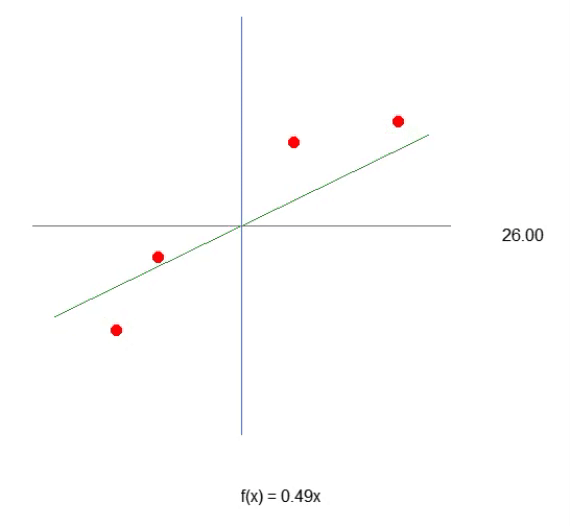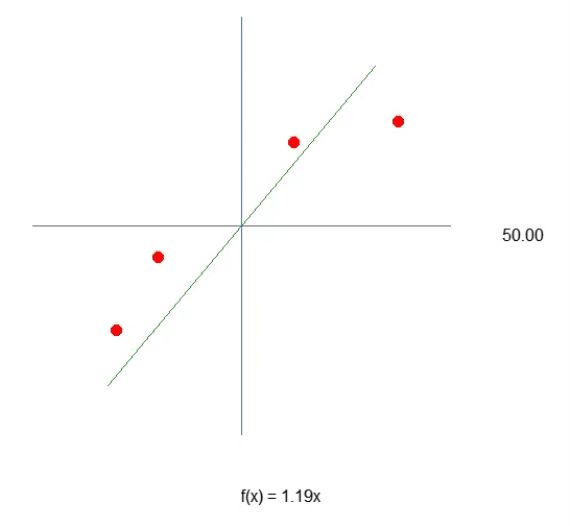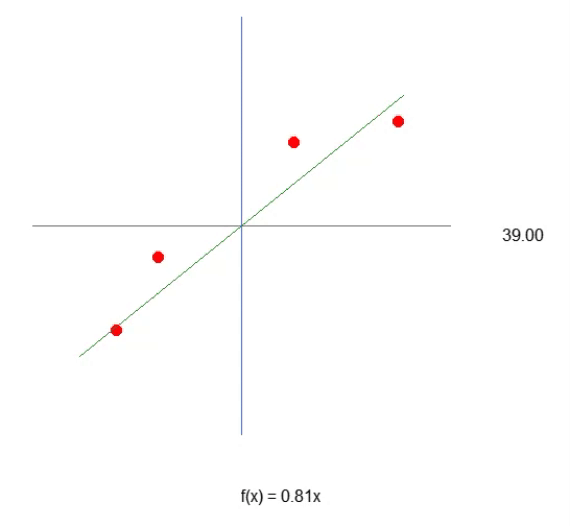
Observa algo interesante tanto en el código como en el resultado visto en la imagen anterior. En la línea seis están los valores utilizados para entrenar la neurona. Claramente, notarás que el valor utilizado en la multiplicación es dos. Sin embargo, la neurona nos indica que el valor es: 1.9804357049081742. Y también podemos notar que el punto de intersección debería ser cero, pero la neurona nos dice que es: 0.054422740828113325. Ok, considerando el hecho de que en la línea 15 aceptamos que el error puede ser de: 0.001, no está tan mal. Esto se debe a que el error final reportado por la neurona fue de: 0.0009994343288155726, es decir, por debajo del margen de error que consideramos aceptable.

Estas diferencias que puedes notar claramente son el índice de probabilidad de que la información sea correcta. Normalmente, esto se representa en términos de porcentaje. Sin embargo, nunca verás un 100%. El número puede ser muy cercano al 100%, pero nunca será exacto debido a esta ligera desviación con respecto al resultado correcto.

A pesar de esto, este índice de probabilidad no es un índice de certeza sobre una información. Aún no estamos trabajando en la generación de este segundo índice. Por ahora, solo estamos entrenando y verificando si la neurona es capaz de establecer una correlación entre los datos de entrenamiento. Pero es posible que ya estés pensando lo siguiente: "Este tema de la neurona es inútil, ya que de la forma en que lo estás creando, no sirve para nada más. Solo sirve para buscar un número que ya sabemos cuál es. Lo que realmente quiero es un sistema que pueda decirme cosas, escribir un texto, o incluso un código. Quién sabe, tal vez hasta un programa que pueda operar en el mercado financiero y darme dinero siempre que lo necesite.

Ciertamente, tienes grandes intereses en mente. Pero si tú, mi querido lector, piensas y estás buscando aprender sobre redes neuronales o inteligencia artificial con la intención de ganar dinero, siento decirte que no lo lograrás. Las únicas personas que realmente van a ganar dinero con esto son aquellas que vendan los sistemas de redes neuronales o inteligencia artificial. Esto ocurre cuando logran convencer a los demás de que la inteligencia artificial o las redes neuronales pueden superar a un buen profesional. Aparte de estas personas, que van a sacar todo el dinero de los demás vendiendo tales productos, nadie más ganará dinero con esto. Si así fuera, ¿por qué escribiría estos artículos explicando cómo funciona? O incluso, ¿por qué algunas personas igualmente conocedoras del funcionamiento de estos mecanismos explicarían cómo trabajan? No tiene sentido. Podrían simplemente guardar silencio, ganar dinero con una red neuronal bien entrenada y listo. Pero no es así como funcionan las cosas en la práctica. Por esta razón, olvídate de la idea de que vas a crear una red neuronal y, sin ningún conocimiento, lograrás ganar dinero solo recogiendo fragmentos de código de aquí y de allá.

Sin embargo, nada te impide, mi estimado lector, crear una pequeña red neuronal cuyo objetivo sea ayudarte en la toma de decisiones, ya sea para comprar, vender o incluso para ayudarte a visualizar ciertos aspectos en el mercado de capitales. ¿Es posible hacerlo? Sí. De hecho, estudiando todo lo que sea necesario, tú, aunque lentamente y con mucho esfuerzo y dedicación, podrás entrenar una red neuronal para ese fin. Pero, como acabo de decir, tendrás que esforzarte para conseguirlo. Sin embargo, es perfectamente posible.

Muy bien, ya tenemos nuestra primera neurona. Pero antes de que te emociones y empieces a pensar en formas de usarla, veamos un poco mejor cómo está esquematizada. Para facilitar la visualización, observa la imagen a continuación.

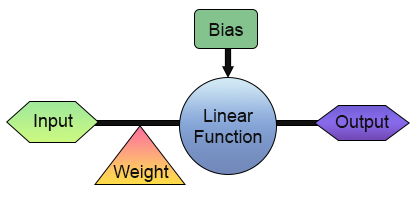
En esta imagen, podemos ver lo que está implementado en nuestra neurona. Fíjate que tiene una entrada y una salida. Esta única entrada recibe un peso. Tal vez esto no sea tan útil después de todo, ya que ¿cuál es el sentido de tener una entrada y una salida? Está bien, comprendo tu escepticismo ante lo que acabamos de crear. Pero tal vez no sepas, ya que esto depende de cuánto conoces sobre diversos temas, que en la electrónica digital existe un circuito que tiene una entrada y una salida. En realidad, hay dos. Uno es el inversor y el otro es un buffer. Ambos son partes integrales de componentes aún más complejos. Y esta neurona puede aprender cómo funcionan ambos circuitos. Solo necesitas entrenarla para eso. Para entrenarla, lo único que sería necesario es cambiar la matriz de entrenamiento por una de las que se muestran a continuación.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 1},
                    {1, 0},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

Al usar este fragmento de código, obtendrás algo parecido a lo que se muestra en la imagen de abajo:

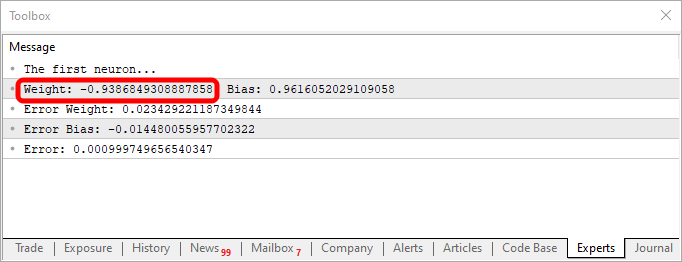
Observa que el valor de weight es negativo. Esto implica que estaremos invirtiendo el valor que entra. Es decir, tenemos un inversor. Usando el fragmento que se ve a continuación, tendríamos otra salida.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+

La salida, en este caso, se muestra en la imagen a continuación.

Observa que ahora el valor de weight es positivo. Esto implica que estamos almacenando la entrada directamente en la salida. Es decir, tenemos un buffer. Nota lo divertido que es jugar con esto.

El simple hecho de cambiar la información en la base de conocimiento, o base de datos, que en nuestro caso es un array de dos dimensiones, ya permite que el mismo código cree una ecuación para representar las cosas. Y por esta razón, todos, absolutamente todos los que se interesan por la programación, disfrutan trabajando con redes neuronales. Son muy entretenidas para trabajar.

Sin embargo, esta primera neurona es bastante limitada, no por su diseño, sino porque solo nos permite una entrada. En la práctica, las neuronas de redes neuronales pueden tener tantas entradas como sea necesario. Del mismo modo, también pueden tener tantas salidas como sean necesarias para realizar sus tareas. Estoy presentando las cosas poco a poco para no abrumarte. Quiero que comprendas cómo y por qué este mecanismo funciona. Claro, por mucho que yo, o cualquier otra persona, intentemos, jamás lograremos mostrar todo lo que se puede hacer con este mecanismo. Esto se debe a que las posibilidades dependen únicamente de tu creatividad. Pero en este momento lo haremos un poco más interesante y, al mismo tiempo, más entretenido.

Función sigmoidea

A partir de ahora, cualquier cosa que te muestre será solo la punta del iceberg. No importa lo genial, divertido, complicado o emocionante que pueda parecer programar esto. Todo, absolutamente todo, de aquí en adelante, será solo un pequeño vistazo de lo que podemos hacer. Entonces, mi querido lector, desde este momento debes comenzar a estudiar de manera un poco más independiente. Solo quiero guiarte por un camino que te inspire para nuevos descubrimientos. Siéntete completamente libre de experimentar y divertirte con lo que se te mostrará. Porque, como se mencionó antes, el único factor limitante será tu imaginación.

Para que nuestra única neurona pueda aprender con más entradas disponibles, solo necesitarás entender un pequeño y simple detalle. Esto se puede ver en la imagen a continuación.

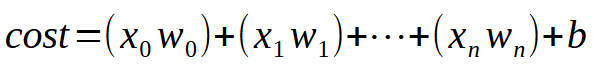
O de manera más resumida, la misma ecuación se muestra justo a continuación.

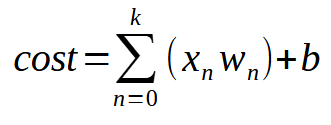
El valor < k > es el número de entradas que nuestra neurona podrá tener. Así que, no importa cuántas entradas sean necesarias, lo único que necesitamos hacer es añadir la cantidad de entradas necesaria para que la neurona aprenda a manejar cada nueva situación. Sin embargo, a partir de la segunda entrada, la función deja de ser una ecuación de línea recta y pasa a ser una ecuación con cualquier forma posible. Esto para que la neurona pueda encontrar la mejor forma de manejar diferentes tipos de entrenamiento.

Ahora la cosa se pone realmente seria, ya que podemos hacer que una única neurona aprenda diversas cosas diferentes. Sin embargo, existe un pequeño problema al dejar de manejar una ecuación de línea recta. Para entender esto, vamos a modificar el programa de forma que quede como se muestra a continuación:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow(((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < 3000) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

Cuando ejecutes este código, obtendrás un resultado similar al de la imagen a continuación:

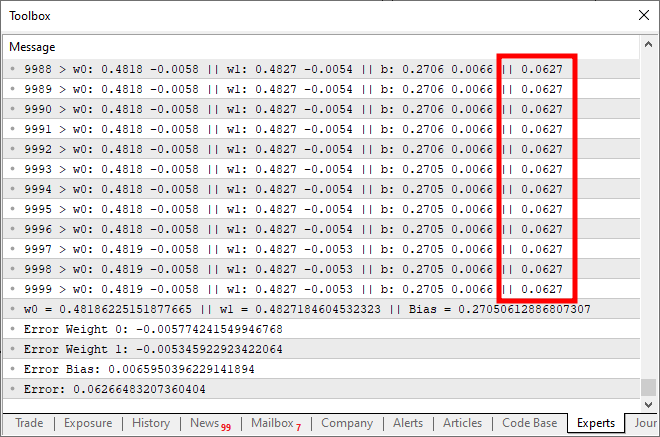
Bueno, ¿qué está mal aquí? Observa que en el código simplemente añadimos la posibilidad de nuevas entradas, lo cual está bien hecho. Pero presta atención a algo: cerca de las diez mil iteraciones, el costo simplemente dejó de disminuir, o si está disminuyendo, lo hace muy lentamente. ¿Por qué sucede esto? El motivo es que falta algo en la neurona. Algo que no era necesario con una única entrada, pero que se vuelve crucial cuando queremos añadir nuevas entradas. Además, es algo utilizado cuando trabajamos con capas de neuronas, lo cual es común en el aprendizaje profundo. Pero eso lo veremos más adelante. Por ahora, concentrémonos en el punto principal. Observa que la neurona está llegando a un punto de estancamiento, donde no puede reducir más el costo. Este problema se resuelve añadiendo una función de activación justo en la salida. La función y cómo suceden las cosas aquí dependen mucho del tipo de tarea que queramos realizar. No existe una única manera de resolver esta parte, ya que se pueden usar diversas funciones de activación. Sin embargo, normalmente se utiliza una sigmoidea, y el motivo es simple. Esta función nos permite llevar valores que van desde más infinito hasta menos infinito a un rango que va de 0 a 1. En algunos casos, la modificamos para que este rango esté entre 1 y -1, pero aquí utilizaremos la versión básica. La función sigmoidea se presenta con la siguiente fórmula:

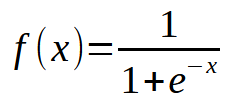
Bien, pero ¿cómo aplicamos esto en nuestro código? Podría parecer algo muy complicado. En realidad, querido lector, es más sencillo de lo que parece. En el mismo código mostrado anteriormente, será necesario cambiar muy poco, como puedes ver a continuación:

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (ulong c = 0; (c < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); c++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
        PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", c, w0, ew0, w1, ew1, bias, eb, err);
    }
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);
}
//+------------------------------------------------------------------+

Y al ejecutar el código mostrado arriba, el resultado será algo similar al que ves en la imagen a continuación.

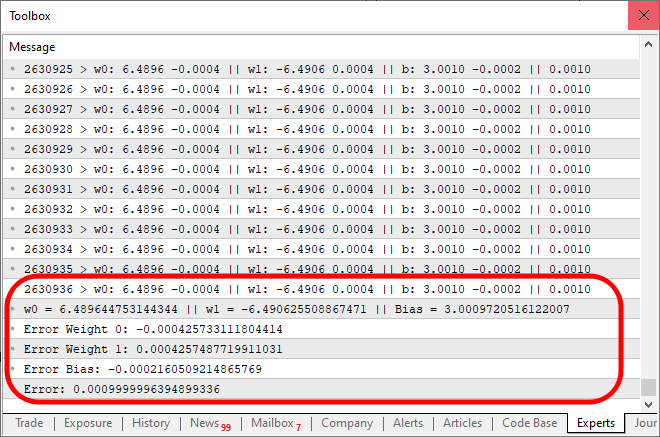
Nota que fueron necesarias 2.630.936 iteraciones para alcanzar el resultado esperado dentro del margen de error. Lo cual no está nada mal. Puede que tengas la impresión de que el programa empieza a volverse un poco lento, ya que estamos usando solo la CPU. Pero esta impresión se debe precisamente al hecho de que estamos imprimiendo un mensaje en cada iteración del código. Podemos hacer que el código sea un poco más rápido si cambiamos esta forma de mostrar las cosas por un método nuevo. Al mismo tiempo, también añadiremos un pequeño código para probar la capacidad de la neurona. Así que el código final es el que puedes observar justo a continuación.

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
#define macroSigmoid(a) (1.0 / (1 + MathExp(-a)))
//+------------------------------------------------------------------+
double Train[][3] {
                    {0, 0, 0},
                    {0, 1, 1},
                    {1, 0, 1},
                    {1, 1, 1},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 3;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double  w0, w1, err, ew0, ew1, eb, bias;
    ulong count;

    Print("The Mini Neuron...");
    MathSrand(512);
    w0 = (double)macroRandom;
    w1 = (double)macroRandom;
    bias = (double)macroRandom;

    for (count = 0; (count < ULONG_MAX) && ((err = Cost(w0, w1, bias)) > eps); count++)
    {
        ew0 = (Cost(w0 + eps, w1, bias) - err) / eps;
        ew1 = (Cost(w0, w1 + eps, bias) - err) / eps;
        eb  = (Cost(w0, w1, bias + eps) - err) / eps;
        w0 -= (ew0 * eps);
        w1 -= (ew1 * eps);
        bias -= (eb * eps);
    }
    PrintFormat("%I64u > w0: %.4f %.4f || w1: %.4f %.4f || b: %.4f %.4f || %.4f", count, w0, ew0, w1, ew1, bias, eb, err);
    Print("w0 = ", w0, " || w1 = ", w1, " || Bias = ", bias);
    Print("Error Weight 0: ", ew0);
    Print("Error Weight 1: ", ew1);
    Print("Error Bias: ", eb);
    Print("Error: ", err);

    Print("Testing the neuron...");
    for (uchar p0 = 0; p0 < 2; p0++)
        for (uchar p1 = 0; p1 < 2; p1++)
            PrintFormat("%d OR %d IS %f", p0, p1, macroSigmoid((p0 * w0) + (p1 * w1) + bias));
}
//+------------------------------------------------------------------+

Al ejecutar este código, podrías ver un mensaje como el que se muestra en la imagen a continuación, apareciendo en el terminal.

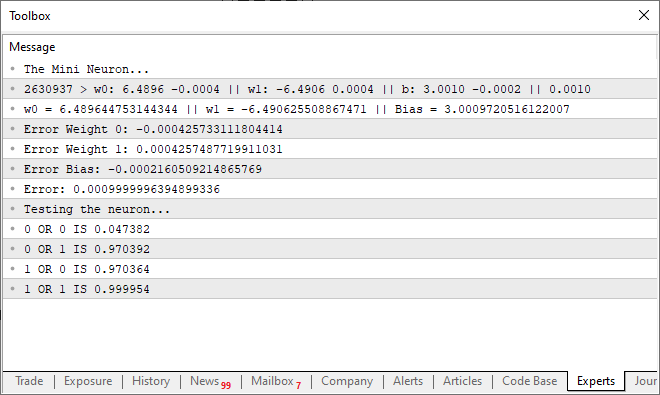
Es decir, logramos que nuestra sencilla neurona entendiera cómo una PUERTA OR funciona. Ahora estamos entrando en un camino sin retorno, ya que nuestra única neurona ya comienza a aprender cosas un poco más complejas que simplemente saber si algo está o no relacionado entre sí.

Consideraciones finales

En este artículo, comenzamos a crear algo que a muchos les sorprende ver funcionando. Pues esta simple y modesta neurona, que logramos programar con muy poco código en MQL5, ha demostrado su capacidad. Muchos dicen que se necesitan mil y un recursos para hacer lo que hemos hecho aquí. Pero espero que tú, querido lector, hayas entendido cómo va evolucionando el proceso. En pocos artículos, he resumido un largo tiempo de trabajo realizado por varios investigadores. Aunque sea algo relativamente sencillo, diseñar cómo se deben implementar las cosas llevó su tiempo. Tanto es así que aún hoy en día hay investigaciones que buscan hacer que todos estos cálculos se ejecuten de manera más fluida, o mejor dicho, más rápida. Aquí estamos usando solo una neurona con dos entradas, cinco parámetros y una salida. Y aun así, nota que el sistema toma algo de tiempo para encontrar la ecuación correcta.

Claro, podríamos usar OpenCL para comenzar a acelerar las cosas utilizando la GPU. Pero, en mi opinión, aún es temprano para pensar en esa solución. Podemos avanzar un poco más antes de que sea necesario realmente usar la GPU para los cálculos. Sin embargo, si deseas profundizar en el tema de redes neuronales, te sugiero encarecidamente que pienses en adquirir una GPU, ya que acelerará significativamente ciertos tipos de actividades en la red neuronal.

En el anexo, puedes acceder al último código presentado en este artículo. Úsalo a tu gusto, experimenta y diviértete. Observa cómo esta neurona es capaz de manejar diversas situaciones y trata de encontrar sus limitaciones, porque las tiene. Por esta razón, todavía tendremos que explorar más temas.