MQL5 Wizard Techniques you should know (Part 66): Using Patterns of FrAMA and the Force Index with the Dot Product Kernel
1 599
0
Introduction
From our last article, where we introduced the pair of these indicators as a source of entry signal patterns for an Expert Advisor, the forward walk results were not as promising. We provided a few reasons why this was and also caveated that the training and optimization we perform is for only 1 year and therefore for any pattern, it is imperative to test as extensively as possible on vasts amount of history. We follow up that piece as always by examining those patterns that were able to forward walk. This is with machine learning.
When applying machine learning algorithms in MQL5, OpenCL is always an option, however this often requires one to have GPU hardware. This is nice to have, but Python’s code library has become quite extensive, a lot of efficiencies can be reaped with just a CPU. That is what we are exploring in these article series and so for this piece, as we have done on some in the past, we code our neural networks in Python because the coding, and training in Python is very efficient.
Of our ten patterns that we optimized or trained in the last article, only 2 were able to walk. Pattern-6 and Pattern-9. We therefore test these further with a neural network, as we did in past particles, the difference being that we are using a convolution neural network aka CNN. This CNN will implement the dot product kernel. First, however, as always with Python implementations, we define the indicator functions first that we need to provide signals to our network.
Fractal Adaptive Moving Average (FrAMA) Function
The FrAMA is a moving average that is dynamic, which adapts its smoothing depending on the fractal dimensions of price movements. This tends to make it more responsive to major price changes and less reactive to noise. We implement this function in Python as follows;
def FrAMA(df, period=14, price_col='close'): """ Calculate Fractal Adaptive Moving Average (FrAMA) for a DataFrame with price data. Args: df: Pandas DataFrame with a price column (default 'close'). period: Lookback period for fractal dimension (default 20). price_col: Name of the price column (default 'close'). Returns: Pandas DataFrame with a single column 'main' containing FrAMA values. """ prices = df[price_col] frama = pd.Series(index=prices.index, dtype=float) for t in range(period, len(prices)): # 1. High-Low range (volatility proxy) high = prices.iloc[t-period:t].max() low = prices.iloc[t-period:t].min() range_hl = high - low # 2. Fractal Dimension (simplified) fd = 1.0 + (np.log(range_hl + 1e-9) / np.log(period)) # Avoid log(0) # 3. Adaptive EMA smoothing factor alpha = 2.0 / (period * fd + 1) # 4. Update FrAMA (recursive EMA) frama.iloc[t] = alpha * prices.iloc[t] + (1 - alpha) * frama.iloc[t-1] return pd.DataFrame({'main': frama})
Our function above give us input flexibility since it accepts a pandas data frame with customizable price column and period parameters. It uses a volatility proxy for high-low range to estimate market volatility and computes a simplified fractal dimension to gauge price complexity. Our function updates the FrAMA via a recursive EMA.
If we go through our code, the first thing we do is extract the specified price column from the input data frame. This extraction ensures the function works with any price column as specified by the user. We avoid hard-coding and maintain compatibility. When using this, it may be a good idea to improve our function by: verifying that the input price column exists in the data frame; and ensuring that the price data is clean without NaNs or missing values, given that FrAMA is sensitive to price inputs.
Next, we initialize an empty pandas series with the same index given that this pre-allocates memory for FrAMA values ensuring alignment with the input data frame’s index, for efficient iterative updates. When using this, FrAMA requires a look back window to compute which means first values are NaN and need to be managed or made zeros. It is also important to ensure the index of prices is consistent, such as with price-time pairing, in order to avoid misalignment.
With this, we get into the for loop, where we calculate the high-low range over the look back period to estimate volatility. For each time step t, we take the maximum and minimum prices in the t-period window and computes their difference. The high-low range serves as a proxy for market volatility, which is important for determining the fractal dimension. A larger range means higher volatility, which influences the adaptive nature of FrAMA. In implementation, an error handling mechanism looking out for NaNs can go some way in addressing missing data.
We then compute the simplified fractal dimension using the logarithmic ratio of the high-low range. The 1e-9 epsilon equivalent term, prevents division by zero or log of zero in the even that range-hl is zero. The fractal dimension, fd, measures price complexity or trendiness. A higher fd, that is closer to 2, means we are in a choppy, noisy market. On the other hand, a lower fd, that is closer to 1, suggests trending markets. This parameter thus drives the adaptability of FrAMA. The 1e9 is a numerical stability trick that ensures it is small enough not to distort results. Also, the fractal dimension used here is a simplified version; more complicated formats can use box-counting methods. After this, we compute the smoothing factor, alpha.
This is a smoothing factor for the exponential moving average based on the fractal dimension and period. It is important because the adaptive alpha determines how responsive FrAMA is to new prices. A higher fd which is got in a noisier market, reduces alpha, slowing the EMA to filter noise. A lower fd which is got in trending markets, increases alpha making FrAMA more responsive to price changes.
This formula therefore balances responsiveness and smoothness. The period can be adjusted to control sensitivity. It is important to ensure that the denominator period * fd + 1 is positive to avoid division issues.
Our next line of code updates FrAMA value at time t using the EMA formula; which is a weighted combination of the current price and the prior FrAMA value. This is important because the recursive EMA calculation is the core to FrAMA and produces a smoothed adaptive moving average that adjusts to market conditions via alpha. Changes that can be made to this implementation include first FrAMA values are not NaNs, and these checks should also include the edge cases of the FrAMA buffer.
The final code line of the FrAMA function returns the FrAMA values as a pandas data frame with a single column named main. This standardizes the output format for compatibility with other technical analysis tools or plotting libraries. The use of ‘main’ column name is conventional for indicators with a single buffer. When integrating in different settings where this name is a calling point, it can be customized to ‘FrAMA’ or something more specific. There is also a need to ensure that the returned data frame aligns with the input data frame index.
Force Index Oscillator Function
This oscillator measures the strength of moves in price by bringing together changes in price and trade volume. This is smoothed with an EMA to emphasize trends or reversals. We implement this in Python as follows:
def ForceIndex(df, period=14, price_col='close', volume_col='tick_volume'): """ Calculate Force Index for a DataFrame with price and volume data. Args: df: Pandas DataFrame with columns for price and volume (default 'close' and 'volume'). period: Smoothing window for EMA (default 13). price_col: Name of the price column (default 'close'). volume_col: Name of the volume column (default 'volume'). Returns: Pandas DataFrame with a single column 'main' containing Force Index values. """ closes = df[price_col] volumes = df[volume_col] # 1. Raw Force Index = Price Delta * Volume price_delta = closes.diff() raw_force = price_delta * volumes # 2. Smooth with EMA alpha = 2.0 / (period + 1) force_index = pd.Series(index=closes.index, dtype=float) for t in range(1, len(raw_force)): if pd.isna(raw_force.iloc[t]): force_index.iloc[t] = np.nan else: force_index.iloc[t] = alpha * raw_force.iloc[t] + (1 - alpha) * force_index.iloc[t-1] return pd.DataFrame({'main': force_index})
Our function above also like the FrAMA offers input flexibility since it accepts customizable price and volume columns. It uses raw force calculation by combining price change and volume to gauge buying and selling pressure. Performs EMA smoothing to reduce noise and emphasize sustained movements. Handle NaNs. Finally, it standardizes the output by returning a data frame for easy integration.
If we go through the lines, the first thing we are doing is extracting the ‘close’ price and volume from the input data frame of the pandas' series. This is important because it isolates the relevant data for calculations, allowing flexibility in column names and efficient processing. Possible changes to this can be validating that price_col and volume_col exist in the data frame to prevent errors; and ensuring volume data is non-negative and that price data is clean, since the Force Index relies on both.
Next, we set the price delta to be the difference in close prices. The method we use in Python returns a buffer that computes the difference between consecutive closing prices in order to measure price movement. This matters because the price change reflects the direction and magnitude of the market’s volume-weighted-drift, which is a key component of the Force Index. NaN value for the first index needs to be handled by converting to zero, and cases of missing values also need to be addressed.
We follow up with determining the raw force index value that is the product of price delta and our volumes. Python simplifies a lot of coding by multiplying buffers/arrays as if they were scalar values. This product represents the strength of price movement. It combines price momentum with volume to quantify buying or selling pressure. A large price change with high volume usually indicates stronger market conviction. In performing this vector product, on top of our code shared above, it is a good idea to ensure the volumes and price delta buffers are aligned by index to avoid miscalculations. It is also noteworthy that this raw force index can be noisy and therefore smoothing can be applied at a later stage.
Next we set the alpha value. This is the calculation of the EMA smoothing factor based on the specified period while using the standard EMA formula of 2/(N + 1). This is important because it determines the weight of new data versus historical data in the smoothed Force Index. A smaller alpha, which comes from a larger period, tends to produce smoother results. We use a default period of 14, and this is common. However, adjustments should be made depending on the timeframe that is used. Typically, shorter periods' server well with intraday trading, while longer periods could work with daily or larger timeframes. It is also important to ensure that the period value is positive to avoid zero division errors.
We then initialize the actual force index buffer from the input pandas data frame. This simply fills an empty buffer with the same index as the price data to store smoothed Force Index values. It is important because it serves as a way of pre-allocating memory and also ensure index alignment, two things that facilitate iterative EMA calculations. Initial NaN values are expected, as the first Force Index requires a prior value.
We therefore check for this by verifying if the raw Force Index at time t is NaN. This ensures robustness by explicitly handling missing data, which prevents invalid EMA calculations. Real-world data often contains gaps, so as jejune as this seems, it should not be overlooked. In fact, logging or flagging NaN values when debugging is good practice.
We then update the force index buffer at each time t, using the EMA formula. This combines the current raw force index with the previous smoothed value. This is important as it is a core smoothing step that reduces noise in the raw force index and highlights sustained trends or reversals. At this step, it is important to ensure that force_index[t-1] is initialized properly, since NaN is often the value for early indices. The edge cases of this buffer, therefore, need to be handled properly.
With this done, we then return the smoothed force index values as a pandas data frame with a single column named main. The standardized output format, as already argued with FrAMA above, allows for better integration and visualization to secondary formats or tools depending on user requirements. The ‘main’ tag tends to align with technical analysis ‘conventions’. It is important to ensure that the data frame’s index matches the input for seamless merging.
Having defined our indicator functions in Python, it is now time to look at the two signal patterns that were able to forward walk in the last article. These were pattern-6 and pattern-9. We are implementing these as a simple 2-bit vector that acts as an input into our neural network. These ‘bits’ are for bullishness and bearishness, with values at each index being either 0 or 1. To recap, the input vector has a size of 2 and at the first index we log 0 if the ALL bullish conditions are not met or 1if they are all met. Similarly, at the second index, we log 0 if ALL bearish conditions are not met or 1 if they as ALL met.
Previously, we have considered scenarios where we broke down each of the constituent parts of the bullish and bearish signal in order to have more elaborate input vectors into our neural networks. The forward walks from this were not as promising, and it seemed more akin to the approach we tried of combining multiple patterns into a single Expert Advisor, also in a previous article.
This analysis might be off, though, so readers can use and modify the attached source code and perform independent testing to come to their own conclusions. The attached code is meant to be used in the MQL5 wizard, and there are guides here on how to do this.
Feature-6 Function
Our Pattern-6 function implementation in Python generates a 2D array of binary signals of 0 or 1 as explained above. We start by initializing our feature output array with zeroes. This output is a NumPy 2D array, the equivalent of a 2-column matrix. The number of rows of this ‘matrix’ is set to the size or length of one of the input data frames ‘one_df’. This initialization sets up the output structure to store bullish and bearish signals separately. The zero initialization means no signals are generated unless pattern conditions a met, providing a ‘clean slate’.
When implementing this, it is important to ensure that the length of the first input, pandas data frame matches that of the second ‘two_df’ as well as the price data frame ‘price_df’ in order to avoid index mis-alignment. The 2D-structure is key in distinguishing bearish and bullish signals, therefore it is important to check that the shape matches expectations. This is how we implement it:
def feature_6(one_df, two_df, price_df): """ Generate binary signals based on sustained price-FrAMA alignment and Force Index momentum. Args: one_df: DataFrame with FrAMA values ('main' column). two_df: DataFrame with Force Index values ('main' column). price_df: DataFrame with price data ('close' column). Returns: 2D NumPy array with bullish (column 0) and bearish (column 1) signals. """ feature = np.zeros((len(one_df), 2)) feature[:, 0] = ((price_df['close'] > one_df['main']) & (price_df['close'].shift(1) > one_df['main'].shift(1)) & (price_df['close'].shift(2) > one_df['main'].shift(2)) & (two_df['main'] > 0.0) & (two_df['main'].shift(1) < two_df['main'].shift(2))).astype(int) feature[:, 1] = ((price_df['close'] < one_df['main']) & (price_df['close'].shift(1) < one_df['main'].shift(1)) & (price_df['close'].shift(2) < one_df['main'].shift(2)) & (two_df['main'] < 0.0) & (two_df['main'].shift(1) < two_df['main'].shift(2))).astype(int) feature[0, :] = 0 feature[1, :] = 0 return feature
We then proceed to define our bullish expectations or the first index value at each row. To recap from the last article, if the current price is above FrAMA; and the previous price is also above the prior FrAMA; and two periods ago this same setup was the case; and the current force index is positive; plus one period ago the force index was below where it is now as well as two periods ago; then we have a bullish setup.
This first column line encapsulates the bullish case, ensuring the signal is only triggered when the price trend is consistently above the adaptive FrAMA, which indicates an uptrend. The force index serves to confirm strong buying pressure. The three period check adds robustness, while the force index check omits weak moves. On implementation, it is important to check all input data frames align index wise and contain valid data. The shift() operations create NaNs for early rows, which need to be handled before indicator values can be returned.
The second column defines the bearish signal with the analogous conditions of: current price being below FrAMA; previous price also being below FrAMA; the same condition happening two periods ago; the current force index being negative; and the force index one period ago is above the current force index and the force index two periods ago. The n-shape in the force index, indicating an increase in negative volume or sentiment.
This pattern mirrors the bullish pattern for selling opportunities. It identifies sustained downtrends with strong selling pressure. The symmetry ensures consistent logic across both patterns. Similar to the bullish pattern, it is vital to ensure data alignment. There should also be tests for a sufficient frequency of this pattern. The force index’s momentum check of (`shift(1) < shift(2)`) may act differently in bearish vs. bullish markets. It is therefore important to analyse historical performance in order to verify its reliability.
The next thing we do is set the first two rows of the feature array to zero since ‘.shift(1)’ and `.shift(2)’ operations produce NaNs for these rows, which makes these conditions undefined. This prevents invalid signals in the initial rows where historical data is insufficient and ensures clean and usable output without manual post-processing. This check is critical for robustness and since this pattern can be implemented by having more than two shifts (such as when periods compared exceed 2), then it is important to verify that setting only the first two rows is sufficient based on the used maximum no. of shifts. If additional shifts are added, then this should be adjusted accordingly.
To sum up our feature-6, the bullish pattern focuses on a sustained price - FrAMA long crossover of at least 3 periods with a positive and recently U shaped force index. It confirms if uptrends ave staying power. The bearish pattern is an inverse to this by dwelling on sustained price - FrAMA bearish crossover for at least 3 periods plus a negative force index with a recent n shape pattern. It also confirms that downtrends are intact.
A key-difference between the two besides being symmetric and opposite is that the force index sentiment check uniquely requires a recent increase in magnitude, which may behave differently in bullish vs bearish markets due to asymmetry. For instance, markets tend to fall faster than they rise.
Feature-9 Function
This Python implementation of signal-9 focuses on single-period sentiment alignment across price, FrAMA, and force index, making them more sensitive to short term changes than ‘feature_6’. We start off as we did with feature-9 by initializing our target output with zeroes. This is a similar setup to feature-6 with the initial size of the output 2D NumPy array being set to match the length of one of the input data frames, one-df. We implement it in Python as follows:
def feature_9(one_df, two_df, price_df): """ Generate binary signals based on single-period momentum alignment of price, FrAMA, and Force Index. Args: one_df: DataFrame with FrAMA values ('main' column). two_df: DataFrame with Force Index values ('main' column). price_df: DataFrame with price data ('close' column). Returns: 2D NumPy array with bullish (column 0) and bearish (column 1) signals. """ feature = np.zeros((len(one_df), 2)) feature[:, 0] = ((price_df['close'] > price_df['close'].shift(1)) & (one_df['main'] > one_df['main'].shift(1)) & (two_df['main'] > two_df['main'].shift(1))).astype(int) feature[:, 1] = ((price_df['close'] < price_df['close'].shift(1)) & (one_df['main'] < one_df['main'].shift(1)) & (two_df['main'] < two_df['main'].shift(1))).astype(int) feature[0, :] = 0 feature[1, :] = 0 return feature
For both feature functions, one-df is meant to be the FrAMA data frame, while two-df is the force index data frame. It thus follows, as we mentioned in feature-6, we need to check that one-data-frame, two-data-frame, and the price-data-frame have the same length to avoid shape mismatches. This matrix/2D array separates bullish and bearish patterns, so verifying its row size is important.
The bullish condition is also what we check for initially with this pattern, next. Its conditions are: current price being higher than the previous close; current FrAMA being higher than the previous FrAMA, and the current force index being above the last value. This captures short-term bullish momentum where price, FrAMA, and force index are all rising, in a sign of aligned buying pressure. It is also a bit more sensitive than feature-6 because it only checks for a single period. This could make it more suitable for scalping or short term trading.
When in use, it is important to ensure data alignment across all inputs to avoid misaligned comparisons. Since this pattern is sensitive to single-period changes, we need to test its signal frequency to avoid over trading in the event markets run into noisy data. Visualizing signals on a price chart to ensure they align with expected volume sentiment can be constructive as well.
We set the bearish pattern for feature-9 as fulfilling the conditions: current price being lower than prior price; current FrAMA being lower than prior FrAMA; and the current force index being lower than previous force index. This grabs short-term bearish sentiment where all three metrics are declining, which indicates aligned selling pressure. The single-period focus tends to make it reactive to immediate downturns.
Once again, just like we saw with the bullish pattern, validation of data integrity and testing for signal frequency, is vital. Bearish signals may trigger more frequently in volatile markets, therefore an analysis of historical performance is important when fine-tuning this strategy.
We then set first rows of the output array to zero because of our use of shift as already mentioned above, and then return the array as the function’s output.
CNN with Dot Product Kernel
Our choice of machine learning algorithm for extending the patterns of FrAMA and the force index is a convolution neural network that uses the dot product kernel. We accomplish this via the class DotProductConv1D. This class is a PyTorch neural network module that combines 1D convolutions with a dot product attention mechanism, as inspired by Transformer architecture.
It does process input data of shape [batch, channels, width] and outputs a single value per sample in the range [0, 1]. Towards 0 would be a bearish forecast, while towards 1 would be bullish. The dot product attention mechanism allows the network to focus on relevant parts of the input sequence, while the convolutional layers project the data into a suitable space for attention computation.
The use of this kernel within a CNN is beneficial for a number of reasons. Firstly, it allows a selective focus on relevant features. The dot product attention mechanism computes similarity scores between query and key vectors, which allows the network to weigh important key steps or features more heavily. This can be beneficial in some time series, for instance where certain periods are more informative e.g. volatile periods vs non-volatile. Secondly, it introduces a global contextual awareness.
Unlike traditional CNNs which rely on fixed-size kernels, and local receptive fields, the dot product attention allows each time step to attend to all other time steps, thus capturing long-range dependencies without having an increase in kernel size. Thirdly, the dynamic weighting where attention scores are computed dynamically based on input makes the model adaptive to varying patterns in the data such as different market conditions within the time series.
Finally, there are complementary strengths from combination with CNNs, which are good for local feature extraction and the dot product kernel that is good for global relationships. The dot product attention is also computationally efficient in moderate sequence lengths, while the 1D CNN reduce the inputs' dimensionality, making the entire model lightweight compared to full transformer models. Our listing for this network class is as follows:
class DotProductConv1D(nn.Module): def __init__(self, in_channels=1, out_channels=1, kernel_size=3): super().__init__() self.kernel_size = kernel_size self.padding = kernel_size // 2 # Projections for dot product attention (1D convolution) self.query = nn.Conv1d(in_channels, out_channels, kernel_size=1) self.key = nn.Conv1d(in_channels, out_channels, kernel_size=1) self.value = nn.Conv1d(in_channels, out_channels, kernel_size=1) # Output projection to produce a single value per sample self.proj = nn.Sequential( nn.Conv1d(out_channels, 1, kernel_size=1), nn.AdaptiveAvgPool1d(1), # Reduce width to 1 (global average pooling) nn.Sigmoid() # Ensures output in [0, 1] ) def forward(self, x): B, C, W = x.shape # [Batch, Channels, Width] # Compute Q/K/V (all [B, out_channels, W]) q = self.query(x) k = self.key(x) v = self.value(x) # Dot product attention attn = torch.bmm(q.transpose(1, 2), k) # [B, W, W] attn = F.softmax(attn / (W ** 0.5), dim=-1) # Scaled softmax # Apply attention to values out = torch.bmm(v, attn.transpose(1, 2)) # [B, out_channels, W] # Project to [B, 1, 1] and squeeze to [B, 1] out = self.proj(out) # [B, 1, 1] return out.squeeze(-1) # [B, 1]
First thing we do above is define the class as a subclass of PyTorch’s ‘nn.module’. This allows it to be used as a neural network module with automatic parameter management and GPU support. Then we initialize the module with parameters for input channels, output channels for attention projections, and a kernel size for padding calculations. These parameters define the network’s capacity and compatibility with input data. We then compute the padding size to maintain the input sequence length after convolution by using integer division to ensure symmetric padding.
Next, we define three 1D convolutional layers that we’ll use to project the input into query, key and value tensors for the attention mechanism. Each has a kernel of size 1 and acts as a per-time-step linear transformation. We then define the output projection pipeline. It reduces the attention output’s channel to 1. It applies global average pooling to collapse the temporal dimension to a single value. Finally, it transforms the output in to a single scalar in the range [0, 1].
With this ‘class header’ defined, we proceed to outline the forward function. The first thing we do within the forward is to apply the query, key, and value convolutional layers to the input tensor ‘x’ that is shaped ‘[B, C, W]’ producing three tensors of shape [B, out_channels, W]. With this done, we compute the dot product attention scores by performing batch matrix multiplication (‘bmm’) between the transposed query tensor (`[B, W, out_channels]`) and the key tensor (`[B, out_channels, W]`) yielding an attention matrix of shape [B, W, W].
We then apply a scaled soft max to the attention scores by dividing the square root of the sequence length in order to stabilize the gradients. Finally, we normalize along the last dimension to produce attention weights that sum up to 1. The output of the forward function is what we define, next, by performing batch matrix multiplication between ‘v’ (‘[B, out_channels, W]’) and the transposed attention matrix (‘[B, W, W]’) in order to produce an output shape of ‘[B, out_channels, W]’.
We then pass the attention output through the projection pipeline (‘self.proj’) to produce a tensor of the shape ‘[B, 1, 1]’. Following this, we simply squeeze out the last dimension such that our returned output is shape ‘[B, 1]’.
Test Runs
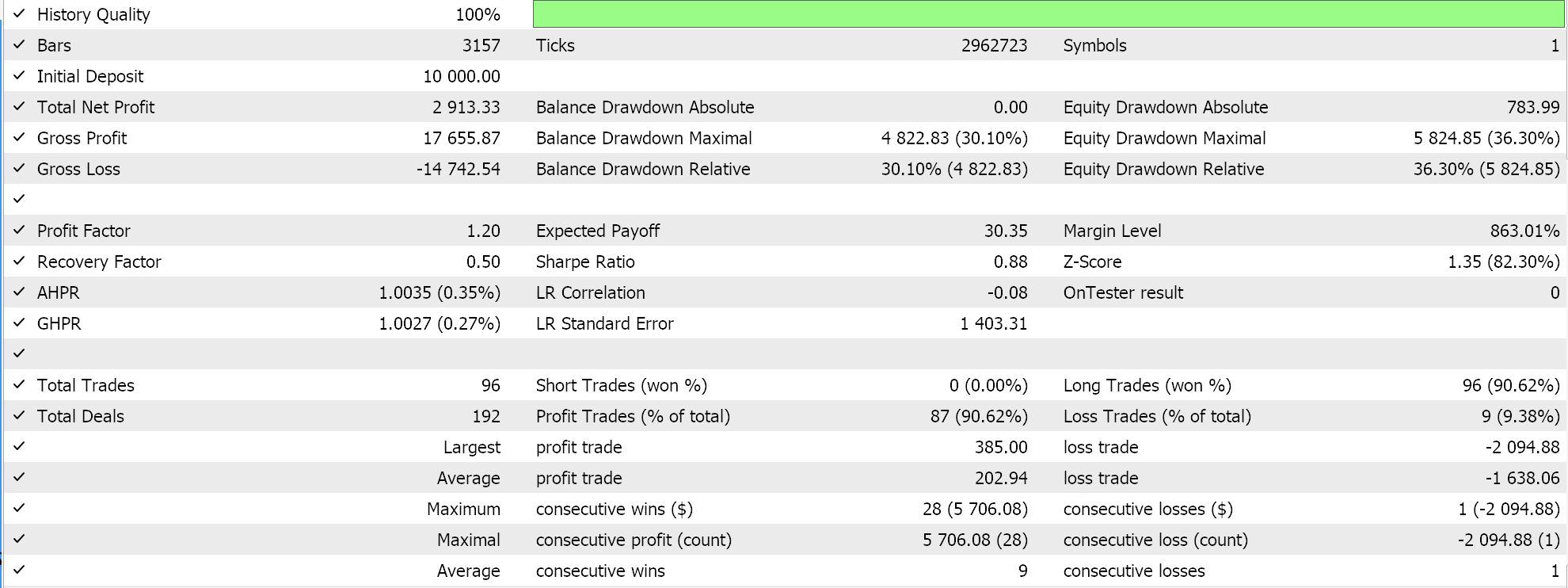
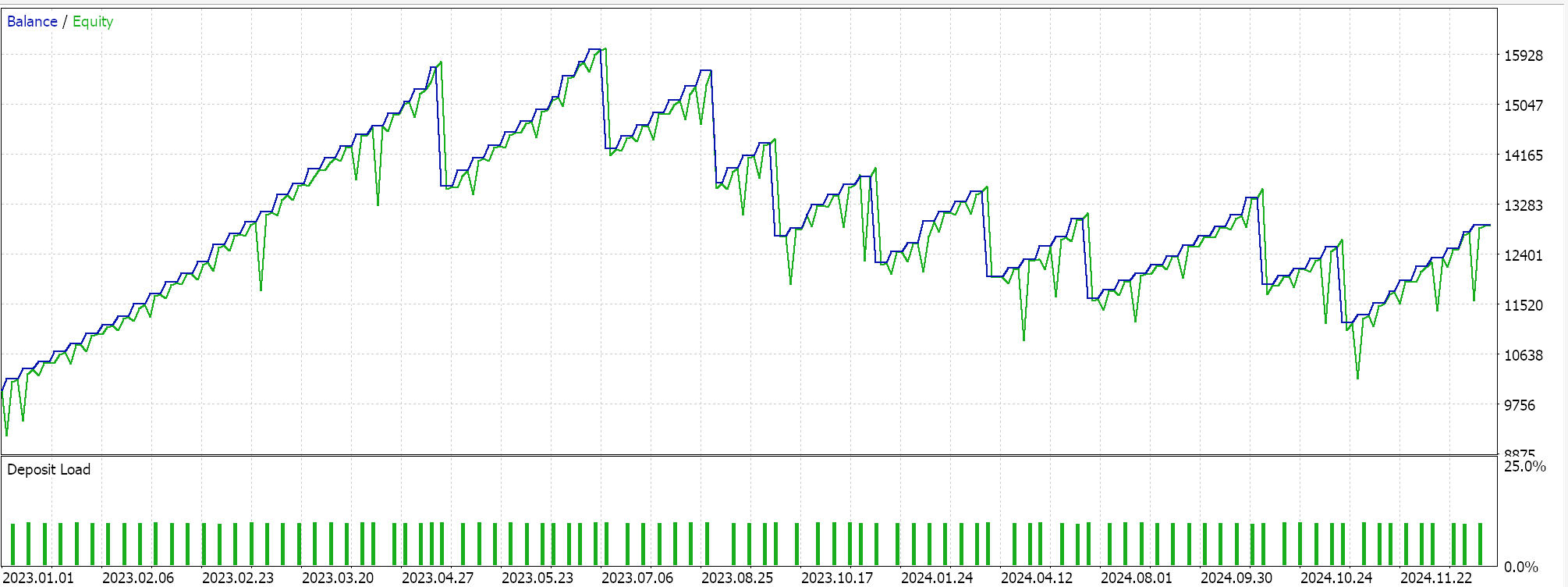
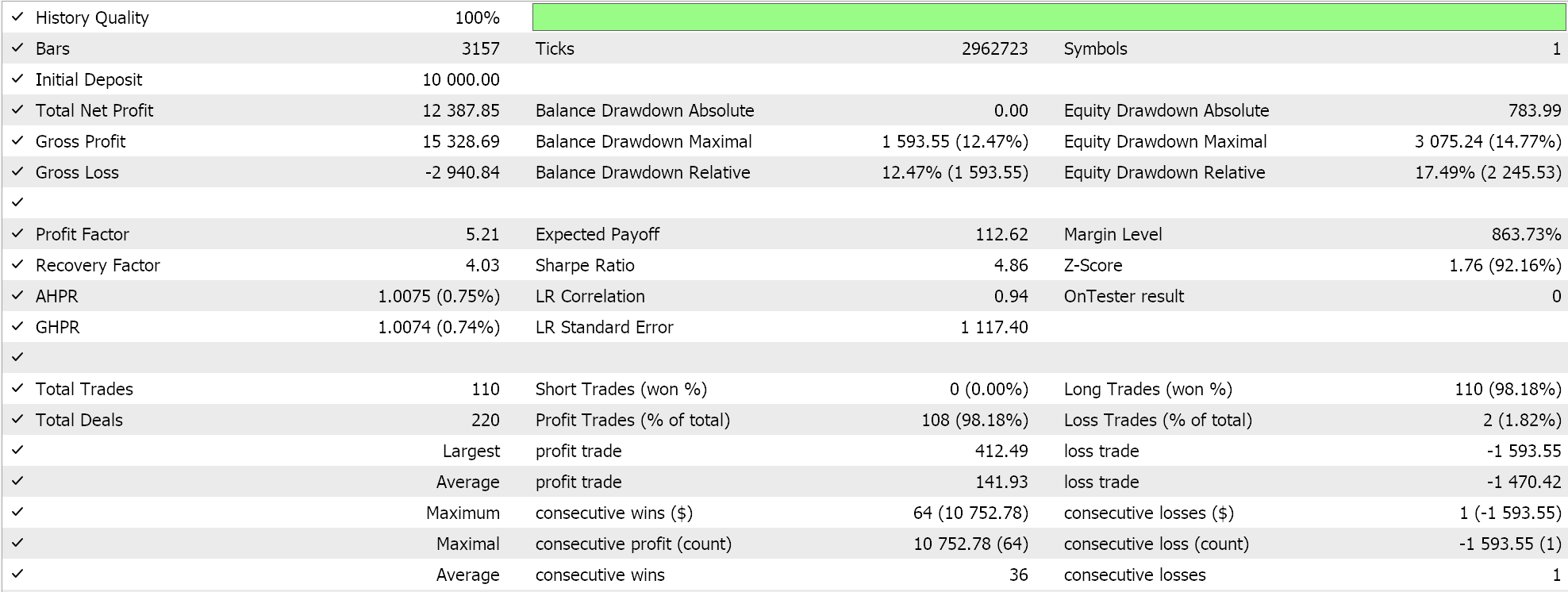
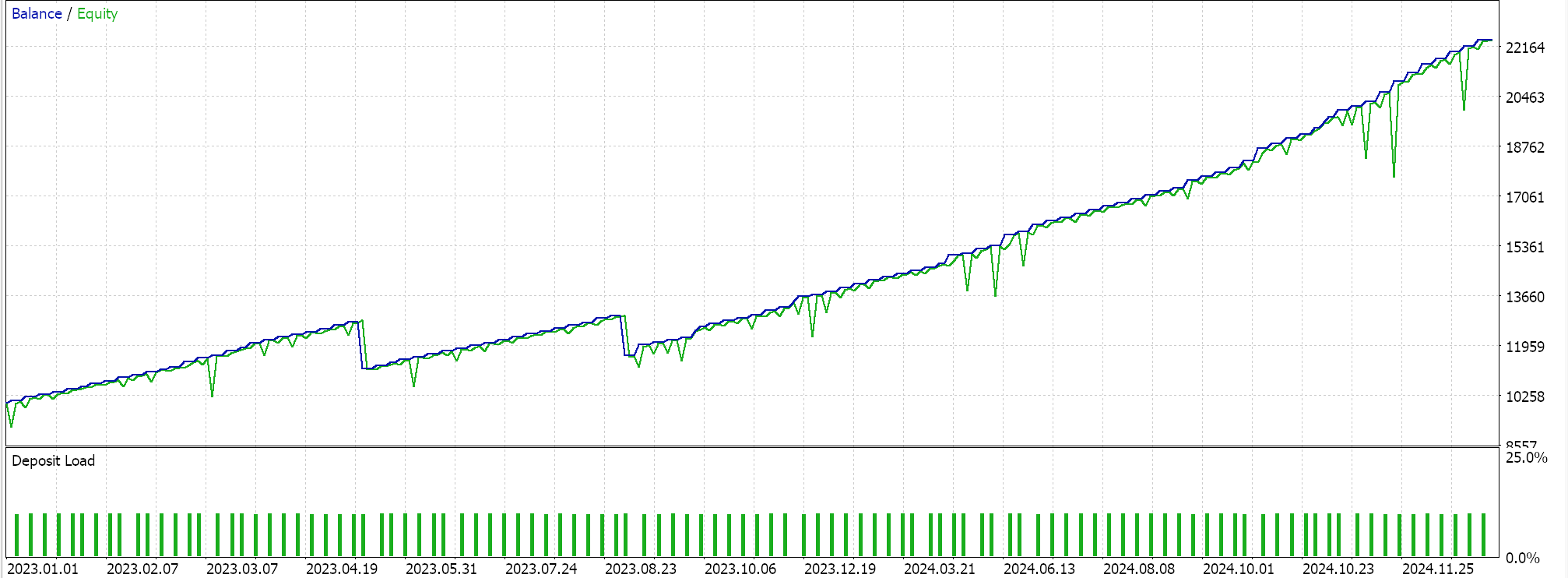
Results of test runs for the two feature patterns 6, and 9 are presented below. Both appear to forward walk but as always our training was based on a very limited data set and therefore more diligence extensive testing is always required on the part of the reader before any long term conclusions can be drawn from testing reports:
For pattern-6.
For pattern-9.
Conclusion
We have demonstrated how machine learning with the use of a product kernel can be used to extend and possibly capitalise on the preliminary potential indicated from the signals of the FrAMA indicator and the force Index oscillator. We only tested the two patterns 6, and 9 which is very limiting, however besides the other 8 that we did not consider there are several other implementations of the pairing of just these two indicators that can be explored.
| name | description |
|---|---|
| wz_66.mq5 | Wizard assembled Expert Advisor whose header indicates included files |
| SignalWZ_66.mqh | Custom Signal Class file |
| 66_6.0nnx | Pattern 6 ONNX file |
| 66_9.onnx | Pattern 9 ONNX file |
Developing a Replay System (Part 69): Getting the Time Right (II)
Data Science and ML (Part 41): Forex and Stock Markets Pattern Detection using YOLOv8
Neural Networks in Trading: Controlled Segmentation (Final Part)
Overcoming The Limitation of Machine Learning (Part 2): Lack of Reproducibility
