
Risk manager for algorithmic trading
Contents
- Introduction
- Subclass for algorithmic trading
- Interface for working with a short stop loss
- Slippage control for open orders
- Spread control for opening positions
- Interface implementation
- Implementation of the trading block
- Assembling and testing the project
Introduction
In this article, we will develop a risk manager class to control risks in algorithmic trading. The purpose of this article is to adapt the principles of controlled risk to algorithmic trading and to implement them in a separate class, so that everyone can verify the effectiveness of the risk standardization approach in intraday trading and investing in financial markets. The materials presented here will use and supplement the information summarized in the previous article "Risk manager for manual trading". In the previous article, we saw that risk control can significantly improve the trading results of even a profitable strategy and protect investors from large drawdowns in a short time period.
Following the comments to the previous article, this publication will additionally cover the criteria for choosing implementation methods in order to make the article more understandable for beginners. We will also cover definitions of trading concepts in comments on the code. In turn, experienced developers will be able to use the presented materials to adapt the code to their architectures.
Additional concepts and definitions used in this article:
High\low the high or low symbol price over a certain period of time indicated by a bar or candlestick.
Stop Loss is the limit price for exiting a position with a loss. If the price goes in the direction opposite to the position we have opened, we limit losses on the open position by closing it before the loss exceeds the values. These values are calculated at the time the position is opened.
Take Profit is the limit price for exiting a position with a profit. This price is set to exit the position and lock in the profit received. It is usually set to capture the planned profit on the deposit or in the area where instrument's daily volatility is expected to exhaust. That is, when it becomes clear that the instrument has no further potential for movement in the certain period of time, and then a correction in the opposite direction is more likely.
Technical Stop Loss is the Stop Loss value set based on technical analysis, for example, for candlestick high/low, break, fractal, etc. depending on the trading strategy used. The main distinguishing feature of this method is that we set the stop loss in chart points based on a certain formation. In this case, the entry point can change while the stop loss values can stay the same. In this case we assume that if the price reaches the stop loss value, then the technical formation will be considered broken, and the direction of the instrument will accordingly be no longer relevant.
Calculated Stop Loss is the Stop Loss set based – on a certain calculated value of the symbol's volatility for a certain period. It differs in that it is not linked to any formation on the chart. With this approach, finding the trade entry point is of particular importance, rather than where the stop position is located on the pattern.
Getter is a class method for accessing the value of a protected field of a class or structure. It is used for encapsulating the value of the class within the logic implemented by the class developer, without the possibility of changing its functionality or the value of a protected field with the specified access level in further use.
Slippage occurs when the broker opens an order at the price that differs from the originally requested one. This situation may occur when you trade by market. For example, when sending an order, the position volume is calculated based on the risk set for the trade in the deposit currency and the calculated/technical stop loss in points. Then, when a position is opened by the broker, it may occur that the position was opened at prices other than those at which the stop loss in points was calculated. For example, it may become equal to 150 instead of 100, while the market is unstable. Such position opening cases should be monitored, and if the resulting risk for an open order becomes much greater (for risk manager parameters) than expected, such a deal should be closed early to avoid higher losses.
Intraday trading is a trading style according ti which trading operations are only performed within one day. According to this approach, open positions are not transferred overnight, that is, to the next trading day. This approach to trading does not require taking into account the risks associated with morning gaps, additional fees for position transfer, changing trends the next day, etc. As a rule, if open positions are transferred over to the next day, this trading style can be considered medium-term.
Positional trading is a trading style according to which a position for an instrument is kept on the account without adding volume or reducing it and without executing additional entry deals. In this approach, upon receiving a signal for an instrument, the trader immediately calculates the full risk based on the signal and processes it. Other signals are not taken into account until the previous position is completely closed.
Trading symbol momentum is a unidirectional, with no rollback, movement of a symbol on the given timeframe. The starting point of the momentum will be the starting point of the movement in the same direction without direction changes. If the price returns to the starting point of the momentum, this is usually referred to as a retest. The value of the instrument's no-rollback movement in points depends, among other things, on the current market volatility, important news release, or important price levels for the instrument itself.
Subclass for algorithmic trading
The RiskManagerBase base class we wrote in the previous article contains all the necessary functionality to provide risk control logic for safer work during active intraday trading. In order not to duplicate all this functionality, we will use one of the most important principles of object-oriented MQL5 programming – inheritance. This approach will allow us to use the previously written code and supplement it with the functionality necessary for embedding our class into any trading algorithm.
The project architecture will be built on the following principles:
- Saving time by avoiding re-writing the same functionality
- Adherence to SOLID programming principles
- Easier work with out architecture for multiple development teams
- Providing the possibility for expanding our project to any trading strategy
The first point, as already noted, is intended to significantly save development time. We will use the inheritance functionality to preserve the previously creating logic of operations with limits and events and not to waste time copying and testing new code.
The second point concerns the basic principles of constructing classes in programming. First of all, we will use the "Open closed Principle" principle: our class will expand without losing the basic principles and approaches to risk control. Each individual method we add will allow us to ensure the Single Responsibility Principle for easy development and logical understanding of the code. This leads to the principle described in the next point.
The third point says that we ensure third parties can understand the logic. The use of separate files for each class will make it more convenient for a team of developers to work simultaneously.
Also, we won't restrict inheritance from our RiskManagerAlgo class using the final specifier, to allow its further improvement through the possibility of further inheritance. This will enable flexible adaptation of our subclass to almost any trading system.
With the above principles, our class will look like this:
//+------------------------------------------------------------------+ //| RiskManagerAlgo | //+------------------------------------------------------------------+ class RiskManagerAlgo : public RiskManagerBase { protected: CSymbolInfo r_symbol; // instance double slippfits; // allowable slippage per trade double spreadfits; // allowable spread relative to the opened stop level double riskPerDeal; // risk per trade in the deposit currency public: RiskManagerAlgo(void); // constructor ~RiskManagerAlgo(void); // destructor //---getters bool GetRiskTradePermission() {return RiskTradePermission;}; //---interface implementation virtual bool SlippageCheck() override; // checking the slippage for an open order virtual bool SpreadMonitor(int intSL) override; // spread control }; //+------------------------------------------------------------------+
In addition to the fields and methods of the existing RiskManagerBase base class, in our RiskManagerAlgo subclass we have provided the following elements to provide additional functionality for algorithmic Expert Advisors (EA). First, we will need a getter to get the data of protected level field of the derived class RiskTradePermission from the base class RiskManagerBase. This method will be the primary way to obtain permission from the risk manager to open new positions algorithmically in the order conditions section. The principle of operation is quite simple: if this variable contains 'true', then the EA can continue to place orders in accordance with the signals of its trading strategy; if it's 'false', order cannot be placed even if the trading strategy indicates a new entry point.
We will also provide an instance of the standard CSymbolInfo class of the MetaTrader 5 terminal for working with symbol fields. The CSymbolInfo class provides easy access to the properties of the symbol, which will also allow us to visually shorten the EA code, for more convenient perception and convenience of further maintenance of the class functionality.
Let's provide additional features for slippage and spread control conditions in our class. The 'slippfits' field will store the control state of the user-defined slippage condition, and the spread size condition will be stored in the 'spreadfits' variable. The third required variable will contain the risk size per trade in the deposit currency. It should be noted that a separate variable was declared specifically to control order slippage. As a rule, with intraday trading, the trading system gives many signals. So, there is no need to be limited to one deal with the risk size for the whole day. This means that before trading, the trader knows in advance which signals for which symbols they process and considers the risk per trade equal to the risk per day, taking into account the number of re-entries into the position.
According to this, the sum of all risks for all entries should not exceed the risk for the day. Well, if there is only one entry per day, then this might be the entire risk. However, this is a rare case as there are usually much more entries. Let's declare the following code at the global level. For convenience, we previously "wrapped" it in a named block using the group keyword.
input group "RiskManagerAlgoClass" input double inp_slippfits = 2.0; // inp_slippfits - allowable slippage per open deal input double inp_spreadfits = 2.0; // inp_spreadfits - allowable spread relative to the stop level to open input double inp_risk_per_deal = 100; // inp_risk_per_deal - risk per trade in the deposit currency
This entry will allow you to flexibly configure the monitoring of open positions in accordance with the conditions specified by the user.
In the public section of our RiskManagerAlgo class we declare the virtual functions of our interface to override as follows:
//--- implementation of the interface virtual bool SlippageCheck() override; // checking the slippage for an open order virtual bool SpreadMonitor(int intSL) override; // spread control
Here we have used the 'virtual' keyword, which serves as a function specifier providing a mechanism for selecting dynamically, at run time, an appropriate member among the functions of our RiskManagerBase base class and the RiskManagerAlgo derived class. Their common parent will be our pure virtual function interface.
We perform initialization in the constructor of the RiskManagerAlgo subclass by copying the values entered by the user through the input parameters to the corresponding fields of the class instance:
//+------------------------------------------------------------------+ //| RiskManagerAlgo | //+------------------------------------------------------------------+ RiskManagerAlgo::RiskManagerAlgo(void) { slippfits = inp_slippfits; // copy slippage condition spreadfits = inp_spreadfits; // copy spread condition riskPerDeal = inp_risk_per_deal; // copy risk per trade condition }
It should be noted here that sometimes direct initialization of class fields may be more practical. However, in this case, it will not make much difference, so we will leave initialization via copying for convenience. In turn, you can use the following code:
//+------------------------------------------------------------------+ //| RiskManagerAlgo | //+------------------------------------------------------------------+ RiskManagerAlgo::RiskManagerAlgo(void):slippfits(inp_slippfits), spreadfits(inp_spreadfits), rispPerDeal(inp_risk_per_deal) { }
In the class destructor, we won't need to "manually" clean up the memory, so we leave the function body empty:
//+------------------------------------------------------------------+ //| ~RiskManagerAlgo | //+------------------------------------------------------------------+ RiskManagerAlgo::~RiskManagerAlgo(void) { }
Now that all the necessary functions are declared in the RiskManagerAlgo class, let's move on to choosing a method for implementing our interface for working with a short stop loss of open positions.
Interface for working with a short stop loss
The mql5 programming language enables flexible development and use of the necessary functionality in optimal implementations. Some of this functionality was ported from C++, and some was supplemented and expanded for greater ease of development. To implement the functionality related to the control over positions opened with a short stop loss, we need a generalizing object that we can use as a parent, not only for inheritance in our risk manager class, but also for inheritance in other EA architectures.
To declare a generic data type created to implement and connect certain functionality, we can use both abstract classes in the C++ style and a separate data type, such as interface.
Abstract classes, as well as interfaces, are intended to create generalized entities, on the basis of which a more specific derived class is created. In our case, it is a class for working with positions with a short stop loss. An abstract class is a class that can only be used as a base class for some subclass, so it is not possible to create an object of an abstract class type. If we need to use this generalized entity, the code of our class will look like this:
//+------------------------------------------------------------------+ //| CShortStopLoss | //+------------------------------------------------------------------+ class CShortStopLoss { public: CShortStopLoss(void) {}; // the class will be abstract event if at least one function in it is virtual virtual ~CShortStopLoss(void) {}; // the same applies to the destructor virtual bool SlippageCheck() = NULL; // checking slippage for the open order virtual bool SpreadMonitor(int intSL)= NULL; // spread control };
The MQL5 programming language offers a special data type interface for generalizing entities. Their notation is much more compact and simpler, so we will use this type, since there will be no difference in functionality. In fact, interface is also a class that cannot contain members/fields and cannot have a constructor and/or destructor. All methods declared in the interface are purely virtual, even without explicit definition, which makes its use more elegant and compact. An implementation via a generic entity such as an interface would look like this:
interface IShortStopLoss { virtual bool SlippageCheck(); // checking the slippage for an open order virtual bool SpreadMonitor(int intSL); // spread control };
Now that we have decided on the type of generic entity to use, let's move on to implementing all the necessary functionality of the methods already declared in the interface for our subclass.
Slippage control for open orders
First of all, to implement the SlippageCheck(void) method, we will need to update the data for the symbol of the chart. We will do this using the Refresh() method of our class CSymbolInfo instance. It will update all fields characterizing the symbol for further operations:
r_symbol.Refresh(); // update symbol data Please note that the Refresh() method updates all field data in the CSymbolInfo class, unlike the similar method of the same class RefreshRates(void), which updates only the data on the current prices of the specified symbol. The Refresh() method in this implementation will be called every tick to ensure the use of up-to-date information at each iteration of our EA.
In the scope of the variables of the Refresh() method, we will need dynamic variables to store the data of the properties of the open position, when iterating over all open positions, to calculate the possible slippage when opening. Information on open positions will be stored in the following form:
double PriceClose = 0, // close price for the order PriceStopLoss = 0, // stop loss price for the order PriceOpen = 0, // open price for the order LotsOrder = 0, // order lot volume ProfitCur = 0; // current order profit ulong Ticket = 0; // order ticket string Symbl; // symbol
To obtain data on the tick value in case of a loss, we will use the TickValueLoss() method of the CSymbolInfo class instance declared inside our RiskManagerAlgo class. The value received from it indicates how much the account balance will change when the price changes by one minimum point for a standard lot. We will use this value later to calculate the potential loss at the actual open prices of the position. Here we use the term "potential", since this method will work on every tick and immediately after opening a position. It means that immediately, on the next received tick, we will be able to check how much we can lose with a deal, although the price is still closer to the opening price than to the stop loss price.
double lot_cost = r_symbol.TickValueLoss(); // get tick value bool ticket_sc = 0; // variable for successful closing
Here we will also declare a variable that is necessary for checking the execution of an order to close an open position if the calculation shows that the position needs to be closed due to slippage. This is a bool variable 'ticket_sc'.
Now we can move on to iterate through all open positions within the framework of our slippage control method. We will iterate over open positions by organizing a for loop, limited by the number of open positions in the terminal. To obtain the value of the number of open positions, we will use a predefined terminal function PositionsTotal(). We will select positions by index, using the SelectByIndex() method of the standard terminal class CPositionInfo.
r_position.SelectByIndex(i)
Once a position has been selected, we can start querying the properties of that position using the same standard terminal class CPositionInfo. But first, we need to check whether the selected position corresponds to the symbol on which this EA instance is running. This can be done using the following code in the loop:
Symbl = r_position.Symbol(); // get the symbol if(Symbl==Symbol()) // check if it's the right symbol
Only after we have made sure that the position selected by index belongs to our chart, we can proceed to query other properties to check the open position. Further queries of position properties will also be made using an instance of the standard terminal class CPositionInfo as follows:
PriceStopLoss = r_position.StopLoss(); // remember its stop loss PriceOpen = r_position.PriceOpen(); // remember its open price ProfitCur = r_position.Profit(); // remember financial result LotsOrder = r_position.Volume(); // remember order lot volume Ticket = r_position.Ticket();
Please note that the check can be performed not only by the symbol, but also by the magic number in the MqlTradeRequest structure, used when opening the selected position. This approach is often used to separate trading operations executed by different strategies within a single account. We will not use this approach, since I believe it is better to use separate accounts for separate strategies, from the point of view of ease of analysis and the use of computing resources. If you use other approaches, please share them in the comments to this article. Now, let's move on to the implementation of our method.
Our method includes position closing. Buy positions are closed by selling at the Bid price and sell positions are closed at the Ask price. So, we need to implement the logic for obtaining the closing price depending on the type of the selected open position:
int dir = r_position.Type(); // define order type if(dir == POSITION_TYPE_BUY) // if it is Buy { PriceClose = r_symbol.Bid(); // close at Bid } if(dir == POSITION_TYPE_SELL) // if it is Sell { PriceClose = r_symbol.Ask(); // close at Ask }
We will not consider the logic of partial closing here, although the terminal allows this to be implemented technically provided that this is allowed by your broker. However, this type of closure is not included in our method logic.
After we make sure the selected position meets the requirements and receive all the necessary features, we can move on to calculating the actual risk for it. First, we need to calculate the size of the resulting stop level in minimum points, taking into account the actual opening price, in order to then compare it with the originally expected one.
We calculate the size as the absolute difference between the opening price and the stop loss. For this, we will use the predefined terminal function MathAbs(). To get an integer value in points from a fractional price value, the value received from MathAbs() is divided by the value of one point in fractional value. To find the value one point we use the Point() method of an instance of our standard terminal class CPositionInfo.
int curr_sl_ord = (int) NormalizeDouble(MathAbs(PriceStopLoss-PriceOpen)/r_symbol.Point(),0); // check the resulting stop
Now, to get the actual potential loss value for the selected position, we just need to multiply the obtained stop value in points by the position size in lots and one tick for value the position symbol. This is done as follows:
double potentionLossOnDeal = NormalizeDouble(curr_sl_ord * lot_cost * LotsOrder,2); // calculate risk upon reaching the stop level
Now let's organize check whether the received value is within the user-entered risk deviation for the trade. This value is specified in the 'slippfits' variable. If the value is beyond this range, then we close the selected position:
if( potentionLossOnDeal>NormalizeDouble(riskPerDeal*slippfits,0) && // if the resulting stop exceeds risk per trade given the threshold value ProfitCur<0 && // and the order is at a loss PriceStopLoss != 0 // if stop loss is not set, don't touch )
In this set of conditions, we have added two more checks, which contain the following logic for processing trading situations.
First, the "ProfitCur<0" condition ensures that slippage is processed only in the losing zone of an open position. This is due to the following conditions of the trading strategy. Since slippage usually occurs during high market volatility, the deal is opened with a slippage towards the take profit, thereby increasing the stop and reducing the take values. This reduces the expected risk/reward of the trade and increases the potential loss relative to the planned one, but at the same time it increases the probability of hitting a take profit, since the momentum due to which our position "slipped" will most likely continue in the moment. This condition means that we will close the position only if the momentum caused the slippage and stopped before reaching the take profit, while returning to the losing zone.
The second condition "PriceStopLoss != 0" is necessary to implement the following logic: If the trader has not set a stop loss, we DO NOT close this position as the risk is not limited for this position. This means that when you open a position, you understand that this position can potentially cover your entire risk for the day if the price goes against you. This implies a very high risk as there may not be enough limits for all the symbols you plan to planned trade for the day, while these symbols could potentially be positive and bring profit. A position without a stop loss may simply make these entries impossible. You should decides for yourself whether to include this condition or not, based on your personal trading strategy. In our implementation, we will not trade multiple instruments at the same time, so we will not delete positions without stop loss levels.
If all the conditions required to identify slippage on a position are met, we will close the position using the PositionClose() method of the standard CTrade class declared in our base class RiskManagerBase. As an input parameter, we pass the previously saved ticket number of the position to be closed. The result of calling the closing function is saved in the ticket_sc variable to control the order execution.
ticket_sc = r_trade.PositionClose(Ticket); // close order The entire code of the method is as follows:
//+------------------------------------------------------------------+ //| SlippageCheck | //+------------------------------------------------------------------+ bool RiskManagerAlgo::SlippageCheck(void) override { r_symbol.Refresh(); // update symbol data double PriceClose = 0, // close price for the order PriceStopLoss = 0, // stop loss price for the order PriceOpen = 0, // open price for the order LotsOrder = 0, // order lot volume ProfitCur = 0; // current order profit ulong Ticket = 0; // order ticket string Symbl; // symbol double lot_cost = r_symbol.TickValueLoss(); // get tick value bool ticket_sc = 0; // variable for successful closing for(int i = PositionsTotal(); i>=0; i--) // start loop through orders { if(r_position.SelectByIndex(i)) { Symbl = r_position.Symbol(); // get the symbol if(Symbl==Symbol()) // check if it's the right symbol { PriceStopLoss = r_position.StopLoss(); // remember its stop loss PriceOpen = r_position.PriceOpen(); // remember its open price ProfitCur = r_position.Profit(); // remember financial result LotsOrder = r_position.Volume(); // remember order lot volume Ticket = r_position.Ticket(); int dir = r_position.Type(); // define order type if(dir == POSITION_TYPE_BUY) // if it is Buy { PriceClose = r_symbol.Bid(); // close at Bid } if(dir == POSITION_TYPE_SELL) // if it is Sell { PriceClose = r_symbol.Ask(); // close at Ask } if(dir == POSITION_TYPE_BUY || dir == POSITION_TYPE_SELL) { int curr_sl_ord = (int) NormalizeDouble(MathAbs(PriceStopLoss-PriceOpen)/r_symbol.Point(),0); // check the resulting stop double potentionLossOnDeal = NormalizeDouble(curr_sl_ord * lot_cost * LotsOrder,2); // calculate risk upon reaching the stop level if( potentionLossOnDeal>NormalizeDouble(riskPerDeal*slippfits,0) && // if the resulting stop exceeds risk per trade given the threshold value ProfitCur<0 && // and the order is at a loss PriceStopLoss != 0 // if stop loss is not set, don't touch ) { ticket_sc = r_trade.PositionClose(Ticket); // close order Print(__FUNCTION__+", RISKPERDEAL: "+DoubleToString(riskPerDeal)); // Print(__FUNCTION__+", slippfits: "+DoubleToString(slippfits)); // Print(__FUNCTION__+", potentionLossOnDeal: "+DoubleToString(potentionLossOnDeal)); // Print(__FUNCTION__+", LotsOrder: "+DoubleToString(LotsOrder)); // Print(__FUNCTION__+", curr_sl_ord: "+IntegerToString(curr_sl_ord)); // if(!ticket_sc) { Print(__FUNCTION__+", Error Closing Orders №"+IntegerToString(ticket_sc)+" on slippage. Error №"+IntegerToString(GetLastError())); // output to log } else { Print(__FUNCTION__+", Orders №"+IntegerToString(ticket_sc)+" closed by slippage."); // output to log } continue; } } } } } return(ticket_sc); } //+------------------------------------------------------------------+
This completes the overriding of the slippage control method. Let's move on to describing the method for controlling the spread size before opening a new position.
Spread control for opening positions
Spread control in our implementation of the SpreadMonitor() method will consist of a preliminary comparison of the current spread just before opening a trade with a calculated/technical stop-loss passed as an integer parameter to the method. The function will return true if the current spread size is within the user-acceptable range. Otherwise, if the spread size exceeds this range, the method will return false.
The function result will be stored in a logical bool variable initialized to true by default:
bool SpreadAllowed = true;
We will obtain the value of the current spread for the symbol using the Spread() method of the CSymbolInfo class:
int SpreadCurrent = r_symbol.Spread(); Below is the logical comparison used for this check:
if(SpreadCurrent>intSL*spreadfits) This means that if the current symbol spread is greater than the product of the required stop loss and the user-specified coefficient, the method should return false, and this should prevent the position with the current spread size from opening until the next tick. Here is the method description:
//+------------------------------------------------------------------+ //| SpreadMonitor | //+------------------------------------------------------------------+ bool RiskManagerAlgo::SpreadMonitor(int intSL) { //--- spread control bool SpreadAllowed = true; // allow spread trading and check ratio further int SpreadCurrent = r_symbol.Spread(); // current spread values if(SpreadCurrent>intSL*spreadfits) // if the current spread is greater than the stop and the coefficient { SpreadAllowed = false; // prohibit trading Print(__FUNCTION__+IntegerToString(__LINE__)+ ". Spread is to high! Spread:"+ IntegerToString(SpreadCurrent)+", SL:"+IntegerToString(intSL));// notify } return SpreadAllowed; // return result } //+------------------------------------------------------------------+
When working with this method, you need to take into account that if the spread condition is very strict, the EA will not open positions, and the relevant information will be constantly logged in the EA's journal. As a rule, a coefficient value of at least 2 is used, which means that if the spread is half the stop, then you either need to wait for a smaller spread, or refuse to enter with such a short stop loss, since the closer the stop level is to the size of the spread, the greater the likelihood of getting a loss from such a position.
Interface implementation
The interface will be the first parent of our base class, since mql5 does not support multiple inheritance. But in this case, this is no limitation for us, since we can implement a consistent inheritance scheme for our project.
To do this, we need to supplement our base class RiskManagerBase with inheritance from the previously described IShortStopLoss interface:
//+------------------------------------------------------------------+ //| RiskManagerBase | //+------------------------------------------------------------------+ class RiskManagerBase:IShortStopLoss // the purpose of the class is to control risk in terminal
This notation will allow us to transfer the required functionality to the subclass RiskManagerAlgo. In this situation, the inheritance access level is not important since our interface has purely virtual functions and does not contain fields, a constructor, or a destructor.
The final inheritance structure of our custom RiskManagerAlgo class, showing the encapsulation of public methods to provide full functionality, is shown in Figure 1.

Figure 1. RiskManagerAlgo class inheritance hierarchy
Now, before assembling our algorithm, we only need to implement the decision-making tool in order to test the described functionality of algorithmic risk control.
Implementation of the trading block
In the previous article Risk manager for manual trading, a trading block consisted of a fairly simple TradeModel entity for basic processing of inputs received from fractals. Since the current article, unlike the previous one, is about algorithmic trading, let's also make an algorithmic decision-making tool based on fractals. It will be based on the same logic, but now we will simply implement everything in code, rather than generating signals manually. As an added bonus, we will be able to test what happens over a larger period of historical data, since we won't have to manually generate the necessary inputs.
Let's declare the CFractalsSignal class, which will be responsible for receiving signals from fractals. The logic remains the same: if the price breaks through the upper fractal of the daily chart, then the EA buys; if the current price breaks through the lower fractal, also from the daily chart, then a sell signal appears. Trades will be closed on an intraday day basis, the day they were opened, at the end of the trading day.
Our CFractalsSignal class will have a field containing information about the timeframe used, on which we will analyze fractal breaks. Thus, we can distinguish between the timeframe on which fractals are analyzed and the timeframe on which the EA runs, simply for ease of use. Let's declare an enum variable ENUM_TIMEFRAMES:
ENUM_TIMEFRAMES TF; // timeframe used
Next, we declare a variable pointer to the standard terminal class for working with the technical indicator, CiFractals, which conveniently implements all the functions we need, and we don't have to write it all over again:
CiFractals *cFractals; // fractals We will also need to store data on signals and on how they are processed by the EA. We will use the TradeInputs custom structure which we used in the previous article. However, last time we generated it manually, and now the CFractalsSignal class will generate it for us:
//+------------------------------------------------------------------+ //| TradeInputs | //+------------------------------------------------------------------+ struct TradeInputs { string symbol; // symbol ENUM_POSITION_TYPE direction; // direction double price; // price datetime tradedate; // date bool done; // trigger flag };
We declare the internal variables of our structure separately for buy and sell signals, so that they can be taken into account simultaneously, since we cannot know in advance which price will be hit first:
TradeInputs fract_Up, fract_Dn; // current signal We just need to declare variables that will store the current values received from the CiFractals class to obtain data on newly formed fractals on the daily chart.
To provide the necessary functionality, we need several methods in the public domain of the CFractalsSignal class, which will be responsible for monitoring the latest current fractal price breaks, giving a signal to open positions and monitoring the success of processing these signals.
Our method for controlling the update of the class data state is Process(). It will not return anything and will not take any parameters, but will simply perform data state update on every incoming tick. The methods for receiving a buy and sell signal will be called BuySignal() and SellSignal(). They will not take any parameters but will return a bool value if it is necessary to open a position in the corresponding direction. The BuyDone() and SellDone() methods will need to be called after checking the broker's server response about the successful opening of the corresponding position. The description of our class looks like this:
//+------------------------------------------------------------------+ //| CFractalsSignal | //+------------------------------------------------------------------+ class CFractalsSignal { protected: ENUM_TIMEFRAMES TF; // timeframe used CiFractals *cFractals; // fractals TradeInputs fract_Up, fract_Dn; // current signal double FrUp; // upper fractals double FrDn; // lower fractals public: CFractalsSignal(void); // constructor ~CFractalsSignal(void); // destructor void Process(); // method to start updates bool BuySignal(); // buy signal bool SellSignal(); // sell signal void BuyDone(); // buy done void SellDone(); // sell done };
In the class constructor, we need to initialize the TF timeframe field to the daily interval PERIOD_D1, since the levels from the daily chart are strong enough to give us the necessary momentum to achieve the take profit, and at the same time they occur much more often than the stronger levels from the weekly and monthly charts. Here we can leave the opportunity for everyone to test smaller timeframes, but we will focus on daily ones. We will also create instances of the class object to work with the fractal indicator of our class and initialize by default all the necessary fields in the following sequence:
//+------------------------------------------------------------------+ //| CFractalsSignal | //+------------------------------------------------------------------+ CFractalsSignal::CFractalsSignal(void) { TF = PERIOD_D1; // timeframe used //--- fractal class cFractals=new CiFractals(); // created fractal instance if(CheckPointer(cFractals)==POINTER_INVALID || // if instance not created OR !cFractals.Create(Symbol(),TF)) // variant not created Print("INIT_FAILED"); // don't proceed cFractals.BufferResize(4); // resize fractal buffer cFractals.Refresh(); // update //--- FrUp = EMPTY_VALUE; // leveled upper at start FrDn = EMPTY_VALUE; // leveled lower at start fract_Up.done = true; // fract_Up.price = EMPTY_VALUE; // fract_Dn.done = true; // fract_Dn.price = EMPTY_VALUE; // }
In the destructor, clear the memory of the fractal indicator object that we created in the constructor:
//+------------------------------------------------------------------+ //| ~CFractalsSignal | //+------------------------------------------------------------------+ CFractalsSignal::~CFractalsSignal(void) { //--- if(CheckPointer(cFractals)!=POINTER_INVALID) // if instance was created, delete cFractals; // delete }
In the data update method, we will only call the Refresh() method of the CiFractals class instance to refresh the data on fractal prices, which it inherited from one of the parent classes CIndicator.
//+------------------------------------------------------------------+ //| Process | //+------------------------------------------------------------------+ void CFractalsSignal::Process(void) { //--- cFractals.Refresh(); // update fractals }
Here I would like to note that there is a possibility of additional optimization of this approach as we do not necessarily need to update this data every tick, since the levels of fractal breaks come from the daily chart. We could additionally implement an event method for the emergence of a new bar on the daily chart and update this data only when it is triggered. But we will keep this implementation, since it does not impose a large additional load on the system, and the implementation of additional functionality will require additional costs with a rather small gain in performance.
In the BuySignal(void) method that opens a buy signal, we first request the latest current Ask price:
double ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); // Buy price
Next, we request the current value of the upper fractal via the Upper() method of the CiFractals class instance, passing the index of the required bar as a parameter:
FrUp=cFractals.Upper(3); // request the current value
We pass the value `3` to this method because we will only use the completely formed fractal breaks. Since in timeseries the buffer count goes from the most recent ones (0) to older ones in the upward direction, the value "3" on the daily chart means the day before the day before yesterday. This will exclude fractal breaks that form on the daily chart at a certain moment and then the price on the same day reaches new high/low and the fractal level disappears.
Now let's make a logical check for updating the current fractal break if the price of the last current break on the daily chart has changed. We will compare the current value of the fractal indicator, updated above in the FrUp variable, with the latest current value of the upper fractal stored in the price field of our TradeInputs custom structure. For the 'price' field to always store the value of the last current price without resetting when there is no data returned by the indicator (if a break is not detected) we will add another check for an empty indicator value FrUp != EMPTY_VALUE. The combination of these two conditions will allow us to update only the significant price values of the last fractal (excluding zero values that corresponds to EMPTY_VALUE in the indicator) and not rewrite this variable with an empty value. The checks are shown below:
if(FrUp != fract_Up.price && // if the data has been updated FrUp != EMPTY_VALUE) // skip empty value
At the end of the method we have the following logic for checking if a buy signal is received:
if(fract_Up.price != EMPTY_VALUE && // skip zero values ask >= fract_Up.price && // if the buy price is greater than or equal to the fractal fract_Up.done == false) // the signal has not been processed yet { return true; // generate a signal to process }
In this block, we also first check if the variable of the last current fractal fract_Up is zero — this is done in case of the initial start of the EA after the first initialization of this variable in the class constructor. The next condition checks whether the current market buy price has broken through the last current value of the fractal: ask >= fract_Up.price. This can be considered the main logical condition of this method. Finally, we need to check whether this fractal level has already been processed for this signal. The point here is that signals on fractal breaks come from the daily chart, and if the current market buy price has reached the required value, we must process this signal once a day, since our trading, although intraday, is positional, without increasing positions or simultaneously opening additional ones. If all the three conditions are met, our method will return true for our EA to process this signal.
The complete implementation of the method with the above logic is shown below:
//+------------------------------------------------------------------+ //| BuySignal | //+------------------------------------------------------------------+ bool CFractalsSignal::BuySignal(void) { double ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); // Buy price //--- check fractals update FrUp=cFractals.Upper(3); // request the current value if(FrUp != fract_Up.price && // if the data has been updated FrUp != EMPTY_VALUE) // skip empty value { fract_Up.price = FrUp; // process the new fractal fract_Up.done = false; // not processed } //--- check the signal if(fract_Up.price != EMPTY_VALUE && // skip zero values ask >= fract_Up.price && // if the buy price is greater than or equal to the fractal fract_Up.done == false) // the signal has not been processed yet { return true; // generate a signal to process } return false; // otherwise false }
As noted above, the method that gets a buy signal should work in tandem with the method that monitors the processing of this signal by the broker's server. The method that will be called when a buy signal is processed is quite compact:
//+------------------------------------------------------------------+ //| BuyDone | //+------------------------------------------------------------------+ void CFractalsSignal::BuyDone(void) { fract_Up.done = true; // processed }
The logic is very simple: when calling this public method, we will put a flag of successful signal processing in the corresponding last signal of the fract_Up structure instance, in the 'done' field. Accordingly, this method will be called in the main EA code only when the check for successful order opening by the broker's server is passed.
The logic for the sell method is similar. The only difference is that we will request the Bid price, not Ask. The condition for the current price will accordingly be checked for "less than the fractal break" for selling.
Below is the corresponding method of the sell signal:
//+------------------------------------------------------------------+ //| SellSignal | //+------------------------------------------------------------------+ bool CFractalsSignal::SellSignal(void) { double bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); // bid price //--- check fractals update FrDn=cFractals.Lower(3); // request the current value if(FrDn != EMPTY_VALUE && // skip empty value FrDn != fract_Dn.price) // if the data has been updated { fract_Dn.price = FrDn; // process the new fractal fract_Dn.done = false; // not processed } //--- check the signal if(fract_Dn.price != EMPTY_VALUE && // skip empty value bid <= fract_Dn.price && // if the ask price is less than or equal to the fractal AND fract_Dn.done == false) // signal has not been processed { return true; // generate a signal to process } return false; // otherwise false }
Processing a sell signal has a similar logic. In this case, the 'done' field will be filled in according to the instance of the fract_Dn structure, which is responsible for the last current fractal for selling:
//+------------------------------------------------------------------+ //| SellDone | //+------------------------------------------------------------------+ void CFractalsSignal::SellDone(void) { fract_Dn.done = true; // processed } //+------------------------------------------------------------------+
This completes theimplementation of our method for generating inputs from daily fractal breaks, and we can move on to the general assembly of the project.
Assembling and testing the project
We will start assembling the project by connecting all the files described above, including the necessary code at the beginning of the main file of the project. For this, we use the #include preprocessor command. Files <RiskManagerAlgo.mqh>, <TradeModel.mqh> and <CFractalsSignal.mqh> are our custom classes that we talked about in the previous chapters. The remaining two notations <Indicators\BillWilliams.mqh> and <Trade\Trade.mqh> are standard terminal classes for working with fractals and trading operations, respectively.
#include <RiskManagerAlgo.mqh> #include <Indicators\BillWilliams.mqh> #include <Trade\Trade.mqh> #include <TradeModel.mqh> #include <CFractalsSignal.mqh>
To set up the slippage control method, we introduce another additional integer variable of type int of the input memory class. The user will specify the acceptable stop value in the amount of minimum points for the instrument:
input group "RiskManagerAlgoExpert" input int inp_sl_in_int = 2000; // inp_sl_in_int - a stop loss level for a separate trade
In more detailed fully automatic integrations or implementations, when using this slippage control method, it is better to implement the transfer of this parameter not through user input parameters, but by returning the stop value from the class responsible for setting the technical stop level or the calculated stop from the class working with volatility. In this implementation, we will leave an additional opportunity for the user to change this setting depending on their specific strategy.
Now we declare the necessary pointers to the risk manager, position and fractal classes:
RiskManagerAlgo *RMA; // risk manager CTrade *cTrade; // trade CFractalsSignal *cFract; // fractal
We will initialize the pointers in the event handler function of our EA's initialization OnInit():
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- RMA = new RiskManagerAlgo(); // algorithmic risk manager //--- cFract =new CFractalsSignal(); // fractal signal //--- trade class cTrade=new CTrade(); // create trade instance if(CheckPointer(cTrade)==POINTER_INVALID) // if instance not created, { Print(__FUNCTION__+IntegerToString(__LINE__)+" Error creating object!"); // notify } cTrade.SetTypeFillingBySymbol(Symbol()); // fill type for the symbol cTrade.SetDeviationInPoints(1000); // deviation cTrade.SetExpertMagicNumber(123); // magic number cTrade.SetAsyncMode(false); // asynchronous method //--- return(INIT_SUCCEEDED); }
When setting up the CTrade object, we specify in the SetTypeFillingBySymbol() method parameter the current symbol on which the EA is running. The current symbol on which the EA is running is returned using the predefined Symbol() method. For the maximum acceptable deviation from the requested price in the SetDeviationInPoints() method, we specify a bit larger value. Since this parameter is not so important for our study, we will not implement is as an input but leave it hardcoded. We also statically register the magic number for all positions opened by the EA.
In the destructor, we implement the deletion of the object, clearing the memory by the pointer, if the pointer is valid:
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(CheckPointer(cTrade)!=POINTER_INVALID) // if there is an instance, { delete cTrade; // delete } //--- if(CheckPointer(cFract)!=POINTER_INVALID) // if an instance is found, { delete cFract; // delete } //--- if(CheckPointer(RMA)!=POINTER_INVALID) // if an instance is found, { delete RMA; // delete } }
Now let's describe the main body of our EA at the entry point of the new tick arrival event OnTick(). First, we need to run the main event monitoring method ContoMonitor() of the base class RiskManagerBase, which we did not override in the subclass, from the subclass instance as follows:
RMA.ContoMonitor(); // run the risk manager Next we call the slippage control method SlippageCheck(), which, as mentioned earlier, processes each new tick and checks if actual risk of open positions meets the planned one (relative to the set stop loss):
RMA.SlippageCheck(); // check slippage It should be noted that since our fractal decision-making tool does not imply deep implementation and serves more as a demonstration of the risk manager's capabilities, it will not set stops, but will simply close positions at the end of the trading day, and therefore this method will allow all transactions that will be passed to it. In order for this method to work fully in your implementation, you can send orders to the broker's server only with a non-zero stop-loss value.
Next we need to update the fractal break indicator data through our custom CFractalsSignal class using the public Process() method:
cFract.Process(); // start the fractal process Now that all event methods of all classes are included in the code, we can move on to the block for monitoring the emergence of signals to place orders. The checking of buy and sell signals will be separated in the same way as the corresponding methods of our CFractalsSignal trading decision making tool class. First, let's describe the Buy check using the following two conditions:
if(cFract.BuySignal() && RMA.SpreadMonitor(inp_sl_in_int)) // if there is a buy signal
First of all, we check the availability of a buy signal via the BuySignal() method of the CFractalsSignal class instance. If it gives this signal, then we check if the risk manager confirms that the spread matches the value allowed by the user via the SpreadMonitor() method. As the only parameter to the SpreadMonitor() method, we pass the user input inp_sl_in_int.
If both described conditions are met, we proceed to place orders in the following simplified logical structure:
if(cTrade.Buy(0.1)) // if Buy executed, { cFract.BuyDone(); // the signal has been processed Print("Buy has been done"); // notify } else // if Buy not executed, { Print("Error: buy"); // notify }
We place an order using the Buy() method of the CTrade class instance, passing a lot value equal to 0.1 in a parameter. For a more objective assessment of the risk manager's operation, we will not change this value in order to "smooth out" the statistics for the volume parameter. This means that all inputs will have the same weight in the statistics of our EA's work.
If the Buy() method executed correctly, that is, a positive response is received from the broker and the deal was opened, we immediately call the BuyDone() method to inform our CFractalsSignal class that the signal was processed successfully and no other signal at this price is required. If a buy order could not be placed, we inform the EA about this in the journal and do not call the method of successful signal processing, to allow a new attempt to reopen.
We will implement similar logic for sell orders, calling the methods corresponding to sells in the code sequence.
We will use the block for closing orders at the end of the trading day from the previous article without changes:
MqlDateTime time_curr; // current time structure TimeCurrent(time_curr); // request current time if(time_curr.hour >= 23) // if end of day { RMA.AllOrdersClose(); // close all positions }
The main task of this code is to close all open positions at 23:00 according to the last known server time, since we are implementing the logic of intraday trading here, without overnights. The logic of this code is described in more detail in the previous article. If you want to leave positions overnight, you can simply comment out this block in the EA code or even delete it.
We also need to display the current state of the risk manager data on the screen via the predefined terminal function Comment(), passing the Message() method of the risk manager class to it:
Comment(RMA.Message()); // display the data state in a commentBelow is the code for processing the new tick event:
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { RMA.ContoMonitor(); // run the risk manager RMA.SlippageCheck(); // check slippage cFract.Process(); // start the fractal process if(cFract.BuySignal() && RMA.SpreadMonitor(inp_sl_in_int)) // if there is a buy signal { if(cTrade.Buy(0.1)) // if Buy executed, { cFract.BuyDone(); // the signal has been processed Print("Buy has been done"); // notify } else // if Buy not executed, { Print("Error: buy"); // notify } } if(cFract.SellSignal()) // if there is a sell signal { if(cTrade.Sell(0.1)) // if sell executed, { cFract.SellDone(); // the signal has been processed Print("Sell has been done"); // notify } else // if sell failed, { Print("Error: sell"); // notify } } MqlDateTime time_curr; // current time structure TimeCurrent(time_curr); // request current time if(time_curr.hour >= 23) // if end of day { RMA.AllOrdersClose(); // close all positions } Comment(RMA.Message()); // display the data state in a comment } //+------------------------------------------------------------------+
Now we can build the project and test it on historical data. For testing example, let's take USDJPY pair and test it during 2023 with the following inputs (see. Table 2):
| # | Setting | Value |
|---|---|---|
| 1 | EA | RiskManagerAlgo.ex5 |
| 2 | Symbol | USDJPY |
| 3 | Chart Timeframes | M15 |
| 4 | Time range | 2023.01.01 - 2023.12.31 |
| 5 | Forward testing | NO |
| 6 | Delays | No delays, perfect performance |
| 7 | Simulation | Every Tick |
| 8 | Initial deposit | USD 10,000 |
| 9 | Leverage | 1:100 |
| 10 | Optimization | Slow Complete Algorithm |
Table 1. Strategy tester settings for the RiskManagerAlgo EA
For optimization in the strategy tester, we set parameters based on the principle of the smallest step in order to reduce the training time, but at the same time, to be able to trace the dependence discussed in the previous article: whether the risk manager allows improving the trading results of even profitable strategies. The input parameters for optimization are presented in Table 2:
| # | Parameter name | Start | Step | Stop Sign |
|---|---|---|---|---|
| 1 | inp_riskperday | 0.1 | 0.5 | 1 |
| 2 | inp_riskperweek | 0.5 | 0.5 | 3 |
| 3 | inp_riskpermonth | 2 | 1 | 8 |
| 4 | inp_plandayprofit | 0.1 | 0.5 | 3 |
| 5 | dayProfitControl | false | - | true |
Table 2. Parameters of the strategy optimizer for the RiskManagerAlgo EA
The optimization parameters do not include those parameters that do not directly depend on the strategy effectiveness and do not influence modeling in the tester. For example, inp_slippfits will depend mainly on the quality of the broker's order execution, and not on our entries. The inp_spreadfits parameter directly depends on the spread size, which varies depending on many factors, including, but not limited to, the broker account type, the timing of important news releases, etc. Each person can optimize these parameters independently, based on the brokerage company where they trade.
The optimization results are presented in Figures 2 and 3.
Figure 2. Optimization results of the RiskManagerAlgo EA
The graph of the optimization results shows that most of the results are in the zone of positive mathematical expectation. This is related to the logic of the strategy, when a large volume of market participants' positions is concentrated at strong fractal breaks, and accordingly, testing of these breaks by the price provokes increased market activity, which gives momentum to the instrument.
To confirm the thesis of the presence of momentum in trading fractal levels, you can compare the best and worst iterations for a given set with the parameters specified above. Our risk manager allows us to standardize this momentum in relation to the risks for entering a position. To better understand the role of the risk manager in standardizing risk relative to market momentum, let's look at the relationship between the daily risk and planned daily profit parameters in Figure 3.
Figure 3. Diagram of daily risk vs planned daily profit
Figure 3 shows a break in the daily risk parameter value, where the effectiveness of the fractal breakout strategy first increases as this value increases, and then begins to decrease. This will be the extreme point (break in the function) of our model for these two parameters. At a certain point, the very presence of such a moment in the model, when an increase in the value of the risk parameter per day starts decreasing profits instead of increasing it, proves that the market impulse becomes smaller relative to the risks that we have included in our model. There is a clear excess of the cost of risk relative to the expected profit. This break is clearly visible on the graph and does not require additional mathematical calculations, such as derivatives of functions.
Now, to really make sure that there is market momentum, let's look at the parameters of the best and worst iterations of our EA's optimization results separately, in order to assess the risk-to-reward ratio. Obviously, if the expected profit at entry is several times greater than the planned risk, then the momentum took place: a unidirectional, non-recoiling movement of the instrument in one direction. If the risk value of our levels is equal to or greater than the return, then there are no momentum there.
The break in the risk value for the day will obviously be the optimal point of optimization for the best pass with the following parameters presented in Table 3, which is what the optimizer showed us:
| # | Parameter name | Parameter value |
|---|---|---|
| 1 | inp_riskperday | 0.6 |
| 2 | inp_riskperweek | 3 |
| 3 | inp_riskpermonth | 8 |
| 4 | inp_plandayprofit | 3.1 |
| 5 | dayProfitControl | true |
| 6 | inp_slippfits | 2 |
| 7 | inp_spreadfits | 2 |
| 8 | inp_risk_per_deal | 100 |
| 9 | inp_sl_in_int | 2000 |
Table 3. Parameters of the best pass of the strategy optimizer for the RiskManagerAlgo EA
We see that the planned profit of 3.1 is five times greater than the required cost of risk to achieve it, which is 0.6. In other words, we risk 0.6% of the deposit and earn 3.1%. This clearly indicates the presence of a price momentum at the daily levels of fractal breaks, which give a positive mathematical expectation.
The graph of the best iteration is shown in Figure 4.
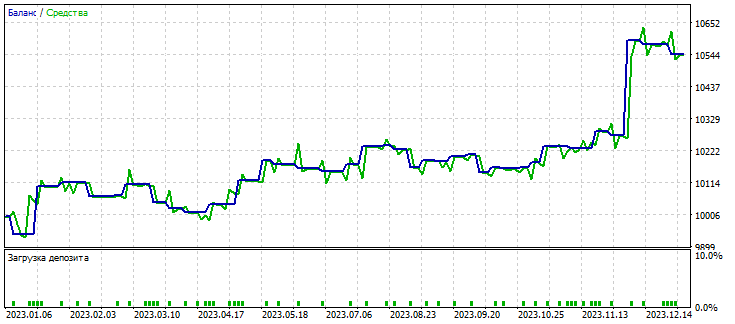
Figure 4. Graph of the best iteration of the strategy optimizer
The deposit growth graph shows that the strategy using risk control forms a fairly smooth graph, where each new rollback does not rewrite the minimum value of the previous rollback. This indicates the result of using risk standardization and our risk manager for investment security. Now, to finally confirm the thesis of the presence of momentum and the need to standardize risks relative to it, let's look at the results of the worst optimizer run.
The risk-return for the worst run with the following parameters can be estimated using the data in Table 4:
| # | Parameter name | Parameter value |
|---|---|---|
| 1 | inp_riskperday | 1.1 |
| 2 | inp_riskperweek | 0.5 |
| 3 | inp_riskpermonth | 2 |
| 4 | inp_plandayprofit | 0.1 |
| 5 | dayProfitControl | true |
| 6 | inp_slippfits | 2 |
| 7 | inp_spreadfits | 2 |
| 8 | inp_risk_per_deal | 100 |
| 9 | inp_sl_in_int | 2000 |
Table 4. Parameters of the worst pass of the strategy optimizer for the RiskManagerAlgo EA
The data in Table 4 show that the worst iteration is exactly in the plane of Figure 3 where we do not standardize risk relative to momentum. That is, we are in a zone where the maximum risk does not provide the necessary return, and we do not use the potential received risk to the maximum, while spending a large amount of the deposit on these entries.
The graph of the worst iteration is shown in Figure 5:
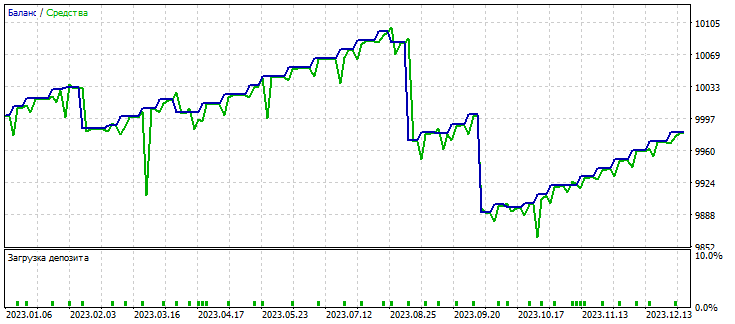
Figure 5. Graph of the worst iteration of the strategy optimizer
According to Figure 5, it is clear that an unbalanced risk to potential return can lead to large drawdowns on the account, both in terms of balance and funds. Based on the optimization results presented in this chapter of the article, we can conclude that the use of a risk manager is mandatory to control risks. It is imperative to select logically justified risks relative to the capabilities of your trading strategy. Now let's move on to the general conclusions of our article.
Conclusion
Based on the materials, models, arguments and calculations presented in the article, the following conclusions can be drawn. It is not enough to find a profitable investment strategy or algorithm. Even in this case, you can lose money due to the unreasonable application of risk to capital. Even with a profitable strategy, the key to the efficient and safe operation in the financial markets is compliance with risk management. A prerequisite for the efficient and secure long-term stable work is the standardization of risk according to the capabilities of the strategy used. I also strongly recommend not to trade on real accounts with the risk manager disabled and without stop losses set on each open position.
Obviously, not all risks in financial markets can be controlled and minimized, but they should always be assessed against the expected return. You can always control the standardized risks with the help of a risk manager. In this article, as in the previous ones, I highly recommend applying the principles of money and risk management.
If you use non-systematic trading without risk control, you can turn any profitable strategy into a losing one. On the other hand, sometimes a losing strategy can be turned into a profitable one if apply a proper risk management. If the materials presented in this article help to save at least one person's deposit, I will consider that the work was not done in vain.
I would appreciate your feedback in the comments to this article. Wishing you all profitable trades!
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/14634
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Developing a multi-currency Expert Advisor (Part 11): Automating the optimization (first steps)
Developing a multi-currency Expert Advisor (Part 11): Automating the optimization (first steps)
 HTTP and Connexus (Part 2): Understanding HTTP Architecture and Library Design
HTTP and Connexus (Part 2): Understanding HTTP Architecture and Library Design
 Data Science and ML(Part 30): The Power Couple for Predicting the Stock Market, Convolutional Neural Networks(CNNs) and Recurrent Neural Networks(RNNs)
Data Science and ML(Part 30): The Power Couple for Predicting the Stock Market, Convolutional Neural Networks(CNNs) and Recurrent Neural Networks(RNNs)
 Creating an MQL5-Telegram Integrated Expert Advisor (Part 7): Command Analysis for Indicator Automation on Charts
Creating an MQL5-Telegram Integrated Expert Advisor (Part 7): Command Analysis for Indicator Automation on Charts
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Top. We all think about how to make money. Professionals think how not to lose
Good phrase) I'll take it into consideration))))