Category Theory in MQL5 (Part 20): A detour to Self-Attention and the Transformer

Introduction

It would be remiss, I think, to carry on with articles in these series while on the subject of category theory & natural transformations, and not touch on the elephant in the room that is chatGPT. By now everyone is acquainted, in some form, with chatGPT and a host of other AI platforms and has witnessed, hopefully appreciated, the potential transformer neural networks have on making not just our research easier, but also taking away much needed time from menial tasks. So I detour in these series and try to address the question whether natural transformations of category theory are in any way key to the Generative Pretrained Transformer algorithms engaged by Open AI.

Besides checking for any synonyms with the ‘transform’ wording, I think it would also be fun to see parts, of the GPT algorithm code in MQL5, and test them on preliminary classification of a security price series.

The transformer, as introduced in the paper, ‘Attention Is All You Need’ was an innovation in neural networks used to perform translations across spoken languages (e.g. Italian to French) that proposed getting rid of recurrence and convolutions. Its suggestion? Self-Attention. It is understood that a lot of AI platforms in use are the brain child of this early effort.

The actual algorithm used by Open AI is certainly under wraps, but none the less it has been understood to use Word-Embedding, Positional Encoding, Self-Attention, and a Feed-Forward network, as part of a stack in a decode-only transformer. None of this is confirmed so you should not take my word for it. And to be clear this reference is on the word/ language translation part of the algorithm. Yes, since most input in chatGPT is text it does form a key almost foundational role in the algorithm but we now know chatGPT does much more than interpret text. For example, if you uploaded an excel file it can not only open it to read its contents but it will plot graphs and even give an opinion on the statistics presented. The point here being the chatGPT algorithm is clearly not being entirely presented here, but only bits of what is understood, it may look like.

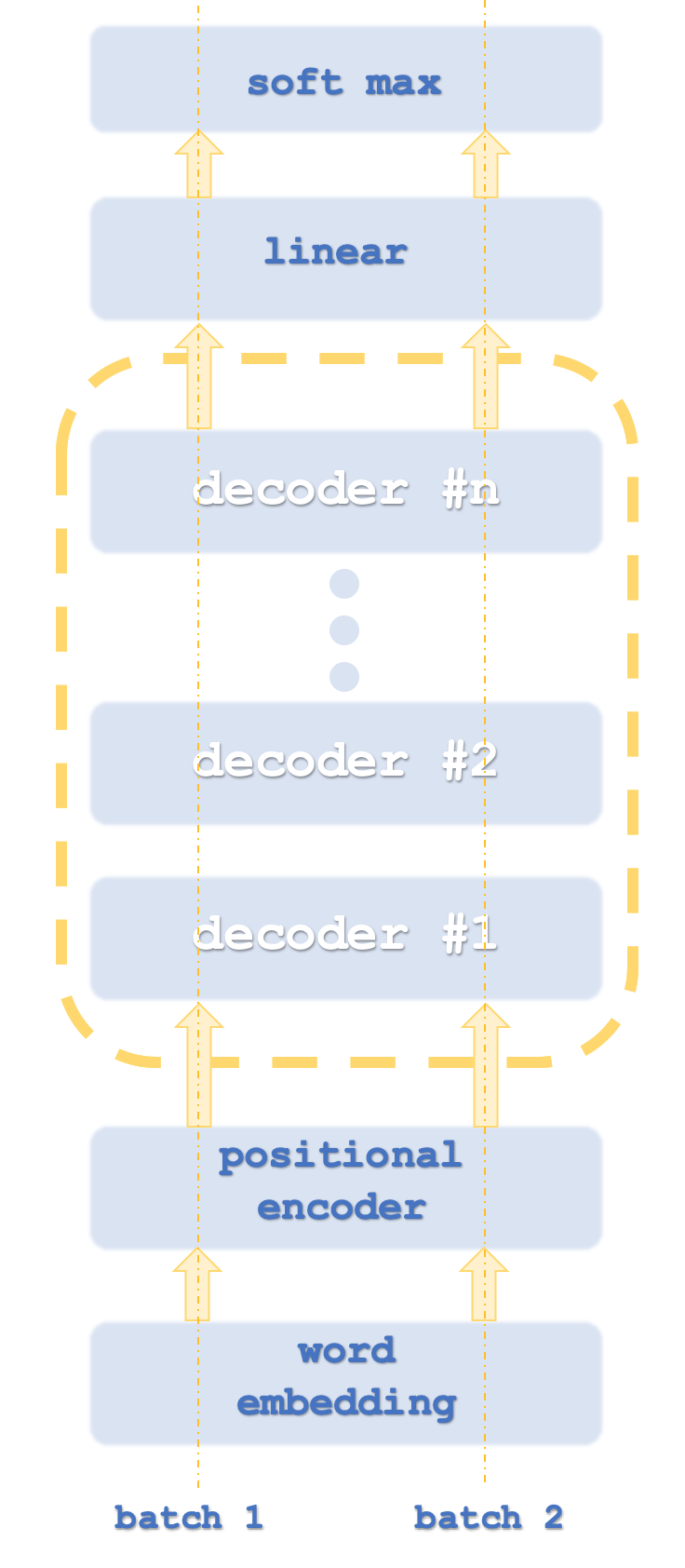
Batch 1 and 2 are analogous to computer threads as transformers typically run network instances in parallel.

Since we are classifying numbers the need for Word-Embedding will not be present. Positional encoding is meant to capture the absolute importance of each word in a sentence thanks to its position. The algorithm for this is straight forward in that each word (aka token) is assigned a reading on a sine wave, from an array of sine waves at different frequencies. The reading from each wave is added up to get the position encoding for that token. This value can be a vector meaning you are summing up values from more than one array of frequencies.

This then leads to Self-Attention. What this does is compute the relative importance of each word in a sentence to words that appear before it in that sentence. This seemingly trivial endeavor is important in sentences that typically feature the word ‘it’, amongst other cases. For example, in the sentence below:

“The dish washer partly cleaned the glass and it cracked it.”

What do the its stand for? To a human this is straight forward but to the learning machine, no so. Mundane as this problem initially seems, it was the ability to quantify this word relative importance that arguably was critical in launching transformer neural nets that were found to be more parallelizable and requiring significantly less time to train than recurrent and convolutional networks, their predecessor.

For this article therefore, Self-Attention will be the crux in our testing signal class. Interestingly though the Self-Attention algorithm does have a semblance to a category in the way words relate to each other. The word relations, that are used to quantify relative importance (similarity), could be thought of as morphisms with the words themselves forming objects. In fact, this relationship is a bit eerie since each word needs to compute its similarity or importance to itself. This is a lot like the identity morphism! In addition, beside inferring morphisms and objects, we could also relate functors and categories respectively as we have seen in the later articles.

Understanding the Transformer Decoder

Typically, a transformer network will contain both encode and decode stacks with each stack representing a repetition in the self-attention and feed-forward networks. It could resemble something similar to what is below:

On top of this, each step is run with parallel ‘threads’, meaning if for example the self-attention and feed-forward step could be represented by a multi-layer perceptron, then if the transformer had 8 threads, there would be 8 multi-layer perceptrons at each stage. This clearly is resource intensive and yet is what gives this approach its edge because even with this resource use it is still more efficient than convoluted networks, the predecessor.

The approach used by Open AI is understood to be a variant of this in that it is decode-only. Its steps were shown roughly in our first diagram. Being decode only apparently does not affect the accuracy of the model while it certainly delivers more on performance since only ‘half’ the transformer is processed. It could be helpful pointing out here that the self-attention mapping when encoding is different from that when decoding in that when encoding all words have their relative importance computed regardless of relative position in a sentence. This is clearly even more resource intensive because as mentioned on the decoder side self-attention (aka similarity calculations) are only done for each word to itself and only those words that come before it in a sentence. Some could argue this even negates the need for positional encoding but for our purposes we will include it in the source. This decode-only approach therefore is our focus.

The role of self-attention and feed-forward networks within a transformer step will is to take position-encoding or previous stack outputs and produce inputs for the linear-SoftMax step of inputs for the next decoder step, depending on the stack.

Position-encoding which some may find overkill for our signal class and article is included here for information purposes. The absolute order of input price bar information could be as important as word sequence within a sentence. We are using a simple algorithm that returns a 4-cardinal vector of double values acting as ‘co-ordinates’ of each input price point.

Some might argue why not use simple indexing for each input. Well it turns out this leads to vanishing and exploding gradients when training networks and therefore a less volatile and normalized format is necessitated. You could think of this as being equivalent to an encryption key that is standard in length, say 128, regardless of what is being encrypted. Yes, it makes cracking the hidden key more difficult but it also provides a more efficient way of generating and storing the keys.

So, what we will use will be 4 sine waves at different frequencies. Occasionally despite these 4 frequencies two words may have the same ‘co-ordinates’, but this should not be a problem as if it does happen then many words (or in our case price points) are being used to negate this slight anomaly. These co-ordinate values are added to the 4 price points of our input vector which represents what we would have got from word-embedding but did not since we are already dealing with numbers in the form of security prices. Our signal class will use price changes. And to sort of ‘normalize’ our position-encoding, the position encoding values which can oscillate about +5.0 to -5.0 and sometimes even beyond, will be multiplied to the point size of the security in question before being added to the price change.

The self-attention mechanism as you may gather from the shared hyperlink(s) above is charged with determining 3 vectors namely the query vector, key vector and values vector. These vectors are got from multiplying the position encoding output vector to a matrix of weights. How are these weights got? From back propagation. For our purposes though we will use instances of the multi-layer perceptron class to initialize and train these weights. Single layer only. A diagrammatic representation of this process for this critical stage could be as follows:

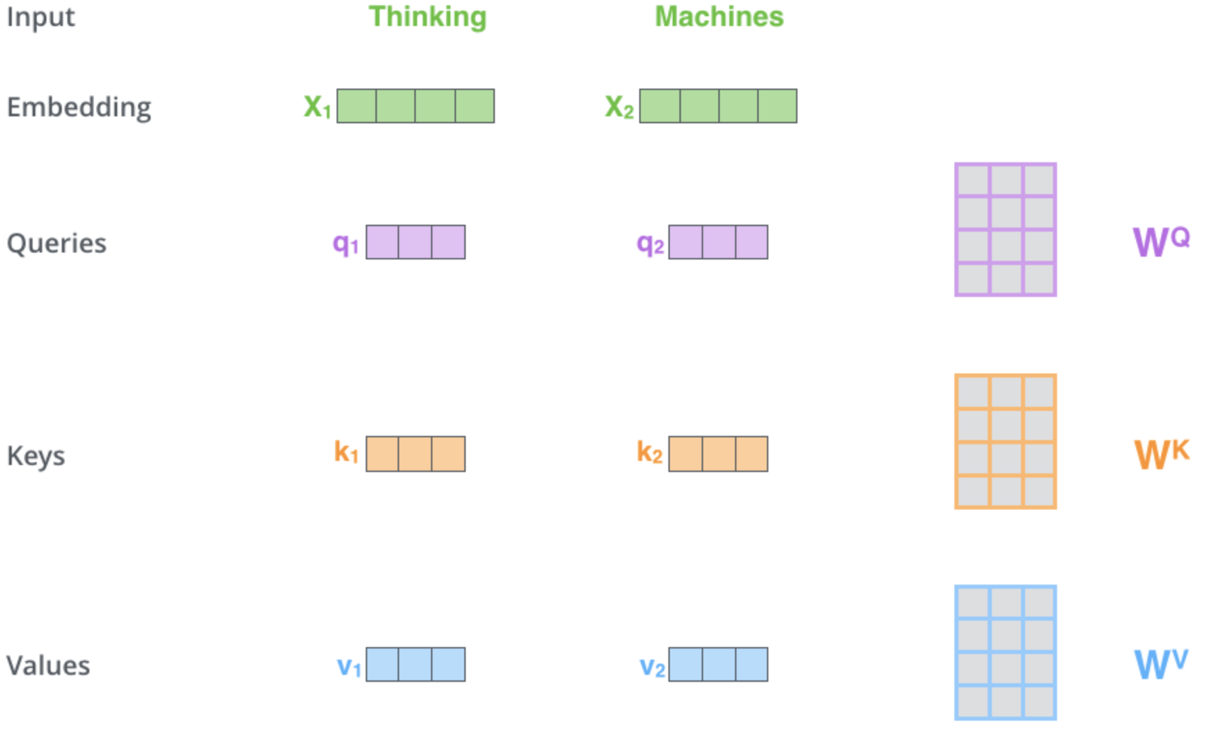
This illustration and some talking points in this article are sourced from this web-page. The image above represents 2 words as inputs (“Thinking”, & “Machines”). On embedding (converting them to numeric vectors), they are converted to vectors in green. The matrices on the right represent the weights we are going to get via Multi-Layer Perceptrons as mentioned above.

So once our networks perform forward pass coming up with the query, key and value vectors, we do a dot product of the query and the key, divide this result by the square root of the cardinal of the key vector and the result is the similarity between the price point with the query vector and the price point with the key vector. These multiplications are done throughout all the price points keeping in line with the self-attention mapping where we only compare price points to itself and those before it. The results got would-be wide-ranging figures which is why they are normalized into a probability distribution using the SoftMax function. The sum of all these probability weights comes to one as expected. They are effectively weighting. In the final step each weight is multiplied with its respective vector value and all these products are summed into a single vector that forms the output of the self-attention layer.

The feed-forward network takes the output vector from self-attention processes it through a multi-layer perceptron and outputs another vector similar in size to the self-attention input vector.

The theoretical framework for implementing the Transformer Decoder in MQL5 will be via simple signal class and not expert advisor. This subject is a bit complex for now since some of these ideas have been around for less than a decade so it is felt that testing and familiarity is more important for now than execution and results. The reader of course is free to take and adopt these ideas further as and when he feels comfortable.

The MQL5 Signal Class: A Glimpse into Self-Attention and Feed-Forward Networks

The signal class attached to this article has a go at forecasting price changes with a transformer decoder that only has one stack and a single thread!! The attached code is adjustable to increase the number of stacks by adjusting the ‘__DECODERS’ definition parameter. As mentioned above the stacks are typically multiple and more often than not in a multiple thread setting. In fact, usually multiple stacks are used within a decoder such that a residual connection is necessary. This again is to avoid vanishing and exploding gradients problem. So, we are working with a simple bare bones transformer and seeing what it can do. The reader can take it from here on further customization to suit his implementation needs.

The positional encoding is probably the simplest of all the functions listed as it simply returns a vector of co-ordinates given a size of inputs. This listing is below:

//+------------------------------------------------------------------+
//| Positional Encoding vector given length.                         |
//+------------------------------------------------------------------+
vector CSignalCT::PositionalEncoding(int Positions)
   {
      vector _positions;
      _positions.Init(Positions);_positions.Fill(0.0);
      
      for(int i=0;i<Positions;i++)
      {
         for(int ii=0;ii<Positions;ii++)
         {
            _positions[i]+=MathSin((((ii+1)/Positions)*(i+1))*__PI);
         }
      }
      
      return(_positions);
   }

So, our signal class references a number of functions but chief among them is the Decode function whose source is listed below:

//+------------------------------------------------------------------+
//| Decode Function.                                                 |
//+------------------------------------------------------------------+
void CSignalCT::Decode(int &DecoderIndex,matrix &Input,matrix &Sum,matrix &Output)
   {
      Input.ReplaceNan(0.0);
      //
      //output matrices
      Sum.Init(1,int(Input.Cols()));Sum.Fill(0.0);
      
      Ssimilarity _s[];
      ArrayResize(_s,int(Input.Cols()));
      
      for(int i=int(Input.Rows())-1;i>=0;i--)
      {
         matrix _i;_i.Init(1,int(Input.Cols()));
         for(int ii=0;ii<int(Input.Cols());ii++)
         {
            _i[0][ii]=Input[i][ii];
         }
         //
         SelfAttention(DecoderIndex,_i,_s[i].queries,_s[i].keys,_s[i].values);
      }
      
      for(int i=int(Input.Cols())-1;i>=0;i--)
      {
         for(int ii=i;ii>=0;ii--)
         {
            matrix _similarity=DotProduct(_s[i].queries,_s[ii].keys);
            Sum+=DotProduct(_similarity,_s[i].values);
         }
      }
      //
      Sum.ReplaceNan(0.0);
      //
      FeedForward(DecoderIndex,Sum,Output);
   }

As you can see it calls both the self-attention function and the feed-forward function and also prepares the input data necessary for both these layer functions.

The self-attention function does the actual matrix weight computations to get the vectors for queries, keys, and values. We have represented these ‘vectors’ as matrices, even though for our signal class’s purposes we will be using one row matrices, because in practice multiple vectors are often fed through a network or multiplied to a matrix system of weights to yield a matrix of queries, keys, and values. The source for this is below:

//+------------------------------------------------------------------+
//| Self Attention Function.                                         |
//+------------------------------------------------------------------+
void CSignalCT::SelfAttention(int &DecoderIndex,matrix &Input,matrix &Queries,matrix &Keys,matrix &Values)
   {
      Input.ReplaceNan(0.0);
      //
      Queries.Init(int(Input.Rows()),int(Input.Cols()));Queries.Fill(0.0);
      Keys.Init(int(Input.Rows()),int(Input.Cols()));Keys.Fill(0.0);
      Values.Init(int(Input.Rows()),int(Input.Cols()));Values.Fill(0.0);
      
      for(int i=0;i<int(Input.Rows());i++)
      {
         double _x_inputs[],_q_outputs[],_k_outputs[],_v_outputs[];
         vector _i=Input.Row(i);ArrayResize(_x_inputs,int(_i.Size()));
         for(int ii=0;ii<int(_i.Size());ii++){ _x_inputs[ii]=_i[ii]; }
         
         m_base_q[DecoderIndex].MLPProcess(m_mlp_q[DecoderIndex],_x_inputs,_q_outputs);
         m_base_k[DecoderIndex].MLPProcess(m_mlp_k[DecoderIndex],_x_inputs,_k_outputs);
         m_base_v[DecoderIndex].MLPProcess(m_mlp_v[DecoderIndex],_x_inputs,_v_outputs);
         
         for(int ii=0;ii<int(_q_outputs.Size());ii++){ if(!MathIsValidNumber(_q_outputs[ii])){ _q_outputs[ii]=0.0; }}
         for(int ii=0;ii<int(_k_outputs.Size());ii++){ if(!MathIsValidNumber(_k_outputs[ii])){ _k_outputs[ii]=0.0; }}
         for(int ii=0;ii<int(_v_outputs.Size());ii++){ if(!MathIsValidNumber(_v_outputs[ii])){ _v_outputs[ii]=0.0; }}
         
         for(int ii=0;ii<int(Queries.Cols());ii++){ Queries[i][ii]=_q_outputs[ii]; }   Queries.ReplaceNan(0.0);
         for(int ii=0;ii<int(Keys.Cols());ii++){ Keys[i][ii]=_k_outputs[ii]; }         Keys.ReplaceNan(0.0);
         for(int ii=0;ii<int(Values.Cols());ii++){ Values[i][ii]=_v_outputs[ii]; }     Values.ReplaceNan(0.0);
      }
   }

The feed-forward function is a straight forward processing of a multi-layer perceptron and there is nothing here specific to the decode transformer, from our perspective. Of course, other implementations could have custom settings here like multiple hidden layers or even different type of networks like Boltzmann machine, but for our purposes this is a simple single hidden layer network.

The dot product function is a bit interesting in that it is a custom implementation of multiplying two matrices. We mostly use it to multiply one row matrices (aka vectors) but it is scalable and could be resourceful since preliminary testing of the inbuilt matrix multiplication function has found it to be buggy, for now.

The SoftMax is an implementation of what is listed in Wikipedia. All we are doing is returning a vector of probabilities given an input array of values. The output vector does have all its values as positive and summing up to one.

So, putting this all together, our signal class loads price data from 2020.01.01 up to 2023.08.01 for the forex pair USDJPY. With the daily time frame we feed a vector of 4 price points that are simply the last 4 changes in close price into the position encode function. This function as mentioned gets the co-ordinates of each price change, normalizes it by multiplying it to the USDJPY point size and adds it to the input price changes.

The output vector for this is fed into the Decode function to compute the query, key, and value vector for each of the 4 inputs in the vector. From self-mapping since similarity is only checked for each price point with itself and the price changes before it, from 4 vector values we end up with 10 vector values that need SoftMax normalization.

Once we run this through the SoftMax we have an array of ten weights of which only one belongs to the first price point, 2 to the second, 3 to the third and 4 to the fourth. So since with each price point we also have a value vector that we got during self-attention function, we multiply this vector with its respective weight that we have got from SoftMax and then sum up all these vectors into a single output vector. By design, its magnitude should match the magnitude of the input vector since the transformer stacks are in sequence. Also, since we are using multi-layer perceptrons it is important to mention the weights initialized with each of the networks will be random and get trained (thus improved), with each successive bar.

Our signal class, when compiled into an expert advisor and optimized for the first 5 months of 2023 and given a walk forward test from 2023.06.01 to 2023.08.01 presents us with the reports below:

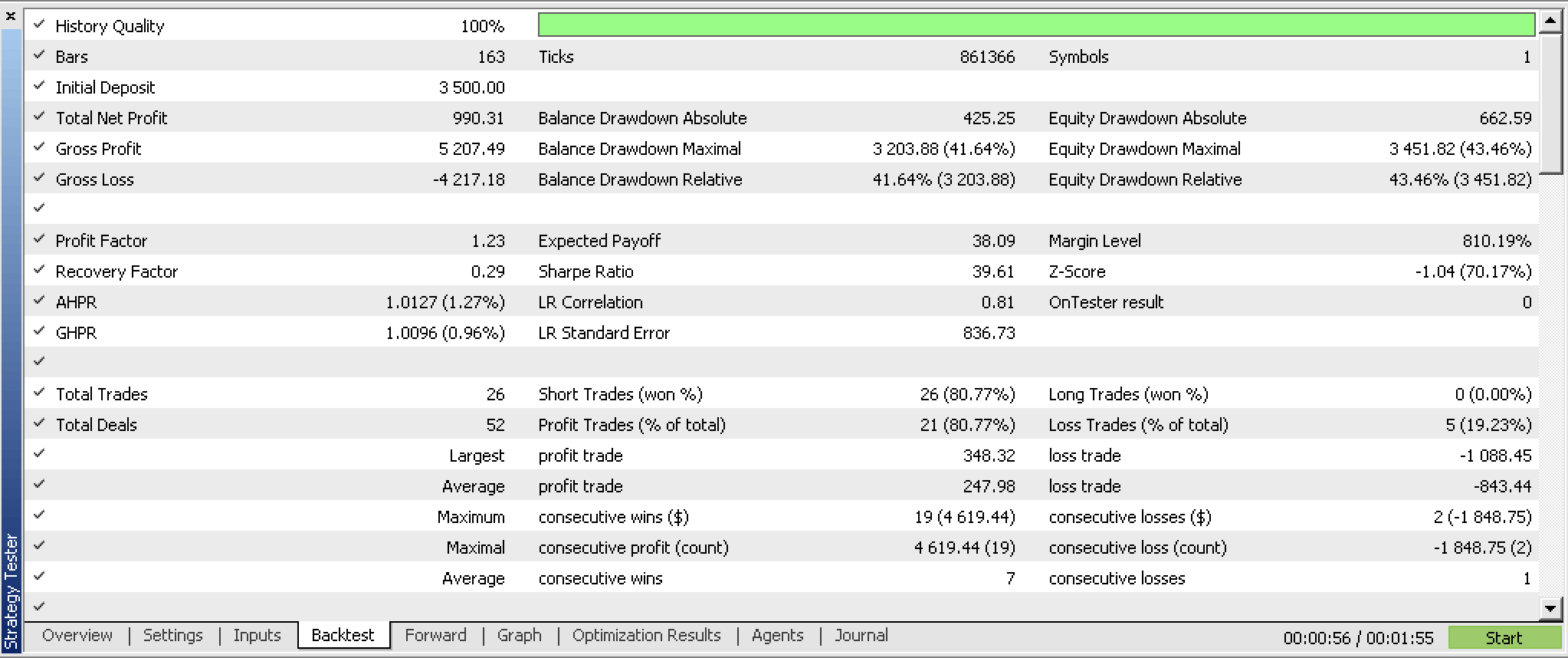
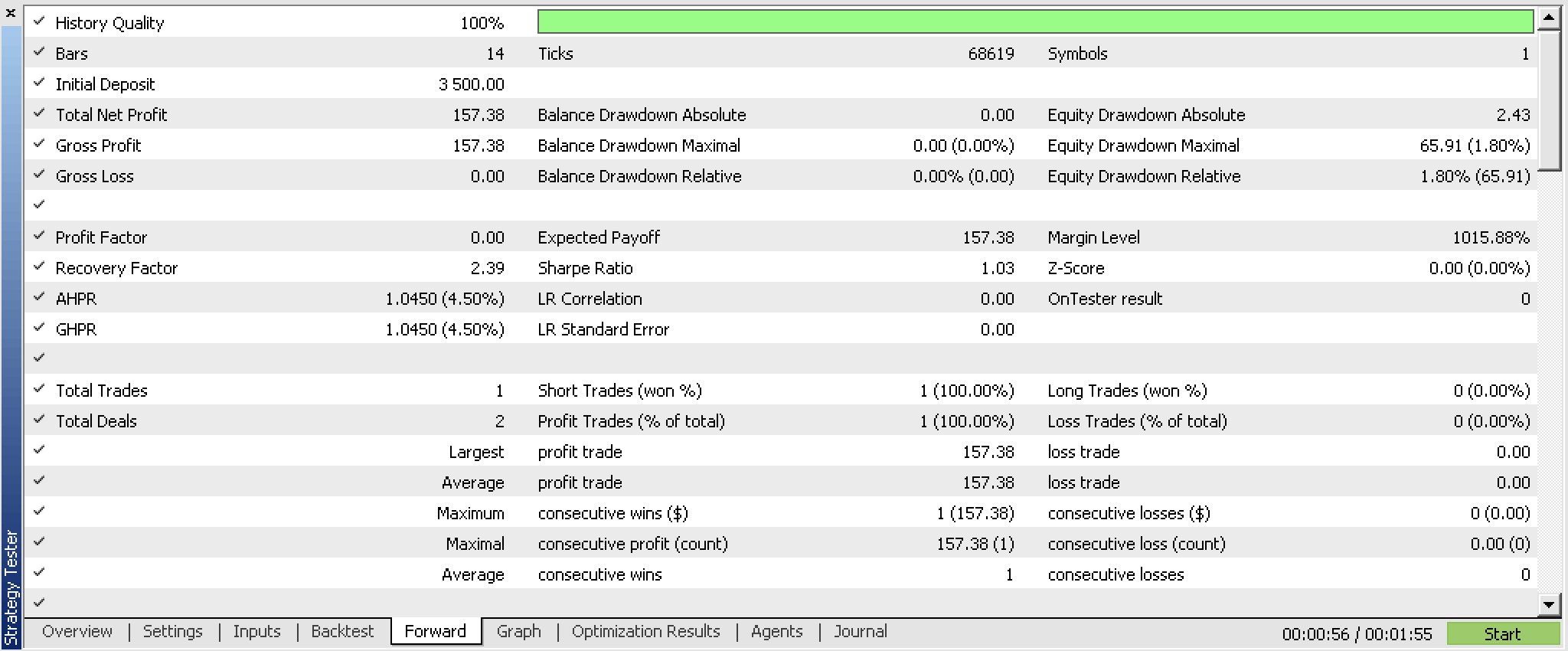
These reports were generated with an expert that had network weights reading and writing features which are not shared in the attached code as implementation is up to the reader. Because weights are not read from a definite source on initialisation, results are bound to be different on each run.

Real-World Applications

The potential applications of this signal class specifically and not the transformer decoder could be in scouting for potential securities to trade with the transformer decoder. If we run tests over multiple securities on time spans over decades we might get a sense of what is worth looking into further with additional testing and system development and what should be avoided.

Within a stack of the decode transformer the self-attention layer is critical and is bound to give us our edge since the feed-forward network used here is pretty straight forward. So, the relative importance of each prior price change gets captured in ways that correlation functions easily gloss over since they focus on averages. The use of multi-layer perceptrons in capturing the weight matrices for the query, key and value vectors is one approach that could be used as there is a plethora of other intermediate machine learning options to accomplish this. On the whole understanding self-attention’s sensitivity to the predictability of the network would be key.

Limitations and Drawbacks

The network training for our signal class is done incrementally on each new bar and the provision to load pre-trained weights is not availed meaning we are bound to get random results a lot. In fact, because of this the reader should expect a different set of results whenever the signal class is run.

In addition, the ability to also save trained weights at the end of the signal class is not availed meaning we cannot build on what is learnt here.

These limitations are critical and need to be addressed, in my opinion, before any one proceeds with developing our transformer decoder further into a trading system. Not only should we use trained weights and also be able to save training weights, testing on out of sample data with trained weights needs to be done before the system could be deployed.

Conclusion

So, to answer the question, is the chatGPT algorithm linked to natural transformations? It could be. This is because if we view the stacks of the decoder transformer as categories then the threads (parallel operations that run through the transformer) would be functors. With this analogy, the difference between the end results of each operation would be equivalent to a natural transformation.

Our decoder Transformer even without proper weights logging and reading has shown some potential. It certainly an interesting system that one could develop further, and even add to his toolkit, as he builds his edge.

In conclusion the self-attention algorithm is adept at quantifying relative similarity among tokens (the inputs in a transformer). In our case these tokens were price changes at different, but sequential points in time. In other models this could have been multiple economic indicators, news events, or investor sentiment values etc. but the process would have been the same, however the result with these different inputs is bound to unveil and thus model the complex and dynamic relationship of these input values, helping the developer understand them better. This in the long term will make the transformer adaptively extract relevant features from the input tokens with each new training session. So even in volatile situations where a lot of news is breaking the model should sift out white noise and be more resilient.

Also, the self-attention algorithm when faced with lagged or input data at different points in time, like we have explored with the attached signal class, it helps in quantifying the relative significance of these different periods and thus captures long range dependencies. This leads to the ability to handle forecasting over different time horizons, another plus for traders. So, to sum up the relative weighting of token inputs should provide insights to traders on not just various economic indicators that may be inputs but also on the different time frames, if lagged time indicators (or prices) are used.

Additional Resources

References are mostly Wikipedia as per the links with the addition of Cornell University Computer Science Publications,Stack Exchange, and this website.

Author's Note

The source code shared in this article is NOT the code used by chatGPT. It is simply an implementation of a decode-only transformer. It is in a signal class format meaning the user needs to compile this with the MQL5 wizard to form a testable expert. There is a guide on that here. In addition he should implement read and write mechanisms for reading and storing learnt network weights.