Estimate future performance with confidence intervals

Introduction

Creation of profitable automated trading systems is no easy task. Even if one happens to make a profitable expert advisor, there are still questions about whether it is worth the risk. We may be satisfied that our strategy will not blow through all capital allocated to it, but this is no  reason to immediately enable live trading. Ultimately, profit is the motive and if we later find that our strategy is indeed profitable, but not profitable enough to justify the risk, or generates poor returns relative to other investment opportunities we will no doubt have serious regrets.

Therefore, in this article we will explore techniques borrowed from the field of statistics that can help us estimate the future performance of an automated trading system, using data collected from out of sample tests.

Is it good enough

When we test a candidate trading system, we naturally end up with a collection of various performance metrics. This data will intuitively give us an indication of the profit potential of the system,but this intuition may not be enough. A strategy that produced plenty profit in testing can garner less than stellar returns when traded live. Is there some way of getting a better idea, of whether performance observed during testing will continue at the same level? If it does not, how bad will the performance get?

This is where standard statistical methods could help. It should be noted that the techniques we will discuss are not meant to be accurate in their estimations, they will never be. What they do is provide methods to identify strategies with a high probability of producing significant or acceptable profit.

I have seen many who use raw Sharpe Ratio figures to make probability based assumptions of future performance. This is dangerous, remember, that past performance is not an indication of future profit. Financial markets are not to be trifled with. Price charts gyrate this way and that, often for unknown reasons. What we want to do is calculate proper probability based performance projections that we can apply in our decision making processes.

Confidence Intervals

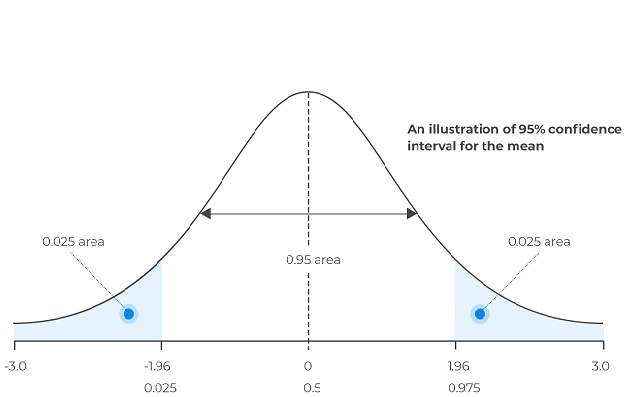
A confidence interval refers to the probability that a certain statistic of a collection of data or population will lie within some range for a proportion of time. They measure the degree of certainty by computing the probability that the levels calculated will contain the true statistic that is being estimated. Statisticians usually use confidence levels of 90% , up to 99%. These intervals can be calculated using various methods. In this article we will concentrate on some common boostrap techniques.

The bootstrap

Bootstrapping in statistics is a procedure in which  a collection of data is used to create numerous other new data sets, by randomly picking or selecting from the original. The new data sets will have the same members as the original but some members in the new datasets will be duplicates.

Original	Bootstrap1	Bootstrap2	Bootstrap3	Bootstrap4
A	A	A	A	B
B	A	B	B	B
C	B	B	B	C
D	C	D	C	D
E	D	E	C	E

The table above illustrates this better. The original column has the original dataset, the other columns represent datasets constructed from the original. As can be seen, the bootstrapped columns have one or more duplicates. By doing this many times over, we are able to generate lots of data that can represent samples that we cannot currently observe or would be unknown. We have already seen examples of the bootstrap applied to trading in the article "Applying the Monte Carlo method for optimizing trading strategies" .

Central to bootstrapping theory is that the original data set should be representative of a larger collection of data, the population, which cannot observe and are trying to model. Therefore when we create these bootstraps they become proxys of the unobservable collection. Statistical properties of these bootstraps along with the original sample can be used to draw conclusions of the unknown and/or unobservable population.

Bootstrapping confidence intervals

Three methods of boostrap confidence intervals  will  be demonstrated. Namely, the pivot method, percentile method and finally the bias corrected and accelerated method (bcd).

The pivot method involves the generation of numerous bootstraps which will be used to calculate  test statistics. A test statistic refers to whatever characteristic of the population we are trying to estimate, this could be its mean or median. The estimated bounds are then found by adjusting the value of the test statistic from the original dateset relative to what is needed to increase the expected value of the bootstrap samples up to the original.

The percentile method considers the distribution of the calculated test statistics from the bootstraped samples.This distribution is assumed to be similar to that of the unknown population. The bounds become the interval between the percentiles of the distribution of calculated test statistics obtained from the bootstraped samples.  

The bias corrected and accelerated method is little more sophisticated. After generating our bootstraps and calculating the test statistic for each. We compute the bias correction factor, which is the proportion of bootstrap estimates less than that of the original dataset. Then the acceleration factor is calculated by employing a method called a jackknife. This is another resampling method  used to estimate the degree to which the variance of the transformed test statistic depends on its value.

The percentile method is then used to calculate the lower and upper bounds which are  modified according to the bias correction and acceleration factors. The final confidence intervals are obtained from the modified values after being sorted.

Lets see how these techniques can be implemented in code.

The CBoostrap class

CBoostrap is a class that encapsulates the calculation of confidence intervals using the three bootstrap methods just described. With it, users will be able to calculate confidence intervals for multiple configurable probabilities and also be able to specify the number of bootstraps to generate.

#include<Math\Alglib\specialfunctions.mqh>
#include<Math\Stat\Math.mqh>
#include<UniformRandom.mqh>

The definition  of the class begins with the inclusion of some essential math utilities from the standard library.

//+------------------------------------------------------------------+
//|Function pointer                                                  |
//+------------------------------------------------------------------+
typedef double(*BootStrapFunction)(double &in[],int stop=-1);

The BootStrapFunction function pointer defines a  function signature to calculate the test statistic or population parameter.

//+------------------------------------------------------------------+
//|Boot strap types                                                  |
//+------------------------------------------------------------------+
enum ENUM_BOOSTRAP_TYPE
  {
   ENUM_BOOTSTRAP_PIVOT=0,
   ENUM_BOOTSTRAP_PERCENTILE,
   ENUM_BOOTSTRAP_BCA
  };

The ENUM_BOOSTRAP_TYPE enumeration facilitates the selection of a particular boostrap calculation method: ie Pivot,Percentile or BCA.

//+------------------------------------------------------------------+
//|Constructor                                                       |
//+------------------------------------------------------------------+
CBootstrap::CBootstrap(const ENUM_BOOSTRAP_TYPE boot_type,const uint nboot,const BootStrapFunction function,double &in_samples[])
  {
//--- set the function pointer
   m_function=function;
//--- optimistic initilization of flag
   m_initialized=true;
//--- set method of boostrap to be applied
   m_boot_type=boot_type;
//--- set number of boostrap iterations
   m_replications=nboot;
//---make sure there are at least 5 boostraps
   if(m_replications<5)
      m_initialized=false;
//--- initilize random number generator
   m_unifrand=new CUniFrand();
   if(m_unifrand!=NULL)
      m_unifrand.SetSeed(MathRand());
   else
      m_initialized=false;
//--- copy samples to internal buffer
   if(ArrayCopy(m_data,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- initialize shuffled buffer
   if(ArrayCopy(m_shuffled,in_samples)!=ArraySize(in_samples))
     {
      Print("Data Copy error ", GetLastError());
      m_initialized=false;
     }
//--- set memory for bootstrap calculations container
   if(ArrayResize(m_rep_cal,(int)m_replications)!=(int)m_replications)
     {
      Print("Memory allocation error ", GetLastError());
      m_initialized=false;
     }
//--- check function pointer
   if(m_function==NULL)
     {
      Print("Invalid function pointer");
      m_initialized=false;
     }
  }

CBoostrap is defined by a parametric constructor, whose input parameters determine the nature of a boostrap operation:

• boot_type  - sets the method of boostrap calculation

• nboot  - represents the number of desired boostrap samples that will be generated, it is recommended to have at least 100, though its more ideal to generate thousands in order to get robust results.

• function -  will point to a user supplied function definition for calculating the population parameter being estimated. The parameters of this function being an array of the data samples used to calculate  the test statistic. The default integer parameter of the function pointer defines the number of array members that will be used in the calculation.

• Lastly, the in_samples array is the container of data from which bootstraps will be generated. This same dataset and bootstrapped variations of it will be passed to the function pointer to calculate the test statistic.

//+------------------------------------------------------------------+
//| public method for calculating confidence intervals               |
//+------------------------------------------------------------------+
bool CBootstrap::CalculateConfidenceIntervals(double &in_out_conf[])
  {
//--- safety check
   if(!m_initialized)
     {
      ZeroMemory(in_out_conf);
      return m_initialized;
     }
//--- check input parameter values
   if(ArraySize(in_out_conf)<=0 ||
      in_out_conf[ArrayMaximum(in_out_conf)]>=1 ||
      in_out_conf[ArrayMinimum(in_out_conf)]<=0)
     {
      Print("Invalid input values for function ",__FUNCTION__,"\n All values should be probabilities between 0 and 1");
      return false;
     }
//--- do bootstrap based on chosen method
   switch(m_boot_type)
     {
      case ENUM_BOOTSTRAP_PIVOT:
         return pivot_boot(in_out_conf);
      case ENUM_BOOTSTRAP_PERCENTILE:
         return percentile_boot(in_out_conf);
      case ENUM_BOOTSTRAP_BCA:
         return bca_boot(in_out_conf);
      default:
         return false;
     }
//---
  }

One of only two publicly available methods for the class CalculateConfidenceIntervals() takes as input an array of probability values. As many as the user wants. These values define the  probabilities that the true parameter value lies within the calculated interval.

For example , in order to calculate confidence intervals whose probability is 90%, the user would supply an array with the value 0.9, then the method will return a pair of values. These returned values will be written to the same array supplied as input. For each single input array member the method will replace with a pair of values, the first of each pair being the lower bound of the interval and the second being the upper bound.

As stated its possible to  request more than one confidence interval with different probabilities. The output will arrange the bounds in order of the lowest probability to the highest specified as input.

Before demonstrating the use of the class we need to define what data we will use to measure the performance of a trading strategy. It is usually standard practice to classify strategy performance according to the return. To calculate this value the equity curve as well as the return series has to be examined.

Using the returns series of a strategy we can calculate various performance metrics. To keep things simple we will use the mean annualized return as the test statistic whose future value we want to estimate with a specified confidence.

Using this test statistic we can gauge the lowest average returns we can expect for a strategy. Also the upper confidence level provides a rough idea of how good performance will get if all goes well.

CReturns class

To collect the series of returns needed to approximate the future mean return, we will use the CReturns class. The class is adapted from code featured in the article "Mathematics in trading: Sharpe and Sortino ratios". A special feature of this version, is the ability to select the type of returns series to be used in performance calculations.

//+------------------------------------------------------------------+
//| Class for calculating Sharpe Ratio in the tester                 |
//+------------------------------------------------------------------+
class CReturns
  {
private:
   CArrayDouble*     m_all_bars_equity;
   CArrayDouble*     m_open_position_bars_equity;
   CArrayDouble*     m_trade_equity;

   CArrayDouble*     m_all_bars_returns;
   CArrayDouble*     m_open_position_bars_returns;
   CArrayDouble*     m_trade_returns;

   int               ProcessHistory(void);
   void              CalculateReturns(CArrayDouble &r,CArrayDouble &e);

public:
                     CReturns(void);
                    ~CReturns(void);

   void              OnNewTick(void);

   bool              GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[]);
   bool              GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[]);
  };

returns.mqh defines an enumeration that determines the type of returns series. ENUM_RETURNS_ALL_BARS defines a series of bar by bar returns for all bars of a test period. ENUM_RETURNS_POSITION_OPEN_BARS is series of returns that constitutes the bar by bar returns for those bars a position was open. ENUM_RETURNS_TRADES defines a returns series of completed trades only, no bar by bar information  is collected with this option.

//+------------------------------------------------------------------+
//| Enumeration specifying granularity of return                     |
//+------------------------------------------------------------------+
enum ENUM_RETURNS_TYPE
  {
   ENUM_RETURNS_ALL_BARS=0,//bar-by-bar returns for all bars
   ENUM_RETURNS_POSITION_OPEN_BARS,//bar-by-bar returns for bars with open trades
   ENUM_RETURNS_TRADES//trade returns
  };

Using the CReturns class the series of equity values defining the equity curve can be retrieved through the GetEquityCurve() method.

//+------------------------------------------------------------------+
//| get equity curve                                                 |
//+------------------------------------------------------------------+
bool CReturns::GetEquityCurve(const ENUM_RETURNS_TYPE return_type,double &out_equity[])
  {
   int m_counter=0;
   CArrayDouble *equity;
   ZeroMemory(out_equity);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         m_counter=m_all_bars_equity.Total();
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         m_counter=m_open_position_bars_equity.Total();
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         m_counter=(m_trade_equity.Total()>1)?m_trade_equity.Total():ProcessHistory();
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(m_counter < 2)
      return false;
//---
   if(ArraySize(out_equity)!=m_counter)
      if(ArrayResize(out_equity,equity.Total()) < m_counter)
         return false;
//---
   for(int i=0; i<equity.Total(); i++)
      out_equity[i]=equity[i];
//---
   return(true);
//---
  }

Similarly GetReturns() can output the series of returns. Both methods take as input, the specific returns series desired as well as an array where the values will be received.

//+------------------------------------------------------------------+
//|Gets the returns into array                                       |
//+------------------------------------------------------------------+
bool CReturns::GetReturns(const ENUM_RETURNS_TYPE return_type,double &out_returns[])
  {
//---
   CArrayDouble *returns,*equity;
   ZeroMemory(out_returns);
//---
   switch(return_type)
     {
      case ENUM_RETURNS_ALL_BARS:
         returns=m_all_bars_returns;
         equity=m_all_bars_equity;
         break;
      case ENUM_RETURNS_POSITION_OPEN_BARS:
         returns=m_open_position_bars_returns;
         equity=m_open_position_bars_equity;
         break;
      case ENUM_RETURNS_TRADES:
         if(m_trade_equity.Total()<2)
            ProcessHistory();
         returns=m_trade_returns;
         equity=m_trade_equity;
         break;
      default:
         return false;
     }
//--- if there are no bars, return 0
   if(equity.Total() < 2)
      return false;
//--- calculate average returns
   CalculateReturns(returns,equity);
//--- return the mean return
   if(returns.Total()<=0)
      return false;
//---
   if(ArraySize(out_returns)!=returns.Total())
      if(ArrayResize(out_returns,returns.Total()) < returns.Total())
         return false;
//---
   for(int i=0; i<returns.Total(); i++)
      out_returns[i]=returns[i];
//---
   return(true);
//---
  }

An example

The Expert Advisor code below shows how to use CReturns to collect the series of returns. In our example the returns series is saved to a binary file. Although its possible to do the confidence interval calculations using CBootstrap within OnTester. In our example, we instead will analyze this series from a separate program.

//+------------------------------------------------------------------+
//|                                           MovingAverage_Demo.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Returns.mqh>
#include <Bootstrap.mqh>
#include <Files\FileBin.mqh>
#include <Trade\Trade.mqh>

input double MaximumRisk        = 0.02;    // Maximum Risk in percentage
input double DecreaseFactor     = 3;       // Descrease factor
input int    MovingPeriod       = 12;      // Moving Average period
input int    MovingShift        = 6;       // Moving Average shift
input ENUM_RETURNS_TYPE rtypes  = ENUM_RETURNS_ALL_BARS; // return types to record
input uint BootStrapIterations  = 10000;
input double BootStrapConfidenceLevel = 0.975;
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input bool   SaveReturnsToFile = true;
input string ReturnsFileName = "MovingAverage_Demo";

//---
int    ExtHandle=0;
bool   ExtHedging=false;
CTrade ExtTrade;
CReturns ma_returns;
#define MA_MAGIC 1234501
//+------------------------------------------------------------------+
//| Calculate optimal lot size                                       |
//+------------------------------------------------------------------+
double TradeSizeOptimized(void)
  {
   double price=0.0;
   double margin=0.0;
//--- select lot size
   if(!SymbolInfoDouble(_Symbol,SYMBOL_ASK,price))
      return(0.0);
   if(!OrderCalcMargin(ORDER_TYPE_BUY,_Symbol,1.0,price,margin))
      return(0.0);
   if(margin<=0.0)
      return(0.0);

   double lot=NormalizeDouble(AccountInfoDouble(ACCOUNT_MARGIN_FREE)*MaximumRisk/margin,2);
//--- calculate number of losses orders without a break
   if(DecreaseFactor>0)
     {
      //--- select history for access
      HistorySelect(0,TimeCurrent());
      //---
      int    orders=HistoryDealsTotal();  // total history deals
      int    losses=0;                    // number of losses orders without a break

      for(int i=orders-1; i>=0; i--)
        {
         ulong ticket=HistoryDealGetTicket(i);
         if(ticket==0)
           {
            Print("HistoryDealGetTicket failed, no trade history");
            break;
           }
         //--- check symbol
         if(HistoryDealGetString(ticket,DEAL_SYMBOL)!=_Symbol)
            continue;
         //--- check Expert Magic number
         if(HistoryDealGetInteger(ticket,DEAL_MAGIC)!=MA_MAGIC)
            continue;
         //--- check profit
         double profit=HistoryDealGetDouble(ticket,DEAL_PROFIT);
         if(profit>0.0)
            break;
         if(profit<0.0)
            losses++;
        }
      //---
      if(losses>1)
         lot=NormalizeDouble(lot-lot*losses/DecreaseFactor,1);
     }
//--- normalize and check limits
   double stepvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);
   lot=stepvol*NormalizeDouble(lot/stepvol,0);

   double minvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
   if(lot<minvol)
      lot=minvol;

   double maxvol=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MAX);
   if(lot>maxvol)
      lot=maxvol;
//--- return trading volume
   return(lot);
  }
//+------------------------------------------------------------------+
//| Check for open position conditions                               |
//+------------------------------------------------------------------+
void CheckForOpen(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- check signals
   ENUM_ORDER_TYPE signal=WRONG_VALUE;

   if(rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=ORDER_TYPE_SELL;    // sell conditions
   else
     {
      if(rt[0].open<ma[0] && rt[0].close>ma[0])
         signal=ORDER_TYPE_BUY;  // buy conditions
     }
//--- additional checking
   if(signal!=WRONG_VALUE)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionOpen(_Symbol,signal,TradeSizeOptimized(),
                               SymbolInfoDouble(_Symbol,signal==ORDER_TYPE_SELL ? SYMBOL_BID:SYMBOL_ASK),
                               0,0);
     }
//---
  }
//+------------------------------------------------------------------+
//| Check for close position conditions                              |
//+------------------------------------------------------------------+
void CheckForClose(void)
  {
   MqlRates rt[2];
//--- go trading only for first ticks of new bar
   if(CopyRates(_Symbol,_Period,0,2,rt)!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(rt[1].tick_volume>1)
      return;
//--- get current Moving Average
   double   ma[1];
   if(CopyBuffer(ExtHandle,0,0,1,ma)!=1)
     {
      Print("CopyBuffer from iMA failed, no data");
      return;
     }
//--- positions already selected before
   bool signal=false;
   long type=PositionGetInteger(POSITION_TYPE);

   if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0])
      signal=true;
   if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0])
      signal=true;
//--- additional checking
   if(signal)
     {
      if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100)
         ExtTrade.PositionClose(_Symbol,3);
     }
//---
  }
//+------------------------------------------------------------------+
//| Position select depending on netting or hedging                  |
//+------------------------------------------------------------------+
bool SelectPosition()
  {
   bool res=false;
//--- check position in Hedging mode
   if(ExtHedging)
     {
      uint total=PositionsTotal();
      for(uint i=0; i<total; i++)
        {
         string position_symbol=PositionGetSymbol(i);
         if(_Symbol==position_symbol && MA_MAGIC==PositionGetInteger(POSITION_MAGIC))
           {
            res=true;
            break;
           }
        }
     }
//--- check position in Netting mode
   else
     {
      if(!PositionSelect(_Symbol))
         return(false);
      else
         return(PositionGetInteger(POSITION_MAGIC)==MA_MAGIC); //---check Magic number
     }
//--- result for Hedging mode
   return(res);
  }
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit(void)
  {
//--- prepare trade class to control positions if hedging mode is active
   ExtHedging=((ENUM_ACCOUNT_MARGIN_MODE)AccountInfoInteger(ACCOUNT_MARGIN_MODE)==ACCOUNT_MARGIN_MODE_RETAIL_HEDGING);
   ExtTrade.SetExpertMagicNumber(MA_MAGIC);
   ExtTrade.SetMarginMode();
   ExtTrade.SetTypeFillingBySymbol(Symbol());
//--- Moving Average indicator
   ExtHandle=iMA(_Symbol,_Period,MovingPeriod,MovingShift,MODE_SMA,PRICE_CLOSE);
   if(ExtHandle==INVALID_HANDLE)
     {
      printf("Error creating MA indicator");
      return(INIT_FAILED);
     }
//--- ok
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick(void)
  {
   ma_returns.OnNewTick();
//---
   if(SelectPosition())
      CheckForClose();
   else
      CheckForOpen();
//---
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Tester function                                                  |
//+------------------------------------------------------------------+
double OnTester()
  {
   double returns[],confidence[],params[];
   ArrayResize(confidence,1);
   confidence[0]=BootStrapConfidenceLevel;
//---
   double ret=0.0;
//---
   if(ma_returns.GetReturns(rtypes,returns))
     {
      CBootstrap minreturn(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,returns);

      if(minreturn.CalculateConfidenceIntervals(confidence))
        {
         ret=confidence[0];
         string fname=ReturnsFileName+"_"+_Symbol+".returns";
         CFileBin file;
         if(SaveReturnsToFile && file.Open(fname,FILE_WRITE|FILE_COMMON)!=INVALID_HANDLE)
            file.WriteDoubleArray(returns);

        }

     }
//---
   return(ret);
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }

A script reads the saved data and passes it to an instance of CBootstrap. The test statistic is calculated by the MeanReturns() function whose signature matches that of BootStrapFunction function pointer. Calling CalculateConfidenceIntervals() with an array with values 0.9, 0.95, 0.975, which corresponds to 90% , 95% and 97.5% confidence intervals.

//+------------------------------------------------------------------+
//|                                       ApproximateMeanReturns.mq5 |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Math.mqh>
#include<Files\FileBin.mqh>
#include<Bootstrap.mqh>
//--- input parameters
input string   FileName="MovingAverage_Demo_EURUSD.returns";//returns file name
input ENUM_BOOSTRAP_TYPE AppliedBoostrapMethod=ENUM_BOOTSTRAP_BCA;
input uint BootStrapIterations=10000;
input string BootStrapProbability="0.975,0.95,0.90";
//---
CBootstrap *meanreturns;
double logreturns[],bounds[],bootstraps[];
string sbounds[];
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int done=StringSplit(BootStrapProbability,StringGetCharacter(",",0),sbounds);
//---
   if(done)
     {
      ArrayResize(bounds,done);
      for(int i=0; i<done; i++)
         bounds[i]=StringToDouble(sbounds[i]);
      if(ArraySort(bounds))
         for(int i=0; i<done; i++)
            sbounds[i]=DoubleToString(bounds[i]);
     }
//---
   if(!done)
     {
      Print("error parsing inputs ", GetLastError());
      return;
     }
//---
   if(!LoadReturns(FileName,logreturns))
      return;
//---
   meanreturns=new CBootstrap(AppliedBoostrapMethod,BootStrapIterations,MeanReturns,logreturns);
//---
   if(meanreturns.CalculateConfidenceIntervals(bounds))
     {
      for(int i=0; i<done; i++)
         Print(EnumToString(AppliedBoostrapMethod)," ",sbounds[i],": ","(",bounds[i*2]," ",bounds[(i*2)+1],")");
     }
//---
   delete meanreturns;
  }
//+------------------------------------------------------------------+
//+------------------------------------------------------------------+
//| Load returns from file                                           |
//+------------------------------------------------------------------+
bool LoadReturns(const string fname,double &out_returns[])
  {
   CFileBin file;
//---
   if(file.Open(fname,FILE_READ|FILE_COMMON)==INVALID_HANDLE)
      return false;
//---
   if(!file.ReadDoubleArray(out_returns))
     {
      Print("File read error ",GetLastError());
      return false;
     }
//---
   return true;
  }
//+------------------------------------------------------------------+
//|the bootstrap function                                            |
//+------------------------------------------------------------------+
double MeanReturns(double &rets[], int upto=-1)
  {
   int stop=(upto<=0)?ArraySize(rets):upto;

   if(!stop)
     {
      Print("in danger of zero divide error ",__FUNCTION__);
      return 0;
     }

   double sum=0;
   for(int i=0; i<stop; i++)
      sum+=rets[i];

   sum/=double(stop);

   switch(Period())
     {
      case PERIOD_D1:
         sum*=252;
         return sum;
      case PERIOD_W1:
         sum*=52;
         return sum;
      case PERIOD_MN1:
         sum*=12;
         return sum;
      default:
         sum*=double(PeriodSeconds(PERIOD_D1) / PeriodSeconds());
         return sum*=252;
     }

  }
//+------------------------------------------------------------------+

Before looking at the final output of the calculated intervals, its always a good idea to take a peak at the distribution plot of the bootstrapped test statistics. This can be done by plotting the data accessed through GetBootStrapStatistics().

Looking at the Moving Average EA results. we see that OnTester returns  a negative number, indicating that future performance could worsen despite the positive results displayed by the single test. -0.12 is the worst case average return we can expect.  

The results at different Confidence intervals are shown below.

ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.90000000: (-0.07040966776550685 0.1134376873958945)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.95000000: (-0.09739322056041048 0.1397669758772337)
ApproximateMeanReturns (EURUSD,D1)      ENUM_BOOTSTRAP_BCA 0.97500000: (-0.12438450770122121 0.1619709975134838)

This example demonstrates calculation of projected probability based mean returns for the Moving Average EA. Its possible to use the same principle for other performance metrics as well. Although a word a caution is necessary. Ratio based performance metrics can be problematic. The reason for this, is because of the denominator in the calculation of the metric. If it becomes really small we end up with very large figures.

The best way to determine the suitability of using these methods to estimate future performance for a particular metric, is to study the distribution of the boostraped sample statistics. What we are looking out for are any heavy tails. Results obtained from distributions with heavy tails should be used with care.

Lets see an example of estimating a worst case sharpe ratio for the same EA.This is accomplished by rewriting the function passed to the function pointer parameter of the CBootstrap constructor.

The results from the test again indicate far worse performance relative to the single test result.

Conclusion

Knowing the range of performance we can expect in the future can help us to make better investment decisions with respect to strategy selection. Although the method demonstrated is based on textbook statistics users should be aware of the inherent limitations.

The computed confidence intervals are only as good as the data they are based on. If the samples used in the calculation  are inadequate , we end up in a classic garbage in garbage out scenario. Its always important to select appropriate samples that are representative of conditions likely to be encountered in the future.

FileName	Description
Mql5files\include\Bootstrap.mqh	contains the definition of the CBootstrap class
Mql5files\include\Returns.mqh	contains the definition of the CReturns class
Mql5files\include\UniformRandom.mqh	this is a class for generating uniformly distributed number between 0 and 1
Mql5files\scripts\ApproximateMeanReturns.mq5	Script that reads file save from the strategy tester and calculates confidence intervals of the project mean returns
Mql5files\experts\ MovingAverage_Demo.mq5	An expert advisor used to demonstrate the application of the CBootstrap and CReturns.