Quick n Dirty Frequency Response
- Indikatoren
- Safwan Rushdi Khalil Arekat
- Version: 1.2
- Aktualisiert: 17 Februar 2023
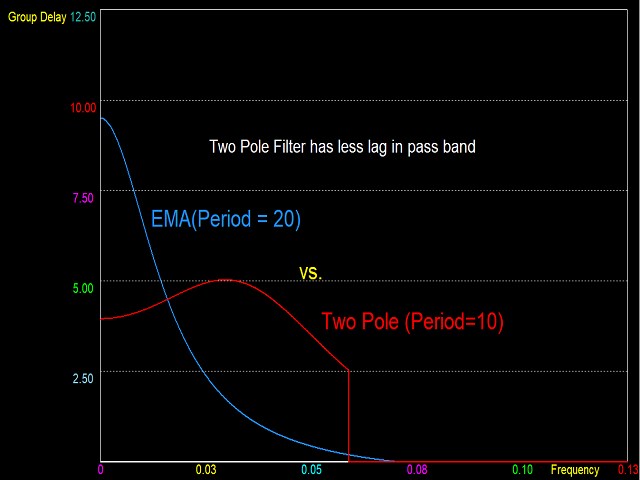
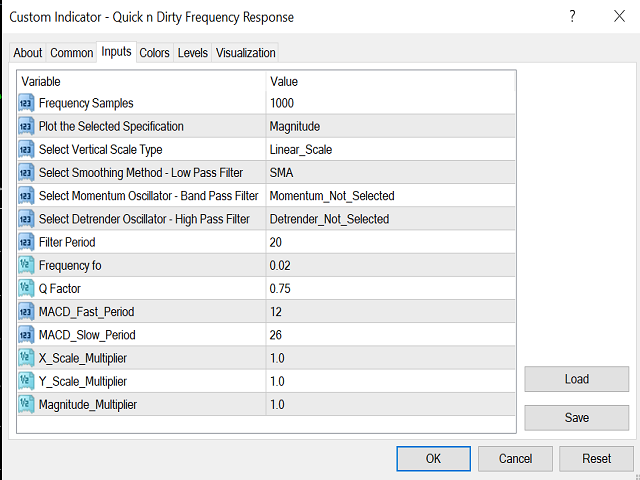
Dieser Indikator verarbeitet nicht die Daten des Kurscharts und liefert keine Handelssignale. Stattdessen handelt es sich um eine Anwendung zur Berechnung und Anzeige der Frequenzantwort vieler herkömmlicher Indikatoren. Gleitende Durchschnitte wie der SMA, der LWMA und der EMA sowie Oszillatoren wie der MACD, der CCI und der Awsome Osc haben alle die Form von digitalen Filtern. Elektronikingenieure verwenden eine spezielle Methode zur Charakterisierung der Leistung dieser Filter, indem sie ihren Frequenzgang untersuchen. Zwei wichtige Größen des Frequenzgangs sind der Amplitudengang und der Gruppenlaufzeitgang. Der Amplitudengang (auch Frequenzspektrum genannt) zeigt das Verhältnis zwischen dem Ausgang des Filters und dem Eingang des Filters bei verschiedenen Frequenzen. Die Gruppenverzögerung ist einfach eine schicke Bezeichnung für die Verzögerung des Ausgangs gegenüber dem Eingang bei verschiedenen Frequenzen (in Einheiten der Anzahl von Balken). Das Spielen mit meinem kostenlosen Indikator(Price Discret Fourier Transform Toy) ist ein guter Einstieg, um das Konzept der Frequenzen in einem digitalen Signal wie dem Preis zu verstehen.
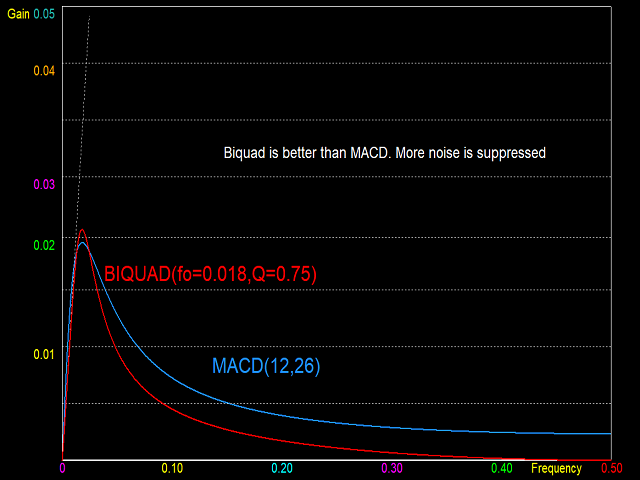
Technische Indikatoren, die digitalen Filtern ähneln, lassen sich je nach ihren Frequenzmerkmalen in drei Typen einteilen. Digitale Filter, die niedrige Frequenzen durchlassen, aber hohe Frequenzen unterdrücken (Low Pass Filter, LPF), fungieren als Preisglätter. Sie eliminieren hochfrequente Volatilität und verzerren den Trend. Die Amplitudenantwort eines LPF hat bei der Frequenz Null einen Wert von Eins oder einen Bereich niedriger Frequenzen (Durchlassbereich genannt). Dies sind die Frequenzen, die durchgelassen werden. Jenseits des Durchlassbereichs sinkt der Amplitudengang auf sehr niedrige Werte bei hohen Frequenzen, die durch das Filter unterdrückt werden (als Sperrbereich bezeichnet). Ein perfektes Filter hat einen sehr scharfen Übergang vom Durchlassbereich zum Sperrbereich. Unter den Glättungsarten in diesem Indikator bietet der "gefensterte Sinus" die beste Reaktion, aber dafür ist eine große Filterperiode erforderlich, was zu einer großen Verzögerung führt (versuchen Sie, fo=0,15 und Filterperiode=50 einzustellen). Beispiele für Indikatoren, die als Glätter fungieren, sind gleitende Durchschnitte und andere Filter, die hier vorgestellt wurden und in zukünftigen Indikatoren von diesem Entwickler vorgestellt werden sollen.
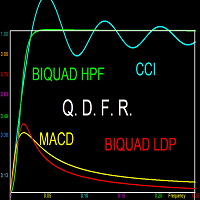
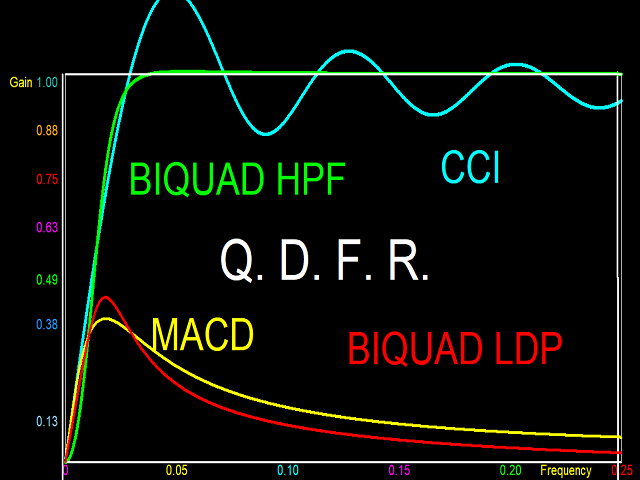
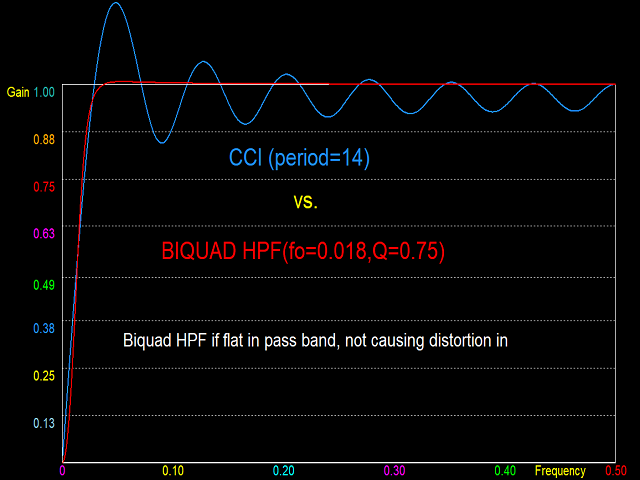
Digitale Filter, die hohe Frequenzen durchlassen, aber tiefe Frequenzen unterdrücken (High Pass Filter, HPF), fungieren als De-Trender. Sie eliminieren den niederfrequenten Trend und heben die zyklische Komponente und die Volatilität auf. Der Amplitudengang eines HPF hat einen Wert von Eins bei der maximalen Frequenz (0,5) oder einen Bereich hoher Frequenzen (Passband genannt). Dies sind die Frequenzen, die durchgelassen werden. Unterhalb des Durchlassbereichs sinkt der Amplitudengang auf sehr niedrige Werte bei niedrigen Frequenzen, die vom Filter unterdrückt werden (als Sperrbereich bezeichnet). Ein perfektes Filter hat einen sehr scharfen Übergang vom Durchlassbereich zum Sperrbereich. Beispiele für Indikatoren, die als HPF-Detrender fungieren, sind der CCI und der DPOsowie andere hier vorgestellte Filter, die in künftigen Indikatoren dieses Entwicklers vorgestellt werden sollen.
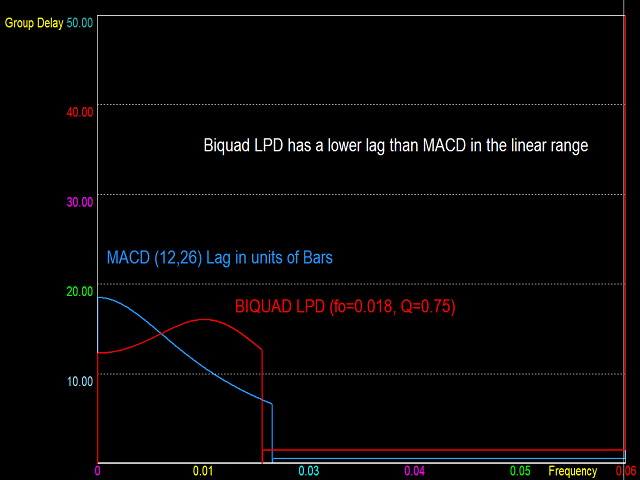
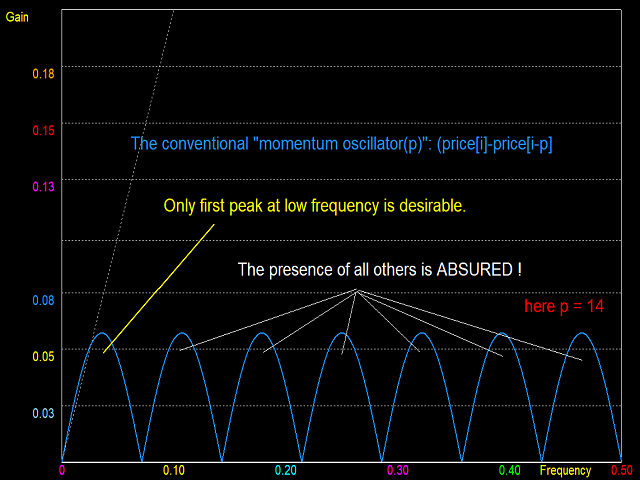
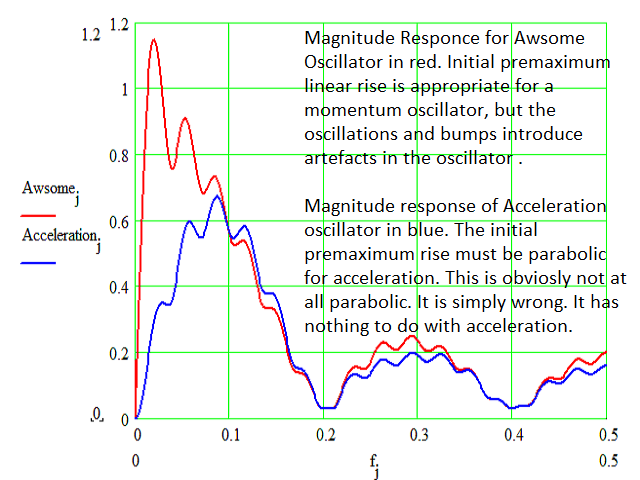
Momentum-Oszillatoren gehören zur dritten Klasse der digitalen Filter, den Bandpassfiltern (BPF). Diese haben zwei Sperrbereiche, einen bei niedriger und einen bei hoher Frequenz, und einen Durchlassbereich dazwischen. Auch hier hat ein perfekter BPF scharfe Übergänge zwischen Durchlass- und Sperrband. Ein Impulsoszillator zeichnet sich jedoch dadurch aus, dass er im Tiefpassbereich eine lineare Amplitudenantwort aufweist. Dies ermöglicht es dem Filter, bei niedrigen Frequenzen als Differenzierer zu wirken. Der Übergang zum hochfrequenten Sperrbereich sollte jedoch scharf sein. Der MACD erfüllt die Anforderungen an einen Impulsoszillator sehr gut. Bessere Momentum-Oszillatoren sind jedoch der Biquad Low Pass Differentiator (LPD) und der Wulf LPD. Weitere Informationen zu diesen Momentum-Oszillatoren werden in zukünftigen Indikatoren von diesem Entwickler bereitgestellt.
(Diese Beschreibung ist in Arbeit .... mehr Details werden bald enthalten sein)