Discrete Fourier Transform of Price

Dieser Indikator ist ein nützliches Instrument zur Visualisierung zyklischer Komponenten im Preis. Er berechnet die diskrete Fourier-Transformation (DFT) eines vom Benutzer ausgewählten Preisdiagrammsegments. Er zeigt die Zyklen, das Spektrum und das synthetisierte Signal in einem separaten Fenster an. Der Indikator ist nur als Lernwerkzeug gedacht und eignet sich nicht für die Bereitstellung tatsächlicher Handelssignale. Laden Sie die Datei herunter - sie ist ein kostenloses Spielzeug. Spielen Sie damit, um zu verstehen, wie Signale durch die Kontrolle ihrer zyklischen Komponenten transformiert werden können. Dies ist die wesentliche Operation, die von digitalen Filtern durchgeführt wird. Viele Standardindikatoren wie gleitende Durchschnitte und Oszillatoren (SMA, LWMA, EMA, MACD, CCI, DPO, AWSOME OSC und Momentum usw.) haben alle die Form solcher linearer digitaler Filter. Dieses Tool hilft, die Funktionsweise dieser Indikatoren zu veranschaulichen. Die Beschreibung enthält nur sehr wenige mathematische Gleichungen, da das Ziel darin besteht, sich auf einen konzeptionellen Rahmen und das Verständnis zu konzentrieren.

Beziehung zur elektronischen digitalen Signalverarbeitung (DSP): Wenn wir uns den Preis als ein Signal in einem digitalen elektronischen System vorstellen, ohne die Situation mit zu vielen technischen Details zu verkomplizieren, können wir den Preis als ein zeitdiskretes digitales Signal definieren, das einmal in sich wiederholenden periodischen linearen Intervallen abgetastet wird. Die beiden Hauptunterschiede zwischen dem Preis und dem elektronischen Digitalsignal sind: Erstens ist der Preis immer eine positiv definierte Größe, und zweitens wird das elektronische Signal in der Regel viel schneller abgetastet als der Preis (für Menschen, nicht für HFT-Systeme). So ist das digitale Preissignal beispielsweise der tägliche, stündliche oder viertelstündliche Schlusskurs, wie er üblicherweise dargestellt wird.

Bei der Betrachtung fast aller Preisdiagramme kann man feststellen, dass sich der Preis auf zwei leicht erkennbare Arten verändert: eine schnelle, sprunghafte Preisänderung zwischen aufeinanderfolgenden Zeiträumen und eine langsamere Veränderung der Gesamtpreiskurve über viele Zeiträume hinweg. In elektronischen Systemen bezeichnen wir die schnellen Veränderungen als "Rauschen" und die langsamere Veränderung als das eigentliche "Signal". In der Handelssprache werden diese als "Volatilität" bzw. "Trend" bezeichnet. Gibt es also einen "richtigen" Weg, diese beiden Merkmale zu entkoppeln, um den gewünschten Trend allein zu erhalten, der die längerfristige, nachhaltige Kursänderung anzeigt? Ein Ansatz ist die Anwendung der DFT.

Die diskrete Fourier-Transformation DFT (manchmal auch FFT genannt): Diese Methode ist eine der Techniken, die zur Analyse und Verarbeitung von diskreten Zeitsignalen in elektronischen Systemen verwendet werden (aber sie findet auch in vielen anderen Bereichen Anwendung), und sie ist nicht einmal die beste Technik, um dies in Schaltkreisen zu tun, aber sie ist einfach genug, um hier betrachtet zu werden. Wir werden nicht auf die langwierige Mathematik eingehen, sondern uns auf eine konzeptionelle Beschreibung konzentrieren, die Sie hoffentlich als ausreichend und zufriedenstellend empfinden werden.

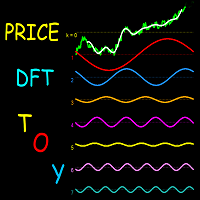
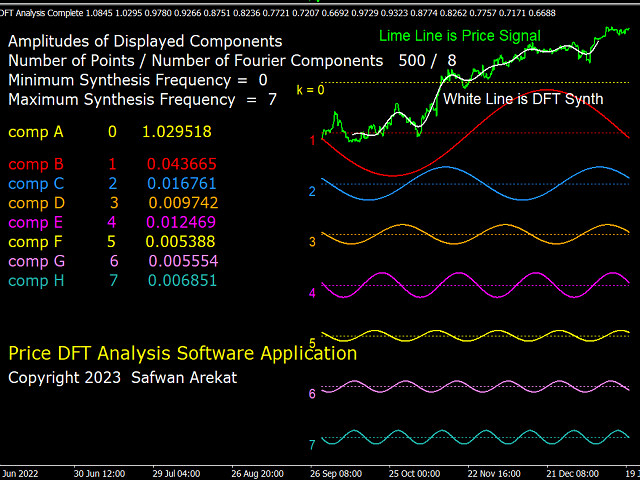
Kurze Beschreibung der DFT: Jedes digitale Signal (oder jede Zeitreihe) mit einer Länge von N Abtastwerten kann in N/2+1 sinusförmige Schwingungskomponenten (Zyklen) mit sequentiell zunehmender Periode (abnehmender Frequenz) "analysiert" werden. Die kleinste Periode ist das Doppelte der Abtastlänge (d. h. zwei Abtastungen), die größte Periode beträgt N/2 Abtastungen. Die Amplitude der Zyklen ist je nach der Form des Signals unterschiedlich. Das ursprüngliche Signal kann durch Addition aller N/2+1 solcher Zyklen "synthetisiert" werden. Wird bei der Synthese nur eine Untergruppe von Zyklen verwendet, so erhält man ein anderes Signal. Man kann also die Synthese entsprechend dem gewünschten Signal anpassen. Dies ist das Wesen der "Filterbanken"-Technik im DSP.

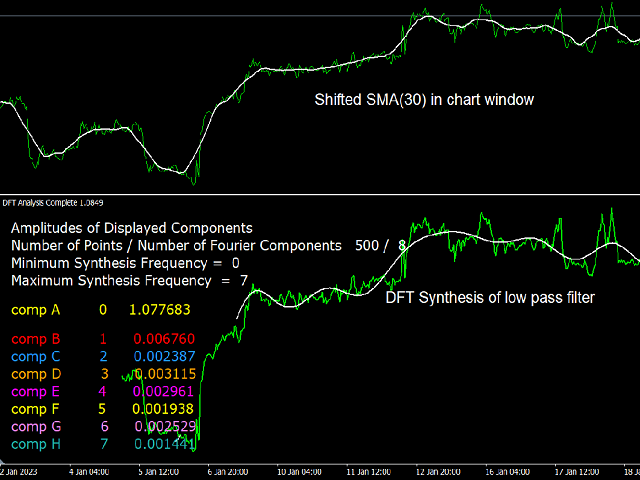
Ein Tiefpassfilter: Diesen Filter erhält man, indem man die Gleichstromkomponente (k=0) und einen Bereich niedriger Frequenzen bis zu einem bestimmten Grenzwert (z.B. k=0 bis k=7) verwendet. Dies hat den Effekt, dass alle höheren Frequenzen ausgelöscht werden, daher der Name Tiefpass. Da das Trendsignal mit niedrigen Frequenzen und die Volatilität mit hohen Frequenzen verbunden ist, entspricht das resultierende Signal einem entrauschten Trendsignal. Es handelt sich also um ein geglättetes Signal, dessen Wert und langsame Veränderung dem ursprünglichen Signal entsprechen.

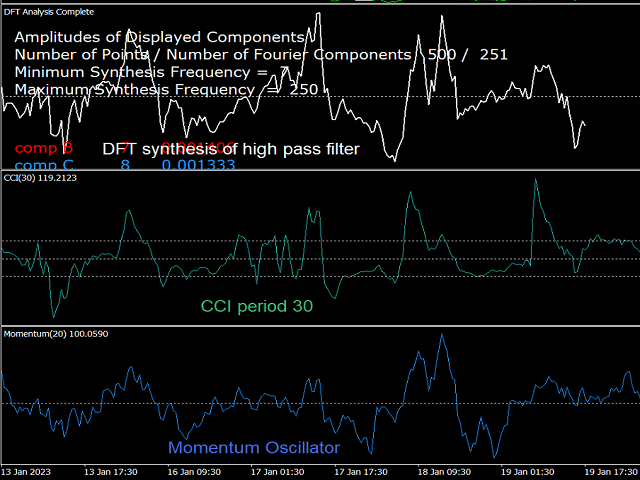
Ein Hochpassfilter: Dieses Filter erhält man, indem man alle Frequenzen oberhalb einer bestimmten Mindestpassfrequenz (zum Beispiel k=7 bis k=N/2) addiert. In jeder Situation, in der die Gleichstromkomponente (k=0) eliminiert wird, ist das resultierende Signal ein Oszillator. Bei einem Hochpass enthält der Oszillator nur die höheren Frequenzkomponenten, so dass die Trendkomponente eliminiert wird. Einige Standardindikatoren sind Hochpassfilter-Oszillatoren, wie z. B. der DPO- und der CCI-Oszillator, da ihr Signal durch Subtraktion eines gleitenden Durchschnitts vom ursprünglichen Signal gewonnen wird, wodurch die Gleichstromkomponente entfernt wird, während die hohen Frequenzen erhalten bleiben.

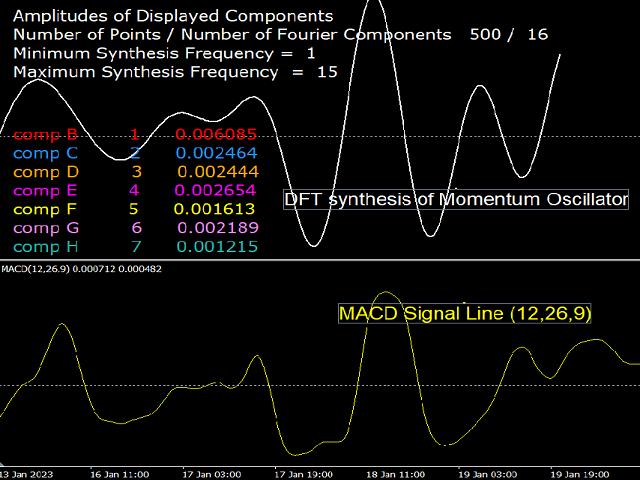
Ein Bandpassfilter: Dieser Filter verwendet einen Frequenzbereich, der die hohen und tiefen Frequenzen nicht enthält. Zum Beispiel k=7 bis k=30. Das resultierende Signal ist ein Oszillator, da das k=0 entfernt wurde. Viele Oszillatoren in der technischen Analyse haben die Form eines Bandpass-Oszillators, der bekannteste ist der MACD, der als Momentum-Oszillator fungieren soll. Aber der Momentum-Oszillator addiert die Frequenzen auf eine vorgeschriebene Weise, wie in anderen kostenlosen Indikatoren von diesem Entwickler erläutert wird.

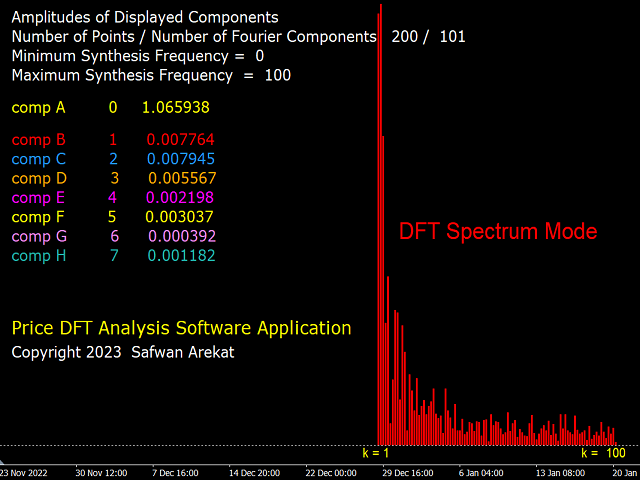
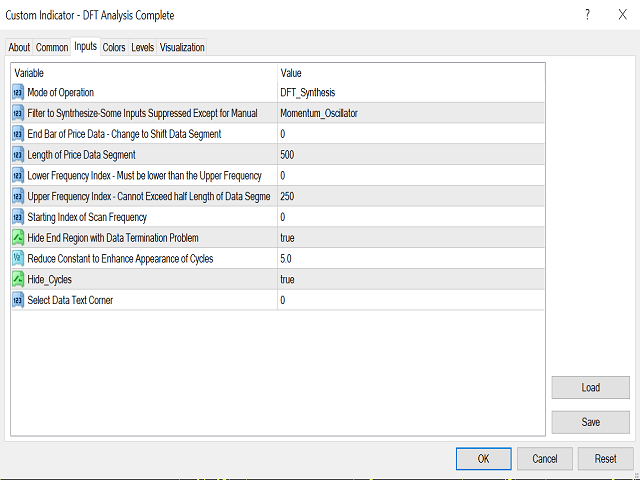
Die Steuerung des Indikators: Es wurde versucht, die Eingabeparameter einfach zu verstehen und zu verwenden. Es gibt drei Betriebsmodi: 1) Die DFT-Analyse, die die im Signal vorhandenen Zyklen anzeigt. 2) Der Synthesemodus, in dem die oben beschriebenen Filter angepasst werden können. 3) DFT-Spektrummodus, der die relative Stärke jedes Zyklus anzeigt. Der Benutzer kann mit diesem System "spielen", um ein besseres Verständnis der Bedeutung und Funktion digitaler Filter zu erlangen und um zu verstehen, wie sie mit vielen der häufig verwendeten technischen Indikatoren zusammenhängen.

Ich wünsche Ihnen viel Spaß beim Lernen und.... viel Spaß!