Maxim Romanov / Profile

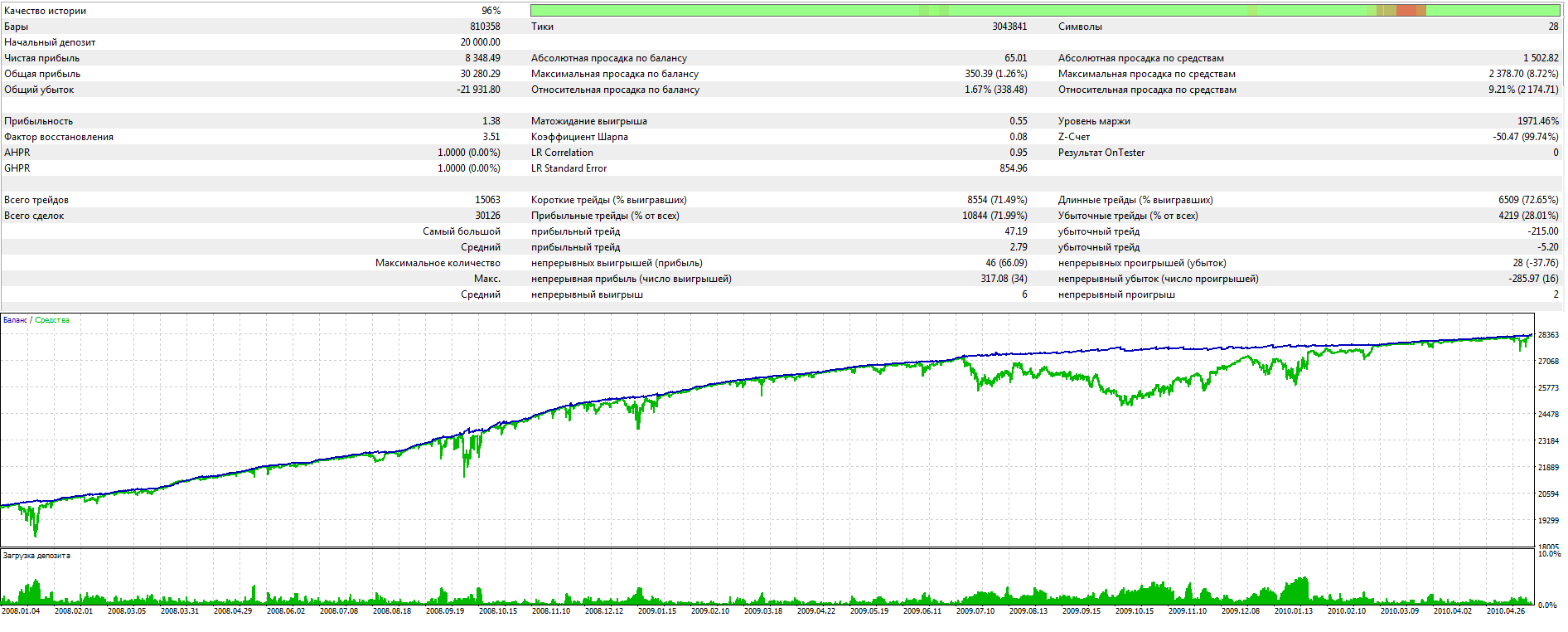
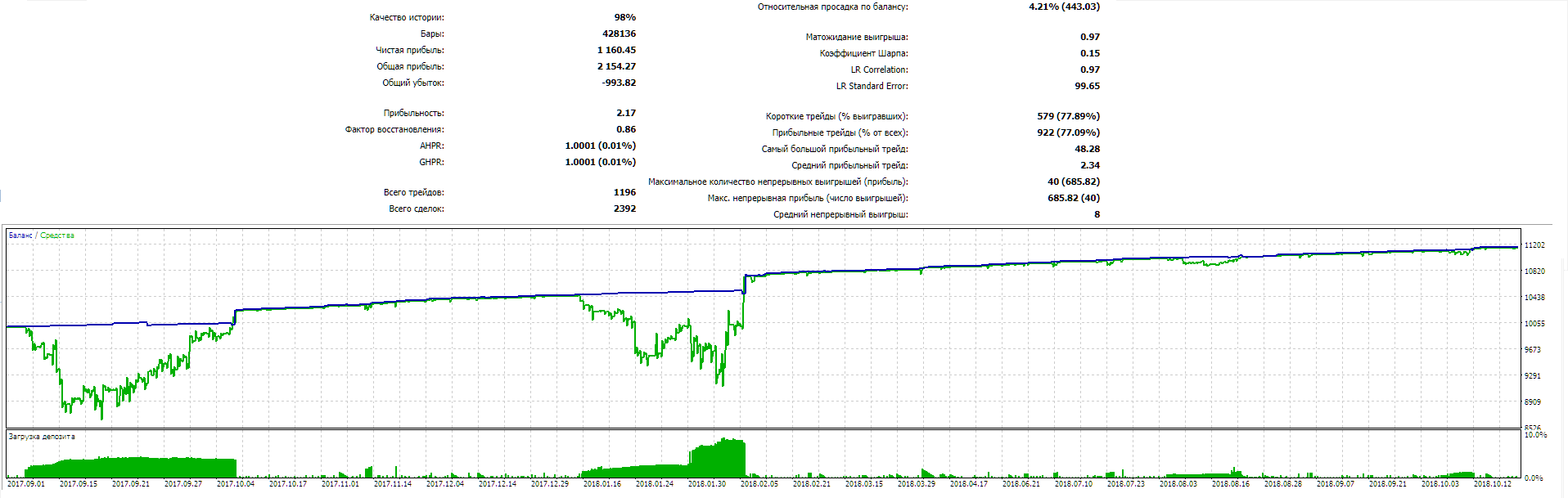
I continue filling the algorithm with the minimum necessary functionality and testing the results. The profitability is quite low but the articles demonstrate the model of the fully automated profitable trading on completely different instruments traded on fundamentally different markets.

It is impossible to get a truly stable algorithm if we use optimization based on historical data to select parameters. A stable algorithm should be aware of what parameters are needed when working on any trading instrument at any time. It should not forecast or guess, it should know for sure.

In this article, I will continue the development of the topic by improving the flexibility of the previously created algorithm. The algorithm became more stable with an increase in the number of candles in the analysis window or with an increase in the threshold percentage of the overweight of falling or growing candles. I had to make a compromise and set a larger sample size for analysis or a larger percentage of the prevailing candle excess.

In the upcoming series of articles, I will demonstrate the development of self-adapting algorithms considering most market factors, as well as show how to systematize these situations, describe them in logic and take them into account in your trading activity. I will start with a very simple algorithm that will gradually acquire theory and evolve into a very complex project.

The article considers the methodology for developing trading algorithms, in which a consistent scientific approach is used to analyze possible price patterns and to build trading algorithms based on these patterns. Development ideals are demonstrated using examples.

Traders often talk about trends and flats but very few of them really understand what a trend/flat really is and even fewer are able to clearly explain these concepts. Discussing these basic terms is often beset by a solid set of prejudices and misconceptions. However, if we want to make profit, we need to understand the mathematical and logical meaning of these concepts. In this article, I will take a closer look at the essence of trend and flat, as well as try to define whether the market structure is based on trend, flat or something else. I will also consider the most optimal strategies for making profit on trend and flat markets.

We usually analyze the market using candlesticks or bars that slice the price series into regular intervals. Doesn't such discretization method distort the real structure of market movements? Discretization of an audio signal at regular intervals is an acceptable solution because an audio signal is a function that changes over time. The signal itself is an amplitude which depends on time. This signal property is fundamental.