Algoritmi Genetici - È Facile!
397
0
Introduzione
L'algoritmo genetico ( AG ) si riferisce all'algoritmo euristico ( AE ) che fornisce una soluzione accettabile al problema nella maggior parte dei casi praticamente significativi, ma la correttezza delle decisioni non è stata dimostrata matematicamente ed è usata più spesso per i problemi, la cui soluzione analitica è molto difficile o addirittura impossibile.
Un classico esempio di un problema di questa classe (classe NP) è un "problema del venditore ambulante" (è uno dei più famosi problemi di ottimizzazione combinatoria). La sfida principale è trovare il percorso più vantaggioso che passa attraverso le città date almeno una volta e poi ritorna alla città iniziale). Ma nulla impedisce di usarli per compiti che si prestano alla formalizzazione.
Gli AE sono ampiamente utilizzati per risolvere problemi di elevata complessità computazionale, invece di passare attraverso tutte le opzioni, il che richiede una notevole quantità di tempo. Sono utilizzati nei campi dell'intelligenza artificiale, come il riconoscimento di modelli, nel software antivirus, nell'ingegneria, nei giochi per computer e in altre aree.
Va detto che MetaQuotes Software Corp. utilizza gli AG nei loro prodotti software di MetaTrader4 / 5. Conosciamo tutti lo strategy tester e quanto tempo e fatica possono essere risparmiati utilizzando un ottimizzatore di strategia integrato, in cui, proprio come con l'enumerazione diretta, è possibile ottimizzare con l'uso di AG. Inoltre, il tester MetaTrader 5 ci consente di utilizzare i criteri di ottimizzazione dell'utente. Forse il lettore sarà interessato a leggere gli articoli sugli AG e i vantaggi, forniti da AE, in contrasto con l'enumerazione diretta.
1. Un po' di storia
Poco più di un anno fa, avevo bisogno di un algoritmo di ottimizzazione per l'addestramento delle reti neurali. Dopo aver rapidamente familiarizzato con i vari algoritmi, ho scelto gli AG. Come risultato della mia ricerca di implementazioni già pronte, ho scoperto che quelle aperte per l'accesso pubblico, hanno limitazioni funzionali, come il numero di parametri che possono essere ottimizzati, o sono troppo "strettamente sintonizzate".
Avevo bisogno di uno strumento universalmente flessibile non solo per addestrare tutti i tipi di reti neurali, ma anche per risolvere in generale eventuali problemi di ottimizzazione. Dopo un lungo studio delle "creazioni genetiche" straniere, non ero ancora in grado di capire come funzionassero. La causa era uno stile di codice elaborato o la mia mancanza di esperienza nella programmazione o, forse, entrambe le cose.
Le principali difficoltà sono sorte dalla codifica dei geni in un codice binario e, quindi, dal lavorare con loro in questa forma. In entrambi i casi, è stato deciso di scrivere un algoritmo genetico da zero, concentrandosi sulla scalabilità e sulla facilità di modifica in futuro.
Non volevo occuparmi di trasformazione binaria e ho deciso di lavorare direttamente con i geni, cioè rappresentare il cromosoma con un insieme di geni sotto forma di numeri reali. È così che è apparso il codice per il mio algoritmo genetico, con una rappresentazione dei cromosomi per numeri reali. Più tardi ho capito che non avevo scoperto nulla di nuovo e che analoghi algoritmi genetici (si chiamano AG con codice reale) esistevano già da più di 15 anni, da quando sono uscite le prime pubblicazioni su di loro.
Lascio la mia visione di approccio all'implementazione e ai principi del funzionamento degli AG al lettore per giudicare, poiché si basa sull'esperienza personale del suo uso in problemi pratici.
2. Descrizione dell’AG
L’AG contiene i principi, presi in prestito dalla natura stessa. Questi sono i principi di ereditarietà e variabilità. L'ereditarietà è la capacità degli organismi di trasferire i loro tratti e le loro caratteristiche evolutive alla loro discendenza. Grazie a questa capacità, tutti gli esseri viventi si lasciano alle spalle le caratteristiche della loro specie nei loro figli.
La variabilità dei geni negli organismi viventi assicura la diversità genetica della popolazione ed è casuale, poiché la natura non ha modo di sapere in anticipo quali caratteristiche saranno preferibili in futuro (cambiamenti climatici, diminuzione / aumento di cibo, l'emergere di specie concorrenti, ecc.). Questa variabilità consente la comparsa di figli con nuovi tratti, che possono sopravvivere e lasciare i figli nelle nuove condizioni alterate dell'habitat.
In biologia, la variabilità, che è sorta a causa dell'emergere di mutazioni, è chiamata mutazionale; la variabilità dovuta a un'ulteriore combinazione incrociata di geni mediante accoppiamento, è chiamata combinazionale. Entrambi questi tipi di variazioni sono implementati nell'AG. Inoltre, c'è un'implementazione della mutagenesi, che imita il meccanismo naturale delle mutazioni (cambiamenti nella sequenza nucleotidica del DNA) - il naturale (spontaneo) e artificiale (indotto).
L'unità più semplice di trasferimento di informazioni sul criterio dell'algoritmo è il gene - unità strutturale e funzionale di ereditarietà che controlla lo sviluppo di un particolare tratto o proprietà. Chiameremo una variabile della funzione il gene. Il gene è rappresentato da un numero reale. L'insieme delle variabili geniche della funzione studiata è la caratteristica caratterizzante del cromosoma - .
Mettiamoci d'accordo per rappresentare il cromosoma sotto forma di colonna. Quindi il cromosoma per la funzione f (x) = x ^ 2, sarebbe simile a questo:
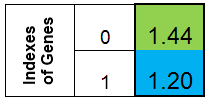
Figura 1. Cromosoma per la funzione f (x) = x ^ 2
dove 0-esimo indice - valore della funzione f (x), chiamato l'adattamento degli individui (chiameremo questa funzione la funzione fitness - FF , e il valore della funzione - VFF ). È conveniente memorizzare il cromosoma in un array unidimensionale. Questo è l’array double Chromosome [] .
Tutti gli esemplari della stessa era evolutiva sono combinati in una popolazione . Inoltre, la popolazione è arbitrariamente divisa in due colonie uguali: le colonie genitori e discendenti. Come risultato dell'incrocio delle specie parentali, che sono selezionate dall'intera popolazione, e di altri operatori dell’AG, c'è una colonia di nuovi figli, che è pari alla metà delle dimensioni della popolazione, che sostituisce la colonia di figli nella popolazione.
La popolazione totale di individui durante una ricerca per il minimo di funzione f (x) = x ^ 2 potrebbe essere simile a questa:
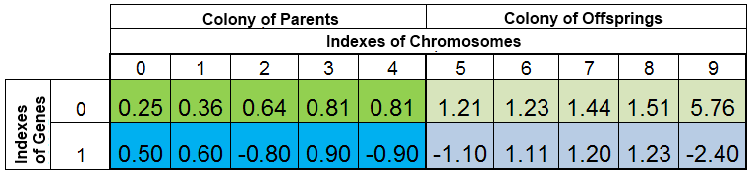
Figura 2. Popolazione totale di individui
La popolazione è ordinata per VFF. Qui, lo 0-esimo indice del cromosoma viene ripreso dal campione con il VFF più piccolo. La nuova discendenza sostituisce completamente solo gli individui nella colonia del discendente, mentre la colonia madre rimane intatta. Tuttavia, la colonia madre potrebbe non essere sempre completa, poiché gli esemplari duplicati vengono distrutti, quindi i nuovi figli riempiono i posti vacanti nella colonia madre e il resto viene collocato nella colonia del discendente.
In altre parole, la dimensione della popolazione è raramente costante e varia da epoca a epoca, quasi allo stesso modo che in natura. Ad esempio, la popolazione prima della riproduzione e dopo la riproduzione può assomigliare a questa:
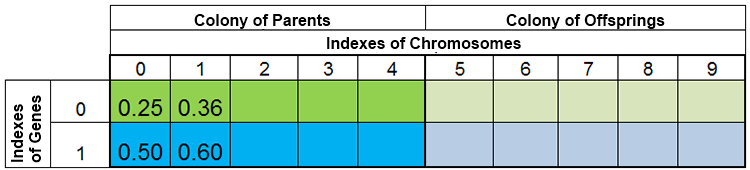
Figura 3. La popolazione prima della riproduzione
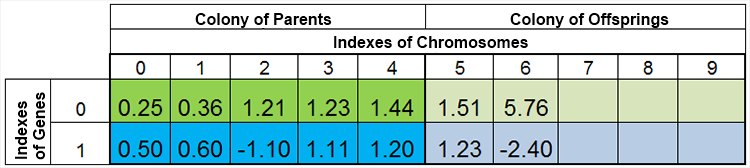
Figure 4. La popolazione dopo la riproduzione
Il meccanismo descritto del "mezzo" adempimento della popolazione da parte dei discendenti, così come la distruzione dei duplicati e il divieto di incrocio di individui con sé stessi, hanno un unico obiettivo: evitare l’”effetto collo di bottiglia" (un termine della biologia, che significa una riduzione del pool genico della popolazione a seguito di una riduzione critica dovuta a una serie di motivi diversi, che può portare a una completa estinzione di una specie, AG sta affrontando la fine della comparsa di cromosomi unici e "rimane bloccato" in uno degli estremi locali.)
3. Descrizione della funzione UGAlib
Algoritmo AG:- Creazione di una proto-popolazione. I geni sono generati in modo casuale all'interno di un determinato intervallo.
- Determinare l'idoneità di ogni individuo, o in altre parole, il calcolo del VFF.
- Preparare la popolazione per la riproduzione, dopo aver rimosso i duplicati cromosomici.
- Isolamento e conservazione del cromosoma di riferimento (con il miglior VFF).
- Operatori di UGA (selezione, accoppiamento, mutazione). Per ogni accoppiamento e mutazione, i nuovi genitori vengono selezionati ogni volta. Preparare la popolazione per la prossima era.
- Confronto dei geni dei figli migliori con i geni del cromosoma di riferimento. Se il cromosoma della migliore discendenza è migliore del cromosoma di riferimento, allora sostituire il cromosoma di riferimento.
Continuare dal paragrafo 5 fino a quando non ci sono più cromosomi, migliori di quelli di riferimento che appaiono, per un determinato numero di ere.
3.1. Variabili globali. Variabili globali
Annunciate le seguenti variabili a livello globale:
//----------------------Global variables----------------------------- double Chromosome[]; //A set of optimized arguments of the function - genes //(for example: the weight of the neuron network, etc.)- of the chromosome int ChromosomeCount =0; //Maximum possible amount of chromosomes in a colony int TotalOfChromosomesInHistory=0;//Total number of chromosomes in the history int ChrCountInHistory =0; //Number of unique chromosomes in the base chromosome int GeneCount =0; //Number of genes in the chromosome double RangeMinimum =0.0;//Minimum search range double RangeMaximum =0.0;//Maximum search range double Precision =0.0;//Search step int OptimizeMethod =0; //1-minimum, any other - maximum int FFNormalizeDigits =0; //Number of symbols after the comma in the fitness value int GeneNormalizeDigits =0; //Number of symbols after the comma in the genes value double Population [][1000]; //Population double Colony [][500]; //Offspring colony int PopulChromosCount =0; //The current number of chromosomes in a population int Epoch =0; //Number of epochs without progress int AmountStartsFF=0; //Number of launches of the fitness function //————————————————————————————————————————————————————————————————————————
3.2. UGA. La funzione principale degli AG
In realtà, la funzione principale degli AG, viene chiamata dal corpo del programma per eseguire i passaggi, elencati sopra, quindi non entreremo nel dettaglio.
Al completamento dell'algoritmo, ha registrato le seguenti informazioni nel registro:
- Quante epoche c'erano in totale (generazioni).
- Quanti difetti totali.
- Il numero di cromosomi unici.
- Il numero totale di lanci di FF.
- Il numero totale di cromosomi nella storia.
- Rapporto percentuale di duplicati per il numero totale di cromosomi nella storia.
- Miglior risultato.
"Il numero di cromosomi unici" e il "Numero totale di lanci di FF" - le stesse dimensioni, ma sono calcolati in modo diverso. Utilizzo per il controllo.
//———————————————————————————————————————————————————————————————————————— //Basic function UGA void UGA ( double ReplicationPortion, // Proportion of replication. double NMutationPortion, // Proportion of natural mutations. double ArtificialMutation, // Proportion of artificial mutations. double GenoMergingPortion, // Proportion of borrowed genes. double CrossingOverPortion, // Proportion of cross -over. //--- double ReplicationOffset, // Coefficient of displacement of interval borders double NMutationProbability // Probability of mutation of each gene in% ) { //generator reset takes place only once MathSrand((int)TimeLocal()); //-----------------------Variables------------------------------------- int chromos=0, gene =0;//indexes of chromosomes and genes int resetCounterFF =0;//counter of resets of "Epochs without progress" int currentEpoch =1;//number of the current epoch int SumOfCurrentEpoch=0;//sum of "Epochs without progress" int MinOfCurrentEpoch=Epoch;//minimum of "epochs without progress" int MaxOfCurrentEpoch=0;//maximum of "Epochs without progress" int epochGlob =0;//total number of epochs // Colony [number of traits(genes)][number of individuals in a colony] ArrayResize(Population,GeneCount+1); ArrayInitialize(Population,0.0); // Colony of offspring [number of traits(genes)][number of individuals in a colony] ArrayResize(Colony,GeneCount+1); ArrayInitialize(Colony,0.0); // Chromosome bank // [number of traits (genes)][number of chromosomes in the bank] double historyHromosomes[][100000]; ArrayResize(historyHromosomes,GeneCount+1); ArrayInitialize(historyHromosomes,0.0); //---------------------------------------------------------------------- //--------------Verification of the correctness of incoming parameters---------------- //...the number of chromosomes mus be less than 2 if(ChromosomeCount<=1) ChromosomeCount=2; if(ChromosomeCount>500) ChromosomeCount=500; //---------------------------------------------------------------------- //====================================================================== // 1) Create a proto- population —————1) ProtopopulationBuilding(); //====================================================================== // 2) Determine the fitness of each individual —————2) //For the 1st colony for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=0;chromos<ChromosomeCount;chromos++) Population[0][chromos]=Colony[0][chromos]; //For the 2nd colony for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos-ChromosomeCount]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) Population[0][chromos]=Colony[0][chromos-ChromosomeCount]; //====================================================================== // 3) Prepare the population for reproduction ————3) RemovalDuplicates(); //====================================================================== // 4) Extract the reference chromosome —————4) for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; //====================================================================== ServiceFunction(); //The main cycle The main cycle of the genetic algorithm from 5 to 6 while(currentEpoch<=Epoch) { //==================================================================== // 5) Operators of UGA —————5) CycleOfOperators ( historyHromosomes, //--- ReplicationPortion, //Proportion of replication. NMutationPortion, //Proportion of natural mutation. ArtificialMutation, //Proportion of artificial mutation. GenoMergingPortion, //Proportion of borrowed genes. CrossingOverPortion,//Proportion of cross- over. //--- ReplicationOffset, //Coefficient of displacement of interval borders NMutationProbability//Probability of mutation of each gene in % ); //==================================================================== // 6) Compare the genes of the best offspring with the genes of the reference chromosome. // If the chromosome of the best offspring is better that the reference chromosome, // replace the reference. —————6) //If the optimization mode is - minimization if(OptimizeMethod==1) { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]<Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Rest the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //If the optimization mode is - minimization else { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]>Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Reset the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //==================================================================== //Another epoch went by.... epochGlob++; } Print("Epochs went by=",epochGlob," Number of resets=",resetCounterFF); Print("MinOfCurrentEpoch",MinOfCurrentEpoch, " AverageOfCurrentEpoch",NormalizeDouble((double)SumOfCurrentEpoch/(double)resetCounterFF,2), " MaxOfCurrentEpoch",MaxOfCurrentEpoch); Print(ChrCountInHistory," - Unique chromosome"); Print(AmountStartsFF," - Total number of launches of FF"); Print(TotalOfChromosomesInHistory," - Total number of chromosomes in the history"); Print(NormalizeDouble(100.0-((double)ChrCountInHistory*100.0/(double)TotalOfChromosomesInHistory),2),"% of duplicates"); Print(Chromosome[0]," - best result"); } //————————————————————————————————————————————————————————————————————————
3.3. Creazione di una Proto-popolazione. Creazione di una proto-popolazione.
Poiché nella maggior parte dei problemi di ottimizzazione non c'è modo di sapere in anticipo dove si trovano gli argomenti della funzione sulla linea numerica, allora la migliore opzione ottimale è la generazione casuale all'interno di un determinato intervallo.
//———————————————————————————————————————————————————————————————————————— //Creating a proto- population void ProtopopulationBuilding() { PopulChromosCount=ChromosomeCount*2; //Fill up the population with chromosomes with random //...genes in the range between RangeMinimum...RangeMaximum for(int chromos=0;chromos<PopulChromosCount;chromos++) { //beginning with the 1st indexes (the 0 index is reserved for VFF) for(int gene=1;gene<=GeneCount;gene++) Population[gene][chromos]= NormalizeDouble(SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); TotalOfChromosomesInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.4. GetFitness. Ottenere la forma fisica
Esegue la funzione ottimizzata per ciascun cromosoma in ordine.
//------------------------------------------------ ------------------------ // Getting the fitness for each individual. void GetFitness ( double &historyHromosomes[][100000] ) { for(int chromos=0;chromos<ChromosomeCount;chromos++) CheckHistoryChromosomes(chromos,historyHromosomes); } //————————————————————————————————————————————————————————————————————————
3.5. CheckHistoryChromosomes. Verifica del cromosoma attraverso la base cromosomica
Il cromosoma di ogni individuo viene verificato attraverso la base - se l’FF è stato calcolato per esso, e se lo era, allora il VFF pronto viene preso dalla base, in caso contrario, allora viene chiamato l’FF. Pertanto, sono esclusi i calcoli ripetitivi ad alta intensità di risorse dell’FF.
//———————————————————————————————————————————————————————————————————————— //Verification of chromosome through the chromosome base. void CheckHistoryChromosomes ( int chromos, double &historyHromosomes[][100000] ) { //-----------------------Variables------------------------------------- int Ch1=0; //Index of the chromosome from the base int Ge =0; //Index of the gene int cnt=0; //Counter of unique genes. If at least one gene is different //- the chromosome is acknowledged unique //---------------------------------------------------------------------- //If at least one chromosome is stored in the base if(ChrCountInHistory>0) { //Enumerate the chromosomes in the base to find an identical one for(Ch1=0;Ch1<ChrCountInHistory && cnt<GeneCount;Ch1++) { cnt=0; //Compare the genes, while the gene index is less than the number of genes and while there are identical genes for(Ge=1;Ge<=GeneCount;Ge++) { if(Colony[Ge][chromos]!=historyHromosomes[Ge][Ch1]) break; cnt++; } } //If there are enough identical genes then we can use a ready- made solution from the base if(cnt==GeneCount) Colony[0][chromos]=historyHromosomes[0][Ch1-1]; //If there is no such chromosome, then we calculate the FF for it... else { FitnessFunction(chromos); //.. and if there is space in the base, then save it if(ChrCountInHistory<100000) { for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } } //If the base is empty, calculate the FF for it and save it in the base else { FitnessFunction(chromos); for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.6. CycleOfOperators. Ciclo di operatori in UGA
A questo punto, il destino della letteratura un'intera epoca di vita artificiale viene deciso - una nuova generazione nasce e muore. Questo accade nel modo seguente: due genitori vengono selezionati per l'accoppiamento o uno per commettere un atto di mutazioni su di lui/lei. Per ogni operatore di AG viene determinato un parametro appropriato. Di conseguenza otteniamo una discendenza. Questo viene ripetuto più e più volte, fino a quando la colonia discendente viene riempita completamente. Quindi la colonia di discendenti viene lasciata uscire nell'habitat, in modo che ogni individuo possa dimostrarsi come potrebbe e calcoliamo il VFF.
Dopo essere stata testata da "tubi di fuoco, acqua e rame", la colonia di discendenti viene collocata nella popolazione. Il prossimo passo nell'evoluzione artificiale sarà il sacro omicidio dei cloni, al fine di prevenire l'esaurimento del "sangue" nelle generazioni future e la successiva classifica della popolazione rinnovata, per il grado di forma fisica.
//———————————————————————————————————————————————————————————————————————— //Cycle of operators of UGA void CycleOfOperators ( double &historyHromosomes[][100000], //--- double ReplicationPortion, //Proportion of replications. double NMutationPortion, //Proportion of natural mutations. double ArtificialMutation, //Proportion of artificial mutations. double GenoMergingPortion, //Portion of borrowed genes. double CrossingOverPortion,//Proportion of cross-over. //--- double ReplicationOffset, //Coefficient of displacement of interval borders double NMutationProbability//Probability of mutation of each gene in % ) { //-----------------------Variables------------------------------------- double child[]; ArrayResize (child,GeneCount+1); ArrayInitialize(child,0.0); int gene=0,chromos=0, border=0; int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,6); ArrayInitialize(fit,0.0); //Counter of planting spots in a new population. int T=0; //---------------------------------------------------------------------- //Set a portion of operators of UGA double portion[6]; portion[0]=ReplicationPortion; //Proportion of replications. portion[1]=NMutationPortion; //Proportion of natural mutations. portion[2]=ArtificialMutation; //Proportion of artificial mutations. portion[3]=GenoMergingPortion; //Proportion of borrowed genes. portion[4]=CrossingOverPortion;//Proportion of cross- overs. portion[5]=0.0; //------------------------Cycle of operators of UGA--------- //Fill up the new colony with offspring while(T<ChromosomeCount) { //============================ for(i=0;i<6;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(portion[i]-portion[5]); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[4][1]); for(u=0;u<5;u++) { if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; } //============================ switch(u) { //--------------------- case 0: //------------------------Replication-------------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { Replication(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 1: //---------------------Natural mutation------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { NaturalMutation(child,NMutationProbability); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 2: //----------------------Artificial mutation----------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { ArtificialMutation(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast-forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 3: //-------------The creation of an individual with borrowed genes----------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { GenoMerging(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One space is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- default: //---------------------------Crossing-Over--------------------------- //If there is place in the new colony, create a new individual if(T<ChromosomeCount) { CrossingOver(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- } }//End of the cycle operators of UGA-- //Determine the fitness of each individual in the colony of offspring GetFitness(historyHromosomes); //Settle the offspring into the main population if(PopulChromosCount>=ChromosomeCount) { border=ChromosomeCount; PopulChromosCount=ChromosomeCount*2; } else { border=PopulChromosCount; PopulChromosCount+=ChromosomeCount; } for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=0;gene<=GeneCount;gene++) Population[gene][chromos+border]=Colony[gene][chromos]; //Prepare the population for the next reproduction RemovalDuplicates(); }//the end of the function //————————————————————————————————————————————————————————————————————————
3.7. Replica. Replica
L'operatore è più vicino al fenomeno naturale, che in biologia è chiamato - replicazione del DNA, anche se, in sostanza, non è la stessa cosa. Ma dal momento che non ho trovato alcun equivalente, più vicino a questo in natura, ho deciso di mantenere questo titolo.
La replicazione è l'operatore genetico più importante, che genera nuovi geni, mentre trasmette i tratti dei cromosomi parentali. L'operatore principale, garantendo la convergenza dell'algoritmo. L’AG può funzionare solo con esso senza l'uso di altri operatori, ma in questo caso il numero di lanci FF sarebbe molto maggiore.
Considerare il principio dell'operatore di Replica. Usiamo due cromosomi parentali. Il nuovo gene della discendenza è un numero casuale dall'intervallo
[C1-((C2-C1)*ReplicationOffset),C2+((C2-C1)*ReplicationOffset)]
dove C1 e C2 geni parentali ReplicationOffset - Coefficiente di spostamento dei bordi dell'intervallo [C1, C2] .
Ad esempio, dall'individuo paterno (blu) e dall'individuo materno (rosa) può essere creato un figlio (verde):
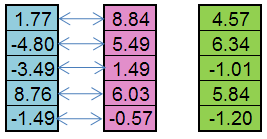
Figura 5. Il principio del lavoro di Replica dell'operatore
Graficamente, la probabilità del gene della discendenza può essere riassunta:
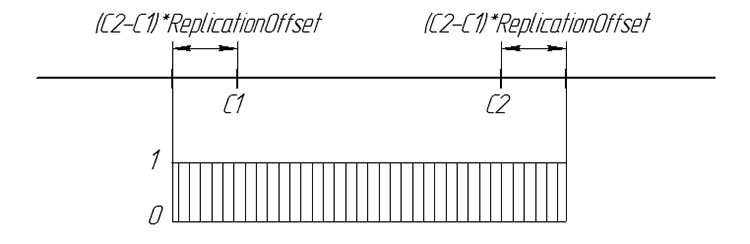
Figura 6. La probabilità della comparsa del gene della discendenza su una linea numerica
Gli altri geni della discendenza sono generati allo stesso modo.
//------------------------------------------------ ------------------------ // Replication void Replication ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- SelectTwoParents(address_mama,address_papa); //-------------------Cycle of gene enumeration-------------------------------- for(int i=1;i<=GeneCount;i++) { //----figure out where the father and mother came from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search had not gone over the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if we С1>C2, swi if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of the created gene Minimum = C1-((C2-C1)*ReplicationOffset); Maximum = C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search has not gone over the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- temp=RNDfromCI(Minimum,Maximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } //————————————————————————————————————————————————————————————————————————3.8. NaturalMutation. Mutazione naturale
Le mutazioni si verificano costantemente nel corso dei processi che si verificano nelle cellule viventi e servono come materiale per la selezione naturale. Sorgono spontaneamente per tutta la vita dell'organismo nelle sue normali condizioni di habitat, con una frequenza di una volta ogni 10 ^ 10 generazioni cellulari.
Noi - i ricercatori curiosi, non abbiamo necessariamente bisogno di aderire all'ordine naturale e aspettare così a lungo per la prossima mutazione del gene. Il parametro NMutationProbability, che è espresso in percentuale e determina la probabilità di mutazione per ciascun gene nel cromosoma, ci aiuterà a farlo.
Nell'operatore NaturalMutation , la mutazione consiste nella generazione di un gene casuale nell'intervallo [RangeMinimum, RangeMaximum] . NMutationProbability = 100% significherebbe una mutazione al 100% di tutti i geni nel cromosoma e NMutationProbability = 0% - completa assenza di mutazioni. L'ultima opzione non è adatta ad essere utilizzata in problemi pratici.
//------------------------------------------------ ------------------------ // The natural mutation. void NaturalMutation ( double &child[], double NMutationProbability ) { //-----------------------Variables------------------------------------- int address=0; double prob=0.0; //---------------------------------------------------------------------- if(NMutationProbability<0.0) prob=0.0; if(NMutationProbability>100.0) prob=100.0; //-----------------Parent selection------------------------ SelectOneParent(address); //--------------------------------------- for(int i=1;i<=GeneCount;i++) if(RNDfromCI(0.0,100.0)<prob) child[i]=NormalizeDouble( SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits ); } //————————————————————————————————————————————————————————————————————————
3.9. ArtificialMutation. Mutazione artificiale
Il compito principale dell'operatore - è la generazione di sangue "fresco". Usiamo due genitori e i geni della discendenza sono selezionati dagli spazi, non allocati dai geni genitori, sulla linea numerica. Protegge l’AG dal rimanere bloccato in uno degli estremi locali. In proporzione maggiore, rispetto ad altri operatori, accelera la convergenza, oppure rallenta, aumentando il numero di lanci di FF.
Proprio come nella replicazione, usiamo due cromosomi parentali. Ma il compito dell'operatore ArtificialMutation non è quello di trasmettere i tratti genitoriali alla discendenza, bensì di rendere il figlio diverso da loro. Pertanto, essendo un completo opposto, usando lo stesso coefficiente di spostamento del bordo dell'intervallo, ma i geni sono generati al di fuori dell'intervallo che sarebbe stato preso dalla replicazione. Il nuovo gene della discendenza è un numero casuale dagli intervalli [RangeMinimum, C1-(C2-C1) * ReplicationOffset] e [C2 + (C2-C1) * ReplicationOffset, RangeMaximum]
Graficamente, la probabilità di un gene nella discendenza ReplicationOffset = 0,25 può essere rappresentata come:
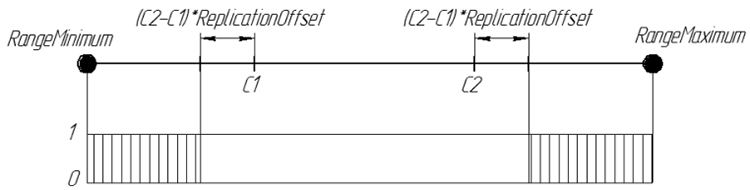
Figura 7. La probabilità di un gene nel discendente ReplicationOffset = 0,25 sull'intervallo di linea reale [RangeMinimum; RangeMaximum]
//———————————————————————————————————————————————————————————————————————— //Artificial mutation. void ArtificialMutation ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0,p=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //-------------------Cycle of genes enumeration------------------------------ for(int i=1;i<=GeneCount;i++) { //----determine where the mother and father are from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search doesn't go beyond the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if С1>C2, we change their places if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of creating the new gene Minimum=C1-((C2-C1)*ReplicationOffset); Maximum=C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search doesn't go beyond the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- p=MathRand(); if(p<16383.5) { temp=RNDfromCI(RangeMinimum,Minimum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } else { temp=RNDfromCI(Maximum,RangeMaximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } } //————————————————————————————————————————————————————————————————————————
3.10 GenoMerging. Geni in prestito
L'operatore AG dato non ha un equivalente naturale. È, infatti, difficile immaginare come questo meraviglioso meccanismo funzionerebbe negli organismi viventi. Tuttavia, ha una notevole proprietà di trasferire geni da un numero di genitori (il numero di genitori è uguale al numero di geni) alla discendenza. L'operatore non genera nuovi geni ed è un meccanismo di ricerca combinatoria.
Funziona così: per il primo gene della discendenza viene selezionato un genitore e il primo gene viene preso da lui, quindi, per il secondo gene, viene selezionato un secondo genitore e il gene viene prelevato da lui, ecc. È consigliabile applicarlo se il numero di geni è più di uno. Altrimenti, dovrebbe essere disabilitato, poiché l'operatore genererà duplicati dei cromosomi
//———————————————————————————————————————————————————————————————————————— //Borrowing genes. void GenoMerging ( double &child[] ) { //-----------------------Variables------------------------------------- int address=0; //---------------------------------------------------------------------- for(int i=1;i<=GeneCount;i++) { //-----------------Selecting parents------------------------ SelectOneParent(address); //-------------------------------------------------------- child[i]=Population[i][address]; } } //————————————————————————————————————————————————————————————————————————
3.11. CrossingOver. Crossing-over
Crossing-over (noto anche in biologia come crossing) - è un fenomeno di scambio di sezioni di cromosomi. Proprio come in GenoMerging, questo è un meccanismo di ricerca combinatoria.
Vengono selezionati due cromosomi parentali. Entrambi sono "tagliati" in un posto casuale. Il cromosoma della discendenza sarà costituito da parti di cromosomi parentali.
È più facile illustrare questo meccanismo in un'immagine:
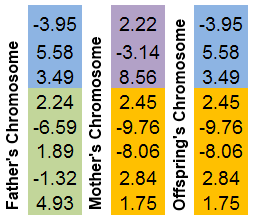
Figura 8. Il meccanismo di scambio delle parti cromosomiche
È consigliabile applicarlo se il numero di geni è più di uno. Altrimenti, dovrebbe essere disabilitato, poiché l'operatore genererà duplicati dei cromosomi
//———————————————————————————————————————————————————————————————————————— //Crossing-over. void CrossingOver ( double &child[] ) { //-----------------------Variables------------------------------------- int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //Determine the breakage point int address_of_gene=(int)MathFloor((GeneCount-1)*(MathRand()/32767.5)); for(int i=1;i<=GeneCount;i++) { //----copy the mother's genes-------- if(i<=address_of_gene+1) child[i]=Population[i][address_mama]; //----copy the father's genes-------- else child[i]=Population[i][address_papa]; } } //————————————————————————————————————————————————————————————————————————
3.12. SelectTwoParents. La selezione di due genitori
Per prevenire l'esaurimento del pool genico, c'è il divieto di incrocio con sé stessi. Dieci tentativi sono fatti per trovare genitori diversi e se non riusciamo a trovare una coppia, permettiamo l'incrocio con sé stessi. Fondamentalmente, otteniamo una copia dello stesso campione.
Da un lato, la probabilità di clonare individui diminuisce, dall'altro - la circolarità della ricerca è impedita, poiché può sorgere una situazione, in cui sarebbe praticamente impossibile farlo (scegliere genitori diversi) in un numero ragionevole di passaggi.
Utilizzato negli operatori Replication, ArtificialMutation e CrossingOver.
//———————————————————————————————————————————————————————————————————————— //Selection of two parents. void SelectTwoParents ( int &address_mama, int &address_papa ) { //-----------------------Variables------------------------------------- int cnt=1; address_mama=0;//address of the mother individual in a population address_papa=0;//address of the father individual in a population //---------------------------------------------------------------------- //----------------------------Selection of parents-------------------------- //Ten attempts to chose different parents. while(cnt<=10) { //For the mother individual address_mama=NaturalSelection(); //For the father individual address_papa=NaturalSelection(); if(address_mama!=address_papa) break; } //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.13. SelectOneParent. La selezione di un genitore
Qui tutto è semplice: un genitore viene selezionato dalla popolazione.
Utilizzato negli operatori NaturalMutation e GenoMerging.
//———————————————————————————————————————————————————————————————————————— //Selection of one parent. void SelectOneParent ( int &address//address of the parent individual in the population ) { //-----------------------Variables------------------------------------- address=0; //---------------------------------------------------------------------- //----------------------------Selecting a parent-------------------------- address=NaturalSelection(); //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.14. NaturalSelection. Selezione naturale
Selezione naturale - il processo che porta alla sopravvivenza e alla riproduzione preferenziale degli individui meglio adattati a queste condizioni ambientali, in possesso di caratteri ereditari utili.
L'operatore è simile all'operatore tradizionale "Roulette" ( Roulette-wheel selection - Selezione di individui con n "lanci" della roulette. La ruota della roulette contiene un settore per ogni membro della popolazione. La dimensione dell'i-esimo settore è proporzionale al corrispondente valore di fitness), ma presenta differenze significative. Tiene conto della posizione degli individui, rispetto a quelli più e meno adatti. Inoltre, anche un individuo che ha i geni peggiori, ha la possibilità di lasciare una discendenza. Questo è giusto, non è vero? Anche se non si tratta di giustizia, ma del fatto che in natura, tutti gli individui hanno l'opportunità di lasciare una discendenza.
Ad esempio, prendi 10 persone, con il seguente VFF nel problema di massimizzazione: 256, 128, 64, 32, 16, 8, 4, 2, 0, -1 - dove i valori più grandi corrispondono a una migliore forma fisica. Questo esempio è preso in modo che potessimo vedere che la "distanza" tra individui vicini è 2 volte più grande rispetto ai due individui precedenti. Tuttavia, sul grafico a torta, la probabilità che ogni individuo lasci una discendenza è la seguente:
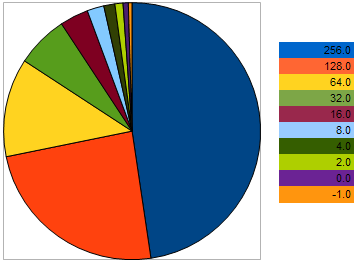
Figura 9. Il grafico delle probabilità di selezione degli individui genitori
dimostra che con l'approccio degli individui al peggio, le loro possibilità peggiorano. Al contrario, più l'individuo si avvicina al campione migliore, maggiori sono le possibilità di riproduzione che ha.
Figura 10. Il grafico delle probabilità di selezione degli individui genitori
//———————————————————————————————————————————————————————————————————————— //Natural selection. int NaturalSelection() { //-----------------------Variables------------------------------------- int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,PopulChromosCount); ArrayInitialize(fit,0.0); double delta=(Population[0][0]-Population[0][PopulChromosCount-1])*0.01-Population[0][PopulChromosCount-1]; //---------------------------------------------------------------------- for(i=0;i<PopulChromosCount;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(Population[0][i]+delta); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[PopulChromosCount-1][1]); for(u=0;u<PopulChromosCount;u++) if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; return(u); } //————————————————————————————————————————————————————————————————————————
3.15. RemovalDuplicates. Eliminazione dei duplicati
La funzione rimuove i cromosomi duplicati nella popolazione e i restanti cromosomi unici (unici per la popolazione dell'epoca attuale) sono ordinati in ordine dal VFF, determinato dal tipo di ottimizzazione, cioè decrescente o crescente.
//———————————————————————————————————————————————————————————————————————— //Removing duplicates sorted by VFF void RemovalDuplicates() { //-----------------------Variables------------------------------------- int chromosomeUnique[1000];//Array stores the unique trait //of each chromosome: 0-duplicate, 1-unique ArrayInitialize(chromosomeUnique,1); //Assume that there are no duplicates double PopulationTemp[][1000]; ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Ge =0; //Index of the gene int Ch =0; //Index of the chromosome int Ch2=0; //Index of the second chromosome int cnt=0; //Counter //---------------------------------------------------------------------- //----------------------Remove duplicates---------------------------1 //Chose the first from the pair for comparison... for(Ch=0;Ch<PopulChromosCount;Ch++) { //If it's not a duplicate... if(chromosomeUnique[Ch]!=0) { //Chose the second from the pair... for(Ch2=0;Ch2<PopulChromosCount;Ch2++) { if(Ch!=Ch2 && chromosomeUnique[Ch2]!=0) { //Zeroize the counter of identical genes cnt=0; //Compare the genes. while there are identical genes present for(Ge=1;Ge<=GeneCount;Ge++) { if(Population[Ge][Ch]!=Population[Ge][Ch2]) break; else cnt++; } //If there are the same amount of identical genes as total genes //..the chromosome is considered a duplicate if(cnt==GeneCount) chromosomeUnique[Ch2]=0; } } } } //The counter calculates the number of unique chromosomes cnt=0; //Copy the unique chromosomes into a temporary array for(Ch=0;Ch<PopulChromosCount;Ch++) { //If the chromosome is unique, copy it, if not, go to the next if(chromosomeUnique[Ch]==1) { for(Ge=0;Ge<=GeneCount;Ge++) PopulationTemp[Ge][cnt]=Population[Ge][Ch]; cnt++; } } //Assigning the variable "All chromosomes" the value of counter of unique chromosomes PopulChromosCount=cnt; //Return unique chromosomes back to the array for temporary storage //..of combined populations for(Ch=0;Ch<PopulChromosCount;Ch++) for(Ge=0;Ge<=GeneCount;Ge++) Population[Ge][Ch]=PopulationTemp[Ge][Ch]; //=================================================================1 //----------------Ranking the population---------------------------2 PopulationRanking(); //=================================================================2 } //————————————————————————————————————————————————————————————————————————
3.16. PopulationRanking. Classifica della popolazione
Lo smistamento viene effettuato dal VFF. Il metodo è simile a ' bubbly (L'algoritmo consiste in passaggi ripetuti attraverso l'array ordinato. Per ogni passaggio, gli elementi vengono successivamente confrontati a coppie, e se l'ordine di una coppia è sbagliato, avviene uno scambio di elementi. I passaggi attraverso l'array vengono ripetuti fino a quando uno dei passaggi mostra che gli scambi non sono più necessari, il che significa che l'array è stato ordinato.
Quando si passa attraverso l'algoritmo, un elemento che si distingue fuori posto, "si apre" nella posizione desiderata, proprio come una bolla nell'acqua, da cui il nome dell'algoritmo, ma c'è una differenza: vengono ordinati solo gli indici dell'array, non il contenuto dell'array. Questo metodo è più veloce e leggermente diverso in velocità dalla semplice copia di un array a un altro. E maggiore è la dimensione dell'array ordinato, minore è la differenza.
//———————————————————————————————————————————————————————————————————————— //Population ranking. void PopulationRanking() { //-----------------------Variables------------------------------------- int cnt=1, i = 0, u = 0; double PopulationTemp[][1000]; //Temporary population ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Indexes[]; //Indexes of chromosomes ArrayResize (Indexes,PopulChromosCount); ArrayInitialize(Indexes,0); int t0=0; double ValueOnIndexes[]; //VFF of corresponding //..chromosome indexes ArrayResize (ValueOnIndexes,PopulChromosCount); ArrayInitialize(ValueOnIndexes,0.0); double t1=0.0; //---------------------------------------------------------------------- //Fill in the indexes in the temporary array temp2 and //...copy the first line from the sorted array for(i=0;i<PopulChromosCount;i++) { Indexes[i] = i; ValueOnIndexes[i] = Population[0][i]; } if(OptimizeMethod==1) { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]>ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } else { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]<ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } //Create a sorted-out array based on the obtained indexes for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) PopulationTemp[i][u]=Population[i][Indexes[u]]; //Copy the sorted-out array back for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) Population[i][u]=PopulationTemp[i][u]; } //————————————————————————————————————————————————————————————————————————
3.17. RNDfromCustomInterval. Il generatore di numeri casuali da un dato intervallo
Solo una funzione utile. È utile in UGA.
//———————————————————————————————————————————————————————————————————————— //Generator of random numbers from the selected interval. double RNDfromCI(double RangeMinimum,double RangeMaximum) { return(RangeMinimum+((RangeMaximum-RangeMinimum)*MathRand()/32767.5));} //————————————————————————————————————————————————————————————————————————
3.18. SelectInDiscreteSpace. La selezione nello spazio discreto
Viene utilizzato per ridurre lo spazio di ricerca. Con il parametro step = 0.0 la ricerca viene effettuata in uno spazio continuo (limitato alle limitazioni del linguaggio, in MQL al 15° simbolo significativo incluso). Per utilizzare l'algoritmo AG con una maggiore precisione, è necessario scrivere una libreria aggiuntiva per lavorare con numeri lunghi.
Il lavoro della funzione in RoundMode = 1 può essere illustrato dalla figura seguente:
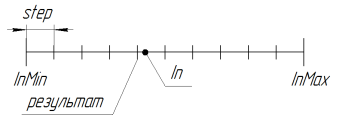
Figura 11. il lavoro della funzione SelectInDiscreteSpace a RoundMode = 1
//———————————————————————————————————————————————————————————————————————— //Selection in discrete space. //Modes: //1-closest below //2-closest above //any closest double SelectInDiscreteSpace ( double In, double InMin, double InMax, double step, int RoundMode ) { if(step==0.0) return(In); // secure the correctness of borders if( InMax < InMin ) { double temp = InMax; InMax = InMin; InMin = temp; } // during a breach - return the breached border if( In < InMin ) return( InMin ); if( In > InMax ) return( InMax ); if( InMax == InMin || step <= 0.0 ) return( InMin ); // bring to the specified scale step = (InMax - InMin) / MathCeil ( (InMax - InMin) / step ); switch( RoundMode ) { case 1: return( InMin + step * MathFloor ( ( In - InMin ) / step ) ); case 2: return( InMin + step * MathCeil ( ( In - InMin ) / step ) ); default: return( InMin + step * MathRound ( ( In - InMin ) / step ) ); } } //————————————————————————————————————————————————————————————————————————
3.19. FitnessFunction. Funzione fitness
Non fa parte dell’AG. La funzione riceve l'indice del cromosoma nella popolazione, per il quale verrà calcolato il VFF. VFF è scritto nell'indice zero del cromosoma trasmesso. Il codice di questa funzione è univoco per ogni attività.
3.20. Funzione di servizio. Funzione di servizio
Non fa parte dell’AG. Il codice di questa funzione è univoco per ogni attività specifica. Può essere utilizzato per implementare il controllo sulle epoche. Ad esempio, al fine di visualizzare il miglior VFF per l'epoca attuale.
4. Esempi di lavoro UGA
Tutti i problemi di ottimizzazione sono risolti per mezzo dell’AE e sono divisi in due tipi:
- Il genotipo è coerente con un fenotipo. I valori dei geni cromosomici sono nominati direttamente dagli argomenti di una funzione di ottimizzazione. Esempio 1.
- Il genotipo non corrisponde al fenotipo. L'interpretazione del significato dei geni cromosomici è necessaria per calcolare la funzione ottimizzata. Esempio 2.
4.1. Esempio 1
Considera il problema con una risposta nota, al fine di assicurarti che l'algoritmo funzioni e poi passa alla risoluzione del problema, la cui soluzione è di interesse per molti trader.
Problema: Trova la funzione minima e massima "Skin":
sul segmento [-5, 5].
Risposta: fmin (3.07021,3.315935) = -4.3182, fmax (-3.315699; -3.072485) = 14.0606.
Figura 12. Il grafico di "Skin" sul segmento [-5, 5]
Per risolvere il problema scriviamo il seguente script:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" #include "Skin.mqh"//testing function //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Gene pool parameter----"; input int ChromosomeCount_P = 50; //Number of chromosomes in a colony input int GeneCount_P = 2; //Number of genes input int FFNormalizeDigits_P = 4; //Number of fitness symbols input int GeneNormalizeDigits_P = 4; //Number of genes input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Operator parameters----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing-over. //--- input double ReplicationOffset_P = 0.5; //Coefficient of interval borders displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = -5.0; //Minimum range search input double RangeMaximum_P = 5.0; //Maximum range search input double Precision_P = 0.0001;//The required accuracy input int OptimizeMethod_P = 1; //Optim.:1-Min,other-Max //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double ERROR=0.0;//Average error in gen //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparing global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum range search RangeMaximum =RangeMaximum_P; //Maximum range search Precision =Precision_P; //Search step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of symbols in fitness GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//Proportion of crossing-over. //--- ReplicationOffset_P, //Coefficient of interval border replacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," mc - Time of implementation"); //---------------------------------- return(0); } //————————————————————————————————————————————————————————————————————————
Ecco l'intero codice dello script per risolvere il problema. Eseguilo, ottieni le informazioni, fornite dalla funzione Comment ():
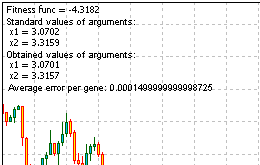
Figura 13. Il risultato della risoluzione del problema
Guardando i risultati, vediamo che l'algoritmo funziona.
4.2. Esempio 2.
È opinione diffusa che l'indicatore ZZ mostri gli input ideali di un sistema di trading ribaltato. L'indicatore è molto popolare tra i sostenitori della "teoria delle onde" e coloro che lo usano per determinare la dimensione delle "figure".
Problema : Determinare se ci sono altri punti di entrata per un sistema di trading ribaltato su dati storici, diversi dai vertici ZZ, dando in somma più punti di guadagno teorico?
Per gli esperimenti selezioneremo una coppia GBPJPY per M1 100 barre. Accetta lo spread di 80 punti (quotazioni a cinque cifre). Per iniziare, è necessario determinare i migliori parametri ZZ. A tale scopo, utilizziamo l'enumerazione semplice per trovare il valore migliore del parametro ExtDepth, utilizzando uno script semplice:
#property script_show_inputs //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input int History=100; input double Spred =80.0; input int Depth =5; //For "one-time" use input bool loop =true;//Use enumeration or not //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- void OnStart() { //-----------------------Variables------------------------------------- double ZigzagBuffer [];//For storing the buffer of the ZZ indicator double PeaksOfZigzag[];//for storing the values of the ZZ extremum int Zigzag_handle; //Indicator marker ArraySetAsSeries(ZigzagBuffer,true); ArrayResize(PeaksOfZigzag,History); int depth=3; double PipsSum=0.0; int PeaksCount=0; bool flag=true; //---------------------------------------------------------------------- if(loop==true) { while(depth<200 && flag==true) { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",depth); //--- reset the code error ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<100;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Could not copy the indicator buffer. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- PipsSum=0.0; PeaksCount=0; for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; //----------------------------------------------------------- if(PeaksCount<=2) flag=false; else { Print(depth," ",PeaksCount," ",PipsSum); depth+=1; } //----------------------------------------------------------- } } else { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",Depth); //--- reser the error code ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<History;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Was not able to copy the buffer indicator. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; } Print(Depth," ",PeaksCount," ",PipsSum); //----------------------------------------------------------- } } //————————————————————————————————————————————————————————————————————————
Eseguendo lo script, otteniamo 4077 punti in ExtDepth = 3. Diciannove vertici indicatore "fit" su 100 barre. Con l'aumento di ExtDepth, il numero di vertici ZZ diminuisce, così come la redditività.
Ora, possiamo trovare i vertici dell'alternativa ZZ, usando UGA. I vertici ZZ possono avere tre posizioni per ogni barra: 1) Alto, 2) Basso, 3) Nessun vertice. La presenza e la posizione del vertice saranno trasportate da ogni gene per ogni barra. Quindi, la dimensione del cromosoma - 100 geni.
Secondo i miei calcoli (e i matematici possono correggermi se sbaglio), su 100 barre puoi costruire 3 ^ 100, o 5.15378e47 opzioni alternative "zigzag" . Questo è il numero esatto di opzioni che devono essere considerate, utilizzando l'enumerazione diretta. Durante il calcolo con una velocità di 100000000 opzioni al secondo, avremo bisogno di 1.6e32 anni ! Questo è più dell'età dell'universo. Ecco quando ho iniziato ad avere dubbi sulla capacità di trovare una soluzione a questo problema.
Ma cominciamo.
Poiché UGA utilizza la rappresentazione del cromosoma con numeri reali, dobbiamo in qualche modo codificare la posizione dei vertici. Questo avviene quando il genotipo del cromosoma non corrisponde al fenotipo. Assegnare un intervallo di ricerca per i geni [0, 5]. Concordiamo sul fatto che l'intervallo [0, 1] corrisponde al vertice di ZZ su High, l'intervallo [4, 5] corrisponde al vertice su Low e l'intervallo (1, 4) corrisponde all'assenza del vertice.
È necessario considerare un punto importante. Poiché la proto-popolazione è generata casualmente con geni nell'intervallo specificato, il primo campione avrà risultati molto scarsi, forse anche con poche centinaia di punti con un segno meno. Dopo alcune generazioni (anche se c'è la possibilità che accada nella prima generazione) vedremo la comparsa di campioni, i cui geni sono coerenti con l'assenza di vertici in generale. Ciò significherebbe l'assenza di scambi e il pagamento dell'inevitabile spread.
Secondo alcuni ex trader: "La migliore strategia di trading - non è fare trading". Questo individuo sarà il vertice dell'evoluzione artificiale. Per far in modo questa evoluzione "artificiale" crei degli individui di trading, cioè che disponga i vertici della ZZ alternativa, assegniamo alla forma fisica degli individui, privi di vertici, il valore di "-100000000.0", ponendolo deliberatamente sul gradino più basso dell'evoluzione, rispetto a qualsiasi altro individuo.
Ecco il codice dello script che utilizza UGA per trovare i vertici dello ZZ alternativo:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Parameters of the gene pool----"; input int ChromosomeCount_P = 100; //Number of chromosomes in the colony input int GeneCount_P = 100; //Number of genes input int FFNormalizeDigits_P = 0; //Number of fitness symbols input int GeneNormalizeDigits_P= 0; //Number of gene symbols input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Parameters of operators----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing - over. input double ReplicationOffset_P = 0.5; //Coefficient of interval border displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = 0.0; //Minimum search range input double RangeMaximum_P = 5.0; //Maximum search range input double Precision_P = 1.0; //Required accuracy input int OptimizeMethod_P = 2; //Optim.:1-Min,other -Max input string Other = "----Other----"; input double Spred = 80.0; input bool Show = true; //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double Hight []; double Low []; datetime Time []; datetime Ti []; double Peaks []; bool show; //———————————————————————————————————————————————————————————————————————— //--------------------------Body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparation of global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum search range RangeMaximum =RangeMaximum_P; //Maximum search range Precision =Precision_P; //Searching step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of fitness symbols GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Preparation of global variables ArraySetAsSeries(Hight,true); CopyHigh (NULL,0,0,GeneCount+1,Hight); ArraySetAsSeries(Low,true); CopyLow (NULL,0,0,GeneCount+1,Low); ArraySetAsSeries(Time,true); CopyTime (NULL,0,0,GeneCount+1,Time); ArrayResize (Ti,GeneCount+1);ArrayInitialize(Ti,0); ArrayResize(Peaks,GeneCount+1);ArrayInitialize(Peaks,0.0); show=Show; //---------------------------------------------------------------------- //local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Очистим экран ObjectsDeleteAll(0,-1,-1); ChartRedraw(0); //launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of replication of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//proportion of crossing- over. //--- ReplicationOffset_P, //Coefficient of interval border displacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- //Display the last result on the screen show=true; ServiceFunction(); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," мс - time of execution"); //---------------------------------- return(0); } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Service function. Called up from UGA. | | //If there is no need for it, leave the function empty, like this: | // void ServiceFunction() | // { | // } | //-----------------------------------------------------------------------+ void ServiceFunction() { if(show==true) { //-----------------------Variables----------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //-------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Chromosome[u]; if(temp<=1.0 ) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } } ObjectsDeleteAll(0,-1,-1); for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; ObjectCreate (0,"BoxBackName"+(string)V,OBJ_TREND,0,Ti[V],Peaks[V],Ti[V+1],Peaks[V+1]); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_COLOR,Black); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_SELECTABLE,true); } ChartRedraw(0); Comment(PipsSum); } //---------------------------------------------------------------------- else return; } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Function of determining the fitness of the individual. Called up from UGA. | //-----------------------------------------------------------------------+ void FitnessFunction(int chromos) { //-----------------------Variables------------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //---------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Colony[u][chromos]; if(temp<=1.0) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); PeaksCount++; } } if(PeaksCount>1) { for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; Colony[0][chromos]=PipsSum; } else Colony[0][chromos]=-10000000.0; AmountStartsFF++; } //————————————————————————————————————————————————————————————————————————
Quando eseguiamo lo script, otteniamo i vertici con un profitto totale di 4939 punti. Inoltre, ci sono volute solo 17.929 volte per contare i punti, rispetto ai 3 ^ 100 necessari attraverso l'enumerazione diretta. Sul mio computer, questo è 21,7 secondi contro 1,6e32 anni!
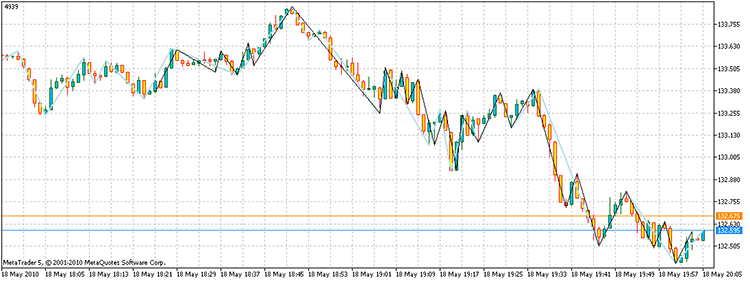
Figura 14. Il risultato della soluzione al problema. I segmenti di colore nero - un indicatore ZZ alternativo, blu cielo - ZZ
Quindi, la risposta alla domanda sarà la seguente: "Esiste."
5. Consigli per lavorare con UGA
- Prova a impostare correttamente le condizioni stimate in FF, per poterti aspettare un risultato adeguato dall'algoritmo. Ripensa all'Esempio 2. Questa è forse la mia raccomandazione principale.
- Non utilizzare un valore troppo piccolo per il parametro Precision. Sebbene l'algoritmo sia in grado di funzionare con un passaggio 0, è necessario richiedere una ragionevole accuratezza della soluzione. Questo parametro ha lo scopo di ridurre la dimensione del problema.
- Variare la dimensione della popolazione e il valore soglia del numero di epoche. Una buona soluzione sarebbe quella di assegnare un parametro Epoch due volte più grande di quello mostrato da MaxOfCurrentEpoch. Non scegliere valori troppo grandi, questo non accelererà la ricerca di una soluzione al problema.
- Sperimenta i parametri degli operatori genetici. Non ci sono parametri universali e dovresti assegnarli sulla base delle condizioni dell'attività che hai di fronte.
Risultati
Insieme a uno strategy tester molto potente per il terminale del personale, il linguaggio MQL5 ti consente di creare non meno di un potente strumento per il trader, permettendoti di risolvere problemi davvero complessi. Otteniamo un algoritmo di ottimizzazione molto flessibile e scalabile. E sono sfacciatamente orgoglioso di questa scoperta, anche se non sono stato il primo a farla.
Poiché l'UGA è stato inizialmente progettato in modo tale da poter essere facilmente modificato ed esteso con operatori aggiuntivi e blocchi di calcolo, il lettore sarà facilmente in grado di contribuire allo sviluppo dell'evoluzione "artificiale".
Auguro al lettore tanto successo nel trovare soluzioni ottimali. Spero di essere stato in grado di aiutarlo in questo. Buona Fortuna!
Nota. L'articolo ha utilizzato l'indicatore ZigZag. Tutti i codici sorgente di UGA sono allegati.
Licenze: I codici sorgente allegati all'articolo (codice UGA) sono distribuiti in condizioni di licenza BSD .
Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/55
Un Esempio di Strategia di Trading Basata sulle Differenze di Fuso Orario nei Diversi Continenti
MQL per "Duri di Comprendonio": Come Progettare e Costruire Classi di Oggetti
Creazione e Pubblicazione di Report di Trading e Notifiche SMS
Creazione di un Indicatore con più Indicatori Buffer per Principianti
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso