Genetic Algorithms - It's Easy!
24 574
20
Introduction
Genetic algorithm ( GA ) refers to the heuristic algorithm ( EA ), which gives an acceptable solution to the problem in the majority of practically significant cases, but the correctness of the decisions has not been proven mathematically, and is used most often for problems, the analytical solution of which is very difficult or even impossible.
A classic example of a problem of this class (class NP) is a "traveling salesman problem" (is one of the most famous combinatorial optimization problems). The main challenge is finding the most advantageous route, which passes through the given cities at least one time, and then returns to the initial city). But nothing prevents to use them for tasks, which yield to formalization.
EA are widely used for solving problems of high computational complexity, instead of going through all of the options, which takes up a significant amount of time. They are used in the fields of artificial intelligence, such as pattern recognition, in antivirus software, engineering, computer games, and other areas.
It should be mentioned that MetaQuotes Software Corp. uses GA in their software products of MetaTrader4 / 5. We all know about the strategy tester and about how much time and effort can be saved by using a built-in strategy optimizer, in which, just like with the direct enumeration, it is possible to optimize with the use of GA. In addition, the MetaTrader 5 tester allows us to use the user optimization criteria. Perhaps the reader will be interested in reading the articles about the GA and the advantages, provided by EA, in contrast to direct enumeration.
1. A little bit of history
Just over a year ago, I needed an optimization algorithm for training neural networks. After quickly acquainting myself with the various algorithms, I chose GA. As a result of my search for ready -made implementations, I found that the ones open for public access, either have functional limitations, such as the number of parameters that can be optimized, or are too "narrowly tuned".
I needed a universally flexible instrument not only for training all types of neural networks, but also for generally solving any optimization problems. After a lengthy study of foreign "genetic creations", I was still not able to understand how they work. The cause of this was either an elaborate code style, or my lack of experience in programming, or possibly both.
The main difficulties arose from coding genes to a binary code and then working with them in this form. Either way, it was decided to write a genetic algorithm from scratch, focusing on scalability and easy modification in the future.
I did not want to deal with binary transformation, and decided to work with the genes directly, ie represent the chromosome with a set of genes in the form of real numbers. This is how the code for my genetic algorithm, with a representation of chromosomes by real numbers, appeared. Later I learned that I didn't discover anything new, and that analogous genetic algorithms (they are called real-coded GA ) already existed for more than 15 years, ever since the first publications about them came out.
I leave my vision of approaching the implementation and principles of GA functioning for the reader to judge, since it is based on personal experience of its use in practical problems.
2. GA Description
GA contains the principles, borrowed from nature itself. These are the principles of heredity and variability. Heredity is the ability of organisms to transfer their traits and evolutionary characteristics to their offspring. Thanks to this ability, all living beings leave behind the characteristics of their species in their offspring.
The variability of genes in living organisms assures the genetic diversity of the population and is random, since nature doesn't have a way of knowing in advance which features will be most preferable in the future (climate change, decrease / increase in food, the emergence of competing species, etc.). This variability allows the appearance of creatures with new traits, which can survive and leave behind offspring in the new, altered conditions of the habitat.
In biology, variability, which arose due to the emergence of mutations, is called mutational, variability due to further cross- combination of genes by mating, is called combinational. Both of these types of variations are implemented in the GA. In addition, there is an implementation of mutagenesis, which mimics the natural mechanism of mutations (changes in the nucleotide sequence of DNA) - the natural (spontaneous) and artificial (induced).
The simplest unit of information transfer on the criterion of the algorithm is gene - structural and functional unit of heredity, which controls the development of a particular trait or property. We will call one variable of the function the gene. The gene is represented by a real number. The set of gene- variables of the studied function is the characterizing feature of the - chromosome .
Let's agree to represent the chromosome in the form of a column. Then the chromosome for the function f (x) = x ^ 2, would look like this:
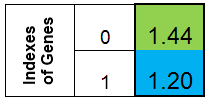
Figure 1. Chromosome for the function f (x) = x ^ 2
where 0-th index - value of the function f (x), called the adaptation of the individuals (we will call this function the fitness function - FF , and the value of the function - VFF ). It is convenient to store the chromosome in a one-dimensional array. This is the double Chromosome [] array.
All specimens of the same evolutionary era are combined into a population . Moreover, the population is arbitrarily divided into two equal colonies - the parent and the descendant colonies. As a result of crossing the parental species, which are selected from the entire population, and other operators of the GA, there is a colony of new offspring, which is equal to half the size of the population, which replaces the colony of the offspring in the population.
The total population of individuals during a search for the minimum of function f (x) = x ^ 2 might look like this:
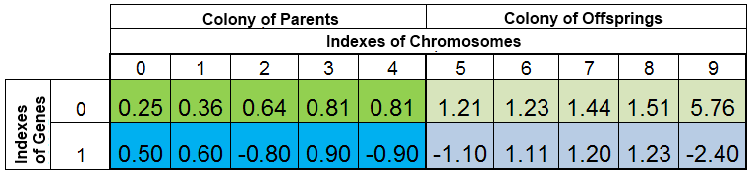
Figure 2. Total population of individuals
The population is sorted by VFF. Here, the 0-th index of the chromosome is taken up by the specimen with the smallest VFF. The new offspring completely replace only the individuals in the descendant's colony, while the parent colony remains intact. However, the parent colony may not always be complete, since the duplicate specimens are destroyed, then the new offspring fill vacancies in the parent colony, and the rest are placed in the descendant's colony.
In other words, the population size is rarely constant, and varies from era to era, almost in the same way as in nature. For example, the population before breeding and after breeding may look like this:
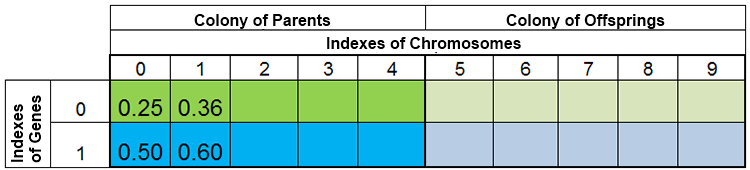
Figure 3. The population before breeding
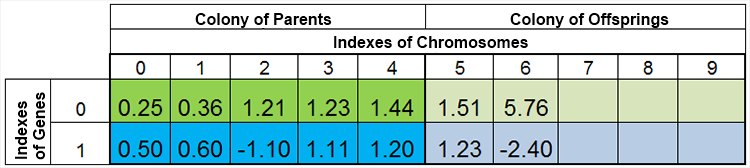
Figure 4. The population after breeding
The described mechanism of the "half" fulfillment of the population by the descendants, as well as the destruction of duplicates and the ban on cross-breeding of individuals with themselves, have a single goal - to avoid the "bottleneck effect" (a term from biology, meaning a reduction of the gene pool of the population as a result of a critical reduction due to a number of different reasons, which can lead to a complete extinction of a specie, GA is facing the end of appearances of unique chromosomes and "getting stuck" in one of the local extrema.)
3. Description of the UGAlib function
Algorithm GA:- Creating a proto- population. Genes are generated randomly within a given range.
- Determining the fitness of each individual, or in other words, the calculation of VFF.
- Preparing the population for reproduction, after removing chromosome duplicates.
- Isolation and preservation of the reference chromosome (with the best VFF).
- Operators of UGA (selection, mating, mutation). For each mating and mutation, new parents are selected each time. Preparing the population for the next era.
- Comparison of genes of the best offspring with the genes of the reference chromosome. If the chromosome of the best offspring is better than the reference chromosome, then replace the reference chromosome.
Continue on from paragraph 5 until the there are no longer chromosomes, better than the reference ones appearing, for a specified number of eras.
3.1. Global variables. Global variables
Announced the following variables on the global level:
//----------------------Global variables----------------------------- double Chromosome[]; //A set of optimized arguments of the function - genes //(for example: the weight of the neuron network, etc.)- of the chromosome int ChromosomeCount =0; //Maximum possible amount of chromosomes in a colony int TotalOfChromosomesInHistory=0;//Total number of chromosomes in the history int ChrCountInHistory =0; //Number of unique chromosomes in the base chromosome int GeneCount =0; //Number of genes in the chromosome double RangeMinimum =0.0;//Minimum search range double RangeMaximum =0.0;//Maximum search range double Precision =0.0;//Search step int OptimizeMethod =0; //1-minimum, any other - maximum int FFNormalizeDigits =0; //Number of symbols after the comma in the fitness value int GeneNormalizeDigits =0; //Number of symbols after the comma in the genes value double Population [][1000]; //Population double Colony [][500]; //Offspring colony int PopulChromosCount =0; //The current number of chromosomes in a population int Epoch =0; //Number of epochs without progress int AmountStartsFF=0; //Number of launches of the fitness function //————————————————————————————————————————————————————————————————————————
3.2. UGA. The main function of the GA
Actually, the main function of GA, called from the body of the program to perform the steps, listed above, therefore we won't go into much details on it.
Upon completion of the algorithm, recorded the following information into the log:
- How many epochs were there in total (generations).
- How many total faults.
- The number of unique chromosomes.
- The total number of launches of FF.
- The total number of chromosomes in history.
- Percentage ratio of duplicates to the total number of chromosomes in the history.
- Best result.
"The number of unique chromosomes" and the "Total number of launches of FF" - the same sizes, but are calculated differently. Use for control.
//———————————————————————————————————————————————————————————————————————— //Basic function UGA void UGA ( double ReplicationPortion, // Proportion of replication. double NMutationPortion, // Proportion of natural mutations. double ArtificialMutation, // Proportion of artificial mutations. double GenoMergingPortion, // Proportion of borrowed genes. double CrossingOverPortion, // Proportion of cross -over. //--- double ReplicationOffset, // Coefficient of displacement of interval borders double NMutationProbability // Probability of mutation of each gene in% ) { //generator reset takes place only once MathSrand((int)TimeLocal()); //-----------------------Variables------------------------------------- int chromos=0, gene =0;//indexes of chromosomes and genes int resetCounterFF =0;//counter of resets of "Epochs without progress" int currentEpoch =1;//number of the current epoch int SumOfCurrentEpoch=0;//sum of "Epochs without progress" int MinOfCurrentEpoch=Epoch;//minimum of "epochs without progress" int MaxOfCurrentEpoch=0;//maximum of "Epochs without progress" int epochGlob =0;//total number of epochs // Colony [number of traits(genes)][number of individuals in a colony] ArrayResize(Population,GeneCount+1); ArrayInitialize(Population,0.0); // Colony of offspring [number of traits(genes)][number of individuals in a colony] ArrayResize(Colony,GeneCount+1); ArrayInitialize(Colony,0.0); // Chromosome bank // [number of traits (genes)][number of chromosomes in the bank] double historyHromosomes[][100000]; ArrayResize(historyHromosomes,GeneCount+1); ArrayInitialize(historyHromosomes,0.0); //---------------------------------------------------------------------- //--------------Verification of the correctness of incoming parameters---------------- //...the number of chromosomes mus be less than 2 if(ChromosomeCount<=1) ChromosomeCount=2; if(ChromosomeCount>500) ChromosomeCount=500; //---------------------------------------------------------------------- //====================================================================== // 1) Create a proto- population —————1) ProtopopulationBuilding(); //====================================================================== // 2) Determine the fitness of each individual —————2) //For the 1st colony for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=0;chromos<ChromosomeCount;chromos++) Population[0][chromos]=Colony[0][chromos]; //For the 2nd colony for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) for(gene=1;gene<=GeneCount;gene++) Colony[gene][chromos-ChromosomeCount]=Population[gene][chromos]; GetFitness(historyHromosomes); for(chromos=ChromosomeCount;chromos<ChromosomeCount*2;chromos++) Population[0][chromos]=Colony[0][chromos-ChromosomeCount]; //====================================================================== // 3) Prepare the population for reproduction ————3) RemovalDuplicates(); //====================================================================== // 4) Extract the reference chromosome —————4) for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; //====================================================================== ServiceFunction(); //The main cycle The main cycle of the genetic algorithm from 5 to 6 while(currentEpoch<=Epoch) { //==================================================================== // 5) Operators of UGA —————5) CycleOfOperators ( historyHromosomes, //--- ReplicationPortion, //Proportion of replication. NMutationPortion, //Proportion of natural mutation. ArtificialMutation, //Proportion of artificial mutation. GenoMergingPortion, //Proportion of borrowed genes. CrossingOverPortion,//Proportion of cross- over. //--- ReplicationOffset, //Coefficient of displacement of interval borders NMutationProbability//Probability of mutation of each gene in % ); //==================================================================== // 6) Compare the genes of the best offspring with the genes of the reference chromosome. // If the chromosome of the best offspring is better that the reference chromosome, // replace the reference. —————6) //If the optimization mode is - minimization if(OptimizeMethod==1) { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]<Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Rest the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //If the optimization mode is - minimization else { //If the best chromosome of the population is better than the reference chromosome if(Population[0][0]>Chromosome[0]) { //Replace the reference chromosome for(gene=0;gene<=GeneCount;gene++) Chromosome[gene]=Population[gene][0]; ServiceFunction(); //Reset the counter of "epochs without progress" if(currentEpoch<MinOfCurrentEpoch) MinOfCurrentEpoch=currentEpoch; if(currentEpoch>MaxOfCurrentEpoch) MaxOfCurrentEpoch=currentEpoch; SumOfCurrentEpoch+=currentEpoch; currentEpoch=1; resetCounterFF++; } else currentEpoch++; } //==================================================================== //Another epoch went by.... epochGlob++; } Print("Epochs went by=",epochGlob," Number of resets=",resetCounterFF); Print("MinOfCurrentEpoch",MinOfCurrentEpoch, " AverageOfCurrentEpoch",NormalizeDouble((double)SumOfCurrentEpoch/(double)resetCounterFF,2), " MaxOfCurrentEpoch",MaxOfCurrentEpoch); Print(ChrCountInHistory," - Unique chromosome"); Print(AmountStartsFF," - Total number of launches of FF"); Print(TotalOfChromosomesInHistory," - Total number of chromosomes in the history"); Print(NormalizeDouble(100.0-((double)ChrCountInHistory*100.0/(double)TotalOfChromosomesInHistory),2),"% of duplicates"); Print(Chromosome[0]," - best result"); } //————————————————————————————————————————————————————————————————————————
3.3. Creating a Proto- population. Creating a proto- population.
Since in most optimization problems there is no way of knowing in advance where the function arguments are located on the number line, then the best optimum option is random generation within a given range.
//———————————————————————————————————————————————————————————————————————— //Creating a proto- population void ProtopopulationBuilding() { PopulChromosCount=ChromosomeCount*2; //Fill up the population with chromosomes with random //...genes in the range between RangeMinimum...RangeMaximum for(int chromos=0;chromos<PopulChromosCount;chromos++) { //beginning with the 1st indexes (the 0 index is reserved for VFF) for(int gene=1;gene<=GeneCount;gene++) Population[gene][chromos]= NormalizeDouble(SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); TotalOfChromosomesInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.4. GetFitness. Getting the fitness
Performs the optimized function for each chromosome in order.
//------------------------------------------------ ------------------------ // Getting the fitness for each individual. void GetFitness ( double &historyHromosomes[][100000] ) { for(int chromos=0;chromos<ChromosomeCount;chromos++) CheckHistoryChromosomes(chromos,historyHromosomes); } //————————————————————————————————————————————————————————————————————————
3.5. CheckHistoryChromosomes. Verification of the chromosome through the chromosome base
The chromosome of each individual is verified through the base - whether the FF has been calculated for it, and if it was, then the ready VFF is taken from the base, if not, then the FF is called for it. Thus, the repeating resource -intensive calculations of FF are excluded.
//———————————————————————————————————————————————————————————————————————— //Verification of chromosome through the chromosome base. void CheckHistoryChromosomes ( int chromos, double &historyHromosomes[][100000] ) { //-----------------------Variables------------------------------------- int Ch1=0; //Index of the chromosome from the base int Ge =0; //Index of the gene int cnt=0; //Counter of unique genes. If at least one gene is different //- the chromosome is acknowledged unique //---------------------------------------------------------------------- //If at least one chromosome is stored in the base if(ChrCountInHistory>0) { //Enumerate the chromosomes in the base to find an identical one for(Ch1=0;Ch1<ChrCountInHistory && cnt<GeneCount;Ch1++) { cnt=0; //Compare the genes, while the gene index is less than the number of genes and while there are identical genes for(Ge=1;Ge<=GeneCount;Ge++) { if(Colony[Ge][chromos]!=historyHromosomes[Ge][Ch1]) break; cnt++; } } //If there are enough identical genes then we can use a ready- made solution from the base if(cnt==GeneCount) Colony[0][chromos]=historyHromosomes[0][Ch1-1]; //If there is no such chromosome, then we calculate the FF for it... else { FitnessFunction(chromos); //.. and if there is space in the base, then save it if(ChrCountInHistory<100000) { for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } } //If the base is empty, calculate the FF for it and save it in the base else { FitnessFunction(chromos); for(Ge=0;Ge<=GeneCount;Ge++) historyHromosomes[Ge][ChrCountInHistory]=Colony[Ge][chromos]; ChrCountInHistory++; } } //————————————————————————————————————————————————————————————————————————
3.6. CycleOfOperators. Cycle of Operators in UGA
At this point, the fate of literary an entire epoch of artificial life is being decided - a new generation is born and dies. This happens in the following way: two parents are selected for mating, or one to commit an act of mutations over him. For each operator of GA an appropriate parameter is determined. As a result we get one offspring. This is repeated over and over, until the descendant colony is filled completely. Then the colony of descendants is let out into the habitat, so that each individual could demonstrate itself as well as it could, and we calculate the VFF.
After being tested by "fire, water, and copper pipes", the colony of descendants is settled into the population. The next step in artificial evolution will be the sacred murder of clones, in order to prevent the depletion of "blood" in future generations, and the subsequent ranking of the renewed population, by the degree of fitness.
//———————————————————————————————————————————————————————————————————————— //Cycle of operators of UGA void CycleOfOperators ( double &historyHromosomes[][100000], //--- double ReplicationPortion, //Proportion of replications. double NMutationPortion, //Proportion of natural mutations. double ArtificialMutation, //Proportion of artificial mutations. double GenoMergingPortion, //Portion of borrowed genes. double CrossingOverPortion,//Proportion of cross-over. //--- double ReplicationOffset, //Coefficient of displacement of interval borders double NMutationProbability//Probability of mutation of each gene in % ) { //-----------------------Variables------------------------------------- double child[]; ArrayResize (child,GeneCount+1); ArrayInitialize(child,0.0); int gene=0,chromos=0, border=0; int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,6); ArrayInitialize(fit,0.0); //Counter of planting spots in a new population. int T=0; //---------------------------------------------------------------------- //Set a portion of operators of UGA double portion[6]; portion[0]=ReplicationPortion; //Proportion of replications. portion[1]=NMutationPortion; //Proportion of natural mutations. portion[2]=ArtificialMutation; //Proportion of artificial mutations. portion[3]=GenoMergingPortion; //Proportion of borrowed genes. portion[4]=CrossingOverPortion;//Proportion of cross- overs. portion[5]=0.0; //------------------------Cycle of operators of UGA--------- //Fill up the new colony with offspring while(T<ChromosomeCount) { //============================ for(i=0;i<6;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(portion[i]-portion[5]); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[4][1]); for(u=0;u<5;u++) { if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; } //============================ switch(u) { //--------------------- case 0: //------------------------Replication-------------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { Replication(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 1: //---------------------Natural mutation------------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { NaturalMutation(child,NMutationProbability); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast- forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 2: //----------------------Artificial mutation----------------------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { ArtificialMutation(child,ReplicationOffset); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast-forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- case 3: //-------------The creation of an individual with borrowed genes----------- //If there is space in the new colony, create a new individual if(T<ChromosomeCount) { GenoMerging(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One space is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- default: //---------------------------Crossing-Over--------------------------- //If there is place in the new colony, create a new individual if(T<ChromosomeCount) { CrossingOver(child); //Settle the new individual into the new colony for(gene=1;gene<=GeneCount;gene++) Colony[gene][T]=child[gene]; //One place is occupied, fast forward the counter T++; TotalOfChromosomesInHistory++; } //--------------------------------------------------------------- break; //--------------------- } }//End of the cycle operators of UGA-- //Determine the fitness of each individual in the colony of offspring GetFitness(historyHromosomes); //Settle the offspring into the main population if(PopulChromosCount>=ChromosomeCount) { border=ChromosomeCount; PopulChromosCount=ChromosomeCount*2; } else { border=PopulChromosCount; PopulChromosCount+=ChromosomeCount; } for(chromos=0;chromos<ChromosomeCount;chromos++) for(gene=0;gene<=GeneCount;gene++) Population[gene][chromos+border]=Colony[gene][chromos]; //Prepare the population for the next reproduction RemovalDuplicates(); }//the end of the function //————————————————————————————————————————————————————————————————————————
3.7. Replication. Replication
The operator is closest to the natural phenomenon, which in biology is called - DNA replication, although, in essence, it is not the same thing. But since I didn't find any equivalent, closer to this in nature, I decided to keep this title.
Replication is the most important genetic operator, which generates new genes, while transmitting the traits of the parental chromosomes. The main operator, ensuring the convergence of the algorithm. GA can only function with it without the use of other operators, but in this case the number of FF launches would be much greater.
Consider the principle of the Replication operator. We use two parental chromosomes. The new offspring gene is a random number from the interval
[C1-((C2-C1)*ReplicationOffset),C2+((C2-C1)*ReplicationOffset)]
where C1 and C2 parental genes ReplicationOffset - Coefficient of displacement of the interval borders [C1, C2] .
For example, from the paternal individual (blue) and the maternal individual (pink) a child (green) can be created:
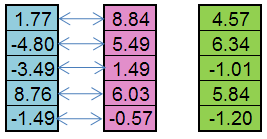
Figure 5. The principle of the operator Replication work
Graphically, the probability of the offspring gene can be summarized:
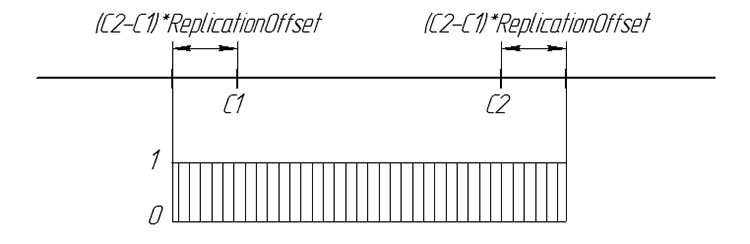
Figure 6. The probability of the appearance of the offspring gene on a number line
The other offspring genes are generated in the same way.
//------------------------------------------------ ------------------------ // Replication void Replication ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- SelectTwoParents(address_mama,address_papa); //-------------------Cycle of gene enumeration-------------------------------- for(int i=1;i<=GeneCount;i++) { //----figure out where the father and mother came from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search had not gone over the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if we С1>C2, swi if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of the created gene Minimum = C1-((C2-C1)*ReplicationOffset); Maximum = C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search has not gone over the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- temp=RNDfromCI(Minimum,Maximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } //————————————————————————————————————————————————————————————————————————3.8. NaturalMutation. Natural mutation
Mutations occur constantly throughout the course of the processes, occurring in living cells, and serve as the material for natural selection. They arise spontaneously throughout the entire life of the organism in its normal habitat conditions, with a frequency of once per 10 ^ 10 cell generations.
We - the curious researchers, do not necessarily need to adhere to the natural order, and wait so long for the next mutation of the gene. The NMutationProbability parameter, which is expressed as a percentage and determines the probability of mutation for each gene in the chromosome, will help us to do this.
In NaturalMutation operator, mutation consists of the generation of a random gene in the interval [RangeMinimum, RangeMaximum] . NMutationProbability = 100% would mean a 100% mutation of all genes in the chromosome, and NMutationProbability = 0% - complete absence of mutations. The latest option is unfit to be used in practical problems.
//------------------------------------------------ ------------------------ // The natural mutation. void NaturalMutation ( double &child[], double NMutationProbability ) { //-----------------------Variables------------------------------------- int address=0; double prob=0.0; //---------------------------------------------------------------------- if(NMutationProbability<0.0) prob=0.0; if(NMutationProbability>100.0) prob=100.0; //-----------------Parent selection------------------------ SelectOneParent(address); //--------------------------------------- for(int i=1;i<=GeneCount;i++) if(RNDfromCI(0.0,100.0)<prob) child[i]=NormalizeDouble( SelectInDiscreteSpace(RNDfromCI(RangeMinimum,RangeMaximum),RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits ); } //————————————————————————————————————————————————————————————————————————
3.9. ArtificialMutation. Artificial mutation
The main task of the operator - is the generation of "fresh" blood. We use two parents, and the genes of the offspring are selected from the, unallocated by the parent genes, spaces on the number line. Protects the GA from getting stuck in one of the local extrema. In a larger proportion, compared to other operators, accelerates the convergence, or else - slows down, increasing the number of launches of FF.
Just as in Replication, we use two parental chromosomes. But the task of the ArtificialMutation operator is not to convey the parental traits to the offspring, but rather to make the child different from them. Therefore, being a complete opposite, using the same coefficient of interval border displacement, but the genes are generated outside the interval, which would have been taken by Replication. The new gene of the offspring is a random number from the intervals [RangeMinimum, C1-(C2-C1) * ReplicationOffset] and [C2 + (C2-C1) * ReplicationOffset, RangeMaximum]
Graphically, the probability of a gene in the offspring ReplicationOffset = 0.25 can be represented as:
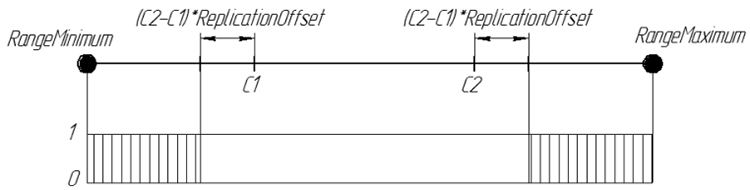
Figure 7. The probability of a gene in the descendant ReplicationOffset = 0.25 on the real line interval [RangeMinimum; RangeMaximum]
//———————————————————————————————————————————————————————————————————————— //Artificial mutation. void ArtificialMutation ( double &child[], double ReplicationOffset ) { //-----------------------Variables------------------------------------- double C1=0.0,C2=0.0,temp=0.0,Maximum=0.0,Minimum=0.0,p=0.0; int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //-------------------Cycle of genes enumeration------------------------------ for(int i=1;i<=GeneCount;i++) { //----determine where the mother and father are from -------- C1 = Population[i][address_mama]; C2 = Population[i][address_papa]; //------------------------------------------ //Mandatory verification to make sure that the search doesn't go beyond the specified range if(C1 < RangeMinimum) C1 = RangeMinimum; if(C1 > RangeMaximum) C1 = RangeMaximum; if(C2 < RangeMinimum) C2 = RangeMinimum; if(C2 > RangeMaximum) C2 = RangeMaximum; //------------------------------------------------------------------ //....determine the largest and smallest of them, //if С1>C2, we change their places if(C1>C2) { temp=C1; C1=C2; C2=temp; } //-------------------------------------------- //Specify the borders of creating the new gene Minimum=C1-((C2-C1)*ReplicationOffset); Maximum=C2+((C2-C1)*ReplicationOffset); //-------------------------------------------- //Mandatory verification to make sure that the search doesn't go beyond the specified range if(Minimum < RangeMinimum) Minimum = RangeMinimum; if(Maximum > RangeMaximum) Maximum = RangeMaximum; //--------------------------------------------------------------- p=MathRand(); if(p<16383.5) { temp=RNDfromCI(RangeMinimum,Minimum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } else { temp=RNDfromCI(Maximum,RangeMaximum); child[i]= NormalizeDouble(SelectInDiscreteSpace(temp,RangeMinimum,RangeMaximum,Precision,3),GeneNormalizeDigits); } } } //————————————————————————————————————————————————————————————————————————
3.10 GenoMerging. Borrowing genes
The given GA operator does not have a natural equivalent. It is in fact difficult to imagine how this wonderful mechanism would function in living organisms. However, it has a remarkable property of transferring genes from a number of parents (the number of parents is equal to the number of genes) to the offspring. The operator does not generate new genes, and is a combinatorial search mechanism.
It works like this: for the first offspring gene a parent is selected, and the first gene is take from him, then, for the second gene, a second parent is selected, and the gene is taken from him, etc. This is advisable to apply if the number of genes is more than one. Otherwise, it should be disabled, since the operator will generate duplicates of the chromosomes.
//———————————————————————————————————————————————————————————————————————— //Borrowing genes. void GenoMerging ( double &child[] ) { //-----------------------Variables------------------------------------- int address=0; //---------------------------------------------------------------------- for(int i=1;i<=GeneCount;i++) { //-----------------Selecting parents------------------------ SelectOneParent(address); //-------------------------------------------------------- child[i]=Population[i][address]; } } //————————————————————————————————————————————————————————————————————————
3.11. CrossingOver. Crossing-over
Crossing-over (also known in biology as crossing) - is a phenomenon of exchanging sections of chromosomes. Just as in GenoMerging, this is a combinatorial search mechanism.
Two parental chromosomes are selected. Both are "cut" in a random place. Chromosome of the offspring will consist of parts of parental chromosomes.
It is easiest to illustrate this mechanism in a picture:
Figure 8. The exchange mechanism of chromosome parts
This is advisable to apply if the number of genes is more than one. Otherwise, it should be disabled, since the operator will generate duplicates of the chromosomes.
//———————————————————————————————————————————————————————————————————————— //Crossing-over. void CrossingOver ( double &child[] ) { //-----------------------Variables------------------------------------- int address_mama=0,address_papa=0; //---------------------------------------------------------------------- //-----------------Selecting parents------------------------ SelectTwoParents(address_mama,address_papa); //-------------------------------------------------------- //Determine the breakage point int address_of_gene=(int)MathFloor((GeneCount-1)*(MathRand()/32767.5)); for(int i=1;i<=GeneCount;i++) { //----copy the mother's genes-------- if(i<=address_of_gene+1) child[i]=Population[i][address_mama]; //----copy the father's genes-------- else child[i]=Population[i][address_papa]; } } //————————————————————————————————————————————————————————————————————————
3.12. SelectTwoParents. The selection of two parents
To prevent the depletion of the gene pool, there is a ban on crossbreeding with oneself. Ten attempts are made to find different parents, and if we fail to find a pair, we allow the crossbreeding with oneself. Basically, we obtain a copy of the same specimen.
On the one hand, the likelihood of cloning individuals decreases, on the other - the circularity of the search is prevented, since a situation can arise, in which it would be practically impossible to do this (choose different parents) in a reasonable number of steps.
Used in the operators Replication, ArtificialMutation, and CrossingOver.
//———————————————————————————————————————————————————————————————————————— //Selection of two parents. void SelectTwoParents ( int &address_mama, int &address_papa ) { //-----------------------Variables------------------------------------- int cnt=1; address_mama=0;//address of the mother individual in a population address_papa=0;//address of the father individual in a population //---------------------------------------------------------------------- //----------------------------Selection of parents-------------------------- //Ten attempts to chose different parents. while(cnt<=10) { //For the mother individual address_mama=NaturalSelection(); //For the father individual address_papa=NaturalSelection(); if(address_mama!=address_papa) break; } //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.13. SelectOneParent. The selection of one parent
Here everything is simple - one parent is selected from the population.
Used in operators NaturalMutation and GenoMerging.
//———————————————————————————————————————————————————————————————————————— //Selection of one parent. void SelectOneParent ( int &address//address of the parent individual in the population ) { //-----------------------Variables------------------------------------- address=0; //---------------------------------------------------------------------- //----------------------------Selecting a parent-------------------------- address=NaturalSelection(); //--------------------------------------------------------------------- } //————————————————————————————————————————————————————————————————————————
3.14. NaturalSelection. Natural selection
Natural selection - the process that leads to the survival and preferential reproduction of individuals, better adapted to these environmental conditions, possessing useful hereditary traits.
The operator is similar to the traditional operator "Roulette" ( Roulette-wheel selection - Selection of individuals with n "launches" of the roulette. The roulette wheel contains one sector for each member of the population. The size of the i-th sector is proportional to the corresponding value of fitness), but has significant differences. It takes into account the position of individuals, relative to the most and the least suited ones. Moreover, even an individual that has the worst genes, has a chance to leave behind an offspring. This is fair, is it not? Although it's not about fairness, but in the fact about the fact that in nature, all individuals have the opportunity to leave behind offspring.
For example, take 10 individuals, having the following VFF in the maximization problem: 256, 128, 64, 32, 16, 8, 4, 2, 0, -1 - where the larger values correspond to better fitness. This example is taken so that we could see that the "distance" between neighboring individuals is 2 times larger than between the two previous individuals. However, on the pie chart, the probability of each individual leaving an offspring is as follows:
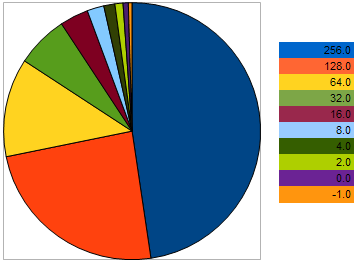
Figure 9. The probability chart of selecting the parent individuals
it demonstrates that with the approach of individuals to the worst, their chances become worse. Conversely - the closer the individual gets to the better specimen, the better chances for reproduction it has.
Figure 10. The probability chart of selecting the parent individuals
//———————————————————————————————————————————————————————————————————————— //Natural selection. int NaturalSelection() { //-----------------------Variables------------------------------------- int i=0,u=0; double p=0.0,start=0.0; double fit[][2]; ArrayResize (fit,PopulChromosCount); ArrayInitialize(fit,0.0); double delta=(Population[0][0]-Population[0][PopulChromosCount-1])*0.01-Population[0][PopulChromosCount-1]; //---------------------------------------------------------------------- for(i=0;i<PopulChromosCount;i++) { fit[i][0]=start; fit[i][1]=start+MathAbs(Population[0][i]+delta); start=fit[i][1]; } p=RNDfromCI(fit[0][0],fit[PopulChromosCount-1][1]); for(u=0;u<PopulChromosCount;u++) if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1]) break; return(u); } //————————————————————————————————————————————————————————————————————————
3.15. RemovalDuplicates. Removing duplicates
The function removes duplicate chromosomes in the population, and the remaining unique chromosomes (unique to the population of the current epoch) are sorted in order by the VFF, determined by the type of optimization, ie decreasing or increasing.
//———————————————————————————————————————————————————————————————————————— //Removing duplicates sorted by VFF void RemovalDuplicates() { //-----------------------Variables------------------------------------- int chromosomeUnique[1000];//Array stores the unique trait //of each chromosome: 0-duplicate, 1-unique ArrayInitialize(chromosomeUnique,1); //Assume that there are no duplicates double PopulationTemp[][1000]; ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Ge =0; //Index of the gene int Ch =0; //Index of the chromosome int Ch2=0; //Index of the second chromosome int cnt=0; //Counter //---------------------------------------------------------------------- //----------------------Remove duplicates---------------------------1 //Chose the first from the pair for comparison... for(Ch=0;Ch<PopulChromosCount;Ch++) { //If it's not a duplicate... if(chromosomeUnique[Ch]!=0) { //Chose the second from the pair... for(Ch2=0;Ch2<PopulChromosCount;Ch2++) { if(Ch!=Ch2 && chromosomeUnique[Ch2]!=0) { //Zeroize the counter of identical genes cnt=0; //Compare the genes. while there are identical genes present for(Ge=1;Ge<=GeneCount;Ge++) { if(Population[Ge][Ch]!=Population[Ge][Ch2]) break; else cnt++; } //If there are the same amount of identical genes as total genes //..the chromosome is considered a duplicate if(cnt==GeneCount) chromosomeUnique[Ch2]=0; } } } } //The counter calculates the number of unique chromosomes cnt=0; //Copy the unique chromosomes into a temporary array for(Ch=0;Ch<PopulChromosCount;Ch++) { //If the chromosome is unique, copy it, if not, go to the next if(chromosomeUnique[Ch]==1) { for(Ge=0;Ge<=GeneCount;Ge++) PopulationTemp[Ge][cnt]=Population[Ge][Ch]; cnt++; } } //Assigning the variable "All chromosomes" the value of counter of unique chromosomes PopulChromosCount=cnt; //Return unique chromosomes back to the array for temporary storage //..of combined populations for(Ch=0;Ch<PopulChromosCount;Ch++) for(Ge=0;Ge<=GeneCount;Ge++) Population[Ge][Ch]=PopulationTemp[Ge][Ch]; //=================================================================1 //----------------Ranking the population---------------------------2 PopulationRanking(); //=================================================================2 } //————————————————————————————————————————————————————————————————————————
3.16. PopulationRanking. Ranking the population
Sorting is made by the VFF. The method is similar to ' bubbly (The algorithm consists of repeated passages through the sorted array. For every pass, the elements are successively compared pairwise, and if the order of a pair is wrong, an exchange of elements take place. Passages through the array are repeated up until one of the passage shows that exchanges are no longer needed, which means - the array has been sorted.
When passing through the algorithm, an element that stands out of place, "pops up" to the desired position, just like a bubble in water, hence the name of the algorithm, but there is a difference - only the indexes of the array are sorted, not the contents of the array. This method is faster and slightly different in speed from simply copying one array to another. And the larger the size of the sorted array, the smaller the difference is.
//———————————————————————————————————————————————————————————————————————— //Population ranking. void PopulationRanking() { //-----------------------Variables------------------------------------- int cnt=1, i = 0, u = 0; double PopulationTemp[][1000]; //Temporary population ArrayResize (PopulationTemp,GeneCount+1); ArrayInitialize(PopulationTemp,0.0); int Indexes[]; //Indexes of chromosomes ArrayResize (Indexes,PopulChromosCount); ArrayInitialize(Indexes,0); int t0=0; double ValueOnIndexes[]; //VFF of corresponding //..chromosome indexes ArrayResize (ValueOnIndexes,PopulChromosCount); ArrayInitialize(ValueOnIndexes,0.0); double t1=0.0; //---------------------------------------------------------------------- //Fill in the indexes in the temporary array temp2 and //...copy the first line from the sorted array for(i=0;i<PopulChromosCount;i++) { Indexes[i] = i; ValueOnIndexes[i] = Population[0][i]; } if(OptimizeMethod==1) { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]>ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } else { while(cnt>0) { cnt=0; for(i=0;i<PopulChromosCount-1;i++) { if(ValueOnIndexes[i]<ValueOnIndexes[i+1]) { //----------------------- t0 = Indexes[i+1]; t1 = ValueOnIndexes[i+1]; Indexes [i+1] = Indexes[i]; ValueOnIndexes [i+1] = ValueOnIndexes[i]; Indexes [i] = t0; ValueOnIndexes [i] = t1; //----------------------- cnt++; } } } } //Create a sorted-out array based on the obtained indexes for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) PopulationTemp[i][u]=Population[i][Indexes[u]]; //Copy the sorted-out array back for(i=0;i<GeneCount+1;i++) for(u=0;u<PopulChromosCount;u++) Population[i][u]=PopulationTemp[i][u]; } //————————————————————————————————————————————————————————————————————————
3.17. RNDfromCustomInterval. The generator of random numbers from a given interval
Just a handy feature. Is handy in UGA.
//———————————————————————————————————————————————————————————————————————— //Generator of random numbers from the selected interval. double RNDfromCI(double RangeMinimum,double RangeMaximum) { return(RangeMinimum+((RangeMaximum-RangeMinimum)*MathRand()/32767.5));} //————————————————————————————————————————————————————————————————————————
3.18. SelectInDiscreteSpace. The selection in discrete space
Is used to reduce the search space. With the parameter step = 0.0 the search is carried out in a continuous space (limited to language limitations, in MQL to the 15th significant symbol inclusive). To use the GA algorithm with a greater accuracy, you need to write an additional library for working with long numbers.
The work of the function at RoundMode = 1 can be illustrated by the following figure:
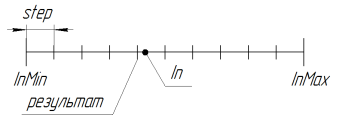
Figure 11. the work of the function SelectInDiscreteSpace at RoundMode = 1
//———————————————————————————————————————————————————————————————————————— //Selection in discrete space. //Modes: //1-closest below //2-closest above //any closest double SelectInDiscreteSpace ( double In, double InMin, double InMax, double step, int RoundMode ) { if(step==0.0) return(In); // secure the correctness of borders if( InMax < InMin ) { double temp = InMax; InMax = InMin; InMin = temp; } // during a breach - return the breached border if( In < InMin ) return( InMin ); if( In > InMax ) return( InMax ); if( InMax == InMin || step <= 0.0 ) return( InMin ); // bring to the specified scale step = (InMax - InMin) / MathCeil ( (InMax - InMin) / step ); switch( RoundMode ) { case 1: return( InMin + step * MathFloor ( ( In - InMin ) / step ) ); case 2: return( InMin + step * MathCeil ( ( In - InMin ) / step ) ); default: return( InMin + step * MathRound ( ( In - InMin ) / step ) ); } } //————————————————————————————————————————————————————————————————————————
3.19. FitnessFunction. Fitness function
Is not part of the GA. The function receives the index of the chromosome in the population, for which the VFF will be calculated. VFF is written in the zero index of the transmitted chromosome. The code of this function is unique for each task.
3.20. ServiceFunction. Service function
Is not part of the GA. The code of this function is unique for each specific task. It can be used to implement control over epochs. For example, in order to display the best VFF for the current epoch.
4. Examples of UGA work
All of the optimization problems are solved by the means of EA, and are divided into two types:
- Genotype is consistent of a phenotype. The values of the chromosome genes are directly appointed by the arguments of an optimization function. Example 1.
- The genotype does not match the phenotype. The interpretation of the meaning of chromosome genes is required to calculate the optimized function. Example 2.
4.1. Example 1
Consider the problem with a known answer, in order to make sure that the algorithm works, and then move on to solving the problem, the solution of which is of interest to many traders.
Problem: Find the minimum and maximum function "Skin":
on the segment [-5, 5].
Answer: fmin (3.07021,3.315935) = -4.3182, fmax (-3.315699; -3.072485) = 14.0606.
Figure 12. The graph of "Skin" on the segment [-5, 5]
To solve the problem we write the following script:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" #include "Skin.mqh"//testing function //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Gene pool parameter----"; input int ChromosomeCount_P = 50; //Number of chromosomes in a colony input int GeneCount_P = 2; //Number of genes input int FFNormalizeDigits_P = 4; //Number of fitness symbols input int GeneNormalizeDigits_P = 4; //Number of genes input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Operator parameters----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing-over. //--- input double ReplicationOffset_P = 0.5; //Coefficient of interval borders displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = -5.0; //Minimum range search input double RangeMaximum_P = 5.0; //Maximum range search input double Precision_P = 0.0001;//The required accuracy input int OptimizeMethod_P = 1; //Optim.:1-Min,other-Max //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double ERROR=0.0;//Average error in gen //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparing global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum range search RangeMaximum =RangeMaximum_P; //Maximum range search Precision =Precision_P; //Search step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of symbols in fitness GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//Proportion of crossing-over. //--- ReplicationOffset_P, //Coefficient of interval border replacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," mc - Time of implementation"); //---------------------------------- return(0); } //————————————————————————————————————————————————————————————————————————
Here is the entire code of the script for solving the problem. Run it, get the information, provided by the function Comment ():
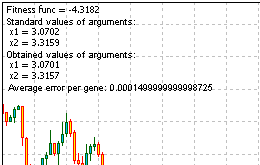
Figure 13. The result of solving the problem
Looking at the results, we see that the algorithm works.
4.2. Example 2
It is widely believed that the indicator ZZ shows the ideal inputs of an overturn trading system. The indicator is very popular among the "wave theory" supporters, and those who use it to determine the size of the "figures".
Problem : Determine whether there are any other entry points for an overturn trading system on historical data, different from the ZZ vertexes, giving in sum more points of theoretical gain?
For the experiments we will select a pair GBPJPY for M1 100 bars. Accept the spread of 80 points (five-digit quotes). To get started, you need to determine the best ZZ parameters. To do this, we use simple enumeration to find the best value of the ExtDepth parameter, using a simple script:
#property script_show_inputs //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input int History=100; input double Spred =80.0; input int Depth =5; //For "one-time" use input bool loop =true;//Use enumeration or not //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //--------------------------The body of the program-------------------------------- void OnStart() { //-----------------------Variables------------------------------------- double ZigzagBuffer [];//For storing the buffer of the ZZ indicator double PeaksOfZigzag[];//for storing the values of the ZZ extremum int Zigzag_handle; //Indicator marker ArraySetAsSeries(ZigzagBuffer,true); ArrayResize(PeaksOfZigzag,History); int depth=3; double PipsSum=0.0; int PeaksCount=0; bool flag=true; //---------------------------------------------------------------------- if(loop==true) { while(depth<200 && flag==true) { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",depth); //--- reset the code error ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<100;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Could not copy the indicator buffer. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- PipsSum=0.0; PeaksCount=0; for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; //----------------------------------------------------------- if(PeaksCount<=2) flag=false; else { Print(depth," ",PeaksCount," ",PipsSum); depth+=1; } //----------------------------------------------------------- } } else { //----------------------------------------------------------- Zigzag_handle=iCustom(NULL,0,"ZigZag",Depth); //--- reser the error code ResetLastError(); //--- attempt to copy the indicator values for(int i=0;i<History;i++) { if(BarsCalculated(Zigzag_handle)>0) break; Sleep(1000); } int copied=CopyBuffer(Zigzag_handle,0,0,History,ZigzagBuffer); if(copied<=0) { Print("Was not able to copy the buffer indicator. Error =",GetLastError()," copied=",copied); return; } //----------------------------------------------------------- for(int u=0;u<History;u++) { if(NormalizeDouble(ZigzagBuffer[u],Digits())>0.0) { PeaksOfZigzag[PeaksCount]=NormalizeDouble(ZigzagBuffer[u],Digits()); PeaksCount++; } } //----------------------------------------------------------- for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(PeaksOfZigzag[V]-PeaksOfZigzag[V+1]))/Point(),Digits())-Spred; } Print(Depth," ",PeaksCount," ",PipsSum); //----------------------------------------------------------- } } //————————————————————————————————————————————————————————————————————————
By running the script, we get 4077 points in ExtDepth = 3. Nineteen indicator vertexes "fit" on 100 bars. With the increase of ExtDepth, the number of ZZ vertexes decreases, and so does the profitability.
Now we can find the vertexes of the alternative ZZ, using UGA. The ZZ vertexes can have three positions for each bar: 1) High, 2) Low, 3) No vertex. The presence and position of the vertex will be carried by every gene for each bar. Thus, the size of the chromosome - 100 genes.
According to my calculations (and mathematicians can correct me if I'm wrong), on 100 bars you can build 3 ^ 100, or 5.15378e47 alternative options "zigzags" . This is the exact number of options that needs to be considered, using direct enumeration. During calculation with a speed of 100000000 options per second, we will need 1.6e32 years ! This is more than the age of the universe. Here is when I began having doubts about the ability of finding a solution to this problem.
But let us begin.
Since UGA uses the representation of the chromosome by real numbers, we need to somehow encode the position of the vertexes. This is precisely the case when the genotype of the chromosome does not match the phenotype. Assign a search interval for the genes [0, 5]. Let's agree that interval [0, 1] corresponds to the vertex of ZZ on High, the interval [4, 5] corresponds to the vertex on Low, and the interval (1, 4) corresponds to the absence of the vertex.
It is necessary to consider one important point. Since the proto- population is randomly generated with genes in the specified interval, the first specimen will have very poor results, possibly even with a few hundred points with a minus sign. After a few generations (although there is the chance of it happening in the first generation)we will see the appearance of specimen, whose genes are consistent with the absence of vertexes in general. This would mean the absence of trade and the payment of the inevitable spread.
According to some former traders: "The best strategy for trade - is not to trade". This individual will be the vertex of the artificial evolution. In order to make this "artificial" evolution give birth to trading individuals, ie make it arrange the vertexes of the alternative ZZ, we assign the fitness of individuals, lacking vertexes, the value of "-10000000.0", deliberately placing it on the lowest rung of evolution, compared to any other individuals.
Here is the script code that uses UGA for finding the vertexes of the alternative ZZ:
#property script_show_inputs //+——————————————————————————————————————————————————————————————————————+ #include "UGAlib.mqh" //+——————————————————————————————————————————————————————————————————————+ //———————————————————————————————————————————————————————————————————————— //----------------------Incoming parameters-------------------------------- input string GenofundParam = "----Parameters of the gene pool----"; input int ChromosomeCount_P = 100; //Number of chromosomes in the colony input int GeneCount_P = 100; //Number of genes input int FFNormalizeDigits_P = 0; //Number of fitness symbols input int GeneNormalizeDigits_P= 0; //Number of gene symbols input int Epoch_P = 50; //Number of epochs without progress //--- input string GA_OperatorParam = "----Parameters of operators----"; input double ReplicationPortion_P = 100.0; //Proportion of replication. input double NMutationPortion_P = 10.0; //Proportion of natural mutations. input double ArtificialMutation_P = 10.0; //Proportion of artificial mutations. input double GenoMergingPortion_P = 20.0; //Proportion of borrowed genes. input double CrossingOverPortion_P = 20.0; //Proportion of crossing - over. input double ReplicationOffset_P = 0.5; //Coefficient of interval border displacement input double NMutationProbability_P= 5.0; //Probability of mutation of each gene in % //--- input string OptimisationParam = "----Optimization parameters----"; input double RangeMinimum_P = 0.0; //Minimum search range input double RangeMaximum_P = 5.0; //Maximum search range input double Precision_P = 1.0; //Required accuracy input int OptimizeMethod_P = 2; //Optim.:1-Min,other -Max input string Other = "----Other----"; input double Spred = 80.0; input bool Show = true; //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //----------------------Global variables----------------------------- double Hight []; double Low []; datetime Time []; datetime Ti []; double Peaks []; bool show; //———————————————————————————————————————————————————————————————————————— //--------------------------Body of the program-------------------------------- int OnStart() { //-----------------------Variables------------------------------------- //Preparation of global variables for UGA ChromosomeCount=ChromosomeCount_P; //Number of chromosomes in the colony GeneCount =GeneCount_P; //Number of genes RangeMinimum =RangeMinimum_P; //Minimum search range RangeMaximum =RangeMaximum_P; //Maximum search range Precision =Precision_P; //Searching step OptimizeMethod =OptimizeMethod_P; //1-minimum, any other - maximum FFNormalizeDigits = FFNormalizeDigits_P; //Number of fitness symbols GeneNormalizeDigits = GeneNormalizeDigits_P;//Number of gene symbols ArrayResize(Chromosome,GeneCount+1); ArrayInitialize(Chromosome,0); Epoch=Epoch_P; //Number of epochs without progress //---------------------------------------------------------------------- //Preparation of global variables ArraySetAsSeries(Hight,true); CopyHigh (NULL,0,0,GeneCount+1,Hight); ArraySetAsSeries(Low,true); CopyLow (NULL,0,0,GeneCount+1,Low); ArraySetAsSeries(Time,true); CopyTime (NULL,0,0,GeneCount+1,Time); ArrayResize (Ti,GeneCount+1);ArrayInitialize(Ti,0); ArrayResize(Peaks,GeneCount+1);ArrayInitialize(Peaks,0.0); show=Show; //---------------------------------------------------------------------- //local variables int time_start=GetTickCount(),time_end=0; //---------------------------------------------------------------------- //Очистим экран ObjectsDeleteAll(0,-1,-1); ChartRedraw(0); //launch of the main function UGA UGA ( ReplicationPortion_P, //Proportion of replication. NMutationPortion_P, //Proportion of replication of natural mutations. ArtificialMutation_P, //Proportion of artificial mutations. GenoMergingPortion_P, //Proportion of borrowed genes. CrossingOverPortion_P,//proportion of crossing- over. //--- ReplicationOffset_P, //Coefficient of interval border displacement NMutationProbability_P//Probability of mutation of each gene in % ); //---------------------------------- //Display the last result on the screen show=true; ServiceFunction(); //---------------------------------- time_end=GetTickCount(); //---------------------------------- Print(time_end-time_start," мс - time of execution"); //---------------------------------- return(0); } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Service function. Called up from UGA. | | //If there is no need for it, leave the function empty, like this: | // void ServiceFunction() | // { | // } | //-----------------------------------------------------------------------+ void ServiceFunction() { if(show==true) { //-----------------------Variables----------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //-------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Chromosome[u]; if(temp<=1.0 ) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); Ti [PeaksCount]=Time[u]; PeaksCount++; } } ObjectsDeleteAll(0,-1,-1); for(int V=0;V<PeaksCount-1;V++) { PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; ObjectCreate (0,"BoxBackName"+(string)V,OBJ_TREND,0,Ti[V],Peaks[V],Ti[V+1],Peaks[V+1]); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_COLOR,Black); ObjectSetInteger(0,"BoxBackName"+(string)V,OBJPROP_SELECTABLE,true); } ChartRedraw(0); Comment(PipsSum); } //---------------------------------------------------------------------- else return; } //———————————————————————————————————————————————————————————————————————— //———————————————————————————————————————————————————————————————————————— //-----------------------------------------------------------------------+ // Function of determining the fitness of the individual. Called up from UGA. | //-----------------------------------------------------------------------+ void FitnessFunction(int chromos) { //-----------------------Variables------------------------------------- double PipsSum=0.0; int PeaksCount=0; double temp=0.0; //---------------------------------------------------------------------- for(int u=1;u<=GeneCount;u++) { temp=Colony[u][chromos]; if(temp<=1.0) { Peaks[PeaksCount]=NormalizeDouble(Hight[u],Digits()); PeaksCount++; } if(temp>=4.0) { Peaks[PeaksCount]=NormalizeDouble(Low[u],Digits()); PeaksCount++; } } if(PeaksCount>1) { for(int V=0;V<PeaksCount-1;V++) PipsSum+=NormalizeDouble((MathAbs(Peaks[V]-Peaks[V+1]))/Point(),FFNormalizeDigits)-Spred; Colony[0][chromos]=PipsSum; } else Colony[0][chromos]=-10000000.0; AmountStartsFF++; } //————————————————————————————————————————————————————————————————————————
When we run the script, we get the vertexes with a total profit of 4939 points. Moreover, it took only 17,929 times to count up the points, in comparison to 3 ^ 100 needed through direct enumeration. On my computer, this is 21.7 seconds against 1.6e32 years!
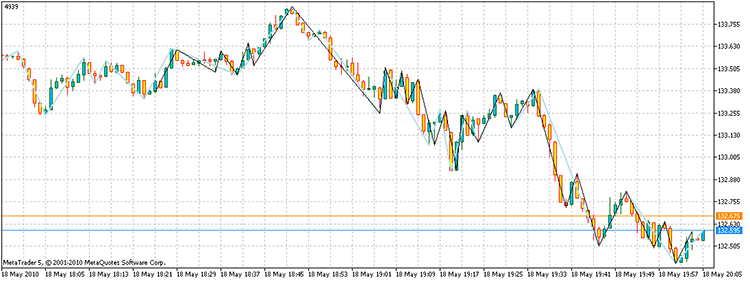
Figure 14. The result of the problem solution. The black colored segments - an alternative ZZ, sky-blue - ZZ indicator
So the answer to the question will read as follows: "Exists."
5. Recommendations for working with UGA
- Try to set the estimated conditions correctly in FF, to be able to expect an adequate result from the algorithm. Think back to Example 2. This is perhaps this is my main recommendation.
- Do not use too small of a value for the Precision parameter. Although the algorithm is able to work with a step 0, you should request a reasonable accuracy of the solution. This parameter is intended to reduce the dimension of the problem.
- Vary the size of the population and the threshold value of the epochs number. A good solution would be to assign a parameter Epoch twice larger than shown by the MaxOfCurrentEpoch. Do not choose too large of a values, this will not accelerate finding solution to the problem.
- Experiment with the parameters of genetic operators. There are no universal parameters, and you should assign them on the basis of the conditions of the task before you.
Findings
Along with a very powerful staffing terminal strategy tester, the MQL5 language allows you to create no less of a powerful instrument for the trader, allowing you to solve truly complex problems. We obtain a very flexible and scalable algorithm of optimization. And I'm unabashedly proud of this discovery, even though I was not the first to establish it.
Because the UGA was initially designed in such a way, that it could be easily modified and extended with additional operators and calculation blocks, the reader will be easily able to contribute to the development of the "artificial" evolution.
I wish the reader success in finding optimal solutions. I hope that I was able to helped him in this. Good luck!
Note. The article used the indicator ZigZag. All source codes of UGA are attached.
Licensing: The source codes attached to the article (UGA code) are distributed under BSD license conditions.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/55
Creating Information Boards Using Standard Library Classes and Google Chart API
A DLL-free solution to communicate between MetaTrader 5 terminals using Named Pipes
Creating an Expert Advisor, which Trades on a Number of Instruments
Guide to writing a DLL for MQL5 in Delphi
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
You're planning to optimize something, aren't you? So you need to present this "something" in the form of FF, it can be for example the number of profit points on the indicator signals. This is the FF.
I have something to ask, about FF, for example, if it is like the advice given, where does the optimization matter, whether this UGA can save the possibility of profit that has been told or something else, and whether when setting the optimal indicator parameter whether it should be I do virtual testing like the EA example I see, and sorry if this offends, Genetic Algorithms are random, how can we be sure it's optimal, and if possible we enter a good condition to make genetic algorithms optimize parameter indicators, for example, we can take it from historical buy and profit conditions with how many points and genetic algorithms use similar data in the future and run the optimization, is that a good way to use it, I can't think of anything else, if it's wrong please tell me a good use example, if without because and when it is executed then optimal results come out, such as entering random numbers, u Fortunately now, enter the random number again and then lose, and so on, isn't it more of a guesswork.
Genetic algorithms use random numbers not by themselves, but by using a probability distribution. Since no one knows the future, people always use the probability distribution to make ANY decisions.You can use the full iteration of the parameters, but you won't use them all. You'll need to decide which option to use, won't you? - the result of applying such manual selection in the future is uncertain in advance, that is, it is not deterministic.
Genetic algorithms use random numbers not by themselves, but by using a probability distribution. Since no one knows the future, people always use the probability distribution to make ANY decisions.You can use the full iteration of the parameters, but you won't use them all. You'll need to decide which option to use, won't you? - the result of applying such manual selection in the future is uncertain in advance, that is, it is not deterministic.
If so, give me advice on which one is good to optimize, if it is a matter of parameter indicators I slightly disagree because the parameters change frequently. is it better to apply in takeprofit and stoploss or is there another better way. Thank you for your response, and if you have any suggestions, thank you. I'd like to share the results of the experiment and maybe a little help in trying this UGA further.
it is difficult to give advice without knowing anything about the trading system